Abstract
This article studies the role of model uncertainties in sensitivity and probability analysis of reliability. The measure of reliability is failure probability. The failure probability is analysed using the Bernoulli distribution with binary outcomes of success (0) and failure (1). Deeper connections between Shannon entropy and variance are explored. Model uncertainties increase the heterogeneity in the data 0 and 1. The article proposes a new methodology for quantifying model uncertainties based on the equality of variance and entropy. This methodology is briefly called “variance = entropy”. It is useful for stochastic computational models without additional information. The “variance = entropy” rule estimates the “safe” failure probability with the added effect of model uncertainties without adding random variables to the computational model. Case studies are presented with seven variants of model uncertainties that can increase the variance to the entropy value. Although model uncertainties are justified in the assessment of reliability, they can distort the results of the global sensitivity analysis of the basic input variables. The solution to this problem is a global sensitivity analysis of failure probability without added model uncertainties. This paper shows that Shannon entropy is a good sensitivity measure that is useful for quantifying model uncertainties.
Keywords:
sensitivity analysis; failure probability; limit states; variance; entropy; model uncertainties; importance measure; computational methods in statistics MSC:
65C50; 60H99
1. Introduction
Structural reliability is a measure of the ability of a structure to function without failure when put into operation [1]. A limit state function indicates success or failure states [2]. A structure is considered reliable if the probability of failure Pf is very small.
In the probability theory, the failure frequency can be studied using the Bernoulli distribution, where Pf is the mean value and Pf(1 − Pf) is the variance. Whereas Pf is a an important variable for assessing reliability, variance Pf(1 − Pf) is useful for the global sensitivity analysis of reliability.
Reliability-oriented sensitivity analysis (ROSA) based on the Sobol–Hoeffding decomposition of Pf(1 − Pf) was first introduced in [3,4]. Since then, ROSAs have been applied in studies of the structural reliability of steel [5,6], concrete [7] and composite [8] beams. The concept [3,4] builds on Sobol [9,10], but with its focus on Pf, it surpasses classical methods examining the correlation [11,12], variance [13,14] or distribution [15,16] of model output without a clear relationship to structural reliability.
A generalisation of all types of global sensitivity indices was presented by Fort using contrast functions [17]. It can be noted that ROSA also includes quantile-oriented sensitivity indices, which are useful in load-carrying capacity analysis based on quantiles as design values of the limit states [18,19,20,21,22]. A comparison of selected ROSA types in applications for limit states was published in [23].
The basis of probabilistic reliability analysis is the estimation of Pf using a stochastic computational model. Although there may be numerous sources of uncertainty in the estimation of Pf, they are generally classified as either aleatory or epistemic. However, the distinction between aleatory and epistemic uncertainties is not clearly defined, but it can be described within the analysis model [24].
In engineering models, uncertainties may be divided into (i) natural variability, (ii) model uncertainty and (iii) statistical uncertainty [1]. The natural variability is due to the natural randomness of model inputs. Model uncertainties are uncertainties related to imperfect knowledge or an idealisation of the mathematical models. Finally, statistical uncertainties are due to the limited sample sizes of the observed quantities.
In general, uncertainty can be defined as any departure from the unachievable ideal of complete determinism [25]. In engineering applications, model uncertainty can be defined as the inability of a model to accurately represent a physical phenomenon due to an insufficient understanding of the phenomenon, conservative assumptions and mathematical simplifications [26].
It Is common practice to treat most uncertainties as random variables [27]; see also [28,29]. If experiments are available, the uncertainty in the resistance model can be directly captured by the ratio between the measured and the calculated quantity; see, e.g., [30,31,32]. However, quantifying uncertainty in load action models is less common; see, e.g., [33,34].
In limit states, model uncertainties can be considered as random variables to cover the imprecision and incompleteness of the relevant theoretical models for the resistance and load effects [27]; see Figure 1.
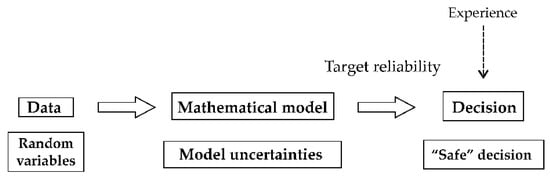
Figure 1.
The model uncertainties in a mathematical model.
Although random input variables are given attention in experimental research, model uncertainties are often a neglected part of probabilistic and especially sensitivity analysis of reliability.
The importance of model uncertainties has been confirmed in numerous studies. Model uncertainties in the shear resistance of reinforced concrete beams were studied in [35,36]. The statistical analysis of model uncertainties was evaluated in [37] by comparing the resistance data from experiments and models of reinforced concrete members. The effects of model uncertainties on the shear resistance of recycled aggregate concrete elements were studied in [38]. A methodology for quantifying model uncertainties of reinforced concrete columns exposed to fire was published in [39]. The model uncertainties of the resistance of steel members under axial compression, bending and combined axial compression and bending were investigated in [40]. For composite structures, studies of resistance models have shown that model uncertainties for buckling are more significant than for flexure [41,42].
Model uncertainties are always present, because each building’s structure is unique, and measurements on many structures of the same type are impossible. Despite this importance, the existing knowledge about model uncertainties and their characteristics seems to suffer from imprecise definitions and a lack of available experimental data [28].
The careless introduction of model uncertainties can lead to an excessively reliable (uneconomical) design. On the contrary, neglecting these uncertainties can lead to an unsafe design. Therefore, they should be quantified very carefully.
There is a complete lack of research into model uncertainties using methods of global sensitivity analysis of Pf. This article attempts to fill this gap with research into ROSA building on [43]. The paper builds on available concepts [27]. The novelty of this work is the formulation of a new methodology for quantifying model uncertainties based on the proposed rule called “variance = entropy”.
2. Probability Analysis of Reliability with Model Uncertainties
The reliability theory is widely used to consider the uncertainties of engineering structures [1]. The general condition of reliability can be described using the limit state function in the form:
where X = (X1, X2, …, XM) is a random input vector with M dimensionality, including the uncertain material characteristic, geometrical characteristics, loads and environmental factors. An example of building construction data is published, e.g., in [44]. The limit state function provides a failure criterion, where Z < 0 is the failure state and Z ≥ 0 is the safety state. The failure probability can be formulated as follows:
where 1Z<0 is a binary random variable, which has a value of 1 with the probability of failure Pf and 0 with the probability of success 1-Pf. The value of Pf is usually small (≈10−5) and must be lower than the target failure probability Pft defined in standards [45].
Z = f(X1, X2, …, XM),
In engineering practice, Equation (1) is usually written in the form of the limit state function of two random variables [46]:
where A is the load action, and R is the resistance. Reliability is generally expressed in probabilistic terms, where A and R are statistically independent random variables [45].
Eurocode [45] distinguishes two limit states at which the structure ceases to perform its intended function satisfactorily. The first limit state (ultimate limit state) deals with strength, overturning, sliding, buckling, fatigue fracture, etc. The second limit state (serviceability limit state) deals with discomfort to occupancy and/or malfunction caused by excessive deflection, crack width, vibration leakage and loss of durability. Both limit states are based on the general concept of action and barrier, where Pf can be calculated according to Equation (2). Structural reliability is verified by computational models using material and geometric characteristics with the application of various limits, such as stress limits [47,48], buckling limits [49,50], deformation limits [51,52], etc.
In Equation (1), the function f is usually not complete and accurate, so failure cannot be predicted without error, even if the statistical characteristics of all random input variables are known. The real outcome Z’ of the experiment can formally be written as:
where variables θi are additional random parameters containing the model uncertainties [27]. The model uncertainties account for random effects disregarded in models and simplifications in mathematical relationships.
Z’ = f’(X1, X2, …, XM, θ1, θ2),
Model uncertainties are ideally determined from a set of representative laboratory experiments and measurements on actual structures with measured and controlled values of Xi [27]. The model uncertainty in such cases is intrinsic in nature. Statistical uncertainty may be significant in the event of a small number of measurements (typical case in building structures). Furthermore, uncertainty may arise due to measurement errors of Xi and Z. In many cases, a good and consistent set of experiments is absent, and the statistical characteristics of model uncertainties are based solely on engineering judgement.
The probability that Z’ < 0 is formulated based on Equation (2) in the form:
In engineering practice, most limit states are based on Equation (3), where X are continuous input random variables, and Pf, Pf’ are small.
When assessing the reliability of a structure, model uncertainties can be related to load effect models evaluating the effects of loads and their combinations or resistance models based on simplified relationships or complex numerical models. The most common way of introducing model uncertainties is by multiplying the model resistance and load effect by factors θ1 and θ2; see, e.g., [38,39]. Equation (3) can be rewritten as:
where θ1 and θ2 are model uncertainties. In Equation (6), a small variation coefficient is assumed for random variables θ1, R, θ2 and A [27,45]. It can be noted that common building structures have variation coefficients of R and A less than 0.2 [45]. The basic probabilistic models of model uncertainty θ1 and θ2 are listed in Table 3.9.1 in JCSS probabilistic model code [27]. For example, a bent steel member has a recommended lognormal probability density function (pdf) with a mean value of 1 and a standard deviation of 0.05 for both random variables θ1 and θ2 [27]. The lognormal pdf is introduced to exclude negative values rather than because of asymmetry since it differs slightly from the Gauss pdf. The main goal of such model uncertainties is to increase the variance (symmetric effect) of R and A; see Figure 2.
Z’ = R’ − A’ = θ1·R − θ2·A,
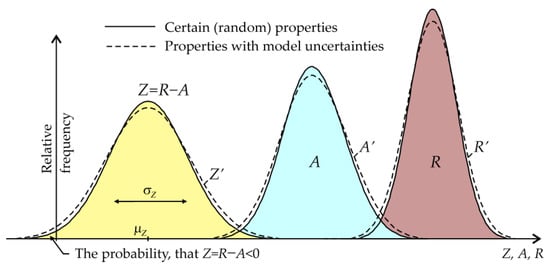
Figure 2.
Model uncertainties in the limit state concept.
The probabilistic model code [27] suggests principles but does not provide details. In practice, there are several ways to account for model uncertainties in computational models; see, e.g., [28,53,54]. Although model uncertainties are justified in the conservative estimation of Pf, their use in sensitivity analysis is debatable. This is because random variables θ1 and θ2 are artificially added inputs, the nature of which must be separated from the basic random input vector X.
3. Reliability-Oriented Sensitivity Measures
The global ROSA aims at quantifying the influence of each input variable of a numerical model on the quantity of interest related to structural failure. The classical concept of global ROSA is based on the Sobol–Hoeffding decomposition of the variance of the Bernoulli distribution of 1Z<0 [3,4].
An alternative measure of uncertainty is entropy. The Shannon discrete entropy [55] of Bernoulli distribution of 1Z<0 can be defined using the formula:
In the Bernoulli distribution, Equations (7) and (8) depend only on Pf, as shown in Figure 3.
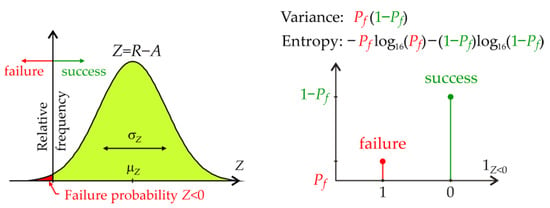
Figure 3.
The failure probability Pf in the Bernoulli trial.
Entropy, by its very nature, only deals with the probabilities of each value, not the values themselves. The variance has this property because of its application to data 0 and 1, which are without units. However, the variance is generally dependent on values and units. Both measures maximise when each outcome occurs with the same probability, i.e., a lot of uncertainty, and minimise when there is only one outcome, i.e., no uncertainty. Both measures are measures of heterogeneity in the data 0 and 1.
A comparison of the plots of Equations (7) and (8) is useful for logarithm base b = 16, where the rise of both domes is the same; see Figure 4a. For b = 16, the variance and Shannon entropy are similar in dome functions with a common peak point. On one level, the functions permit the increase of Pf to Pf1 for Pf < 0.5 or the decrease of Pf to Pf1 for Pf > 0.5. The input of the calculation is the value of Pf, which determines the level, and the output is Pf1 modified by the effects of model uncertainties; see Figure 4a. This is the same effect as the model uncertainties in the computational model and the same effect as the model uncertainty coefficients θi used in [27] for Pf < 0.5. For structural reliability analysis, the cases of Pf < 0.5 for small Pf values are of practical importance.
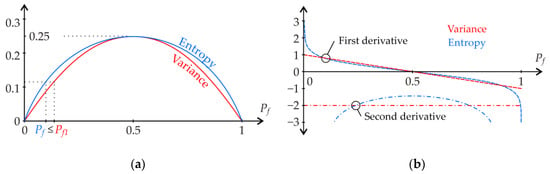
Figure 4.
Sensitivity measures based on entropy and variance: (a) entropy and variance functions; (b) graph of derivatives of functions.
Although the domes are similar, the derivatives at the boundary points are different; see Figure 4b. Shannon entropy at point zero has each odd derivative ∞ and each even derivative −∞. At point one, all derivatives of Shannon entropy are −∞.
The “variance = entropy” rule increases Pf to Pf1 for Pf < 0.5; see Figure 4a. The rule is based on the formal similarity of the dome functions of entropy and variance of the Bernoulli distribution, where 0 and 1 are unitless. This is a new rule that has not yet been published and whose effectiveness is verified by the case studies presented in the next section. The rule in the presented form cannot be transferred to other types of distributions.
Entropic sensitivity analysis is a form of global sensitivity analysis. It decomposes the entropy of the output of a model or system into fragments that can be attributed to inputs or sets of inputs [43]. However, the fragments are not created by the decomposition of the variance as in Sobol. The global sensitivity analysis results are influenced only by the shape of the dome and not by its rise [43]. In practice, the sensitivity measure can be multiplied by a constant having a physical unit to obtain a different physical meaning.
Sensitivity indices based on entropy H(1Z<0) can be written similarly to Sobol indices based on variance V(1Z<0) [43]. For both sensitivity measures, the first-order sensitivity index (main effect) can be written in the form:
where M(Pf) = {V(1Z<0), H(1Z<0)}, but other sensitivity measures are also possible [43]. It is clear from Equation (9) that the amplitude of the measure in the numerator decreases with the amplitude in the denominator. Each measure can have a different amplitude. The sensitivity measure can be multiplied by a non-zero constant having a physical unit and assign physical meaning to the measurement. The second-order sensitivity index can be written as follows:
Higher-order sensitivity indices can be written analogously. However, the sum of all sensitivity indices must be equal to one.
Sensitivity indices based on V(1Z<0) are non-negative and less than one due to Sobol–Hoeffding decomposition [9,10]. Sensitivity indices based on H(1Z<0) have not been proven to be non-negative and less than one, although this property has been observed in numerical studies [43].
The sensitivity indices can be non-negative and less than one in the specific case H(1Z<0) = V(1Z’<0), where Z’ has the same input vector X as Z, but the model uncertainties are added to Z’. The influence of model uncertainties can be considered in Z’ by (i) using added random variables θi or (ii) modifying Z to Z’ without added θi. Then, the sensitivity analysis is based on Sobol–Hoeffding decomposition V(1Z’<0).
The current concept [27] assumes added model uncertainties as random variables θi, and other modifications of the limit state have not yet been introduced. Applying Equations (7) and (8), we can write:
H(1Z<0) = V(1Z’<0).
Upon substituting Equations (7) and (8) into Equation (12), we obtain:
where the left side is computed with Pf from Equation (3), and the right side introduces Pf1 taking into account model uncertainties according to (i) or (ii). The failure probability Pf1 can be obtained by solving Equation (13) in the form:
where the negative sign before the square root is for Pf 0.5, and the positive sign is for Pf > 0.5. Pf 0.5 is relevant for reliability analysis, where the increase from Pf to Pf1 can be performed by using random variables θ1, θ2 or using a specific limit state function Z’ without added random variables. The functional dependence of Pf1 on Pf has two very weakly non-linear (approximately linear) branches; see Figure 5a. Small failure probability values such as Pf ∈ [4.8 × 10−4, 8.5 × 10−6] are relevant for the structural reliability analysis; see the course in a lognormal scale in Figure 5b.
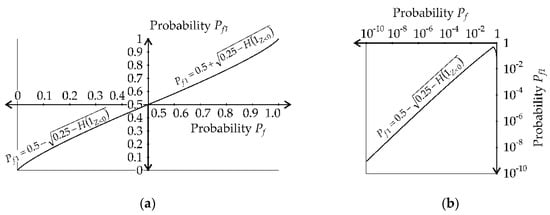
Figure 5.
Dependence between Pf and Pf1: (a) graph for Pf ∈ [0, 1]; (b) graph for Pf ∈ [1 × 10−10, 1].
In the next section, the hypothesis that Equation (12) represents a good general condition for the modification of the limit state leading to rational model uncertainties θ1 and θ2, which have similar statistical characteristics to those recommended in [45], is studied.
4. Calibration of Models of Uncertainties
Why the entropic approach? If model uncertainty is added to the system, its entropy increases. Increasing the variance of R and A leads to H(1Z<0) < H(1Z’<0) and V(1Z<0) < V(1Z’<0); see Figure 2 and Figure 4a. Suppose the increase in entropy is similar for similar models. In that case, the increase in entropy can be a general rule for identifying model uncertainties as random variables in a stochastic model. The issue is the quantification of such an increase.
Let us focus on increasing the variance up to the entropy value according to Equation (12). Why this entropic approach? It will be shown in the case studies that the condition H(1Z<0) = V(1Z’<0) provides approximately the same model uncertainties as published in [27]. This phenomenon has not yet been published and is simply called “variance = entropy”. The following case studies verify and build on this phenomenon.
Numerous ways exist to introduce model uncertainties into the computational model to increase the variance. Practically applicable model uncertainties should be independent of Pf for easy implementation in common design situations, where design (target) failure probabilities are Pfd = {8.5 × 10−6, 7.2 × 10−5, 4.8 × 10−4} [45,56].
The entropy is equal to the variance if the added model uncertainties lead to Pf1, whereas without model uncertainties, it is Pf. Quantifying model uncertainties to achieve Pf1 is treated in case studies in several variants.
4.1. Models Uncertainties Based on Random Variables θ1, θ2
The concept of the case studies is illustrated in Figure 6. Random variable R (X1) has a mean value μR = 11 and a standard deviation σR = 1/√2. Random variable A (X2) has a mean value μA as a parameter and a standard deviation σA = σR. Both variables R and A have a Gauss pdf and are statistically independent; see, e.g., [23]. Then, random variable Z also has a Gauss pdf with a mean value μZ = 11 − μA and a standard deviation σZ = 1. The units of R and A are not important (they can be, e.g., kN); see Figure 6.
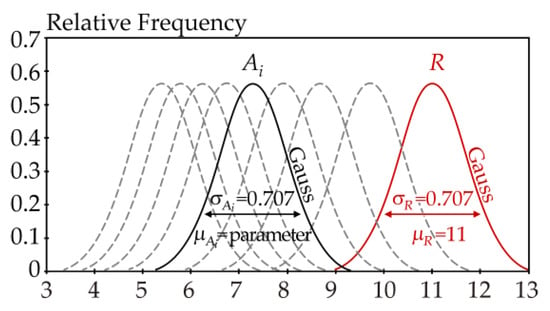
Figure 6.
Gaussian limit state model with parameter μA.
In the case studies, the control parameter μA decreases with a step of 0.05 and gradually has the values 11, 10.95, 10.9, etc. Depending on μA, Pf has the values 0.48, 0.46, 0.44, etc. Pf is estimated using numerical integration with a small step of ∆a taken over [μZ − 10σZ, μZ + 10σZ]. Although μA is the control parameter, the results of the case studies are shown in dependence on Pf, which is a more illustrative variable.
In the first case study, Pf1 is calculated using θ1 and θ2 as random variables in Equation (6). Random variables θ1 and θ2 are considered with a lognormal pdf with mean values μθ1 = μθ2 = 1. Standard deviations σθ1, σθ2 are output values that have to be found such that Pf’ ≈ Pf1, and σθ1 =σθ2. In practice, the procedure is as follows: the value of the input parameter μA is selected; subsequently, the value of Pf is estimated by numerical integration according to Equation (2); then, the value of Pf1 is calculated according to Equation (14). Next, the estimation of σθ1, σθ2 is performed numerically using the bisection method with an accuracy of 1 × 10−5 so that Pf’ converges to Pf1. Finally, the value of Pf’ is estimated according to Equation (5) using 1010 runs of the Monte Carlo method in each step of the bisection method. The output is the estimation of σθ1, σθ2, where σθ1 = σθ2. The point (Pf, σθ) is depicted in the graph plotted in Figure 7. The blue line in Figure 7 is obtained by connecting 120 points (Pf, σθ), where one point is for one value of the control parameter μA.
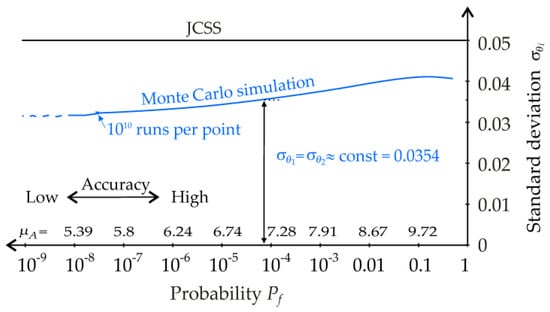
Figure 7.
Course of the standard deviation of model uncertainty compared to [27]—case study 1.
The blue line in Figure 7 shows that the plot of the standard deviations can be approximately replaced by a constant value σθ1 = σθ2 = 0.0354, which is independent of Pf. The constant mean value and standard deviation permit the implementation of θ1 and θ2 into the computational model independently of Pf, which is a crucial requirement. Although the concept of [27] is based on the philosophy of constant moments μθi, σθi, the implementation of model uncertainties into a stochastic model is unclear.
In the second case study, Pf1 is calculated using one random variable, θ1, in Equation (6), whereas the second variable, θ2 = 1, is deterministic. The results of the study are shown in Figure 8. It is apparent that the second model approximates the model uncertainties of [27] more closely. A comparison of Figure 7 and Figure 8 shows that a single random variable θ1 can adequately describe the uncertainty in theoretical models.
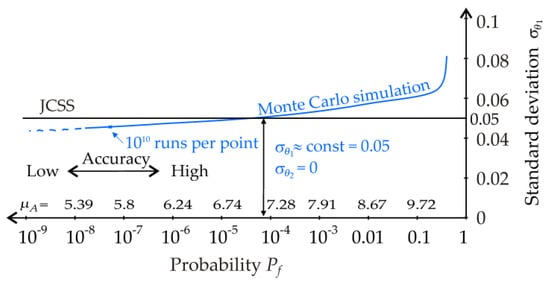
Figure 8.
Course of the standard deviation of model uncertainty compared to [27]—case study 2.
Other ways of introducing model uncertainties have been explored and are possible. However, they are more problematic due to greater misaligned σθ1 and σθ2, according to Pf.
Throughout the article, R and A are statistically independent variables X1 and X2. In this case study, let R and A have artificially introduced weak correlation, and θ1 and θ2 are not considered. The joint pdf of correlated R and A with a Gauss pdf can be written as follows:
The estimate of Pf’ is computed as the numerical integral of Equation (15). In the outer loop, the pdf of A is numerically integrated with a small step ∆a taken over (μA − 10σA, μA + 10σA). In the inner loop, the pdf of R is numerically integrated with a small step ∆r taken over (μR − 10σR, a). The estimation of correlation corr(R, A) is performed with an accuracy of 1 × 10−5 using the bisection method, with the goal of Pf’ → Pf1. The blue line shows the control calculation, where Pf’ is estimated using the Monte Carlo method; see Figure 9.
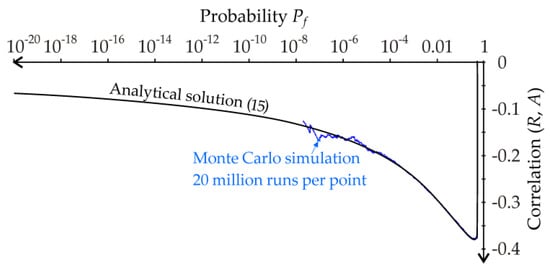
Figure 9.
Course of artificial correlation between R and A—case study 3.
The course of the correlation is non-linear and strongly dependent on Pf. Therefore, the introduction of negative corr(R, A) is an inappropriate implementation of model uncertainties into stochastic models. Moreover, R and A are products of their stochastic models with their random variables. Therefore, the artificial introduction of a correlation between R and A has no basis in real limit states.
4.2. Model Uncertainties Based on Pseudorandom Sequences in Monte Carlo Techniques
Increasing the failure probability can be achieved within the limit state function without added random variables θi. Failure occurs if Z’ < 0, where Z’ is the limit state function supplemented by the influence of model uncertainties in the pseudorandom form.
In the first case, the pseudorandom effect [·] is introduced in the form:
where c0 and c1 are deterministic variables, c0 is a large number, e.g., 109σZ (but not infinity), and c1 is the amplitude of the sine function. The goal is to calibrate the amplitude c1 so that Pf’ = Pf1. The size of c1 is sought using the bisection method with an accuracy of 1 × 10−5 so that Pf’ converges to Pf1. The value of Pf’ is estimated according to Equation (5) using 1010 runs of the Monte Carlo method in each step of the bisection method. The output of the procedure is an estimate c1. Estimation of the values of Pf and c1 is performed 120 times using parameter μA step-by-step according to the method described in the preceding section. Finally, the dependence of c1 vs. Pf is plotted by joining 120 points (Pf, c1); see Figure 10.
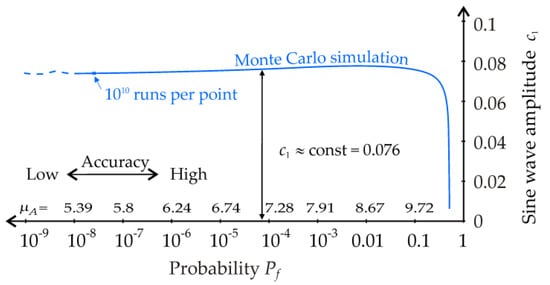
Figure 10.
Parameter of pseudorandom model uncertainty—case study 4.
The blue line in Figure 10 shows that the course of c1 can be approximately replaced by a constant value c1 = 0.076 so that c1 is independent of Pf. The model uncertainty in Equation (16) is based on the product [·] of two random numbers A/R without added θi. For the Monte Carlo method, we can write:
where N is the number of runs of the Monte Carlo method, aj, rj are random realisations of A and R, and c0, c1 are deterministic variables. The numerical results are the same irrespective of whether aj/rj or rj/aj is used. The product [·] based on the sine function is close enough to the pseudorandom number and suits the intended use. It can be shown that substituting c0·A/R for the third independent random variable in sin (·) does not affect the result shown in Figure 10.
In the second case, the pseudorandom number is introduced as a multiple of random variable A:
Calibration is performed according to the procedure described in the previous paragraph, but for variable c2. The graph of c2 vs. Pf is shown in Figure 11.
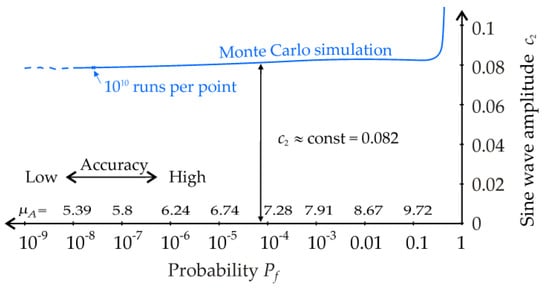
Figure 11.
Parameter of pseudorandom model uncertainty—case study 5.
In order to have c2 independent of Pf, the course of c2 can be approximated by a constant value of c2 = 0.082.
In the third case, the pseudorandom number is introduced as a multiple of both random variables A and R in the form:
where c3 is calibrated using the procedure described in the preceding studies. The course of c3 can be approximated by a constant value of c3 = 0.053; see Figure 12.
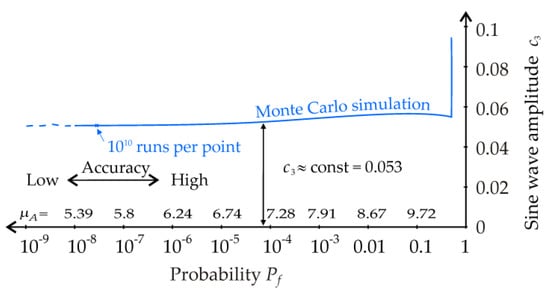
Figure 12.
Parameter of pseudorandom model uncertainty—case study 6.
The fourth case introduces model uncertainties by rewriting the reliability condition Z 0 in the logarithmic form as follows:
The logarithmic condition of reliability Γ 0 is based on the transformation
where model uncertainties can be introduced as pseudorandom fluctuations around zero using the sine function as follows:
The graph of c4 vs. Pf is analysed using the procedure described in the preceding studies; see Figure 13. The course of c4 can be approximated by the constant value c4 = 0.079 at the point Pf = 10−5; see Figure 13. It can be noted that removing the logarithms in Equation (22) does not lead to the parameter c4 with alignment course, and therefore the study is not presented.
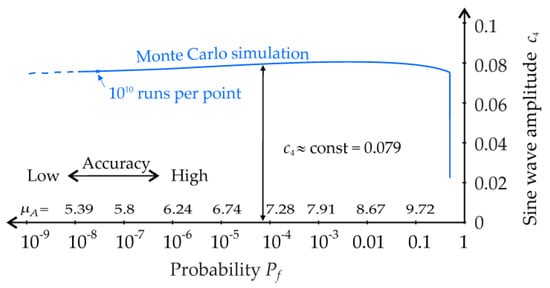
Figure 13.
Parameter of pseudorandom model uncertainty—case study 7.
By introducing Pf independent constants c4 = 0.079 and c0 = 109 into Equation (23), the relationship for estimating Pf1 ≈ Pf’ using the Monte Carlo method can be written as:
where N is the number of runs of the Monte Carlo method, and aj and rj are random realisations of A and R. The results in Figure 14 are treated similarly to the preceding studies, but with the output Pf1. Points Pf1 are calculated for thirty steps of parameter μA, where 1010 steps of the Monte Carlo method are used in each step to estimate Pf1; see Figure 14.
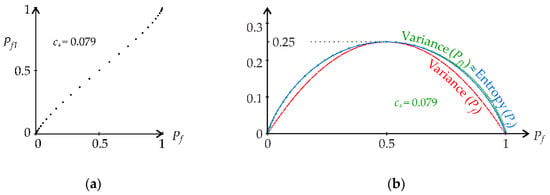
Figure 14.
Comparison of Pf and Pf1 for constant c4 = 0.079: (a) Pf1 from Monte Carlo simulations using steps of μA; (b) variance and entropy for Pf and Pf1.
For Pf < 0.5, it holds that Pf1 > Pf. For Pf > 0.5, it holds that Pf1 < Pf; see Figure 14a. It can be summarised that the entropy H(1Z<0) = H(1Γ<0) can be approximated by the variance V(1Γ’<0) based on Pf1 = E(1Γ’<0) as follows:
The approximation of the left half of the dome, Pf < 0.5, is more accurate because c4 = 0.079 was calibrated for the point Pf = 7.2 × 10−5; see Figure 14b.
The approximation of the other cases H(1Z<0) ≈ V(1Z’<0) based on Z’ can be presented analogously. Figure 10, Figure 11, Figure 12 and Figure 13 show the constants c1 to c4 subtracted from the point Pf = 7.2 × 10−5, representing the common design condition of a building structure [45].
Although pseudorandom sequences can introduce the influence of model uncertainties without added random variables θi, they require the introduction of deterministic parameters, which is not very practical.
4.3. Summary
Case studies 1 and 2 have shown that the “variance = entropy” rule converges to the model uncertainty θi recommended in [27]. The model uncertainties θi have approximately constant statistical characteristics for any Pf < 0.5.
Thus, a reliability assessment including the effect of model uncertainties is possible by calculating Pf1 from Pf, where Pf is failure probability computing without model uncertainties. The failure probability Pf1, including the effect of model uncertainties, is calculated from Equation (25):
where Pft is the target (design) failure probability, e.g., 7.2 × 10−5 [45]. The design of a structure is safe if Pf1 Pft. The rule is called “variance = entropy”. This is a simple yet effective rule taking into account the influence of model uncertainties without adding random variables θi to the stochastic computational model.
This direct application of the “variance = entropy” rule can be recommended for practical use. The advantage of this approach is that both probabilistic and sensitivity analysis are performed in the usual way with only nature random input variables.
5. Global Sensitivity Analysis of Reliability with Model Uncertainties
The influence of model uncertainties and random input variables can be investigated using global ROSA. In the preceding section, the global sensitivity analysis of Pf was performed using μR = 11, μA = 8.6735 and σR = σA = 1/√2. Using these parameters, Pf = 0.01 and Pf1 = 0.02.
In Equation (11), the estimation of sensitivity indices Pi, Pij, etc. is based on the unconditional and conditional estimates of Pf. The unconditional estimate of Pf used ten million MC runs. The conditional estimate of Pf∣Xi used one hundred thousand MC runs, and the estimate of E(M(·)) used one hundred thousand MC runs. Higher-order sensitivity indices are estimated analogously with the same number of runs.
The sensitivity analysis results shown in Figure 15 are based on the Sobol–Hoeffding decomposition of variance V(1Z<0) [3,4] and the fragmentation of Shannon entropy H(1Z<0) introduced in [43]; see Figure 15. The sensitivity indices shown in Figure 15 do not consider the influence of model uncertainties.
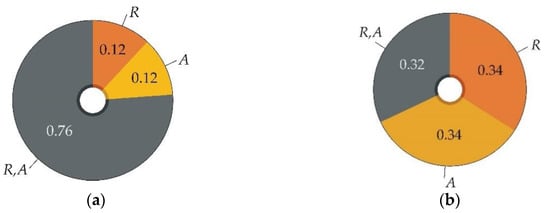
Figure 15.
First- and second-order sensitivity indices from sensitivity analysis of Pf using Z: (a) Sobol sensitivity indices; (b) Shannon’s entropy-based sensitivity indices.
The sensitivity indices in Figure 16 are based on the decomposition of the variance V(1Z’<0) but using a modified function of the limit state Z’. The results in Figure 16a are obtained from Equation (6), where both θ1 and θ2 have a lognormal pdf with μθ1 = μθ2 = 1 and σθ1 = σθ2 = 0.0354. The results in Figure 16b are obtained from Equation (22) with parameters c0 = 109 and c4 = 0.079. The other variants of Z’ lead to results close to Figure 16b.
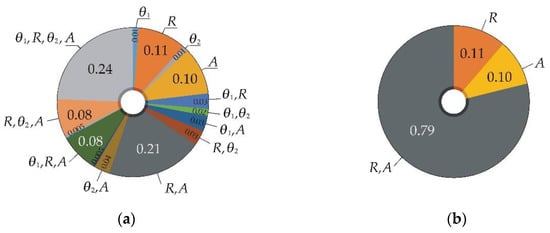
Figure 16.
First- and higher-order variance-based sensitivity indices of global sensitivity analysis of Pf1 using Z’: (a) Z’ based on Equation (6); (b) Z’ based on Equation (22) with c4 = 0.079 and c0 = 109.
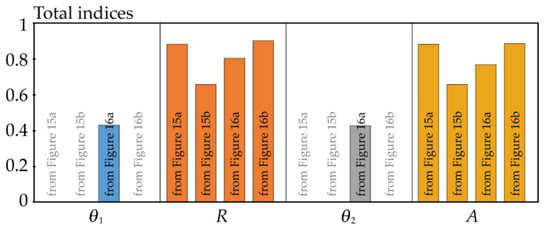
The sensitivity ranking can be determined using total sensitivity indices [57]. The total index measures the contribution to the output variance (entropy) of Xi, including all variance (entropy) caused by its interactions, of any order, with any other input variables. For input random variables R (X1) and A (X2), the total index can be written as P1T = P1 + P12 and P2T = P2 + P12. Total indices are particularly desirable when multiple input random variables with a high proportion of interaction effects are analysed using higher-order indices; see Figure 16a. It can be noted that global sensitivity analysis of small failure probability values has a high proportion of interaction effects when the sensitivity measure is variance [43]. The total indices in Figure 17 are calculated from the sensitivity indices in Figure 15 and Figure 16.
Figure 15 shows the symmetric influence of variables R and A. Figure 16 shows a slightly more significant influence of variable R (compared to A) due to the slightly asymmetric influence of model uncertainties introduced into Z’. The differences between the total indices of R and A are negligible for the same Z’; see Figure 17. Figure 16a presents multiple sensitivity indices and interaction effects due to model uncertainties θ1 and θ2 introduced as random variables. The influence of θ1 and θ2 is relatively large and reaches half of the effects of R and A; see the third column in Figure 17. In the case of a larger number of inputs, random variables θ1 and θ2 may overshadow the influence of the weakest input variables.
6. Global Sensitivity Analysis Based on Rényi Entropy
In this chapter, the results shown in Figure 15b are evaluated using Rényi entropy [58]. The same statistical characteristics μR = 11, μA = 8.6735, and σR = σA = 1/√2 are used.
The theoretical background on Rényi entropy can be found in [59,60]. Rényi entropy is one of the extensions of the Shannon entropy from Equation (8). For a binary random variable, the relationship of Rényi entropy can be written as:
where α is the order of Rényi entropy, and . The limit for α → 1 is Shannon entropy. Other properties of the Renyi entropy can be found, e.g., in [61].
Figure 18a depicts Rényi entropy for the logarithm base b = 16 and α ∈ {0, 0.5, 1, 1.432, 2, ∞}. The variance can be approximated by the Rényi entropy for α ≈ 1.432, where the value of the entropy with its first derivative approximately coincides with the value of the variance and its first derivative. However, the sensitivity indices from Rényi entropy with α = 1.432 differ slightly from Figure 15a. Sensitivity indices for α ∈ [0, 2.425] are depicted in Figure 18b.
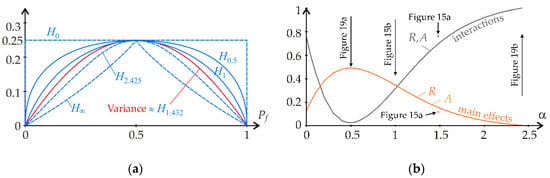
Figure 18.
Global sensitivity analysis of Pf from Z based on Rényi entropy: (a) dependence of Rényi entropy on Pf; (b) first- and second-order sensitivity indices of R and A.
Figure 18b shows that the parameter α significantly changes the ratio of the first- and second-order sensitivity indices. The first-order sensitivity indices are maximum for α ≈ 0.5; see Figure 19a. The second-order sensitivity indices (interaction effects) are equal to one, and the first-order sensitivity indices (main effects) are equal to zero for α ≈ 2.425; see Figure 19b. The first-order sensitivity indices become negative, and the second- (last) order sensitivity index becomes greater than one for α > 2.425.
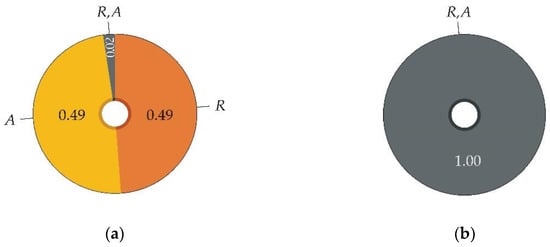
Figure 19.
Global sensitivity analysis of Pf from Z based on Rényi entropy: (a) sensitivity indices for α = 0.5; (b) sensitivity indices for α = 2.425.
The example shows the sensitivity measure’s significant influence on the sensitivity indices’ structure. The sensitivity order of R and A is equal in all cases, but specific values of α provide this information using a large proportion of first-order sensitivity indices (see Figure 19a), whereas others express the same result in an avant-garde way; see Figure 19b.
7. Discussion
Entropy and variance have been investigated in case studies in which the limit states were described using a Bernoulli random variable. Model uncertainties were calibrated from the condition that Shannon entropy is approximated by the variance Pf’ (1 − Pf’) ≈ −Pf log16(Pf) − (1 − Pf)log16(1 − Pf), where Pf’ is the increased value of failure probability due to model uncertainties. Studies have shown that increasing the variance to the entropy value can be achieved by using model uncertainties with statistical characteristics approximately according to the recommendations in [27].
Model uncertainties θi are given for models of building structures, where R and A may depart from the Gaussian distribution due to the small skewness and kurtosis values [62]. The statistical characteristics of θi are approximately the same if the coefficients of variation R and A are small, which is in accordance with [45]. Under these assumptions, R and A can be the product of other data of the building structure (parameters of the computational model), such as load cases [56] or material and geometric characteristics of structures; see, e.g., [44,63].
The limit state Z without model uncertainties gives sensitivity analysis results with a perfectly symmetrical influence of R and A; see Figure 15. The classic Sobol sensitivity analysis based on the variance of Bernoulli distribution has a high proportion of interaction effect of R and A; see Figure 15a. The smaller the analysed Pf, the greater the interaction effects [23,43]. Distinguishing the effects of R from A can be difficult for very small Pf, where the interaction effect is strong (converges to one), and the main effects are weak (converges to zero).
Entropy offers a new sensitivity measure for the sensitivity analysis of small values of Pf. With a strong proportion of first-order indices, the entropy results approach the outputs, which are common in the application of Sobol sensitivity analysis of model outputs [57].
Taking into account model uncertainties as random variables θ1 and θ2 allows us to clarify the proportionality of the influence of both groups. Sensitivity analysis is important in terms of transparency of decision making, because then it is clear which reducible uncertainties have been left unchanged by our decisions [24]. On the other hand, the modified limit states Z’ with hidden model uncertainties give the sensitivity analysis results more clearly solely from the basic input variables without artificially added effects θ1, θ2.
The global ROSA based on entropy does not emanate from the Sobol–Hoeffding decomposition of the variance. The sum of all indices is one, but the indices need not be in the interval [0, 1]. The case study showed that the sensitivity indices based on Rényi entropy could be negative for entropy smaller than the variance. Sensitivity indices based on Shannon entropy have non-negative indices observed in case studies of common engineering tasks [43]. However, the possibility of negative indices does not affect the ability of the indices to identify the sensitivity ranking by comparing indices from lowest to highest.
When the number of random input variables is large, the sensitivity ranking can be determined using first-order indices and total indices, as with Sobol indices [57]. Practically, there is no need to calculate all 2M − 1 indices, but only 2M indices are needed.
The approximation of the entropy by the variance V(1Z’<0) ≈ H(1Z<0) or V(1Γ’<0) ≈ H(1Γ<0) in the modified limit state was achieved by artificially adding model uncertainties to the original limit state Z or Γ. The approximation does not lead to the similarity of the sensitivity indices of variance and entropy. The sensitivity indices based on the decomposition V(1Z’<0) or V(1Γ’<0) remain close to Sobol; see the comparison of Figure 16b with Figure 15a. Although model uncertainties lead to a conservative estimate of the probability of failure, they do not replace the entropic sensitivity measure H(1Z<0) in global sensitivity analysis. The properties of the entropic sensitivity measure were not replicated within the limit state function. The differences between the two sensitivity measures have not yet been explained. The entropic sensitivity measure remains the original sensitivity measure, which gives a good structure of sensitivity indices with a strong representation of first-order sensitivity indices.
The introduction of Rényi entropy in global ROSA showed the sensitivity indices’ dependence on the sensitivity measure’s shape; see Figure 18. The correct setting of parameter α leads to a good structure of sensitivity indices with high first-order effects, whereas the other cases have a large proportion of higher-order effects. The sensitivity index of the last order practically complements the indices of lower orders so that the sum of all indices in Equation (11) is one. If the sensitivity indices are estimated numerically with limited accuracy, then a high value of the sensitivity index of the last order may complicate the determination of the sensitivity ranking.
8. Conclusions
This article deals with the role of model uncertainties in sensitivity and probabilistic reliability analysis. The failure probability Pf was studied using the variance and entropy of the Bernoulli distribution with a binary outcome.
Introducing model uncertainties into a computational model increases the entropy of the system. Introducing model uncertainties in the magnitudes according to the recommendation of [27] increases the variance to the value of Shannon entropy. Shannon entropy is a good sensitivity measure useful for quantifying model uncertainties.
The “variance = entropy” approach presents a sufficiently sensitive and general rule for calibrating model uncertainties of any computational model. The rule increases the failure probability to a safer value, similar to using the model uncertainty factors from [27]. Such a new rule may benefit complex computational models for which recommendation [27] lacks detail. The accurate calibration of model uncertainties is useful, because their inappropriate introduction into a computational model can lead to a less optimal structural design due to a rough estimate of the failure probability.
Shannon entropy provides a useful sensitivity measure, especially for small values of Pf. Rényi entropy presents a sensitivity measure with great flexibility that significantly changes the sensitivity indices’ structure but does not change the information gained from sensitivity analysis. Rational results of sensitivity indices were obtained for dome functions between variance and Shannon entropy.
Funding
This work has been supported and prepared within the project namely “Probability oriented global sensitivity measures of structural reliability” of The Czech Science Foundation (GACR, https://gacr.cz/) no. 20-01734S, Czechia.
Data Availability Statement
Not applicable.
Conflicts of Interest
The author declares no conflict of interest.
References
- Melchers, R.E. Structural Reliability Analysis and Prediction, 2nd ed.; John Wiley: Chichester, UK, 2002. [Google Scholar]
- Ditlevsen, O. Model uncertainty in structural reliability. Struct. Saf. 1982, 1, 73–86. [Google Scholar] [CrossRef]
- Li, L.Y.; Lu, Z.Z.; Feng, J.; Wang, B.T. Moment-independent importance measure of basic variable and its state dependent parameter solution. Struct. Saf. 2012, 38, 40–47. [Google Scholar] [CrossRef]
- Wei, P.; Lu, Z.; Hao, W.; Feng, J.; Wang, B. Efficient sampling methods for global reliability sensitivity analysis. Comput. Phys. Commun. 2012, 183, 1728–1743. [Google Scholar] [CrossRef]
- Li, W.; Yang, R.; Qi, Q.; Zhao, G. Reliability and sensitivity analysis of bridge crane structure. J. Mech. Sci. Technol. 2022, 36, 4419–4431. [Google Scholar] [CrossRef]
- Kala, Z. Estimating probability of fatigue failure of steel structures. Acta Comment. Univ. Tartu. Math. 2019, 23, 245–254. [Google Scholar] [CrossRef]
- Novák, L. On distribution-based global sensitivity analysis by polynomial chaos expansion. Comput. Struct. 2022, 267, 106808. [Google Scholar] [CrossRef]
- Zhou, C.; Li, C.; Zhang, H.; Zhao, H.; Zhou, C. Reliability and sensitivity analysis of composite structures by an adaptive Kriging based approach. Compos. Struct. 2021, 278, 114682. [Google Scholar] [CrossRef]
- Sobol, I.M. Sensitivity estimates for non-linear mathematical models. Math. Model. Comput. Exp. 1993, 1, 407–414. [Google Scholar]
- Sobol, I.M. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates. Math. Comput. Simul. 2001, 55, 271–280. [Google Scholar] [CrossRef]
- Dong, X.; Wang, Y.; Wang, Z. Intelligent meta-model construction and global stochastic sensitivity analysis based on PSO-CNN. Structures 2022, 43, 1516–1529. [Google Scholar] [CrossRef]
- Jindra, D.; Kala, Z.; Kala, J. Buckling curves of stainless steel CHS members: Current state and proposed provisions. J. Constr. Steel. Res. 2022, 198, 107521. [Google Scholar] [CrossRef]
- Kala, Z.; Valeš, J. Imperfection sensitivity analysis of steel columns at ultimate limit state. Arch. Civ. Mech. Eng. 2018, 18, 1207–1218. [Google Scholar] [CrossRef]
- Pan, L.; Novák, L.; Lehký, D.; Novák, D.; Cao, M. Neural network ensemble-based sensitivity analysis in structural engineering: Comparison of selected methods and the influence of statistical correlation. Comput. Struct. 2021, 242, 106376. [Google Scholar] [CrossRef]
- Rykov, V.; Zaripova, E.; Ivanova, N.; Shorgin, S. On sensitivity analysis of steady state probabilities of double redundant renewable system with Marshall-Olkin failure model. Commun. Comput. Inf. Sci. 2018, 919, 234–245. [Google Scholar]
- Plischke, E.; Borgonovo, E. Fighting the curse of sparsity: Probabilistic sensitivity measures from cumulative distribution functions. Risk Anal. 2020, 40, 2639–2660. [Google Scholar] [CrossRef]
- Fort, J.C.; Klein, T.; Rachdi, N. New sensitivity analysis subordinated to a contrast. Commun. Stat. Theory Methods 2016, 45, 4349–4364. [Google Scholar] [CrossRef]
- Kala, Z. From probabilistic to quantile-oriented sensitivity analysis: New indices of design quantiles. Symmetry 2020, 12, 1720. [Google Scholar] [CrossRef]
- Kala, Z. Quantile-based versus Sobol sensitivity analysis in limit state design. Structures 2020, 28, 2424–2430. [Google Scholar] [CrossRef]
- Kala, Z. Quantile-oriented global sensitivity analysis of design resistance. J. Civ. Eng. Manag. 2019, 25, 297–305. [Google Scholar] [CrossRef]
- Kala, Z.; Valeš, J. Sensitivity assessment and lateral-torsional buckling design of I-beams using solid finite elements. J. Constr. Steel. Res. 2017, 139, 110–122. [Google Scholar] [CrossRef]
- Elie-Dit-Cosaque, K.; Maume-Deschamps, V. Goal-oriented Shapley effects with special attention to the quantile-oriented case. SIAM/ASA J. Uncertain. Quantif. 2022, 10, 1037–1069. [Google Scholar] [CrossRef]
- Kala, Z. Sensitivity analysis in probabilistic structural design: A comparison of selected techniques. Sustainability 2020, 12, 4788. [Google Scholar] [CrossRef]
- Kiureghian, A.D.; Ditlevsen, O. Aleatory or epistemic? Does it matter? Struct. Saf. 2009, 31, 105–112. [Google Scholar] [CrossRef]
- Walker, W.E.; Harremoës, P.; Rotmans, J.; van der Sluijs, J.P.; van Asselt, M.B.A.; Janssen, P.; Krayer von Krauss, M.P. Defining uncertainty: A conceptual basis for uncertainty management in model-based decision support. Integr. Assess. 2010, 4, 5–17. [Google Scholar] [CrossRef]
- Hamutcuoglu, O.M. Parametric Uncertainties in Reliability Analysis of Bridge Structures; Oregon State University: Corvallis, OR, USA, 2010. [Google Scholar]
- Joint Committee on Structural Safety (JCSS). Probabilistic Model Code. Available online: https://www.jcss-lc.org/ (accessed on 15 May 2020).
- Holický, M.; Retief, J.V.; Sýkora, M. Assessment of model uncertainties for structural resistance. Probabilistic Eng. Mech. 2016, 45, 188–197. [Google Scholar] [CrossRef]
- Sykora, M.; Holicky, M.; Prieto, M.; Tanner, P. Uncertainties in resistance models for sound and corrosion-damaged RC structures according to EN 1992-1-1. Mater. Struct. 2015, 48, 3415–3430. [Google Scholar] [CrossRef]
- Halvonik, J.; Kalická, J.; Majtánová, L.; Minárová, M. Safety factor for the punching shear resistance model in 2nd Generation of Eurocode 2. J. Build. Eng. 2022, 46, 103788. [Google Scholar] [CrossRef]
- Olalusi, O.B.; Viljoen, C. Model uncertainties and bias in SHEAR strength predictionsof slender stirrup reinforced concrete beams. Struct. Concr. 2020, 21, 316–332. [Google Scholar] [CrossRef]
- Phoon, K.K.; Tang, C. Characterisation of geotechnical model uncertainty. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2019, 13, 101–130. [Google Scholar] [CrossRef]
- Köhler, J.; Sorensen, J.D.; Faber, M.H. Probabilistic modeling of timber structures. Struct. Saf. 2007, 29, 255–267. [Google Scholar] [CrossRef]
- Kang, W.-H.; Uy, B.; Hawkes, D.; Morgan, R. Reliability analysis for load factors in steel bulk material handling structures with respect to AS4324.1. Aust. J. Struct. Eng. 2016, 17, 99–108. [Google Scholar] [CrossRef]
- Olalusi, O.B.; Spyridis, P. Probabilistic studies on the shear strength of slender steel fiber reinforced concrete structures. Appl. Sci. 2020, 10, 6955. [Google Scholar] [CrossRef]
- Olalusi, O.B.; Viljoen, C. Assessment of reliability of EN 1992-1-1 variable strut inclination method of shear design provisions for stirrup failure. Struct. Concr. 2020, 21, 303–315. [Google Scholar] [CrossRef]
- Castaldo, P.; Gino, D.; Bertagnoli, G.; Mancini, G. Resistance model uncertainty in non-linear finite element analyses of cyclically loaded reinforced concrete systems. Eng. Struct. 2020, 211, 110496. [Google Scholar] [CrossRef]
- Pacheco, J.; de Brito, J.; Chastre, C.; Evangelista, L. Eurocode shear design of coarse recycled aggregate concrete: Reliability analysis and partial factor calibration. Materials 2021, 14, 4081. [Google Scholar] [CrossRef]
- Achenbach, M.; Gernay, T.; Morgenthal, G. Quantification of model uncertainties for reinforced concrete columns subjected to fire. Fire Saf. J. 2019, 108, 102832. [Google Scholar] [CrossRef]
- Shi, G.; Zhu, X.; Ban, H. Material properties and partial factors for resistance of high-strength steels in China. J. Constr. Steel. Res. 2016, 121, 65–79. [Google Scholar] [CrossRef]
- Sá, M.F.; Pacheco, J.; Correia, J.R.; Silvestre, N.; Sorensen, J.D. Structural safety of pultruded FRP profiles for global buckling. Part 1: Approach to material uncertainty, resistance models, and model uncertainties. Compos. Struct. 2021, 257, 113304. [Google Scholar] [CrossRef]
- Pacheco, J.; Sá, M.F.; Correia, J.R.; Silvestre, N.; Sorensen, J.D. Structural safety of pultruded FRP profiles for global buckling. Part 2: Reliability-based evaluation of safety formats and partial factor calibration. Compos. Struct. 2021, 257, 113147. [Google Scholar] [CrossRef]
- Kala, Z. New importance measures based on failure probability in global sensitivity analysis of reliability. Mathematics 2021, 9, 2425. [Google Scholar] [CrossRef]
- Hess, P.E.; Bruchman, D.; Assakkaf, I.A.; Ayyub, B.M. Uncertainties in material and geometric strength and load variables. Nav. Eng. J. 2002, 114, 139–166. [Google Scholar] [CrossRef]
- European Committee for Standardization. EN 1990:2002: Eurocode—Basis of Structural Design; European Committee for Standardization: Brussels, Belgium, 2002. [Google Scholar]
- Galambos, T.V.; Ravindra, M.K. Load and resistance factor design. Eng. J. AISC 1981, 18, 78–84. [Google Scholar]
- Melhem, M.M.; Caprani, C.C.; Stewart, M.G. Reliability updating of partial factors for empirical codes: Application to Super-T PSC girders designs at the ultimate limit state in bending. Structures 2022, 35, 233–242. [Google Scholar] [CrossRef]
- Koteš, P.; Vičan, J. Influence of fatigue crack formation and propagation on reliability of steel members. Appl. Sci. 2021, 11, 11562. [Google Scholar] [CrossRef]
- Yousuf, L.S. Largest lyapunov exponent parameter of stiffened carbon fiber reinforced epoxy composite laminated plate due to critical buckling load using average logarithmic divergence approach. Mathematics 2022, 10, 2020. [Google Scholar] [CrossRef]
- Jindra, D.; Kala, Z.; Kala, J. Flexural buckling of stainless steel CHS columns: Reliability analysis utilizing FEM simulations. J. Constr. Steel. Res. 2022, 188, 107002. [Google Scholar] [CrossRef]
- Arrayago, I.; Rasmussen, K.J.R. Reliability of stainless steel frames designed using the Direct Design Method in serviceability limit states. J. Constr. Steel. Res. 2022, 196, 107425. [Google Scholar] [CrossRef]
- Norkus, A.; Martinkus, V. Experimental study on bearing resistance of short displacement pile groups in dense sands. J. Civ. Eng. Manag. 2019, 25, 551–558. [Google Scholar] [CrossRef]
- Aven, T.; Nokland, T.E. On the use of uncertainty importance measures in reliability and risk analysis. Reliab. Eng. Syst. Saf. 2010, 95, 127–133. [Google Scholar] [CrossRef]
- Peng, X.; Xu, X.; Li, J.; Jiang, S. A Sampling-based sensitivity analysis method considering the uncertainties of input variables and their distribution parameters. Mathematics 2021, 9, 1095. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423, 623–656. [Google Scholar] [CrossRef]
- Kala, Z. Reliability analysis of the lateral torsional buckling resistance and the ultimate limit state of steel beams with random imperfections. J. Civ. Eng. Manag. 2015, 21, 902–911. [Google Scholar] [CrossRef]
- Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Gatelli, D.; Saisana, M.; Tarantola, S. Global Sensitivity Analysis: The Primer; John Wiley & Sons: West Sussex, UK, 2008. [Google Scholar]
- Rényi, A. On measures of entropy and information. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 20–30 June 1961; pp. 547–561. [Google Scholar]
- Rényi, A. Probability Theory; North-Holland: Amsterdam, The Netherlands, 1970. [Google Scholar]
- Rényi, A. Selected Papers of Alfréd Rényi, 2nd ed.; Akademia Kiado: Budapest, Hungary, 1976. [Google Scholar]
- Jizba, P.; Lavička, H.; Tabachová, Z. Causal inference in time series in terms of Rényi transfer entropy. Entropy 2022, 24, 855. [Google Scholar] [CrossRef] [PubMed]
- Szalai, J.; Papp, F. On the probabilistic evaluation of the stability resistance of steel columns and beams. J. Constr. Steel. Res. 2009, 65, 569–577. [Google Scholar] [CrossRef]
- Arrayago, I.; Rasmussen, K.J.R.; Real, E. Statistical analysis of the material, geometrical and imperfection characteristics of structural stainless steels and members. J. Constr. Steel. Res. 2020, 175, 106378. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).