Protection Strategy Selection Model Based on Genetic Ant Colony Optimization Algorithm
Abstract
1. Introduction
- Assess the risk of ICS using the Common Vulnerability Scoring System and the Bayesian attack graph.
- The target attack path is predicted by the combination of the maximum probability attack path and the maximum risk attack path.
- Combining the advantages of the Genetic Algorithm and Ant Colony Optimization Algorithm, the optimal protection strategy selection problem under limited budget is calculated.
- Reinforcement learning is used to dynamically select relevant parameters of the Genetic Ant Colony Optimization Algorithm.
2. Related Work
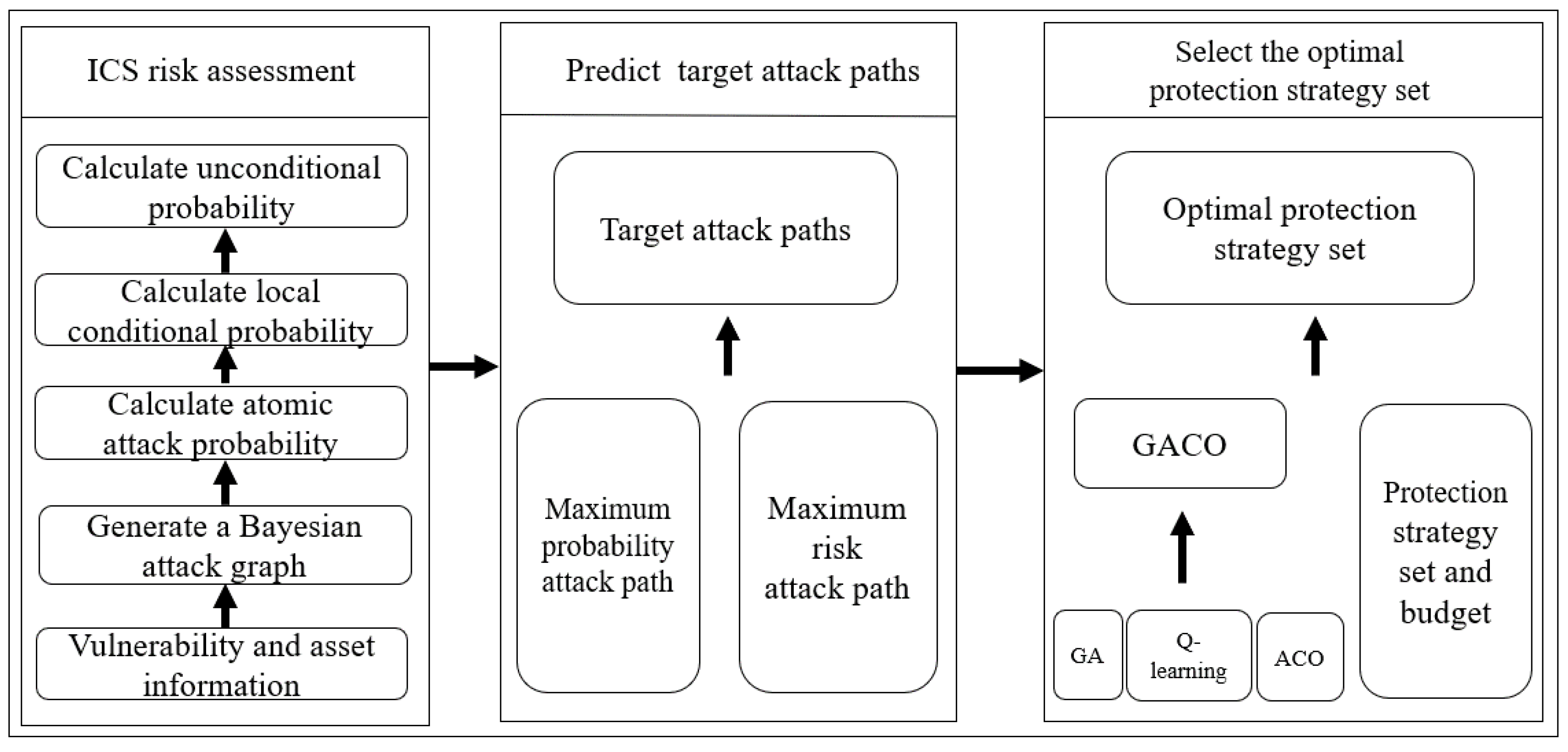
3. Model Structure
- ICS risk assessment: Firstly, a Bayesian attack graph is generated based on the detected vulnerability information and asset information. Then, the atomic attack probability of each edge in the attack graph is calculated according to the Common Vulnerability Scoring System, and the local conditional probability of the attribute node is calculated according to the atomic attack probability. Finally, the unconditional probability of the attribute node is calculated according to the above probability, so as to evaluate the risk of ICS.
- Predict target attack paths: This paper predicts the target attack path from two perspectives. One is the probability angle, which calculates the maximum probability attack path according to the unconditional probability of the attribute node, so as to predict the target path with the lowest attack difficulty. The other is the angle of probability and profit, which calculates the maximum risk attack path according to the unconditional probability of the attribute node and the attack benefit, so as to predict the target path with the most damage.
- Select the optimal protection strategy set: Firstly, the Genetic Ant Colony Optimization Algorithm (GACO) is constructed by combining the Genetic Algorithm (GA), Ant Colony Optimization Algorithm (ACO) and Q-learning Algorithm. Then, the Genetic Ant Colony Optimization Algorithm is used to select the optimal protection strategy set that does not exceed the budget from the protection strategy set to be selected.
4. ICS Risk Assessment
4.1. Definition of Bayesian Attack Graph
4.2. Probability Calculation Based on Bayesian Attack Graph
4.2.1. Atomic Attack Probability
4.2.2. Local Conditional Probability
4.2.3. Unconditional Probability
5. Predict Target Attack Paths
5.1. Maximum Probability Attack Path
5.2. Maximum Risk Attack Path
6. Select the Optimal Protection Strategy Set
6.1. Quantitative Protection Metrics
6.2. Reinforcement Learning
6.3. Genetic Ant Colony Optimization Algorithm
6.3.1. The Basic Idea of Genetic Ant Colony Optimization Algorithm
6.3.2. Using Q-Learning to Update the Parameters of the Algorithm
6.3.3. Steps of Genetic Ant Colony Optimization Algorithm
| Algorithm 1 GACO |
|
7. Experiment and Discussion
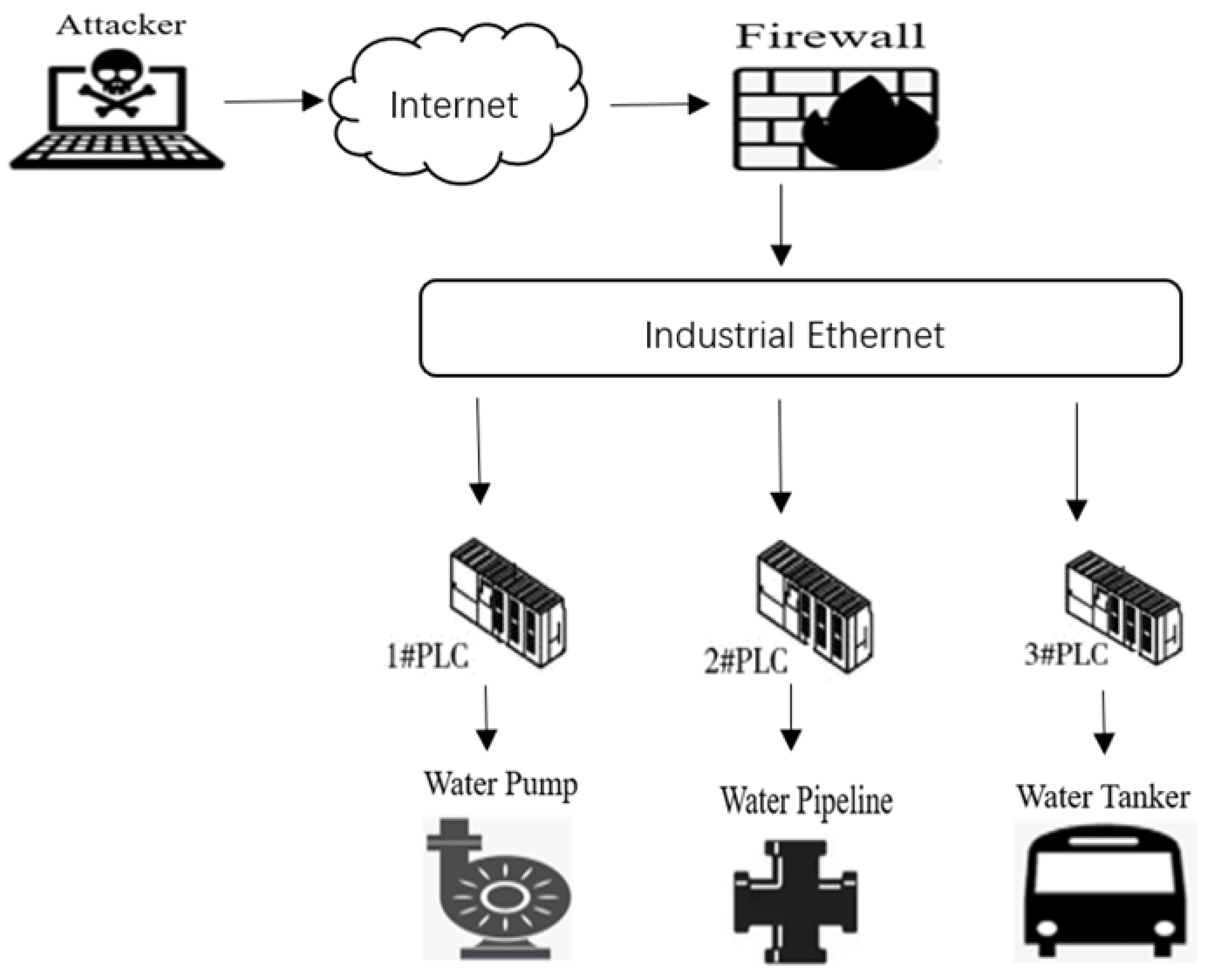
7.1. Experimental Scene
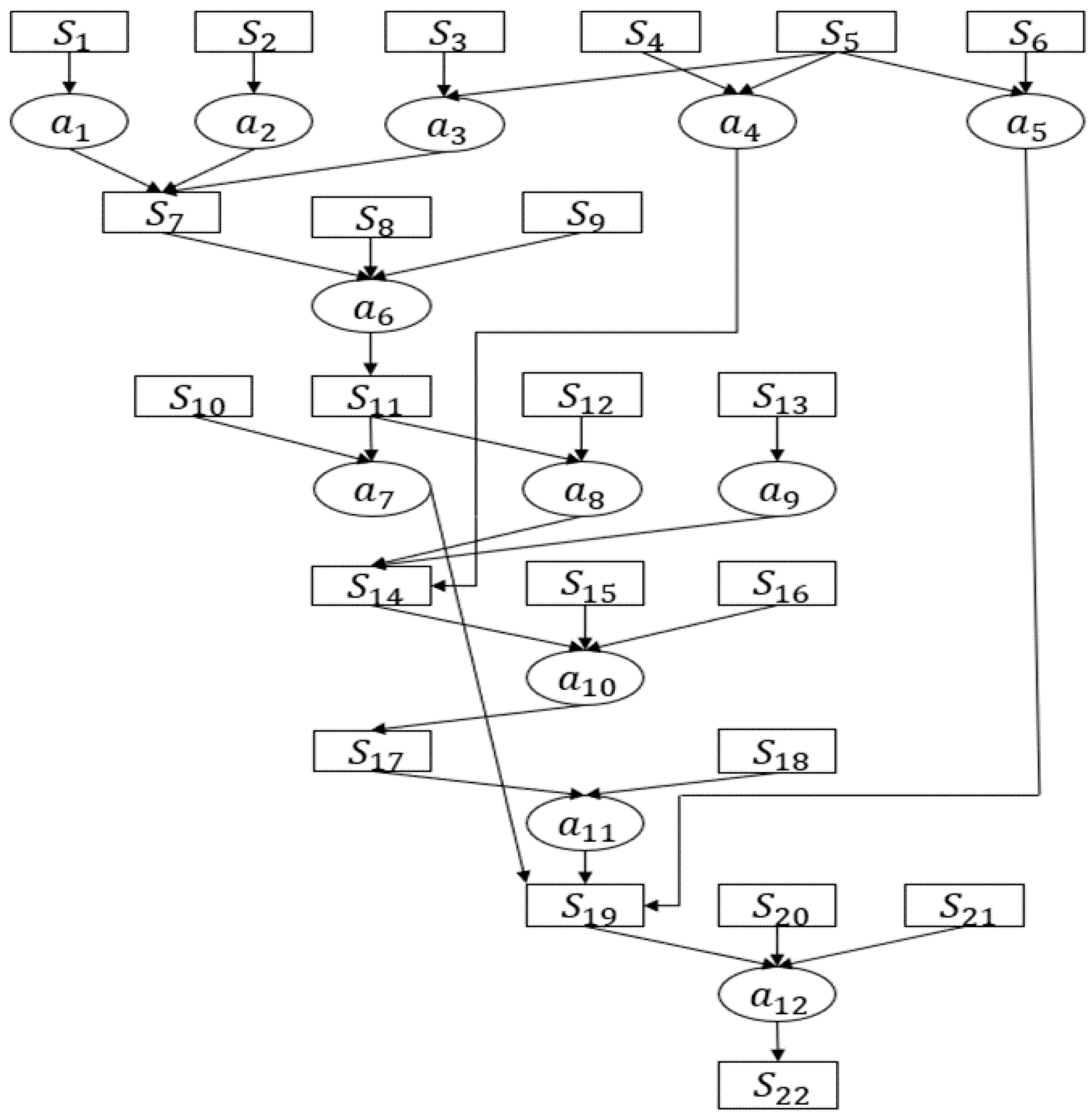
7.2. Generate a Bayesian Attack Graph
7.3. Unconditional Probability of a Node
7.4. Quantify Protection Costs and Attack Benefits
7.5. Predict Attack Paths
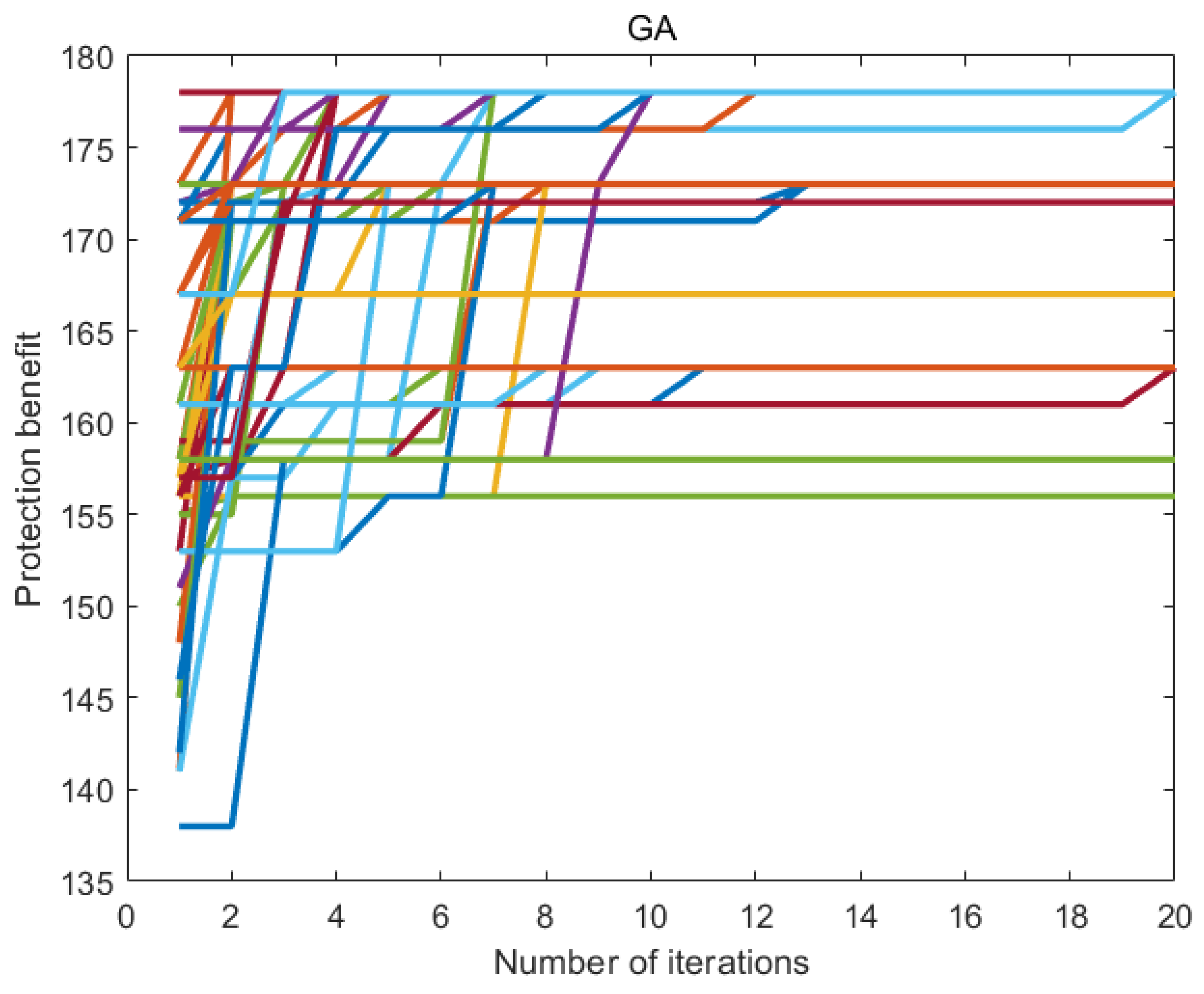
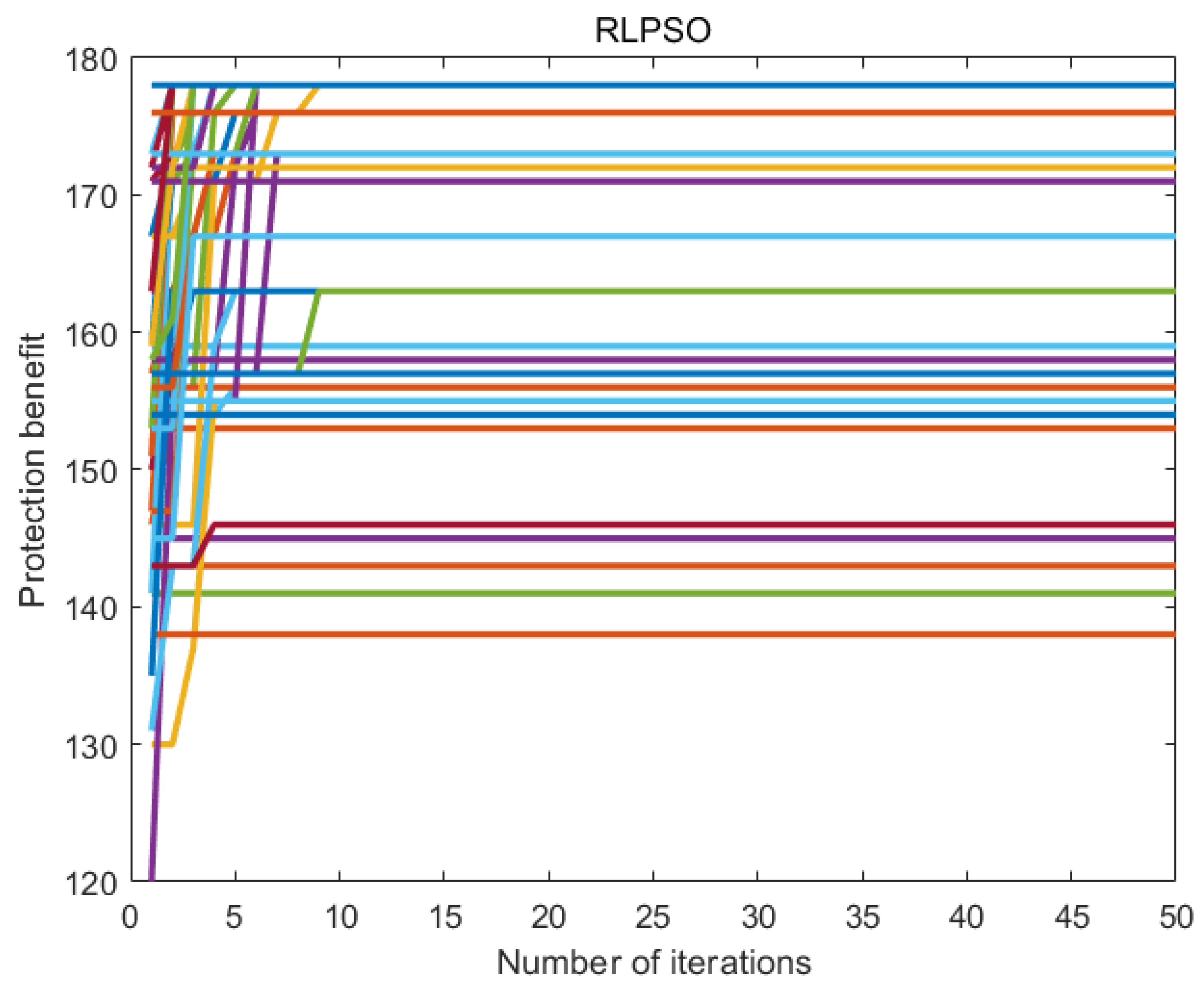
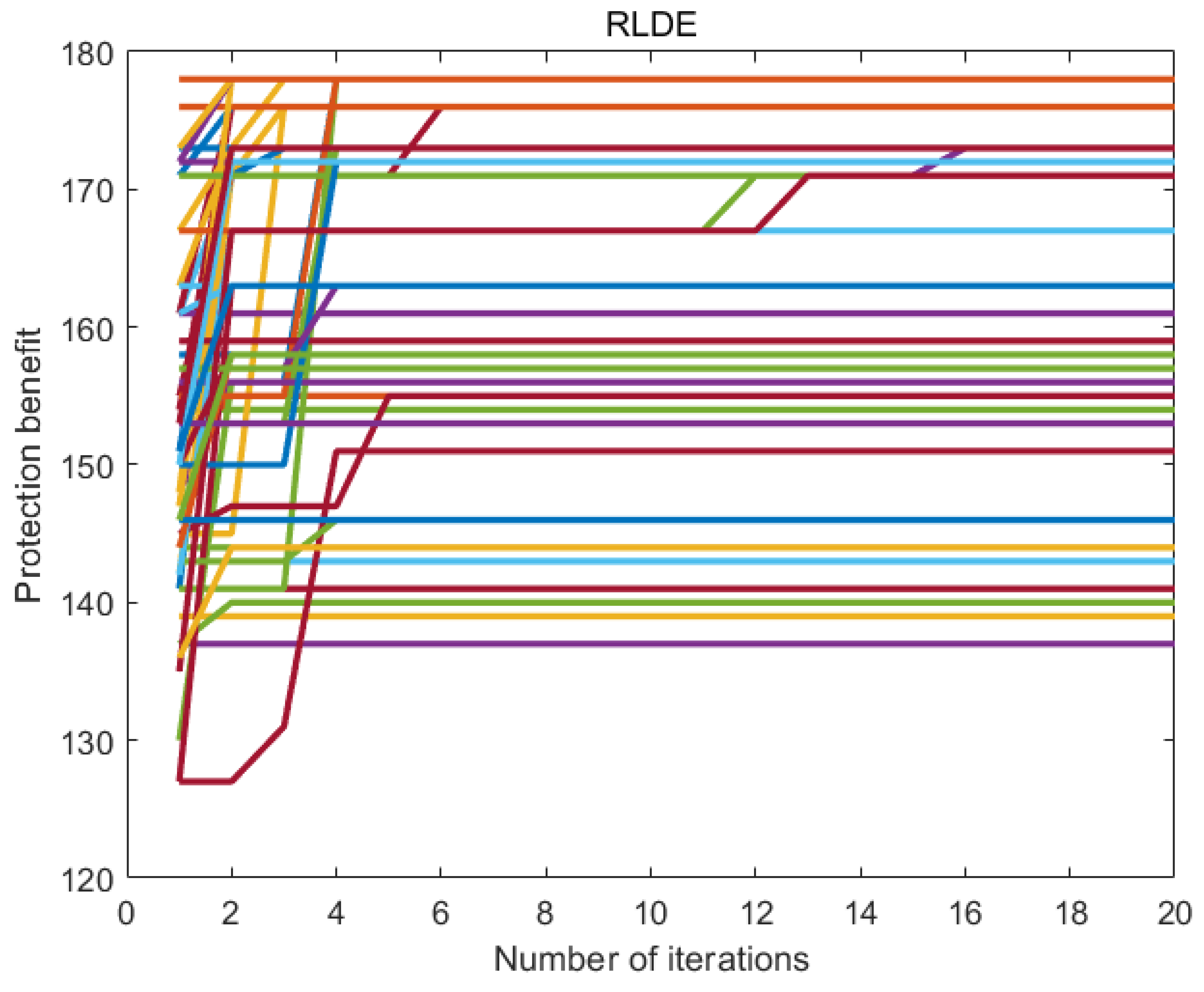
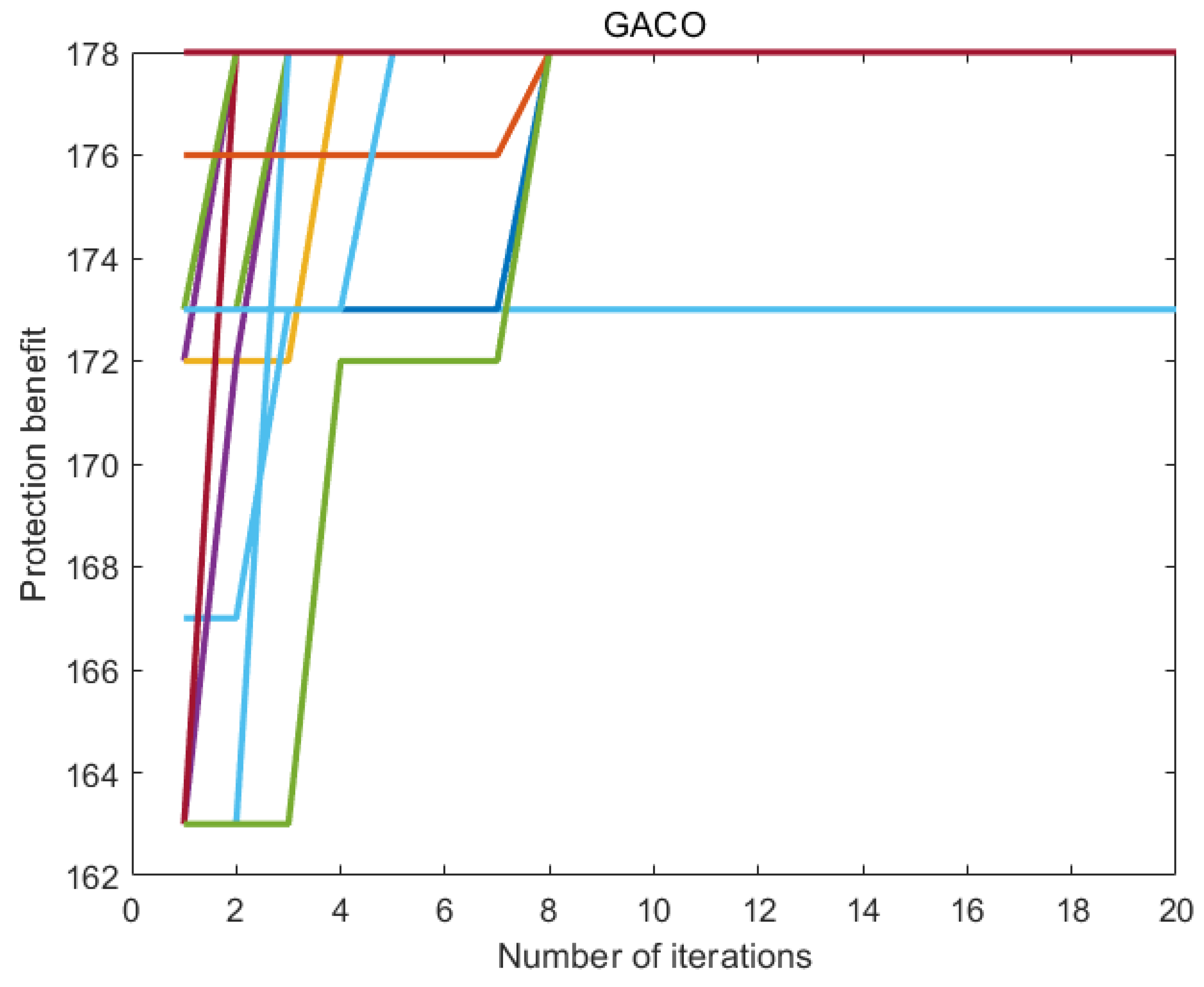
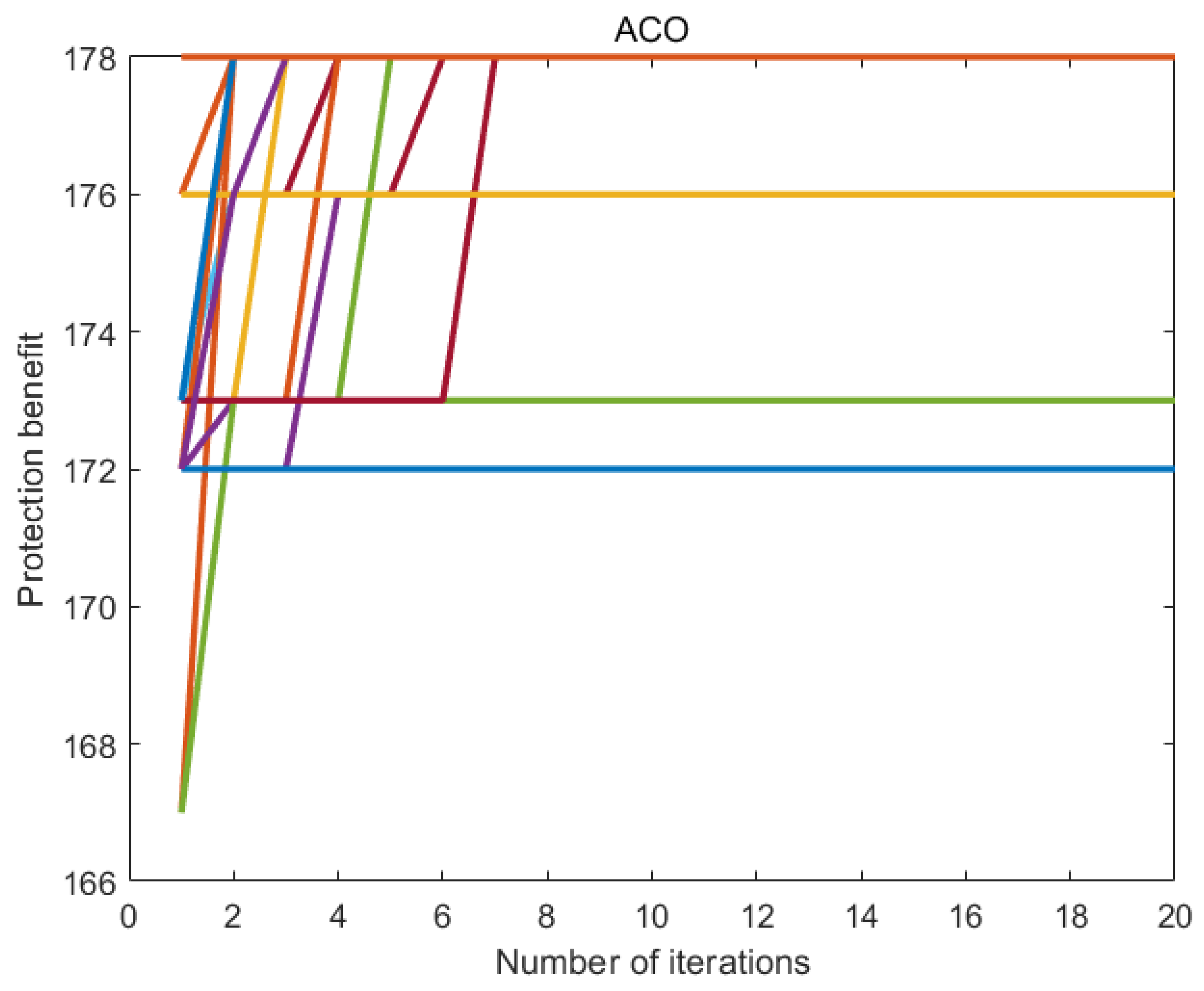
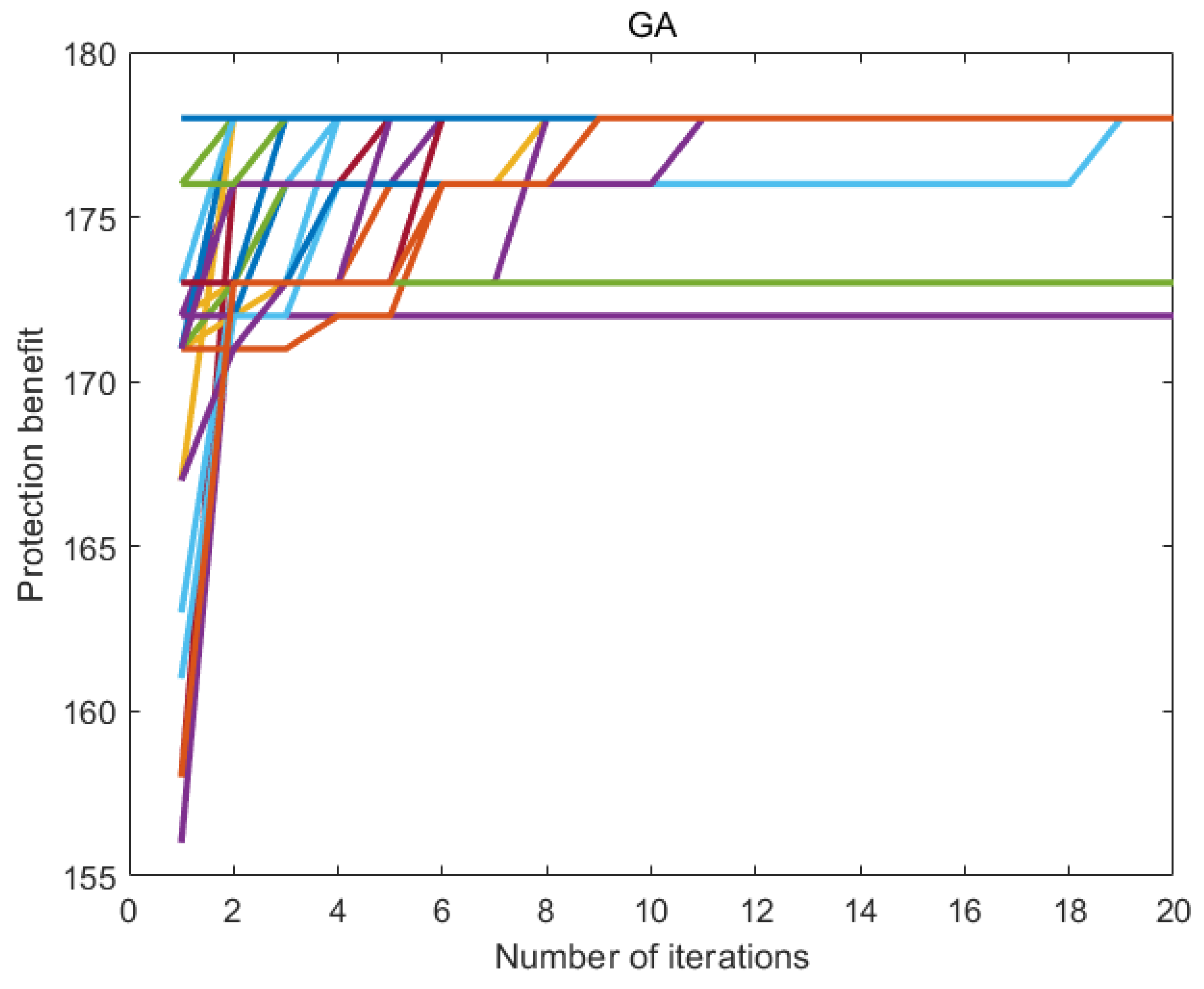
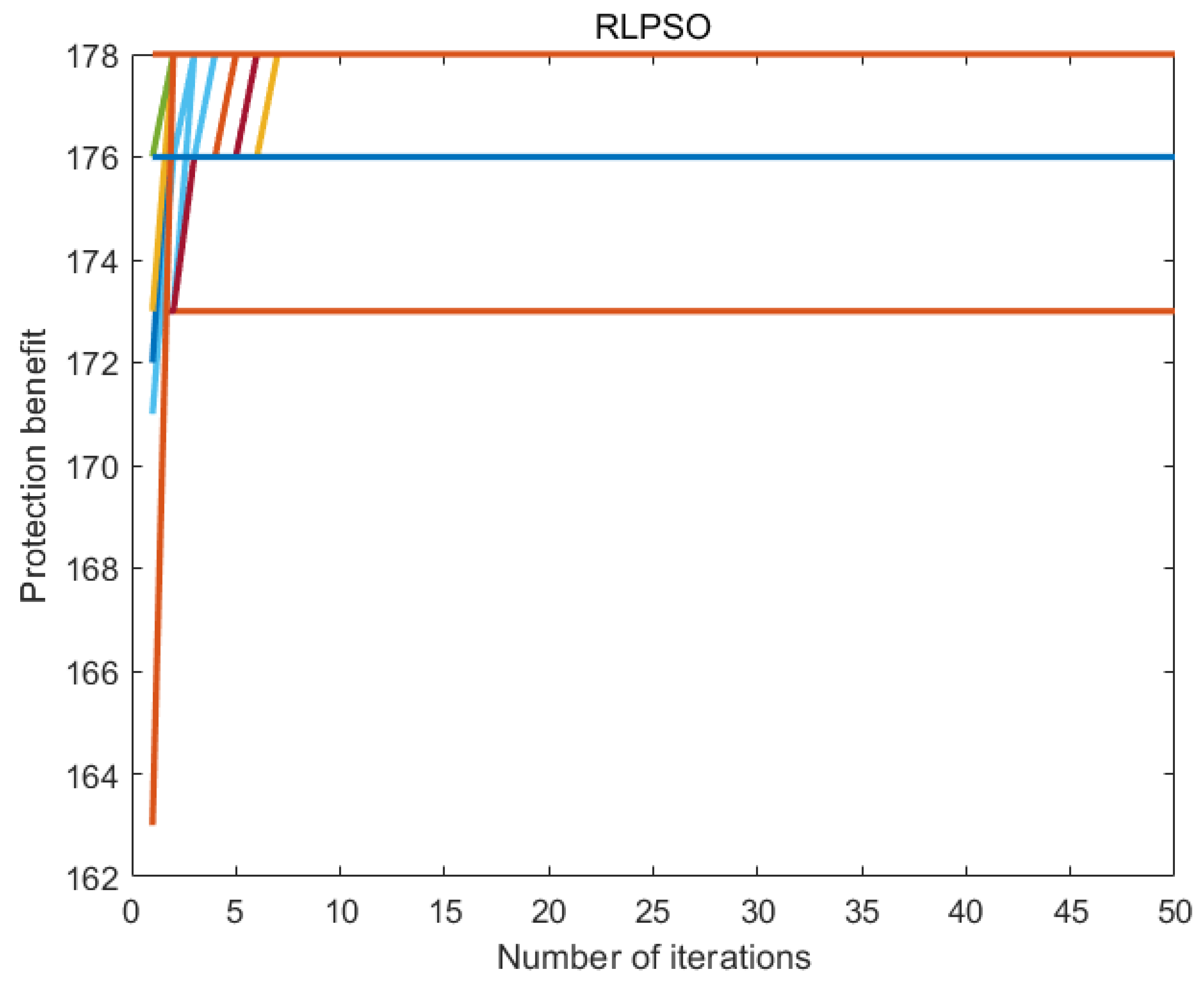
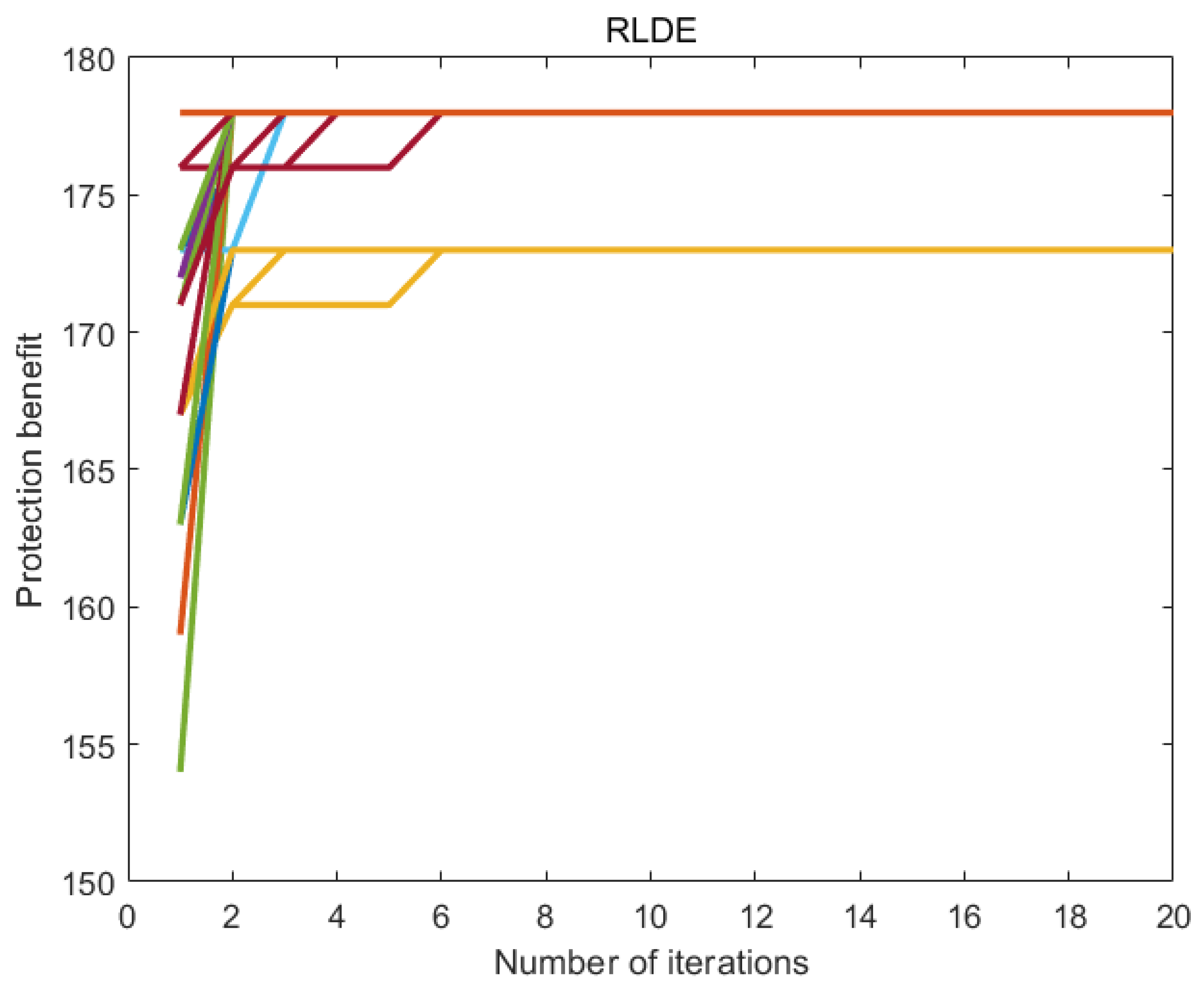
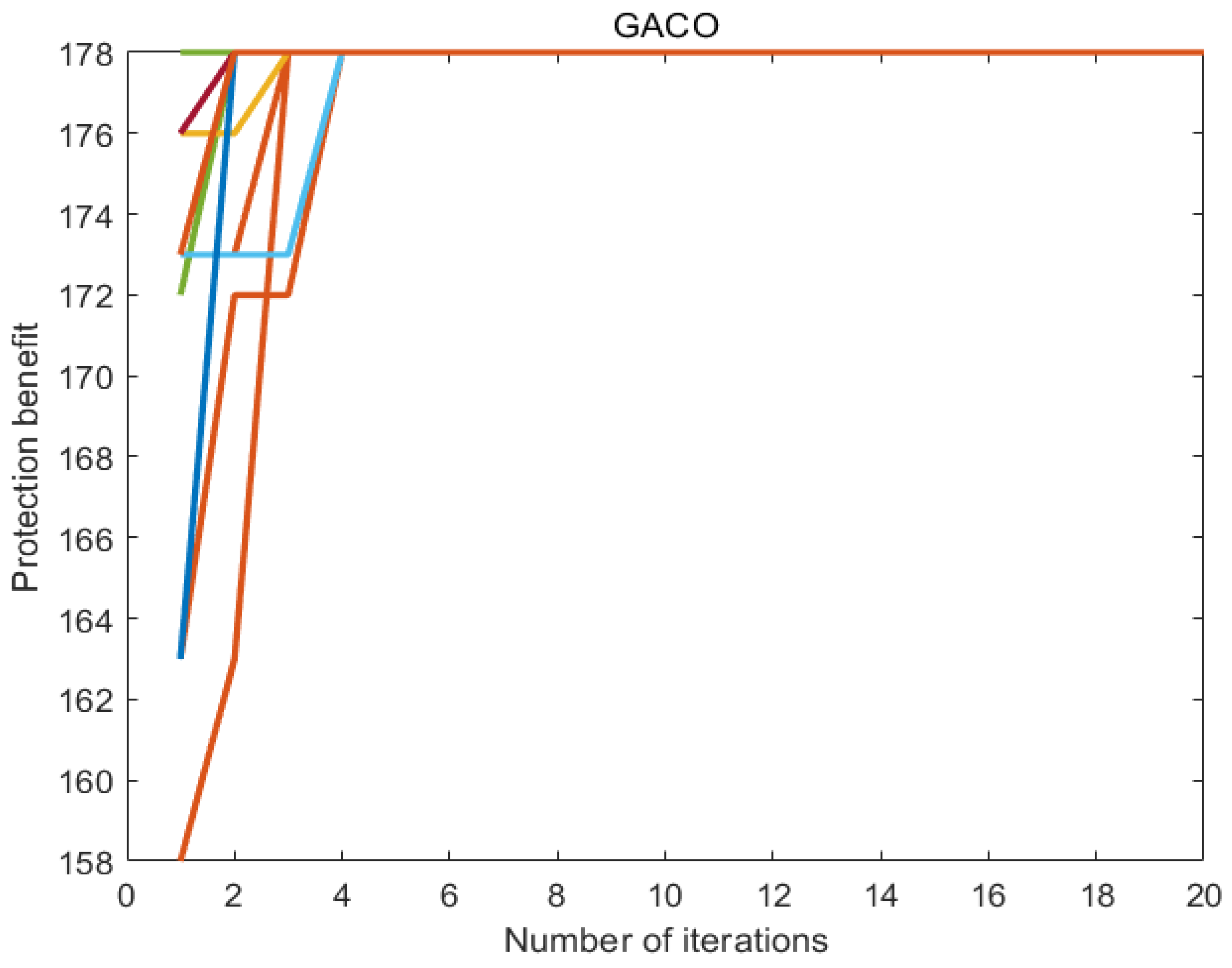
7.6. Experimental Results
7.7. Discussion
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Parameters | Descriptions |
|---|---|
| S | the set of attribute nodes |
| A | the set of atomic attacks |
| R | the relationship between parent and child nodes |
| E | the set of directed edges |
| the atomic attack probability against vulnerability | |
| the local conditional probability of attribute node | |
| the unconditional probability of attribute node | |
| the attack reachability probability of the path W | |
| the risk value of attribute node | |
| the overall risk of the path W | |
| M | a set of protection strategies |
| C | a set of protection cost |
| MC | the total protection cost |
| MV | the total protection benefit |
| the state of the agent at time t | |
| the action that the agent can perform at time t | |
| the reward obtained by performing the action at time t | |
| the learning rate | |
| the discount factor | |
| the reward value of the action corresponding to the state at time t | |
| the cumulative reward the agent obtains at time t | |
| the probability that the kth ant chooses strategy | |
| (t) | the pheromone concentration of strategy at time t |
| the visibility of strategy | |
| the relative importance of pheromone concentration | |
| the relative importance of visibility | |
| the strategy set selected by the kth ant | |
| the volatility coefficient of pheromone | |
| Q | a constant |
| the total benefit of the protection strategy set corresponding to the kth ant | |
| the total cost of the protection strategy set corresponding to the kth ant |
References
- Fan, X.; Fan, K.; Wang, Y.; Zhou, R. Overview of cyber-security of industrial control system. In Proceedings of the 2015 International Conference on Cyber Security of Smart Cities, Industrial Control System and Communications (SSIC), Shanghai, China, 5–7 August 2015; pp. 1–7. [Google Scholar]
- Xu, L.; Wang, B.; Wu, X.; Zhao, D.; Zhang, L.; Wang, Z. Detecting Semantic Attack in SCADA System: A Behavioral Model Based on Secondary Labeling of States-Duration Evolution Graph. IEEE Trans. Netw. Sci. Eng. 2021, 9, 703–715. [Google Scholar] [CrossRef]
- Knowles, W.; Prince, D.; Hutchison, D.; Disso, J.F.P.; Jones, K. A survey of cyber security management in industrial control systems. Int. J. Crit. Infrastruct. Prot. 2015, 9, 52–80. [Google Scholar] [CrossRef]
- Zhao, D.; Wang, L.; Wang, Z.; Xiao, G. Virus propagation and patch distribution in multiplex networks: Modeling, analysis, and optimal allocation. IEEE Trans. Inf. Forens. Secur. 2019, 14, 1755–1767. [Google Scholar] [CrossRef]
- Zhao, D.; Xiao, G.; Wang, Z.; Wang, L.; Xu, L. Minimum dominating set of multiplex networks: Definition, application, and identification. IEEE Trans. Syst. Man Cybern. Syst. 2020, 51, 7823–7837. [Google Scholar] [CrossRef]
- Hemsley, K.E.; Fisher, E. History of Industrial Control System Cyber Incidents; Technical Report; Idaho National Lab (INL): Idaho Falls, ID, USA, 2018. [Google Scholar]
- Sun, C.C.; Hahn, A.; Liu, C.C. Cyber security of a power grid: State-of-the-art. Int. J. Electr. Power Energy Syst. 2018, 99, 45–56. [Google Scholar] [CrossRef]
- Dewri, R.; Ray, I.; Poolsappasit, N.; Whitley, D. Optimal security hardening on attack tree models of networks: A cost-benefit analysis. Int. J. Inf. Secur. 2012, 11, 167–188. [Google Scholar] [CrossRef]
- Whitley, D. A genetic algorithm tutorial. Stat. Comput. 1994, 4, 65–85. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, Z.; Kadobayashi, Y. Exploring attack graph for cost-benefit security hardening: A probabilistic approach. Comput. Secur. 2013, 32, 158–169. [Google Scholar] [CrossRef]
- Dorigo, M.; Maniezzo, V.; Colorni, A. Ant system: Optimization by a colony of cooperating agents. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 1996, 26, 29–41. [Google Scholar] [CrossRef]
- Liu, Y.; Lu, H.; Cheng, S.; Shi, Y. An adaptive online parameter control algorithm for particle swarm optimization based on reinforcement learning. In Proceedings of the 2019 IEEE Congress on Evolutionary Computation (CEC), Wellington, New Zealand, 10–13 June 2019; pp. 815–822. [Google Scholar]
- Huynh, T.N.; Do, D.T.; Lee, J. Q-Learning-based parameter control in differential evolution for structural optimization. Appl. Soft Comput. 2021, 107, 107464. [Google Scholar] [CrossRef]
- Zuoguang, W.; Wei, Q.; Liu, W.W. Quantitative risk assessment of industrial control systems based on attack-tree and CVSS. Appl. Res. Comput. 2016, 12, 3785–3790. [Google Scholar]
- Meng, Z.; Yang, C. Two-stage differential evolution with novel parameter control. Inf. Sci. 2022, 596, 321–342. [Google Scholar] [CrossRef]
- Zamani, H.; Nadimi-Shahraki, M.H.; Gandomi, A.H. QANA: Quantum-based avian navigation optimizer algorithm. Eng. Appl. Artif. Intell. 2021, 104, 104314. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.H.; Taghian, S.; Mirjalili, S. An improved grey wolf optimizer for solving engineering problems. Expert Syst. Appl. 2021, 166, 113917. [Google Scholar] [CrossRef]
- Zamani, H.; Nadimi-Shahraki, M.H.; Gandomi, A.H. Starling murmuration optimizer: A novel bio-inspired algorithm for global and engineering optimization. Comput. Methods Appl. Mech. Eng. 2022, 392, 114616. [Google Scholar] [CrossRef]
- Chakraborty, S.; Saha, A.K.; Chakraborty, R.; Saha, M. An enhanced whale optimization algorithm for large scale optimization problems. Knowl.-Based Syst. 2021, 233, 107543. [Google Scholar] [CrossRef]
- Wu, H.; Gu, Y.; Cheng, G.; Zhou, Y. Effectiveness Evaluation Method for Cyber Deception Based on Dynamic Bayesian Attack Graph. In Proceedings of the 2020 3rd International Conference on Computer Science and Software Engineering, Beijing, China, 22–24 May 2020; pp. 1–9. [Google Scholar]
- Zhang, Y.; Wang, B.; Wu, C.; Wei, X.; Wang, Z.; Yin, G. Attack Graph-based Quantitative Assessment for Industrial Control System Security. In Proceedings of the 2020 Chinese Automation Congress (CAC), Shanghai, China, 6–8 November 2020; pp. 1748–1753. [Google Scholar]
- Xu, K.; Wang, X.; Xu, H.; Dong, N.; Han, M.; Zhou, X. A vulnerability scanning scheme based on attack graph for smart grid industrial control system. In Proceedings of the IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2021; Volume 645, p. 012060. [Google Scholar]
- Yang, J.; Yang, Y. Optimal Security Protection Selection Strategy Based on Markov Model Attack Graph. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2021; Volume 2132, p. 012020. [Google Scholar]
- Boudermine, A.; Khatoun, R.; Choyer, J.H. Attack Graph-based Solution for Vulnerabilities Impact Assessment in Dynamic Environment. In Proceedings of the 2022 5th Conference on Cloud and Internet of Things (CIoT), Marrakech, Morocco, 28–30 March 2022; pp. 24–31. [Google Scholar]
- Wang, L.; Islam, T.; Long, T.; Singhal, A.; Jajodia, S. An attack graph-based probabilistic security metric. In Proceedings of the IFIP Annual Conference on Data and Applications Security and Privacy; Springer: Berlin/Heidelberg, Germany, 2008; pp. 283–296. [Google Scholar]
- Poolsappasit, N.; Dewri, R.; Ray, I. Dynamic security risk management using bayesian attack graphs. IEEE Trans. Dependable Secur. Comput. 2011, 9, 61–74. [Google Scholar] [CrossRef]
- Liu, G.; Li, Q.; Zhang, H. Defense strategy generation method for network security based on state attack-defense graph. J. Comput. Appl. 2013, 33 (Suppl. S1), 121–125. [Google Scholar]
- Zukhri, Z.; Paputungan, I.V. A hybrid optimization algorithm based on genetic algorithm and ant colony optimization. Int. J. Artif. Intell. Appl. 2013, 4, 63. [Google Scholar] [CrossRef]
- Ye, Z.; Guo, Y.; Wang, C.; Ju, A.K. Survey on application of attack graph technology. J. Commun. 2017, 38, 121–132. [Google Scholar]
- Chung, C.J.; Khatkar, P.; Xing, T.; Lee, J.; Huang, D. NICE: Network intrusion detection and countermeasure selection in virtual network systems. IEEE Trans. Dependable Secur. Comput. 2013, 10, 198–211. [Google Scholar] [CrossRef]
- Luo, Z.; Yang, X.; Liu, J.; Xu, R. Network intrusion intention analysis model based on Bayesian attack graph. J. Commun. 2020, 41, 160–169. [Google Scholar]
- Li, Y.; Wang, C.Z.; Huang, G.Q.; Zhao, X.; Zhang, B.; Li, Y.C. A survey of architecture and implementation method on cyber security situation awareness analysis. Acta Electon. Sin. 2019, 47, 927. [Google Scholar]
- Xiu-juan, W.; Bo, S.; Yan-wen, L.; Cong-bin, X. Computer Network Vulnerability Assessment Based on Bayesian Attribute Network. J. Beijing Univ. Posts Telecommun. 2015, 38, 110. [Google Scholar]
- Mell, P.; Scarfone, K.; Romanosky, S. Common vulnerability scoring system. IEEE Secur. Priv. 2006, 4, 85–89. [Google Scholar] [CrossRef]
- Ruohonen, J. A look at the time delays in CVSS vulnerability scoring. Appl. Comput. Inform. 2019, 15, 129–135. [Google Scholar] [CrossRef]
- Ye, Y.; Xu, X.S.; Jia, Y.; Qi, Z.C. An attack graph-based probabilistic computing approach of network security. Chin. J. Comput. 2010, 33, 1987–1996. [Google Scholar] [CrossRef]
- Chen, X.; Fang, B.; Tan, Q.; Zhang, H. Inferring attack intent of malicious insider based on probabilistic attack graph model. Chin. J. Comput. 2014, 37, 62–72. [Google Scholar]
- Gao, N.; Gao, L.; He, Y.; Wang, F. Optimal security hardening measures selection model based on Bayesian attack graph. Comput. Eng. Appl. 2016, 52, 125–130. [Google Scholar]
- Babu, B.; Ijyas, T.; Muneer, P.; Varghese, J. Security issues in SCADA based industrial control systems. In Proceedings of the 2017 2nd International Conference on Anti-Cyber Crimes (ICACC), Abha, Saudi Arabia, 26–27 March 2017; pp. 47–51. [Google Scholar]
- Harrison, L.; Spahn, R.; Iannacone, M.; Downing, E.; Goodall, J.R. Nv: Nessus vulnerability visualization for the web. In Proceedings of the Ninth International Symposium on Visualization for Cyber Security, Seattle, WA, USA, 15 October 2012; pp. 25–32. [Google Scholar]
- Ou, X.; Govindavajhala, S.; Appel, A.W. MulVAL: A Logic-based Network Security Analyzer. In Proceedings of the USENIX Security Symposium, Baltimore, MD, USA, 31 July–5 August 2005; Volume 8, pp. 113–128. [Google Scholar]


| Index | Rank | Score |
|---|---|---|
| Access Vector (AV) | local access | 0.395 |
| local network accessible | 0.646 | |
| network accessible | 1.0 | |
| Access Complexity (AC) | high | 0.35 |
| medium | 0.61 | |
| low | 0.71 | |
| Authentication (AU) | multiple instances of authentication | 0.45 |
| single instance of authentication | 0.56 | |
| no authentication | 0.704 |
| Q Table | action1 | action2 | action3 | action4 | action5 | action6 |
|---|---|---|---|---|---|---|
| state1 | ||||||
| state2 |
| action1 | action2 | action3 | action4 | action5 | action6 |
|---|---|---|---|---|---|
| (1, 1) | (2, 2) | (3, 3) | (4, 4) | (5, 5) | (6, 6) |
| action1 | action2 | action3 | action4 | action5 | action6 |
|---|---|---|---|---|---|
| (1, 1) | (2, 2) | (3, 3) | (4, 4) | (5, 5) | (6, 6) |
| Host | Vulnerability ID |
|---|---|
| 198.168.0.1 | CVE-1999-0517 |
| 198.168.0.2 | CVE-1999-0517 |
| 198.168.0.10 | CVE-1999-0517 |
| Node | Probability | Node | Probability | Node | Probability |
|---|---|---|---|---|---|
| 1.0000 | 1.0000 | 1.0000 | |||
| 1.0000 | 1.0000 | 1.0000 | |||
| 0.5000 | 1.0000 | 0.9960 | |||
| 1.0000 | 1.0000 | 1.0000 | |||
| 1.0000 | 0.5000 | 1.0000 | |||
| 0.9863 | 0.8372 | 1.0000 | |||
| 0.5000 | 1.0000 | 0.9530 | |||
| 0.5000 |
| Attack | Strategy | Protective Action | Cost | Value |
|---|---|---|---|---|
| Disable multi-hop access 192.168.0.1–192.168.0.10 | 33 | 50 | ||
| Disable multi-hop access 192.168.0.2–192.168.0.10 | 33 | 50 | ||
| Disable direct network access 192.168.0.10 | 30 | 52 | ||
| Disable direct network access 192.168.0.2 | 30 | 52 | ||
| Disable direct network access 192.168.0.1 | 30 | 52 | ||
| Limit remote visit 192.168.0.10 | 20 | 5 | ||
| Patch CVE-1999-0517 192.168.0.10 | 15 | 25 | ||
| Disable multi-hop access 192.168.0.10 | 14 | 26 | ||
| Disable multi-hop access 192.168.0.2–192.168.0.10 | 33 | 50 | ||
| Disable multi-hop access 192.168.0.1–192.168.0.2 | 30 | 56 | ||
| Limit remote visit 192.168.0.2 | 33 | 15 | ||
| Patch CVE-1999-0517 192.168.0.2 | 17 | 30 | ||
| Disable multi-hop access 192.168.0.1–192.168.0.2 | 30 | 56 | ||
| Limit remote visit 192.168.0.1 | 18 | 8 | ||
| Patch CVE-1999-0517 192.168.0.1 | 19 | 40 |
| Index | Attack Path | Probability | Risk |
|---|---|---|---|
| 1 | --------- | 0.119 | 92.000 |
| 2 | -------------- | 0.049 | 169.674 |
| 3 | --------- | 0.119 | 92.000 |
| 4 | -------------- | 0.049 | 144.671 |
| 5 | ---------- | 0.119 | 93.000 |
| 6 | --------------- | 0.049 | 170.674 |
| 7 | ---------- | 0.098 | 115.674 |
| 8 | ----- | 0.238 | 50.000 |
| 9 | --------- | 0.098 | 117.674 |
| Algorithm | Parameter | Value |
|---|---|---|
| GACO | 0.1 | |
| 0.9 | ||
| 0.1 | ||
| Q | 1 | |
| 1 | ||
| , | [(1,2),(1,3),(1,4),(2,3),(2,4),(2,5)] | |
| , | [(0.8,0.2),(0.7,0.2),(0.6,0.2), | |
| (0.8,0.1),(0.7,0.1),(0.6,0.1)] | ||
| GA | 0.8 | |
| 0.1 | ||
| ACO | 1 | |
| 3 | ||
| 0.1 | ||
| Q | 1 | |
| 1 | ||
| RLPSO | 0.9 | |
| 0.1 | ||
| w, c1, c2 | [(0.8,2,1.5),(0.8,1.5,2),(0.8,2,2), | |
| (0.6,2,1.5),(0.6,1.5,2),(0.6,2,2)] | ||
| RLDE | 0.9 | |
| 0.1 | ||
| F, Cr | [(0.6,0.7),(0.6,0.8),(0.7,0.7), | |
| (0.8,0.7),(0.8,0.9),(0.9,0.9)] |
| Population Size | Algorithm | The Number of Occurrences |
|---|---|---|
| 15 | GACO | 9 |
| GA | 37 | |
| ACO | 43 | |
| RLPSO | 70 | |
| RLDE | 65 | |
| 100 | GACO | 0 |
| GA | 15 | |
| ACO | 19 | |
| RLPSO | 8 | |
| RLDE | 6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Zhou, Y.; Li, X.; Xu, L.; Zhao, D. Protection Strategy Selection Model Based on Genetic Ant Colony Optimization Algorithm. Mathematics 2022, 10, 3938. https://doi.org/10.3390/math10213938
Li X, Zhou Y, Li X, Xu L, Zhao D. Protection Strategy Selection Model Based on Genetic Ant Colony Optimization Algorithm. Mathematics. 2022; 10(21):3938. https://doi.org/10.3390/math10213938
Chicago/Turabian StyleLi, Xinzhan, Yang Zhou, Xin Li, Lijuan Xu, and Dawei Zhao. 2022. "Protection Strategy Selection Model Based on Genetic Ant Colony Optimization Algorithm" Mathematics 10, no. 21: 3938. https://doi.org/10.3390/math10213938
APA StyleLi, X., Zhou, Y., Li, X., Xu, L., & Zhao, D. (2022). Protection Strategy Selection Model Based on Genetic Ant Colony Optimization Algorithm. Mathematics, 10(21), 3938. https://doi.org/10.3390/math10213938






