Open-Source Computational Photonics with Auto Differentiable Topology Optimization
Abstract
1. Introduction
2. Materials and Methods
2.1. Finite Element Method
2.2. Fourier Modal Method
2.3. Plane Wave Expansion Method
2.4. Automatic Differentiation
2.5. Topology Optimization
3. Results
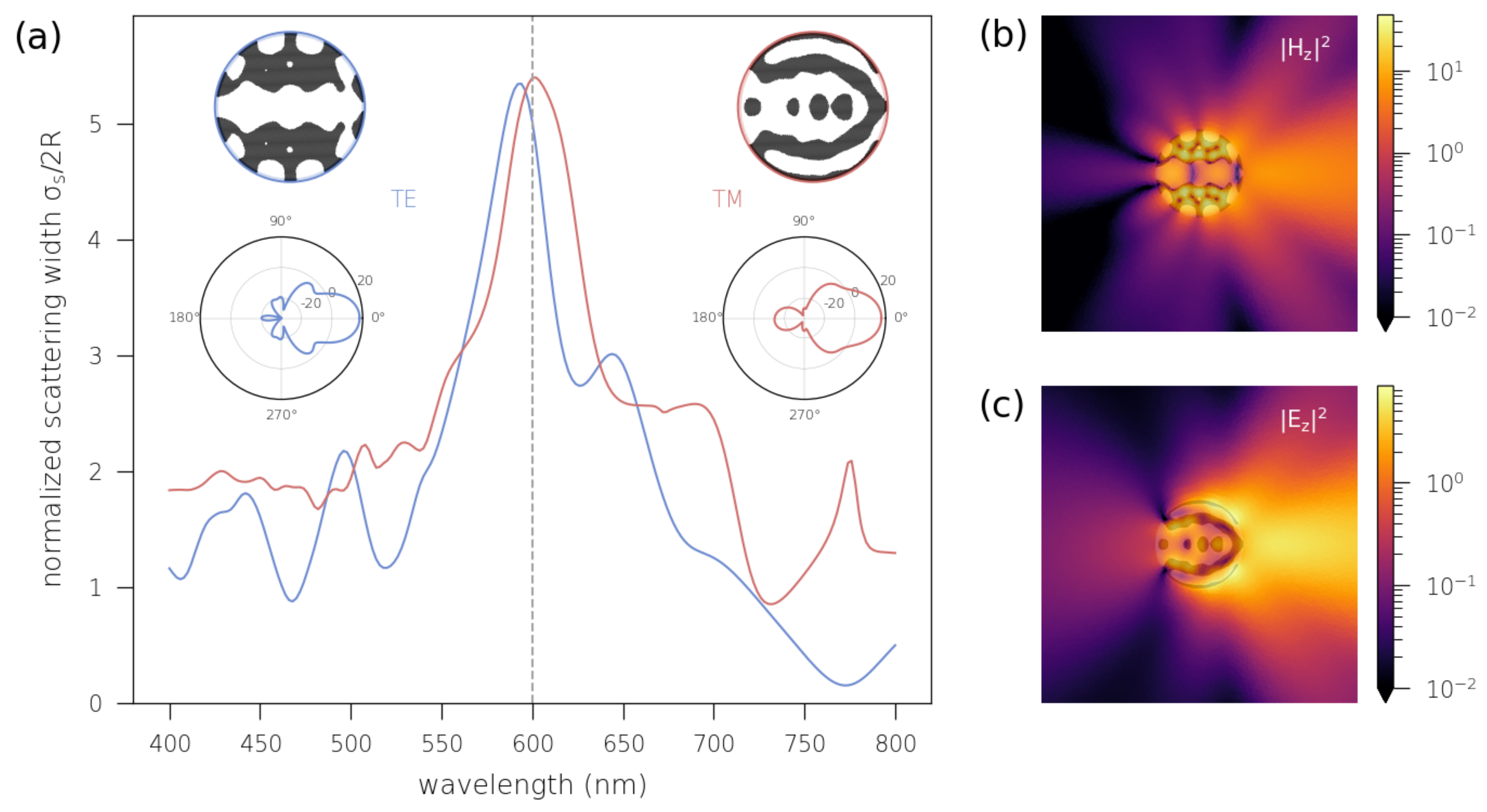
3.1. Superscatterer
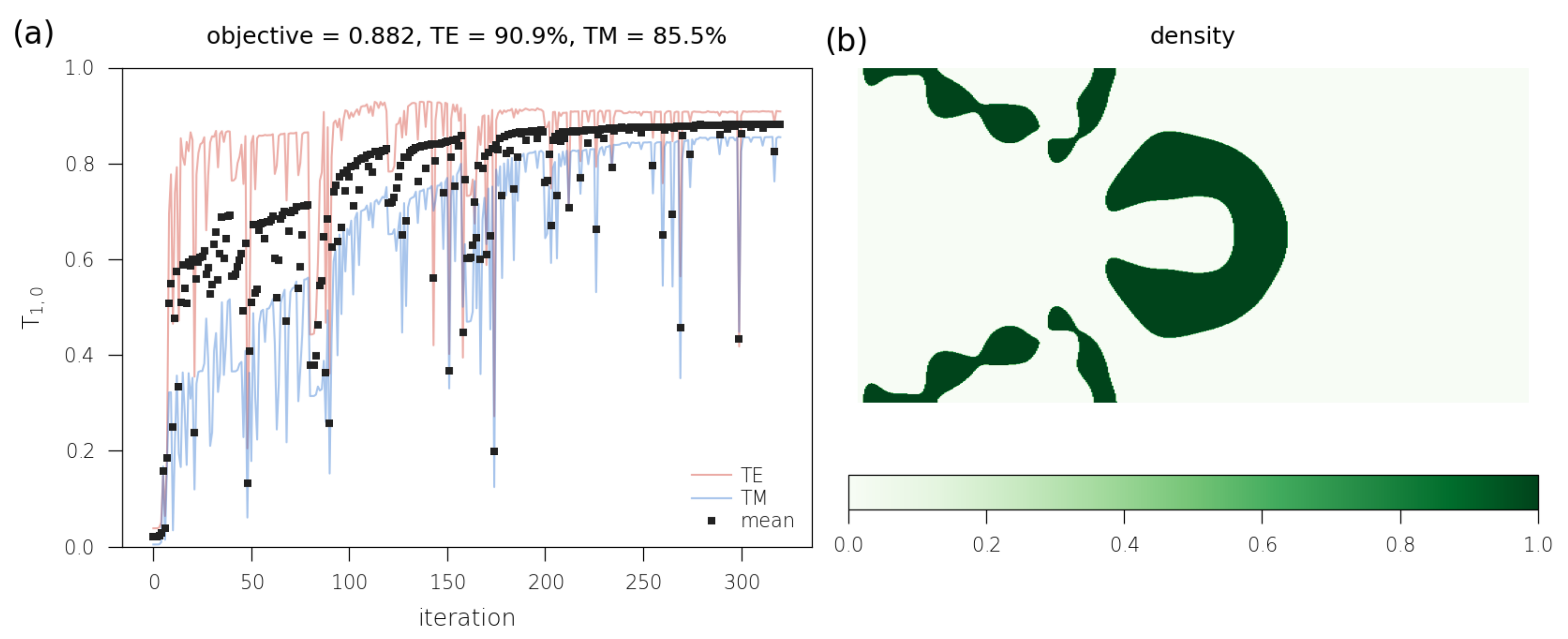
3.2. Deflective Metasurface
3.3. Bandgap and Dispersion Engineering in Photonic Crystals
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| FEM | Finite Element Method |
| FMM | Fourier Modal Method |
| RCWA | Rigorous Coupled Wave Analysis |
| PWEM | Plane Wave Expansion Method |
| AD | Automatic Differentiation |
| RBME | Plane Wave Expansion Method |
Appendix A. Code Validation
- FEM: https://gyptis.gitlab.io/examples (accessed on 17 October 2022)
- FMM: https://nannos.gitlab.io/examples (accessed on 17 October 2022)
- PWEM: https://protis.gitlab.io/examples (accessed on 17 October 2022)
Appendix A.1. FEM

Appendix A.2. FMM
| Diffraction Order | −1 | 0 | 1 |
|---|---|---|---|
| −1 | 4.345 | 12.816 | 6.130 |
| 0 | 12.816 | 17.765 | 12.816 |
| 1 | 6.130 | 12.816 | 4.345 |
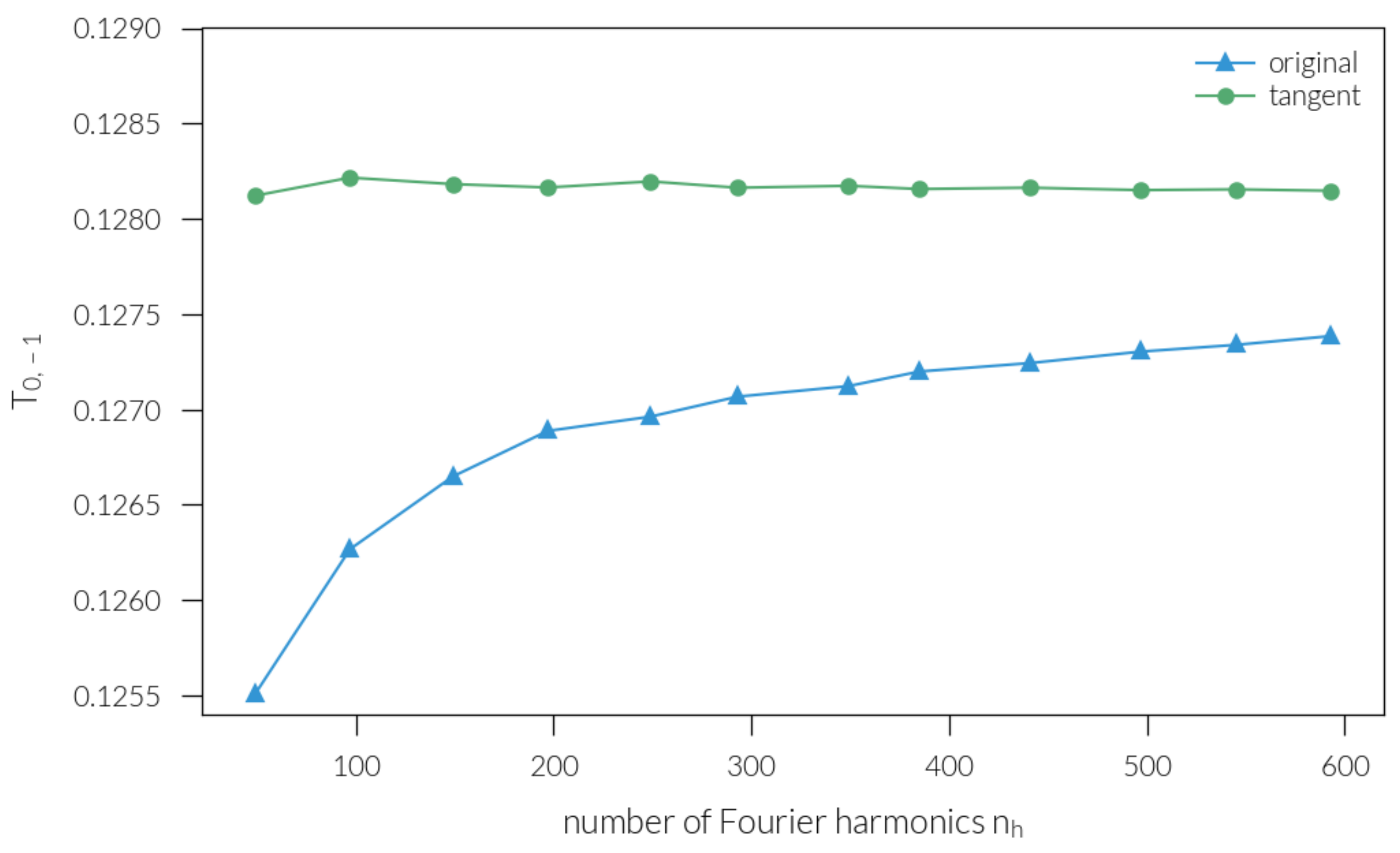
Appendix A.3. PWEM
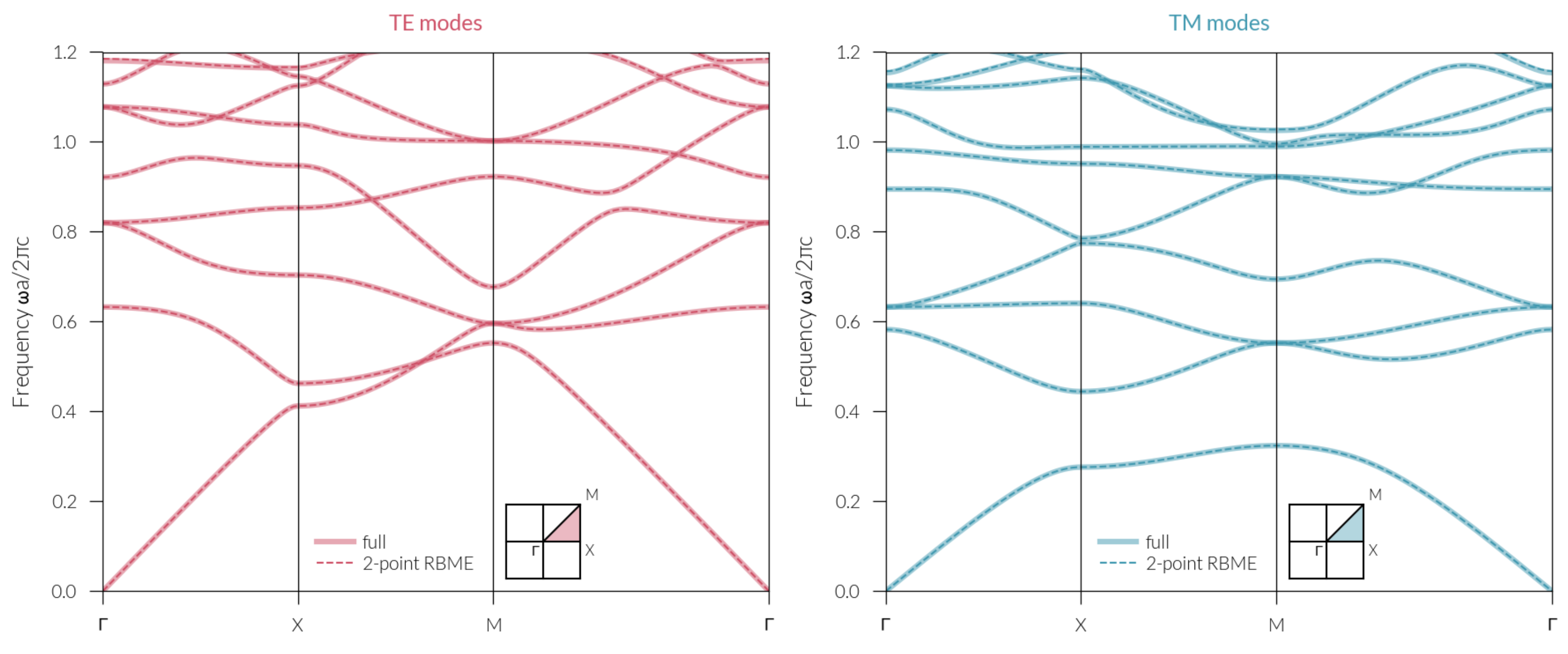
References
- Bendsoe, M.P.; Sigmund, O. Topology Optimization: Theory, Methods, and Applications; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Molesky, S.; Lin, Z.; Piggott, A.Y.; Jin, W.; Vucković, J.; Rodriguez, A.W. Inverse Design in Nanophotonics. Nat. Photonics 2018, 12, 659–670. [Google Scholar] [CrossRef]
- Andkjær, J.; Sigmund, O. Topology Optimized Low-Contrast All-Dielectric Optical Cloak. Appl. Phys. Lett. 2011, 98, 021112. [Google Scholar] [CrossRef]
- Vial, B.; Hao, Y. Topology Optimized All-Dielectric Cloak: Design, Performances and Modal Picture of the Invisibility Effect. Opt. Express 2015, 23, 23551. [Google Scholar] [CrossRef] [PubMed]
- Vial, B.; Torrico, M.M.; Hao, Y. Optimized Microwave Illusion Device. Sci. Rep. 2017, 7, 3929. [Google Scholar] [CrossRef] [PubMed]
- Jensen, J.S.; Sigmund, O. Systematic Design of Photonic Crystal Structures Using Topology Optimization: Low-Loss Waveguide Bends. Appl. Phys. Lett. 2004, 84, 2022–2024. [Google Scholar] [CrossRef]
- Jensen, J.S.; Sigmund, O. Topology Optimization of Photonic Crystal Structures: A High-Bandwidth Low-Loss T-Junction Waveguide. J. Opt. Soc. Am. Opt. Phys. 2005, 22, 1191. [Google Scholar] [CrossRef]
- Diaz, A.R.; Sigmund, O. A Topology Optimization Method for Design of Negative Permeability Metamaterials. Struct. Multidisc. Optim. 2009, 41, 163–177. [Google Scholar] [CrossRef]
- Nishi, S.; Yamada, T.; Izui, K.; Nishiwaki, S.; Terada, K. Isogeometric Topology Optimization of Anisotropic Metamaterials for Controlling High-Frequency Electromagnetic Wave. Int. J. Numer. Methods Eng. 2020, 121, 1218–1247. [Google Scholar] [CrossRef]
- Lin, Z.; Liu, V.; Pestourie, R.; Johnson, S.G. Topology Optimization of Freeform Large-Area Metasurfaces. Opt. Express 2019, 27, 15765–15775. [Google Scholar] [CrossRef]
- Fan, J.A. Freeform Metasurface Design Based on Topology Optimization. MRS Bull. 2020, 45, 196–201. [Google Scholar] [CrossRef]
- Pestourie, R.; Pérez-Arancibia, C.; Lin, Z.; Shin, W.; Capasso, F.; Johnson, S.G. Inverse Design of Large-Area Metasurfaces. Opt. Express 2018, 26, 33732–33747. [Google Scholar] [CrossRef]
- Christiansen, R.E.; Christiansen, R.E.; Sigmund, O.; Sigmund, O. Inverse Design in Photonics by Topology Optimization: Tutorial. JOSA B 2021, 38, 496–509. [Google Scholar] [CrossRef]
- Jensen, J.; Sigmund, O. Topology Optimization for Nano-Photonics. Laser Photon. Rev. 2010, 5, 308–321. [Google Scholar] [CrossRef]
- Demésy, G.; Zolla, F.; Nicolet, A.; Commandré, M.; Fossati, C. The Finite Element Method as Applied to the Diffraction by an Anisotropic Grating. Opt. Express 2007, 15, 18089–18102. [Google Scholar] [CrossRef]
- Berenger, J.P. A Perfectly Matched Layer for the Absorption of Electromagnetic Waves. J. Comput. Phys. 1994, 114, 185–200. [Google Scholar] [CrossRef]
- Vial, B.; Zolla, F.; Nicolet, A.; Commandré, M.; Tisserand, S. Adaptive Perfectly Matched Layer for Wood’s Anomalies in Diffraction Gratings. Opt. Express 2012, 20, 28094. [Google Scholar] [CrossRef]
- Vial, B. Gyptis. Zenodo. 2022. Available online: https://zenodo.org/record/6636134#.Y1CkJExBxPY (accessed on 17 October 2022).
- Geuzaine, C.; Remacle, J.F. Gmsh: A 3-D Finite Element Mesh Generator with Built-in Pre- and Post-Processing Facilities. Int. J. Numer. Methods Eng. 2009, 79, 1309–1331. [Google Scholar] [CrossRef]
- Alnæs, M.; Blechta, J.; Hake, J.; Johansson, A.; Kehlet, B.; Logg, A.; Richardson, C.; Ring, J.; Rognes, M.E.; Wells, G.N. Archive of Numerical Software. The FEniCS Project Version 1.5. 2015. Available online: https://journals.ub.uni-heidelberg.de/index.php/ans/article/view/20553 (accessed on 17 October 2022).
- Whittaker, D.M.; Culshaw, I.S. Scattering-Matrix Treatment of Patterned Multilayer Photonic Structures. Phys. Rev. B 1999, 60, 2610–2618. [Google Scholar] [CrossRef]
- Liu, V.; Fan, S. S4: A Free Electromagnetic Solver for Layered Periodic Structures. Comput. Phys. Commun. 2012, 183, 2233–2244. [Google Scholar] [CrossRef]
- Popov, E.; Nevière, M. Maxwell Equations in Fourier Space: Fast-Converging Formulation for Diffraction by Arbitrary Shaped, Periodic, Anisotropic Media. JOSA A 2001, 18, 2886–2894. [Google Scholar] [CrossRef]
- Moharam, M.G.; Gaylord, T.K. Rigorous Coupled-Wave Analysis of Planar-Grating Diffraction. JOSA 1981, 71, 811–818. [Google Scholar] [CrossRef]
- Li, L. New Formulation of the Fourier Modal Method for Crossed Surface-Relief Gratings. JOSA A 1997, 14, 2758–2767. [Google Scholar] [CrossRef]
- Schuster, T.; Ruoff, J.; Kerwien, N.; Rafler, S.; Osten, W. Normal Vector Method for Convergence Improvement Using the RCWA for Crossed Gratings. JOSA A 2007, 24, 2880–2890. [Google Scholar] [CrossRef] [PubMed]
- Götz, P.; Schuster, T.; Frenner, K.; Rafler, S.; Osten, W. Normal Vector Method for the RCWA with Automated Vector Field Generation. Opt. Express 2008, 16, 17295–17301. [Google Scholar] [CrossRef]
- Li, L. Fourier Modal Method for Crossed Anisotropic Gratings with Arbitrary Permittivity and Permeability Tensors. J. Opt. Pure Appl. Opt. 2003, 5, 345–355. [Google Scholar] [CrossRef]
- Li, L. Formulation and Comparison of Two Recursive Matrix Algorithms for Modeling Layered Diffraction Gratings. JOSA A 1996, 13, 1024–1035. [Google Scholar] [CrossRef]
- Hussein, M.I. Reduced Bloch Mode Expansion for Periodic Media Band Structure Calculations. Proc. R. Soc. Math. Phys. Eng. Sci. 2009, 465, 2825–2848. [Google Scholar] [CrossRef]
- Griewank, A.; Walther, A. Evaluating Derivatives; Other Titles in Applied Mathematics; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2008. [Google Scholar] [CrossRef]
- Corliss, G.; Faure, C.; Griewank, A.; Hascoet, L.; Naumann, U. Automatic Differentiation of Algorithms: From Simulation to Optimization; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Baydin, A.G.; Pearlmutter, B.A.; Radul, A.A.; Siskind, J.M. Automatic Differentiation in Machine Learning: A Survey. J. Mach. Learn. Res. 2017, 18, 5595–5637. [Google Scholar]
- Mitusch, S.K.; Funke, S.W.; Dokken, J.S. Dolfin-Adjoint 2018.1: Automated Adjoints for FEniCS and Firedrake. J. Open Source Softw. 2019, 4, 1292. [Google Scholar] [CrossRef]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array Programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef]
- Bradbury, J.; Frostig, R.; Hawkins, P.; Johnson, M.J.; Leary, C.; Maclaurin, D.; Necula, G.; Paszke, A.; VanderPlas, J.; Wanderman-Milne, S.; et al. JAX: Composable Transformations of Python+NumPy Programs. 2018. Available online: https://github.com/google/jax3 (accessed on 17 October 2022).
- Maclaurin, D.; Duvenaud, D.; Adams, R.P. Autograd: Effortless Gradients in Numpy. Proc. ICML 2015, 238, 5. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Advances in Neural Information Processing Systems 32; Wallach, H., Larochelle, H., Beygelzimer, A., d’Alché-Buc, F., Fox, E., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2019; pp. 8024–8035. [Google Scholar]
- Paszke, A.; Gross, S.; Chintala, S.; Chanan, G.; Yang, E.; DeVito, Z.; Lin, Z.; Desmaison, A.; Antiga, L.; Lerer, A. Automatic Differentiation in PyTorch. In Proceedings of the NIPS-W, Long Beach, CA, USA, 9 December 2017. [Google Scholar]
- Lazarov, B.S.; Sigmund, O. Filters in Topology Optimization Based on Helmholtz-type Differential Equations. Int. J. Numer. Methods Eng. 2011, 86, 765–781. [Google Scholar] [CrossRef]
- Wang, F.; Lazarov, B.S.; Sigmund, O. On Projection Methods, Convergence and Robust Formulations in Topology Optimization. Struct. Multidisc. Optim. 2010, 43, 767–784. [Google Scholar] [CrossRef]
- Bendsøe, M.; Sigmund, O. Material Interpolation Schemes in Topology Optimization. Arch. Appl. Mech. Ing. Arch. 1999, 69, 635–654. [Google Scholar] [CrossRef]
- Svanberg, K. A Class of Globally Convergent Optimization Methods Based on Conservative Convex Separable Approximations. SIAM J. Optim. 2002, 12, 555–573. [Google Scholar] [CrossRef]
- Johnson, S.G. The NLopt Nonlinear-Optimization Package. Available online: http://github.com/stevengj/nlopt (accessed on 17 October 2022).
- Aslan, K.; Lakowicz, J.R.; Geddes, C.D. Plasmon Light Scattering in Biology and Medicine: New Sensing Approaches, Visions and Perspectives. Curr. Opin. Chem. Biol. 2005, 9, 538–544. [Google Scholar] [CrossRef]
- Guo, X.; Ying, Y.; Tong, L. Photonic Nanowires: From Subwavelength Waveguides to Optical Sensors. Acc. Chem. Res. 2014, 47, 656–666. [Google Scholar] [CrossRef]
- Lee, B.; Lee, I.M.; Kim, S.; Oh, D.H.; Hesselink, L. Review on Subwavelength Confinement of Light with Plasmonics. J. Mod. Opt. 2010, 57, 1479–1497. [Google Scholar] [CrossRef]
- Powell, A.W.; Mrnka, M.; Hibbins, A.P.; Sambles, J.R. Superscattering and Directive Antennas via Mode Superposition in Subwavelength Core-Shell Meta-Atoms. Photonics 2022, 9, 6. [Google Scholar] [CrossRef]
- Wee, W.H.; Pendry, J.B. Shrinking Optical Devices. New J. Phys. 2009, 11, 073033. [Google Scholar] [CrossRef]
- Yang, T.; Chen, H.; Luo, X.; Ma, H. Superscatterer: Enhancement of Scattering with Complementary Media. Opt. Express 2008, 16, 18545–18550. [Google Scholar] [CrossRef]
- Ruan, Z.; Fan, S. Superscattering of Light from Subwavelength Nanostructures. Phys. Rev. Lett. 2010, 105, 013901. [Google Scholar] [CrossRef]
- Ruan, Z.; Fan, S. Design of Subwavelength Superscattering Nanospheres. Appl. Phys. Lett. 2011, 98, 043101. [Google Scholar] [CrossRef]
- Mirzaei, A.; Miroshnichenko, A.E.; Shadrivov, I.V.; Kivshar, Y.S. Superscattering of Light Optimized by a Genetic Algorithm. Appl. Phys. Lett. 2014, 105, 011109. [Google Scholar] [CrossRef]
- Frezza, F.; Mangini, F.; Tedeschi, N. Introduction to Electromagnetic Scattering: Tutorial. JOSA A 2018, 35, 163–173. [Google Scholar] [CrossRef]
- Ching, E.S.C.; Leung, P.T.; Maassen van den Brink, A.; Suen, W.M.; Tong, S.S.; Young, K. Quasinormal-Mode Expansion for Waves in Open Systems. Rev. Mod. Phys. 1998, 70, 1545–1554. [Google Scholar] [CrossRef]
- Zolla, F.; Nicolet, A.; Demésy, G. Photonics in Highly Dispersive Media: The Exact Modal Expansion. Opt. Lett. 2018, 43, 5813–5816. [Google Scholar] [CrossRef] [PubMed]
- Lalanne, P.; Yan, W.; Gras, A.; Sauvan, C.; Hugonin, J.P.; Besbes, M.; Demésy, G.; Truong, M.D.; Gralak, B.; Zolla, F.; et al. Quasinormal Mode Solvers for Resonators with Dispersive Materials. JOSA A 2019, 36, 686–704. [Google Scholar] [CrossRef] [PubMed]
- Vial, B.; Zolla, F.; Nicolet, A.; Commandré, M. Quasimodal Expansion of Electromagnetic Fields in Open Two-Dimensional Structures. Phys. Rev. At. Mol. Opt. Phys. 2014, 89, 023829. [Google Scholar] [CrossRef]
- Yu, N.; Genevet, P.; Kats, M.A.; Aieta, F.; Tetienne, J.P.; Capasso, F.; Gaburro, Z. Light Propagation with Phase Discontinuities: Generalized Laws of Reflection and Refraction. Science 2011, 334, 333–337. [Google Scholar] [CrossRef]
- Kildishev, A.V.; Boltasseva, A.; Shalaev, V.M. Planar Photonics with Metasurfaces. Science 2013, 339, 1232009. [Google Scholar] [CrossRef]
- Sell, D.; Yang, J.; Doshay, S.; Yang, R.; Fan, J.A. Large-Angle, Multifunctional Metagratings Based on Freeform Multimode Geometries. Nano Lett. 2017, 17, 3752–3757. [Google Scholar] [CrossRef]
- Lin, Z.; Groever, B.; Capasso, F.; Rodriguez, A.W.; Lončar, M. Topology-Optimized Multilayered Metaoptics. Phys. Rev. Appl. 2018, 9, 044030. [Google Scholar] [CrossRef]
- Roques-Carmes, C.; Lin, Z.; Christiansen, R.E.; Salamin, Y.; Kooi, S.E.; Joannopoulos, J.D.; Johnson, S.G.; Soljačić, M. Toward 3D-Printed Inverse-Designed Metaoptics. ACS Photonics 2022, 9, 43–51. [Google Scholar] [CrossRef]
- Yang, J.; Fan, J.A. Topology-Optimized Metasurfaces: Impact of Initial Geometric Layout. Opt. Lett. 2017, 42, 3161–3164. [Google Scholar] [CrossRef]
- Sigmund, O.; Hougaard, K. Geometric Properties of Optimal Photonic Crystals. Phys. Rev. Lett. 2008, 100, 153904. [Google Scholar] [CrossRef]
- Men, H.; Lee, K.Y.K.; Freund, R.M.; Peraire, J.; Johnson, S.G. Robust Topology Optimization of Three-Dimensional Photonic-Crystal Band-Gap Structures. Opt. Express 2014, 22, 22632–22648. [Google Scholar] [CrossRef]
- Minkov, M.; Williamson, I.A.D.; Andreani, L.C.; Gerace, D.; Lou, B.; Song, A.Y.; Hughes, T.W.; Fan, S. Inverse Design of Photonic Crystals through Automatic Differentiation. ACS Photonics 2020, 7, 1729–1741. [Google Scholar] [CrossRef]
- Vercruysse, D.; Sapra, N.V.; Su, L.; Vuckovic, J. Dispersion Engineering with Photonic Inverse Design. IEEE J. Sel. Top. Quantum Electron. 2020, 26, 1–6. [Google Scholar] [CrossRef]
- Lin, Z.; Pick, A.; Lončar, M.; Rodriguez, A.W. Enhanced Spontaneous Emission at Third-Order Dirac Exceptional Points in Inverse-Designed Photonic Crystals. Phys. Rev. Lett. 2016, 117, 107402. [Google Scholar] [CrossRef]
- Vial, B. Nannos. Zenodo. 2022. Available online: https://doi.org/10.5281/zenodo.6636104 (accessed on 17 October 2022).
- Vial, B. Protis. Zenodo. 2022. Available online: https://doi.org/10.5281/zenodo.6636141 (accessed on 17 October 2022).
- Ruppin, R. Scattering of Electromagnetic Radiation by a Perfect Electromagnetic Conductor Cylinder. J. Electromagn. Waves Appl. 2006, 20, 1853–1860. [Google Scholar] [CrossRef]
- Jandieri, V.; Meng, P.; Yasumoto, K.; Liu, Y. Scattering of Light by Gratings of Metal-Coated Nanocylinders on Dielectric Substrate. J. Opt. Soc. Am. A 2015, 32, 1384. [Google Scholar] [CrossRef]
- Joannopoulos, J.D.; Johnson, S.G.; Winn, J.N.; Meade, R.D. Photonic Crystals: Molding the Flow of Light, 2nd ed.; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vial, B.; Hao, Y. Open-Source Computational Photonics with Auto Differentiable Topology Optimization. Mathematics 2022, 10, 3912. https://doi.org/10.3390/math10203912
Vial B, Hao Y. Open-Source Computational Photonics with Auto Differentiable Topology Optimization. Mathematics. 2022; 10(20):3912. https://doi.org/10.3390/math10203912
Chicago/Turabian StyleVial, Benjamin, and Yang Hao. 2022. "Open-Source Computational Photonics with Auto Differentiable Topology Optimization" Mathematics 10, no. 20: 3912. https://doi.org/10.3390/math10203912
APA StyleVial, B., & Hao, Y. (2022). Open-Source Computational Photonics with Auto Differentiable Topology Optimization. Mathematics, 10(20), 3912. https://doi.org/10.3390/math10203912






