Parametric Distributions for Survival and Reliability Analyses, a Review and Historical Sketch
Abstract
1. Introduction
2. Fundamentals of Survival Analysis
2.1. Definition of Survival Time
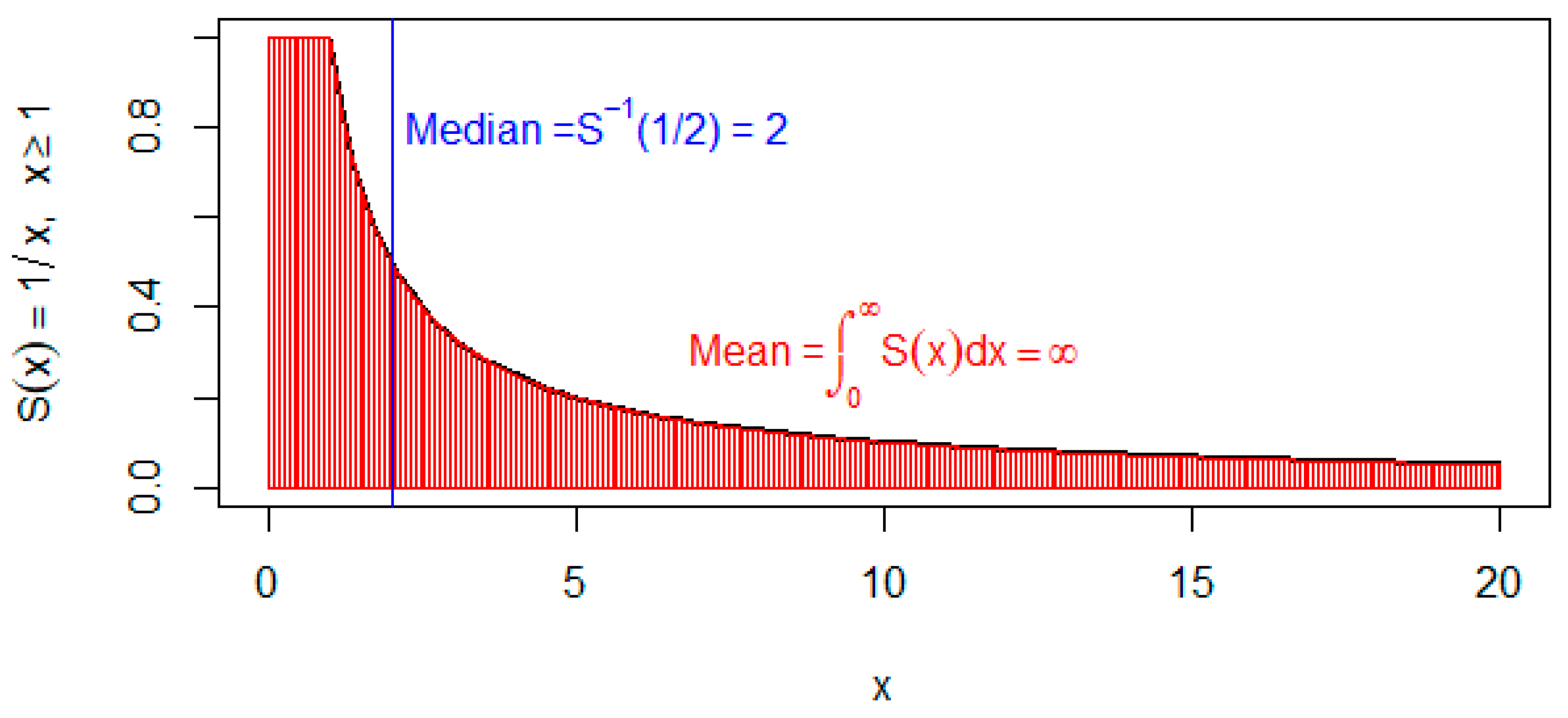
2.2. Survival Function
2.3. Hazard Function
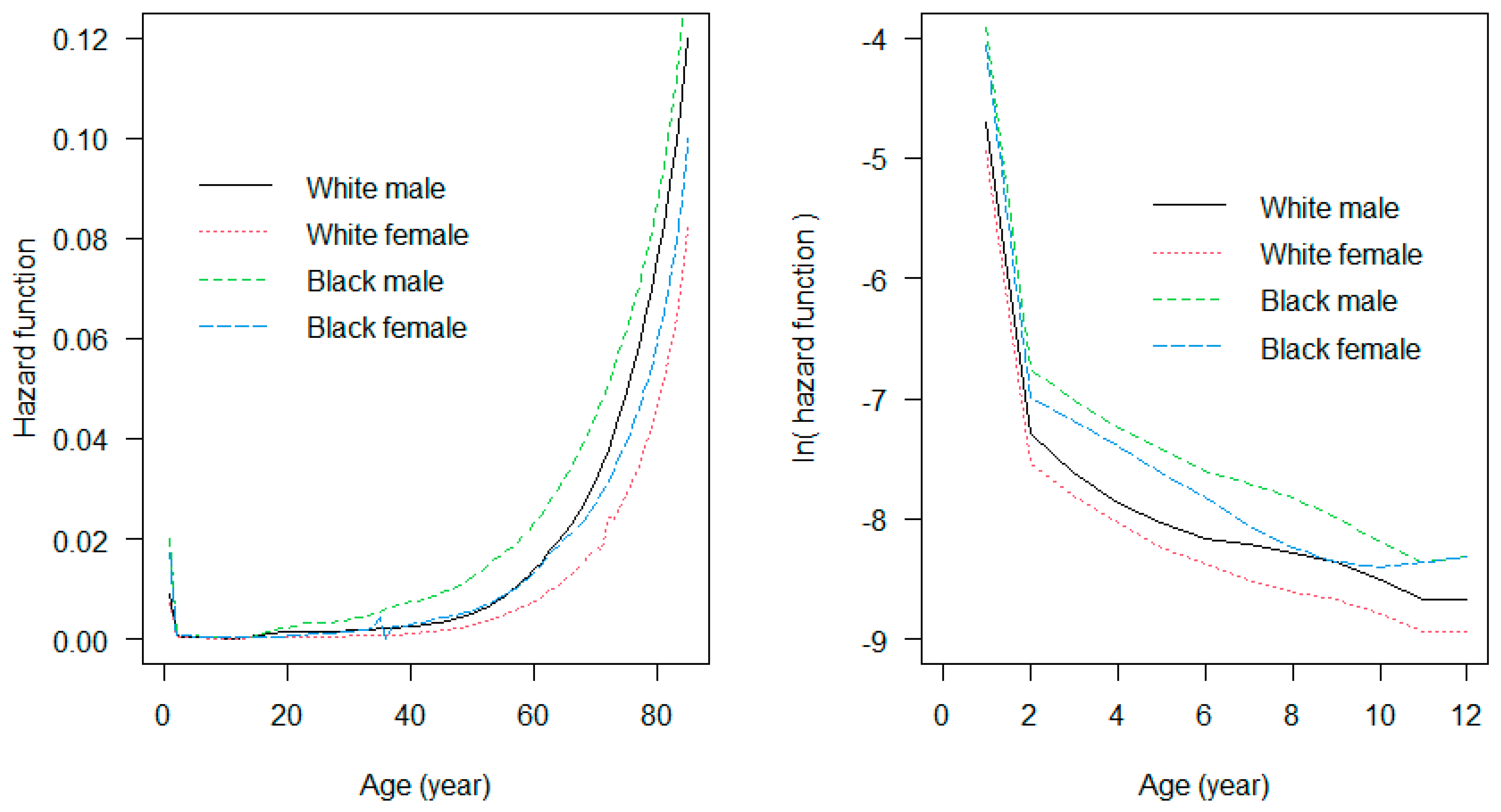
2.4. Shape of Hazard Function
3. Parametric Models
3.1. Exponential Distribution and Its Variants
3.2. Weibull Distribution
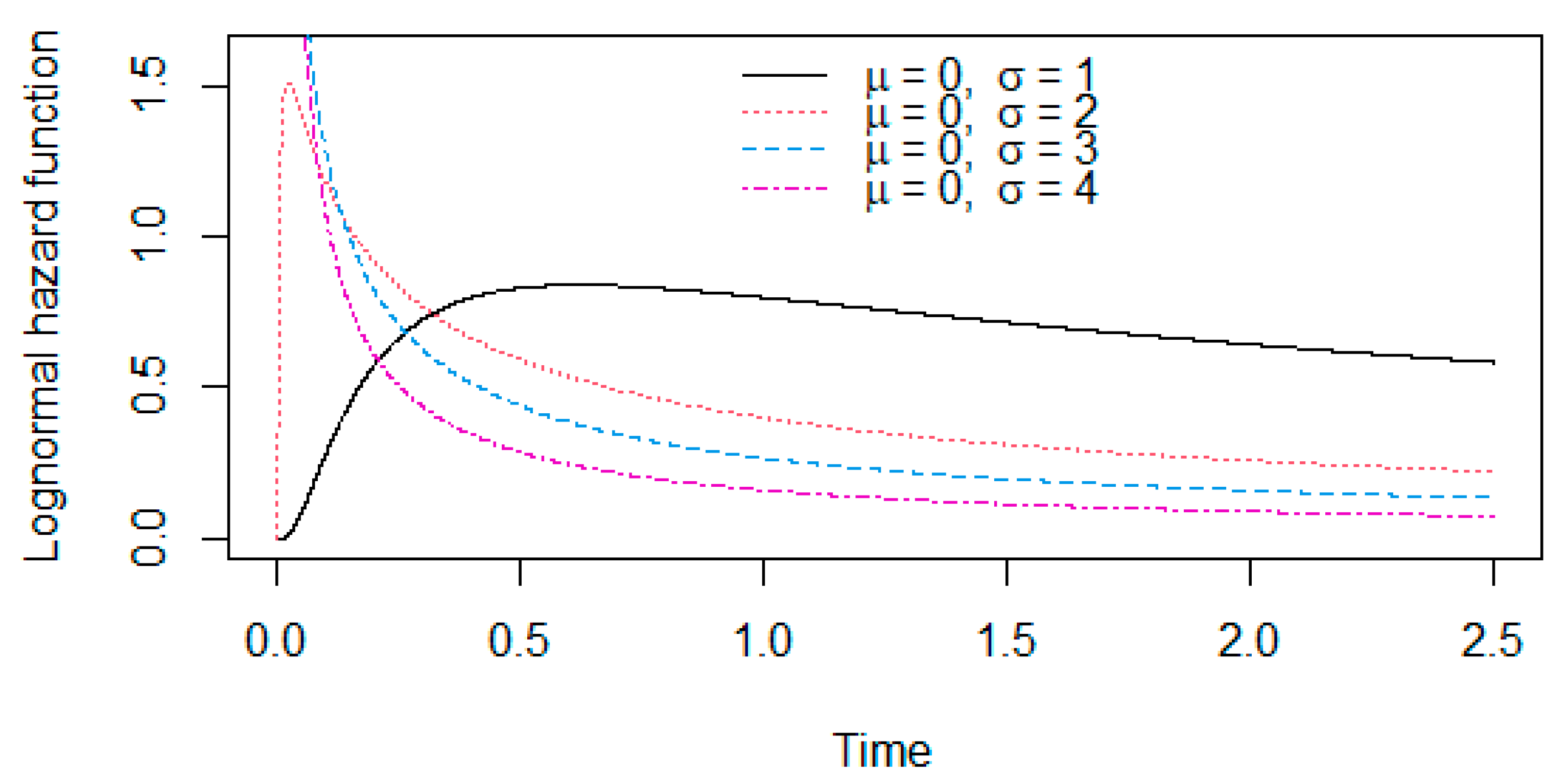
3.3. Lognormal Distribution
3.4. Log-Logistic Distribution
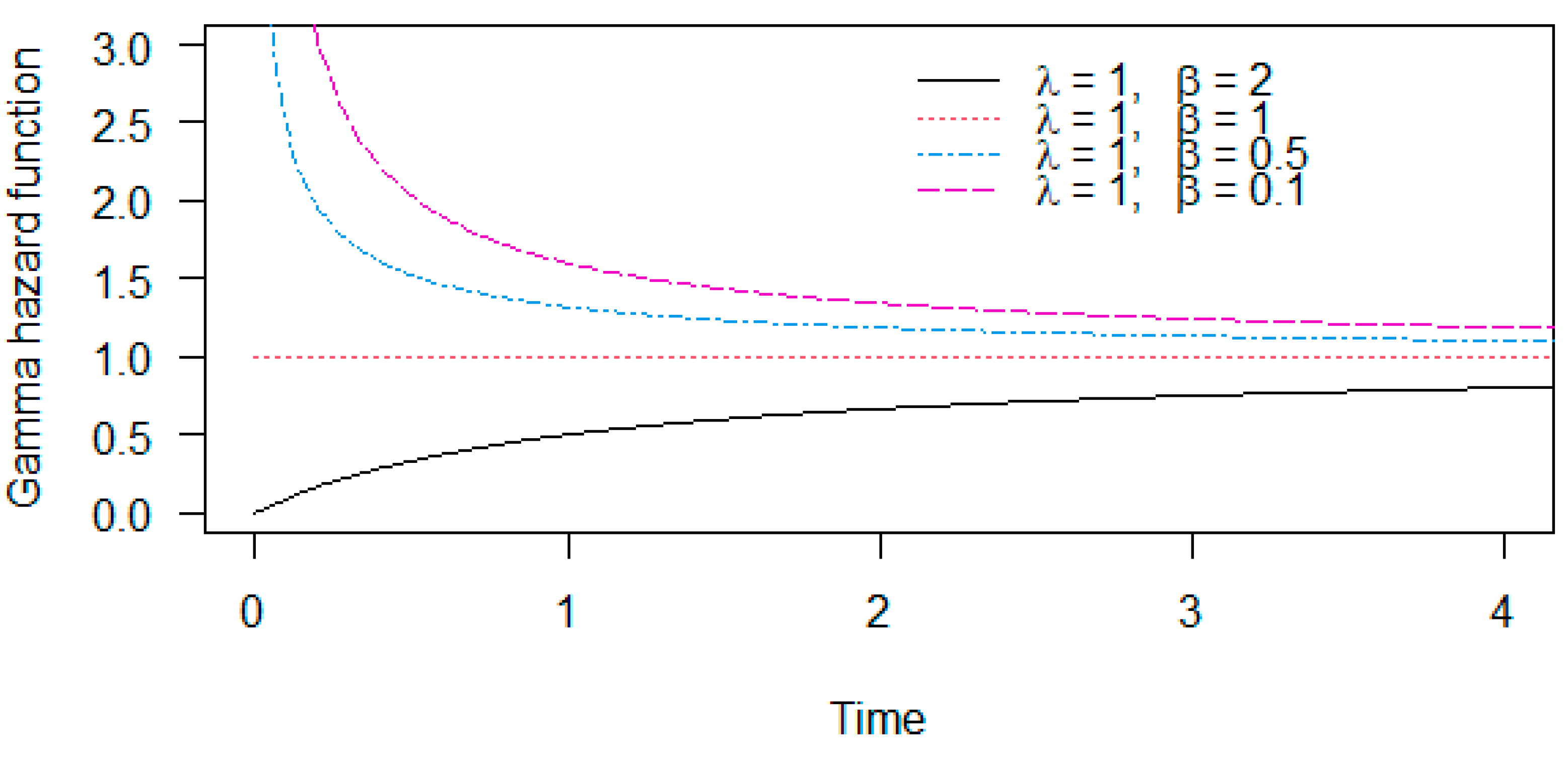
3.5. Gamma Distribution
3.6. Generalized Gamma Distribution
3.7. Burr Distributions
3.8. Pareto Distributions
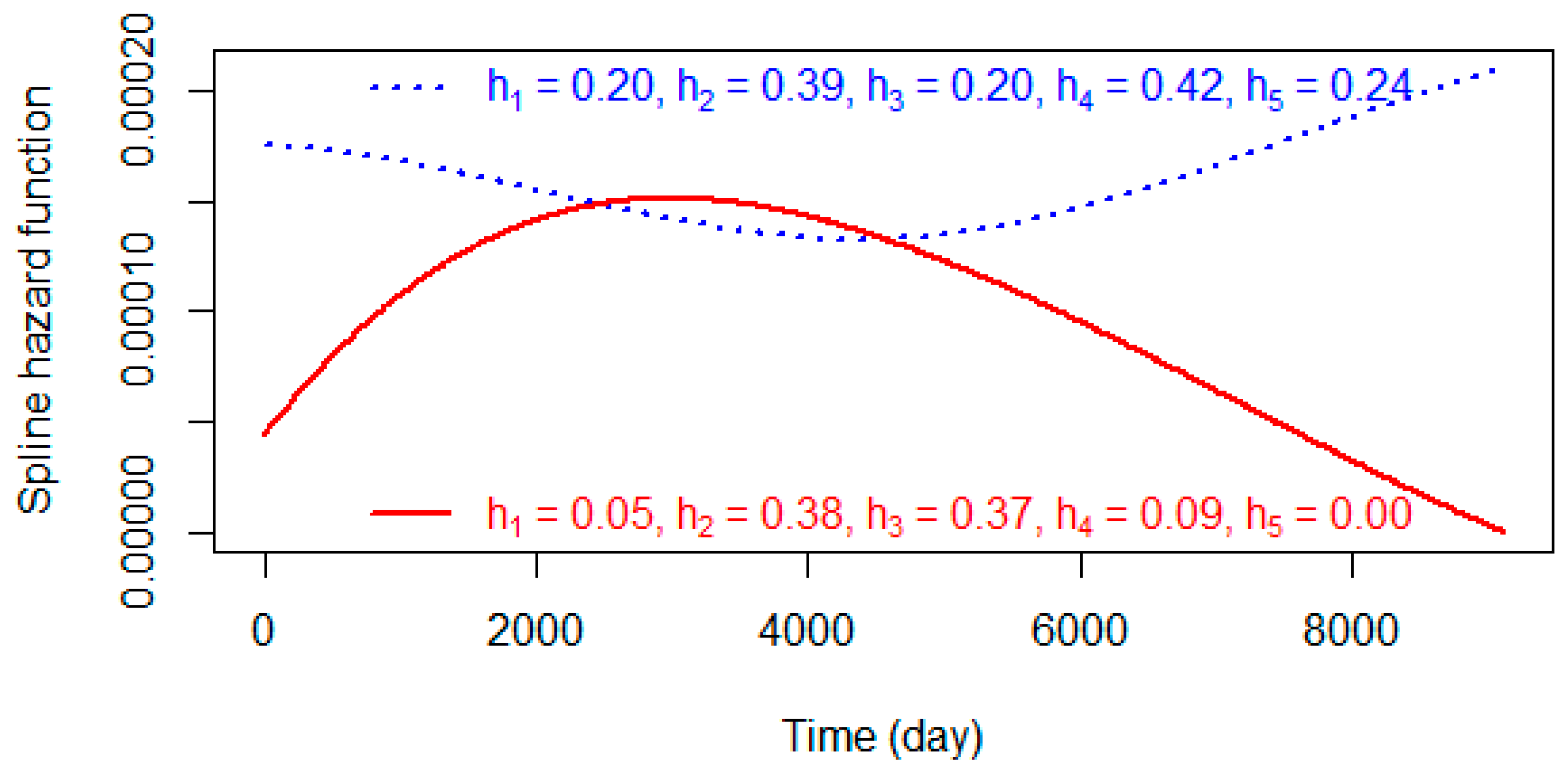
3.9. Spline Distributions
3.10. Other Distributions
4. Data Analysis
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. How We Searched a List of Parametric Distributions?
Appendix B. Five-Parameter Spline Basis Functions
Appendix C. Maximum Likelihood Estimator (MLE)
- The exponential distribution:
- The Weibull distribution:
- The lognormal distribution:
- The Pareto type I distribution:
References
- Halley, E. An estimate of the degrees of the mortality of mankind, drawn from curious tables of the births and funerals at the city of Breslaw; with an attempt to ascertain the price of annuities upon lives. Phil. Trans. R. Soc. London 1693, 17, 596–610. [Google Scholar] [CrossRef]
- Bellhouse, D.R. A new look at Halley’s life table. J. R. Stat. Soc. Ser. A 2011, 174, 823–832. [Google Scholar] [CrossRef]
- Bernoulli, D. Essai d’une Nouvelle Analyse de la Mortalite Cause e par la Petite Verole, et des Avantages de L’inoculation pour le Prevenir; Histoire avec le Memoires; Academie Royal des Sciences: Paris, France, 1760; pp. 11–45. [Google Scholar]
- Kalbfleisch, J.D.; Prentice, R.L. The Statistical Analysis of Failure Time Data, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2002. [Google Scholar]
- Klein, J.P.; Moeschberger, M.L. Survival Analysis: Techniques for Censored and Truncated Data, 2nd ed.; Springer: New York, NY, USA, 2003. [Google Scholar]
- Collett, D. Modelling Survival Data in Medical Research, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Commenges, D.; Jacqmin-Gadda, H. Dynamical Biostatistical Models; CRC Press: Boca Raton, FL, USA, 2015; Volume 86. [Google Scholar]
- Emura, T.; Chen, Y.H. Analysis of Survival Data with Dependent Censoring: Copula-Based Approaches; Springer: Singapore, 2018. [Google Scholar]
- Emura, T.; Matsui, S.; Rondeau, V. Survival Analysis with Correlated Endpoints, Joint Frailty-Copula Models; JSS Research Series in Statistics; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Cohen, A.C.; Whitten, B.J. Parameter Estimation in Reliability and Life Span Models; CRC Press: Boca Raton, FL, USA, 1988. [Google Scholar]
- Cohen, A.C. Truncated and Censored Samples: Theory and Applications; CRC Press: Boca Raton, FL, USA, 1991. [Google Scholar]
- Lawless, J.F. Statistical Models and Methods for Lifetime Data; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Nelson, W.B. Applied Life Data Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2003; Volume 521. [Google Scholar]
- Nelson, W.B. Accelerated Testing: Statistical Models, Test Plans, and Data Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Meeker, W.Q.; Escobar, L.A.; Pascual, F.G. Statistical Methods for Reliability Data; John Wiley & Sons: Hoboken, NJ, USA, 1998. [Google Scholar]
- Cox, D.R.; Oakes, D. Analysis of Survival Data; Chapman: London, UK; Hall/CRC: Boca Raton, FL, USA, 1984. [Google Scholar]
- Klein, J.P.; Van Houwelingen, H.C.; Ibrahim, J.G.; Scheike, T.H. (Eds.) Handbook of Survival Analysis; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Johnson, N.L.; Kotz, S.; Balakrishnan, N. Continuous Univariate Distributions, Volume 1; John Wiley & Sons: Hoboken, NJ, USA, 1994. [Google Scholar]
- Johnson, N.L.; Kotz, S.; Balakrishnan, N. Continuous Univariate Distributions, Volume 2; John Wiley & Sons: Hoboken, NJ, USA, 1995. [Google Scholar]
- Balakrishnan, N.; Nevzorov, V.B. A Primer on Statistical Distributions; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Krishnamoorthy, K. Handbook of Statistical Distributions with Applications; Chapman & Hall: London, UK, 2006. [Google Scholar]
- Shewa, F.; Endale, S.; Nugussu, G.; Abdisa, J.; Zerihun, K.; Banbeta, A. Time to Kidneys Failure Modeling in the Patients at Adama Hospital Medical College: Application of Copula Model. J. Res. Health Sci. 2022, 22, e00549. [Google Scholar] [CrossRef]
- Huang, X.; Xu, J. Subgroup Identification and Regression Analysis of Clustered and Heterogeneous Interval-Censored Data. Mathematics 2022, 10, 862. [Google Scholar] [CrossRef]
- Huang, X.; Xu, J.; Zhou, Y. Profile and Non-Profile MM Modeling of Cluster Failure Time and Analysis of ADNI Data. Mathematics 2022, 10, 538. [Google Scholar] [CrossRef]
- Lipowski, C.; Lo, S.; Shi, S.; Wilke, R.A. Competing risks regression with dependent multiple spells: Monte Carlo evidence and an application to maternity leave. Jpn. J. Stat. Data Sci. 2021, 4, 953–981. [Google Scholar] [CrossRef]
- Scheike, T.H.; Keiding, N. Design and analysis of time-to-pregnancy. Stat. Method Med. Res. 2006, 15, 127–140. [Google Scholar] [CrossRef]
- Emura, T.; Wang, H. Approximate tolerance limits under the log-location-scale models in the presence of censoring. Technometrics 2010, 52, 313–323. [Google Scholar] [CrossRef]
- Chiang, J.Y.; Lio, Y.L.; Ng, H.K.T.; Tsai, T.R.; Li, T. Robust bootstrap control charts for percentiles based on model selection approaches. Comp. Indus. Eng. 2018, 123, 119–133. [Google Scholar] [CrossRef]
- Wong, K.L. The physical basis for the roller-coaster hazard rate curve for electronics. Qual. Reliab. Eng. Int. 1991, 7, 489–495. [Google Scholar] [CrossRef]
- Andreopoulos, P.; Bersimis, G.F.; Tragaki, A.; Rovolis, A. Mortality modeling using probability distributions. Application in Greek mortality data. Commun. Stat. Theory Methods 2019, 48, 127–140. [Google Scholar] [CrossRef]
- Olkin, I. Life distributions: A brief discussion. Comm. Stat. Simul. Comp. 2016, 45, 1489–1498. [Google Scholar] [CrossRef]
- Shih, J.H.; Emura, T. Penalized Cox regression with a five-parameter spline model. Commun. Stat. Theory Methods 2021, 50, 3749–3768. [Google Scholar] [CrossRef]
- Thach, T.T. A Three-Component Additive Weibull Distribution and Its Reliability Implications. Symmetry 2022, 14, 1455. [Google Scholar] [CrossRef]
- Nelson, W.B. Theory and applications of hazard plotting for censored failure data. Technometrics 1972, 14, 945–966. [Google Scholar] [CrossRef]
- Li, H.; Wen, D.; Lu, Z.; Wang, Y.; Deng, F. Identifying the probability distribution of fatigue life using the maximum entropy principle. Entropy 2016, 18, 111. [Google Scholar] [CrossRef]
- Gupta, R.D.; Kundu, D. Generalized exponential distributions. Aust. New Zealand J. Stat. 1999, 41, 173–188. [Google Scholar] [CrossRef]
- Nadarajah, S.; Gupta, A.K. On the moments of the exponentiated Weibull distribution. Commun. Stat. Theory Methods 2005, 34, 253–256. [Google Scholar] [CrossRef]
- Carrasco, J.M.; Ortega, E.M.; Cordeiro, G.M. A generalized modified Weibull distribution for lifetime modeling. Comp. Stat. Data Anal. 2008, 53, 450–462. [Google Scholar] [CrossRef]
- Epstein, B. Estimation from life test data. Technometrics 1960, 2, 447–454. [Google Scholar] [CrossRef]
- Weißbach, R.; Wied, D. Truncating the exponential with a uniform distribution. Stat. Pap. 2021, 63, 1247–1270. [Google Scholar] [CrossRef]
- Weißbach, R.; Dörre, A. Retrospective sampling of survival data based on a Poisson birth process: Conditional maximum likelihood. Statistics 2022, 56, 844–866. [Google Scholar] [CrossRef]
- Li, Z.; Chinchilli, V.M.; Wang, M. A Bayesian joint model of recurrent events and a terminal event. Biom. J. 2019, 61, 187–202. [Google Scholar] [CrossRef] [PubMed]
- Ling, M.H. Optimal constant-stress accelerated life test plans for one-shot devices with components having exponential lifetimes under gamma frailty models. Mathematics 2022, 10, 840. [Google Scholar] [CrossRef]
- Hu, J.; Zhuang, Y.; Goldiner, C. Fixed-accuracy confidence interval estimation of P (X <Y) under a geometric–exponential model. Jpn. J. Stat. Data Sci. 2021, 4, 1079–1104. [Google Scholar]
- Wang, Y.; Yan, Z.; Chen, Y. E-Bayesian and H-Bayesian Inferences for a Simple Step-Stress Model with Competing Failure Model under Progressively Type-II Censoring. Entropy 2022, 24, 1405. [Google Scholar] [CrossRef]
- Smith, R.M.; Bain, L.J. An exponential power life-testing distribution. Commun. Stat. Theory Methods 1975, 4, 469–481. [Google Scholar]
- Furukawa, K.; Preston, D.L.; Misumi, M.; Cullings, H.M. Handling incomplete smoking history data in survival analysis. Stat. Method Med. Res. 2017, 26, 707–723. [Google Scholar] [CrossRef]
- Emura, T.; Michimae, H. A copula-based inference to piecewise exponential models under dependent censoring, with application to time to metamorphosis of salamander larvae. Environ. Ecol. Stat. 2017, 24, 151–173. [Google Scholar] [CrossRef]
- Schneider, S.; Demarqui, F.N.; Colosimo, E.A.; Mayrink, V.D. An approach to model clustered survival data with dependent censoring. Biom. J. 2020, 62, 157–174. [Google Scholar] [CrossRef]
- Schneider, S.; Demarqui, F.N.; de Freitas Costa, E. Free-ranging dogs’ lifetime estimated by an approach for long-term survival data with dependent censoring. Environ. Ecol. Stat. 2022, 1–43. [Google Scholar] [CrossRef]
- Zhang, Z.; Charalambous, C.; Foster, P. A Gaussian copula joint model for longitudinal and time-to-event data with random effects. arXiv 2022, arXiv:2112.01941. [Google Scholar]
- Rosin, P.; Rammler, E. The laws governing the fineness of powdered coal. J. Inst. Fuel 1933, 7, 29–36. [Google Scholar]
- Weibull, W. A Statistical Theory of Strength of Materials; Generalstabens Litografiska Anstalts Förlag: Stockholm, Sweden, 1939. [Google Scholar]
- Weibull, W. A statistical distribution function of wide applicability. J. Appl. Mech. 1951, 18, 293–297. [Google Scholar] [CrossRef]
- Anzures-Cabrera, J.; Hutton, J.L. Competing risks, left truncation and late entry effect in A-bomb survivors cohort. J. Appl. Stat. 2010, 37, 821–831. [Google Scholar] [CrossRef][Green Version]
- Fan, T.H.; Wang, Y.F.; Ju, S.K. A competing risks model with multiply censored reliability data under multivariate Weibull distributions. IEEE Trans. Reliab. 2019, 68, 462–475. [Google Scholar] [CrossRef]
- Wang, Y.C.; Emura, T.; Fan, T.H.; Lo, S.M.; Wilke, R.A. Likelihood-based inference for a frailty-copula model based on competing risks failure time data. Qual. Reliab. Eng. Int. 2020, 36, 1622–1638. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, C.; Tripathi, Y.M.; Dey, S.; Wu, S.J. Reliability analysis of Weibull multicomponent system with stress-dependent parameters from accelerated life data. Qual. Reliab. Eng. Int. 2021, 37, 2603–2621. [Google Scholar] [CrossRef]
- Shu, M.H.; Wu, C.W.; Hsu, B.M.; Wang, T.C. Standardized lifetime-capability and warranty-return-rate-based suppliers qualification and selection with accelerated Weibull-life type II testing data. Commun. Stat. Theory Methods 2022, 51, 8186–8204. [Google Scholar] [CrossRef]
- Emura, T.; Pan, C.H. Parametric likelihood inference and goodness-of-fit for dependently left-truncated data, a copula-based approach. Stat. Pap. 2020, 61, 479–501. [Google Scholar] [CrossRef]
- Michimae, H.; Emura, T. Likelihood Inference for Copula Models Based on Left-Truncated and Competing Risks Data from Field Studies. Mathematics 2022, 10, 2163. [Google Scholar] [CrossRef]
- Wu, B.H.; Michimae, H.; Emura, T. Meta-analysis of individual patient data with semi-competing risks under the Weibull joint frailty–copula model. Comput. Stat. 2020, 35, 1525–1552. [Google Scholar] [CrossRef]
- Shinohara, S.; Lin, Y.H.; Michimae, H.; Emura, T. Dynamic lifetime prediction using a Weibull-based bivariate failure time model: A meta-analysis of individual-patient data. Comm. Stat. Simul Comp. 2020, 1–20. [Google Scholar] [CrossRef]
- Huang, X.W.; Wang, W.; Emura, T. A copula-based Markov chain model for serially dependent event times with a dependent terminal event. Jpn. J. Stat. Data Sci. 2021, 4, 917–951. [Google Scholar] [CrossRef]
- Zhang, Z.; Charalambous, C.; Foster, P. Joint modelling of longitudinal measurements and survival times via a multivariate copula approach. J. Appl. Stat. 2022, 1–21. [Google Scholar] [CrossRef]
- Lee, L. Multivariate distributions having Weibull properties. J Mult. Anal. 1979, 9, 267–277. [Google Scholar] [CrossRef]
- Yeh, H.C. Characterizations of the general multivariate Weibull distributions. Commun. Stat. Theory Methods 2012, 41, 76–87. [Google Scholar] [CrossRef]
- Kundu, D.; Gupta, A.K. Bayes estimation for the Marshall–Olkin bivariate Weibull distribution. Comp. Stat. Data Anal. 2013, 57, 271–281. [Google Scholar] [CrossRef]
- Rehman, H.; Chandra, N. Inferences on cumulative incidence function for middle censored survival data with Weibull regression. Jpn. J. Stat. Data Sci. 2022, 5, 65–86. [Google Scholar] [CrossRef]
- Gupta, S.S. Life test sampling plans for normal and lognormal distributions. Technometrics 1962, 4, 151–175. [Google Scholar] [CrossRef]
- Emura, T.; Shiu, S.-K. Estimation and model selection for left-truncated and right-censored lifetime data with application to electric power transformers analysis. Commun. Stat.Simul. 2016, 45, 3171–3189. [Google Scholar] [CrossRef]
- Ranjan, R.; Sen, R.; Upadhyay, S.K. Bayes analysis of some important lifetime models using MCMC based approaches when the observations are left truncated and right censored. Reliab. Eng. Syst. Saf. 2021, 214, 107747. [Google Scholar] [CrossRef]
- Dörre, A.; Huang, C.Y.; Tseng, Y.K.; Emura, T. Likelihood-based analysis of doubly-truncated data under the location-scale and AFT model. Comp. Stat. 2021, 36, 375–408. [Google Scholar] [CrossRef]
- Emura, T.; Michimae, H. Left-truncated and right-censored field failure data: Review of parametric analysis for reliability. Qual. Reliab. Eng. Int. 2022, 24, 151–173. [Google Scholar] [CrossRef]
- Aldeni, M.; Wagaman, J.; Amezziane, M.; Ahmed, S.E. Pretest and shrinkage estimators for log-normal means. Comput. Stat. 2022, 1–24. [Google Scholar] [CrossRef]
- Dey, A.K.; Kundu, D. Discriminating between the log-normal and log-logistic distributions. Commun. Stat. Theory Methods 2009, 39, 280–292. [Google Scholar] [CrossRef]
- de Freitas Costa, E.; Schneider, S.; Carlotto, G.B.; Cabalheiro, T.; de Oliveira Júnior, M.R. Zero-inflated-censored Weibull and gamma regression models to estimate wild boar population dispersal distance. Jpn. J. Stat. Data Sci. 2021, 4, 1133–1155. [Google Scholar] [CrossRef]
- Dörre, A. Bayesian estimation of a lifetime distribution under double truncation caused by time-restricted data collection. Stat. Pap. 2020, 61, 945–965. [Google Scholar] [CrossRef]
- Dörre, A. Semiparametric likelihood inference for heterogeneous survival data under double truncation based on a Poisson birth process. Jpn. J. Stat. Data Sci. 2021, 4, 1203–1226. [Google Scholar] [CrossRef]
- Stacy, E.W. A generalization of the gamma distribution. Ann. Math. Stat. 1962, 3, 1187–1192. [Google Scholar] [CrossRef]
- Stacy, E.W.; Mihram, G.A. Parameter estimation for a generalized gamma distribution. Technometrics 1965, 7, 349–358. [Google Scholar] [CrossRef]
- Özsoy, V.S.; Ünsal, M.G.; Örkcü, H.H. Use of the heuristic optimization in the parameter estimation of generalized gamma distribution: Comparison of GA, DE, PSO and SA methods. Comput. Stat. 2020, 35, 1895–1925. [Google Scholar] [CrossRef]
- Farewell, V.T.; Prentice, R.L. A study of distributional shape in life testing. Technometrics 1977, 19, 69–75. [Google Scholar]
- Balakrishnan, N.; Pal, S. An EM algorithm for the estimation of parameters of a flexible cure rate model with generalized gamma lifetime and model discrimination using likelihood-and information-based methods. Comp. Stat. 2015, 30, 151–189. [Google Scholar] [CrossRef]
- He, Z.; Emura, T. The COM-Poisson cure rate model for survival data-computational aspects. J. Chin. Stat. Assoc. 2019, 57, 1–42. [Google Scholar]
- Burr, I.W. Cumulative frequency functions. Ann. Math. Stat. 1942, 13, 215–232. [Google Scholar] [CrossRef]
- Nadarajah, S.; Pogány, T.K.; Saxena, R.K. On the characteristic function for Burr distributions. Statistics 2012, 46, 419–428. [Google Scholar] [CrossRef]
- Lindsay, S.R.; Wood, G.R.; Woollons, R.C. Modelling the diameter distribution of forest stands using the Burr distribution. J. Appl. Stat. 1996, 23, 609–620. [Google Scholar] [CrossRef]
- Paranaíba, P.F.; Ortega, E.M.; Cordeiro, G.M.; Pescim, R.R. The beta Burr XII distribution with application to lifetime data. Comp. Stat. Data Anal. 2011, 55, 1118–1136. [Google Scholar] [CrossRef]
- Elbatal, I.; Khan, S.; Hussain, T.; Elgarhy, M.; Alotaibi, N.; Semary, H.E.; Abdelwahab, M.M. A New Family of Lifetime Models: Theoretical Developments with Applications in Biomedical and Environmental Data. Axioms 2022, 11, 361. [Google Scholar] [CrossRef]
- Lio, Y.; Tsai, T.R.; Wang, L.; Cecilio Tejada, I.P. Inferences of the Multicomponent Stress–Strength Reliability for Burr XII Distributions. Mathematics 2022, 10, 2478. [Google Scholar] [CrossRef]
- Escarela, G.; Carriere, J.F. Fitting competing risks with an assumed copula. Stat. Method Med. Res. 2003, 12, 333–349. [Google Scholar] [CrossRef]
- Almuhayfith, F.E.; Darwish, J.A.; Alharbi, R.; Marin, M. Burr XII Distribution for Disease Data Analysis in the Presence of a Partially Observed Failure Mode. Symmetry 2022, 14, 1298. [Google Scholar] [CrossRef]
- Dagum, C. A Model of Income Distribution and the Conditions of Existence of Moments of Finite Order. Bull. Int. Stat. Inst. 1975, 46, 199–205. [Google Scholar]
- Domma, F.; Giordano, S.; Zenga, M.A. Maximum likelihood estimation in dagum distribution from censored samples. J. Appl. Statist. 2011, 38, 2971–2985. [Google Scholar] [CrossRef]
- Domma, F.; Latorre, G.; Zenga, M.A. Reliablity studies of Dagum distribution. Stat. E Appl. 2012, 10, 97–113. [Google Scholar]
- Domma, F.; Condino, F. The beta-Dagum distribution: Definition and properties. Commun. Stat. Theory Methods 2013, 42, 4070–4090. [Google Scholar] [CrossRef]
- Mokhlis, N.A. Reliability of a stress-strength model with Burr type III distributions. Commun. Stat. Theory Methods 2005, 34, 1643–1657. [Google Scholar] [CrossRef]
- Domma, F.; Giordano, S. A copula-based approach to account for dependence in stress-strength models. Stat. Pap. 2013, 54, 807–826. [Google Scholar] [CrossRef]
- Shih, J.H.; Emura, T. Likelihood-based inference for bivariate latent failure time models with competing risks under the generalized FGM copula. Comp. Stat. 2018, 33, 1293–1323. [Google Scholar] [CrossRef]
- Shih, J.H.; Emura, T. Bivariate dependence measures and bivariate competing risks models under the generalized FGM copula. Stat. Pap. 2019, 60, 1101–1118. [Google Scholar] [CrossRef]
- Domma, F. Some properties of the bivariate Burr type III distribution. Statistics 2010, 44, 203–215. [Google Scholar] [CrossRef]
- Jenkins, S.P. Pareto models, top incomes and recent trends in UK income inequality. Economica 2017, 84, 261–289. [Google Scholar] [CrossRef]
- Amin, Z.H. Bayesian inference for the Pareto lifetime model under progressive censoring with binomial removals. J. Appl. Stat. 2008, 35, 1203–1217. [Google Scholar] [CrossRef]
- Lin, Y.H.; Sun, L.H.; Tseng, Y.J.; Emura, T. The Pareto type I joint frailty-copula model for clustered bivariate survival data. Comm. Stat. Simul Comp. 2022, 1–25. [Google Scholar] [CrossRef]
- Saldaña-Zepeda, D.P.; Vaquera-Huerta, H.; Arnold, B.C. A goodness of fit test for the Pareto distribution in the presence of type II censoring, based on the cumulative hazard function. Comp. Stat. Data Anal. 2010, 54, 833–842. [Google Scholar] [CrossRef]
- Lomax, K.S. Business failures. Another example of the analysis of failure data. J. Am. Statist. Assoc. 1954, 49, 847–852. [Google Scholar] [CrossRef]
- Mitra, D.; Kundu, D.; Balakrishnan, N. Likelihood analysis and stochastic EM algorithm for left truncated right censored data and associated model selection from the Lehmann family of life distributions. Jpn. J. Stat. Data Sci. 2021, 4, 1019–1048. [Google Scholar] [CrossRef]
- Lindley, D.V.; Singpurwalla, N.D. Multivariate distributions for the reliability of a system of components having a common environment. J. Appl. Probab. 1986, 23, 418–431. [Google Scholar] [CrossRef]
- Sankaran, P.G.; Nair, N.U. A bivariate Pareto model and its applications to reliability. Naval. Res. Logist. 1993, 40, 1013–1020. [Google Scholar] [CrossRef]
- Noughabi, M.S.; Kayid, M. Bivariate quantile residual life: A characterization theorem and statistical properties. Stat. Pap. 2019, 60, 2001–2012. [Google Scholar] [CrossRef]
- Sankaran, P.G.; Kundu, D. A bivariate Pareto model. Statistics 2014, 48, 241–255. [Google Scholar] [CrossRef]
- Shih, J.H.; Lee, W.; Sun, L.H.; Emura, T. Fitting competing risks data to bivariate Pareto models. Commun. Stat. Theory Methods 2019, 48, 1193–1220. [Google Scholar] [CrossRef]
- Mardia, K.V. Families of Bivariate Distributions; No. 27; Lubrecht & Cramer Limited: Port Jervis, NY, USA, 1970. [Google Scholar]
- Klotz, J. Spline smooth estimates of survival. Surviv. Anal. Lect. Notes-Monogr. Ser. 1982, 2, 14–25. [Google Scholar]
- Jarjoura, D. Smoothing hazard rates with cubic splines. Commun. Stat. Simul. Comput. 1988, 17, 377–392. [Google Scholar] [CrossRef]
- O’Sullivan, F. Fast computation of fully automated log-density and log-hazard estimation. SIAM J. Sci. Stat. Comput. 1988, 9, 363–379. [Google Scholar] [CrossRef]
- Ramsay, J.O. Monotone regression splines in action. Stat. Sci. 1988, 3, 425–441. [Google Scholar] [CrossRef]
- Kwon, S.; Ha, I.D.; Shih, J.H.; Emura, T. Flexible parametric copula modeling approaches for clustered survival data. Pharm. Stat. 2022, 21, 69–88. [Google Scholar] [CrossRef]
- Emura, T.; Nakatochi, M.; Murotani, K.; Rondeau, V. A joint frailty-copula model between tumour progression and death for meta-analysis. Stat. Method. Med. Res. 2017, 26, 2649–2666. [Google Scholar] [CrossRef]
- Emura, T.; Shih, J.H.; Ha, I.D.; Wilke, R.A. Comparison of the marginal hazard model and the sub-distribution hazard model for competing risks under an assumed copula. Stat. Method. Med. Res. 2020, 29, 2307–2327. [Google Scholar] [CrossRef]
- Emura, T.; Michimae, H.; Matsui, S. Dynamic risk prediction via a joint frailty-copula model and IPD meta-analysis: Building web applications. Entropy 2022, 24, 589. [Google Scholar] [CrossRef] [PubMed]
- Birnbaum, Z.W.; Saunders, S.C. A new family of life distributions. J. Appl. Prob. 1969, 6, 319–327. [Google Scholar] [CrossRef]
- Achcar, J.A. Inferences for the Birnbaum—Saunders fatigue life model using Bayesian methods. Comp. Stat. Data Anal. 1993, 15, 367–380. [Google Scholar] [CrossRef]
- Wang, M.; Zhao, J.; Sun, X.; Park, C. Robust explicit estimation of the two-parameter Birnbaum–Saunders distribution. J. Appl. Stat. 2013, 40, 2259–2274. [Google Scholar] [CrossRef]
- Wang, M.; Sun, X.; Park, C. Bayesian analysis of Birnbaum–Saunders distribution via the generalized ratio-of-uniforms method. Comp. Stat. 2016, 31, 207–225. [Google Scholar] [CrossRef]
- Teimouri, M. Fast Bayesian inference for Birnbaum-Saunders distribution. Comp. Stat. 2022, 1–33. [Google Scholar] [CrossRef]
- Hjorth, U. A reliability distribution with increasing, decreasing, constant and bathtub-shaped failure rates. Technometrics 1980, 22, 99–107. [Google Scholar] [CrossRef]
- Demirci Bicer, H.; Bicer, C.; Bakouch, H.S.H. A geometric process with Hjorth marginal: Estimation, discrimination, and reliability data modeling. Qual. Reliab. Eng. Int. 2022, 38, 2795–2819. [Google Scholar] [CrossRef]
- Mudholkar, G.S.; Srivastava, D.K.; Freimer, M. The exponentiated Weibull family: A reanalysis of the bus-motor-failure data. Technometrics 1995, 37, 436–445. [Google Scholar] [CrossRef]
- Sattari, M.; Haidari, A.; Barmalzan, G. Orderings for series and parallel systems comprising heterogeneous new extended Weibull components. Commun. Stat. Theory Methods. 2022, 1–16. [Google Scholar] [CrossRef]
- Tahmasbi, R.; Rezaei, S. A two-parameter lifetime distribution with decreasing failure rate. Comput. Stat. Data Anal. 2008, 52, 3889–3901. [Google Scholar] [CrossRef]
- Chesneau, C.; Tomy, L.; Jose, M.; Jayamol, K.V. Odd Exponential-Logarithmic Family of Distributions: Features and Modeling. Math. Comput. Appl. 2022, 27, 68. [Google Scholar] [CrossRef]
- Akaike, H. Information theory and an extension of the maximum likelihood principle. In Selected Papers of Hirotugu Akaike; Springer: New York, NY, USA, 1998; pp. 199–213. [Google Scholar]
- Korkmaz, M.Ç.; Altun, E.; Alizadeh, M.; El-Morshedy, M. The Log Exponential-Power Distribution: Properties, Estimations and Quantile Regression Model. Mathematics 2021, 9, 2634. [Google Scholar] [CrossRef]
- Santoro, K.I.; Gómez, H.J.; Barranco-Chamorro, I.; Gómez, H.W. Extended Half-Power Exponential Distribution with Applications to COVID-19 Data. Mathematics 2022, 10, 942. [Google Scholar] [CrossRef]
- Nayak, T.K. Testing equality of conditionally independent exponential distributions. Commun. Stat. Theory Methods 1988, 17, 807–820. [Google Scholar] [CrossRef]
- Andersen, P.K. Recent developments in survival analysis. Stat. Method Med. Res. 2010, 19, 3–4. [Google Scholar] [CrossRef] [PubMed]
- Datta, S.; del Carmen Pardo, M.; Scheike, T.; Yuen, K.C. Special issue on advances in survival analysis. Comp. Stat. Data Anal. 2016, 93, 255–256. [Google Scholar] [CrossRef]
- Emura, T.; Ha, I.D. Special feature: Recent statistical methods for survival analysis. Jpn. J. Stat. Data Sci. 2018, 4, 889–894. [Google Scholar] [CrossRef]
- Crowder, M.J. Multivariate Survival Analysis and Competing Risks; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Ha, I.D.; Lee, Y. A review of h-likelihood for survival analysis. Jpn. J. Stat. Data Sci. 2021, 4, 1157–1178. [Google Scholar] [CrossRef]
- Su, C.L.; Lin, F.C. Analysis of cyclic recurrent event data with multiple event types. Jpn. J. Stat. Data Sci. 2021, 4, 895–915. [Google Scholar] [CrossRef]
- Li, D.; Hu, X.J.; Wang, R. Evaluating Association Between Two Event Times with Observations Subject to Informative Censoring. J.Am. Stat. Assoc. 2021, 1–3. [Google Scholar] [CrossRef]
- Wang, Y.C.; Emura, T. Multivariate failure time distributions derived from shared frailty and copulas. Jpn. J. Stat. Data Sci. 2021, 4, 1105–1131. [Google Scholar] [CrossRef]
- Kleinbaum, D.G.; Klein, M. Survival Analysis: A Self-Learning Text; Springer: New York, NY, USA, 2012; Volume 3. [Google Scholar]



| Distribution | Parameter | Hazard Function | Survival Function | Expectation |
|---|---|---|---|---|
| Exponential | ||||
| Piecewise Exponential | - | |||
| Weibull | ||||
| Rayleigh | ||||
| Gamma | ||||
| Lognormal | ||||
| Log-logistic | , | |||
| Pareto I | ||||
| Pareto II | ||||
| Pareto IV | ||||
| Hjorth | ||||
| Burr III | ||||
| Burr XII | ||||
| Exponential power | - | |||
| Gompertz | ||||
| Generalized Gamma | ||||
| Birnbaum–Saunders | ||||
| Exponential-logarithmic | ||||
| Generalized-Exponential | Gupta and Kundu [36] | |||
| Exponentiated-Weibull | Nadarajah and Gupta [37] | |||
| G-modified Weibull | Carrasco et al. [38] | |||
| M-spline | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Taketomi, N.; Yamamoto, K.; Chesneau, C.; Emura, T. Parametric Distributions for Survival and Reliability Analyses, a Review and Historical Sketch. Mathematics 2022, 10, 3907. https://doi.org/10.3390/math10203907
Taketomi N, Yamamoto K, Chesneau C, Emura T. Parametric Distributions for Survival and Reliability Analyses, a Review and Historical Sketch. Mathematics. 2022; 10(20):3907. https://doi.org/10.3390/math10203907
Chicago/Turabian StyleTaketomi, Nanami, Kazuki Yamamoto, Christophe Chesneau, and Takeshi Emura. 2022. "Parametric Distributions for Survival and Reliability Analyses, a Review and Historical Sketch" Mathematics 10, no. 20: 3907. https://doi.org/10.3390/math10203907
APA StyleTaketomi, N., Yamamoto, K., Chesneau, C., & Emura, T. (2022). Parametric Distributions for Survival and Reliability Analyses, a Review and Historical Sketch. Mathematics, 10(20), 3907. https://doi.org/10.3390/math10203907








