Vaccination’s Role in Combating the Omicron Variant Outbreak in Thailand: An Optimal Control Approach
Abstract
1. Introduction
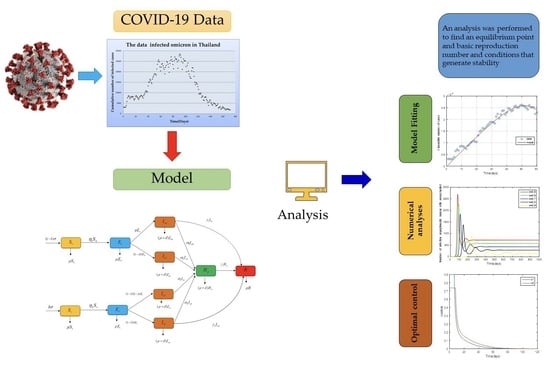
2. Materials and Methods
2.1. Mathematical Model
2.2. Stability Analysis
2.2.1. Equilibrium Point
2.2.2. The Basic Reproduction Number
2.2.3. Global Stability Analysis
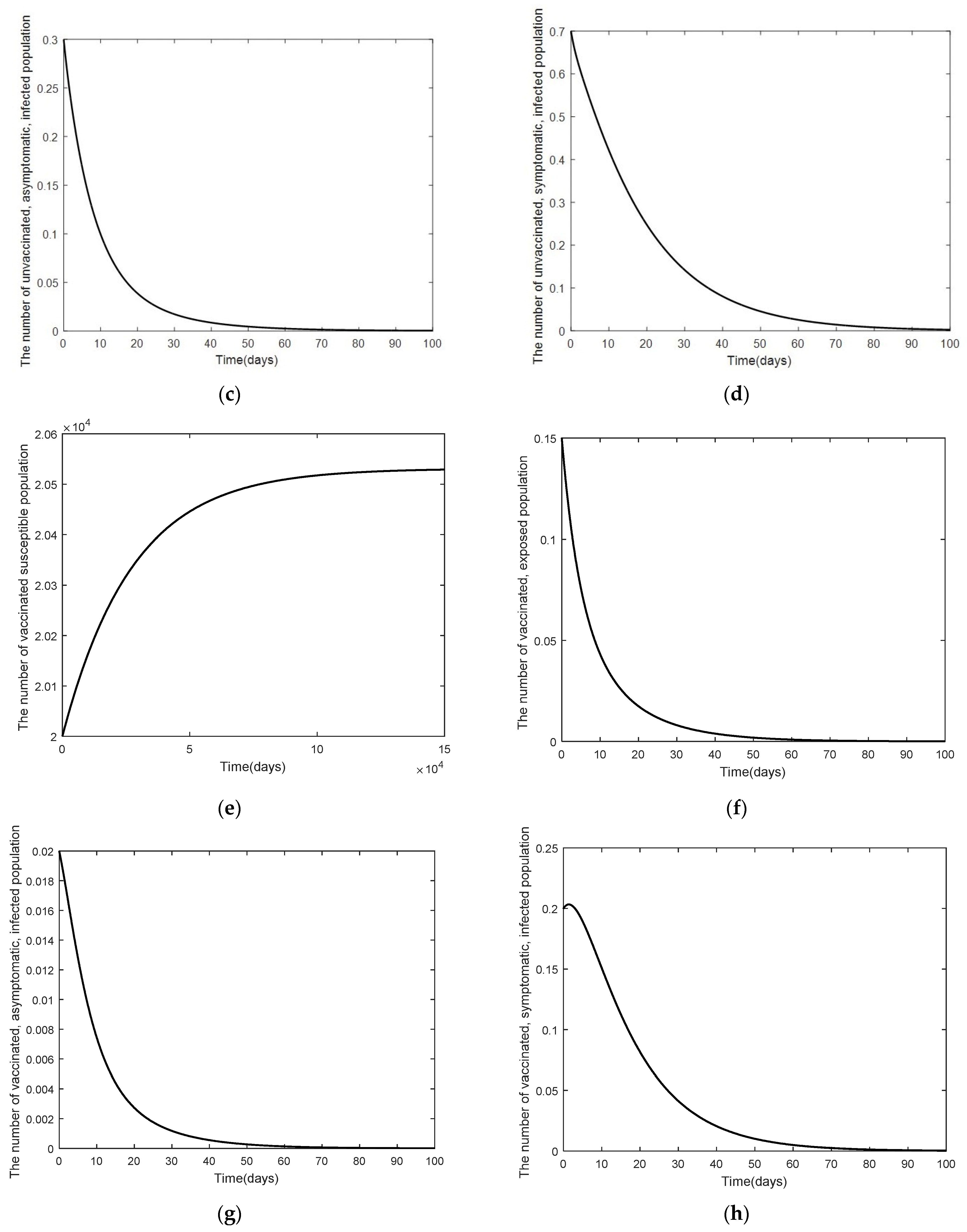
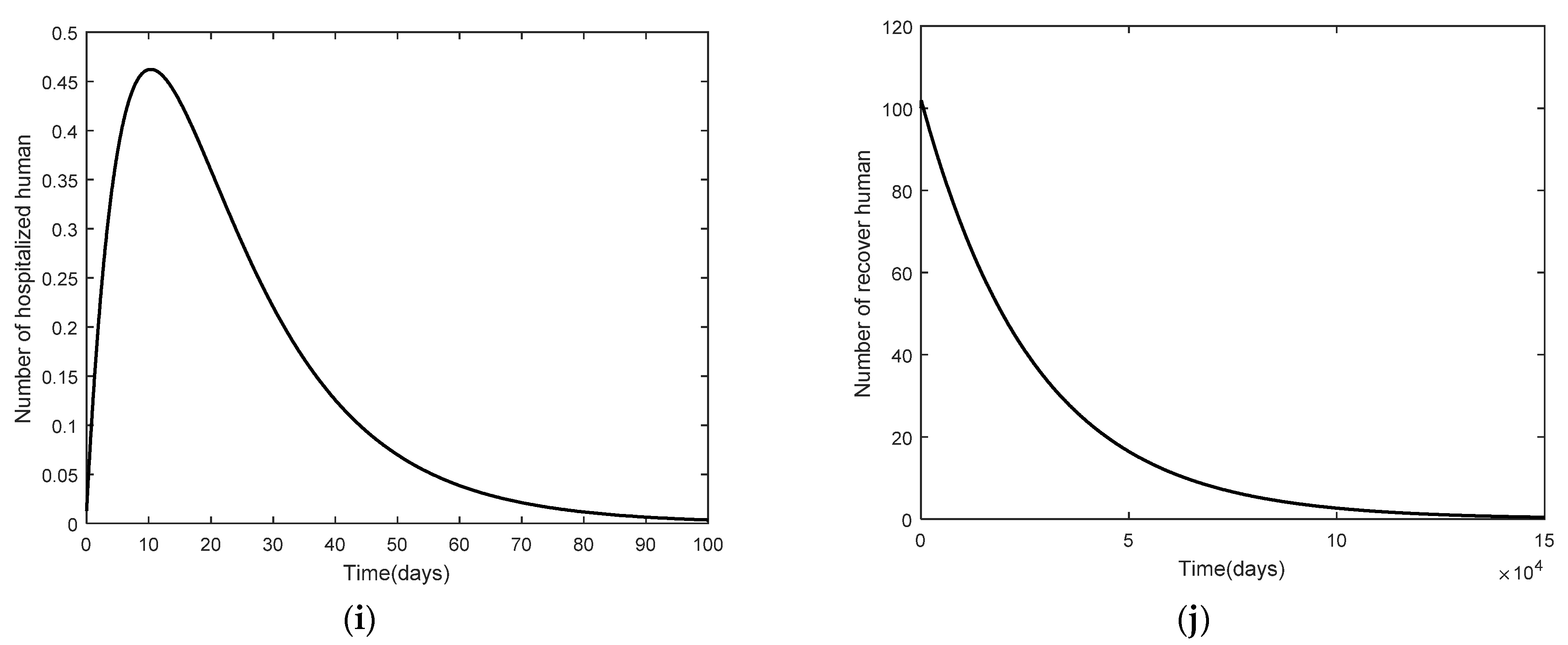
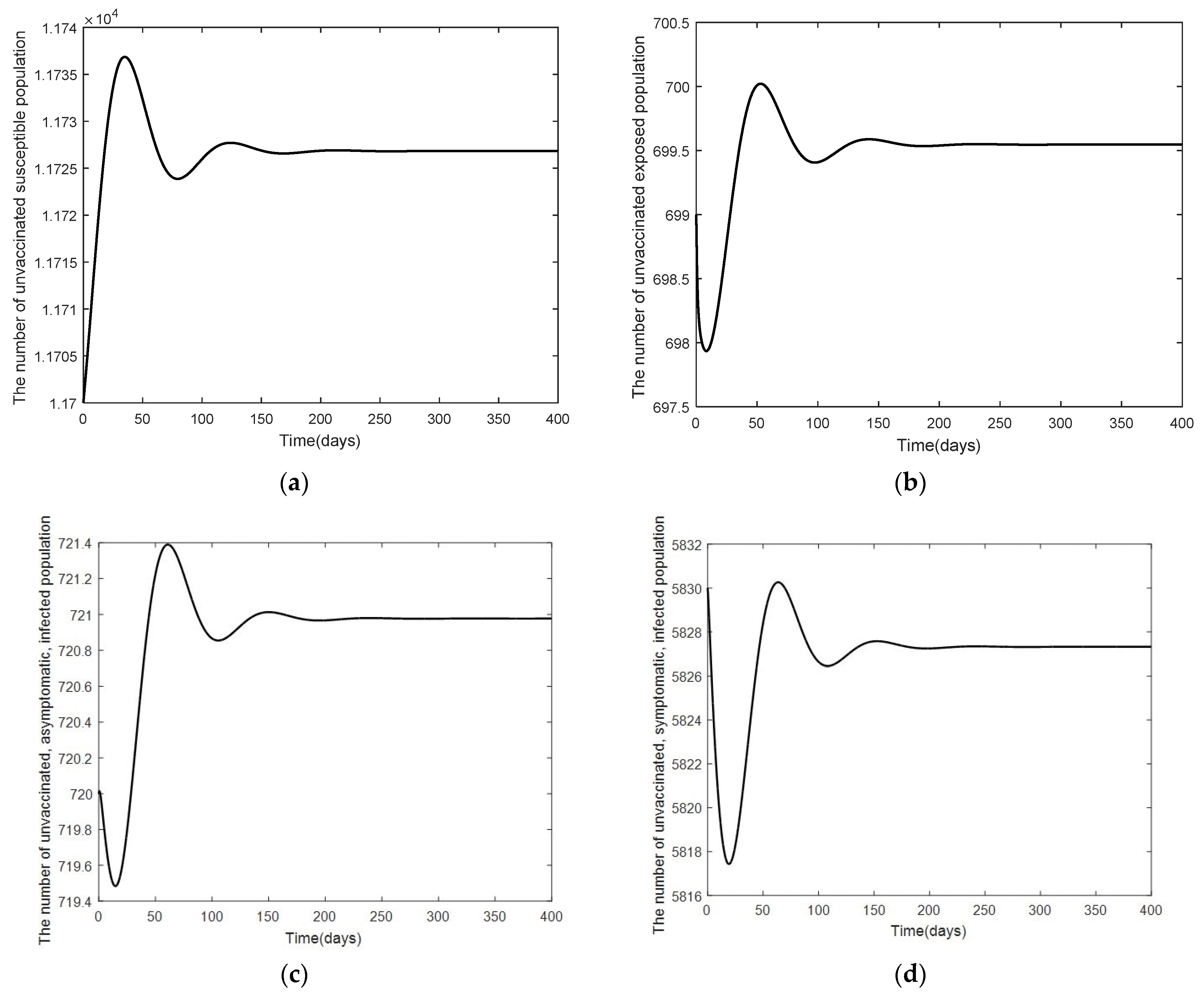
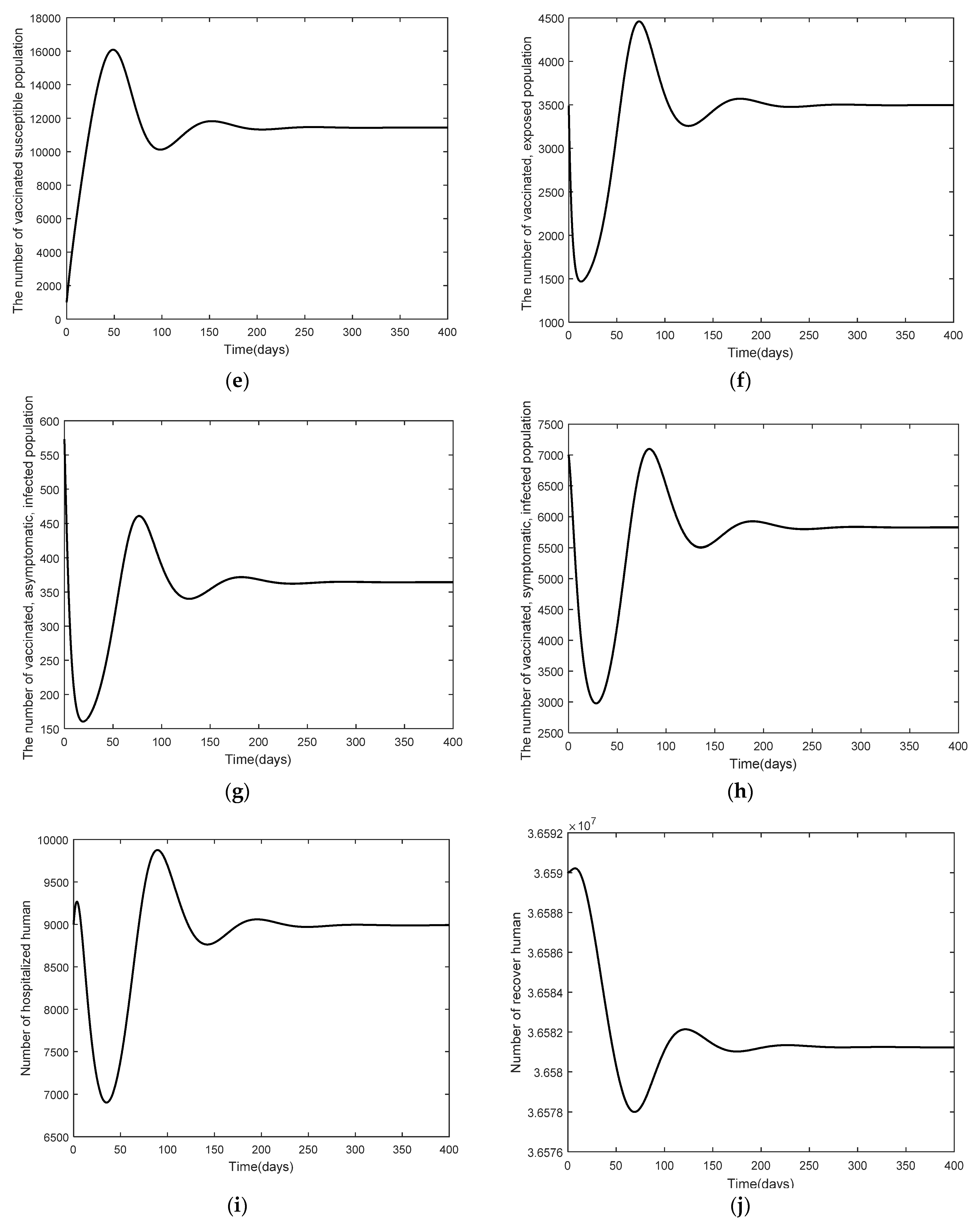
3. Numerical Analysis Result
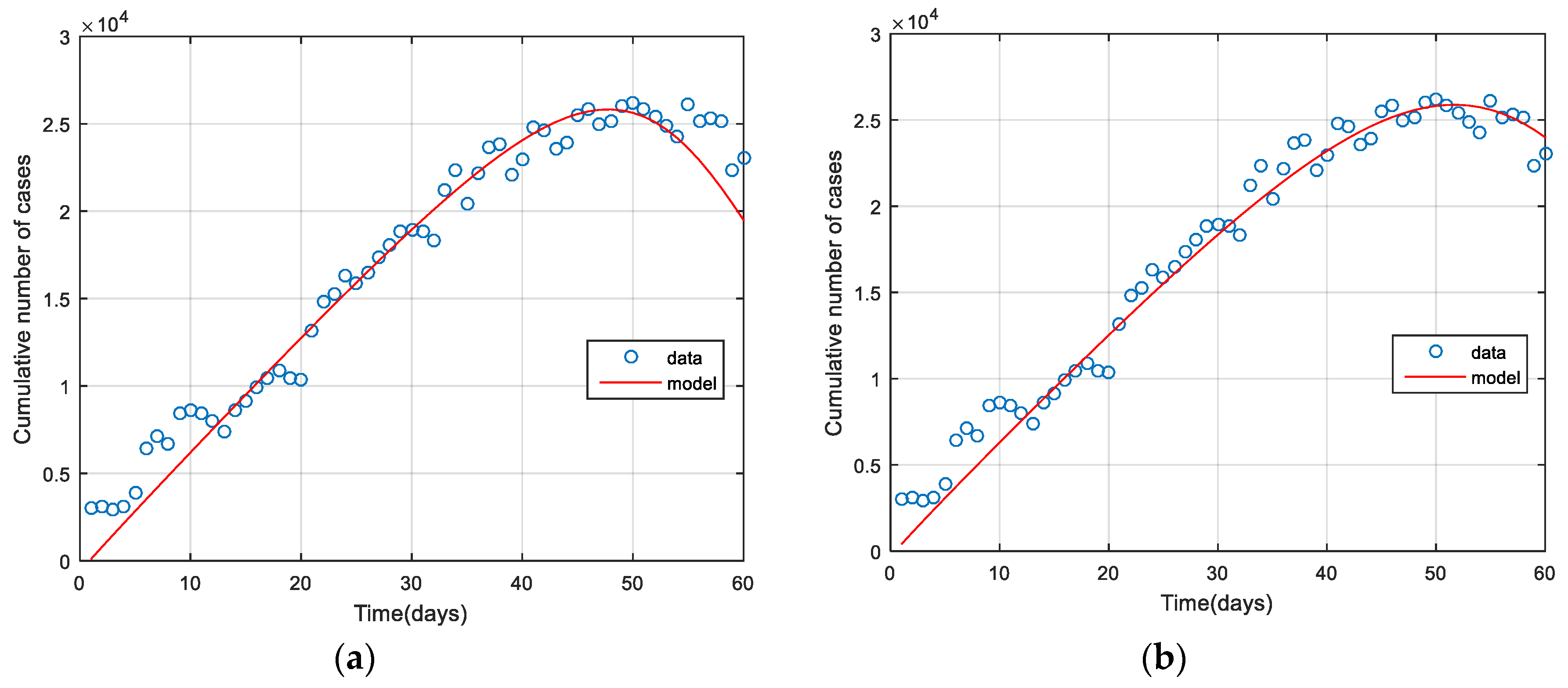
3.1. Model Fitting
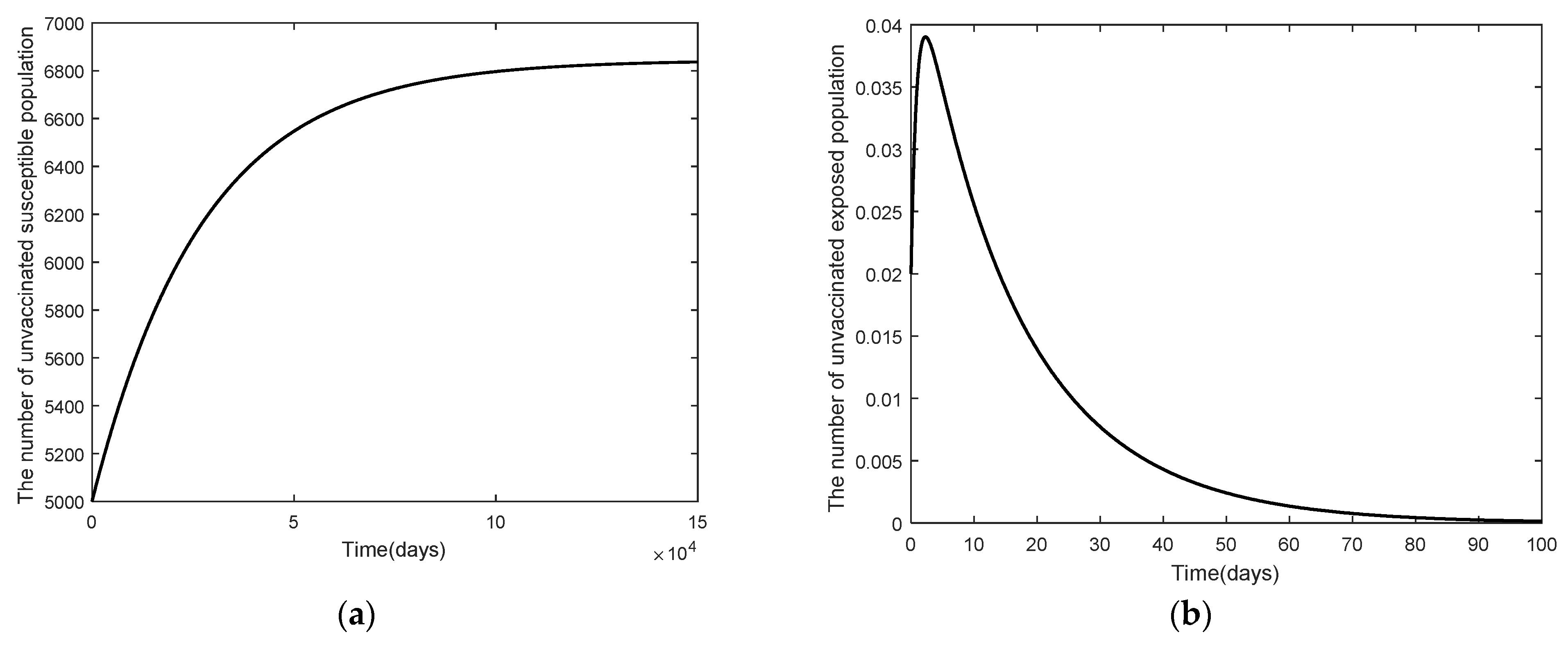
3.2. Numerical Analysis Result
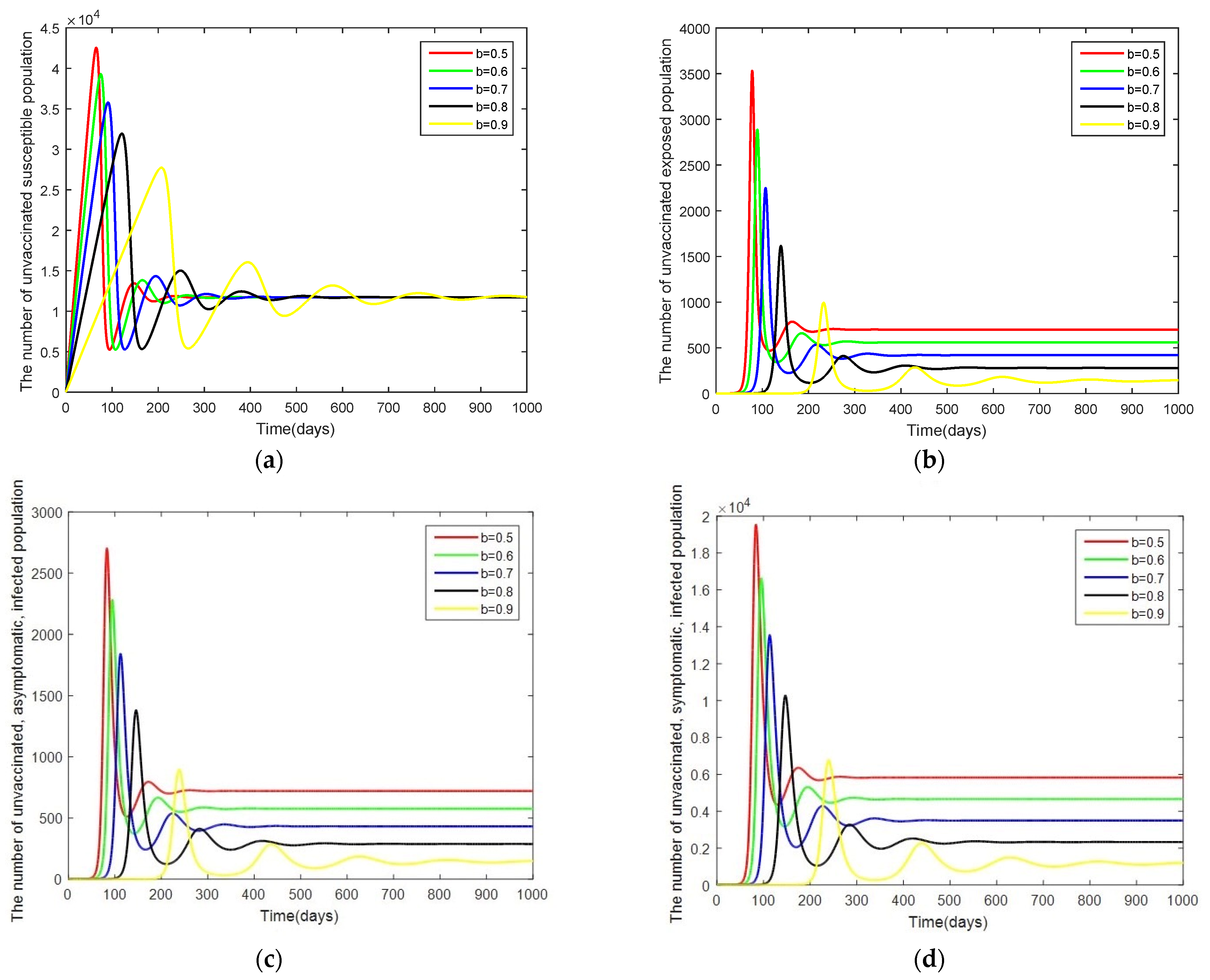
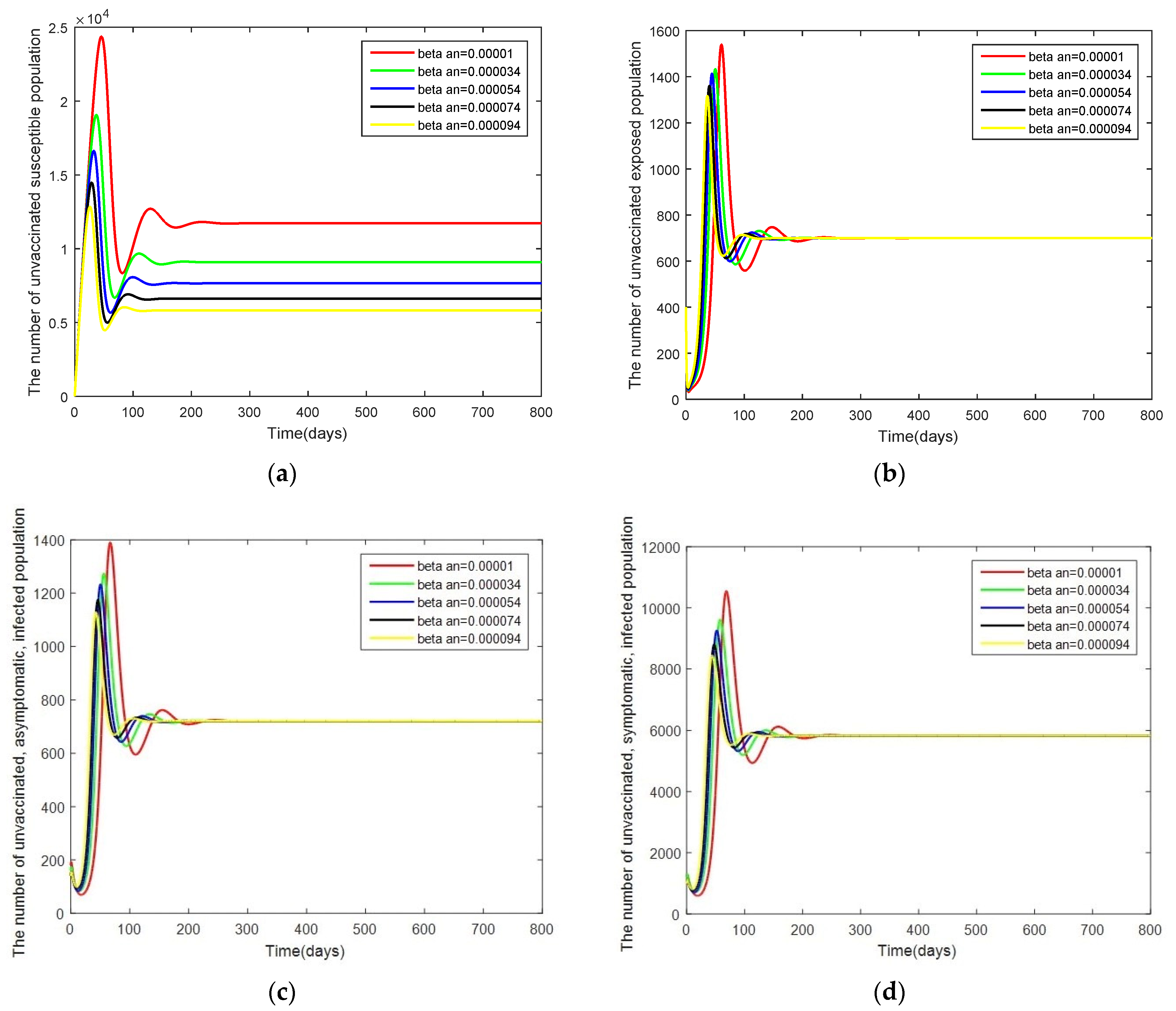
- Case 1: Changes in . Here, the system is simulated with = [0.00001, 0.000034, 0.000054, 0.000074, 0.000094] while keeping the other parameters as given by Table 2.
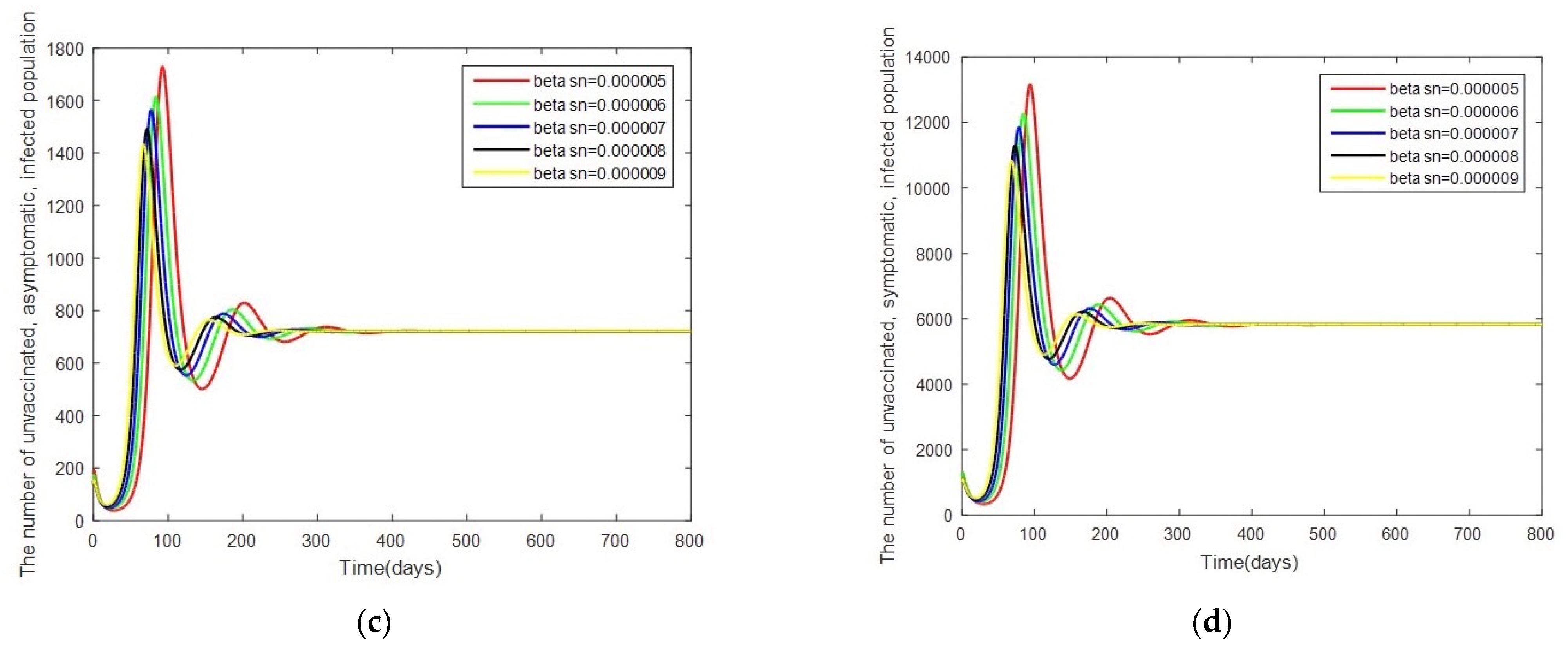
- Case 2: Changes in . In this case, the system is resimulated with = [0.000005, 0.000006, 0.000007, 0.000008, 0.000009] while keeping the other parameters as given by Table 2.
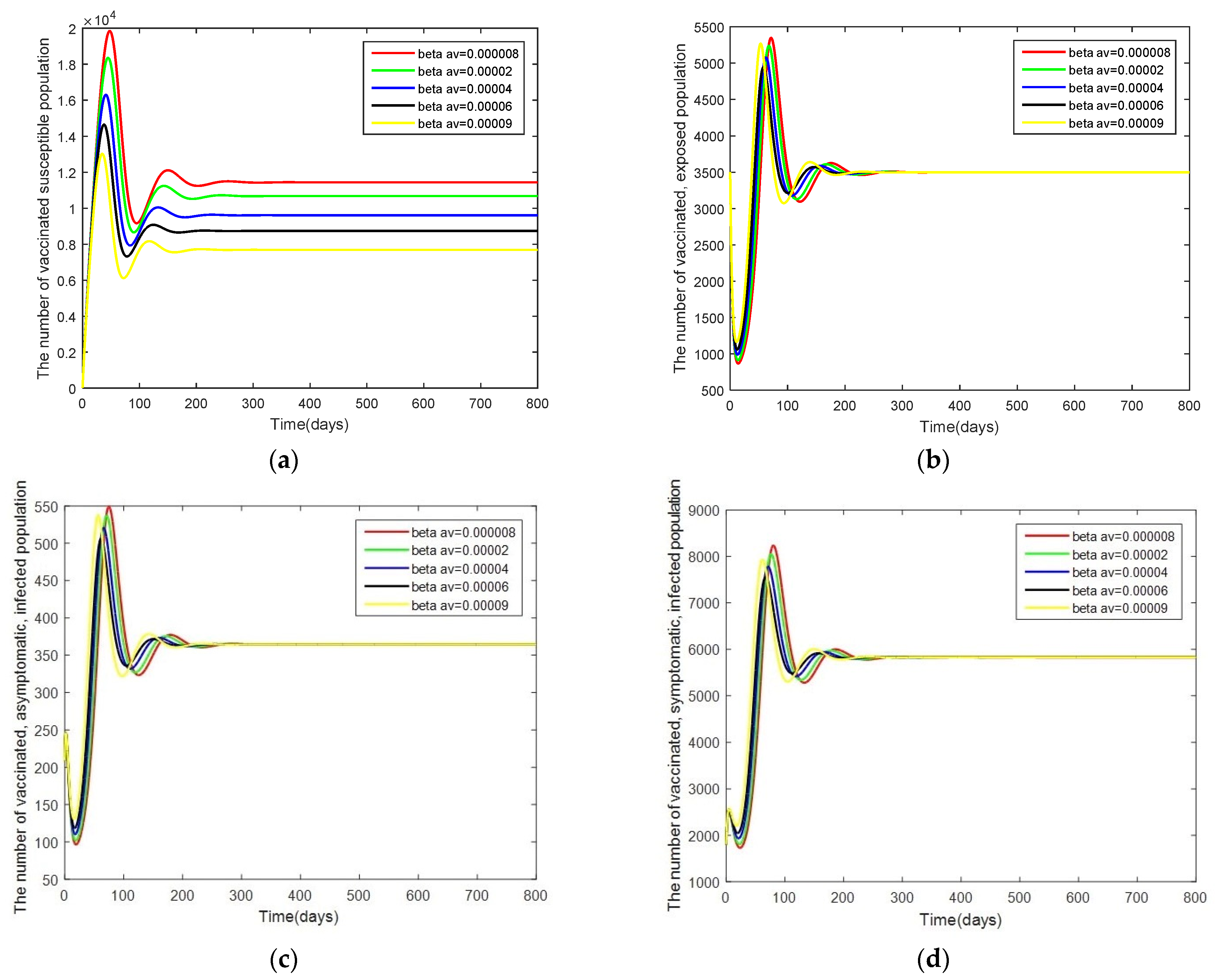
- Case 3: Changes in . In this case, the system is resimulated with = [0.000008, 0.00002, 0.00004, 0.00006, 0.00009] while keeping the other parameters as given by Table 2.
- Case 4: Changes in . In this case, the system is resimulated with = [0.000003, 0.000004, 0.000005, 0.000006, 0.00001] while keeping the other parameters as given by Table 2.
3.3. Sensitivity Analysis of Parameters
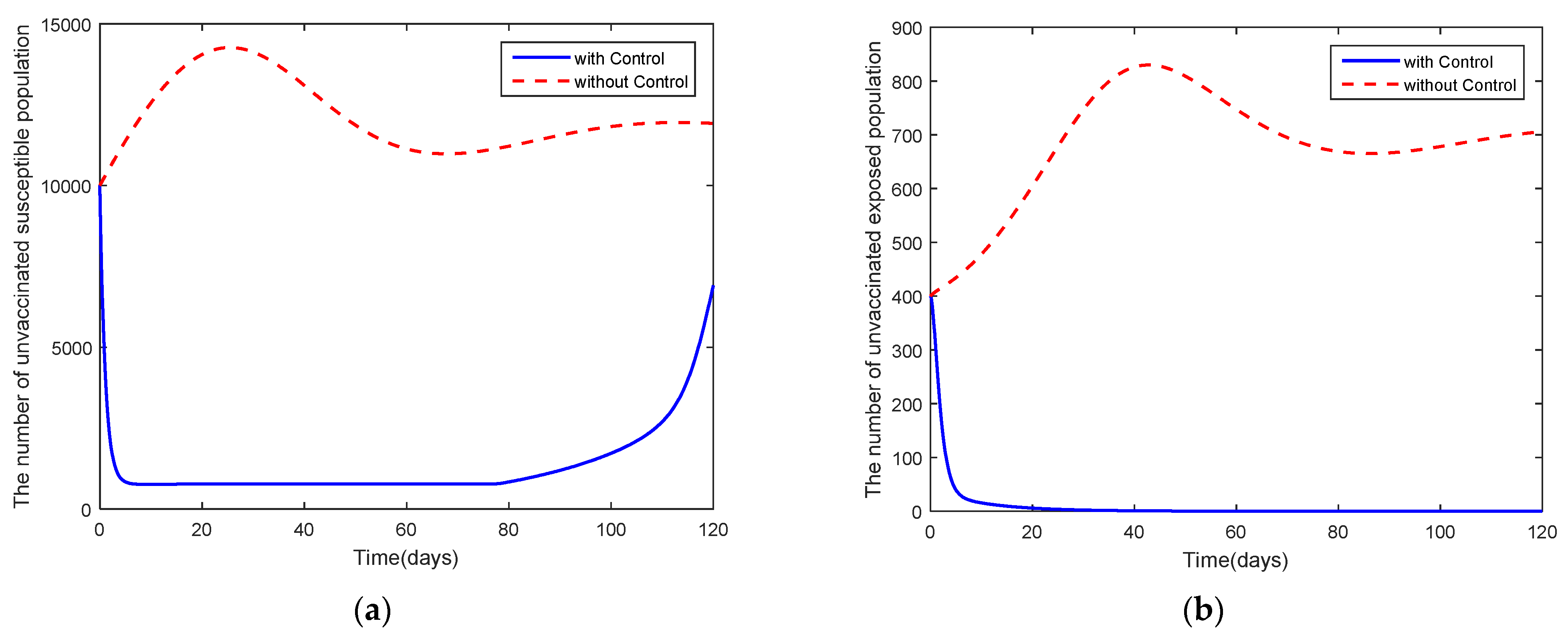
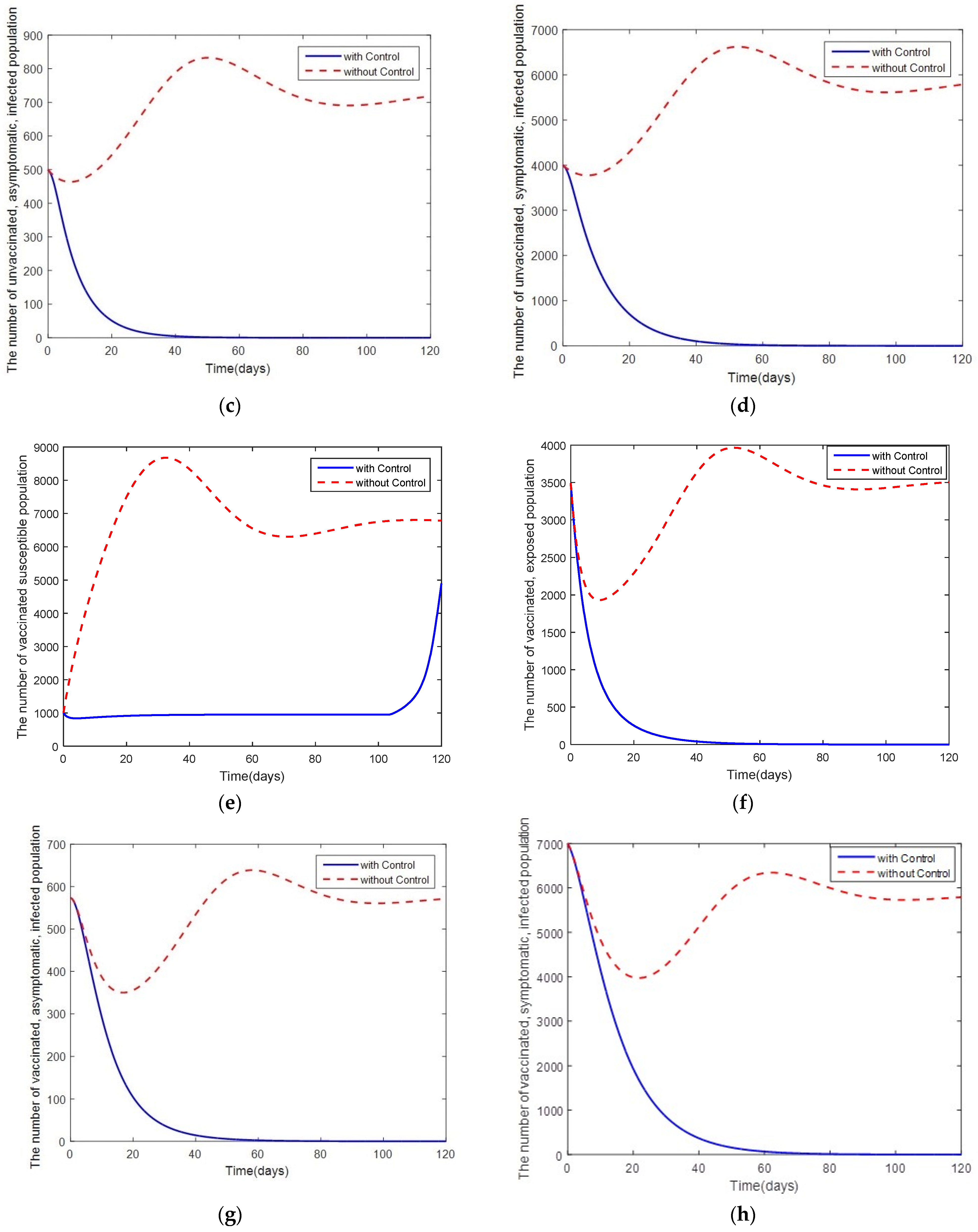
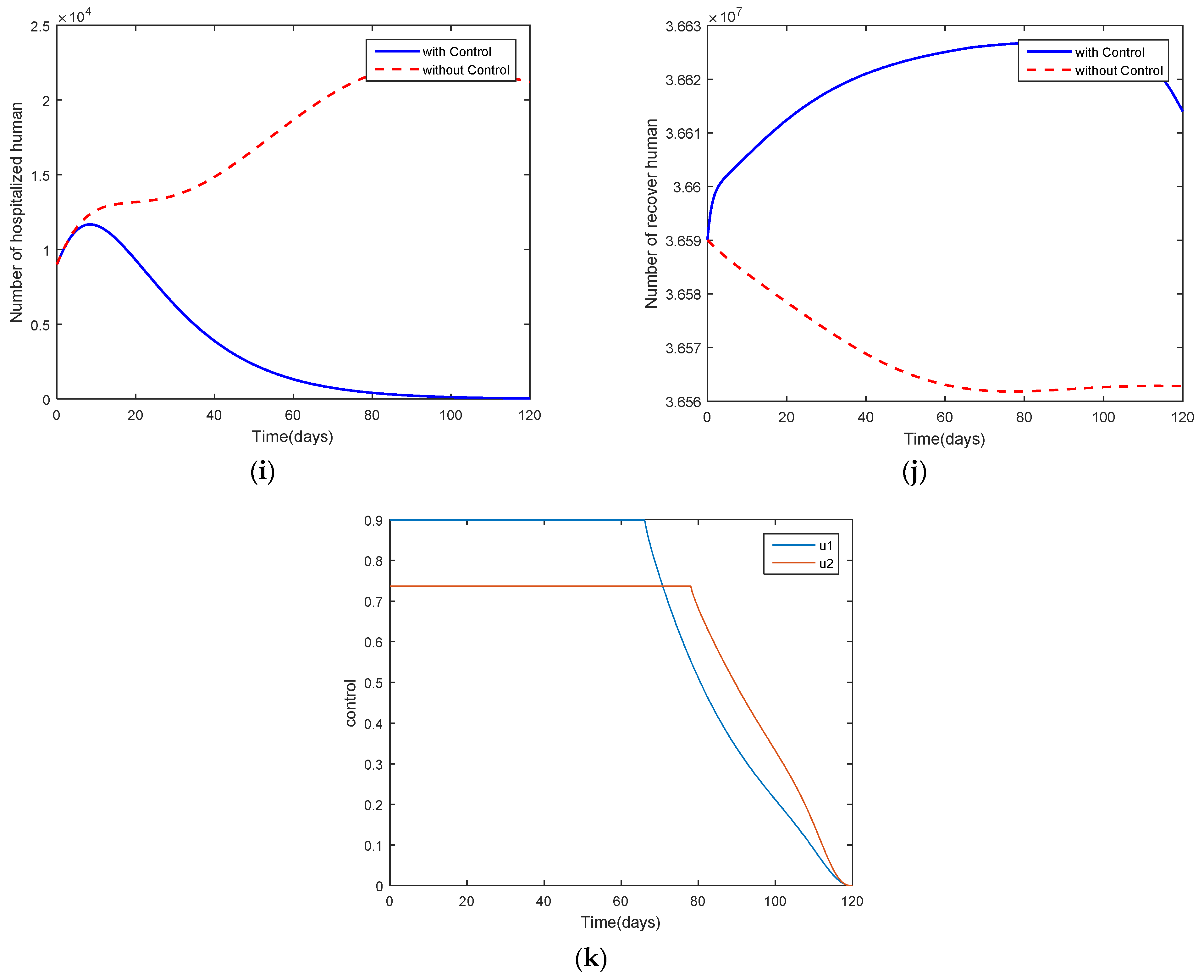
4. Optimal Control Problem
5. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chaharborj, S.S.; Hassanzadeh, J.; Phang, P.C. Controlling of pandemic COVID-19 using optimal control theory. Results Phys. 2021, 26, 104311. [Google Scholar] [CrossRef]
- Jankhonkhan, J.; Sawangtong, W. Model Predictive Control of COVID-19 pandemic Concerning Social Isolation and Vaccination Policies in Thailand. Axioms 2021, 10, 274. [Google Scholar] [CrossRef]
- Lina, Q.; Zhaob, S.; Gaod, D.; Loue, Y.; Yangf, S.; Musae, S.S.; Wangb, M.H.; Caig, Y.; Wangg, W.; Yangh, L.; et al. A conceptual model for the coronavirus disease 2019 (COVID-19) outbreak in Wuhan, China with individual reaction and governmental action. Int. J. Infect. Dis. 2020, 93, 211–216. [Google Scholar] [CrossRef]
- Feng, L.X.; Jing, S.L.; Hu, S.K.; Wang, D.F.; Huo, H.F. Modelling the effects of media coverage and quarantine on the COVID-19 infections in the UK. Math. Biosci. Eng. 2020, 17, 3618–3636. [Google Scholar] [CrossRef]
- Prathumwan, D.; Trachoo, K.; Chaiya, I. Mathematical Modeling for Prediction Dynamics of the Coronavirus Disease 2019 (COVID-19) Pandemic, Quarantine Control Measures. Symmetry 2020, 12, 1404. [Google Scholar] [CrossRef]
- Win, Z.T.; Eissa, M.A.; Tian, B. Stochastic Epidemic Model for COVID-19 Transmission under Intervention Strategies in China. Mathematics 2022, 10, 3119. [Google Scholar] [CrossRef]
- Yang, C.; Wang, J. Modeling the transmission of COVID-19 in the US-A case study. Infect. Dis. Model. 2021, 6, 195–211. [Google Scholar] [CrossRef]
- Zhanga, Z.; Jain, S. Mathematical model of Ebola and Covid-19 with fractional differential operators: Non-Markovian process and class for virus pathogen in the environment. Chaos Solit. Fract. 2020, 140, 110175. [Google Scholar] [CrossRef]
- Diagne, M.L.; Rwezaura, H.; Tchoumi, S.Y.; Tchuenche, J.M. A Mathematical Model of COVID-19 with Vaccination and Treatment. Comput. Math. Methods Med. 2021, 2021, 1250129. [Google Scholar] [CrossRef]
- Iboi, E.A.; Sharomi, O.; Ngonghala, C.N.; Gumel, A.B. Mathematical modeling and analysis of COVID-19 pandemic in Nigeria. Math. Biosci. Eng. 2020, 17, 7192–7220. [Google Scholar] [CrossRef]
- Ndaïrou, F.; Area, L.; Nietoc, J.J.; Torres, D.F.M. Mathematical modeling of COVID-19 transmission dynamics with a case study of Wuhan. Chaos Solit. Fract. 2020, 135, 109846. [Google Scholar] [CrossRef] [PubMed]
- Faruk, O.; Kar, S. A Data Driven Analysis and Forecast of COVID-19 Dynamics during the Third Wave Using SIRD Model in Bangladesh. COVID 2021, 1, 43. [Google Scholar] [CrossRef]
- Wang, L.; Dai, Y.; Wang, R.; Sun, Y.; Zhang, C.; Yang, Z.; Sun, Y. SEIARN: Intelligent Early Warning Model of Epidemic Spread Based on LSTM Trajectory Prediction. Mathematics 2022, 10, 3046. [Google Scholar] [CrossRef]
- World Health Organization. COVID-19—WHO Thailand Situation Reports. Available online: https://www.who.int/thailand/emergencies/novel-coronavirus-2019/situation-reports (accessed on 29 June 2022).
- Kermack, W.O.; McKndrick, A.G.; Walker, G.T. A contribution to the mathematical theory of epidemics. R. Soc. Lond. Ser. A Contain. Pap. Math. Phys. Charact. 1927, 115, 700–721. [Google Scholar]
- Lamwong, J.; Pongsumpun, P.; Tang, I.M.; Wongvanich, N. The Lyapunov Analyses of MERS-Cov Transmission in Thailand. Curr. Appl. Sci. Technol. 2019, 19, 112–123. [Google Scholar]
- Etbaigha, F.; Willms, A.R.; Poljak, Z. An SEIR model of influenza A virus infection and reinfection within a farrow-to-finish swine farm. PLoS ONE 2018, 13, e0202493. [Google Scholar] [CrossRef]
- Islam, R.; Biswas, M.H.A.; Jamali, A.R.M. Mathematical analysis of Epidemiological Model of Influenza A (H1N1) Virus Transmission Dynamics in Bangladesh Perspective. GANIT J. Bangladesh. Math. Soc. 2017, 37, 39–50. [Google Scholar] [CrossRef]
- Rezapour, S.; Mohammadi, H. A study on the AH1N1/09 influenza transmission model with the fractional Caputo–Fabrizio derivative. Adv. Diff. Equ. 2020, 2020, 488. [Google Scholar] [CrossRef]
- Chanprasopchai, P.; Pongsumpun, P.; Tang, I.M. Effect of Rainfall for the Dynamical Transmission Model of the Dengue Disease in Thailand. Comput. Math. Methods Med. 2017, 2017, 17. [Google Scholar] [CrossRef]
- Bhuju, G.; Phaijoo, G.R.; Gurung, D.B. Fuzzy Approach Analyzing SEIR-SEI Dengue Dynamics. Biomed. Res. Int. 2020, 2020, 11. [Google Scholar] [CrossRef]
- Gardner, L.M.; Rey, D.; Heywood, A.E.; Toms, R.; Wood, J.; Travis Waller, S.; Raina MacIntyre, C. A scenario-based evaluation of the Middle East respiratory syndrome coronavirus and the Hajj. Risk. Anal. 2014, 34, 1391–1400. [Google Scholar] [CrossRef] [PubMed]
- Sen, D.; Sen, D. Use of a Modified SIRD Model to Analyze COVID-19 Data. Ind. Eng. Chem. Res. 2021, 60, 4251–4260. [Google Scholar] [CrossRef]
- Kumar, H.; Arora, P.K.; Pant, M.; Kumar, A.; Shahroz, A.K. A simple mathematical model to predict and validate the spread of Covid-19 in India. Mater. Today Proc. 2021, 47, 3859–3864. [Google Scholar] [CrossRef] [PubMed]
- Hezam, I.M.; Foul, A.; Alrasheedi, A. A dynamic optimal control model for COVID-19 and cholera co-infection in Yemen. Adv. Differ. Equ. 2021, 2021, 108. [Google Scholar] [CrossRef]
- Riyapan, P.; Shuaib, S.E.; Intarasit, A. A Mathematical Model of COVID-19 Pandemic: A Case Study of Bangkok, Thailand COVID-19. Comput. Math. Methods Med. 2021, 2021, 6664483. [Google Scholar] [CrossRef]
- Rajput, A.; Sajid, M.; Tanvi; Shekhar, C.; Aggarwal, R. Optimal control strategies on COVID-19 infection to bolster the efcacy of vaccination in India. Sci. Rep. 2021, 11, 20124. [Google Scholar] [CrossRef]
- Dipo Aldila, D.; Shahzad, M.; Khoshnaw, A.H.A.; Ali, M.; Sultan, F.; Islamilova, A.; Anwar, Y.R.; Samiadji, B.M. Optimal control problem arising from COVID-19 transmission model with rapid-test. Results Phys. 2020, 37, 105501. [Google Scholar] [CrossRef]
- Tchoumi, S.Y.; Diagne, M.L.; Rwezaurac, H.; Tchuenche, J.M. Malaria and COVID-19 co-dynamics: A mathematical model and optimal control. Appl. Math. Model. 2021, 99, 294–327. [Google Scholar] [CrossRef]
- Driessche, P.V.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2020, 180, 29–48. [Google Scholar] [CrossRef]
- Abioye, A.I.; Peter, O.J.; Ogunseye, H.A.; Oguntolu, F.A.; Oshinubi, K.; Ibrahim, A.A.; Khan, I. Mathematical model of COVID-19 in Nigeria with optimal control. Results Phys. 2020, 28, 104598. [Google Scholar] [CrossRef]
- La Salle, J.P. The Stability of Dynamical Systems; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1976. [Google Scholar]
- Adepoju, O.A.; Samson Olaniyi, S. Stability and optimal control of a disease model with vertical transmission and saturated incidence. Sci. Afri. 2021, 12, e00800. [Google Scholar] [CrossRef]
- Gatyeni, S.P.; Chirove, F.; Nyabadza, F. Modelling the Potential Impact of Stigma on the Transmission Dynamics of COVID-19 in South Africa. Mathematics 2022, 10, 3253. [Google Scholar] [CrossRef]
- Lahodny, G. Curve Fitting and Parameter Estimation; Springer: Berlin/Heidelberg, Germany, 2015; pp. 1–18. [Google Scholar]
- Arruda, E.F.; Das, S.S.; Dias, C.M.; Pastore, D.H. Modelling and optimal control of multi strain epidemics, with application to COVID-19. PLoS ONE 2021, 16, e0257512. [Google Scholar] [CrossRef] [PubMed]
- Lamwong, J.; Tang, I.; Pongsumpun, P. Mers model of Thai and South Korean population. Curr. Appl. Sci. Technol. 2018, 18, 45–57. [Google Scholar]
- Husniah, H.; Ruhanda, R.; Supriatna, A.K.; Biswas, M.H.A. SEIR Mathematical Model of Convalescent Plasma Transfusion to Reduce COVID-19 Disease Transmission. Mathematics 2021, 9, 2857. [Google Scholar] [CrossRef]
- Chitnis, N.; Hyman, J.M.; Cushing, J.M. Determining important parameters in the spread of malaria through the sensitivity analysis of a mathematical model. Bull. Math. Biol. 2008, 70, 1272–1296. [Google Scholar] [CrossRef]
- Lenhart, S.; Workman, J.T. Optimal Control Applied to Biological Models; Chapman & Hall/CRC: London, UK, 2007. [Google Scholar]
- Pontryagin, L.S.; Boltyanskii, V.G.; Gamkrelidze, R.V.; Mishchenko, E.F. The Mathematical Theory of Optimal Processes; Wiley: New York, NY, USA, 1962. [Google Scholar]
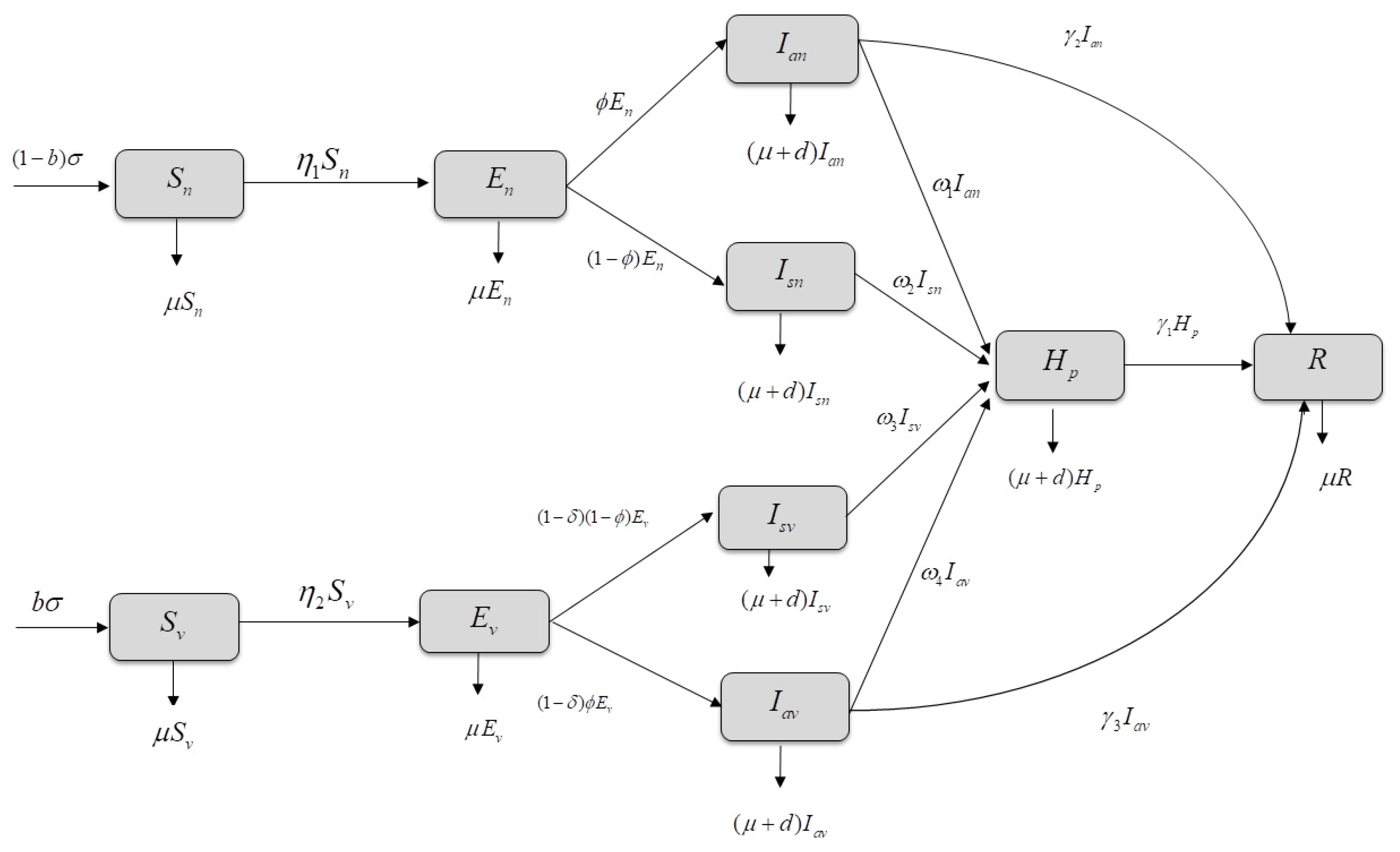





| Variables and Parameters | Description |
|---|---|
| The number in the unvaccinated, susceptible population. | |
| The number in the unvaccinated, exposed population. | |
| The number in the unvaccinated, asymptomatic, infected population. | |
| The number in the unvaccinated, symptomatic, infected population. | |
| The number in the vaccinated, susceptible population. | |
| The number in the vaccinated, exposed population. | |
| The number in the vaccinated, asymptomatic, infected population. | |
| The number in the vaccinated, symptomatic, infected population. | |
| The number in the hospitalized population. | |
| The number in the recovered population. | |
| Efficacy of vaccination. | |
| Initial number in the population. | |
| Infection rate of the unvaccinated, asymptomatic, infected population. | |
| Infection rate of the unvaccinated, symptomatic, infected population. | |
| Infection rate of the vaccinated, asymptomatic, infected population. | |
| Infection rate of the vaccinated, symptomatic, infected population. | |
| Incubation period of the disease. | |
| Efficacy of the vaccination against COVID-19. | |
| Hospitalization rate of the unvaccinated, asymptomatic, infected population. | |
| Hospitalization rate of the unvaccinated, symptomatic, infected population. | |
| Hospitalization rate of the vaccinated, asymptomatic, infected population. | |
| Hospitalization rate of the vaccinated, symptomatic, infected population. | |
| Recovery rate after hospitalization. | |
| Recovery rate of the unvaccinated, asymptomatic, infected population. | |
| Recovery rate of the vaccinated, asymptomatic, infected population. | |
| Death rate from natural causes. | |
| Death rate from COVID-19. | |
| Total number in the human population. |
| Parameters | The Disease-Free | The Endemic | Reference |
|---|---|---|---|
| 0.5 | 0.5 | Estimated | |
| 1 | 1400 | Estimated | |
| 0.00001 | 0.00001 | Data fitted | |
| 0.000009 | 0.000009 | Data fitted | |
| 0.000008 | 0.000008 | Data fitted | |
| 0.00001 | 0.00001 | Data fitted | |
| 1/7 | 1/7 | [7,36] | |
| 0.8 | 0.8 | Assumed | |
| 0.1 | 0.1 | [5,7] | |
| 0.1 | 0.1 | [5,7] | |
| 0.1 | 0.1 | [5,7] | |
| 0.1 | 0.1 | [5,7] | |
| 1/7 | 1/7 | [7] | |
| 1/14 | 1/14 | [10] | |
| 1/14 | 1/14 | [7] | |
| 0.0000365 | 0.0000365 | [37,38] | |
| 0.00286 | 0.00286 | [31] |
| Parameters | Sensitivity Indices |
|---|---|
| +1.0000 | |
| +1.0000 | |
| +0.1209 | |
| +0.8791 | |
| +0.0730 | |
| +0.9270 | |
| +0.0007 | |
| −0.0026 | |
| −0.0872 | |
| −0.8544 | |
| −0.9009 | |
| −0.0419 | |
| −0.0311 | |
| −0.0299 | |
| −1.0004 | |
| −0.0269 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lamwong, J.; Pongsumpun, P.; Tang, I.-M.; Wongvanich, N. Vaccination’s Role in Combating the Omicron Variant Outbreak in Thailand: An Optimal Control Approach. Mathematics 2022, 10, 3899. https://doi.org/10.3390/math10203899
Lamwong J, Pongsumpun P, Tang I-M, Wongvanich N. Vaccination’s Role in Combating the Omicron Variant Outbreak in Thailand: An Optimal Control Approach. Mathematics. 2022; 10(20):3899. https://doi.org/10.3390/math10203899
Chicago/Turabian StyleLamwong, Jiraporn, Puntani Pongsumpun, I-Ming Tang, and Napasool Wongvanich. 2022. "Vaccination’s Role in Combating the Omicron Variant Outbreak in Thailand: An Optimal Control Approach" Mathematics 10, no. 20: 3899. https://doi.org/10.3390/math10203899
APA StyleLamwong, J., Pongsumpun, P., Tang, I.-M., & Wongvanich, N. (2022). Vaccination’s Role in Combating the Omicron Variant Outbreak in Thailand: An Optimal Control Approach. Mathematics, 10(20), 3899. https://doi.org/10.3390/math10203899