Abstract
The study of convective heat transfer in differently shaped fins with radiation, internal heat generation and variable thermal conductivity was considered. The energy equation of the model was converted into the dimensionless form by adopting the proper variables, which was later solved using the differential transformation method. The impact of the parameters on the thermal performance, efficiency and heat transfer of the fins was analyzed graphically and also by performing thermal analysis on the fins. It was noticed that there was a significant effect on the thermal performance of the fins with different shapes, and also the heat transfer rate of the fin increased for improved values of the internal heat generation and radiation parameters. The exponential profile showed better results than other profiles, and the results obtained were supported by thermal analysis using ANSYS software.
Keywords:
convection-radiation heat transfer; thermal analysis; differential transformation method; internal heat generation and variable heat conductivity MSC:
76-10; 76R10
1. Introduction
Heat enchantment has become an important factor that has captured the interest of many researchers. Increasing the heat transfer mainly depends on the heat transfer coefficient, the surface area available and the temperature difference between the surface and surrounding fluid. Fins are used as heat dissipators by increasing the surface area of the heated surface that is exposed to an ambient fluid. In particular, fins are electronic components, and diodes, transistors, etc., are made up of fins. Karus et al. [1] presented a general overview of fins. Using the above concepts, Gireesha and Sowmya [2] solved fin problems with heat distribution in an inclined fin. The study of horizontal fins with natural convection was considered by Popiel et al. [3]. In most cases, the electrical current generates internal heat that can be detected in electrical filaments or nuclear reactors exposed to the temperature. This is a nonlinear factor that does not allow an analytical solution. It can be solved using numerical or semi-analytical methods. A mathematical study of the fin with an internal heat source was studied by Minkler and Rouleau [4]. Recently, many researchers [5,6,7] have used a numerical approach to solve the fins of various shapes with an internal heat source. Sobamowo [8] investigated the effect of internal heat initiation and temperature-dependent heat conduction. Turkyilmazoglu [9] used variable heat conduction and heat distribution coefficients to obtain the rate of heat transfer through radial fins. Variable thermal properties in straight fins were reported by Ndlovu and Moitsheki [10]. Rohit et al. [11] studied temperature-relative heat transfer in a moving fin using the decomposition method. In recent years, thermal enhancement flow problems have been analyzed by a few authors [12,13]. The study of heat conduction between fins with a motion and in the presence of convection energy using the homotopy scheme was performed by Aziz and Khani [14]. Sowmya et al. [15] examined the heat performance in longitudinal fins with a heat source due to natural convection. A study of a porous medium and the radiation parameter was conducted by Hatami and Ganji [16] in a circular fin. Heat transfer and temperature distribution in circular convective radiative porous fins of different shapes were analyzed by Pasha [17]. Heat propagation in fins with radiation for different geometries was studied by Tarobi et al. [18]. A handful of researchers studied the effect of rectangular fins used in heat exchange systems and determined the dimensions of the fin to achieve better efficiency [19,20,21]. Shi et al. [22] studied the bio-convection flow of magneto-cross nanofluid containing gyrotactic microorganisms with activation energy.
Fins are widely used in industries to reduce the heat transfer rate of the appliances produced by them. As an example, Farhad et al. [23,24] studied the application of fins in air-conditioning and ice storage systems by arranging the fins in different combinations. Their study revealed that the length, shape and arrangement of the fins expedited heat transfer. Sabu et al. [25] studied the significance of nanoparticles’ shape and thermo-hydrodynamic slip constraints on MHD alumina-water nanoliquid flows over a rotating heated disk. Jamal et al. [26] considered partially inclined baffles in a rectangular enclosure to study the turbulent and thermal behaviors of air using the finite volume method. They reported that the thermal performance of a heat exchanger and the reduction in pressure loss by adopting the designs that allow the maximum heat transfer rate with minimum energy coincide with the results of Demartini et al. [27]. Moreover, they found out that the heat transfer rate is directly related to the number of baffles present in the system. Meanwhile, Omid et al. [28] studied the performance of airflow in rectangular-shaped solar heaters with V-shaped ribs. Increasing the inclination of the ribs produces higher velocity and heat transfer. In this article, the DTM was used to solve the nonlinear energy equation describing the temperature distribution in fins with variable thermal conductivity, radiation and internal heat generation. DTM is a semi-analytical technique proposed by Zho [29] in 1986 to solve the initial value problems in electrical circuits to obtain precise nth derivative values. The solution for a system of differential equations by the DTM was explained by Fatma [30]. Two-dimensional DTM used to solve the differential equation was developed by Chen and Ho [31]. Ayaz [32] proved that DTM is better to solve a nonlinear problem than the Taylor series method. The DTM has been used to solve various problems in applied mathematics and physics such as systems of differential equations [33]. Fallo et al. [34] applied the 3D DTM for the first time to study heat transfer in a cylindrical spine fin with variable thermal properties. Chiba et al. [35] solved the one-dimensional phase change problem in a slab of finite thickness using the DTM. The finite Taylor series and the iteration operation described by the transformed equations derived from the original equation employing differential transformation operations can be utilized to assess the approximating solution. Several authors used the DTM concept to solve various types of equations [36,37,38,39].
This work aims to study the heat transfer of longitudinal fins with different geometries in the presence of a temperature-dependent heat source, thermal radiation and variable thermal conductivity by providing an analytical solution for the heat equation using the DTM approximation technique. A review of the above literature shows no attempt has been made to analyze the heat transfer for the above-considered profiles and effects using the DTM. Graphical comparison of heat transfer rate between the three profiles and the efficiency of the fins are discussed in this study, and also our study is supported by performing thermal analysis using ANSYS software.
2. Fundamental Operations of DTM
Let be a function that is continuously differentiable in the domain D. Power series can be used for the representation of and can be articulated in terms of the Taylor series [40] as follows:
The Maclaurin series is obtained by taking in Equation (1) and can be expressed as:
Franco [41] explained the use of differential transforms and expressed the function as follows:
is the converted function, and is the initial function. The differential function is restricted to where H is a permanent value and is assumed to be unity. The inverse differential transform can be expressed as:
The functions and transformations used in our study are presented in Table 1. From this, it can be deduced that the differential transform is similar to the Taylor series. To get more accuracy, we consider a higher number of terms in the above series.

Table 1.
Fundamental definitions of DTM.
3. Mathematical Formulation
The fin length is L with the variable area as shown in Figure 1. is base temperature, is ambient temperature, and the tip is presumed to be in convection. Constant heat is maintained throughout the fin, while thermal conduction is temperature dependent and varies linearly. The energy equation is obtained considering the following assumptions:
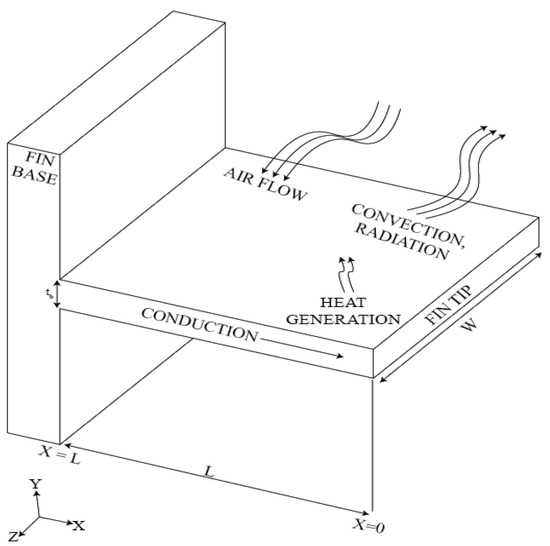
Figure 1.
Representation of a rectangular fin.
- The temperature is a function of and remains constant over time.
- The temperature variance due to fin thickness is neglected.
- The fin bed is kept at a steady temperature.
- Solid matrix and fluid are in a dynamic state of equilibrium.
- Fin is considered to be in a steady state.
The balanced energy equation under the above assumptions for the small element is:
The corresponding boundary constraints are defined as:
Here, the variable heat conduction is stated as:
where is heat conduction at ambient temperature, and is persistent. The fin is segregated into different profiles according to the difference in thickness along its length.
where is the girth, and is thickness along the length. Various geometries can be considered as shown in Figure 2:
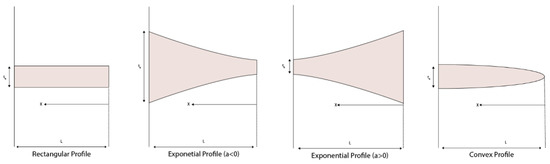
Figure 2.
Schematic representation of fins with different profiles.
- For quadrilateral fin
- For exponential fin
- For convex finDimensionless parameters are:
By applying equations in Equations (7)–(11) into Equation (5), we obtain:
- For rectangular profile
- For exponential profile
- For convex profilewhere and convective environment boundary conditions are:
4. Solution Method with DTM
Equations (12)–(14) are reduced to the Taylor series using the properties mentioned in Table 1. We obtain:
- For rectangular profile
- For exponential profile
- For convex profile
Boundary conditions can be reduced to:
Considering and using boundary constraints with the assistance of MATLAB software, the terms of the series can be obtained as follows:
- For rectangular profileand so forth
- For exponential profile…and so forth
- For convex profile…and so forth
By substituting Equation (19) in Equation (4) for
- For rectangular profile
To obtain the values of , we use Equation (18)
Solving Equation (23) using MATLAB software we obtain the exact value of . The same procedure is repeated for the other profiles.
Fin Efficiency
The amount of heat transferred in a fin is determined with the help of the parameter called efficiency. It is a correlation between the actual heat shift in a fin to heat that would be transmitted if a complete fin is of the temperature of the fin bed. The non-dimensional equation for the efficiency of a rectangular profile is given by:
5. Results
The current investigation presents the exploration of temperature differences associated with variable thermal conductivity, internal heat generation and radiation over the longitudinal fin of different profiles. The dimensionless energy equations of the fins are solved using the DTM. Results mainly referring to temperature field and thermal profiles are depicted graphically for three types of fins, namely rectangular, exponential and convex. The effects of Nr, G, Nc, and on temperature fields are analyzed and discussed. Moreover, for all results reported here, the following values of variables are used unless otherwise indicated by the graphs or tables: . Thermal analysis is performed and discussed using ANSYS software. The results of the present study are compared with the existing results of Languri et al. [42] and Arslanturk [43] (Table 2).

Table 2.
Comparison of obtained by different studies for rectangular fins by considering and .
The fluctuation in fin temperature due to variable heat conduction is shown in Figure 3 for three different profiles. From this graph, it is noticed that the thermal gradient reduces gradually from the base to the tip of the fin for different values of . The increment in enhances the temperature field due to heat loss to the surrounding fluid from the fin surface. The results show that the fin-tip temperature for exponential profiles is greater than that of the other profiles.
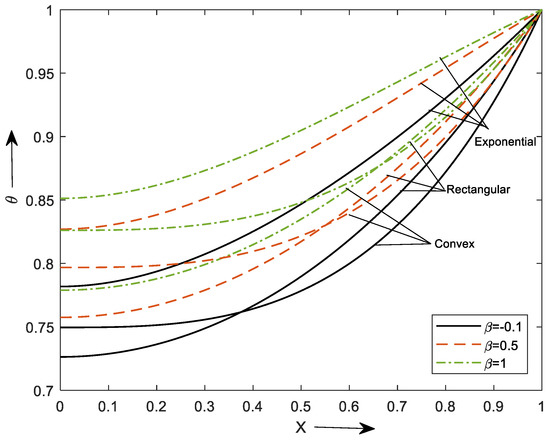
Figure 3.
Temperature distribution of different profiles for diverse values of .
Figure 4 shows the influence of the N on the thermal attribute of the fin. As the parameter N intensifies, the enriched heating pattern in the fin is noted which reduces the temperature rise. The contribution of this flow parameter is significant for enhancing the thermal transport of the fin. From the graph, we can notice that the exponential profile shows better performance which is followed by the rectangular and convex for various values on radiation parameters.
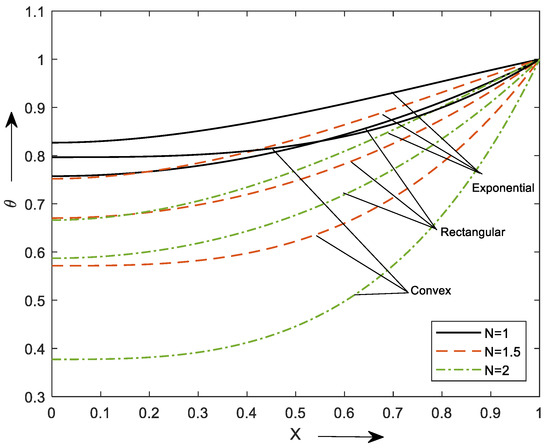
Figure 4.
Temperature distribution of different profiles for diverse values of .
The effect of the internal heat generation parameter is depicted in Figure 5. For this, it is observed that the temperature of the fin can be enhanced with the values of . Higher heat generation enhances fin temperature in steady-state conditions owing to the fact of larger dissipation of the heating environment due to the fin.
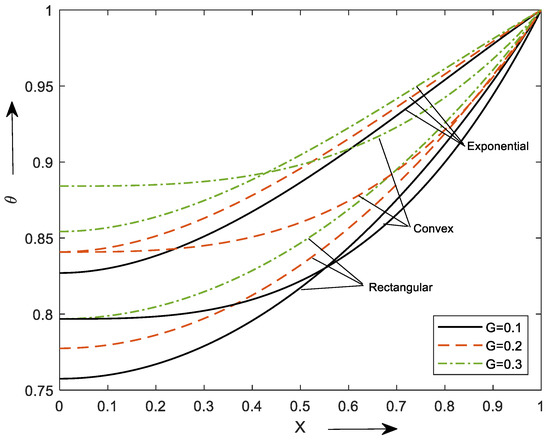
Figure 5.
Temperature distribution of different profiles for diverse values of .
The radiative parameter impact (Nr) is shown in Figure 6. With an increment in the radiation number, the thermal profile θ decreases steadily. The lower temperature inside the fin indicates a loss of ambient fluid temperature with radiative parameters.
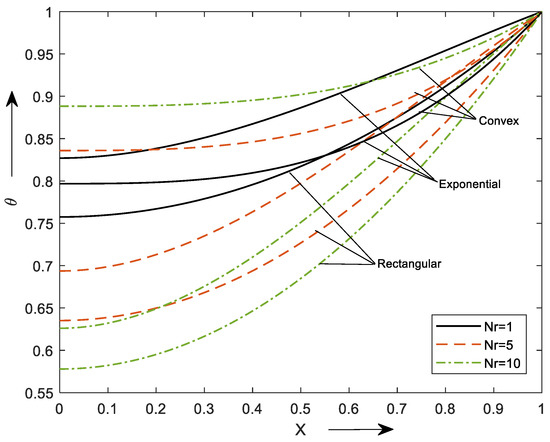
Figure 6.
Behavior Nr on θ.
The Figure 7 shows variation in dimensionless ambient temperature on the temperature field. As increases, the temperature of the surrounding liquid increases, which affects the rate of heat transmission from fin to surface. This is noted with a rise in .
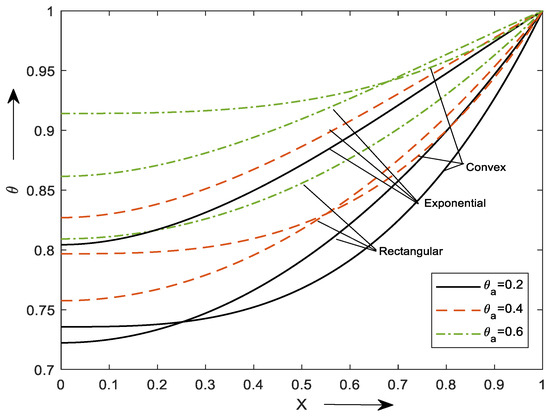
Figure 7.
Behavior on θ.
The effect of parameters on temperature for rectangular, exponential and convex profiles is obtained on the same graph to understand the difference between each profile. Similar observations discussed above can be seen in the other two profiles. Meanwhile, the exponential-shaped fins exhibit better performance than the others. Heat transference at the fin base is an important study, which has many applications and is of the form
The effect of simultaneously varying with N for two different values of and can be seen in Figure 8a,b, respectively, for all three profiles. From the graphs, it can be concluded that the value of is inversely related to the values of and . Heat transfer is more at the base and then reduces to become constant at the fin tip. Which shows that the fin cools down earlier at the tip.
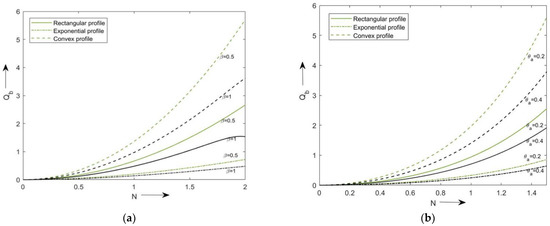
Figure 8.
(a) Variation of with for several assigned values of . (b) Variation of with for several assigned values of .
6. Thermal Analysis
ANSYS is a tool that helps us understand the routine of a model from our study in a virtual environment. It uses governing equations to study the behaviors of the problem. To investigate the thermal behaviors, the following assumption is made on the fins:
- Aluminum alloy (AA6061) is considered a fin material as it is a good thermal and electrical conductor with heat conduction of 300 W/m K.
- Heat conduction is considered 1D and longitudinal.
- h is considered to be 39.9 W/m2K above the fin surface.
- The fin base is kept at 550 K, and 283 is the ambient temperature.
Figure 9a–c illustrate longitudinal fin thermal propagation for rectangular, exponential and convex profiles, respectively. The maximum temperature observed was 550 K in all three profiles, and the fin tip temperature was 546 K, 530.28 K and 545 K, respectively. The temperature gradually decreased from the bed of the fin to the tip. Exponential fins have better results compared to other profiles. The results are drawn from the thermal analysis, which agrees well with our numerical results.
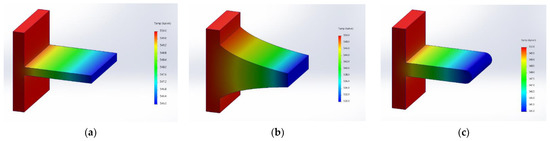
Figure 9.
Temperature distribution of (a) rectangular; (b) exponential; (c) convex profile for aluminum alloy (AA6061).
The efficiency of the fin for several values of internal heat generation versus the thermal expansion coefficient can be seen in Figure 10a. From the graph, we can depict that a smaller value of efficiency is higher and decreases gradually. Moreover, as the value of heat production is increased, the efficiency is enhanced. This shows that by keeping the values of smaller and values of higher we can obtain efficient fins. A similar observation can be observed with the three different profiles considered in our study, but the exponential fin has fin efficiency in general.
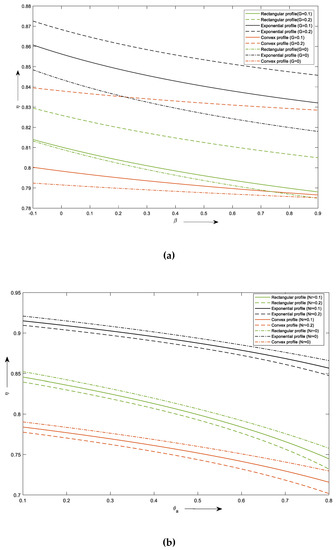
Figure 10.
Influence of: (a) G and on fin efficiency; (b) Nr and on fin efficiency.
Figure 10b shows the efficiency of the fin versus for different values of a radiative parameter. It can be observed that for a lower value of a radiative parameter and the efficiency is higher and reduces gradually as the values are increased. An exponential profile with a lower value of and can be used to obtain the higher efficiency of the fin.
7. Conclusions
The framework for temperature rate is presented in a longitudinal fin subject to internal heating, variable thermal conductivity and convective radiation. The Rosseland theory is used to determine the features of a radiative phenomenon. DTM approximations are followed for the simulation process. Graphical explanations are manifested for the consequence of parameters in the heat transfer of the fin. The key findings of this analysis are as follows:
- Upon enhancing the convection–conduction parameter, the thermal dispersal in the fin lowers.
- A strengthened heat transfer fine is observed for the radiative-conduction constant.
- The thermal rate of the fin improves with an augmented change in a heat-generating parameter.
- This scrutiny convinces us that DTM algorithms are efficient and convenient methods for nonlinear differential systems.
- Thermal radiation and natural convection have a significant influence on the cooling of a fin.
- In the steady state, fins dissipate heat to the environment because heat production within a fin surges the temperature of the fins.
- The temperature scatters of a fin for different profiles are calculated using the ANSYS software, considering aluminum alloy (AA6061) as the fin body material. The fin base has a higher temperature and reduces drastically toward the fin tip.
This work can be extended by considering the porous fins in the presence of a magnetic field and also by considering the porous fins with the nano and hybrid nanofluid with the effect of the shape factor.
Author Contributions
Conceptualization, M.K.A. and P.V.A.S.; Data curation, S.V.K.V.; Formal analysis, P.J.; Funding Hacquisition, P.J.; Methodology, A.M.Z.; Software, B.N.H.; Validation, C.S.K.R.; Writing—original draft, P.V.A.S.; Writing—review & editing, N.A.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work received no external funds.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All the data are present in this article.
Acknowledgments
The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University, Abha 61413, Saudi Arabia, for funding this work through a research group program under grant number R.G.P.-2/21/43. This research received funding support from the NSRF via the Program Management Unit for Human Resources & Institutional Development, Research and Innovation, (grant number B05F650018).
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| fin cross-section (m2) | |
| exponential parameter | |
| heat transfer coefficient (wm−1k−1) | |
| heat conduction (wm−1k−1) | |
| radiative parameter | |
| heat generation parameter | |
| fin length (m) | |
| convective parameter | |
| temperature (k) | |
| transformed function | |
| original analytic function | |
| fin base temperature | |
| thermal expansion coefficient (K−1) | |
| dimensional constant (K−1) | |
| efficiency of the fin | |
| transformed equation | |
| dimensionless temperature | |
| ambient temperature | |
| base of the fin |
References
- Kraus, A.D.; Aziz, A.; Welty, J.R. Extended Surface Heat Transfer; John Wiley: Hoboken, NJ, USA, 2002. [Google Scholar]
- Gireesha, B.J.; Sowmya, G. Heat transfer analysis of an inclined porous fin using Differential Transform Method. Int. J. Ambient Energy 2022, 43, 3189–3195. [Google Scholar] [CrossRef]
- Oleśkowicz-Popiel, C.; Blanch, R.O.; Wojtkowiak, J. Efficiency of the horizontal single pin fin subjected to free convection and radiation heat transfer. Heat Transf. Eng. 2007, 28, 299–309. [Google Scholar] [CrossRef]
- Minkler, W.S.; Rouleau, W.T. The Effects of Internal Heat Generation on Heat Transfer in Thin Fins. Nucl. Sci. Eng. 1960, 7, 400–406. [Google Scholar] [CrossRef]
- Venkitesh, V.; Mallick, A. Thermal analysis of a convective–conductive–radiative annular porous fin with variable thermal parameters and internal heat generation. J. Anal. Calorim. 2022, 147, 1519–1533. [Google Scholar] [CrossRef]
- Majhi, T.; Kundu, B. New Approach for Determining Fin Performances of an Annular Disc Fin with Internal Heat Generation. In Advances in Mechanical Engineering; Springer: Singapore, 2020; pp. 1033–1043. [Google Scholar]
- Das, R.; Kundu, B. Prediction of Heat-Generation and Electromagnetic Parameters from Temperature Response in Porous Fins. J. Thermophys. Heat Transf. 2021, 35, 761–769. [Google Scholar] [CrossRef]
- Sobamowo, M.G. Analysis of convective longitudinal fin with temperature-dependent thermal conductivity and internal heat generation. Alex. Eng. J. 2017, 56, 1–11. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Exact heat-transfer solutions to radial fins of general profile. J. Heat Trans. 2016, 30, 89–93. [Google Scholar] [CrossRef]
- Ndlovu, P.L.; Moitsheki, R.J. Steady state heat transfer analysis in a rectangular moving porous fin. Propuls. Power Res. 2020, 9, 188–196. [Google Scholar] [CrossRef]
- Singla, R.K.; Das, R. Application of decomposition method and inverse prediction of parameters in a moving fin. Energy Convers. Manag. 2014, 84, 268–281. [Google Scholar] [CrossRef]
- Shah, N.A.; Wakif, A.; El-Zahar, E.R.; Ahmad, S.; Yook, S.-J. Numerical simulation of a thermally enhanced EMHD flow of a heterogeneous micropolar mixture comprising (60%)-ethylene glycol (EG), (40%)-water (W), and copper oxide nanomaterials (CuO). Case Stud. Therm. Eng. 2022, 35, 102046. [Google Scholar] [CrossRef]
- Sajjan, K.; Shah, N.A.; Ahammad, N.A.; Raju, C.S.K.; Kumar, M.D.; Weera, W. Nonlinear Boussinesq and Rosseland approximations on 3D flow in an interruption of Ternary nanoparticles with various shapes of densities and conductivity properties. AIMS Math. 2022, 7, 18416–18449. [Google Scholar] [CrossRef]
- Aziz, A.; Khani, F. Convection-radiation from a continuously moving fin of variable thermal conductivity. J. Frankl. Inst. 2011, 348, 640–651. [Google Scholar] [CrossRef]
- Sowmya, G.; Sarris, I.E.; Vishalakshi, C.s.; Kumar, R.S.V.; Prasannakumara, B.C. Analysis of transient thermal distribution in a convective–radiative moving rod using two-dimensional differential transform method with MULTIVARIATE pade approximant. Symmetry 2021, 13, 1793. [Google Scholar] [CrossRef]
- Hatami, M.; Ganji, D.D. Thermal performance of circular convective-radiative porous fins with different section shapes and materials. Energy Convers. Manag. 2013, 76, 185–193. [Google Scholar] [CrossRef]
- Pasha, A.v.; Jalili, P.; Ganji, D.D. Analysis of unsteady heat transfer of specific longitudinal fins with Temperature-dependent thermal coefficients by DTM. Alex. Eng. J. 2018, 57, 3509–3521. [Google Scholar] [CrossRef]
- Torabi, M.; Aziz, A.; Zhang, K. A comparative study of longitudinal fins of rectangular, trapezoidal and concave parabolic profiles with multiple nonlinearities. Energy 2013, 51, 243–256. [Google Scholar] [CrossRef]
- Zhang, H.; Sun, K. Conduction from longitudinal fin of rectangular profile with exponential vary heat transfer coefficient. Adv. Mater. Res. 2013, 614–615, 311–314. [Google Scholar] [CrossRef]
- Buikis, A.; Pagodkina, I. Comparison of Analytical and Numerical Solutions for a Two-Dimensinal Longitudinal Fin of Rectangular Profile. Latv. J. Phys. Technol. Sci. 1996, 33, 177–187. [Google Scholar]
- Kezzar, M.; Tabet, I.; Eid, M.R. A new analytical solution of longitudinal fin with variable heat generation and thermal conductivity using DRA. Eur. Phys. J. Plus 2020, 135, 120. [Google Scholar] [CrossRef]
- Shi, Q.H.; Hamid, A.; Khan, M.I.; Naveen Kumar, R.; Punith Gowda, R.J.; Prasannakumara, B.C.; Shah, N.A.; Khan, S.U.; Chung, J.D. Numerical study of bio-convection flow of magneto-cross nanofluid containing gyrotactic microorganisms with activation energy. Sci Rep. 2021, 11, 16030. [Google Scholar] [CrossRef] [PubMed]
- Afsharpanah, F.; Ajarostaghi, S.S.M.; Arıcı, M. Parametric study of phase change time reduction in a shell-and-tube ice storage system with anchor-type fin design. Int. Commun. Heat Mass Transf. 2022, 137, 106281. [Google Scholar] [CrossRef]
- Afsharpanah, F.; Cheraghian, G.; Hamedani, F.A.; Shokri, E.; Soheil, S.; Ajarostaghi, M. Utilization of Carbon-Based Nanomaterials and Plate-Fin Networks in a Cold PCM Container with Application in Air Conditioning of Buildings. Nanomaterials 2022, 12, 1927. [Google Scholar] [CrossRef] [PubMed]
- Sabu, A.S.; Wakif, A.; Areekara, S.; Mathew, A.; Shah, N.A. Significance of nanoparticles’ shape and thermo-hydrodynamic slip constraints on MHD alumina-water nanoliquid flows over a rotating heated disk: The passive control approach. Int. Commun. Heat and Mass Transf. 2021, 129, 105711. [Google Scholar] [CrossRef]
- Salhi, J.E.; Ajarostaghi, S.S.M.; Zarrouk, T.; Pour, M.S.; Salhi, N.; Salhi, M. Turbulence and thermo-flow behavior of air in a rectangular channel with partially inclined baffles. Energy Sci. Eng. 2022, 10, 3540–3558. [Google Scholar] [CrossRef]
- Demartini, L.C.; Vielmo, H.A.; Möller, S.v. Numeric and Experimental Analysis of the Turbulent Flow through Channel With Baffle Plates. J. Braz. Soc. Mech. Sci. Eng. 2004, 28, 233–241. [Google Scholar] [CrossRef]
- Kadijani, O.N.; Moghadam, H.K.; Ajarostaghi, S.S.M.; Asadi, A.; Pour, M.S. Hydrothermal performance of humid air flow in a rectangular solar air heater equipped with V-shaped ribs. Energy Sci. Eng. 2022, 10, 2276–2289. [Google Scholar] [CrossRef]
- Zhou, J.K. Differential Transformation Method and Its Application for Electrical Circuits; Hauzhang University Press: Wuhan, China, 1986. [Google Scholar]
- Ayaz, F. Solutions of the system of differential equations by differential transform method. Appl. Math. Comput. 2004, 147, 547–567. [Google Scholar] [CrossRef]
- Chen, C.K.; Ho, S.H. Solving partial differential equations by two-dimensional differential transform method. Appl. Math. Comput. 1999, 106, 171–179. [Google Scholar]
- Ayaz, F. On the two-dimensional differential transform method. Appl. Math. Comput. 2003, 143, 361–374. [Google Scholar] [CrossRef]
- Kanth, A.S.V.R.; Aruna, K. Differential transform method for solving linear and non-linear systems of partial differential equations. Phys. Lett. Sect. A Gen. At. Solid State Phys. 2008, 372, 6896–6898. [Google Scholar] [CrossRef]
- Fallo, N.; Moitsheki, R.J.; Makinde, O.D. Analysis of heat transfer in a cylindrical spine fin with variable thermal properties. Defect Diffus. Forum 2018, 387, 10–22. [Google Scholar] [CrossRef]
- Chiba, R. A Series Solution for Heat Conduction Problem with Phase Change in a Finite Slab. Abstr. Appl. Anal. 2014, 684293. [Google Scholar] [CrossRef]
- Moradi, A.; Hayat, T.; Alsaedi, A. Convection-radiation thermal analysis of triangular porous fins with temperature-dependent thermal conductivity by DTM. Energy Convers. Manag. 2014, 77, 70–77. [Google Scholar] [CrossRef]
- Ndlovu, P.L. Analytical study of transient heat transfer in a triangular moving porous fin with temperature dependant thermal properties. Defect Diffus. Forum 2019, 393, 31–46. Available online: www.scientific.net/DDF.393.31 (accessed on 1 August 2022). [CrossRef]
- Abbasi, H.; Javed, A. Implementation of differential transform method (DTM) for large deformation analysis of cantilever beam. IOP Conf. Ser. Mater. Sci. Eng. 2020, 899, 012003. [Google Scholar] [CrossRef]
- Aksoy, G. Application of differential transformation method for an annular fin with variable thermal conductivity. Therm. Sci. 2021, 315. [Google Scholar] [CrossRef]
- Joneidi, A.A.; Ganji, D.D.; Babaelahi, M. Differential Transformation Method to determine fin efficiency of convective straight fins with temperature dependent thermal conductivity. Int. Commun. Heat Mass Transf. 2009, 36, 757–762. [Google Scholar] [CrossRef]
- Franco, A. An analytical method for the optimum thermal design of convective longitudinal fin arrays. Heat Mass Transf. 2009, 45, 1503–1517. [Google Scholar] [CrossRef][Green Version]
- Languri, E.M.; Ganji, D.D.; Jamshidi, N. Variational Iteration and Homotopy perturbation methods for fin efficiency of convective straight fins with temperature dependent thermal conductivity. In Proceedings of the 5th WSEAS International Conference on Fluid Mechanics (Fluids 08), Acapulco, Mexico, 25–27 January 2008; Volume 25. [Google Scholar]
- Arslanturk, C. A decomposition method for fin efficiency of convective straight fins with temperature-dependent thermal conductivity. Int. Commun. Heat Mass Transf. 2005, 32, 831–841. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).