Abstract
In recent years, the issue of maximizing submodular functions has attracted much interest from research communities. However, most submodular functions are specified in a set function. Meanwhile, recent advancements have been studied for maximizing a diminishing return submodular (DR-submodular) function on the integer lattice. Because plenty of publications show that the DR-submodular function has wide applications in optimization problems such as sensor placement impose problems, optimal budget allocation, social network, and especially machine learning. In this research, we propose two main streaming algorithms for the problem of maximizing a monotone DR-submodular function under cardinality constraints. Our two algorithms, which are called and , have , of approximation ratios and , , respectively. We conducted several experiments to investigate the performance of our algorithms based on the budget allocation problem over the bipartite influence model, an instance of the monotone submodular function maximization problem over the integer lattice. The experimental results indicate that our proposed algorithms not only provide solutions with a high value of the objective function, but also outperform the state-of-the-art algorithms in terms of both the number of queries and the running time.
MSC:
03G10; 06C05; 06D99; 30E10; 65K10
1. Introduction
Submodular function maximization problems have recently received great interest in the research community. A satisfactory explanation for this attraction is the prevalence of optimization problems related to submodular functions in many real-world applications [1]. Prominent examples include sensor placement problems [2,3] and facility location [4] in operational improvement, the influence maximization problem in viral marketing [5,6], document summarization [7], experiment design [8], dictionary learning [9] in machine learning, etc. These problems can be presented with the concept of submodularity, and effective algorithms have been developed taking advantage of the submodular function [10]. Given a ground set E, a function f: is called submodular if for all ,
The submodularity of a submodular function f is equivalent to the property diminishing return, i.e., for any and , it holds.
and the set function f is called monotone if
The submodular function maximization problem aims to select a subset A of the ground set E to maximize .
Most existing studies of the submodular function maximization problem consider submodular functions identified over a set function. It means that the problem has the input as a subset of the ground set and returns an actual value. However, there are many real-world situations in which it is crucial to know whether an element is selected and how many copies of that element should be chosen. In other words, the problem considers submodular functions over a multiset, under the name submodular function on the integer lattice [11]. The submodularity defined on the integer lattice differs from set functions because it does not equate to the diminishing return property. Some notable examples include the optimal budget allocation problem [12], document summarization and sensor placement [13], the submodular welfare problem [14], and maximization of influence spread with partial incentives [15]. The definitions of a submodular function and diminishing return submodular function on the integer lattice are as follows:
A function is a submodular function on the integer lattice if for all
where and denote the coordinate-wise min and max operations, respectively.
A function is called diminishing return submodular (DR-submodular), if for all with
where and denote the unit vector with coordinate e being 1 and the other elements are 0.
The submodularity defined on the integer lattice differs from the set functions because it does not equate to the diminishing return property. In other words, lattice submodularity is weaker than DR-submodularity, i.e., a lattice submodular function may not be a DR-submodular function, but any DR-submodular function is a lattice submodular one [11]. Due to this cause, developing approximation algorithms is challenging; even for a single cardinality constraint, we need a more complicated method, such as partial enumeration [12,13]. Nevertheless, the diminishing return property of the DR-submodular function maximization problem often plays a fundamental role in some practical problems, such as optimizing budget allocation among channels and influencers [12], optimal budget allocation [13], and online submodular welfare maximization [14].
There have been many approaches to solving the problem of maximizing the submodular function under different constraints and contexts in the last decade. Two notable approaches to this problem are greedy algorithms [16,17,18,19] and streaming algorithms [20,21,22]. Plenty of studies show that the greedy method is often used for this optimization problem because it outputs a better result than other methods due to its “greedy” operation [16,23,24]. Understandably, the greedy method always scans data many times to find the best. However, this causes its algorithms to have a long runtime; it cannot even be applied to big data. Contrary to the greedy method, the streaming method scans the data once. As each element in the dataset arrives in order, the streaming algorithm must decide whether that element is selected before the next element arrives. Thus, the result of this method may not be as good as the result of greedy, because the elements it selects are not the best, but meet the selection condition. However, the outstanding advantage of the streaming method is that it runs much faster than the greedy method [25]. There are many studies that have used the streaming method to resolve the issue of submodular function maximization. Those studies have shown the advantages of the streaming method compared to the greedy method. Some prominent studies include using the streaming algorithm for maximizing k-submodular functions under budget constraints [26], optimizing a submodular function under noise by streaming algorithms [27], maximizing a monotone submodular function by multi-pass streaming algorithms [20], and using fast streaming for the problem of submodular maximization [22].
Attracted by the usefulness of the maximizing DR-submodular function on the integer lattice issue in many practical problems, numerous studies on this problem have recently been published. These publications consider the problem under many different constraints and use greedy or streaming methods as the standard approach. Some prominent examples include the use of a fast double greedy algorithm to maximize the non-monotone DR submodular function [24], using a threshold greedy algorithm to maximize the monotone DR submodular constraint knapsack over an integer lattice [28], combining the threshold greedy algorithm with a partial element enumeration technique to maximize the monotone DR submodular knapsack constraint over an integer lattice [11], using a streaming method to maximize DR-submodular functions with d-knapsack constraints [29], using a one-pass streaming algorithm for DR-submodular maximization with a knapsack constraint over the integer lattice [30], and using streaming algorithms for maximizing a monotone DR-submodular function with a cardinality constraint on the integer lattice [31].
Our contribution. In this paper, we focus on the maximization of monotone DR-submodular function under cardinality constraint on the integer lattice (the problem in Definition 2). In surveying the literature, there are two novel methods for this problem. First, Soma et al. [11] proposed the Cardinality constraint/DR-submodular algorithm (called ), which interpolates between the classical greedy algorithm and a truly continuous algorithm. This algorithm achieves an approximation ratio of () in complexity. Second, Zhang et al. [31] first devised a streaming algorithm based on Sieve streaming [32]. Zhang’s method achieves an approximation ratio of () in memory and query complexity. Inspired by Zhang’s method [31], our study based on the streaming method devises two improved streaming algorithms for the problem and obtains some positive results compared to state-of-the-art algorithms. Specifically, our main contributions are as follows.
- To resolve the problem, we first devise an algorithm (called ) to handle each element by scanning the data with the assumption of a known optimal value (). We prove that guarantees the theoretical result with an approximation ratio of . Next, we devise a -approximation streaming algorithm (called Stepping-Stone algorithm), which has the procedure role to calculate the threshold for the main algorithm. Later, based on and Stepping-Stone algorithms, we provide two main streaming algorithms to solve this problem. They are named and . Because cannot be determined in actual situations, we estimate based on a conventional method by observing where . Based on estimated , , a one-pass streaming algorithm, has an approximation ratio of () and takes queries. For , we first find a temporary result that satisfies the cardinality constraint by the Stepping-Stone algorithm. Subsequently, we increase the approximation solution ratio in by finding elements that hold the threshold restriction of the above temporary result. The is a multi-pass streaming algorithm that scans passes, takes queries, and returns an approximation ratio of .
- We further investigate the performance of our algorithms by performing some experiments on some datasets of practical applications. We run four algorithms, , [11], and [31], to compare their performance. The results indicate that our algorithms provide solutions with a theoretically guaranteed value of the objective function and outperform the state-of-the-art algorithm in both the number of queries and the runtime.
Table 1 shows how our algorithms compare theoretical properties with current state-of-the-art algorithms for the problem of maximizing monotone DR submodular functions with a cardinality constraint in the integer lattice.

Table 1.
State-of-the-art algorithms for the problem of monotone DR-submodular function maximization with a cardinality constraint on the integer lattice in terms of time complexity.
Organization. The structure of our paper is as follows: Section 1 introduces the development situation of the submodular function maximization on a-set and multi-set. Primarily, we focus on maximizing the monotone DR-submodular function on the integer lattice under cardinality constraint and present the main contributions of our study. Section 2 reviews the related work. The definition of the problem and some notation are introduced in Section 3. Section 4 contains our proposed algorithms and theoretical analysis. Section 5 shows the experimental results and evaluation. Finally, Section 6 concludes the paper and future work.
2. Related Work
A considerable amount of literature has been published on the maximization of monotone submodular functions under many different constraints over many decades. Nemhauser et al. [33] are pioneers in studying the approximations for maximizing submodular set functions in combinatorial optimization and machine learning. They proved that the standard greedy algorithm gives a ()-approximation under a matroid constraint and a ()-approximation under a cardinality constraint. Their method served as a model for further development. Later, Sviridenko [34] developed an improved greedy algorithm for maximizing a submodular set function subject to a knapsack constraint. This algorithm achieves a ()-approximation with time complexity for a knapsack constraint. Subsequently, Calinescu et al. [35] first devise a ()-approximation algorithm for maximizing a monotone submodular function subject to a matroid constraint. This method combines a continuous greedy algorithm and pipage rounding. The pipage rounding rounds the approximate fractional solution of the continuous greedy approach to obtain an integral feasible solution. Recently, Badanidiyuru et al. [36] design a ()-approximation algorithm with any fixed constraint for maximizing submodular functions. This algorithm takes time complexity for the cardinality constraint.
Several studies have recently begun investigating the maximization of DR-submodular functions on the integer lattice under various constraints. Soma et al. (2014) [13] studied the monotone DR-submodular function maximization over integer lattices under a knapsack constraint. They proposed a simple greedy algorithm, which has an approximation ratio of () and a pseudo-polynomial time complexity. Next, Soma et al. (2018) [11] continued to develop polynomial-time approximation algorithms for the problem of DR-submodular function maximization under a cardinality constraint, a knapsack constraint, and a polymatroid constraint on the integer lattice, respectively. For the cardinality constraint, they devised an algorithm based on the decreasing threshold greedy framework. For the polymatroid constraint, they developed an algorithm based on an extension of continuous greedy algorithms. For the knapsack constraint, they used the decreasing threshold greedy framework as the algorithm of the cardinality constraint. However this algorithm takes its initial solution as an input, whereas the algorithm for cardinality constraints always uses the zero vector as the initial solution. All three algorithms have polynomial time and achieve a ()-approximation ratio. Besides, Some et al. (2017) [37] also studied the problem of non-monotone DR-submodular function maximization. They proposed a double greedy algorithm, which has -approximation and . Subsequently, Gu et al. (2020) [24] study the problem of maximizing the non-monotone DR-submodular function on the bounded integer lattice. They propose a fast double greedy algorithm that improves runtime. Their result achieves a -approximation algorithm with a time complexity. Liu et al. (2021) [29] develop two streaming algorithms for maximizing DR-submodular functions under the d-knapsack constraints. The first is a one-pass streaming algorithm that achieves a -approximation with memory complexity and update time per element, where and are the upper and lower bounds for the cost of each item in the stream. The second is an improved streaming algorithm to reduce the memory complexity to with an unchanged approximation ratio and query complexity. Zhang et al. (2021) [31] based on the Sieve streaming method to develop a streaming algorithm for the problem of monotone DR-submodular function under cardinality constraint on the integer lattice. This algorithm achieves an approximation ratio of and takes complexity. This is the problem that we study in this paper. Most recently, Tan et al. (2022) [30] design an one-pass streaming algorithm for the problem of DR-submodular maximization with a knapsack constraint over the integer lattice, called DynamicMRT, which achieves a -approximation ratio, a memory complexity , and query complexity per element for the knapsack constraint K. Meanwhile, Gong et al. (2022) [28] consider the problem of non-negative monotone DR-submodular function maximization over a bounded integer lattice. They present a deterministic algorithm and theoretically reduce its runtime to a new record, , (where and is a cost function defined in E) with the approximate ratio of ().
All the studies mentioned above consider the problem of maximizing the submodular function on a set function or maximizing the DR-submodular function on the integer lattice under different constraints. Only the studies of Soma et al. in [11] and Zhang et al. in [31] consider the problem of , as mentioned in the contribution section. Motivated by these studies, we proposed two improved streaming algorithms for the problem. Our algorithms achieve better than state-of-the-art methods through theoretical analysis and experimental results.
3. Preliminaries
This section introduces the definitions of the monotone DR-submodular, problem and its associated notations. Table 2 summarizes the usually used notations in this paper.

Table 2.
Table of the usually used notations in this paper.
3.1. Notation
For a positive integer , denotes the set . Given a ground set , we denote the i-th entry of a vector by , and for each , we define the e-th unit vector with if and if .
For , denotes the multiset where the element e appears times and with a subset , and . According to the definition of the vector norm, we have and .
For two vectors , signifies then . Furthermore, given , and denote the coordinate-wise maximum and minimum, respectively. This means that and . In addition, denotes the multiset where the element e appears + times. Thus, we can infer .
3.2. Definition
For function , we define .
Definition 1
(Monotone DR-submodular function). A function is monotone if ) for all with and f is said to be diminishing return submodular (DR-submodular), if
Definition 2
(Maximization of monotone DR-submodular function under cardinality constraint on the integer lattice— problem). Let , and an integer , we consider the DR-submodular function under cardinality constraint as follows
4. Proposed Algorithm
This section presents descriptions and theoretical analysis of the algorithms we have proposed for the problem, including a streaming algorithm with the assumption that the optimal value is known (), the Stepping-Stone algorithm and two main streaming algorithms ().
4.1. Streaming Algorithm with Approximation Ratio of
First, we propose , a single-pass streaming algorithm for the problem under the assumption that the optimal value of the objective function is known. Afterwards, we use the traditional method to estimate the optimal value and devise the main one-pass streaming algorithm called .
4.1.1. Algorithm with Knowing Optimal Value—
Algorithm description. The detail of is fully presented in Algorithm 1.
| Algorithm 1: |
Input: ,, k, , a guess of optimal value v Output: A vector 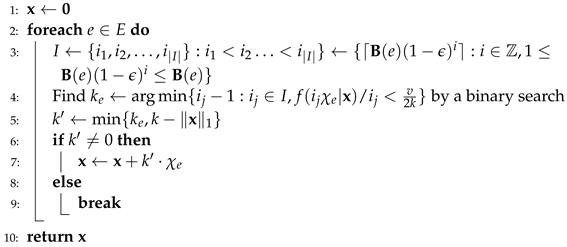 |
We assume that the optimal value of the objective function of is already known. is created to find vector using this . Given a known optimal value v that satisfies for any . When each element e arrives, we find a set I, which is the set of positive integers predicted to be the number of copies of e. Then, we use the binary search with threshold to find the minimum that holds . We denote by the number of copies of e that adds the result vector . The value is the minimum of two values and the rest of elements ’ in the cardinality k. If is equal to 0, then e is not selected in . Otherwise, e is selected in with copies.
Theoretical analysis. Lemma 1, Theorem 1, and their proofs demonstrate the theoretical solution guarantee of . On the basis of that, we devise the first main streaming algorithm for the problem.
Lemma 1.
We have .
Proof.
Assume that where with some . We have and
Therefore, . From the combination of the selection and the monotonicity of f, we have the following.
The proof is completed. □
Theorem 1.
For any and , the Algorithm 1 takes queries and returns a solution satisfying .
Proof.
The Algorithm 1 scans only one time over E and each incoming element e, it takes queries to find . The total number of required queries of the algorithm is .
Denote and as the solution at the beginning of iteration i and the additional vector in the current solution at iteration i, respectively. We consider two following cases:
Case 1. If , we have thus:
Case 2. If , after ending the main loop, we have for all . Therefore:
where the second equality follows from the lattice identity for . We have . The proof is completed. □
4.1.2. -Approximation Streaming Algorithm— Algorithm
Algorithm description. The detail of this algorithm is fully presented in Algorithm 2.
| Algorithm 2: Streaming-I algorithm () |
Input: ,, k, Output: A -approximation solution  |
Based on the analysis of , and the working frame of the Sieve streaming algorithm [38], we design the algorithm for the problem with the following main idea. We find a set of solutions of , where and O is the set of values that changes according to the maximum value of the unit standard vector on the arriving elements. Besides, we find a set I, which contains positive integers predicted to be the number of copies of each element e if e is selected in . For each solution , , the algorithm finds , is the smallest value in I so that the current element e satisfies the condition in line 8 by binary search. Then, we choose , which is the minimum value between and . If is not equal to 0, this means that e is selected in with copies. Otherwise, e is not selected in . In the end, the result is , which makes maximal.
Theoretical analysis. We analyze the complexity of , stated in Theorem 2.
Theorem 2.
is a single-pass streaming algorithm, has an approximation ratio of and takes queries.
Proof.
By the definition of O, there exists an integer i such that
By applying the proof of Theorem 1, and the working frame of the Sieve streaming algorithm in [38], we obtain:
The proof is completed. □
4.2. Streaming Algorithm with Approximation Ratio of
In this section, we introduce two more algorithms for the problem, including one with the role of a stepping stone (called Stepping-Stone algorithm) and the second main algorithm (called algorithm) in our study.
4.2.1. -Approximation Streaming Algorithm—Stepping-Stone Algorithm
Algorithm description. The detail of this algorithm is fully presented in Algorithm 3.
| Algorithm 3: -approximation algorithm (Stepping-Stone algorithm) |
Input: ,, k, Output: A vector 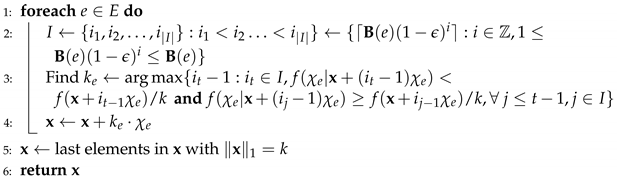 |
We design the Stepping-Stone algorithm, which is a -approximation streaming algorithm. The Stepping-Stone algorithm differs from and in that it only selects elements for exactly one solution and has an approximately constant value. In contrast, the other two algorithms find multiple solution candidates and choose the best candidate.
In more detail, the main idea of this algorithm differs from , that is, the Stepping-Stone algorithm is a single-pass streaming algorithm and finds without relying on a given v. In this way, after finding the set I as , for each element , is the largest so that it meets the conditions in line 3. Finally, the output contains the last elements of with .
Theoretical analysis. Lemmas 2–4, and Theorem 3 clarify the theoretical analysis of the Stepping-Stone algorithm.
Lemma 2.
After each iteration of the Stepping-Stone algorithm, we have .
Proof.
Due to the definition of I, after each iteration of the main loop, we have . Similarly to the proof of Lemma 2, we have . By selection of the algorithm, for we have
Therefore:
The proof is completed. □
Lemma 3.
After the main loop of the Stepping-Stone algorithm, we have .
Proof.
Denote is right before the element e starts to proceed. We have the following.
which implies the proof. □
Lemma 4.
At the end of the Stepping-Stone algorithm, we have .
Proof.
If , then and Lemma 4 holds. We consider the case . Assume that , , and where is added to immediately after and .
We further consider two cases.
Case 1. If , we have and
Case 2. If . Denote and . We have and . Similarly to the proof of Lemma 2, we have and thus . Let , then
implying that . Therefore:
Hence, . Combined with the fact that , we have , which completes the proof. □
Theorem 3.
The Stepping-Stone algorithm is a single-pass streaming algorithm that takes and provides an approximation ratio of .
Proof.
The algorithm scans only one time over the ground set E and each element e, it calculates for all to find . This task takes at most queries. Thus, the total number of required queries is . For the proof of the approximation ratio, by using Lemmas 3 and 4, we have:
The proof is completed. □
4.2.2. -Approximation Streaming Algorithm— Algorithm
Algorithm description. The detail of is fully presented in Algorithm 4.
| Algorithm 4: -approximation algorithm () |
Input: ,, k, Output: A vector  |
We propose a -approximation algorithm, called . It is a multi-pass streaming algorithm and is based on the output of the Stepping-Stone algorithm (Algorithm 3) to compute the threshold of of each element e. The of each e is the minimal value , so that . The threshold decreases times after each iteration.
Theoretical analysis. Lemma 5 and Theorem 4 clearly demonstrate the theoretical solution-ability guarantee of the algorithm.
Lemma 5.
In the algorithm, at any iteration of the outer loop, we have:
Proof.
For the first iteration of the outer loop, we have , and thus
Thus, , Lemma 5 is valid. For the latter iterations, the marginal gain of any element e with current vector is less than the threshold of previous iterations of the outer loop, i.e, for . Then,
The proof is completed. □
Theorem 4.
The algorithm is a multi-pass streaming algorithm that scans passes over the ground set, takes queries, and returns an approximation ratio of .
Proof.
We consider following cases:
Case 1. If , after the last iteration of the outer loop we have:
Hence, .
Case 2. If . Denote as after i-th update, is the vector added to at the i-th update, and the final solution , Lemma 5 gives
Rearrange the above inequality for , and we have:
Therefore, , the proof is completed. □
5. Experiment
We conducted experiments based on the budget allocation problem over the bipartite influence model [39]. This problem is an instance of the monotone submodular function maximization problem over the integer lattice under a constraint [3]. As mentioned above, we consider the problem under a cardinality constraint.
Suppose that we consider the context of the algorithmic marketing approach. The budget allocation problem can be explained as follows. In a marketing strategy, one of the crucial choices is deciding how much of a given budget to spend on different media, including television, websites, newspapers, and social media, to reach as many potential customers as possible. In other words, given a bipartite graph , where V is a bipartition of the vertex set, denotes the set of source nodes (such as ad sources), denotes the set of target nodes (such as people/customers), and is the edge set. Each source node has a capacity , which represents the number of available budgets of the ad source corresponding to . Each edge is associated with a probability , which means that putting an advertisement to a slot of activated customer with probability . Each source node will be allocated a budget such that where denotes a total budget capacity. The object value function f, which means the expected number of target vertices activated by , is defined as follows [3].
All experiments are carried out to compare the performance of , , and . We evaluated the performance of each algorithm based on the number of oracle queries, runtime, and influence .
5.1. Experimental Setting
Datasets. For the exhaustive experiment, we choose two datasets of different sizes regarding the number of nodes and edges. They are two real networks that are bipartite, undirected type and weighted of the KONECT (http://konect.cc) (accessed on 1 September 2022) project [40]: the network of the FilmTrust ratings project, and the NIPS is a doc-word dataset of NIPS full papers. The weighted of the rating datasets is the rating value, and one of the doc-word datasets is the number of occurrences of the word in the document. The description of the datasets is presented in Table 3.

Table 3.
Statistics of datasets. All datasets have the type of bipartite and undirected.
Environment. We conducted our experiments on a Linux machine with Intel Xeon Gold 6154 (720) @ 3.700 GHz CPUs and 3TB RAM. Our implementation is written in Python.
Parameter Setting. We set the parameters as follows: , for all experiments. Because FilmTrust has a small set of nodes, . Meanwhile, NIPS has a large set of nodes and edges, so . Besides, we do a simple preprocessing for the edge-weighted of the datasets, which refers to the probability . For FilmTrust, edge weighted is the ratio of the rated value and the maximum rated value (). While, it is the ratio of the number of the word’s occurrences in the document and the number of words in the document () for NIPS.
5.2. Experimental Results
This section discusses the experimental results to clarify the benefits and drawbacks of the algorithms through three metrics: number of oracle queries, runtime, and influence. Two outstanding advantages of our algorithms over and are (1) our algorithms’ runtime and the number of oracle queries are faster many times than those of and ;(2) the influence of our algorithms is often smaller than that of and . However, for some datasets, the influence of and can be equal to or greater than that of and if we suitably set parameters B and k for the dataset. Figure 1 clearly shows the results achieved.
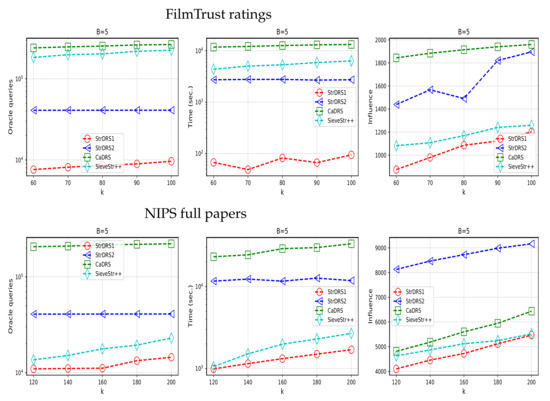
Figure 1.
The results of the experimental comparison of algorithms on the datasets.
Oracle queries and Runtime. Because most of the execution time of the algorithms is consumed by the number of queries to compute the function f, the runtime is directly proportional to the number of oracle queries. In detail, for comparing to , the number of oracle queries of is to times smaller than ; and the runtime of is to times faster than . For comparing to , the number of oracle queries of is to times smaller than ; and the runtime of is to times faster than . Especially, even if k increases many times, the number of queries and runtime of only increase very small compared to the other algorithms. This cause makes it possible for us to mistake them for constants when looking at the charts. Table 4 clearly shows the variation in the number of queries.

Table 4.
Statistics of the number of queries.
Influence. Through the analysis of experimental results, the difference in the influence value of the algorithms is as follows. For the comparison of and , the influence of is to times smaller than . For the comparison of and , the influence of is to times smaller than for FilmTrust dataset. However, for NIPS dataset, the influence of is to times greater than in this parameters set. Generally, because uses a greedy technique, the influence of this algorithm is always at its best. As k increases, this value of can reach the best values. On the contrary, the remaining three algorithms use streaming techniques, so it is difficult to achieve the same influence as ’s. However, the difference in the influence of streaming and greedy algorithms is not too large. Especially, this gap will decrease as k increases. Thus, the time benefit of our algorithms is a significant strength against this disparity in influence.
For the convenience of the readers, we summarize the experimental results in Table 5.

Table 5.
Statistical comparison of experimental results.
6. Conclusions and Future Work
This paper studies the maximization of monotone DR-submodular functions with a cardinality constraint on the integer lattice. We propose two streaming algorithms that have determined approximation ratios and significantly reduce query and time complexity compared to state-of-the-art algorithms. We conducted some experiments to evaluate the efficiency of our algorithms and novel algorithms for this problem. The results indicate that our algorithms are highly scalable and outperform the compared algorithms in terms of both runtime and number of queries, and the influence is slightly smaller.
For our future work, one direction is to study the monotone DR-submodular function maximization problem under a polymatroid constraint and knapsack constraint. In another direction, we consider the maximization of the non-monotone DR-submodular function under a cardinality constraint.
Author Contributions
Conceptualization, B.-N.T.N. and V.S.; formal analysis, B.-N.T.N.; investigation, B.-N.T.N. and P.N.H.P.; methodology, B.-N.T.N., P.N.H.P. and V.-V.L.; project administration, B.-N.T.N.; resources, B.-N.T.N.; software, B.-N.T.N. and P.N.H.P.; supervision, V.S.; validation, V.S.; writing—original draft, B.-N.T.N.; Writing—review and editing, B.-N.T.N., P.N.H.P., V.-V.L. and V.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by Ho Chi Minh City University of Food Industry (HUFI), Ton Duc Thang University (TDTU), and VŠB-Technical University of Ostrava (VŠB-TUO).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All real-world network datasets used in the experiment can be downloaded at http://konect.cc/ (accessed on 1 September 2022).
Acknowledgments
The authors would like to give thanks for the support of Ho Chi Minh City University of Food Industry (HUFI), Ton Duc Thang University (TDTU), and VŠB-Technical University of Ostrava (VŠB-TUO).
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Correction Statement
This article has been republished with a minor correction to the correspondence contact information. This change does not affect the scientific content of the article.
References
- Tohidi, E.; Amiri, R.; Coutino, M.; Gesbert, D.; Leus, G.; Karbasi, A. Submodularity in action: From machine learning to signal processing applications. IEEE Signal Process. Mag. 2020, 37, 120–133. [Google Scholar] [CrossRef]
- Krause, A.; Guestrin, C.; Gupta, A.; Kleinberg, J. Near-optimal sensor placements: Maximizing information while minimizing communication cost. In Proceedings of the 5th International Conference on Information Processing in Sensor Networks, Nashville, TN, USA, 19–21 April 2006; pp. 2–10. [Google Scholar]
- Soma, T.; Yoshida, Y. A generalization of submodular cover via the diminishing return property on the integer lattice. In Proceedings of the Advances in Neural Information Processing Systems 28: Annual Conference on Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015; pp. 847–855. [Google Scholar]
- Cornuejols, G.; Fisher, M.; Nemhauser, G.L. On the uncapacitated location problem. Ann. Discret. Math. 1977, 1, 163–177. [Google Scholar]
- Nguyen, B.-N.T.; Pham, P.N.; Tran, L.H.; Pham, C.V.; Snášel, V. Fairness budget distribution for influence maximization in online social networks. In Proceedings of the International Conference on Artificial Intelligence and Big Data in Digital Era, Ho Chi Minh City, Vietnam, 18–19 December 2021; pp. 225–237. [Google Scholar]
- Pham, C.V.; Thai, M.T.; Ha, D.; Ngo, D.Q.; Hoang, H.X. Time-critical viral marketing strategy with the competition on online social networks. In Proceedings of the International Conference on Computational Social Networks, Ho Chi Minh City, Vietnam, 2–4 August 2016; pp. 111–122. [Google Scholar]
- Lin, H.; Bilmes, J. A class of submodular functions for document summarization. In Proceedings of the 49th Annual Meeting of the Association for Computational Linguistics: Human Language Technologies, Portland, OR, USA, 19–24 June 2011; pp. 510–520. [Google Scholar]
- Agrawal, R.; Squires, C.; Yang, K.; Shanmugam, K.; Uhler, C. Abcd-strategy: Budgeted experimental design for targeted causal structure discovery. In Proceedings of the 22nd International Conference on Artificial Intelligence and Statistics, PMLR, Naha, Japan, 16–18 April 2019; pp. 3400–3409. [Google Scholar]
- Das, A.; Kempe, D. Submodular meets spectral: Greedy algorithms for subset selection, sparse approximation and dictionary selection. In Proceedings of the 28th International Conference on Machine Learning, ICML, Bellevue, WA, USA, 28 June–2 July 2011; pp. 1057–1064. [Google Scholar]
- Liu, S. A review for submodular optimization on machine scheduling problems. Complex. Approx. 2020, 12000, 252–267. [Google Scholar]
- Soma, T.; Yoshida, Y. Maximizing monotone submodular functions over the integer lattice. Math. Program. 2018, 172, 539–563. [Google Scholar] [CrossRef]
- Alon, N.; Gamzu, I.; Tennenholtz, M. Optimizing budget allocation among channels and influencers. In Proceedings of the 21st International Conference on World Wide Web, Lyon, France, 16–20 April 2012; pp. 381–388. [Google Scholar]
- Soma, T.; Kakimura, N.; Inaba, K.; Kawarabayashi, K.-I. Optimal budget allocation: Theoretical guarantee and efficient algorithm. In Proceedings of the International Conference on Machine Learning, PMLR, Beijing, China, 21–26 June 2014; pp. 351–359. [Google Scholar]
- Kapralov, M.; Post, I.; Vondrák, J. Online submodular welfare maximization: Greedy is optimal. In Proceedings of the Twenty-Fourth Annual ACM-SIAM Symposium on Discrete Algorithms, SIAM, New Orleans, LA, USA, 6–8 January 2013; pp. 1216–1225. [Google Scholar]
- Demaine, E.D.; Hajiaghayi, M.; Mahini, H.; Malec, D.L.; Raghavan, S.; Sawant, A.; Zadimoghadam, M. How to influence people with partial incentives. In Proceedings of the 23rd International Conference on World Wide Web, Seoul, Korea, 7–11 April 2014; pp. 937–948. [Google Scholar]
- Bian, A.; Buhmann, J.; Krause, A.; Tschiatschek, S. Guarantees for greedy maximization of non-submodular functions with applications. In Proceedings of the 34th International Conference on Machine Learning, PMLR, Sydney, Australia, 6–11 August 2017; pp. 498–507. [Google Scholar]
- Feldman, M.; Naor, J.; Schwartz, R. A unified continuous greedy algorithm for submodular maximization. In Proceedings of the 2011 IEEE 52nd Annual Symposium on Foundations of Computer Science, Palm Springs, CA, USA, 22–25 October 2011; pp. 570–579. [Google Scholar]
- Korula, N.; Mirrokni, V.; Zadimoghaddam, M. Online submodular welfare maximization: Greedy beats 1/2 in random order. In Proceedings of the Forty-Seventh Annual ACM Symposium on Theory of Computing, Portland, OR, USA, 14–17 June 2015; pp. 889–898. [Google Scholar]
- Ha, D.T.; Pham, C.V.; Hoang, H.X. Submodular Maximization Subject to a Knapsack Constraint Under Noise Models. Asia-Pac. J. Oper. Res. 2022, 2250013. [Google Scholar] [CrossRef]
- Huang, C.; Kakimura, N. Multi-pass streaming algorithms for monotone submodular function maximization. Theory Comput. Syst. 2022, 66, 354–394. [Google Scholar] [CrossRef]
- Chekuri, C.; Gupta, S.; Quanrud, K. Streaming algorithms for submodular function maximization. Int. Colloq. Autom. Lang. Program. 2015, 9134, 318–330. [Google Scholar]
- Buschjäger, S.; Honysz, P.; Pfahler, L.; Morik, K. Very fast streaming submodular function maximization. In Proceedings of the Joint European Conference on Machine Learning and Knowledge Discovery in Databases, Bilbao, Spain, 13–17 September 2021; pp. 151–166. [Google Scholar]
- Pham, C.; Pham, D.; Bui, B.; Nguyen, A. Minimum budget for misinformation detection in online social networks with provable guarantees. Optim. Lett. 2022, 16, 515–544. [Google Scholar] [CrossRef]
- Gu, S.; Shi, G.; Wu, W.; Lu, C. A fast double greedy algorithm for non-monotone dr-submodular function maximization. Discret. Math. Algorithms Appl. 2020, 12, 2050007. [Google Scholar] [CrossRef]
- Mitrovic, S.; Bogunovic, I.; Norouzi-Fard, A.; Tarnawski, J.; Cevher, V. Streaming robust submodular maximization: A partitioned thresholding approach. In Proceedings of the Advances in Neural Information Processing Systems 30: Annual Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 4557–4566. [Google Scholar]
- Pham, C.; Vu, Q.; Ha, D.; Nguyen, T.; Le, N. Maximizing k-submodular functions under budget constraint: Applications and streaming algorithms. J. Comb. Optim. 2022, 44, 723–751. [Google Scholar] [CrossRef]
- Nguyen, B.; Pham, P.; Pham, C.; Su, A.; Snášel, V. Streaming Algorithm for Submodular Cover Problem Under Noise. In Proceedings of the 2021 RIVF International Conference on Computing and Communication Technologies (RIVF), Hanoi, Vietnam, 19–21 August 2021; pp. 1–6. [Google Scholar]
- Gong, S.; Nong, Q.; Bao, S.; Fang, Q.; Du, D.-Z. A fast and deterministic algorithm for knapsack-constrained monotone dr-submodular maximization over an integer lattice. J. Glob. Optim. 2022, 1–24. [Google Scholar] [CrossRef]
- Liu, B.; Chen, Z.; Du, H.W. Streaming algorithms for maximizing dr-submodular functions with d-knapsack constraints. In Proceedings of the Algorithmic Aspects in Information and Management—15th International Conference, AAIM, Virtual Event, 20–22 December 2021; Volume 13153, pp. 159–169. [Google Scholar]
- Tan, J.; Zhang, D.; Zhang, H.; Zhang, Z. One-pass streaming algorithm for dr-submodular maximization with a knapsack constraint over the integer lattice. Comput. Electr. Eng. 2022, 99, 107766. [Google Scholar] [CrossRef]
- Zhang, Z.; Guo, L.; Wang, Y.; Xu, D.; Zhang, D. Streaming algorithms for maximizing monotone dr-submodular functions with a cardinality constraint on the integer lattice. Asia Pac. J. Oper. Res. 2021, 38, 2140004:1–2140004:14. [Google Scholar] [CrossRef]
- Kazemi, E.; Mitrovic, M.; Zadimoghaddam, M.; Lattanzi, S.; Karbasi, A. Submodular streaming in all its glory: Tight approximation, minimum memory and low adaptive complexity. In Proceedings of the 36th International Conference on Machine Learning, PMLR, Long Beach, CA, USA, 9–15 June 2019; Volume 97, pp. 3311–3320. [Google Scholar]
- Nemhauser, G.L.; Wolsey, L.A.; Fisher, M.L. An analysis of approximations for maximizing submodular set functions—I. Math. Program. 1978, 14, 265–294. [Google Scholar] [CrossRef]
- Sviridenko, M. A note on maximizing a submodular set function subject to a knapsack constraint. Oper. Res. Lett. 2004, 32, 41–43. [Google Scholar] [CrossRef]
- Cálinescu, G.; Chekuri, C.; Pxaxl, M.; Vondrxaxk, J. Maximizing a monotone submodular function subject to a matroid constraint. SIAM J.Comput. 2011, 40, 1740–1766. [Google Scholar] [CrossRef]
- Badanidiyuru, A.; Vondrák, J. Fast algorithms for maximizing submodular functions. In Proceedings of the Twenty-Fifth Annual ACM-SIAM Symposium on Discrete Algorithms, SODA, SIAM, Portland, OR, USA, 5–7 January 2014; pp. 1497–1514. [Google Scholar]
- Soma, T.; Yoshida, Y. Non-Monotone DR-Submodular Function Maximization. In Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; pp. 898–904. [Google Scholar]
- Badanidiyuru, A.; Mirzasoleiman, B.; Karbasi, A.; Krause, A. Streaming submodular maximization: Massive data summarization on the fly. In Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, KDD’14, Association for Computing Machinery, New York, NY, USA, 24–27 August 2014; pp. 671–680. [Google Scholar]
- Hatano, D.; Fukunaga, T.; Maehara, T.; Kawarabayashi, K. Lagrangian decomposition algorithm for allocating marketing channels. In Proceedings of the Twenty-Ninth AAAI Conference on Artificial Intelligence, Austin, TX, USA, 25–30 January 2015; pp. 1144–1150. [Google Scholar]
- Kunegis, J. KONECT: The koblenz network collection. In Proceedings of the 22nd International World Wide Web Conference, WWW’13, ACM, Rio de Janeiro, Brazil, 13–17 May 2013; pp. 1343–1350. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).