Artificial Neural Network as a Tool for Estimation of the Higher Heating Value of Miscanthus Based on Ultimate Analysis
Abstract
1. Introduction
2. Materials and Methods
2.1. Crop Establishment and Data Collection
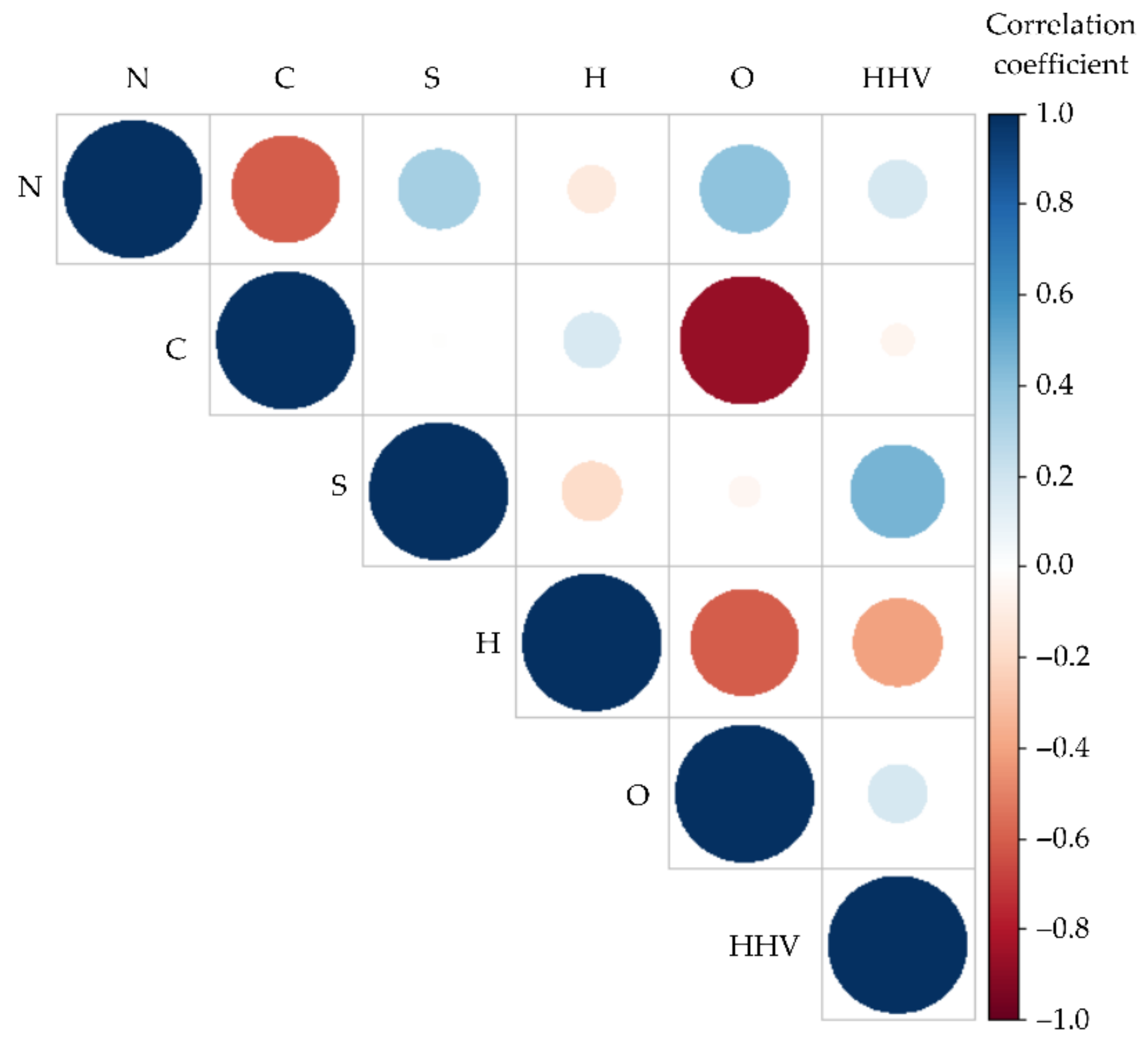
2.2. Statistical Analysis
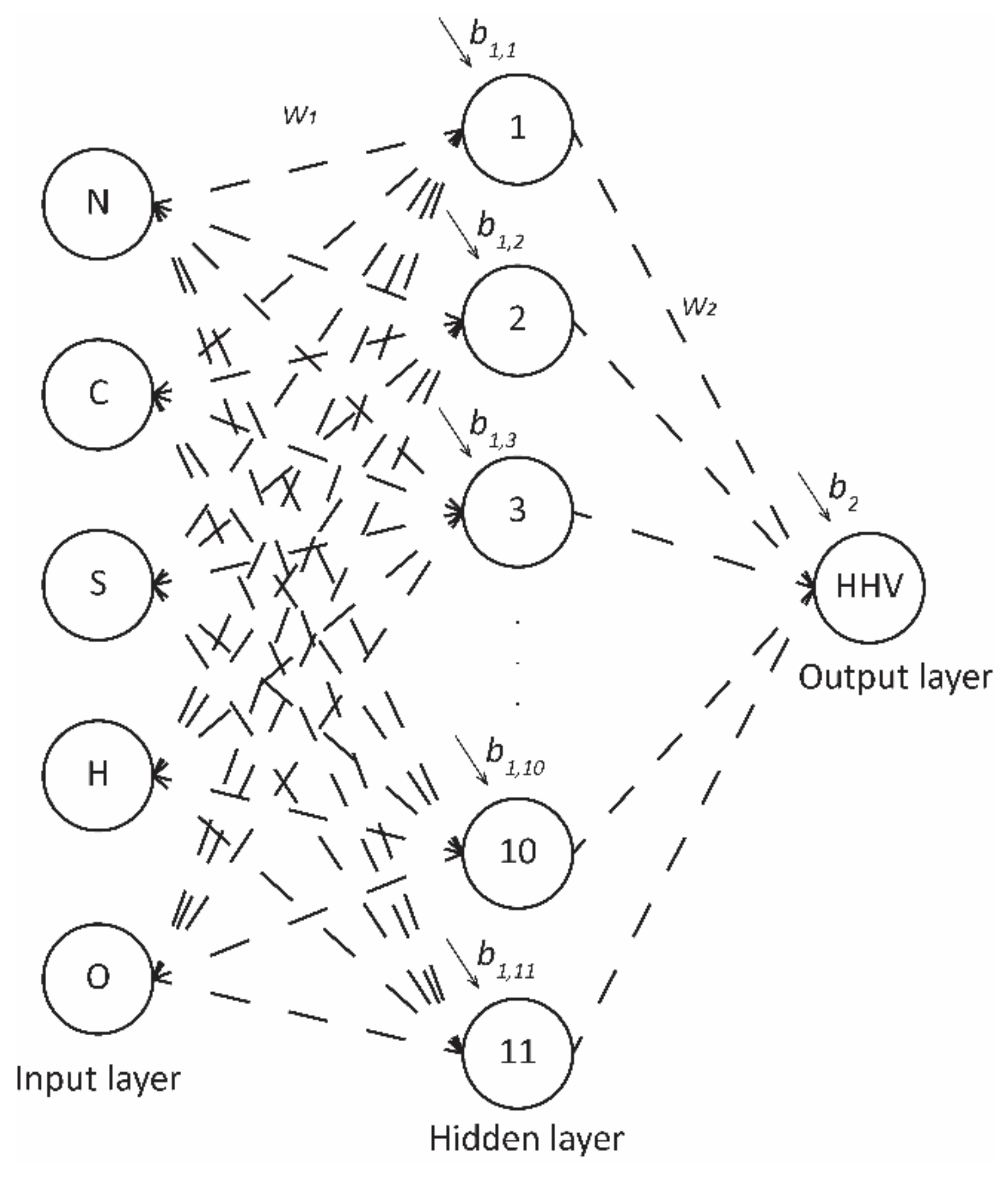
2.3. ANN Modeling
2.4. Regression Models
3. Results
4. Discussion
4.1. Prediction of HHV Using Developed Regression Models
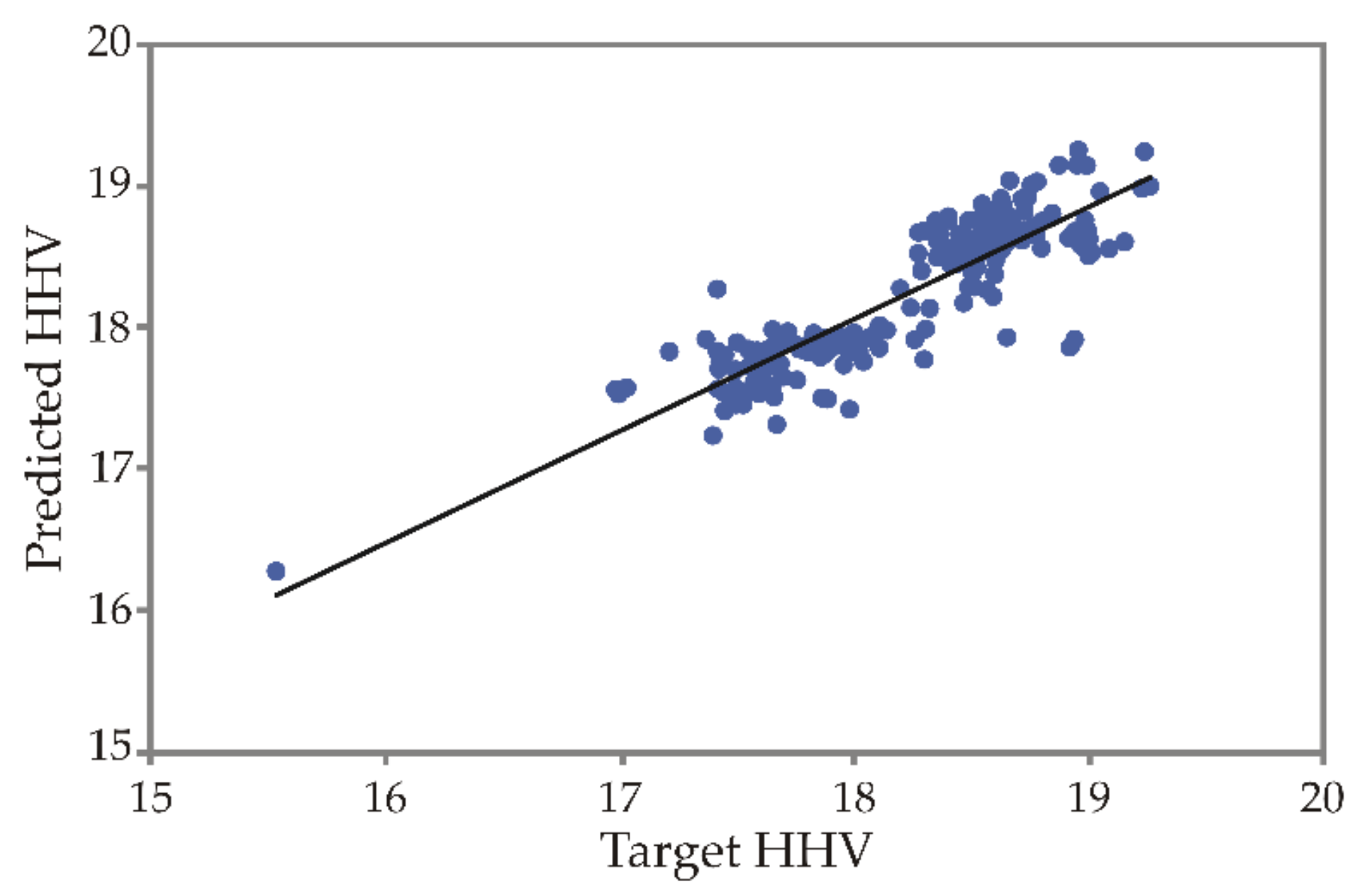
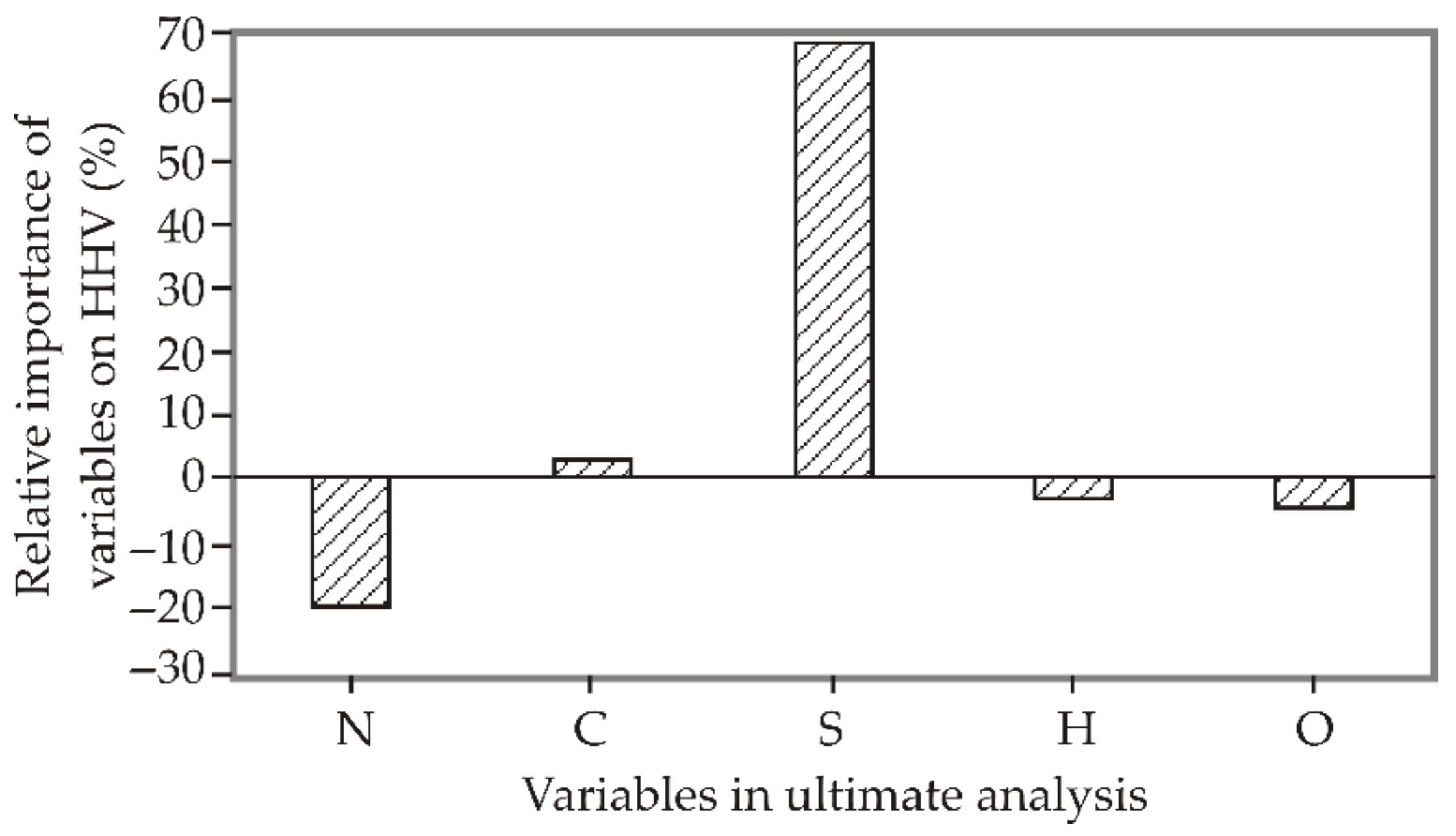
4.2. ANN Model
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Koçar, G.; Civaş, N. An overview of biofuels from energy crops: Current status and future prospects. Renew. Sustain. Energy Rev. 2013, 28, 900–916. [Google Scholar] [CrossRef]
- Long, H.; Li, X.; Wang, H.; Jia, J. resources and their bioenergy potential estimation: A review. Renew. Sustain. Energy Rev. 2013, 26, 344–352. [Google Scholar] [CrossRef]
- Baxter, X.C.; Darvell, L.I.; Jones, J.M.; Barraclough, T.; Yates, N.E.; Shield, I. Miscanthus combustion properties and variations with Miscanthus agronomy. Fuel 2014, 117, 851–869. [Google Scholar] [CrossRef]
- Yi, L.; Feng, J.; Qin, Y.H.; Li, W.Y. Prediction of elemental composition of coal using proximate analysis. Fuel 2017, 193, 315–321. [Google Scholar] [CrossRef]
- Sheng, C.; Azevedo, J.L.T. Estimating the higher heating value of biomass fuels from basic analysis data. Biomass Bioenergy 2005, 28, 499–507. [Google Scholar] [CrossRef]
- Dai, Z.; Chen, Z.; Selmi, A.; Jermsittiparsert, K.; Denić, N.M.; Nešić, Z. Machine learning prediction of higher heating value of biomass. Biomass Convers. Biorefin. 2021, 1–9. [Google Scholar] [CrossRef]
- Giwa, S.O.; Adekomaya, S.O.; Adama, K.O.; Mukaila, M.O. Prediction of selected biodiesel fuel properties using artificial neural network. Front. Energy 2015, 9, 433–445. [Google Scholar] [CrossRef]
- Dashti, A.; Noushabadi, A.S.; Raji, M.; Razmi, A.; Ceylan, S.; Mohammadi, A.H. Estimation of biomass higher heating value (HHV) based on the proximate analysis: Smart modeling and correlation. Fuel 2019, 257, 115931. [Google Scholar] [CrossRef]
- Pattanayak, S.; Loha, C.; Hauchhum, L.; Sailo, L. Application of MLP-ANN models for estimating the higher heating value of bamboo biomass. Biomass Convers. Biorefin. 2021, 11, 2499–2508. [Google Scholar] [CrossRef]
- Vardiambasis, I.O.; Kapetanakis, T.N.; Nikolopoulos, C.D.; Trang, T.K.; Tsubota, T.; Keyikoglu, R.; Khataee, A.; Kalderis, D. Hydrochars as emerging biofuels: Recent advances and application of artificial neural networks for the prediction of heating values. Energies 2020, 13, 4572. [Google Scholar] [CrossRef]
- Özveren, U. An artificial intelligence approach to predict gross heating value of lignocellulosic fuels. J. Energy Inst. 2017, 90, 397–407. [Google Scholar] [CrossRef]
- Olatunji, O.O.; Akinlabi, S.; Madushele, N.; Adedeji, P.A.; Felix, I. Multilayer perceptron artificial neural network for the prediction of heating value of municipal solid waste. AIMS Energy 2019, 7, 944–956. [Google Scholar] [CrossRef]
- Kartal, F.; Özveren, U. A deep learning approach for prediction of syngas lower heating value from CFB gasifier in Aspen plus®. Energy 2020, 209, 118457. [Google Scholar] [CrossRef]
- Ahmed, A.A.M. Prediction of dissolved oxygen in Surma River by biochemical oxygen demand and chemical oxygen demand using the artificial neural networks (ANNs). J. King Saud Univ. Eng. Sci. 2017, 29, 151–158. [Google Scholar] [CrossRef]
- Alizadeh, M.J.; Kavianpour, M.R. Development of wavelet-ANN models to predict water quality parameters in Hilo Bay, Pacific Ocean. Mar. Pollut. Bull. 2015, 98, 171–178. [Google Scholar] [CrossRef]
- Noushabadi, A.S.; Dashti, A.; Ahmadijokani, F.; Hu, J.; Mohammadi, A.H. Estimation of higher heating values (HHVs) of biomass fuels based on ultimate analysis using machine learning techniques and improved equation. Renew. Energy 2021, 179, 550–562. [Google Scholar] [CrossRef]
- Voća, N.; Leto, J.; Karažija, T.; Bilandžija, N.; Peter, A.; Kutnjak, H.; Šurić, J.; Poljak, M. Energy properties and biomass yield of miscanthus x giganteus fertilized by municipal sewage sludge. Molecules 2021, 26, 4371. [Google Scholar] [CrossRef] [PubMed]
- Meehan, P.G.; Finnan, J.M.; Donnell, K.P.M. The effect of harvest date and harvest method on the combustion characteristics of Miscanthus X giganteus. GCB Bioenergy 2013, 5, 487–496. [Google Scholar] [CrossRef]
- Khalil, S.A.; Shaffie, A.M. A comparative study of total, direct and diffuse solar irradiance by using different models on horizontal and inclined surfaces for Cairo, Egypt. Renew. Sustain. Energy Rev. 2013, 27, 853–863. [Google Scholar] [CrossRef]
- Arsenović, M.; Pezo, L.; Stanković, S.; Radojević, Z. Factor space differentiation of brick clays according to mineral content: Prediction of final brick product quality. Appl. Clay Sci. 2015, 115, 108–114. [Google Scholar] [CrossRef]
- Yoon, Y.; Swales, G.; Margavio, T.M. A Comparison of Discriminant Analysis versus Artificial Neural Networks. J. Oper. Res. Soc. 1993, 44, 51–60. [Google Scholar] [CrossRef]
- Mesroghli, S.; Jorjani, E.; Chehreh Chelgani, S. Estimation of gross calorific value based on coal analysis using regression and artificial neural networks. Int. J. Coal Geol. 2009, 79, 49–54. [Google Scholar] [CrossRef]
- Cinar, A.C. Training Feed-Forward Multi-Layer Perceptron Artificial Neural Networks with a Tree-Seed Algorithm. Arab. J. Sci. Eng. 2020, 45, 10915–10938. [Google Scholar] [CrossRef]
- Darvishan, A.; Bakhshi, H.; Madadkhani, M.; Mir, M.; Bemani, A. Application of MLP-ANN as a novel predictive method for prediction of the higher heating value of biomass in terms of ultimate analysis. Energy Source Part A 2018, 40, 2960–2966. [Google Scholar] [CrossRef]
- Grieu, S.; Faugeroux, O.; Traoré, A.; Claudet, B.; Bodnar, J.L. Artificial intelligence tools and inverse methods for estimating the thermal diffusivity of building materials. Energy Build. 2011, 43, 543–554. [Google Scholar] [CrossRef]
- Voca, N.; Pezo, L.; Peter, A.; Suput, D.; Loncar, B.; Kricka, T. Modelling of corn kernel pre-treatment, drying and processing for ethanol production using artificial neural networks. Ind. Crop. Prod. 2021, 162, 113293. [Google Scholar] [CrossRef]
- Pezo, L.L.; Ćurčić, B.L.; Filipović, V.S.; Nićetin, M.R.; Koprivica, G.B.; Mišljenović, N.M.; Lević, L.B. Artificial neural network model of pork meat cubes osmotic dehydratation. Hem. Ind. 2013, 67, 465–475. [Google Scholar] [CrossRef]
- Kollo, T.; von Rosen, D. Advanced Multivariate Statistics with Matrices; Springer: Dordrecht, The Netherlands, 2005. [Google Scholar]
- Garijo, D. A Bernstein Broyden–Fletcher–Goldfarb–Shanno collocation method to solve non-linear beam models. Int. J. Nonlinear Mech. 2021, 131, 103672. [Google Scholar] [CrossRef]
- Nhuchhen, D.R.; Afzal, M.T. HHV predicting correlations for torrefied biomass using proximate and ultimate analyses. Bioengineering 2017, 4, 7. [Google Scholar] [CrossRef]
- Callejón-Ferre, A.J.; Velázquez-Martí, B.; López-Martínez, J.A.; Manzano-Agugliaro, F. Greenhouse crop residues: Energy potential and models for the prediction of their higher heating value. Renew. Sustain. Energy Rev. 2011, 15, 948–955. [Google Scholar] [CrossRef]
- Bilandžija, N.; Voća, N.; Leto, J.; Jurišić, V.; Grubor, M.; Matin, A.; Krička, T. Yield and Biomass Composition of Miscanthus x Giganteus in the Mountain Area of Croatia. In Transactions of FAMENA; University of Zagreb: Zagreb, Croatia, 2018; Volume 42, pp. 51–60. [Google Scholar]
- Rutledge, D.N. Comparison of Principal Components Analysis, Independent Components Analysis and Common Components Analysis. J. Anal. Test. 2018, 2, 235–248. [Google Scholar] [CrossRef]
- Agahian, S.; Akan, T. Battle royale optimizer for training multi-layer perceptron. Evol. Syst. 2021, 123456789. [Google Scholar] [CrossRef]
- Geladi, P.; Manley, M.; Lestander, T. Scatter plotting in multivariate data analysis. J. Chemometr. 2003, 17, 503–511. [Google Scholar] [CrossRef]
- Keim, D.A.; Hao, M.C.; Dayal, U.; Janetzko, H.; Bak, P. Generalized scatter plots. Inform. Visual. 2010, 9, 301–311. [Google Scholar] [CrossRef]

| Sr.no. | Proposed Equations from the Literature | References |
|---|---|---|
| 1 | HHV = a + b · C | [31] |
| 2 | HHV − a + b · H | [31] |
| 3 | HHV − a + b · O | [31] |
| 4 | [31] | |
| 5 | [31] | |
| 6 | HHV = a + b · C + c · H + d · C2 + e · H2 | [31] |
| 7 | [31] | |
| 8 | HHV = a · C − b | [5] |
| 9 | HHV = a + b · C2 + c · C + d · H + e · C · H + g · N | [30] |
| 10 | [31] |
| Sample | N | C | S | H | O | HHV |
|---|---|---|---|---|---|---|
| MxG1 | 0.24 ± 0.15 a | 51.49 ± 0.58 a | 0.11 ± 0.04 a | 5.82 ± 0.32 a | 42.33 ± 0.74 a | 18.21 ± 0.54 a |
| MxG2 | 0.19 ± 0.13 a | 51.3 ± 0.53 a | 0.14 ± 0.06 a | 5.85 ± 0.2 a | 42.53 ± 0.42 a | 18.16 ± 0.37 a |
| MxG3 | 0.23 ± 0.15 a | 50.9 ± 0.96 a | 0.14 ± 0.06 a | 5.82 ± 0.2 a | 42.91 ± 0.89 a | 18.22 ± 0.58 a |
| MxG4 | 0.22 ± 0.13 a | 51.75 ± 0.73 a | 0.21 ± 0.3 a | 5.83 ± 0.33 a | 41.99 ± 0.69 a | 18.24 ± 0.64 a |
| MxG5 | 0.2 ± 0.09 a | 51.38 ± 0.8 a | 0.14 ± 0.08 a | 5.84 ± 0.33 a | 42.44 ± 0.82 a | 18.37 ± 0.48 a |
| MxG6 | 0.31 ± 0.21 a | 51.53 ± 0.86 a | 0.21 ± 0.2 a | 5.89 ± 0.23 a | 42.06 ± 0.88 a | 18.45 ± 0.61 a |
| MxG7 | 0.2 ± 0.13 a | 51.33 ± 0.93 a | 0.12 ± 0.09 a | 5.82 ± 0.33 a | 42.54 ± 0.92 a | 17.97 ± 0.73 a |
| MxG8 | 0.2 ± 0.11 a | 51.65 ± 1.33 a | 0.11 ± 0.06 a | 5.88 ± 0.27 a | 42.16 ± 1.18 a | 18.23 ± 0.64 a |
| MxG9 | 0.21 ± 0.12 a | 51.76 ± 0.77 a | 0.13 ± 0.05 a | 5.85 ± 0.35 a | 42.05 ± 0.86 a | 18.35 ± 0.32 a |
| MxG10 | 0.18 ± 0.1 a | 51.48 ± 0.97 a | 0.11 ± 0.05 a | 5.83 ± 0.33 a | 42.4 ± 0.85 a | 18.1 ± 0.61 a |
| MxG11 | 0.22 ± 0.16 a | 51.09 ± 1.14 a | 0.11 ± 0.05 a | 5.85 ± 0.27 a | 42.74 ± 1.12 a | 18.06 ± 0.33 a |
| MxG12 | 0.19 ± 0.11 a | 51.6 ± 0.82 a | 0.12 ± 0.06 a | 5.86 ± 0.35 a | 42.24 ± 0.97 a | 18.51 ± 0.5 a |
| MxG13 | 0.27 ± 0.22 a | 51.15 ± 0.8 a | 0.15 ± 0.09 a | 5.79 ± 0.36 a | 42.64 ± 0.86 a | 18.24 ± 0.6 a |
| MxG14 | 0.2 ± 0.14 a | 51.53 ± 0.82 a | 0.09 ± 0.03 a | 5.31 ± 1.71 a | 42.86 ± 2.12 a | 17.83 ± 0.81 a |
| MxG15 | 0.25 ± 0.15 a | 51.73 ± 0.99 a | 0.12 ± 0.05 a | 5.83 ± 0.38 a | 42.08 ± 1.19 a | 18.09 ± 0.4 a |
| MxG16 | 0.18 ± 0.12 a | 51.11 ± 1.12 a | 0.11 ± 0.05 a | 5.83 ± 0.33 a | 42.77 ± 1.15 a | 18.02 ± 0.43 a |
| Model | x2 | RMSE | MBE | MPE | SSE | R2 | Skewness | Kurtosis | SD | Variance |
|---|---|---|---|---|---|---|---|---|---|---|
| Model 1 | 0.31 | 0.01 | 0.01 | 854.24 | 59.66 | 0.00 | −0.63 | 1.47 | 0.56 | 0.31 |
| Model 2 | 0.19 | 0.01 | 0.01 | 578.45 | 35.56 | 0.40 | −1.32 | 9.26 | 0.43 | 0.19 |
| Model 3 | 0.30 | 0.01 | 0.01 | 810.35 | 57.95 | 0.03 | −0.67 | 2.10 | 0.55 | 0.30 |
| Model 4 | 0.31 | 0.01 | 0.01 | 830.08 | 58.92 | 0.02 | −0.65 | 1.81 | 0.56 | 0.31 |
| Model 5 | 0.19 | 0.01 | 0.01 | 623.98 | 36.77 | 0.38 | −1.19 | 6.78 | 0.44 | 0.19 |
| Model 6 | 0.22 | 0.01 | 0.01 | 582.07 | 42.91 | 0.36 | −1.53 | 12.54 | 0.47 | 0.22 |
| Model 7 | 0.19 | 0.01 | 0.01 | 585.55 | 35.77 | 0.40 | −1.28 | 8.67 | 0.43 | 0.19 |
| Model 8 | 0.31 | 0.01 | 0.01 | 854.24 | 59.66 | 0.00 | −0.63 | 1.47 | 0.56 | 0.31 |
| Model 9 | 0.17 | 0.01 | 0.01 | 526.96 | 31.57 | 0.47 | −1.79 | 13.09 | 0.41 | 0.17 |
| Model 10 | 0.31 | 0.01 | 0.01 | 853.32 | 59.64 | 0.00 | −0.63 | 1.49 | 0.56 | 0.31 |
| ANN | 0.07 | 0.27 | -0.03 | 1.10 | 13.74 | 0.77 | 0.53 | 2.29 | 0.27 | 0.07 |
| Input Layer | Output Layer | ||||||
|---|---|---|---|---|---|---|---|
| Weight | Bias | Weight | Bias | ||||
| N | C | S | H | O | HHV | ||
| −1.74 | 10.34 | −30.08 | −7.41 | 1.90 | 1.62 | −1.76 | 2.06 |
| −0.28 | 3.37 | 1.69 | 2.99 | −4.61 | −0.37 | 1.18 | |
| 2.58 | −0.83 | −5.02 | −0.40 | −0.37 | −1.56 | 0.20 | |
| 4.23 | −0.73 | −6.78 | −0.79 | 0.10 | −1.40 | −0.31 | |
| 10.55 | −3.52 | −15.48 | 12.93 | −0.96 | −2.58 | −1.91 | |
| 1.08 | 1.54 | 1.49 | −2.03 | −3.48 | −1.57 | −0.44 | |
| 3.56 | −2.75 | −8.74 | 1.54 | 1.03 | −2.09 | −1.30 | |
| −3.67 | 1.30 | 2.92 | 2.02 | −2.74 | −0.87 | 0.48 | |
| −2.72 | −0.49 | 6.47 | −0.49 | 0.34 | 0.75 | −0.60 | |
| 2.25 | 2.01 | 6.90 | −5.15 | 1.20 | 3.20 | 0.47 | |
| −1.14 | 1.93 | 2.53 | 0.98 | −1.49 | 0.71 | −1.56 | |
| Net. Name | Train. Perf. | Test Perf. | Valid. Perf. | Train. Error | Test Error | Valid. Error | Train. Algorithm | Error Function | Hidden Activation | Output Activation |
|---|---|---|---|---|---|---|---|---|---|---|
| MLP 5-11-1 | 0.861 | 0.902 | 0.951 | 0.042 | 0.026 | 0.021 | BFGS 71 | SOS | Tanh | Logistic |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brandić, I.; Pezo, L.; Bilandžija, N.; Peter, A.; Šurić, J.; Voća, N. Artificial Neural Network as a Tool for Estimation of the Higher Heating Value of Miscanthus Based on Ultimate Analysis. Mathematics 2022, 10, 3732. https://doi.org/10.3390/math10203732
Brandić I, Pezo L, Bilandžija N, Peter A, Šurić J, Voća N. Artificial Neural Network as a Tool for Estimation of the Higher Heating Value of Miscanthus Based on Ultimate Analysis. Mathematics. 2022; 10(20):3732. https://doi.org/10.3390/math10203732
Chicago/Turabian StyleBrandić, Ivan, Lato Pezo, Nikola Bilandžija, Anamarija Peter, Jona Šurić, and Neven Voća. 2022. "Artificial Neural Network as a Tool for Estimation of the Higher Heating Value of Miscanthus Based on Ultimate Analysis" Mathematics 10, no. 20: 3732. https://doi.org/10.3390/math10203732
APA StyleBrandić, I., Pezo, L., Bilandžija, N., Peter, A., Šurić, J., & Voća, N. (2022). Artificial Neural Network as a Tool for Estimation of the Higher Heating Value of Miscanthus Based on Ultimate Analysis. Mathematics, 10(20), 3732. https://doi.org/10.3390/math10203732








