Effects of the Nonlocal Thermoelastic Model in a Thermoelastic Nanoscale Material

Abstract

In this work, a novel nonlocal model without energy dissipations is presented to investigate the impacts of the nonlocal thermoelastic parameters in a nanoscale material by the eigenvalue approach. The basic equations are applied under the Green and Naghdi model without energy dissipations. To obtain this model, the theory of the non-local continuum suggested by Eringen is applied. The Laplace transformation technique is used for the basic formulations to obtain the analytical solutions of the thermal stress, the displacement, and the temperature during the nanoscale thermo-electric medium. The inverse of the Laplace transformation is used with the numerical technique to obtain the complete solutions of the studying fields in the time–space domains. The main physical fields are displayed graphically and theoretically discussed under the influence of nonlocal parameters.

1. Introduction

In recent years, the thermoelasticity theories, which assume finite velocity for thermal signals, have received many attentions. These theories are called generalized thermoelasticity theories. Lord and Shulman [1] established the generalized thermoelasticity theory with one delay time while Green and Lindsay [2] established the generalized thermoelasticity theory with two thermal delay times. Green and Naghdi [3,4,5] presented three types of models (GN-III, GN-II, and GN-I). The constitutive formulations of G-N models are linearized, GN-I is similar to classical coupled thermo-elastic theory, type II shows the propagation of thermal signals with finite speed without energy dissipation, and type III suggests the finite velocity of propagation with energy dissipation.

With the rapid development of nanomechanical electromechanical systems (NEMS) technologies, high-performance nanostructures, i.e., nanotubes, nanofilms, and nanowires, have been widely adopted as resonators, probes, sensors, transistors, actuators, etc. It is important to understand the exact characterizations of the thermal and mechanical properties of such nanostructures, as suggested in [6]. The authors have paid considerable attention to corresponding theories of nonlocal beams due to their impacts at the nanoscale. Classically, the strain state defines the stress condition at the same point. However, non-local continuation models consider the stress states at points as the functions of the strain states of all points of the body. The nonlocal elasticity theory was first advocated by Eringen [7]. After two years, the nonlocal thermoelastic theory was explored by Eringen [8]. He reviewed the constitutive relations, the basic equations, the laws of equilibrium in continuum mechanics, and the displacement equations/temperature under the nonlocal elastic theory. Eringen [9] studied nonlocal electromagnetic solids and superconductivity under the elastic theory. Non-local theories of field elasticity have been explained in detail by Eringen [10] with regard to continuum mechanics. Povstenko [11] recommended the non-local elastic theory to take into account the forces of actions between atoms. Marin et al. [12] have discussed the effect of intrinsic rotation, microstructural expansions, and contraction in initial and boundary values problems of thermo-elastic bodies. Abbas et al. [13] studied the response of heat sources in transversely isotropic thermoelastic material without energy dissipations with the two-temperatures model. Marin [14] has discussed the domain of influences theory for a micro stretch elastic material. Sarkar et al. [15] have studied the waves propagation in nonlocal thermo-elastic solids without energy dissipation. Zenkour and Kutbi [16] have investigated the thermo-elastic interaction in a hollow cylinder caused by continuous thermal sources without energy dissipations. Marin [17] presented a partition of energy in a micro-stretch thermo-elastic body. Lata and Kaur [18] investigated the thermo-mechanical interaction in transversely isotropic magneto-thermo-elasticity solids without energy dissipations under the two-temperatures model. Youssef [19] presented the two-temperatures thermoelastic theory without energy dissipations. A model of the nonlocal thermoelastic model without energy dissipation was investigated by Zenkour [20] to consider the vibrations behaviors for nano-machined resonators. Mondal et al. [21] discussed the propagations of time-harmonic plane waves in an infinite nonlocal DPL thermoelastic material with voids. Sarkar and Tomar [22] investigated the plane waves in a nonlocal thermoelasticity solid with voids. Sarkar [23] investigated the thermo-elastic responses of a non-local elastic rod due to nonlocal heat conduction. Ansari and Gholami [24] studied the nonlocal free vibrations in the pre-and post-buckled states of electro-magneto-thermoelastic rectangular nanoplates with different edge conditions. Mahinzare et al. [25] investigated the size-dependent impacts on the critical flow speed of an SWCNT-conveying viscous fluid based on a nonlocal strain gradient cylindrical shell model. Bachher and Sarkar [26] studied the nonlocal model of thermo-elastic medium with voids and fractional derivative heating transfer. Bayones et al. [27] have discussed the impacts of moving thermal sources on a magneto-thermo-elastic rod under a nonlocal model and three-phase lag with memory-dependent derivatives. Zhou and Li [28] studied the nonlocal dual-phase-lag thermo-elastic damping in circular and rectangular micro/nanoplates resonators. Singh and Bijarnia [29] investigated the nonlocal effect on the propagations of waves in a generalized thermoelastic solid half-space. Lata and Singh [30] studied the propagations of the Stoneley waves in nonlocal isotropic magneto-thermoelastic solid under the multi-dual-phase-lag model. Kaur et al. [31] presented the study of transversely isotropic nonlocal thermo-elastic thin nano-beam resonators under a multi-dual-phase-lag model. Biswas [32] studied the Rayleigh wave in the porous nonlocal orthotropic thermoelastic layer lying over the porous nonlocal orthotropic thermoelastic half-space. Over the last few decades, many problems have been solved by generalized thermoelasticity theories [33,34,35,36,37,38,39].

In the present article, a theoretical technique is used when the nonlocal thermoelastic model without energy dissipation is applied during interactions process for the nanoscale medium. The analytical solutions of the basic fields are obtained when the Laplace transforms domain is used. Without any assumed restrictions on the actual physical quantities, the eigenvalue approach gives new analytical solutions in the Laplace domain. Finally, the numerical computations of the main physical fields distribution are displayed graphically with changes in nonlocal parameters with discussions.

2. Basic Equations

Following Eringen [40] and Green and Naghdi [5,41], the basic formulations for nonlocal thermo-elastic material in the absence of heat source and body forces are taken as:

$$\rho \left(1-s_e{\alpha }^2{\nabla }^2\right)\frac{{\partial }^2{u}_i}{\partial t^2}=\mu u_{i,jj}+\left(\lambda +\mu \right)u_{j,ij}-{\gamma }_t{T}_{,i},$$

(1)

$$\rho c_e\left(1-s_t{\alpha }^2{\nabla }^2\right)\frac{{\partial }^{2}T}{\partial t^2}=K^{*}{\nabla }^{2}T-{\gamma }_t{T}_o\left(1-s_t{\alpha }^2{\nabla }^2\right)\frac{{\partial }^2{u}_{i,i}}{\partial t^2},$$

(2)

$$\left(1-s_e{\alpha }^2{\nabla }^2\right){\sigma }_{ij}=\left(\lambda u_{k,k}-{\gamma }_{t}T\right){\delta }_{ij}+\mu \left(u_{i,j}+u_{j,i}\right),$$

(3)

where ${\sigma }_{ij}$ are the stress components, $K^{*}$ is the material constant, $\alpha$ is the non-local parameter, $T_o$ is the reference temperature, $T=T^{*}-T_o$, $T^{*}$ are the temperature variations, $\lambda ,\mu$ are the Lame’s constants, $c_e$ is the specific heating at constant strain, $\rho$ is the density of the material, $u_i$ is the displacements, $t$ is the time, ${\gamma }_t=\left(3\lambda +2\mu \right){\alpha }_t,{\alpha }_t$ is the linear thermal expansion coefficient. Now, we consider a half-space ($x\ge 0$) with the x-axis pointing into the mediums. To simplify the analysis, the one-dimensional problem is considered. The components of displacement for one-dimension medium and the relations between the components of displacement and the component of strain are defined by:

$$u_x=u\left(x,t\right),u_y=0,u_z=0,e_{xx}=\frac{\partial u}{\partial x}.$$

(4)

From Equation (4) in Equations (1)–(3), the governing equations can be expressed by

$$\rho \left(1-s_e{\alpha }^2\frac{{\partial }^2}{\partial x^2}\right)\frac{{\partial }^{2}u}{\partial t^2}=\left(\lambda +2\mu \right)\frac{{\partial }^{2}u}{\partial x^2}-{\gamma }_t\frac{\partial T}{\partial x},$$

(5)

$$\rho c_e\left(1-s_t{\alpha }^2\frac{{\partial }^2}{\partial x^2}\right)\frac{{\partial }^{2}T}{\partial t^2}=K^{*}\frac{{\partial }^{2}T}{\partial x^2}-{\gamma }_t{T}_o\left(1-s_t{\alpha }^2\frac{{\partial }^2}{\partial x^2}\right)\frac{{\partial }^{3}u}{\partial t^2\partial x},$$

(6)

$$\left(1-s_e{\alpha }^2\frac{{\partial }^2}{\partial x^2}\right){\sigma }_{xx}=\sigma =\left(\lambda +2\mu \right)\frac{\partial u}{\partial x}-{\gamma }_{t}T.$$

(7)

3. Initial and Boundary Conditions

The problem homogeneous initial conditions i.e.,

$$T\left(x,0\right)=0,\frac{\partial T\left(x,0\right)}{\partial t}=0,u\left(x,0\right)=0,\frac{\partial u\left(x,0\right)}{\partial t}=0.$$

(8)

While the mechanical and thermal boundary conditions can be supposed by

$$u=0.$$

(9)

The surface $x=0$ is caused by heat flux with the exponentially decaying pulse [42].

$$-K^{*}{\frac{\partial T\left(x,t\right)}{\partial x}|}_{x=0}=q_o\frac{t^2{e}^{-\frac{t}{t_p}}}{16t_p^2},$$

(10)

where $t_p$ is the characteristic pulse time of heat flux and $q_o$ is a constant. To obtain the main fields in non-dimensional form, the following the non-dimensional variables are given by

$$\left(x^{\prime },u^{\prime },{\alpha }^{\prime }\right)=\eta c\left(x,u,\alpha \right),T^{\prime }=\frac{{\gamma }_{t}T}{\rho c^2},\left(t^{\prime },t_p^{\prime }\right)=\eta c^2\left(t,t_p\right),{\sigma }^{\prime }=\frac{\sigma }{\rho c^2},$$

(11)

where $c^2=\frac{\lambda +2\mu }{\mathsf{\rho }}$, $\eta =\frac{\rho c_e}{K}$ and $k$ is the heat conductivity. By using the non-dimension variables (11), the governing equations with the ignoring of the dashes can be written by:

$$\left(1-s_e{\alpha }^2\frac{{\partial }^2}{\partial x^2}\right)\frac{{\partial }^{2}u}{\partial t^2}=\frac{{\partial }^{2}u}{\partial x^2}-\frac{\partial T}{\partial x},$$

(12)

$${\beta }_1\left(1-s_t{\alpha }^2\frac{{\partial }^2}{\partial x^2}\right)\frac{{\partial }^{2}T}{\partial t^2}=\frac{{\partial }^{2}T}{\partial x^2}-{\beta }_2\left(1-s_t{\alpha }^2\frac{{\partial }^2}{\partial x^2}\right)\frac{{\partial }^{3}u}{\partial t^2\partial x},$$

(13)

$$\sigma =\frac{\partial u}{\partial x}-T,$$

(14)

$$\frac{\partial T\left(x,0\right)}{\partial t}=0,u\left(x,0\right)=0,\frac{\partial u\left(x,0\right)}{\partial t}=0,$$

(15)

$$u=0,\frac{\partial T}{\partial x}=-q_o\frac{t^2{e}^{-\frac{t}{t_p}}}{16t_p^2}\mathrm{on}x=0,$$

(16)

where ${\beta }_1=\frac{\rho c_e{c}^2}{K^{*}}$ and ${\beta }_2=\frac{{\gamma }_t{\gamma }_t{T}_o}{\rho K^{*}}$.

4. Laplace Transforms

The definition of Laplace transforms is given by

$$\overline{f}\left(x,p\right)=L\left[f\left(x,t\right)\right]={\displaystyle \underset{0}{\overset{\infty }{\int }}}f\left(x,t\right)e^{-pt}dt.$$

(17)

Now, the basic Equations (12)–(16) by applying the Laplace transforms can be written by

$$\frac{d^2\overline{u}}{d{x}^2}-\frac{d\overline{T}}{dx}=\left(1-s_e{\alpha }^2\frac{d^2}{d{x}^2}\right)p^2\overline{u},$$

(18)

$$\frac{d^2\overline{T}}{d{x}^2}={\beta }_1{p}^2\left(1-s_t{\alpha }^2\frac{d^2}{d{x}^2}\right)\overline{T}+\left(1-s_t{\alpha }^2\frac{d^2}{d{x}^2}\right)p^2{\beta }_2\frac{d\overline{u}}{dx},$$

(19)

$$\overline{\sigma }=\frac{d\overline{u}}{dx}-\overline{T},$$

(20)

$$\overline{u}=0,\frac{d\overline{T}}{dx}=\frac{-q_o{t}_p}{8{\left(p{t}_p+1\right)}^3}.$$

(21)

Equations (18) and (19) can be taken the form

$$\frac{d^2\overline{u}}{d{x}^2}=b_{31}\overline{u}+b_{34}\frac{d\overline{T}}{dx},$$

(22)

$$\frac{d^2\overline{T}}{d{x}^2}=b_{42}\overline{T}+b_{43}\frac{d\overline{u}}{dx},$$

(23)

where $b_{31}=\frac{p^2}{\left(1+s_e{\alpha }^2{p}^2\right)},b_{34}=\frac{1}{\left(1+s_e{\alpha }^2{p}^2\right)}$, $b_{42}=\frac{{\beta }_1{p}^2}{\left(1+{\beta }_1{p}^2{s}_t{\alpha }^2+s_t{\alpha }^2{p}^2{\beta }_2{b}_{34}\right)}$, $b_{43}=\frac{\left(p^2{\beta }_2-s_t{\alpha }^2{p}^2{\beta }_2{b}_{31}\right)}{\left(1+{\beta }_1{p}^2{s}_t{\alpha }^2+s_t{\alpha }^2{p}^2{\beta }_2{b}_{34}\right)}$.

Now, it is possible to obtain the solution of coupled differential Equations (22) and (23) by using the eigenvalue method [43,44,45]:

$$\frac{dV}{dx}=BV,$$

(24)

where $V={\left[\begin{array}{cccc}\overline{u}& \overline{T}& \frac{d\overline{u}}{dx}& \frac{d\overline{T}}{dx}\end{array}\right]}^T$ and $B=\left(\begin{array}{cccc}0& 0& 1& 0\\ 0& 0& 0& 1\\ b_{31}& 0& 0& b_{34}\\ 0& b_{42}& b_{43}& 0\end{array}\right)$.

Thus, the characteristic relation of the matrix $A$ is taken as

$${\omega }^4-{\omega }^2\left(b_{34}{b}_{43}+b_{31}+b_{42}\right)+b_{42}{b}_{31}=0.$$

(25)

The eigenvalue of matrix $B$ is the four roots of Equation (24) which are named here as $\pm {\omega }_1$ and $\pm {\omega }_2$. Thus, the corresponding eigenvectors are determined by:

$$X=\left(\begin{array}{c}{b}_{34}\omega \\ {\omega }^2-b_{31}\\ b_{34}{\omega }^2\\ \left({\omega }^2-b_{31}\right)\omega \end{array}\right).$$

(26)

So, the analytical solution of Equation (24) is written by:

$$V\left(x,p\right)={\sum }_{i=1}^4{A}_i{X}_i{e}^{{\omega }_{i}x}.$$

(27)

Due to the regularity conditions of the solution, the increasing exponential nature in the spatial variable $x$ is set aside to infinity, so the general solution of Equation (27) can be given as

$$V\left(x,p\right)={\sum }_{i=1}^2{A}_i{X}_i{e}^{{\omega }_{i}x},$$

(28)

where $A_1$ and $A_2$ are constants that are computed by using the boundary conditions of the problem. From Equations (28) and (24), the general solutions of the field variables with respect to $x$ and $p$ can be expressed by:

$$\overline{u}\left(x,p\right)={\sum }_{i=1}^2{A}_i{u}_i{e}^{{\omega }_{i}x},$$

(29)

$$\overline{T}\left(x,p\right)={\sum }_{i=1}^2{A}_i{T}_i{e}^{{\omega }_{i}x},$$

(30)

$$\overline{\sigma }\left(x,p\right)={\sum }_{i=1}^2{A}_i\left({\omega }_i{u}_i-T_i\right)e^{{\omega }_{i}x},$$

(31)

where $u_i$ and $T_i$ are the corresponding eigenvectors for displacement and temperature respectively. Now, a numerical scheme for the inverse of Laplace transforms is adopted to obtain the final solutions of the temperature, the displacement, and the stress distributions. The Stehfest approach [46] is used as a numerical inversion method to obtain the general solutions of the temperature, the displacement, and the stress distributions as

$$\overline{V}\left(x,t\right)=\frac{ln2}{t}{\sum }_{j=1}^M{H}_j\overline{V}\left(x,j\frac{ln2}{t}\right),$$

(32)

where

$$H_j={\left(-1\right)}^{\frac{M}{2}+1}{\sum }_{k=\frac{i+1}{2}}^{min\left(i,\frac{M}{2}\right)}\frac{k^{\frac{M}{2}+1}\left(2k\right)!}{\left(\frac{M}{2}-k\right)!k!\left(i-k\right)!\left(2k-1\right)!},$$

(33)

Thus, in the physical space–time domain, the solutions of variables can be expressed by

$$u\left(x,t\right)=\frac{ln2}{t}{\sum }_{j=1}^M{H}_j\overline{u}\left(x,j\frac{ln2}{t}\right),$$

(34)

$$T\left(x,t\right)=\frac{ln2}{t}{\sum }_{j=1}^M{H}_j\overline{T}\left(x,j\frac{ln2}{t}\right),$$

(35)

$$\sigma \left(x,t\right)=\frac{ln2}{t}{\sum }_{j=1}^M{H}_j\overline{\sigma }\left(x,j\frac{ln2}{t}\right).$$

(36)

5. Results and Discussions

The physical quantities distribution in an elastic material is investigated. For numerical calculation, the thermoelastic properties values for the material characteristics of the copper materials whose physical dataset are provided below [27].

$${\alpha }_t=1.78\times {10}^{-5}({\mathrm{k}}^{-1}),\lambda =7.76\times {10}^{10}(\mathrm{N})({\mathrm{m}}^{-2}),c_e=383.1({\mathrm{m}}^2)({\mathrm{k}}^{-1}),$$

$$\mu =3.86\times {10}^{10}(\mathrm{N})({\mathrm{m}}^{-2}),\rho =8954(\mathrm{k}\mathrm{g})({\mathrm{m}}^{-3}),T_o=293(\mathrm{k}),$$

$$t_p=0.3,K=386(\mathrm{N})({\mathrm{k}}^{-1})({\mathrm{s}}^{-1}),t=0.3,\alpha =0.3.$$

Based on the above parameters, Figure 1, Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6 show that the variations of physical quantities are calculated numerically along the distance x. Numerical calculations are carried out for the temperature, the displacement, and the stress variations along the x-axis under nonlocal thermoelastic model. Figure 1, Figure 2 and Figure 3 show the four curves predicted by different values of the nonlocal parameter considering the time $\left(t=0.3\right)$, while Figure 4, Figure 5 and Figure 6 represent the three curves predicted by different values of the characteristic pulse time of heat flux.

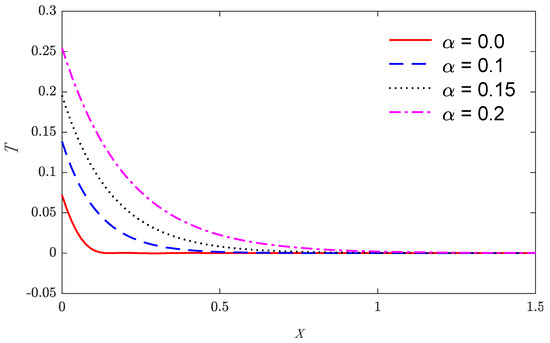
Figure 1. The temperature distributions versus the distance $x$ for various values of the non-local parameter.

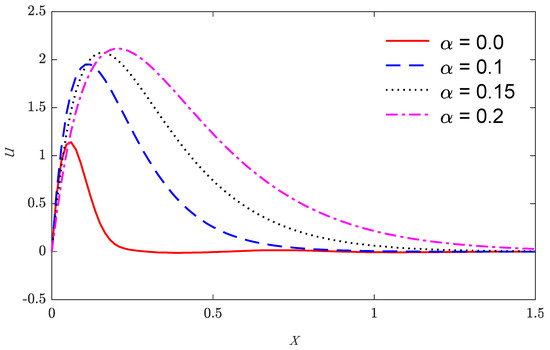
Figure 2. The displacement distributions versus the distance $x$ for various values of the non-local parameter.

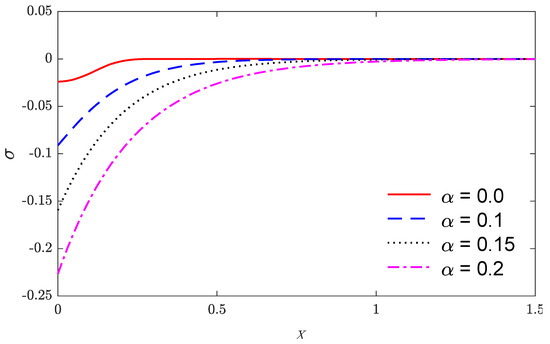
Figure 3. The stress distributions along the distance $x$ for various values of the non-local parameter.

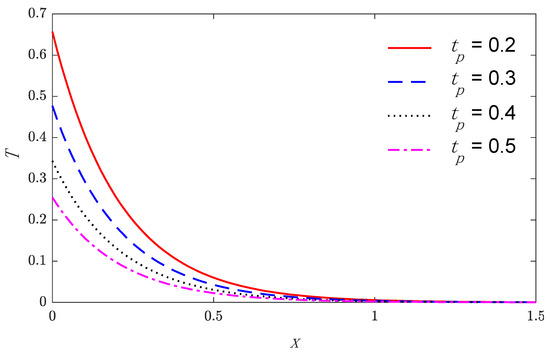
Figure 4. The temperature distribution along the distance $x$ for four values of the characteristic time pulse heat flux.

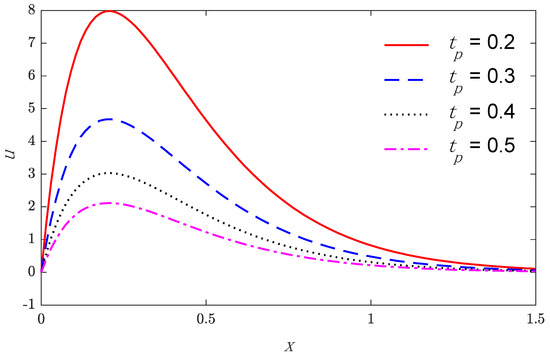
Figure 5. The displacement distributions along the distance $x$ for four values of the characteristic time pulse heat flux.

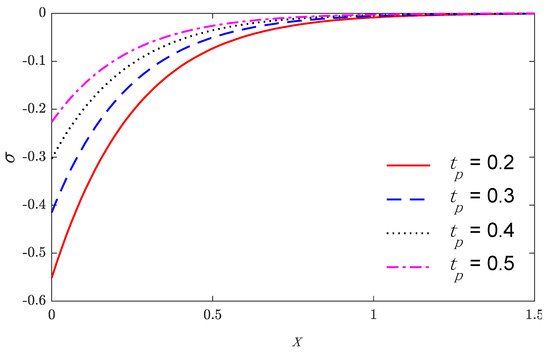
Figure 6. The stress distributions versus the distance $x$ for four values of the characteristic time pulse heat flux.

Figure 1 and Figure 4 suggest that the temperature starts by its maximum values at $x=0$ and gradually reduces with the rising of the distance $x$ until vanishing, which obeys the wavefront for the thermoelastic theory. The variation of displacement versus the distance $x$ is displayed in Figure 2 and Figure 5. It is observed that the displacement starts from zero at the surface $x=0$ that satisfies the problem boundary condition; after that, they attain maximum values and then continuously reduce to zero values. Figure 3 and Figure 6 show the variations of stress with respect to the distance $x$. Curves start from the negative value, increasing in the domain $x>0$ until vanishing. As expected, it can be found that the characteristic pulse time of heat flux has a great impact on the values of all the studied fields.

Finally, the following results are concluded in light of the figures. With the increase in the non-local parameter, the temperature, the displacement, and the stress magnitudes increased. With the increase in the characteristic time pulse heat flux, the temperature, the displacement, and the stress magnitudes decreased.

6. Conclusions

This present work explored non-local thermoelastic interactions in a nanoscale material caused by heat flow with the exponentially decaying pulse. The basic equations are applied under the model of Green and Naghdi without energy dissipation. It obtained the analytical expressions concerning the displacement, the temperature, and the stress in the material. We can conclude that the non-local thermoelasticity theory (non-local thermal conduction and elasticity) has an important effect on the variations of physical quantities.