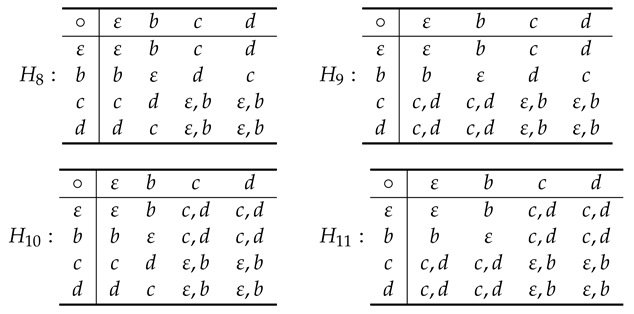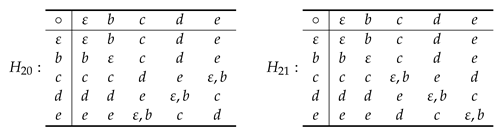G-Hypergroups: Hypergroups with a Group-Isomorphic Heart

Abstract

Hypergroups can be subdivided into two large classes: those whose heart coincide with the entire hypergroup and those in which the heart is a proper sub-hypergroup. The latter class includes the family of 1-hypergroups, whose heart reduces to a singleton, and therefore is the trivial group. However, very little is known about hypergroups that are neither 1-hypergroups nor belong to the first class. The goal of this work is to take a first step in classifying G-hypergroups, that is, hypergroups whose heart is a nontrivial group. We introduce their main properties, with an emphasis on G-hypergroups whose the heart is a torsion group. We analyze the main properties of the stabilizers of group actions of the heart, which play an important role in the construction of multiplicative tables of G-hypergroups. Based on these results, we characterize the G-hypergroups that are of type U on the right or cogroups on the right. Finally, we present the hyperproduct tables of all G-hypergroups of size not larger than 5, apart of isomorphisms.

1. Introduction

Hypercompositional algebra is a branch of Algebra that falls under the many generalizations of group theory [1]. Therefore, it is not surprising that there is a great deal of overlap between the tools and problems of group theory and those of hypergroup theory. In fact, one of the best developed research areas in hypergroup theory is that of their classification. Although a complete classification of hypergroups is well beyond any current research horizon, several important results have been obtained in characterizing classes of hypergroups having certain properties. For example, the class of D-hypergroups consists of those hypergroups that are isomorphic to the quotient set of a group with respect to a non-normal subgroup, and is a subclass of cogroups [2,3,4], and cogroups appear as generalizations of C-hypergroups, that were introduced as hyperstructures having an identity element and a weak form of the cancellation law [5,6].

A strong link between group theory and hypergroup theory is established by the relation $\beta$, which is the smallest equivalence relation defined on a hypergroup H such that the corresponding quotient set $H/\beta$ is a group [7,8,9]. This relation is a very expressive tool for classifying significant families of hypergroups. In particular, the $\beta$-class of the identity of the quotient group $H/\beta$ is called heart [10,11,12]. The heart is a special sub-hypergroup of H that gives detailed informations on the partition of H determined by $\beta$. Notably, a 1-hypergroup is a hypergroup whose heart consists of only one element [13,14]. In this case, that element is also the identity of the hypergroup. In [15,16], the authors characterized 1-hypergroups in terms of the height of their heart and provided a classification of the 1-hypergroups with $\left|H\right|\le 6$ based on the partition of H induced by $\beta$. By means of this technique, the authors were able to enumerate all 1-hypergroups of size up to 6 and construct explicitly all non-isomorphic 1-hypergroups of size up to 5.

Motivated by these studies, in this paper we consider the class of hypergroups whose heart is isomorphic to a group. These hypergroups are called G-hypergroups. Clearly, this class contains that of 1-hypergroups as the heart of a 1-hypergroup is the trivial group. The plan of this paper is the following. In the next section, we introduce basic definitions and notations to be used throughout the paper. In Section 3, we introduce G-hypergroups and their main properties, and give a flexible construction of G-hypergroups that allows to prescribe arbitrarily both the heart and the quotient group $H/\beta$. Moreover, we analyze G-hypergroups whose the heart is isomorphic to a torsion group. We denote this sub-class of G-hypergroups with $\mathfrak{T}\left(H\right)$. If $(H,\circ )\in \mathfrak{T}\left(H\right)$ then the identity $\epsilon$ of ${\omega }_H$ is also identity of $(H,\circ )$, that is $x\in x\circ \epsilon \cap \epsilon \circ x$ for all $x\in H$. Consequently, we prove that the singleton $\left\{\epsilon \right\}$ is an invertible sub-hypergroup of $(H,\circ )$ and the family of right (or left) cosets $\epsilon \circ x$ (or $x\circ \epsilon$, respectively) is a partition of H. Moreover, all $\beta$-classes are a disjoint union of right (left) cosets of $\left\{\epsilon \right\}$. In Section 4, we analyze the main properties of the stabilizers of special actions of ${\omega }_H$ on the set families $\mathfrak{L}=\{x\circ g|x\in H-{\omega }_H,g\in {\omega }_H\}$ and $\mathfrak{R}=\{g\circ x|x\in H-{\omega }_H,g\in {\omega }_H\}$. These stabilizers play an important role in the construction of multiplicative tables of G-hypergroups, as they fix the hyperproducts $g\circ x$ and $x\circ g$ for all $g\in {\omega }_H$ and $x\in H$. The results of Section 5 concern products of elements $x,y\in H-{\omega }_H$ such that $x\circ y\subseteq {\omega }_H$. In Section 6, we characterize the G-hypergroups in $\mathfrak{T}\left(H\right)$ that are of type U on the right. Moreover, we find a sufficient condition for a G-hypergroup of type U on the right to be a cogroup. Finally, in Section 7, we classify the G-hypergroups of size $\le 5$ and $|{\omega }_H|\in \{2,3,4\}$. Apart of isomorphisms, all the multiplicative tables of these hypergroups are listed and, using the results on 1-hypergroups found in [16], we conclude that there are 48 non-isomorphic G-hypergroups of size $\le 5$.

2. Fundamentals of Hypergroup Theory

Throughout this paper, we will use standard definitions of fundamental concepts in hyperstructure theory, such as hyperproduct, semi-hypergroup, hypergroup, and sub-hypergroup, see, e.g., in [17,18,19]. To keep the exposition self-contained, we recall below some auxiliary definitions and results that will be needed in the sequel.

A sub-hypergroup K of a hypergroup $(H,\circ )$ is invertible on the right (resp., on the left) if for all $x,y\in H$, $x\in y\circ K\Rightarrow y\in x\circ K$ (resp., $x\in K\circ y\Rightarrow y\in K\circ x$). Moreover, if K is invertible both on the right and on the left then it is called invertible.

A sub-hypergroup K of a hypergroup $(H,\circ )$ is said to be conjugable if for all $x\in H$ there exists $x^{\prime }\in H$ such that $x{x}^{\prime }\subseteq K$.

An element $\epsilon$ of a semihypergroup $(H,\circ )$ is an identity if $x\in x\circ \epsilon \cap \epsilon \circ x$, for all $x\in H$. Moreover, if $\left\{x\right\}=x\circ \epsilon =\epsilon \circ x$ then $\epsilon$ is a scalar identity.

Given a semihypergroup $(H,\circ )$, the relation ${\beta }^{*}$ of H is the transitive closure of the relation $\beta ={\cup }_{n\ge 1}{\beta }_n$, where ${\beta }_1$ is the diagonal relation in H and, for every integer $n>1$, ${\beta }_n$ is defined as follows:

$$x{\beta }_{n}y⟺\exists (z_1,\dots ,z_n)\in H^n:\{x,y\}\subseteq z_1\circ z_2\circ \cdots \circ z_n.$$

The relations $\beta$ and ${\beta }^{*}$ are among the so-called fundamental relations [7,9,11,20]. Their relevance in hyperstructure theory stems from the following facts. If $(H,\circ )$ is a semihypergroup (resp., a hypergroup), then the quotient set $H/{\beta }^{*}$ endowed with the operation ${\beta }^{*}\left(x\right)\otimes {\beta }^{*}\left(y\right)={\beta }^{*}\left(z\right)$ for $x,y\in H$ and $z\in x\circ y$ is a semigroup (resp., a group) [21,22]. The canonical projection $\phi :H\to H/{\beta }^{*}$ verifies the identity $\phi (x\circ y)=\phi \left(x\right)\otimes \phi \left(y\right)$ for all $x,y\in H$, that is, $\phi$ is said to be a good homomorphism. Moreover, if $(H,\circ )$ is a hypergroup then $\beta$ is transitive [8], $H/\beta$ is a group and the kernel ${\omega }_H={\phi }^{-1}\left(1_{H/\beta }\right)$ of $\phi$ is the heart of $(H,\circ )$.

If A is a non-empty set of a semihypergroup $(H,\circ )$, then we say that A is a complete part if for every $n\ge 1$ and $(x_1,x_2,\dots ,x_n)\in H^n$,

$$(x_1\circ x_2\circ \dots \circ x_n)\cap A\ne \varnothing ⟹x_1\circ x_2\circ \cdots \circ x_n\subseteq A.$$

The transposed hypergroup of a hypergroup $(H,\circ )$ is the hypergroup $(H,★)$ where $x★y=y\circ x$ for all $x,y\in H$.

For later reference, we collect in the following theorem some classic results of hypergroup theory, see in [8,17].

Theorem 1.

Let $(H,\circ )$ be a hypergroup. Then,

1. 

the relation β is transitive;

2. 

if K is a subhypergroup invertible on the right (resp., on the left) of $(H,\circ )$, then the family ${\{x\circ K\}}_{x\in H}$ (resp., ${\{K\circ x\}}_{x\in H}$) is a partition of H;

3. 

a subhypergroup K of $(H,\circ )$ is a complete part if and only if it is conjugable;

4. 

the heart ${\omega }_H$ is the intersection of all conjugable subhypergroups (or complete parts) of $(H,\circ )$;

5. 

the heart ${\omega }_H$ is a reflexive subhypergroup of $(H,\circ )$, that is, $x\circ y\cap {\omega }_H\ne \varnothing \Rightarrow y\circ x\cap {\omega }_H\ne \varnothing$.

3. $G$-Hypergroups

The heart of a hypergroup $(H,\circ )$ allows us to explicitly compute the partition determined by $\beta$, as $\beta \left(x\right)=w_H\circ x=x\circ w_H$ for all $x\in H$. For this reason, the heart of hypergroups has been the subject of much research, in particular, to characterize it as the union of particular hyperproducts [12]. A special class of hypergroups is that of 1-hypergroups, where the heart is a singleton. Clearly, the heart of a 1-hypergroup is isomorphic to a trivial group and if $w_H=\left\{\epsilon \right\}$ then the element $\epsilon$ is an identity since $x\in \beta \left(x\right)=\epsilon \circ x=x\circ \epsilon$. Other relevant results on 1-hypergroups can be found, e.g., in [13,14,15,16]. In this section, we will study the main properties of hypergroups whose heart is isomorphic to a group G, which we call G-hypergroups.

Notably, the class of G-hypergroups is closed under direct product. Indeed, if $(H,\circ )$ and $(H^{\prime },★)$ are G-hypergroups then the direct product $H\times H^{\prime }$ is a G-hypergroup as ${\omega }_{H\times H^{\prime }}={\omega }_H\times {\omega }_H^{\prime }$. Indeed, for all $(x,y)\in H\times H^{\prime }$, we have ${\beta }_{H\times H^{\prime }}(x,y)={\beta }_H\left(x\right)\times {\beta }_{H^{\prime }}\left(y\right)$. Non-trivial examples of G-hypergroups can be built by means of the construction shown in Example 2 of [15], which we recall hereafter. Let $Aut\left(H\right)$ be the automorphism group of a hypergroup $(H,\circ )$. For $f\in Aut\left(H\right)$, let $⟨f⟩$ denote the subgroup of $Aut\left(H\right)$ generated by f. In $H\times ⟨f⟩$, define the following hyperproduct: for $(a,f^m),(b,f^n)\in H\times ⟨f⟩$, let

$$(a,f^m)★(b,f^n)=\left\{(c,f^{m+n})\right|c\in a\circ f^m\left(b\right)\}=(a\circ f^m\left(b\right))\times \left\{f^{m+n}\right\}.$$

with respect to this hyperproduct $(H\times ⟨f⟩,★)$ is a hypergroup whose heart is ${\omega }_H\times \left\{f^0\right\}$. Clearly, if $(H,\circ )$ is a G-hypergroup then also $(H\times ⟨f⟩,★)$ is a G-hypergroup.

3.1. A Construction of G-Hypergroups

Let T and G be groups with $\left|T\right|\ge 2$. Consider a family $\mathfrak{F}={\left\{A_k\right\}}_{k\in T}$ of non-empty and pairwise disjoint sets such that $A_{1_T}=G$ and $|A_i|=|G|$, for all $i\in T$. In these hypotheses we pose $A_i={\left\{a_{i,h}\right\}}_{h\in G}$, for all $i\ne 1_T$. In the set $H={\bigcup }_{k\in T}{A}_k$ we consider the hyperproduct $\circ :H\times H\to {\mathcal{P}}^{*}\left(H\right)$ defined as follows: for all $x,y\in H$,

$$x\circ y=\left\{\begin{array}{cc}\left\{xy\right\}\hfill & \mathrm{if}x,y\in A_{1_T};\hfill \\ \left\{a_{i,hy}\right\}\hfill & \mathrm{if}x=a_{i,h},y\in A_{1_T}\mathrm{and}i\ne 1_T;\hfill \\ A_{ij}\hfill & \mathrm{if}x\in A_i,y\in A_j\mathrm{and}j\ne 1_T;\hfill \end{array}\right.$$

(1)

We note that, by definition of hyperproduct ∘, we have $x\circ 1_G=\left\{x\right\}$ and $x\in 1_G\circ x$ for all $x\in H$. Moreover, for every $i,j\in T$ and $x\in A_j$ we obtain

$$A_i\circ x=A_{ij},x\circ A_i=A_{ji}.$$

(2)

Indeed, if $j\ne 1_T$ then $A_i\circ x={\bigcup }_{y\in A_i}y\circ x=A_{ij}$. Otherwise, if $i=j=1_T$ then $A_{1_T}\circ x=Gx=G=A_{1_T}$. Moreover, if $i\ne 1_T$ and $j=1_T$ then we obtain $A_i\circ x={\bigcup }_{h\in G}{a}_{i,h}\circ x={\bigcup }_{h\in G}\left\{a_{i,hx}\right\}=A_i$. By analogous arguments, we can deduce that $x\circ A_i=A_{ji}$. These simple remarks yield the basis of the following result, where we prove that $(H,\circ )$ is a G-hypergroup with some special properties.

Theorem 2.

In the previous notations, the hyperoperation ∘ defined in (1) is associative. Moreover, we have

1. 

for every integer $n\ge 3$ and for every $(z_1,z_2,\dots ,z_n)\in H^n$, there exists $r\in T$ such that $z_1\circ z_2\circ \dots \circ z_n\subseteq A_r$;

2. 

for all $i\in T$ there exist $x,y\in H$ such that $x\circ y=A_i$;

3. 

$(H,\circ )$ is a hypergroup such that $\beta ={\beta }_2$;

4. 

${\omega }_H=A_{1_T}=G$ and $\beta \left(x\right)=A_k$, for all $x\in A_k$ and $k\in T$;

5. 

$H/\beta \cong T$.

Proof. 

Let $x\in A_i$, $y\in A_j$ and $z\in A_k$ with $i,j,k\in T$. If $i=j=k=1_T$ then we have immediately $(x\circ y)\circ z=x\circ (y\circ z)$ since $A_{1_T}=G$ is a group. Otherwise, we have the following cases:

• Only two of the three elements $i,j,k$ coincide with $1_T$;
• Only one of the three elements $i,j,k$ coincides with $1_T$;
• $i,j,k\in T-\left\{1_T\right\}$.

In the first case, if we assume that $i=j=1_T$ and $k\ne 1_T$, then we have $(x\circ y)\circ z=\left\{xy\right\}\circ z=A_k=x\circ A_k=x\circ (y\circ z)$.

If $i=k=1_T$ and $j\ne 1_T$, we obtain $(x\circ y)\circ z=x\circ (y\circ z)=A_j$.

If $j=k=1_T$ and $i\ne 1_T$, we have $(x\circ y)\circ z=x\circ (y\circ z)=A_i$.

In the second case, suppose $i=1_T$ and $j,k\in T-\left\{1_T\right\}$, we have $(x\circ y)\circ z=A_j\circ z=A_{jk}=x\circ A_{jk}=x\circ (y\circ z)$.

If $j=1_T$ and $i,k\in T-\left\{1_T\right\}$, we obtain $(x\circ y)\circ z=x\circ (y\circ z)=A_{ik}$ because $x\circ y\subseteq A_i$, $z\in A_k$ and $y\circ z=A_k$.

If $i,j\in T-\left\{1_T\right\}$ and $k=1_T$, we deduce $(x\circ y)\circ z=x\circ (y\circ z)=A_{ij}$ as $x\circ y=A_{ij}$, $x\in A_i$ and $y\circ z\subseteq A_j$.

In the last case we have $(x\circ y)\circ z=x\circ (y\circ z)=A_{ijk}$. Thus, ∘ is associative. Now, we complete the proof of the remaining claims.

1.

To prove this claim it suffices to proceed by induction on n, based on (2) and the associativity of hyperproduct ∘.

2.

Let $i\in T$. If $i\ne 1_T$ then we have $x\circ y=A_i$, for all $x\in A_{1_T}$ and $y\in A_i$. If $i=1_T$, since $\left|T\right|\ge 2$, there exists $j,k\in T-\left\{1_T\right\}$ such that $jk=1_T$ and so $x\circ y=A_{jk}=A_{1_T}$, for all $x\in A_j$ and $y\in A_k$.

3.

To prove that $(H,\circ )$ is a hypergroup we only need to prove reproducibility. Let $x\in A_i$. As $iT=T$, using (2) we obtain

$$x\circ H=x\circ \left(\bigcup _{j\in T}{A}_j\right)=\bigcup _{j\in T}x\circ A_j=\bigcup _{j\in T}{A}_{ij}=H.$$

Analogously, we can prove that $H\circ x=H$ for every $x\in H$. Now, being $(H,\circ )$ a hypergroup, we have the chain of inclusions

$${\beta }_1\subseteq {\beta }_2\subseteq {\beta }_3\subseteq \cdots \subseteq {\beta }_n\cdots$$

Thus, if $a\beta b$ then there exists $n\ge 3$ such that $a{\beta }_{n}b$. For points $1.$ and $2.$, there exist $r\in T$ and $x,y\in H$ such that $\{a,b\}\subseteq A_r=x\circ y$, so we obtain $x{\beta }_{2}y$.

4.

Clearly $A_1=G$ is a subhypergroup of H. Moreover, G is conjugable as for all $x\in H-G$ and $x\in A_j$ there exists $x^{\prime }\in A_{j^{-1}}$ such that $x\circ x^{\prime }=A_{1_T}=G$. By point $4.$ of Theorem 1, we have ${\omega }_H\subseteq G$. Moreover, $G\subseteq {\omega }_H$ because ${\omega }_H$ is a complete part of H and $G=x\circ x^{\prime }\bigcap {\omega }_H\ne \varnothing$. Finally, by (2) we have $\beta \left(x\right)={\omega }_H\circ x=G\circ x=A_k$, for all $x\in A_k$ and $k\in T$.

5.

The application $f:T\mapsto H/\beta$ such that $f\left(k\right)=A_k$ is a group isomorphism.

□

3.2. If G Is a Torsion Group

In this subsection, we denote by $\epsilon$ the identity of the heart of a G-hypergroup $(H,\circ )$. Moreover, we denote by $\mathfrak{T}\left(H\right)$ the class of G-hypergroups whose heart is a torsion group. For each element x of a hypergroup $(H,\circ )$, we identify $x^1$ with the singleton $\left\{x\right\}$ and, for any integer $n\ge 2$, we set

$$x^n=\underset{n \mathrm{times}}{\underbrace{x\circ x\circ \cdots \circ x}}.$$

Moreover, define

$$\breve{x}=\bigcup _{k=1}^{\infty }{x}^k.$$

The set $\breve{x}$ is the cyclic semihypergroup generated by x. This hypercompositional analogue of cyclic semigroups has attracted the interest of many researchers, being a powerful tool for the construction and study of remarkable families of hypergroups. We point the interested reader to the detailed reviews in [23,24].

In what follows, we exploit cyclic sub-semihypergroups to derive some properties of hypergroups in $\mathfrak{T}\left(H\right)$. Specifically, we prove that the identity of the heart ${\omega }_H$ of a hypergroup $(H,\circ )\in \mathfrak{T}\left(H\right)$ is an invertible sub-hypergroup of $(H,\circ )$. We will use these properties in the subsequent section to describe the group actions of ${\omega }_H$ on families of hyperproducts $g\circ x$ and $x\circ g$ for $g\in {\omega }_H$ and $x\in H$.

Theorem 3.

Let $(H,\circ )\in \mathfrak{T}\left(H\right)$. Then, ε is an identity of $(H,\circ )$.

Proof. 

Let $x\in H-G$. There exists $e\in {\omega }_H$ such that $x\in x\circ e$ by reproducibility of $(H,\circ )$. Moreover, $x\in x\circ e\subseteq (x\circ e)\circ e=x\circ (e\circ e)=x\circ e^2$ and, by an inductive argument, $x\in x\circ e^n$ for all $n\ge 1$. Finally, as ${\omega }_H$ is a torsion group, there exists $m\ge 1$ such that $e^m=\left\{\epsilon \right\}$, thus $x\in x\circ \epsilon$. By analogous arguments we also have $x\in \epsilon \circ x$. □

Proposition 1.

Let $(H,\circ )$ an G-hypergroup and $x\in H$. The following conditions are equivalent:

1. 

$\epsilon \circ y=\left\{y\right\}$ (resp., $y\circ \epsilon =\left\{y\right\}$) for all $y\in \beta \left(x\right)$;

2. 

$|g\circ y|=1$ (resp., $|y\circ g|=1$) for all $g\in {\omega }_H$ and $y\in \beta \left(x\right)$.

Proof. 

$1.\Rightarrow 2.$ Let $g\in {\omega }_H$ and $y\in \beta \left(x\right)$. The thesis is obvious if $\beta \left(x\right)={\omega }_H$, so let $x\in H-{\omega }_H$ and $a\in g\circ y$. We have $a\in g\circ y\subseteq {\omega }_H\circ y=\beta \left(y\right)=\beta \left(x\right)$ and so $\epsilon \circ a=\left\{a\right\}$. Moreover, $g^{-1}\circ a\subseteq g^{-1}\circ (g\circ y)=(g^{-1}\circ g)\circ y=\epsilon \circ y=\left\{y\right\}$. Hence $g^{-1}\circ a=\left\{y\right\}$. Consequently, $g\circ y=g\circ (g^{-1}\circ a)=(g\circ g^{-1})\circ a=\epsilon \circ a=\left\{a\right\}$. Therefore $|g\circ y|=1$. In the same way we prove that $|y\circ g|=1$ if $y\circ \epsilon =\left\{y\right\}$ for all $y\in \beta \left(x\right)$.

The converse implication, $2.\Rightarrow 1.$, is an immediate consequence of Theorem 3. □

Corollary 1.

Let $(H,\circ )\in \mathfrak{T}\left(H\right)$. Then ε is a left scalar identity (resp., right scalar identity) of $(H,\circ )$ if and only if $|g\circ x|=1$ (resp., $|x\circ g|=1$), for all $g\in {\omega }_H$ and $x\in H$.

Theorem 4.

Let $(H,\circ )\in \mathfrak{T}\left(H\right)$. If S is a finite sub-semihypergroup of $(H,\circ )$ then we have:

1. 

$\epsilon \in S$;

2. 

S is a sub-hypergroup of $(H,\circ )$.

Proof. 

$1.$ Let $\phi :H\to H/\beta$ be the canonical projection. As S is finite, there exists $x\in S$ such that $\breve{x}$ has minimal size.

If $x\in x^2$ then $\phi \left(x\right)=\phi \left(x\right)\otimes \phi \left(x\right)$. Hence $\phi \left(x\right)=1_{H/\beta }$ and $x\in {\omega }_H$. As ${\omega }_H$ is a torsion group, there exists a positive integer n such that $x^n=\left\{\epsilon \right\}$ and so $\epsilon \in S$.

If $x\notin x^2$ then there exists $y\in x^2$ such that $y\ne x$. Clearly, we have $\breve{y}\subseteq \breve{x}$ and consequently $\breve{y}=\breve{x}$ as $\breve{x}$ has minimal size. Therefore, $x\in \breve{y}$ and there exists a integer $n\ge 2$ such that $x\in y^n\subseteq {\left(x^2\right)}^n=x^{2n}=x\circ x^{2n-1}$. Therefore, there exists $a\in x^{2n-1}$ such that $x\in x\circ a$ and $\phi \left(x\right)=\phi \left(x\right)\otimes \phi \left(a\right)$. Thus, $\phi \left(a\right)=1_{H/\beta }$ and $a\in {\omega }_H$. Finally, there exists a integer positive m such that $a^m=\left\{\epsilon \right\}$ and $\epsilon \in {\left(x^{2n-1}\right)}^m=x^{(2n-1)m}\subseteq \breve{x}\subseteq S$.

$2.$ We must show that $x\circ S=S\circ x=S$, for all $x\in S$. By point $1.$ and Theoreme 3, $\epsilon \in S$ and $\epsilon$ is identity in $(H,\circ )$. Therefore, we have $S\subseteq \epsilon \circ S\subseteq S\circ S\subseteq S$ and so $\epsilon \circ S=S\circ S=S$. Now, if $x\in S$, the subset $x\circ \breve{x}$ is a finite sub-semihypergroup of $(H,\circ )$ as S is finite, $x\circ \breve{x}\subseteq S$ and $(x\circ \breve{x})\circ (x\circ \breve{x})=x\circ x\circ \breve{x}\circ \breve{x}\subseteq x^2\circ \breve{x}\subseteq x\circ \breve{x}$. Thus, for point $1.$, we obtain $\epsilon \in x\circ \breve{x}$. Finally,

$$S=\epsilon \circ S\subseteq x\circ \breve{x}\circ S\subseteq x\circ S\circ S\subseteq x\circ S\subseteq S\circ S=S.$$

Therefore, $x\circ S=S$ for all $x\in S$. In the same way we prove that $S\circ x=S$. □

Theorem 5.

Let $(H,\circ )\in \mathfrak{T}\left(H\right)$. The singleton $S=\left\{\epsilon \right\}$ is a invertible sub-hypergroup of $(H,\circ )$.

Proof. 

We prove that $S=\left\{\epsilon \right\}$ is invertible on the left, that is $x\in S\circ y\Rightarrow y\in S\circ x$, for all $x,y\in H$. In the same way, it is proved that S is invertible on the right. Let $x\in S\circ y=\epsilon \circ y$. If $y\in {\omega }_H$, we have $x=y$ and $y\in \epsilon \circ x=S\circ x$. Now, we suppose $y\in H-{\omega }_H$. Clearly, we have $\epsilon \circ x\subseteq \epsilon \circ y$. Moreover, we obtain $x\in {\omega }_H\circ y=\beta \left(y\right)$ and so $y\in \beta \left(x\right)={\omega }_H\circ x$. Therefore, there exists $g\in {\omega }_H$ such that $y\in g\circ x$. Consequently, $y\in g\circ x\subseteq g\circ (\epsilon \circ y)\subseteq g\circ (\epsilon \circ (g\circ x))=g^2\circ x$ and $y\in g^2\circ x$. By induction, we deduce that $y\in g^n\circ x$, for all integer $n\ge 1$. As ${\omega }_H$ is a torsion group, there exists a positive integer m such that $g^m=\left\{\epsilon \right\}$ and so $y\in \epsilon \circ x=S\circ x$. □

Remark 1.

The invertibility on the left (resp., on the right) of the sub-hypergroup $S=\left\{\epsilon \right\}$ implies that the family of right cosets (resp., left cosets) of $S=\left\{\epsilon \right\}$ is a partition of H. Since for each element y of a β-class $\beta \left(x\right)$ we have $\epsilon \circ y\subseteq {\omega }_H\circ x=\beta \left(x\right)$ (resp., $y\circ \epsilon \subseteq x\circ {\omega }_H=\beta \left(x\right)$), then every β-class is a disjoint union of right cosets of S (resp., left cosets of S).

3.3. The Cosets of $\left\{\epsilon \right\}$

As suggested by Remark 1, the families of right and left cosets of $S=\left\{\epsilon \right\}$ are relevant to determine the structure of G-hypergroups in $\mathfrak{T}\left(H\right)$. In this subsection we deepen the knowledge of these cosets. We will only do proofs for right cosets because properties that are true for a hypergroup are also true for its transposed hypergroup.

Proposition 2.

Let $(H,\circ )\in \mathfrak{T}\left(H\right)$. For all $x\in H$ and $g\in {\omega }_H$ we have:

1. 

$x\in g\circ x\iff g\circ x=\epsilon \circ x$;

2. 

$g\circ x\cap \epsilon \circ x\ne \varnothing \iff g\circ x=\epsilon \circ x$;

3. 

$x\in x\circ g\iff x\circ g=x\circ \epsilon$;

4. 

$x\circ g\cap x\circ \epsilon \ne \varnothing \iff x\circ g=x\circ \epsilon$;

Proof. 

$1.$ The implication ⇐ is a consequence of Theorem 3. Now, suppose that $x\in g\circ x$. Clearly, we have $\epsilon \circ x\subseteq \epsilon \circ (g\circ x)=(\epsilon \circ g)\circ x=g\circ x$. Moreover, $g\circ x\subseteq g\circ (g\circ x)=g^2\circ x$ and, by induction, we obtain the chain of inclusions $\epsilon \circ x\subseteq g\circ x\subseteq g^2\circ x\subseteq \cdots \subseteq g^n\circ x\subseteq \cdots .$ As ${\omega }_H$ is a torsion group, there exists a positive integer m such that $g^m=\left\{\epsilon \right\}$ and so $\epsilon \circ x\subseteq g\circ x\subseteq \epsilon \circ x$. Therefore, $\epsilon \circ x=g\circ x$.

Concerning point $2.$, it is enough to prove the implication ⇒. Let $z\in \epsilon \circ x\cap g\circ x$. As $S=\left\{\epsilon \right\}$ is a invertible subhypergroup of H, we have $\epsilon \circ x=\epsilon \circ z$ and so $z\in g\circ x=g\circ \epsilon \circ x=g\circ \epsilon \circ z=g\circ z$. Therefore, by point $1.$, we obtain $\epsilon \circ z=g\circ z$. Consequently, we deduce $\epsilon \circ x=\epsilon \circ z=g\circ z=g\circ \epsilon \circ z=g\circ \epsilon \circ x=g\circ x$.

Points $3.$ and $4.$ follow from $1.$ and $2.$ by considering the transposed hypergroup of $(H,\circ )$. □

Proposition 3.

Let $(H,\circ )\in \mathfrak{T}\left(H\right)$. For all $x,y\in H$ and $g,g^{\prime }\in {\omega }_H$ we have

1. 

$y\in g\circ x\iff \epsilon \circ y=g\circ x$;

2. 

$g\circ x\cap g^{\prime }\circ y\ne \varnothing \iff g\circ x=g^{\prime }\circ y$;

3. 

if $y\in g\circ x$, then $\epsilon \circ x\cap g\circ x=\varnothing \iff \epsilon \circ y\cap g\circ y=\varnothing$;

4. 

$y\in x\circ g\iff y\circ \epsilon =x\circ g$;

5. 

$x\circ g\cap y\circ g^{\prime }\ne \varnothing \iff x\circ g=y\circ g^{\prime }$;

6. 

if $y\in x\circ g$, then $x\circ \epsilon \cap x\circ g=\varnothing \iff y\circ \epsilon \cap y\circ g=\varnothing$.

Proof. 

$1.$ The implication ⇐ is a consequence of the Theorem 3. Let $y\in g\circ x$. We have $g^{-1}\circ y\subseteq g^{-1}\circ g\circ x=\epsilon \circ x$. Taking an element $z\in g^{-1}\circ y$, we obtain $\epsilon \circ z\subseteq \epsilon \circ x$. Therefore, for invertibility of subhypergroup $S=\left\{\epsilon \right\}$ in $(H,\circ )$, $\epsilon \circ z=\epsilon \circ x$. Consequently, as $\epsilon \circ z\subseteq g^{-1}\circ y\subseteq \epsilon \circ x$, we deduce $g^{-1}\circ y=\epsilon \circ x$ and so $\epsilon \circ y=g\circ x$.

$2.$ Let $z\in g\circ x\cap g^{\prime }\circ y$. By point $1.$ of Proposition 3, we have $\epsilon \circ z=g\circ x$ and $\epsilon \circ z=g^{\prime }\circ y$. Therefore, $g\circ x=g^{\prime }\circ y$.

$3.$ As $y\in g\circ x$, by point $1.$ of Proposition 3, we have $\epsilon \circ y=g\circ x$ and so $\epsilon \circ x=g^{-1}\circ (g\circ x)=g^{-1}\circ (\epsilon \circ y)=g^{-1}\circ y$. Consequently, $\epsilon \circ x\cap g\circ x=\varnothing \iff g^{-1}\circ y\cap \epsilon \circ y=\varnothing \iff \epsilon \circ y\cap g\circ y=\varnothing$.

Points $4.$, $5.$, and $6.$ follow from $1.$, $2.$, and $3.$ by considering the transposed hypergroup of $(H,\circ )$. □

4. Actions of ${\mathit{\omega }}_{\mathit{H}}$

If $\varphi :(g,e)\mapsto ge$ is a group action of G on the set E, the sets $O\left(e\right)=\left\{ge\right|g\in G\}$ and $Sta{b}_G\left(e\right)=\{g\in G|ge=e\}$ are the orbit and the stabilizer of element $e\in E$, respectively. The orbits family ${\left\{O\left(e\right)\right\}}_{e\in E}$ is a partition of E and the stabilizer $Sta{b}_G\left(e\right)$ is a subgroup of G. If e and $e^{\prime }$ belong to the same orbit the stabilizers are conjugates. Moreover, we have $\left|O\left(e\right)\right|=[G:Sta{b}_G\left(e\right)]$ and when G is finite we obtain that $\left|O\right(e\left)\right|$ divides the size of G.

If $(H,\circ )\in \mathfrak{T}\left(H\right)$, we denote by $\mathfrak{L}$ and $\mathfrak{R}$ the following sets:

$$\mathfrak{L}=\{x\circ g|x\in H-{\omega }_H,g\in {\omega }_H\},\mathfrak{R}=\{g\circ x|x\in H-{\omega }_H,g\in {\omega }_H\}.$$

On $\mathfrak{L}$ and $\mathfrak{R}$ we consider the actions ${\varphi }_l:{\omega }_H\times \mathfrak{L}\to \mathfrak{L}$ e ${\varphi }_r:{\omega }_H\times \mathfrak{R}\to \mathfrak{R}$ such that

$${\varphi }_l(h,x\circ g)=x\circ (g\circ h)\text{e}{\varphi }_r(h,g\circ x)=(h\circ g)\circ x,$$

for all $x\circ g\in \mathfrak{L}$, $g\circ x\in \mathfrak{R}$ and $h\in {\omega }_H$.

For simplicity, let $Sta{b}_{{\omega }_H}(x\circ \epsilon )={}_{x}S$ and ${}_{x}O=O(x\circ \epsilon )=\{x\circ g|g\in {\omega }_H\}$ be the stabilizer and the orbit of $x\in H-{\omega }_H$ with respect to the action ${\varphi }_l$, and let $Sta{b}_{{\omega }_H}(x\circ \epsilon )={}_{x}S$ and ${}_{x}O=O(x\circ \epsilon )=\{x\circ g|g\in {\omega }_H\}$ be those with respect to ${\varphi }_r$.

If $y\in \beta \left(x\right)$ then there exists $g\in {\omega }_H$ such that $y\in g\circ x$. By Proposition 3, we deduce $\epsilon \circ y=g\circ x$. Conversely, again for the Proposition 3, if $g\circ x\in O_x$ and $y\in g\circ x$ we have $\epsilon \circ y=g\circ x$ with $y\in \beta \left(x\right)$. Therefore, we obtain

$$O_x=\{g\circ x|g\in {\omega }_H\}=\{\epsilon \circ y|y\in \beta \left(x\right)\}.$$

(3)

$${}_{x}O=\{x\circ g|g\in {\omega }_H\}=\{y\circ \epsilon |y\in \beta \left(x\right)\}.$$

(4)

Next, we establish a connection between the sizes of $O_x$, ${}_{x}O$, ${\omega }_H$, and $\beta \left(x\right)$. For brevity, we only expose results for the action ${\varphi }_r$. The corresponding results for the action ${\varphi }_l$ follow trivially by recurring to transposed hypergroups.

Lemma 1.

Let $(H,\circ )\in \mathfrak{T}\left(H\right)$ and $x\in H-{\omega }_H$.

1. 

$S_x=\left\{\epsilon \right\}$ (resp., ${}_{x}S=\left\{\epsilon \right\}$) if and only if $g\circ x\cap g^{\prime }\circ x=\varnothing$ (resp., $x\circ g\cap x\circ g^{\prime }=\varnothing$), for all $\{g,g^{\prime }\}\subseteq {\omega }_H$ and $g\ne g^{\prime }$;

2. 

if $S_x=\left\{\epsilon \right\}$ (resp., ${}_{x}S=\left\{\epsilon \right\}$) then $|O_x|=|{\omega }_H|\le |\beta \left(x\right)|$ (resp., $|{}_{x}O|=|{\omega }_H|\le |\beta \left(x\right)|$;

3. 

$S_x={\omega }_H$ (resp., ${}_{x}S={\omega }_H$) if and only if $\beta \left(x\right)=\epsilon \circ x$ (resp., $\beta \left(x\right)=x\circ \epsilon$).

Proof. 

$1.$ If $S_x=\left\{\epsilon \right\}$ then $\left|O\left(x\right)\right|=[{\omega }_H:\left\{\epsilon \right\}]=\left|{\omega }_H\right|$ and, by Proposition 3, $g\circ x\cap g^{\prime }\circ x=\varnothing$, for all $\{g,g^{\prime }\}\subseteq {\omega }_H$ and $g\ne g^{\prime }$. Conversely, if $g\in S_x$ then $g\circ x=\epsilon \circ x$ and $g=\epsilon$ by hypothesis.

$2.$ By point $1.$, we have $E_x=O_x$ and so $|E_x|=|O\left(x\right)|=[{\omega }_H:\left\{\epsilon \right\}]=\left|{\omega }_H\right|$. Moreover, as the hyperproducts $g\circ x$ in $O\left(x\right)$ have size $\ge 1$ and $g\circ x\subseteq \beta \left(x\right)$, for all $g\in {\omega }_H$, we deduce $|{\omega }_H|\le |\beta \left(x\right)|$.

$3.$ If $S_x={\omega }_H$ then $g\circ x=\epsilon \circ x$, for all $g\in {\omega }_H$. Therefore, $\beta \left(x\right)={\omega }_H\circ x={\cup }_{g\in {\omega }_H}g\circ x=\epsilon \circ x$. Conversely, if $\beta \left(x\right)=\epsilon \circ x$ then ${\omega }_H\circ x=\epsilon \circ x$ and $g\circ x=g\circ (\epsilon \circ x)=g\circ {\omega }_H\circ x={\omega }_H\circ x=\epsilon \circ x$, for all $g\in {\omega }_H$. Hence $S_x={\omega }_H$. □

Proposition 4.

Let $(H,\circ )\in \mathfrak{T}\left(H\right)$ and let x be an element of $H-{\omega }_H$ such that $\epsilon \circ y=\left\{y\right\}$ (resp., $y\circ \epsilon =\left\{y\right\}$), for every $y\in \beta \left(x\right)$. Then $\left|\beta \left(x\right)\right|\le |{\omega }_H|$ and equality holds if and only if $S_x=\left\{\epsilon \right\}$ (resp., ${}_{x}S=\left\{\epsilon \right\}$).

Proof. 

By Proposition 1, we have $|g\circ y|=1$, for every $g\in {\omega }_H$ and $y\in \beta \left(x\right)$. Therefore, $\left|\beta \left(x\right)\right|=|{\omega }_H\circ x|=|{\cup }_{g\in {\omega }_H}g\circ x|\le |{\omega }_H|$. Now, if $S_x=\left\{\epsilon \right\}$ then $\left|\beta \left(x\right)\right|=|{\omega }_H|$ by point $2.$ of Lemma 1. Conversely, if $\left|\beta \left(x\right)\right|=|{\omega }_H|$, then $g\circ x\cap g^{\prime }\circ x=\varnothing$, for all $g,g^{\prime }\in {\omega }_H$ and $g\ne g^{\prime }$. Thus, by point $1.$ of Lemma 1, $S_x=\left\{\epsilon \right\}$. □

A consequence of the previous proposition is the following result:

Theorem 6.

Let $(H,\circ )\in \mathfrak{T}\left(H\right)$ be such that ε is a left scalar identity and $S_x=\left\{\epsilon \right\}$, for all $x\in H-{\omega }_H$ (resp., ε is a right scalar identity and ${}_{x}S=\left\{\epsilon \right\}$, for all $x\in H-{\omega }_H$). Then $\left|\beta \left(x\right)\right|=|{\omega }_H|$, for all $x\in H$. Moreover, if $(H,\circ )$ is finite then $\left|H\right|=|H/\beta |·|{\omega }_H|$.

Now, if $(H,\circ )\in \mathfrak{T}\left(H\right)$ and $x,y\in H$, we denote by $L_x\left(y\right)$ and ${}_{x}L\left(y\right)$ the following sets: $L_x\left(y\right)=\{g\in {\omega }_H|g\circ x=\epsilon \circ y\},{}_{x}L\left(y\right)=\{g\in {\omega }_H|x\circ g=y\circ \epsilon \}.$ Clearly, we have $L_x\left(x\right)=S_x$ and ${}_{x}L\left(x\right)={}_{x}S$.

Proposition 5.

If $(H,\circ )\in \mathfrak{T}\left(H\right)$ and $x,y\in H-{\omega }_H$ then the following conditions are equivalent:

1. 

$L_x\left(y\right)\ne \varnothing$ (resp., ${}_{x}L\left(y\right)\ne \varnothing$);

2. 

$\beta \left(x\right)=\beta \left(y\right)$;

3. 

$O_x=O_y$ (resp., ${}_{x}O={}_{y}O$).

Proof. 

$1.\iff 2.$ If $L_x\left(y\right)\ne \varnothing$ then there exists $g\in {\omega }_H$ such that $g\circ x=\epsilon \circ y$, and so ${\omega }_H\circ x\cap {\omega }_H\circ y\ne \varnothing$. Thus $\beta \left(x\right)=\beta \left(y\right)$. On the other hand, if $\beta \left(x\right)=\beta \left(y\right)$ then $y\in \beta \left(x\right)={\omega }_H\circ x$ and there exists $g\in {\omega }_H$ such that $y\in g\circ x$. By point $1.$ of Proposition 3, we have $g\circ x=\epsilon \circ y$ and so $g\in L_x\left(y\right)$.

$2.\iff 3.$ Let $\beta \left(x\right)=\beta \left(y\right)$. By (3), $\epsilon \circ y\in O_x\cap O_y$ and $O_x=O_y$ since the orbits are a partition of $H-{\omega }_H$. Now, let $O_x=O_y$. There exist $g\circ x\in O_x$ and $h\circ y\in O_y$ such that $g\circ x=h\circ y$. Consequently, we have ${\omega }_H\circ x\cap {\omega }_H\circ y\ne \varnothing$ and $\beta \left(x\right)=\beta \left(y\right)$. □

Proposition 6.

Let $(H,\circ )\in \mathfrak{T}\left(H\right)$ and let $x,y\in H-{\omega }_H$ such that $\beta \left(x\right)=\beta \left(y\right)$. Then, we have

1. 

$|L_x\left(y\right)|=|S_x|$ (resp., $|{}_{x}L\left(y\right)|=|{}_{x}S|$);

2. 

the subgroups $S_x$ and $S_y$ (resp., ${}_{x}S$ and ${}_{y}S$) are conjugates;

3. 

if $S_x$ or $S_y$ (resp., ${}_{x}S$ or ${}_{y}S$) is a normal subgroup or ${\omega }_H$ is abelian, then $S_x=S_y$ (resp., ${}_{x}S={}_{y}S$);

4. 

$|L_x\left(y\right)|=|S_x|=|S_y|=|L_y\left(x\right)|$;

5. 

$|{}_{x}L\left(y\right)|=|{}_{x}S|=|{}_{y}S|=|{}_{y}L\left(x\right)|$.

Proof. 

$1.$ By Proposition 5, the sets $L_x\left(y\right)$ and $L_y\left(x\right)$ are not empty as $\beta \left(x\right)=\beta \left(y\right)$. Fixed an element $h\in L_y\left(x\right)$, we have $h\circ y=\epsilon \circ x=g\circ x$ for all $g\in S_x$. Therefore, $(h^{-1}\circ g)\circ x=\epsilon \circ y$ and $h^{-1}\circ g\in L_x\left(y\right)$. Clearly, the application ${\phi }_{h^{-1}}:S_x\to L_x\left(y\right)$ such that ${\phi }_{h^{-1}}\left(g\right)=h^{-1}\circ g$, for all $g\in S_x$, is injective and so $|S_x|\le |L_x\left(y\right)|$. On the other hand, as $h\circ y=\epsilon \circ x$, we obtain $\epsilon \circ y=h^{-1}\circ x$. Therefore, $g\in L_x\left(y\right)\Rightarrow g\circ x=\epsilon \circ y=h^{-1}\circ x\Rightarrow h\circ g\circ x=\epsilon \circ x\Rightarrow h\circ g\in S_x$. Finally, the application ${\varphi }_h:L_x\left(y\right)\to S_x$ such that ${\varphi }_h\left(g\right)=h\circ g$, for all $g\in L_x\left(y\right)$, is injective and so $|L_x\left(y\right)|\le |S_x\left({\omega }_H\right)|$.

$2.$ By Proposition 5, we have $O_x=O_y$. Thus, the elements $\epsilon \circ x$, $\epsilon \circ y$ of $\mathfrak{R}$ belong to the same orbit. Consequently, the stabilizers $S_x$ and $S_y$ are conjugates.

Point $3.$ is an immediate consequence of $2.$, and points $4.$ and $5.$ follow from $1.$ and $2.$ because conjugated subgroups have the same size. □

An immediate consequence of point $3.$ in Proposition 6 is the following result:

Corollary 2.

Let $(H,\circ )\in \mathfrak{T}\left(H\right)$ and let x, y be elements of $H-{\omega }_H$ such that $\beta \left(x\right)=\beta \left(y\right)$. Then,

1. 

$S_x=\left\{\epsilon \right\}\iff S_y=\left\{\epsilon \right\}$ (resp., ${}_{x}S=\left\{\epsilon \right\}\iff {}_{y}S=\left\{\epsilon \right\}$);

2. 

$S_x={\omega }_H\iff S_y={\omega }_H$ (resp., ${}_{x}S={\omega }_H\iff {}_{y}S={\omega }_H$).

5. Properties of the Hyperproducts $\mathit{x}\circ \mathit{y}\subseteq {\mathit{\omega }}_{\mathit{H}}$ with $\mathit{x},\mathit{y}\in \mathit{H}-{\mathit{\omega }}_{\mathit{H}}$

In this section, we prove certain properties of products of elements $x,y\in H-{\omega }_H$ such that $x\circ y\subseteq {\omega }_H$. These properties will be utilized in the next section in the construction of G-hypergroups of small size. Note that $x\circ y\cap {\omega }_H\ne ⌀⟹x\circ y\subseteq {\omega }_H$, for all $x,y\in H$ as ${\omega }_H$ is a complete part of H by point 4. of Theorem 1.

Proposition 7.

Let $(H,\circ )\in \mathfrak{T}\left(H\right)$ and let $x,y\in H-{\omega }_H$ such that $x\circ y\cap {\omega }_H\ne \varnothing$. If $S_x={\omega }_H$ and $S_y\in \{\left\{\epsilon \right\},{\omega }_H\}$ (alternatively, if ${}_{y}S={\omega }_H$ and ${}_{x}S\in \{\left\{\epsilon \right\},{\omega }_H\}$) then $x\circ y=y\circ x={\omega }_H$.

Proof. 

Let $S_x={\omega }_H$ and $x\circ y\cap {\omega }_H\ne \varnothing$. By Lemma 1 we have $\beta \left(x\right)={\omega }_H\circ x=\epsilon \circ x$. Thus,

$$x\circ y=\epsilon \circ (x\circ y)=(\epsilon \circ x)\circ y=({\omega }_H\circ x)\circ y={\omega }_H\circ (x\circ y)={\omega }_H.$$

Moreover, we have $y\circ x\subseteq {\omega }_H$ because ${\omega }_H$ is a reflexive subhypergroup of $(H,\circ )$. Now, by hypothesis, two cases are possible: $S_y={\omega }_H$ or $S_y=\left\{\epsilon \right\}$. If $S_y={\omega }_H$ then $y\circ x={\omega }_H$ follows by transposing the previous arguments, and the claim follows. On the other hand, if $S_y=\left\{\epsilon \right\}$ then, by Lemma 1, we have $g\circ y\cap g^{\prime }\circ y=\varnothing$ for all $\{g,g^{\prime }\}\subseteq {\omega }_H$ and $g\ne g^{\prime }$. Consequently, if by absurd we suppose that ${\omega }_H\ne y\circ x$ then we deduce the contradiction

$$\beta \left(y\right)=y\circ {\omega }_H=y\circ (x\circ y)=(y\circ x)\circ y=\bigcup _{g\in y\circ x}g\circ y\ne \bigcup _{t\in {\omega }_H}t\circ y={\omega }_H\circ y=\beta \left(y\right).$$

Therefore, also in this case $y\circ x={\omega }_H$ and $x\circ y=y\circ x={\omega }_H$. When ${}_{y}S={\omega }_H$ and ${}_{x}S\in \{\left\{\epsilon \right\},{\omega }_H\}$ the claim follows by transposition. □

Remark 2.

If the heart ${\omega }_H$ of a hypergroup $(H,\circ )\in \mathfrak{T}\left(H\right)$ is isomorphic to a group of size a prime number p then $S_x\in \{\left\{\epsilon \right\},{\omega }_H\}$, for every $x\in H-{\omega }_H$. In this case, if $x,y\in H-{\omega }_H$, $x\circ y\cap {\omega }_H\ne \varnothing$ and at least one of the subgroups $S_x,S_y$ is different from $\left\{\epsilon \right\}$, then $x\circ y=y\circ x={\omega }_H$. This fact is not true if $S_x=S_y=\left\{\epsilon \right\}$. For example, consider the hypergroup represented by the following table:

Here, ${\omega }_H=\{\epsilon ,b\}\cong {\mathbb{Z}}_2$, $S_c=S_d=\left\{\epsilon \right\}$, and $c\circ d=d\circ c=\left\{b\right\}\ne {\omega }_H$. Recall that the 1-hypergroups are a special class of G-hypergroups and their sub-hypergroups are conjugable. The same property is not true if the heart of a G-hypergroup is not trivial. Indeed, if ε is the identity of the heart then $\left\{\epsilon \right\}$ is a non-conjugable sub-hypergroup of H. On the other hand, there are G-hypergroups that have non-trivial non-conjugable sub-hypergroups. For instance, the hypergroup of the previous table has five non-trivial sub-hypergroups different from H and ${\omega }_H$, that is, $G_1=\{\epsilon ,c\}$, $G_2=\{\epsilon ,d\}$, $G_3=\{\epsilon ,b,c,d\}$, $K_1=\{\epsilon ,b,e\}$, $K_2=\{\epsilon ,b,f\}$. Note that $G_1$ and $G_2$ are isomorphic to ${\mathbb{Z}}_2$ and are not conjugable.

Proposition 8.

Let $(H,\circ )\in \mathfrak{T}\left(H\right)$ and let $x,y\in H-{\omega }_H$ such that $\epsilon \in x\circ y$. Then, $S_x\cup {}_{y}S\subseteq x\circ y$.

Proof. 

We have $x\circ y\subseteq {\omega }_H$ as $\epsilon \in x\circ y$. If $g\in S_x$ then $g\circ x=\epsilon \circ x$ and so $g\in g\circ \epsilon \subseteq g\circ (x\circ y)=(g\circ x)\circ y=(\epsilon \circ x)\circ y=\epsilon \circ (x\circ y)=x\circ y$. Therefore, $S_x\subseteq x\circ y$. In the same way, we prove that ${}_{y}S\subseteq x\circ y$. □

An immediate consequence of Propositions 7 and 8 is the following:

Corollary 3.

Let $(H,\circ )\in \mathfrak{T}\left(H\right)$ and let $x,y\in H-{\omega }_H$ such that $\epsilon \in x\circ y$. If ${\omega }_H$ is isomorphic to a group of size a prime number and $S_x\ne \left\{\epsilon \right\}$ or ${}_{y}S\ne \left\{\epsilon \right\}$, then $x\circ y={\omega }_H$.

Proposition 9.

Let $(H,\circ )\in \mathfrak{T}\left(H\right)$ and let $x,y\in H-{\omega }_H$ such that $x\circ y\subseteq {\omega }_H$. Then, $|a\circ b|=|x\circ y|$, for all $a\in \beta \left(x\right)$ and $b\in \beta \left(y\right)$.

Proof. 

By hypothesis $x\circ y\subseteq {\omega }_H$. Moreover, as $a\in \beta \left(x\right)={\omega }_H\circ x$ and $b\in \beta \left(y\right)=y\circ {\omega }_H$, there exist $h,k\in {\omega }_H$ such that $a\in h\circ x$ and $b\in y\circ k$. By Proposition 3, we have $\epsilon \circ a=h\circ x$ and $b\circ \epsilon =y\circ k$. As $a\circ b\subseteq \beta \left(x\right)\circ \beta \left(y\right)=x\circ {\omega }_H\circ y\circ {\omega }_H=x\circ y\circ {\omega }_H={\omega }_H$, we have $a\circ b=\epsilon \circ a\circ b\circ \epsilon =h\circ x\circ y\circ k$. Finally, the application $f:x\circ y\to a\circ b$ such that $f\left(g\right)=h\circ g\circ k$, for all $g\in x\circ y$, is bijective and so $|x\circ y|=|a\circ b|$. □

Lemma 2.

Let $(H,\circ )\in \mathfrak{T}\left(H\right)$ and let P be a normal subgroup of ${\omega }_H$. Moreover, let $a,b\in H-{\omega }_H$ and $h\in {\omega }_H$. Then, we have

1. 

if $a\circ b=h\circ P$, then for all $z\in \beta \left(b\right)$ there exists $z^{\prime }\in \beta \left(a\right)$ such that $z^{\prime }\circ z\subseteq P$;

2. 

if $|H/\beta |=2$ and $P\ne {\omega }_H$ then $a\circ b\ne h\circ P$.

Proof. 

$1.$ Let $a\circ b=h\circ P$. If $z\in \beta \left(b\right)=b\circ {\omega }_H$, there exists $k\in {\omega }_H$ such that $z\in b\circ k$. Now, taken $z^{\prime }\in k^{-1}\circ h^{-1}\circ a$, we have $z^{\prime }\in {\omega }_H\circ a=\beta \left(a\right)$. Moreover, as P is a normal subgroup and $a\circ b=h\circ P$, we deduce $z^{\prime }\circ z\subseteq k^{-1}\circ h^{-1}\circ a\circ b\circ k\subseteq k^{-1}\circ h^{-1}\circ h\circ P\circ k=P$.

$2.$ By absurdity, let $a\circ b=h\circ P$. As $|H/\beta |=2$ and $a,b\in H-{\omega }_H$, we have $\beta \left(a\right)=\beta \left(b\right)=H-{\omega }_H$. Now, let $z\in H$. Clearly, if $z\in {\omega }_H$ then $z^{-1}\circ z=\left\{\epsilon \right\}\subseteq P$. If $z\in H-{\omega }_H$, we have $z\in \beta \left(a\right)$ and, by point $1.$, there exists $z^{\prime }\in \beta \left(b\right)$ such that $z^{\prime }\circ z\subseteq P$. Hence, P is a conjugable subhypergroup of $(H,\circ )$ and we have ${\omega }_H\subseteq P\subseteq {\omega }_H$; impossible as $P\ne {\omega }_H$. □

Proposition 10.

Let $(H,\circ )\in \mathfrak{T}\left(H\right)$ such that $|H/\beta |=2$ and $|{\omega }_H|\ge 2$. We have

1. 

$|a\circ b|\ge 2$, for all $a,b\in H-{\omega }_H$;

2. 

if there exists $x\in H-{\omega }_H$ such that $S_x={\omega }_H$ or ${}_{x}S={\omega }_H$, then $a\circ b={\omega }_H$, for all $a,b\in H-{\omega }_H$;

3. 

if $|{\omega }_H|=2$ then $a\circ b={\omega }_H$, for all $a,b\in H-{\omega }_H$.

Proof. 

$1.$ By hypothesis $S=\left\{\epsilon \right\}$ is a proper normal subgroup of ${\omega }_H$ and $a\circ b\subseteq {\omega }_H$, for all $a,b\in H-{\omega }_H$. If there exist $a,b\in H-{\omega }_H$ such that $|a\circ b|=1$, we can suppose that $a\circ b=\left\{h\right\}$, with $h\in {\omega }_H$. Therefore, we have $a\circ b=\left\{h\right\}=h\circ S$, that is impossible by point $2.$ of Lemma 2.

$2.$ Let $x\in H-{\omega }_H$ and $S_x={\omega }_H$. For reproducibility, there exists $y\in H-{\omega }_H$ such that $\epsilon \in x\circ y$. By Proposition 8, we have $x\circ y={\omega }_H$. Consequently, from Proposition 9, we deduce $a\circ b={\omega }_H$, for all $a,b\in H-{\omega }_H$. We get the same result if ${}_{x}S={\omega }_H$.

$3.$ is an immediate consequence of $1.$ □

Corollary 4.

Let $(H,\circ )\in \mathfrak{T}\left(H\right)$ and let x be an element of $H-{\omega }_H$ such that $\left|\beta \left(x\right)\right|<|{\omega }_H|$. If $(H,\circ )$ is finite and ${\omega }_H$ is a group of size a prime number p then $y\circ g=g\circ y=\beta \left(x\right)$, for all $y\in \beta \left(x\right)$ and $g\in {\omega }_H$. Moreover, if $|H/\beta |=2$ then $x\circ y=y\circ x={\omega }_H$, for all $x,y\in H-{\omega }_H$.

Proof. 

Since $|{\omega }_H|$ is a prime number p and $\left|\beta \left(x\right)\right|<|{\omega }_H|$, by Lemma 1, $S_x={}_{x}S={\omega }_H$ and $\epsilon \circ x=x\circ \epsilon =\beta \left(x\right)$. Now, if $y\in \beta \left(x\right)$, $g\in {\omega }_H$ and $a\in g\circ y$ (resp., $a\in y\circ g$), by Proposition 3, we have $\epsilon \circ a=g\circ y=\beta \left(y\right)=\beta \left(x\right)$ (resp., $a\circ \epsilon =y\circ g=\beta \left(y\right)=\beta \left(x\right)$). Furthermore, by Proposition 10, if $|H/\beta |=2$ and $x,y\in H-{\omega }_H$ then $x\circ y=y\circ x$$={\omega }_H$. □

Example 1.

In the next table we show a hypergroup $(H,\circ )\in \mathfrak{T}\left(H\right)$ such that $|H/\beta |=2$, ${\omega }_H\cong {\mathbb{Z}}_3$, $\left|H\right|=|{\omega }_H|·|H/\beta |$ and all hyperproducts $a\circ b$ have size 2, for all $a,b\in H-{\omega }_H$.

According to Proposition 10, necessarily we have here $S_x\ne {\omega }_H$ and ${}_{x}S\ne {\omega }_H$, for all $x\in H-{\omega }_H$.

In the previous example, each element of the heart is contained in exactly six hyperproducts $x\circ y\subset {\omega }_H$. This fact finds full justification in the next proposition. A new notation is entered: For all $x,y\in H$ such that $x\circ y\subseteq {\omega }_H$ and $g\in {\omega }_H$, let $N_g^{x,y}=\{(a,b)\in \beta \left(x\right)\times \beta \left(y\right)|g\in a\circ b\}$. Clearly, $N_g^{x,y}\ne \varnothing$ as $\beta \left(x\right)\circ \beta \left(y\right)=x\circ {\omega }_H\circ y\circ {\omega }_H=x\circ y\circ {\omega }_H\circ {\omega }_H={\omega }_H$.

Proposition 11.

Let $(H,\circ )\in \mathfrak{T}\left(H\right)$, $x,y\in H-{\omega }_H$ and $x\circ y\subseteq {\omega }_H$. If $\epsilon \circ a=\left\{a\right\}$, for all $a\in \beta \left(x\right)$ (resp., $b\circ \epsilon =\left\{b\right\}$, for all $b\in \beta \left(y\right)$), then $|N_g^{x,y}|$ is the same for all $g\in {\omega }_H$.

Proof. 

Let $(a,b)\in N_g^{x,y}$. There exists $h\in {\omega }_H$ such that $\left\{g^{\prime }\right\}=h\circ g$. Clearly, $h\circ a\subseteq {\omega }_H\circ a=\beta \left(a\right)=\beta \left(x\right)$, with $|h\circ a|=1$ by Proposition 1. Moreover, if $h\circ a=\left\{a^{\prime }\right\}$ then $\left\{g^{\prime }\right\}=h\circ g\subseteq h\circ (a\circ b)=(h\circ a)\circ b=a^{\prime }\circ b$ and so $(a^{\prime },b)\in N_{g^{\prime }}^{x,y}$. Finally, the application ${\phi }_h:N_g^{x,y}\to N_{g^{\prime }}^{x,y}$ such that ${\phi }_h(a,b)=(a^{\prime },b)$, with $h\circ a=\left\{a^{\prime }\right\}$, is injective because $h\circ a_1=h\circ a_2\iff a_1=a_2$, for all $a_1,a_2\in \beta \left(x\right)$. Therefore, $|N_g^{x,y}|\le |N_{g^{\prime }}^{x,y}|$. Similarly, we have $|N_{g^{\prime }}^{x,y}|\le |N_g^{x,y}|$. □

Corollary 5.

Let $(H,\circ )$ be a finite hypergroup in $\mathfrak{T}\left(H\right)$, and let $x,y\in H-{\omega }_H$ such that $x\circ y\subseteq {\omega }_H$. If $\epsilon \circ a=\left\{a\right\}$, for all $a\in \beta \left(x\right)$ (resp., $b\circ \epsilon =\left\{b\right\}$, for all $b\in \beta \left(y\right)$), then $|a\circ b|·\left|\beta \left(x\right)\right|·\left|\beta \left(y\right)\right|=|{\omega }_H|·|N_g^{x,y}|$ for all $a\in \beta \left(x\right)$, $b\in \beta \left(y\right)$ and $g\in {\omega }_H$. In particular, if $|{\omega }_H|$ is a prime number then $a\circ b={\omega }_H$ or $|{\omega }_H|$ divides $\left|\beta \right(x\left)\right|$ or $\left|\beta \right(y\left)\right|$.

Proof. 

Let $n^{x,y}=\left|N_g^{x,y}\right|$. By Proposition 9, $|a\circ b|=|x\circ y|$ for all $a\in \beta \left(x\right)$ and $b\in \beta \left(y\right)$. Thus, taking $a\in \beta \left(x\right)$ and $b\in \beta \left(y\right)$, by Proposition 11 and $\beta \left(x\right)\circ \beta \left(y\right)={\omega }_H$, we obtain $|a\circ b|·\left|\beta \left(x\right)\right|·\left|\beta \left(y\right)\right|=|{\omega }_H|·n^{x,y}$ counting in two different ways. Finally, as $a\circ b\subseteq {\omega }_H$, if $|{\omega }_H|$ is a prime number then $a\circ b={\omega }_H$ or $|{\omega }_H|$ divides $\left|\beta \right(x\left)\right|$ or $\left|\beta \right(y\left)\right|$. □

In Proposition 11, the hypothesis $\epsilon \circ a=\left\{a\right\}$ for all $a\in \beta \left(x\right)$ is essential. Indeed, consider the following hypergroup:

Here, we have ${\omega }_H\cong {\mathbb{Z}}_3$, $|H/\beta |=2$, $|N_{\epsilon }^{d,e}|=16$ and $|N_b^{d,e}|=|N_c^{d,e}|=17$. In this example, Proposition 11 cannot be applied because $\epsilon \circ d\ne \left\{d\right\}$.

6. Hypergroups of Type $\mathit{U}$ in $\mathfrak{T}\left(\mathit{H}\right)$

Among the best-known classes of hypergroups are undoubtedly those of type U, type C, and the cogroups. A hypergroup of type U on the right is a hypergroup $(H,\circ )$ with a right scalar identity $\epsilon$ that fulfills the condition $a\in a\circ b\Rightarrow b=\epsilon$, for all $a,b\in H$, see [25,26,27]. A hypergroup of type C on the right is a hypergroup $(H,\circ )$ of type U on the right that fulfills the condition $a\circ b\cap a\circ c\ne \varnothing \Rightarrow \epsilon \circ b=\epsilon \circ c$, for all $a,b,c\in H$, see [5,6]. A cogroup on the right is a hypergroup of type C on the right such that $|a\circ c|=|b\circ c|$ for all $a,b,c\in H$, see in [2,3,4]. The transposed of a hypergroup of type U on the right is a hypergroup of type type U on the left, and analogously for hypergroup of type C and cogroups. The purpose of this subsection is to characterize the hypergroups in $\mathfrak{T}\left(H\right)$ that are of type U on the right or cogroups on the right. We have the following result:

Theorem 7.

Let $(H,\circ )\in \mathfrak{T}\left(H\right)$. Then, $(H,\circ )$ is of type U on the right if and only if ${}_{x}S=\left\{\epsilon \right\}$ and $x\circ \epsilon =\left\{x\right\}$, for all $x\in H-{\omega }_H$.

Proof. 

If $(H,\circ )$ is of type U on the right, $x\in H-{\omega }_H$, and $g\in {}_{x}S$ then $x\circ g=x\circ \epsilon =\left\{x\right\}$ and so we have $g=\epsilon$. Conversely, let ${}_{x}S=\left\{\epsilon \right\}$ and $x\circ \epsilon =\left\{x\right\}$, for all $x\in H-{\omega }_H$. If $a,u$ are elements of H such that $a\in a\circ u$ then $u\in {\omega }_H$. Indeed, if $\phi :H\to H/\beta$ is the canonical projection then $\phi \left(a\right)=\phi \left(a\right)\otimes \phi \left(u\right)$ and $\phi \left(u\right)=1_{H/\beta }$. Clearly, if $a\in {\omega }_H$ then $u=\epsilon$ because $a\in a\circ u$ and ${\omega }_H$ is isomorphic to a group. If $a\in H-{\omega }_H$ then, using Proposition 2, we have $a\circ \epsilon =a\circ u$ and $u\in {}_{a}S=\left\{\epsilon \right\}$. Thus, $u=\epsilon$ and so $(H,\circ )$ is of type U on the right. □

We note that if $(H,\circ )\in \mathfrak{T}\left(H\right)$ is a 1-hypergroup of type U on the right then ${\omega }_H=\left\{\epsilon \right\}$ and $H/\left\{\epsilon \right\}\cong H$ as $\epsilon$ is a right scalar identity. In this case H is isomorphic to a group. Consequently, we have the following result.

Corollary 6.

A hypergroup $(H,\circ )\in \mathfrak{T}\left(H\right)$ is isomorphic to a group if and only if $(H,\circ )$ is a 1-hypergroup of type U on the right.

In reference to Theorem 7 and the previous corollary, we note that the hypergroup shown in Example 1 is of type U both on the right and on the left. Indeed, in that hypergroup we have $|{\omega }_H|\ge 2$, ${}_{x}S=S_x=\left\{\epsilon \right\}$ and $x\circ \epsilon =\epsilon \circ x=\left\{x\right\}$, for all $x\in H-{\omega }_H$. The next result provides a sufficient condition for a hypergroup of type U on the right to be also a cogroup.

Theorem 8.

Let $(H,\circ )\in \mathfrak{T}\left(H\right)$ be of type U on the right. If $S_x={\omega }_H$ for all $x\in H-{\omega }_H$ then $(H,\circ )$ is a cogroup.

Proof. 

The thesis is obvious if $(H,\circ )$ is a group. Therefore, we suppose that $|{\omega }_H|\ge 2$. Let $S_x={\omega }_H$, for all $x\in H-{\omega }_H$. If $a\circ b\cap a\circ c\ne \varnothing$, we obtain $\phi \left(b\right)=\phi \left(c\right)$ and so $\beta \left(b\right)=\beta \left(c\right)$. Hence, $b\in {\omega }_H$ if and only if $c\in {\omega }_H$. Now, if $b\in H-{\omega }_H$, by point $3.$ of Lemma 1, then $\epsilon \circ b=\beta \left(b\right)=\beta \left(c\right)=\epsilon \circ c$. If $b\in {\omega }_H$ and $a\in H-{\omega }_H$, by point $5.$ of Proposition 3, we obtain $a\circ b=a\circ c$ and so $b\circ c^{-1}\in {}_{a}S=\left\{\epsilon \right\}$ as $(H,\circ )$ is of type U on the right. Therefore, $b=c$ and $\epsilon \circ b=\epsilon \circ c$. We get the same result if we suppose that $a,b\in {\omega }_H$. Thus, $(H,\circ )$ is of type C on the right. Now, we distinguish two cases to prove that $|b\circ a|=|c\circ a|$, for all $a,b,c\in H$. We note that, by Theorem 6, we have that $\left|\beta \left(x\right)\right|=|{\omega }_H|$, for all $x\in H$.

If $a\in {\omega }_H$ then we have $|b\circ a|=|c\circ a|=1$ by Corollary 1. On the other hand, if $a\in H-{\omega }_H$ and $x\in H$ then, from point $3.$ of Lemma 1, we have $\epsilon \circ a=\beta \left(a\right)=a\circ {\omega }_H$ and so

$$\begin{array}{cc}\hfill x\circ a=(x\circ \epsilon )\circ a& =x\circ (\epsilon \circ a)\hfill \\ \hfill & =x\circ (a\circ {\omega }_H)\hfill \\ \hfill & =(x\circ a)\circ {\omega }_H=\bigcup _{y\in x\circ a}y\circ {\omega }_H=\bigcup _{y\in x\circ a}\beta \left(y\right).\hfill \end{array}$$

Finally, as $\beta \left(y\right)=\beta \left(z\right)$, for all $y,z\in x\circ a$, we obtain that $x\circ a=\beta \left(y\right)$, for all $y\in x\circ a$. Therefore, $|x\circ a|=\left|\beta \left(y\right)\right|=|{\omega }_H|$. Thus, if $a\in H-{\omega }_H$ and $b,c\in H$ then $|b\circ a|=|{\omega }_H|=|c\circ a|$ and the proof is over. □

The hypothesis $S_x={\omega }_H$ in Theorem 7 is sufficient but not necessary for a hypergroup of type U on the right to be a cogroup. Indeed, the following hypergroup is a cogroup on the right in $\mathfrak{T}\left(H\right)$ but $S_x\ne {\omega }_H$, for all $x\in H-{\omega }_H$.

In this case the heart ${\omega }_H=\{\epsilon ,b,c,d\}$ is isomorphic to ${\mathbb{Z}}_4$ and $S_x=\{\epsilon ,c\}$ for all $x\in H-{\omega }_H$.

7. $\mathbf{G}$-Hypergroups of Minimal Size

In [16] the authors classified the 1-hypergroups of size $\le 6$. Hereafter, we classify the G-hypergroups of size $\le 5$ and $\left|G\right|\ge 2$, apart of isomorphisms. Recall that $\epsilon$ denotes the identity of G. Furthermore, let $\mathfrak{T}(G,p,q)$ be the subclass of $\mathfrak{T}\left(H\right)$ such that ${\omega }_H=G$, $\left|H\right|=p$ and $|H/\beta |=q$. With these notations, using the results in Section 3, we classify the hypergroups of the subclasses $\mathfrak{T}({\mathbb{Z}}_n,p,q)$ with $2\le n\le 4$, $3\le p\le 5$, $2\le q\le 4$ and $\mathfrak{T}({\mathbb{Z}}_2\times {\mathbb{Z}}_2,5,2)$.

Apart of isomorphisms, the classes $\mathfrak{T}({\mathbb{Z}}_2,3,2)$, $\mathfrak{T}({\mathbb{Z}}_2,4,3)$, $\mathfrak{T}({\mathbb{Z}}_3,4,2)$, $\mathfrak{T}({\mathbb{Z}}_3,5,2)$, $\mathfrak{T}({\mathbb{Z}}_3,5,3)$, $\mathfrak{T}({\mathbb{Z}}_4,5,2)$, and $\mathfrak{T}({\mathbb{Z}}_2\times {\mathbb{Z}}_2,5,2)$ consist of only one hypergroup. We list their tables respecting the order in which the previous classes are written.

We note that the table of hypergroup in $\mathfrak{T}({\mathbb{Z}}_3,5,2)$ is a consequence of Corollary 4. The other tables are deduced by considering the quotient group $H/\beta$.

Class: $\mathfrak{T}({\mathbb{Z}}_2,4,2)$. Using the Propositions 6 and 10, we have the following four hypergroups, apart of isomorphisms:

According to Theorems 7 and 8, and Corollary 6, $H_8$ is a hypergroups of type U on the right and on the left, $H_9$ is a cogroup on the left and $H_{10}$ is a cogroup on the right. We note that if $(G,·)$ is a group and S is a non-normal subgroup of G then the quotient $G/S$ (resp. $S\backslash G$) is a hypergroup with hyperproduct $xh\otimes yh=\left\{zh\right|z\in xhyh\}$ (resp. $hx\otimes hy=\left\{hz\right|z\in hxhy\}$). These hypergroups are called D-hypergroups [3]. The hypergroups $H_9$ and $H_{10}$ are isomorphic to $S\backslash D_4$ and $D_4/S$ respectively, being $D_4$ is the dihedral group of size 8 and S is a non-normal subgroup of size 2. Moreover, $H_{10}$ can be obtained from the construction shown in Section 3.1 with $G=T\cong {\mathbb{Z}}_2$.

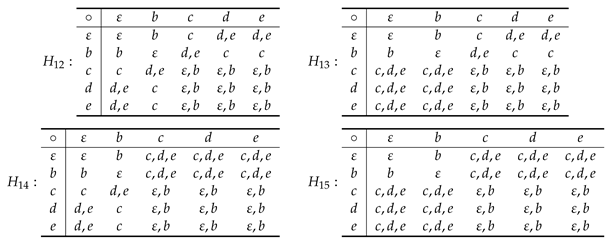
Class: $\mathfrak{T}({\mathbb{Z}}_2,5,2)$. The element $\epsilon$ is not a left scalar identity (resp., right scalar identity) otherwise, by Proposition 1, we have $|g\circ y|=1$, for all $g\in {\omega }_H$ and $y\in H-{\omega }_H$. Consequently, as $|{\omega }_H|=2$, if $y\in H-{\omega }_H$ then we have the contradiction $3=|H-{\omega }_H|=|\beta \left(y\right)|=|{\omega }_H\circ y|=2$. Furthermore, in this case, using the Propositions 6 and 10, we obtain the following four hypergroups, apart of isomorphisms:

Class: $\mathfrak{T}({\mathbb{Z}}_2,5,3)$. If the $\beta$-classes are ${\omega }_H=\{\epsilon ,b\}$, $\beta \left(c\right)=\{c,d\}$ and $\beta \left(e\right)=\left\{e\right\}$, the quotient group $H/\beta$ returns the partial table:

By Propositions 2 and 6, we obtain the following four tables, apart of isomorphisms:

Class: $\mathfrak{T}({\mathbb{Z}}_2,5,4)$. Apart of isomorphisms, we obtain two hypergroups according to that $H/\beta$ is isomorphic to ${\mathbb{Z}}_4$ or ${\mathbb{Z}}_2\times {\mathbb{Z}}_2$.

Therefore, the following result is obtained:

Theorem 9.

There are 21 non-isomorphic G-hypergroup of size $\le 5$ and $|{\omega }_H|\in \{2,3,4\}$, as summarized in Table 1.

Table 1. The G-hypergroups with $\left|H\right|\le 5$.

$\left|\mathit{H}\right|$	3	4	5
$|{\omega }_H|=2$	$H_1$	$H_2,H_{8\dots 11}$	$H_{12\dots 21}$
$|{\omega }_H|=3$	-	$H_3$	$H_{4,5}$
$|{\omega }_H|=4$	-	-	$H_{6,7}$

The G-hypergroups with $|{\omega }_H|=1$ are 1-hypergroups, which include groups. In [16], the authors classified the 1-hypergroups of size $\le 6$. In particular, those of size $\le 5$ are 27. Thus, we have the following result.

Corollary 7.

There are 48 non-isomorphic G-hypergroup of size $\le 5$.

Remark 3.

In every G-hypergroup $(H,\circ )$ with $\left|H\right|\le 5$ all subgroups $S\subset H$ satisfy the condition that ${\omega }_H\subseteq S$ or $S\subseteq {\omega }_H$. On the other hand, the hypergroup shown in Remark 2 has order 6 and contains a subgroup S such that neither $S\subseteq {\omega }_H$ nor ${\omega }_H\subseteq S$. Therefore, that hypergroup is minimal with respect to this property.

8. Conclusions and Directions for Further Research

If $(H,\circ )$ is a hypergroup then the kernel ${\omega }_H$ of the canonical projection $\phi :H\mapsto H/\beta$ is a sub-hypergroup called heart [10,12]. If $|{\omega }_H|=1$ then $(H,\circ )$ is a 1-hypergroup [13,14,16]. However, very little is known about hypergroups that have a heart that does not consist of either a single element or the entire hypergroup. This paper provides a contribution to the knowledge of such hypergroups. To achieve this goal, we generalized the notion of 1-hypergroup to hypergroups whose heart is isomorphic to a group. We analyzed in detail this class of hypergroups, here called G-hypergroups, with a special emphasis on the sub-class $\mathfrak{T}\left(H\right)$ of G-hypergroups whose heart is a torsion group. In the future, these results can hopefully lead to a more general construction than the one presented in Section 3.1, allowing all G-hypergroups to be constructed.

Among our main results, we characterized the G-hypergroups that are also of type U on the right or cogroups on the right. Furthermore, we enumerated all non-isomorphic G-hypergroups with $\left|H\right|\le 5$. The results achieved in Section 7 describe all G-hypergroups with $\left|H\right|\in \{3,4,5\}$ and $|{\omega }_H|\in \{2,3,4\}$, and are condensed in Table 2. We note that the hypergroups $H_9$ and $H_{10}$ are also cogroups. Cogroups are one of the best known classes of hypergroups. A most notable problem with them is characterizing cogroups that are also D-hypergroups, i.e., quotient hypergroups $G/S$ of a group G with respect to a non-normal subgroup S. This problem was solved in greater generality by L. Haddad and Y. Sureau in [3,4] by considering the group of permutations $\sigma$ of H such that $\sigma (x\circ y)=\sigma \left(x\right)\circ y$, for all $x,y\in H$. The cogroups $H_9$ and $H_{10}$ are D-hypergroups isomorphic to $S\backslash D_4$ and $D_4/S$, respectively, being $D_4$ the dihedral group of size 8 and S a non-normal subgroup of size 2.

Table 2. Number of non-isomorphic G-hypergroups with $\left|H\right|\le 5$, depending on the size of their hearts.

$\left|\mathit{H}\right|$	1	2	3	4	5
$|{\omega }_H|=1$	1	1	2	4	19
$|{\omega }_H|=2$	-	-	1	5	10
$|{\omega }_H|=3$	-	-	-	1	2
$|{\omega }_H|=4$	-	-	-	-	2
Total	1	1	3	10	33

At the conclusion of this work we would like to indicate some possible topics for further investigation. First of all, it would be interesting to verify whether the cogroups in $\mathfrak{T}\left(H\right)$ are also D-hypergroups. A challenging problem related to the research carried out, e.g., in [16], which is classifying G-hypergroups of size greater than 5.

Finally, we observe that all G-hypergroups $(H,\circ )$ produced by the construction shown in Section 3.1 are such that the identity of ${\omega }_H$ is also identity of $(H,\circ )$, also when ${\omega }_H$ is not a torsion group. At present, we are not able to prove or disprove that this is always the case. Hence, a problem that remains open after our findings can be formulated as the following conjecture: if $(H,\circ )$ is a G-hypergroup then the scalar identity of ${\omega }_H$ is also the identity of $(H,\circ )$.