Typed Angularly Decorated Planar Rooted Trees and Ω-Rota-Baxter Algebras
Abstract
:1. Introduction
1.1. Rota–Baxter Algebras
1.2. Motivations of -Rota–Baxter Algebras
2. Ω-Rota–Baxter Algebras and Ω-Dendriform Algebras
2.1. -Rota Baxter Algebras
2.2. -Dendriform Algebras
- (a)
- An Ω-Rota-Baxter algebra of weight λ induces an Ω-dendriform algebra , where
- (b)
- An Ω-Rota-Baxter algebra of weight 0 induces an Ω-dendriform algebra , where
- (c)
- An Ω-Rota-Baxter algebra of weight λ induces an Ω-tridendriform algebra , where
- (d)
- An Ω-tridendriform algebra induces two Ω-dendriform algebras and , where
- (a)
- For any and , we have
- (b)
- This follows from Item (a) by taking
- (c)
- For and , we have
- (d)
- For and , we haveWe also have
3. Free Ω-Rota–Baxter Algebras on Typed Angularly Decorated Rooted Trees
3.1. Typed Angularly Decorated Planar Rooted Trees

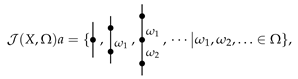


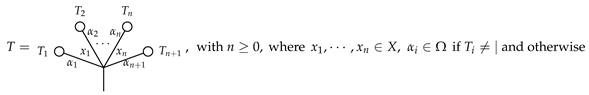
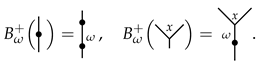
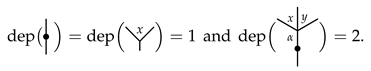
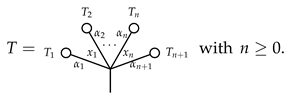
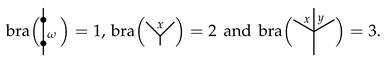
3.2. The Product ⋄ on Typed Angularly Decorated Planar Rooted Trees

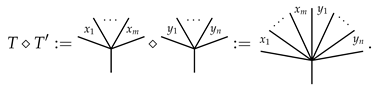

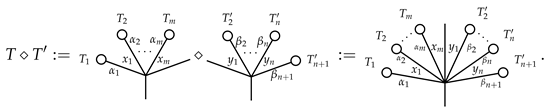

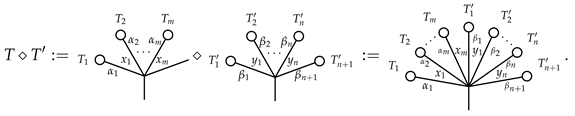
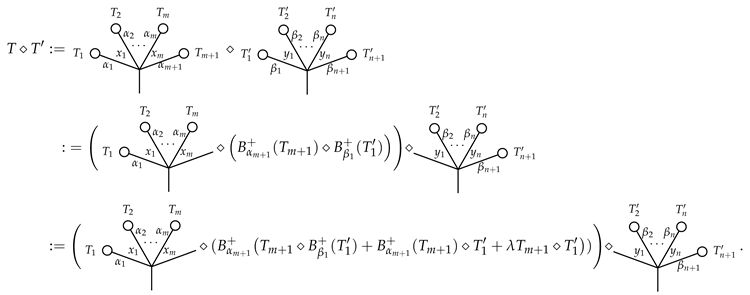

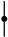 is the identity of ⋄.
is the identity of ⋄.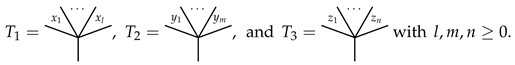
 and the associativity of ⋄ follows directly. Assume
and the associativity of ⋄ follows directly. Assume
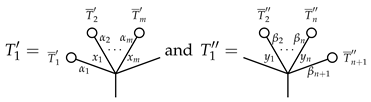
 be a set map. Then, we have the following result.
be a set map. Then, we have the following result.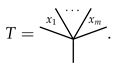

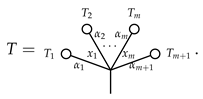
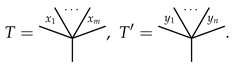
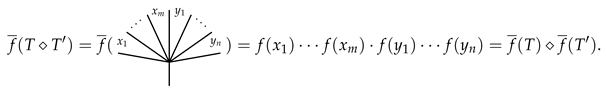

4. Conclusions and Future Studies
- (a)
- In 2000, Aguiar established the relationship between Rota–Baxter algebras and Loday’s dendriform algebras. Later, Bai, Guo and Vallete promoted and deepened this connection from the perspective of operad. Operad provides a unified approach to systematically study the relationship between algebraic operations, which helps us to better understand these algebraic structures.
- (b)
- The Representation theory and homology theory of Rota–Baxter algebras have always been important topics. However, at present, there are just a few articles on the representation of multiple Rota–Baxter algebras, and the theory is still not mature. This leads us to consider the representation theory and homology theory of algebraic structures with a family of operators.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Baxter, G. An analytic problem whose solution follows from a simple algebraic identity. Pac. J. Math 1960, 10, 731–742. [Google Scholar] [CrossRef]
- Rota, G.-C. Baxter algebras and combinatorial identities I, II. Bull. Am. Math. Soc. 1969, 75, 325–334. [Google Scholar] [CrossRef] [Green Version]
- Rota, G.-C. Baxter operators, an introduction. Gian-Carlo Rota on Combinatorics, Introductory Papers and Commentaries. 1995, pp. 504–512. Available online: https://www.amazon.com/Gian-Carlo-Rota-Combinatorics-Introductory-Mathematicians/dp/0817637133 (accessed on 13 November 2021).
- Cartier, P. On the structure of free Baxter algebras. Adv. Math. 1972, 9, 253–265. [Google Scholar] [CrossRef] [Green Version]
- Connes, A.; Kreimer, D. Renormalization in quantum field theory and the Riemann-Hilbert problem. I. The Hopf algebra structure of graphs and the main theorem. Commun. Math. Phys. 2000, 210, 249–273. [Google Scholar] [CrossRef] [Green Version]
- Aguiar, M. Prepoisson algebras. Lett. Math. Phys. 2000, 54, 263–277. [Google Scholar] [CrossRef]
- Guo, L.; Keigher, W. Baxter algebras and shuffle products. Adv. Math. 2000, 150, 117–149. [Google Scholar] [CrossRef] [Green Version]
- Guo, L.; Keigher, W. On free Baxter algebras: Completions and the internal construction. Adv. Math. 2000, 151, 101–127. [Google Scholar] [CrossRef] [Green Version]
- Guo, L.; Zhang, B. Polylogarithms and multiple zeta values from free Rota-Baxter algebras. Sci. China Math. 2010, 53, 2239–2258. [Google Scholar] [CrossRef] [Green Version]
- Guo, L.; Lang, H.L.; Sheng, Y.H. Integration and geometrization of Rota-Baxter Lie algebras. Adv. Math. 2021, 387, 107834. [Google Scholar] [CrossRef]
- Zhang, T.; Gao, X.; Guo, L. Hopf algebras of rooted forests, cocyles, and free Rota-Baxter algebras. J. Math. Phys. 2016, 57, 101701. [Google Scholar] [CrossRef] [Green Version]
- Zheng, H.H.; Guo, L.; Zhang, L.Y. Rota-Baxter paired modules and their constructions from Hopf algebras. J. Algebra 2020, 559, 601–624. [Google Scholar] [CrossRef]
- Pei, J.; Bai, C.; Guo, L. Splitting of operads and Rota-Baxter operators on operads. Appl. Categ. Struct. 2017, 25, 505–538. [Google Scholar] [CrossRef]
- Bai, C.; Guo, L.; Ni, X. Generalizations of the classical Yang-Baxter equation and O-operators. J. Math. Phys. 2011, 52, 063515. [Google Scholar] [CrossRef] [Green Version]
- Bai, C.; Guo, L.; Ni, X. O-operators on associative algebras and associative Yang-Baxter equations. Pacifica J. Math. 2012, 256, 257–289. [Google Scholar] [CrossRef] [Green Version]
- Bardakov, V.G.; Gubarev, V. Rota-Baxter groups, skew left braces, and the Yang-Baxter equation. arXiv 2021, arXiv:2105.00428. [Google Scholar] [CrossRef]
- Smoktunowicz, A.; Vendramin, L. On skew braces (with an appendix by N. Byott and L. Vendramin). J. Comb. Algebra 2018, 2, 47–86. [Google Scholar] [CrossRef] [Green Version]
- Bai, C.; Gao, X.; Guo, L.; Zhang, Y. Operator forms of nonhomogeneous associative classical Yang-Baxter equation. arXiv 2020, arXiv:2007.10939. [Google Scholar]
- Chen, D.; Luo, Y.F.; Zhang, Y.; Zhang, Y.Y. Free Ω-Rota-Baxter algebras and Gröbner-Shirshov bases. Int. J. Algebra Comput. 2020, 30, 1359–1373. [Google Scholar] [CrossRef]
- Kurosh, A.G. Free sums of multiple operators algebras. Sib. Math. J. 1960, 1, 62–70. [Google Scholar]
- Guo, L. Operated monoids, Motzkin paths and rooted trees. J. Algebr. Comb. 2009, 29, 35–62. [Google Scholar] [CrossRef] [Green Version]
- Foissy, L. Algebraic structures on typed decorated planar rooted trees. SIGMA 2021, 17, 86. [Google Scholar]
- Foissy, L. Typed binary trees and generalized dendrifom algebras. J. Algebra 2021, 586, 1–61. [Google Scholar] [CrossRef]
- Zhang, Y.; Gao, X.; Guo, L. Matching Rota-Baxter algebras, matching dendriform algebras and matching pre-Lie algebras. J. Algebra 2020, 552, 134–170. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.Y.; Gao, X. Free Rota-Baxter family algebras and (tri)dendriform family algebras. Pac. J. Math. 2019, 301, 741–766. [Google Scholar] [CrossRef]
- Zhang, Y.Y.; Gao, X.; Manchon, D. Free Rota-Baxter family algebras and free (tri)dendriform family algebras. arXiv 2020, arXiv:2002.04448v4. [Google Scholar] [CrossRef]
- Aguiar, M. Dendriform algebras relative to a semigroup. Symmetry Integr. Geom. Methods Appl. 2020, 16, 15. [Google Scholar] [CrossRef]
- Ma, T.; Li, J. Rota-Baxter Hopf π-(co)algebras. arXiv 2021, arXiv:2104.05529. [Google Scholar]
- Cayley, A. On the theory of the analytical forms called trees. Philos. Mag. 1857, 13, 172–176. [Google Scholar] [CrossRef]
- Brouder, C. Runge-Kutta methods and renormalization. Eur. Phys. J. C 2000, 12, 521–534. [Google Scholar] [CrossRef] [Green Version]
- Connes, A.; Kreimer, D. Hopf algebras, renormalization and non-commutative geometry. Commun. Math. Phys. 1998, 199, 203–242. [Google Scholar] [CrossRef] [Green Version]
- Chapoton, F.; Livernet, M. Pre-Lie algebras and rooted trees operad. Int. Math. Res. Not. 2001, 8, 396–408. [Google Scholar]
- Bruned, Y.; Hairer, M.; Zambotti, L. Algebraic renormalisation of regularity structures. Invent. Math. 2019, 215, 1039–1156. [Google Scholar] [CrossRef] [Green Version]
- Ebrahimi-Fard, K.; Gracia-Bondía, J.M.; Patras, F. A Lie theoretic approach to renormalization. Commun. Math. Phys. 2007, 276, 519–549. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.Y.; Gao, X.; Manchon, D. Free (tri)dendriform family algebras. J. Algebra 2020, 547, 456–493. [Google Scholar] [CrossRef] [Green Version]
- Guo, L. An Introduction to Rota-Baxter Algebra; International Press: Vienna, Austria, 2012. [Google Scholar]
- Stanley, R.P. Enumerative Combinatorics, Volume 2: Number 62 in Cambridge Studies in Advanced Mathematics; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Peng, X.; Zhang, Y. Typed Angularly Decorated Planar Rooted Trees and Ω-Rota-Baxter Algebras. Mathematics 2022, 10, 190. https://doi.org/10.3390/math10020190
Zhang Y, Peng X, Zhang Y. Typed Angularly Decorated Planar Rooted Trees and Ω-Rota-Baxter Algebras. Mathematics. 2022; 10(2):190. https://doi.org/10.3390/math10020190
Chicago/Turabian StyleZhang, Yi, Xiaosong Peng, and Yuanyuan Zhang. 2022. "Typed Angularly Decorated Planar Rooted Trees and Ω-Rota-Baxter Algebras" Mathematics 10, no. 2: 190. https://doi.org/10.3390/math10020190
APA StyleZhang, Y., Peng, X., & Zhang, Y. (2022). Typed Angularly Decorated Planar Rooted Trees and Ω-Rota-Baxter Algebras. Mathematics, 10(2), 190. https://doi.org/10.3390/math10020190




