Abstract
As a generalization of Rota–Baxter algebras, the concept of an -Rota–Baxter could also be regarded as an algebraic abstraction of the integral analysis. In this paper, we introduce the concept of an -dendriform algebra and show the relationship between -Rota–Baxter algebras and -dendriform algebras. Then, we provide a multiplication recursion definition of typed, angularly decorated rooted trees. Finally, we construct the free -Rota–Baxter algebra by typed, angularly decorated rooted trees.
PACS:
16W99; 08B20; 17B38
1. Introduction
1.1. Rota–Baxter Algebras
A Rota–Baxter algebra is an associative algebra equipped with a linear operator that generalizes the algebra of continuous functions with the integral operator. More precisely, for a given commutative ring and , a Rota–Baxter k-algebra of weight is a k-algebra R, together with a k-linear map , such that
for all Such a linear operator is called a Rota–Baxter operator of weight . The concept of a Rota–Baxter algebra could be regarded as an algebraic framework of the integral analysis. Let R be the -algebra of continuous function on . Define as the integration
Then, the integration by parts formula
is just Equation (1) with . The concept of Rota–Baxter algebra was introduced in 1960 by Glen Baxter [1] in his probability study of fluctuation theory, and then studied in the 1960s and 1970s by Cartier and Gian-Carlo Rota [2,3,4] in connection with combinatorics. Apparently, this algebra remained inactive until 2000, when new motivations were found, coming from interesting applications in the prominent work of Connes and Kreimer [5] on the renormalization of perturbative quantum field theory, and from the close relationship with the associative Yang–Baxter equation [6] and the construction of free Rota–Baxter algebras related to the shuffle product [7,8]. Since then, the Rota–Baxter operator has appeared in a wide range of areas in mathematics and mathematical physics, such as number theory [9], pre-Lie and Lie algebra [6,10], Hopf algebras [11,12], operads [13], -operators [14,15], Rota–Baxter groups and skew left braces [16,17], classical Yang–Baxter equations and associative Yang–Baxter equations [14,18].
1.2. Motivations of -Rota–Baxter Algebras
The study of -Rota–Baxter algebras was also partly motivated by the formula of partial integrations. Now, we consider the -algebra of continuous functions on . Let be a nonempty subset of . Define a set of linear operators by the integration
It follows from the formula of partial integration that
which leads to the emergence of a general notation--Rota–Baxter algebras [19]. See Example 1 below.
The second motivation comes from -operated algebras. The concept of algebras with (one or more) linear operators was introduced by A.G. Kurosch [20]. Later, Guo [21] called such algebras -operated algebras and constructed their free objects by Motzkin paths, rooted forests and bracketed words.
Definition 1.
Let Ω be a nonempty set. An Ω-operated algebra is an algebra R together with a family of operators
Recently, many scholars have studied multiple operator algebras. Foissy [22,23] studied multiple algebra structure on typed decorated trees. The authors introduced the concepts dendriform family algebras and matching dendriform algebras [24,25,26]. Aguiar [27] introduced some notions of an S-relative algebras in order to provide a simple uniform perspective on these algebras. Ma and Li [28] combined Rota-Baxter family algebras and Hopf -(co)algebras, and integrate the Rota-Baxter operator into Hopf -(co)algebra, which leads to the concept of Rota-Baxter(Hopf) -(co)algebra.
Rooted trees are useful for several areas of mathematics, such as in the study of vector fields [29], numerical analysis [30] and quantum field theory [31]. The work of the British mathematician Cayley in the 1850s can now be considered as the prehistory of pre-Lie algebras. Chapoton and Livernet [32] first showed that the free pre-Lie algebra generated by a set X is given by grafting of X-decorated rooted trees. Recently, typed decorated trees are used by Bruned, Hairer and Zambotti in [33] to give a systematic description of a canonical renormalization procedure of stochastic PDEs. The authors constructed the free dendriform family algebras [26] and the free matching dendriform algebras [24] respectively via typed decorated trees whose vertices are decorated by elements of a set X and edges are decorated by elements of a semigroup . In this paper, we aim at constructing the free -Rota-Baxter algebra by typed angularly decorated planar rooted trees.
The outline of this paper. In Section 2, we first recall the concept of -Rota-Baxter algebras and show that Rota–Baxter algebras induce -Rota–Baxter algebras. Then, we provide a definition of -dendriform algebras and prove that -Rota–Baxter algebras induce -dendriform algebras. Section 3 is devoted to typed angularly decorated planar rooted trees. We provide a multiplication of typed, angularly decorated planar rooted trees; then, we construct the free -Rota–Baxter algebras on them.
Notation. Throughout this paper, let be a unitary commutative ring, which will be the base ring of all modules, algebras, and linear maps. Algebras are unitary associative algebras but not necessary commutative.
2. Ω-Rota–Baxter Algebras and Ω-Dendriform Algebras
In this section, we first recall -Rota–Baxter algebras and introduce the concept of -dendriform algebras. We then construct an -Rota–Baxter algebra arising from a Rota–Baxter operator of an augmented algebra.
2.1. -Rota Baxter Algebras
In this section, we mainly investigate some basic properties of Ω-Rota–Baxter algebras.
Definition 2
([19]). Let λ be a given element of k and Ω a nonempty set. An Ω-Rota–Baxter algebra of weight λ, or simple an Ω-RBA of weight λ, is a pair consisting of an algebra R and a set of linear operators , that satisfy the Ω-Rota–Baxter equation
Any Rota–Baxter algebra of weight λ can be viewed as an Ω-Rota–Baxter algebra of weight λ by taking Ω as a singleton set.
Remark 1.
Another notion of algebras with multiple Rota–Baxter operators, called a Rota–Baxter family algebra, was suggested by Guo in [34]. See also [21,35]. The difference is that, there, the index set Ω is a semigroup and the Rota–Baxter equation in Rota–Baxter family algebras is defined by
The following example shows that an -Rota–Baxter algebra could be regarded as an algebraic framework of the integral analysis, parallel to the fact that a differential algebra could be considered an algebraic abstraction of differential equations.
Example 1
([19]). (Integration (we thank professor L. Guo for suggesting this example)) Let R be the -algebra of continuous functions on and Ω a nonempty subset of . Define a set of linear operators by the integration
Then, the pair is an Ω-Rota–Baxter algebra of weight zero. This follows from the integration by parts formula, as follows. For any and , set
Then, we have
Thus, the integration by parts formula
can be rewritten as
In other words,
which implies that
Rearranging the terms, we have
The following result shows that an -Rota–Baxter algebra can be constructed from a Rota–Baxter operator of an augmented algebra.
Proposition 1.
Let A be a unitary generalized augmented algebra together with a family of augmentation maps and Ω a set of augmentation maps. Suppose that P is a Rota–Baxter operator on A. Define
Then, is an Ω-Rota–Baxter algebra of weight λ.
Proof.
For any and , we have
Similarly,
Thus, we obatin
This completes the proof. □
2.2. -Dendriform Algebras
In this subsection, we mainly introduce the concept of -dendriform algebras. Then, we investigate the relationship between -Rota–Baxter algebras and -dendriform algebras.
Definition 3.
Let Ω be a nonempty set. An -dendriform algebra or more precisely an -multiple dendriform algebra, is a module D together with a family of binary operations , such that, for any and satisfying
Definition 4.
Let Ω be a set. An -tridendriform algebra is a -module T equipped with a set of linear operations and a binary operation · such that, for and ,
As Rota–Baxter family algebras induce (tri)dendriform family algebras [26] and matching Rota–Baxter algebras induce matching dendriform algebras [24], we will prove that -Rota–Baxter algebras induce the so-called multiple -dendriform algebras [19].
Proposition 2.
- (a)
- An Ω-Rota-Baxter algebra of weight λ induces an Ω-dendriform algebra , where
- (b)
- An Ω-Rota-Baxter algebra of weight 0 induces an Ω-dendriform algebra , where
- (c)
- An Ω-Rota-Baxter algebra of weight λ induces an Ω-tridendriform algebra , where
- (d)
- An Ω-tridendriform algebra induces two Ω-dendriform algebras and , where
Proof.
- (a)
- For any and , we have
- (b)
- This follows from Item (a) by taking
- (c)
- For and , we have
- (d)
- For and , we haveWe also have
This completes the proof. □
3. Free Ω-Rota–Baxter Algebras on Typed Angularly Decorated Rooted Trees
In this section, we construct free Ω-Rota–Baxter algebras in terms of typed angularly decorated planar rooted trees.
3.1. Typed Angularly Decorated Planar Rooted Trees
First, we recall some notations of planar rooted trees; for more details, see [21,26,36,37]. A is a finite graph, connected and without cycles, with a special vertex called the . A is a rooted tree with a fixed embedding into the plane. The first few planar rooted trees are listed below (note that we view the root and the leaves of a tree as edges rather than vertices):
 where the root of a tree is on the bottom.
where the root of a tree is on the bottom.

An edge of a planar rooted tree T is called an inner edge if it is neither a leaf nor the root of T. Let be the set of inner edges of T. For each vertex, v yields a (possibly empty) set of angles , with an angle being a pair of adjacent incoming edges for v. Let be the set of angles of T. We now recall the notation of an X-angularly decorated -typed from [26].
Let X and be two sets. An X-angularly decorated -typed (abbr. typed angularly decorated) planar rooted tree is a planar rooted tree T, together with two maps and . For , let be the set of X-angularly decorated -typed planar rooted trees with leaves and define
The following are some examples of X-angularly decorated Ω-typed planar rooted trees in .
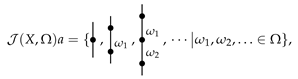





Graphically, an element
is of the form:
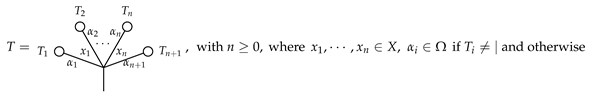 does not exist for .
does not exist for .
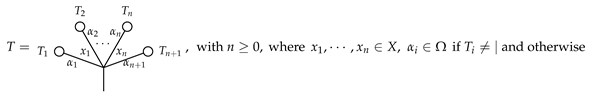
For each , there is a grafting operator
that grafts a tree to a new root and satisfies that the new inner edge between the new root and the root of the tree is typed by . For example,
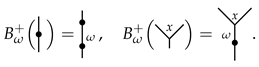
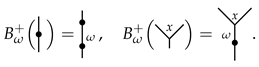
The depth of a rooted tree T is defined as the maximal length of linear chains from the root to the leaves of the tree. For example,
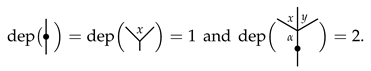
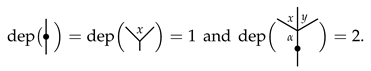
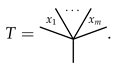
For later use, we add the “zero-vertex tree” | to the picture, and set . For each typed, angularly decorated planar rooted tree T, define the number of branches of T to be if . Otherwise, and T is of the form
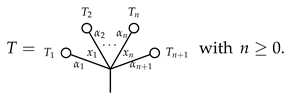 Here, any branch is of a depth that is, at most, one less than the depth of T, and equal to zero if, and only if, . We define . For example,
Here, any branch is of a depth that is, at most, one less than the depth of T, and equal to zero if, and only if, . We define . For example,
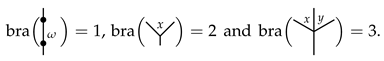

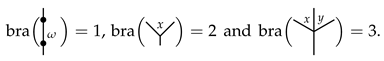
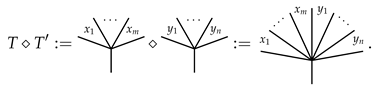
3.2. The Product ⋄ on Typed Angularly Decorated Planar Rooted Trees
Let X be a set and let be a set. We now define a product ⋄ on by induction. For , we define by induction on . For the initial step , we have and are of the form


Define

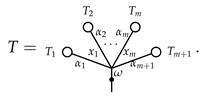
For the induction step , the trees T and are of the form


There are four cases to consider.
Case 1:. Define
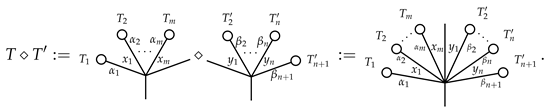

Case 2:. Define


Case 3:. Define
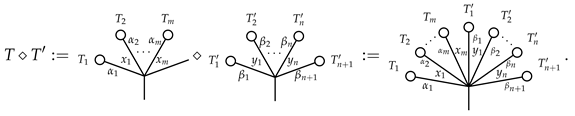

Case 4:. Define
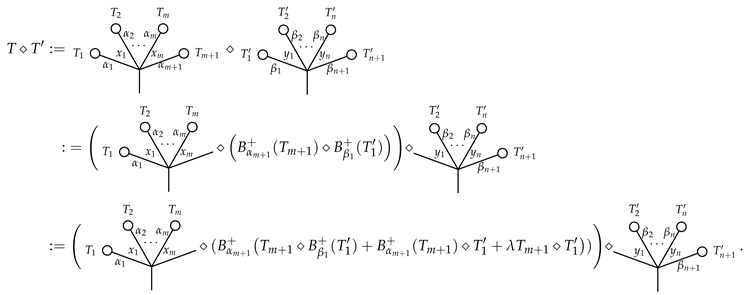

Here, the first ⋄ is defined by Case 3, the second, third and fourth ⋄ are defined by induction and the last ⋄ is defined by Case 2. This completes the inductive definition of the multiplication ⋄ on . Extending by linearity, we can expand the ⋄ to . Now, we have the following result.
Example 2.
Let X be a set and Ω a nonempty set. For and , we have
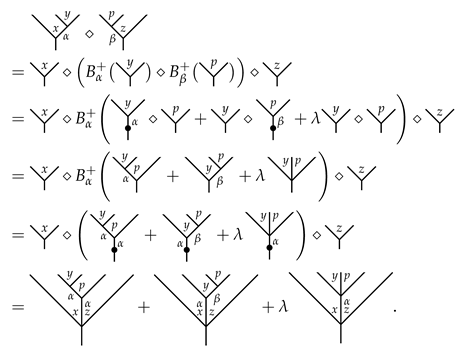
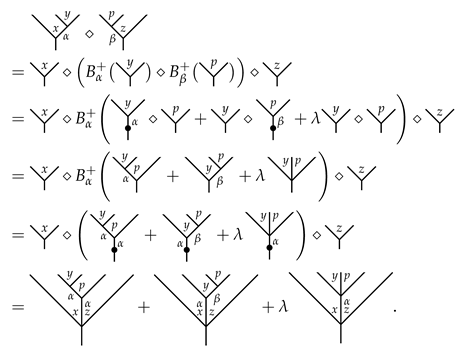
Lemma 1.
Let Ω be a set. Then is an Ω-Rota-Baxter algebra.
Proof.
We prove that is an -Rota–Baxter algebra. From Case 4, when , we immediately obtain , satisfying the -Rota–Baxter equation. By the construction of is closed under ⋄ and 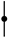 is the identity of ⋄.
is the identity of ⋄.
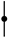 is the identity of ⋄.
is the identity of ⋄.Now, we show the associativity of ⋄, i.e.
We prove Equation (18) by induction on the sum of depths . If , then and are of the form
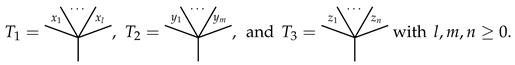
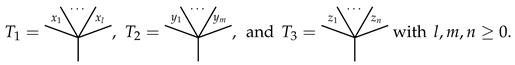
Then by direct calculation.
If , we use induction on the sum of branches . If and one of has depth 1, then this tree must be of the form  and the associativity of ⋄ follows directly. Assume
then
and the associativity of ⋄ follows directly. Assume
then
 and the associativity of ⋄ follows directly. Assume
and the associativity of ⋄ follows directly. Assume
If , then at least one of have branches greater than or equal to 2. If , then there are of the form
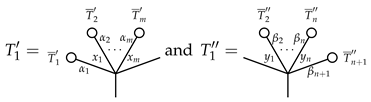 such that . Hence
such that . Hence
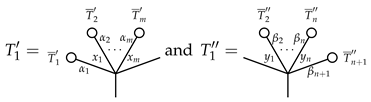
If or , the associativity can be similarly proved. □
Let 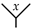 be a set map. Then, we have the following result.
be a set map. Then, we have the following result.
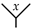 be a set map. Then, we have the following result.
be a set map. Then, we have the following result.Proposition 3.
Let Ω be a set. together with the map i is the free Ω-Rota–Baxter algebra generated by X.
Proof.
By Lemma 1 and the definition of ⋄, is an -Rota–Baxter algebra. Now, we show the freeness of .
Let be an -Rota–Baxter algebra and a set map. We extend f to an -Rota–Baxter algebra morphism as follows: For , we define by induction on . If , then T is of the form

Define . Suppose was defined for all trees of depth , where is a fixed integer. Consider the case of , we define by induction on the branches of T. If , then T is of the form

Define
If , then T is of the form

Define
By the construction of , for all . Next, we show that is an algebra homomorphism, i.e.,
We prove that Equation (19) holds by induction on the sum of depth . If , then and
Then
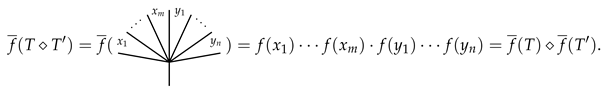
Assume that Equation (19) holds when for a given and consider the case of . We reduce to the induction on . For the initial step of , we have and . Then
Suppose that Equation (19) holds for , with p a fixed integer. Consider the case of . If is in the Case 1, 2 or 3, we can get by the definition of ⋄ and . Hence, we only need to consider Case 4.


Then, we can obtain that is an algebra homomorphism such that for all . Moreover, this is a unique way to extend f as an -Rota-Baxter algebra morphism. Hence, is the free -Rota–Baxter algebra generated by X. □
4. Conclusions and Future Studies
Root tree is a good language for constructing free objects. We can intuitively construct algebraic structures through it. In this paper, we mainly construct the free -Rota–Baxter algebra by typed angularly decorated rooted trees. Further, we hope to provide a more profound characterization from the perspective of operad, representation and homology.
- (a)
- In 2000, Aguiar established the relationship between Rota–Baxter algebras and Loday’s dendriform algebras. Later, Bai, Guo and Vallete promoted and deepened this connection from the perspective of operad. Operad provides a unified approach to systematically study the relationship between algebraic operations, which helps us to better understand these algebraic structures.
- (b)
- The Representation theory and homology theory of Rota–Baxter algebras have always been important topics. However, at present, there are just a few articles on the representation of multiple Rota–Baxter algebras, and the theory is still not mature. This leads us to consider the representation theory and homology theory of algebraic structures with a family of operators.
Author Contributions
Writing—original draft, Y.Z. (Yi Zhang), X.P. and Y.Z. (Yuanyuan Zhang). All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by China Postdoctora Sciencel Foundation (Grant No. FJ3050A0670286).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Baxter, G. An analytic problem whose solution follows from a simple algebraic identity. Pac. J. Math 1960, 10, 731–742. [Google Scholar] [CrossRef]
- Rota, G.-C. Baxter algebras and combinatorial identities I, II. Bull. Am. Math. Soc. 1969, 75, 325–334. [Google Scholar] [CrossRef] [Green Version]
- Rota, G.-C. Baxter operators, an introduction. Gian-Carlo Rota on Combinatorics, Introductory Papers and Commentaries. 1995, pp. 504–512. Available online: https://www.amazon.com/Gian-Carlo-Rota-Combinatorics-Introductory-Mathematicians/dp/0817637133 (accessed on 13 November 2021).
- Cartier, P. On the structure of free Baxter algebras. Adv. Math. 1972, 9, 253–265. [Google Scholar] [CrossRef] [Green Version]
- Connes, A.; Kreimer, D. Renormalization in quantum field theory and the Riemann-Hilbert problem. I. The Hopf algebra structure of graphs and the main theorem. Commun. Math. Phys. 2000, 210, 249–273. [Google Scholar] [CrossRef] [Green Version]
- Aguiar, M. Prepoisson algebras. Lett. Math. Phys. 2000, 54, 263–277. [Google Scholar] [CrossRef]
- Guo, L.; Keigher, W. Baxter algebras and shuffle products. Adv. Math. 2000, 150, 117–149. [Google Scholar] [CrossRef] [Green Version]
- Guo, L.; Keigher, W. On free Baxter algebras: Completions and the internal construction. Adv. Math. 2000, 151, 101–127. [Google Scholar] [CrossRef] [Green Version]
- Guo, L.; Zhang, B. Polylogarithms and multiple zeta values from free Rota-Baxter algebras. Sci. China Math. 2010, 53, 2239–2258. [Google Scholar] [CrossRef] [Green Version]
- Guo, L.; Lang, H.L.; Sheng, Y.H. Integration and geometrization of Rota-Baxter Lie algebras. Adv. Math. 2021, 387, 107834. [Google Scholar] [CrossRef]
- Zhang, T.; Gao, X.; Guo, L. Hopf algebras of rooted forests, cocyles, and free Rota-Baxter algebras. J. Math. Phys. 2016, 57, 101701. [Google Scholar] [CrossRef] [Green Version]
- Zheng, H.H.; Guo, L.; Zhang, L.Y. Rota-Baxter paired modules and their constructions from Hopf algebras. J. Algebra 2020, 559, 601–624. [Google Scholar] [CrossRef]
- Pei, J.; Bai, C.; Guo, L. Splitting of operads and Rota-Baxter operators on operads. Appl. Categ. Struct. 2017, 25, 505–538. [Google Scholar] [CrossRef]
- Bai, C.; Guo, L.; Ni, X. Generalizations of the classical Yang-Baxter equation and O-operators. J. Math. Phys. 2011, 52, 063515. [Google Scholar] [CrossRef] [Green Version]
- Bai, C.; Guo, L.; Ni, X. O-operators on associative algebras and associative Yang-Baxter equations. Pacifica J. Math. 2012, 256, 257–289. [Google Scholar] [CrossRef] [Green Version]
- Bardakov, V.G.; Gubarev, V. Rota-Baxter groups, skew left braces, and the Yang-Baxter equation. arXiv 2021, arXiv:2105.00428. [Google Scholar] [CrossRef]
- Smoktunowicz, A.; Vendramin, L. On skew braces (with an appendix by N. Byott and L. Vendramin). J. Comb. Algebra 2018, 2, 47–86. [Google Scholar] [CrossRef] [Green Version]
- Bai, C.; Gao, X.; Guo, L.; Zhang, Y. Operator forms of nonhomogeneous associative classical Yang-Baxter equation. arXiv 2020, arXiv:2007.10939. [Google Scholar]
- Chen, D.; Luo, Y.F.; Zhang, Y.; Zhang, Y.Y. Free Ω-Rota-Baxter algebras and Gröbner-Shirshov bases. Int. J. Algebra Comput. 2020, 30, 1359–1373. [Google Scholar] [CrossRef]
- Kurosh, A.G. Free sums of multiple operators algebras. Sib. Math. J. 1960, 1, 62–70. [Google Scholar]
- Guo, L. Operated monoids, Motzkin paths and rooted trees. J. Algebr. Comb. 2009, 29, 35–62. [Google Scholar] [CrossRef] [Green Version]
- Foissy, L. Algebraic structures on typed decorated planar rooted trees. SIGMA 2021, 17, 86. [Google Scholar]
- Foissy, L. Typed binary trees and generalized dendrifom algebras. J. Algebra 2021, 586, 1–61. [Google Scholar] [CrossRef]
- Zhang, Y.; Gao, X.; Guo, L. Matching Rota-Baxter algebras, matching dendriform algebras and matching pre-Lie algebras. J. Algebra 2020, 552, 134–170. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.Y.; Gao, X. Free Rota-Baxter family algebras and (tri)dendriform family algebras. Pac. J. Math. 2019, 301, 741–766. [Google Scholar] [CrossRef]
- Zhang, Y.Y.; Gao, X.; Manchon, D. Free Rota-Baxter family algebras and free (tri)dendriform family algebras. arXiv 2020, arXiv:2002.04448v4. [Google Scholar] [CrossRef]
- Aguiar, M. Dendriform algebras relative to a semigroup. Symmetry Integr. Geom. Methods Appl. 2020, 16, 15. [Google Scholar] [CrossRef]
- Ma, T.; Li, J. Rota-Baxter Hopf π-(co)algebras. arXiv 2021, arXiv:2104.05529. [Google Scholar]
- Cayley, A. On the theory of the analytical forms called trees. Philos. Mag. 1857, 13, 172–176. [Google Scholar] [CrossRef]
- Brouder, C. Runge-Kutta methods and renormalization. Eur. Phys. J. C 2000, 12, 521–534. [Google Scholar] [CrossRef] [Green Version]
- Connes, A.; Kreimer, D. Hopf algebras, renormalization and non-commutative geometry. Commun. Math. Phys. 1998, 199, 203–242. [Google Scholar] [CrossRef] [Green Version]
- Chapoton, F.; Livernet, M. Pre-Lie algebras and rooted trees operad. Int. Math. Res. Not. 2001, 8, 396–408. [Google Scholar]
- Bruned, Y.; Hairer, M.; Zambotti, L. Algebraic renormalisation of regularity structures. Invent. Math. 2019, 215, 1039–1156. [Google Scholar] [CrossRef] [Green Version]
- Ebrahimi-Fard, K.; Gracia-Bondía, J.M.; Patras, F. A Lie theoretic approach to renormalization. Commun. Math. Phys. 2007, 276, 519–549. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.Y.; Gao, X.; Manchon, D. Free (tri)dendriform family algebras. J. Algebra 2020, 547, 456–493. [Google Scholar] [CrossRef] [Green Version]
- Guo, L. An Introduction to Rota-Baxter Algebra; International Press: Vienna, Austria, 2012. [Google Scholar]
- Stanley, R.P. Enumerative Combinatorics, Volume 2: Number 62 in Cambridge Studies in Advanced Mathematics; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).