Abstract
Increasingly amounts of biological data promote the development of various penalized regression models. This review discusses the recent advances in both linear and logistic regression models with penalization terms. This review is mainly focused on various penalized regression models, some of the corresponding optimization algorithms, and their applications in biological data. The pros and cons of different models in terms of response prediction, sample classification, network construction and feature selection are also reviewed. The performances of different models in a real-world RNA-seq dataset for breast cancer are explored. Finally, some future directions are discussed.
Keywords:
penalized regression model; RNA-seq data; sample classification; network construction; gene selection; crucial gene MSC:
92B15; 92B10; 62J05; 62J12
1. Introduction
With the rapid development of high-throughput technologies, researchers can easily obtain various omics data (genomics, transcriptomics, proteomics, metabonomics, phenomics, etc.) for interested species [1,2,3,4,5,6]. The obtained omics data can quantify the expression of biomolecules (genes, RNAs, proteins, metabolites, etc.) or phenotype features under well-designed experimental conditions, and therefore help people to explore factors that affect phenotypes and the underlying biomolecular mechanisms [7].
Since RNA-seq allows the entire transcriptome to be explored in a high-throughput and quantitative manner [1], when we mention biological data, we are using RNA-seq data as examples. Based on RNA-seq, researchers can catalogue all species of transcripts (mRNAs, non-coding RNAs, etc.); researchers can also determine a gene’s transcriptional structure and quantify the expression of each transcript under given experimental conditions [1]. There are many challenges in exploring RNA-seq data, such as efficient methods to store, retrieve and process massive data, sequence assembly, sequence mapping and alignment, identifying novel splicing events, data-driven network inference, crucial gene identification and so on [1,6,8,9,10,11,12]. Among these issues, the statistical exploration of sample clustering or classification and crucial gene selection are intriguing yet important.
Many data-driven statistical methods have been proposed to tackle sample clustering or classification [13,14,15,16]. On the one hand, various traditionally distance-based or similarity-based methods, e.g., support vector machine (SVM), posterior probability, Bayesian discriminant analysis, and Fisher’s discriminant analysis, have been developed. However, since the number of observations is often far less than the detected genes, the associated sample covariance or dispersion matrices are always singular ones; methods that rely on the inverse of the covariance matrices are invalid. For example, the traditional Mahalanobis distance and Fisher’s discriminant methods are all invalid, since they all rely on the inverse of the sample dispersion matrix. On the other hand, different from the traditional distance or similarity-based methods, penalized logistic regression models have been extensively used to perform sample classification [17]. Researchers have developed various binary or multinomial logistic regression models to realize sample classification under different cases. Penalized logistic regression models can not only serve as predictors and classifiers with strong statistical meaning, but can also be used to perform gene selection and network construction using biological data [5].
Except for sample clustering or classification, gene identification is one of the most important issues in exploring biological data. For functionally crucial gene identification from biological data, there are generally two frequently used approaches [12]. The first approach relies on the topological features of the complex interaction networks or co-expression networks among biomolecules [18]. Based on the structural features of the networks that reflect the relationships among biomolecules, researchers have proposed the centrality–lethality rule [19], the guilt-by-association rule [20,21,22,23,24,25] and the guilt-by-rewiring rule [26,27]. However, the network-based approaches rely on the reliable construction of biomolecular networks. Data-driven network construction is another interesting topic in systems biology and network science [5,27]. Penalized linear or logistic regressions can also be used to infer network structure, which will be discussed in the following sections. The second approach relies on well-developed statistical models. Traditionally, as a regular bioinformatics analysis process, gene differential expression analysis has been a necessary process in all RNA-seq experiments. Through gene differential expression analysis, researchers can determine which genes are differentially expressed under treatment in comparison with those under control. However, differential expression analysis relies on hard thresholds of fold change (FC) and the hypothesis test P value. The selected genes severely depend on the chosen threshold. Moreover, the selected genes are often difficult to further explain, and some actually crucial genes may be neglected due to their trivial expression changes between treatments and controls [27,28]. Except for differential expression analysis, various regression models have been successively developed to realize gene selection [29,30] or screen single-nucleotide polymorphisms that are associated with diseases via genome-wide association studies (GWAS) [31,32,33,34,35]. Especially, penalized logistic regression models can be used to realize response prediction, crucial gene selection, network construction and sample classification under different circumstances. Moreover, researchers have developed various penalizations to realize reliable informative gene selection [5,17], including bridge regression [36,37], ridge regression [38,39], penalty [40], LASSO [41], adaptive LASSO [42], elastic net [43], group LASSO [29,44], SCAD [45] and so on. With the rapid development and application of high-dimensional penalized regression models, it is interesting to comprehensively review the associated theories and the advances of applications in biological data.
This review focuses on the recent advances of penalized linear and logistic regression models for biological data, where we mainly consider their applications in response prediction, sample classification, informative gene selection and network construction. The main contents are summarized in Figure 1. To formulate this review, extensive surveys on existing references have been performed. Rigorous searching criteria for references were made. The main platforms for searching the related references include “web of science” and “Pubmed”. To collect the related papers, firstly, we summarized some frequently used penalizations (such as LASSO, adaptive LASSO, elastic net, ridge regression, bridge regression, etc.), and then, based on the original papers that proposed the associated penalizations, we downloaded the most relevant papers (especially for methods that have been used to explore biological data) that cited the original works. The searching keywords include “linear regression”, “logistic regression”, “LASSO”, “penalty”, “biological data”, etc. In this review, we mainly considered the most relevant references published in recent 5 years. Except this, some high-impact papers were also surveyed. For each penalization model, roughly 5 to 10 of the most relevant papers were considered. The organization of this review is as follows: Section 2 introduces a mathematical description of biological data and various data normalization methods; Section 3 reviews various penalized linear regression models, some of the numerical algorithms and some of their applications in biological data; Section 4 reviews the advances of various penalized logistic regression models and their applications in biological data. In particular, we will discuss both binary and multinomial logistic regression models. Optimization algorithms for some penalized logistic regression models will also be discussed. Section 5 gives numerical simulation results from some of the penalized models in a breast cancer dataset, where both penalized linear and logistic regression models are considered and compared. Several potential future research directions and concluding remarks will be presented in Section 6.
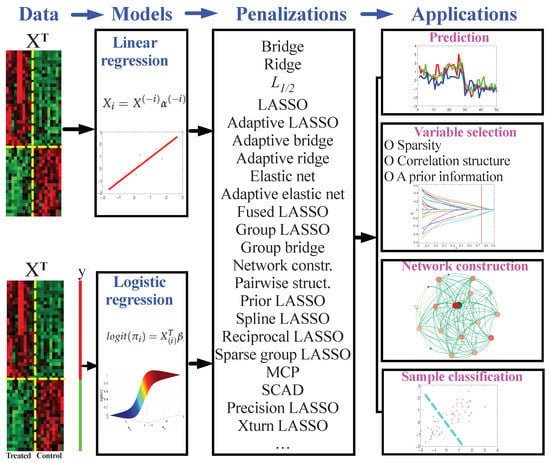
Figure 1.
The main contents and structure of this review. This review focuses on linear and logistic regression models for biological data. Models with various penalizations are discussed, and the applications of penalized regression models in response prediction, variable selection, network construction and sample classification are explored.
2. Mathematical Description of Biological Data
RNA-seq data, as an example, can be explored at different levels, including sample, gene, transcript and exon levels [6,12]. For gene-level analysis, RNA-seq technologies enable us to quantify genome-wide gene expression patterns and perform differential expression analysis. Normalization is a critical step for gene expression analysis. Typical normalization approaches include RPKM [46], FPKM [47], and TPM [48]. The three popular measures all remove the effects of total sequencing depths and gene lengths; different methods have different advantages, but we will give no detailed discussion on this topic. For other biological data, various data normalization processes can be similarly performed.
For a specific species under certain experimental conditions, suppose the expression of p genes (variables) in n samples has been detected, which can be described by the following observational data matrix:
In Equation (1), denotes the i’th observation for the p genes. represents the expression vector for the j’th gene ( can be seen as a random variable, is the observation vector of , similarly hereinafter). For convenience, we assume the data matrix X has been scaled in a column-wise manner, where has zero mean and unit variance. Additionally, denote as the response vector, where each element characterizes the category of the corresponding sample. For binary classification, if the i’th sample is experimentally treated (diseased, treated, positive, etc.); otherwise, (normal, untreated, negative, control, etc.). For multinomial classification problems, , where C denotes the total categories of samples.
In RNA-seq data, based on the observed data X and y, differentially expressed genes (DEGs) can be determined via and statistical hypothesis test [12]. The quantifies the relative expression difference of a gene under treatments and controls. The hypothesis test P value from the adjusted t test can help to further judge whether the expressions of a gene under two experimental conditions are significantly different. Traditionally, are taken as thresholds to screen DEGs from gene expression data. Besides differential expression analysis, various penalized linear or logistic regression models can also be established. If we obtained prior information or determined the interested genes as dependent variables, we could set the other genes as covariates, and thus linear regression models can be established. However, for the cases with categorical response (y), we can establish logistic regression models that reflect the correlation between X and y. Hereinafter, we review the two types of models in detail.
3. Penalized Linear Regression Models for Biological Data
Mathematical and statistical models are powerful tools for exploring useful information from biological data. Linear regression models are primary models, which typically consider the linear relationships among variables. Through linear regression models, one can explore the correlations among genes, and therefore infer the co-expression network for genes [5]; one can also predict the response of certain genes given the expression of the other genes [17]; most importantly, one can select the most relevant genes that are responsible to the response variable [29,30]. Without loss of generality, taking the i’th gene as the response variable and the other genes as covariates, and suppose each variable has been normalized, one can establish the following linear regression model without considering the intercept term [17]:
Here, are regression coefficients to be estimated; the error term independently for different i, which is unobservable. Given n samples, as shown in Equation (1) and based on Equation (2), we obtain the following set of equations:
Equivalently, the matrix form of Equation (3) can be written as:
Here, represents the matrix, which corresponds to the data matrix X without the i’th column; is the parameter vector. Equation (3) or (4) can be used to estimate parameters in Equation (2). It is noted that the parameters in Equation (3) or (4) represent the estimation of parameters in Equation (2). For convenience, we do not distinguish the symbols between parameters and their estimation unless otherwise noted.
3.1. Penalized Linear Regression Models
For , can be estimated via the ordinary least square (OLS) estimation by minimizing the following function:
Whereas a typical feature of most omics data is . For , Equation (5) fails to obtain the unique estimation of . Fortunately, researchers have developed various penalized strategies, which are described as:
Some frequently used penalization functions are summarized in Table 1. For convenience, we relabeled the parameter vector as vector . Here, for model (6), . In , are tuning parameters, which control the final model, similarly hereinafter.

Table 1.
Some typical penalization functions . Detailed explanations of different penalization functions are provided in the main text.
Different penalization functions actually impose different constraints on the regression model. For example, the bridge regression [36,37] minimizes the loss function (5) that is subjected to the constraint . Here, is a constant and . For different q, the constraints are quite different [17,37]. Moreover, of the bridge regression corresponds to the penalization; corresponds to the LASSO [41] or penalty.
LASSO continuously shrinks toward 0 with the increase in , and it encourages many coefficients to shrink to exactly 0 if is large enough [42]. Additionally, LASSO can often improve prediction accuracy owing to the bias-variance trade-off [36,42]. However, the selected number of variables from LASSO will be no more than n, and LASSO can only screen one out of a set of highly correlated variables, which means that the solution of LASSO is unstable. of the bridge regression corresponds to the Tikhonov regularization or ridge regression [38,39]. The ridge regression shrinks the OLS estimator towards 0; compared with the OLS estimation, the ridge regression yields a biased estimation with smaller variance [38,39]. However, the ridge regression cannot generate a sparse solution, which indicates that it has poor interpretability. Different from LASSO, the adaptive LASSO introduces a weight parameter for each parameter . is defined as ; here, is an estimation of , such as the OLS estimation. The adaptive LASSO has the oracle property, and it can be solved by the same efficient algorithm for solving LASSO [42]. The in the adaptive bridge, the adaptive ridge regression and the adaptive elastic net are similar to that in the adaptive LASSO. with corresponding to the elastic net [43]; numerical simulations reveal that the elastic net frequently outperforms LASSO, and it has similar sparsity. The elastic net has been shown to be particularly useful when the parameters are far more than the observations [43]. The fused LASSO is developed for features that are ordered in a meaningful way [51], which encourages sparsity in the coefficients and also sparsity in their differences [51]. represents the group LASSO [29,44]. Here, G is the total number of groups for which the m features can be classified; denotes the j‘th group of parameters; represents the number of features in group j. The group LASSO can realize variable selection in a group-wise manner, which is invariant under group-wise orthogonal reparameterizations [29]. In the network-constrained regularization, W denotes the graph Laplacian matrix. The network-constrained regularization can incorporate the network information for variables, which increases the explainability of the obtained results [53]. In the pairwise-structured penalization, ; represents the weight of and , which measures the similarity between them [54].
Except for the above penalizations, there are many others, including SCAD [45], prior LASSO (pLASSO) [55], group regularized elastic net [56], spline LASSO [57], reciprocal LASSO [58], smoothed group LASSO [61], octagonal shrinkage and clustering algorithm for regression (OSCAR) [64], precision LASSO [65], xturn LASSO [66], adaptive huber [67] and so on. In the SCAD, is defined as [45]:
Here, , . The estimation result from the SCAD is simultaneously unbiased, sparse and continuous [68]. This penalty function makes larger coefficients less penalized and makes the solution continuous. In the pLASSO [55], represents the predicted response that summarizes the a priori information. is a tuning parameter that matches the current dataset and its a prior information, if , pLASSO degenerates into the LASSO. For , pLASSO will only depend on the a priori information. For the group regularized elastic net, represents the variables in the g’th group; is a group-specific penalty weight. The spline LASSO can well capture the effects of different features within a group. The reciprocal LASSO overcomes some drawbacks of the existing penalty functions, which gives small coefficients strong penalties, and therefore avoids selecting overly dense models [58].
In the smoothed group LASSO, is the empirical sample covariance matrix for the j’th group; is the same as that in the group LASSO; is a weight that measures the correlation between the j’th and ’th groups; is the largest group size. The smoothed group LASSO encourages sparsity and smooth coefficients for adjacent groups [61]. The OSCAR can simultaneously select variables and perform supervised clustering in the context of linear regression [64]. The tunning parameter in the OSCAR controls the relative weighting of the norms. In the MCP [62,63], ; is a parameter. Given certain thresholds for variable selection and unbiasedness, the MCP guarantees the convexity of the penalized loss in sparse regions to the utmost degree [62]. The precision LASSO is a variant of the LASSO, which encourages stable and consistent variable selection with highly linearly correlated variables. In Table 1, represents the trace norm, which is defined as the sum of the matrix eigenvalues [69]. is used to make the singular matrix invertible for . Both parts of the penalty term add different weights to the variables: the first term addresses instability and the second term addresses the inconsistencies. t is similar to that in the elastic net, which is used to control the weights of the first term and the second term. The xturn LASSO gives each coefficient a different penalty parameter based on the a priori information. In the penalty function, the penalty parameter vector is defined as , where the matrix Z is the meta-feature data matrix representing the observations for a priori genes; is a parameter vector that links external information Z to individual penalties. The xturn LASSO allows the a priori integration of external meta-features, which improves prediction performance as well as model interpretation [66].
3.2. Algorithms to Solve Penalized Linear Regression Models
In this section, taking the ridge regression and the LASSO as examples, we introduce some algorithms to solve the penalized linear regression problems. For the ridge regression, since the optimization function
is continuously differentiable with respect to , we set
Thus, we obtain the estimation of as:
Here, I is the identity matrix. The ridge regression is a biased estimation of , which is complementary to the traditional OLS estimation:
Although the ridge regression is biased, it is appropriate for the case when is singular. Moreover, the ridge regression has high computational accuracy.
The LASSO needs to solve the following optimization problem:
Different from the ridge regression, the loss function is non-differentiable at . For , set
Here, if , and if . Since the data matrix has been normalized in a column-wise manner, we have , and
can serve as an OLS estimation of . Thus, if and , we have
If and , we have
When and have reverse signs, or equivalently, , it must be that Thus, we obtain the following soft-threshold function for the LASSO problem (10):
Based on the soft-threshold function (12), researchers have developed a coordinate-wise descent algorithm [70] to iteratively obtain the estimation of each parameter, and the iteration stops when it converges.
It is noted that, except for the coordinate-wise descent algorithm, there are also many other algorithms to solve the linear regression models with LASSO, such as the least angle regression [71]. Due to space limitation, no details will be given for the other algorithms. It is also noted that some effective software packages have been developed, such as the glmnet package [72]. The glmnet implements the coordinate descent method for many popular models, which allows us to easily use the linear regression model with LASSO to explore real-world data.
3.3. Applications of Penalized Linear Regression Models in Biological Data
The penalized linear regression model can be applied to realize response prediction, variable selection and network construction in biological data. Firstly, prediction is an important application of regression models. Based on the final fitted model and a given observation, the response can be predicted. Secondly, variables in the model with non-zero estimated coefficients can be selected as informative variables. Finally, the penalized linear regression models can also be used to reconstruct biological networks. In fact, each gene can be iteratively treated as response variable, and it connects with the other genes that are selected by the penalized linear regression model.
3.3.1. Prediction
Penalized linear regression models have been widely used to predict the response under given conditions and predict the association between certain phenotypes and clinical factors. For example, LASSO and elastic net have been used to predict pain intensity in patients with chronic back pain (CBP). To verify whether the severity of CBP is associated with changes in the dynamics of functional brain network topology, Li et al. firstly generated dynamic functional networks for 34 patients with CBP and 34 age-matched healthy controls (HC) through a sliding window method, and then they obtained the nodal degree, clustering coefficient, and participation coefficient of all windows as features to describe the temporal alterations of network structure [73]. A feature called temporal grading index (TGI) was proposed, which can quantify the temporal deviation of each network property of CBP patients to HCs [73]. Linear regression models with LASSO and elastic net are considered to predict the correlation between pain intensity and the TGI of the three features. They reported that brain regions that most correlated with pain intensity have higher clustering coefficients and lower participation coefficients across time windows in the CBP cohort, in comparison with HCs. The investigations revealed spatio-temporal changes in the functional network structure in CBP patients, which can serve as a potential biomarker for evaluating the sensation of pain in the brain.
For association relationship prediction, regression models have been used to predict the association between phenotypes and genotypes [25,31,32,33,34,35]. LASSO and group LASSO have been used to find targets associated with drug resistance. In order to explore the mechanism of EGFR inhibitors in lung cancer and to identify new targets for drug resistance, Yuan et al. [74] studied drug sensitivity from the perspective of DNA methylation, and revealed DNA methylation sites associated with EGFR inhibitor-sensitive genes. The expression profiles of 24,643 genes (RNA-seq) and the beta values of 418,677 methylation sites for 153 lung cancer cell lines are studied [74]. In order to identify genes that are closely related to EGFR inhibitor effectiveness, the authors establish a group LASSO linear regression model. Then, they identify the methylation sites associated with the drug sensitivity genes via LASSO regression. It is reported that the predicted methylation sites are related to regulatory elements [74]. Correlation analysis reveals that the methylation sites located in the promoter region are more correlated with EGFR inhibitor sensitivity genes than those located in the enhancer region and the TFBS [74]. Moreover, they reported that changes in the methylation level of some sites may affect the expression of the corresponding EGFR inhibitor-responsive genes. Therefore, they suggested that DNA methylation may be an important regulatory factor, which can affect the sensitivity of EGFR inhibitors in patients with lung cancer [74].
Except for the above works, in the year 2021, Walco et al. established a multivariate linear regression model and studied the correlation between the etiology and timing of rapid response team (RRT) activation in postoperative patients [75]. The data include 2390 adult surgical inpatients with RRT activated within 7 days of surgery. The authors selected six covariates, including gender, surgical service, obesity, intraoperatively managed red blood cell volume, peripheral vascular disease and trigger category [75]. Combining with the chi-squared test of association and analysis of variance, researchers reported that respiratory triggers were significantly associated with the timing of postoperative RRT calls, and clinical decompensation due to respiratory etiologies tended to occur later postoperatively. Richie-Halford et al. explored informative features in human-brain white matter via the liner regression model with sparse group LASSO. They declared that the associated model can make accurate phenotypic predictions and can discover the most correlated features of the white matter [76].
3.3.2. Variable Selection
Variable selection can also be seen as a kind of prediction. Since variable selection is a widely discussed issue, we cover this topic in great detail. For variable selection in biological data, we mainly consider three categories of works.
The first category of model evaluates the sparsity of the finally selected variables. Typical models include methods of the LASSO family, bridge regression, penalty and so on. In 1996, Tibshirani proposed LASSO [41] and applied it to a prostate cancer dataset [77] to examine the correlation between prostate-specific antigen levels and multiple clinical indicators. The prostate cancer dataset contains eight clinical variables from 97 male patients aged from 41 to 79 years old. LASSO selects three variables lcavol, lweight and svi. The coefficients obtained by LASSO are smaller than those of OLS estimation, which is related to the coefficient shrinkage of LASSO. Fu [37] further explored the prostate cancer dataset by bridge regression, OLS, LASSO and ridge regression. The results showed that the bridge regression performed better than LASSO and ridge regression. However, Fu pointed out that bridge regression does not always perform the best in estimation and prediction compared to the other shrinking models, since the penalty in bridge regression is nonlinear [37]. Zou et al. [42] compared the performances of elastic net with OLS, ridge regression and LASSO in the prostate cancer dataset, and declared that the elastic net is the best among all competitors according to prediction accuracy and sparsity. Xu et al. also explored the prostate cancer dataset via linear regression models with penalty [40]. They showed that LASSO selects five variables, penalty selects four variables, and the prediction error of the is lower than that of LASSO. Therefore, tends to produce a sparser model than LASSO, and has better prediction performance in the prostate cancer dataset. Besides the prostate cancer dataset and the mentioned studies, there are many other works. For example, Qin et al. applied the LASSO linear regression model to identify molecular descriptors that significantly affected biological activity [78]. Yang et al. established the LASSO linear regression model and studied imaging genetic associations [79]. The adaptive LASSO has been used to select metabolites associated with chronic obstructive pulmonary disease [80], the five selected metabolites with the highest weights include vanillylmandelate, N1-methyladenosine, glutamine, 2-hydroxypalmitate and choline phosphate. The selected metabolites are enriched in arginine biosynthesis, aminoacyl-tRNA biosynthesis and the metabolism of glycine, serine and threonine. The spline LASSO and the fused LASSO encourage both sparsity in the coefficients and their differences, which have been applied to protein mass spectroscopy and gene expression data [51,57].
The second category of models considers both sparsity and the correlation structure among genes. In fact, genes always play functions via complex interaction networks and cluster into modulars [29,44,81]. Group LASSO is a well-known penalty that considers the correlation between variables, which retains a few group of variables that are strongly correlated with the dependent variable. Yuan and Lin applied group LASSO to a real birth weight dataset [82]. The weights of newborn babies are predicted, and variables that are strongly correlated with the weights of newborn babies are identified. The results show that the prediction error of the group LASSO is smaller than that of the stepwise regression method. The network-constrained penalty combines LASSO and the penalty induced by the Laplace matrix of the network for the considered variables, which is effective in screening genes and subnetworks that are correlated with disease, and has higher sensitivity than the other methods [53]. In a glioblastoma microarray gene-expression dataset, the network-constrained penalty method identified several subnetworks that are related to survival from glioblastoma [83]. The largest subnetwork identified by the network-constrained penalty includes genes involved in the MAPK signaling pathway (such as PLCE1, PRKCG, MAP2K7, ZAK, KBKG, TRAF2 and MAPK11) and related pathways (e.g., PI3K/AKT pathway), as well as its target gene FOXO1A [83]. The sparse group LASSO was applied to select supracortical and intracortical features related to brain age [84]. Among 150 covariates, the sparse group LASSO selected 94 features, containing 93 cortical regions of interest and education. By visualizing brain features that contribute significantly to age estimation, they found that age-related cortical thinning arises in regions that are responsible for executive processing tasks, spatial cognition, vocabulary learning, episodic memory retrieval, and age-related cognitive decline [84]. Frost and Amos [85] developed a gene set selection method via LASSO penalized regression, which is called SLPR. Based on TCGA data, they demonstrated that the SLPR outperforms the existing multiset methods in some cases [85].
The third category of models considers the effect of a prior information during gene selection. With the development of bioinformatics, rich a prior information including functional annotations, pathway information and knowledge from previous studies for genes has been accumulated, which can be used to improve model performance. The xturn LASSO incorporates a prior information into linear regression model with LASSO to select informative genes, which has been applied to bone density [86] and breast cancer datasets [87]. In the bone density dataset, the relationship between gene expression profiles and bone density was analyzed. This dataset contains the expression profiles of 22,815 genes from 84 women. Compared with LASSO and adaptive LASSO, the xturn LASSO selects fewer genes and has the best prediction performance. Among the genes selected by the xturn LASSO, the genes SOST and DKK1 are involved in the WNT pathway, while the WNT pathway is the core of bone turnover. The breast cancer dataset contains 29,476 gene expression profiles and three clinical variables. A total of 594 samples make up the training set and 564 samples comprise the testing set. Zeng et al. [66] applied the xturn LASSO model to the breast cancer dataset and predicted the five-year survival of patients. The results show that the xturn LASSO exhibits a better prediction performance than LASSO and the adaptive LASSO, and it tends to produce a model that is sparser and more interpretable than LASSO.
3.3.3. Network Construction and Network Dynamics Inference
The application of penalized linear regression models for network construction and dynamics inference is another research focus [5,88,89,90,91,92,93]. Network construction is a typical inverse problem in systems biology and network science, which aims to clarify the pairwise relationship among variables from data. In 2015, Han et al. [91] established the LASSO framework to realize robust network construction from sparse and noisy data. The authors decomposed the reconstruction task of the network to infer local structures for each node [94], where the LASSO linear regression model was used. Based on reverse phase protein arrays, Erdem et al. measured the expression profiles of 134 proteins in 21 breast cancer cell lines, which were stimulated with IGF1 or insulin for up to 48 h [92], and they inferred the directed protein expression networks from three approaches, one of which was based on LASSO linear regression. Finkle et al. [90] proposed the Sliding Window Inference for Network Generation (SWING) framework to determine the network structure from time-series data. The SWING first divided time series data into several windows with a user-defined width, and then inferences were made for each window by iteratively solving regression models between response and covariates (genes). Edges from each regression model were finally integrated into a single network that represents the biological interactions among genes [90]. Roy et al. proposed PoLoBag to determine the signed gene regulatory network from expression data [88]. The PoLoBag is an ensemble regression model with a bagging framework, where the weights estimated from LASSO for bootstrap samples are averaged [88]. The results demonstrated that the PoLoBag was often more accurate in inferring signed gene regulatory network than the existing algorithms [88]. In 2020, we converted the data-driven weighted network construction problem into parameter estimations of penalized linear regression problems, and a variational Bayesian framework was developed to solve the problems. Numerical simulations revealed that the variational Bayesian framework outperformed LASSO in terms of accuracy and computational speed [93]. Penalized regression models can also be used to infer system dynamics. Recently, in order to realize the autonomous inference of the dynamics of complex networks, a two-phase approach has been proposed [89]. Based on the established libraries of elementary functions and observed data, Gao and Yan converted the dynamics inference tasks into penalized regression problems to identify the necessary elementary functions and learn their precise coefficients [89]. It is noted that Gaussian graphical models are also based on various penalizations to realize sparse network construction [95,96,97]. Except for the mentioned works, there are many other related investigations, due to space limitation, for which no more details will be given.
4. Penalized Logistic Regression Models for Biological Data
4.1. Penalized Binary Logistic Regression Models
Based on the binary response vector y and the gene expression data matrix X, one can establish the following logistic regression model to simultaneously realize response prediction, gene selection and sample classification. Specifically, suppose that , and denote . For simplicity, it is also assumed that X is normalized in a column-wise manner. Then, based on the n observations, the sample regression function can be written as [17]:
Here, is the logit function. To estimate the parameter vector , different from the linear regression, since Equation (13) is nonlinear, we can use maximum likelihood estimation (MLE) rather than OLS estimation. For the case of , the parameter can be estimated via maximizing the following likelihood function:
Considering that
we can easily prove that the optimization problem (14) is equivalent to minimizing the following negative logarithmic likelihood function, also known as the loss function:
For the case of , similar to the linear regression, the parameter can be estimated via the following penalized negative logarithmic likelihood function [29,44,54,98,99]:
Here, the penalization term is similar to the linear regression with in Table 1. Most of the penalizations can be extended to the logistic regression models, such as LASSO, group LASSO, ridge regression and so on.
4.2. Penalized Multinomial Logistic Regression Models
Multinomial logistic regression is also called as softmax regression, which is a natural extension of the binary logistic model to cases where the response variable has three or more possible categories [100,101,102,103,104]. Suppose the response variable has C possible categories: there are two approaches to establish the multinomial logistic regression models. Given the observations as shown in Section 2, the first model is non-symmetrical [105,106]:
Here, are parameter vectors to be estimated. Under model (17), we can obtain the following probability distribution:
Based on MLE, one can minimize the following negative logarithmic likelihood function to estimate parameters :
Here, if and only if ; otherwise, if . satisfies and
The second multinomial logistic regression model is a symmetrical one [100,107], which can be written as:
The corresponding loss function can be established as:
Different from Equation (19), in Equation (21), if and only if , and it satisfies .
Besides the above models, the multinomial logistic regression model can also be converted into a series of binary logistic regression models [108]. Three approaches can be considered: one-versus-one, one-versus-rest and many-versus-many. For the one-versus-one approach, we can extract any two of the C categories as treatment and control, respectively, and consider binary logistic regression models. For the one-versus-rest approach, we can treat one of the interested categories as treatment, and treat the rest categories as the control. For the many-versus-many approach, we can combine multiple categories as the treatment, and the combination of the rest categories as the control.
4.3. Algorithms to Solve the Penalized Logistic Regression Models
Taking the binary logistic regression with group LASSO as an example, we review numerical algorithms to solve the optimization problem. Based on Equation (16) and Table 1, the loss function for the binary logistic regression with group LASSO is as follows:
The first term can be expanded at to its second order as follows [81]:
where is the gradient of at ; ,
is the Hessian matrix of at ; is a diagonal matrix with elements . Since the right-hand side of Equation (23) is continuous differentiable, after setting its first-order derivative with respect to as , we can obtain the following Newton–Raphson algorithm [44] to numerically obtain the approximated optimal solution for as:
Here, can be seen as a temporary working response variable [81], where
In fact, Equation (24) can be seen as the solution of the following reweighted least square estimation problem [54,81,109]:
Therefore, the optimization problem (22) can be approximated by the following reweighted least square problem with group LASSO [81]:
Similar to the discussions in the linear regression and the method introduced in reference [29], further assume that the data have been normalized, satisfying . represents the subset of X with the dimensions and . One obtains the iteration algorithm for the parameter group as
Here, , and
Based on Equation (27), researchers have developed group-wise coordinate descent algorithms [29,44,110] to obtain the numerical estimation of . It is noted that, since Equation (27) requires , one needs to be orthogonalized. It is also noted that when the group number , the group LASSO degenerates into LASSO, and algorithms for the logistic regression model with LASSO can be also obtained, similar to the linear regression with LASSO. Due to space limitation, we omit any detailed discussion.
4.4. Applications of Penalized Logistic Regression Models in Biological Data
For biological data with categorical response and continuous gene expression data, depending on the total categories of the response variable, one can establish penalized binary or multinomial logistic regression models. Based on the established penalized logistic regression models, we can not only predict the probability of each sample that belongs to a certain category, but also select genes that are responsible for the response variable and realize gene network inference. Moreover, based on the established logistic regression model, we can also evaluate the odds ratio of a gene associated with a certain phenotype, or how strong a gene is associated with exposure.
4.4.1. Prediction, Sample Classification and Gene Selection
Penalized logistic regression models play important roles in tackling response prediction, sample classification and variable selection [17,111]. Liao et al. proposed a parametric bootstrap method for penalized logistic regression models to more accurately realize disease classification in microarray data [99]. Lin et al. proposed a disease risk scoring system using logistic regression with group LASSO, and applied it to the survey data of porcine reproductive and respiratory syndrome (PRRS) [112]. The investigated dataset contains 896 samples and 127 variables. Among the samples, 499 had PRRS outbreaks, and the rest did not. The results showed that the logistic group LASSO-based risk scoring system had the highest AUC . Its AUC was significantly higher than that of the other models (such as the models based on expert opinion or logistic regression models based on variable significance selection) [112]. This algorithm can help swine producers to reduce their reliance on expert advice, and identify variables that could potentially lead to PRRS outbreaks. Zhang et al. explored the application of the logistic regression model in detecting key risk factors for heart disease [113]. Three datasets were considered: the California dataset contains 270 samples with 46 clinical features; the Hungarian dataset contains 245 samples with 37 clinical features; the Long Beach VA dataset contains 103 samples with 50 clinical features. The prediction accuracy of in the Cleveland, Hungarian and Long Beach VA datasets reached , and , respectively. Thus, this illustrates that penalized logistic regression based on is an effective technique in practical classification problems. They reported that sex- and exercise-induced angina were commonly selected features in two different datasets, and the feature height at rest in the Hungarian dataset and the feature ramus in the Long Beach VA dataset were only selected by the regularization [113]. Based on elastic net logistic regression, Torang et al. proposed a classifier for immune cells and T helper cell subsets [114]. To evaluate the performance of the proposed classifier in immune cell classification, two single-cell RNA-seq (scRNA-seq) datasets were considered. The first dataset contained malignant, mesenchymal, immune and endothelial cells from 15 melanoma tissues [115]. The second dataset comprised 317 epithelial breast cancer cells, 175 immune cells and 23 noncancerous stromal cells from 11 patients with breast cancer [116]. The simulation results show that the developed classifier addresses the problem of identifying immune cell types from noisy scRNA-seq signatures. The elastic net logistic regression was also used to detect brain function and structural changes in female, schizophrenic patients [117] and to determine predictors of dengue patients, as well as to predict the length of hospital stay [118]. In the year 2021, in order to diagnose early Alzheimer’s disease (AD), Cui et al. proposed an adaptive LASSO penalized logistic regression model based on particle swarm optimization (PSO-ALLR) [119]. A dataset from the AD Neuroimaging Initiative database was considered, which contained MRI images of 197 subjects, including 51 samples with AD, 50 healthy controls (HC), and 96 MCI (including 51 converted MCI (cMCI) and 45 stable MCI (sMCI)) [119]. Three classification missions were designed, AD vs. HC, MCI vs. HC and cMCI vs. sMCI; 70% of the dataset was used as the training set, and 30% of the dataset served as the testing set. The simulation results showed that the PSO-ALLR selected 17 features in AD vs. HC, 23 features in MCI vs. HC, and 16 features in cMCI vs. sMCI [119]. The classification accuracies of AD vs. HC, MCI vs. HC, cMCI vs. sMCI can reach 96.27%, 84.81%, and 76.13%, respectively.
Recently, Yang et al. applied the LASSO logistic regression model to find biomarkers from a breast cancer dataset [120]. The breast cancer dataset was from TCGA-BRCA, which contained 1070 samples. To explore genes that were related with lymphatic metastasis, patients with breast cancer were partitioned into two groups: those without lymphatic metastasis and those with lymphatic metastasis. A total of 15 hub genes with prognostic value for overall survival were identified by the LASSO logistic regression model. Further investigations revealed that the selected BAHD1 gene could predict lymph node metastasis and prognosis. In vitro investigations have revealed that BAHD1 significantly affected the proliferation, migration and invasion of breast cancer cells, and that the down-regulation of BAHD1 can induce cell cycle arrest in the G1 phase [120,121]. Moreover, the mRNA levels of CCND1, CDK1 and YWHAZ decreased after BAHD1 silencing [120,121]. The obtained results indicated that BAHD1 was crucial during the development and progression of breast cancer. Except for this, the LASSO logistic regression models were also applied to explore the risk factors of venous thrombosis [122]; the sparse logistic regression with a penalty has been applied to gene selection and cancer classification [123]; the network-regularized logistic model has been used to identify molecular pathway that related to certain phenotype [124]. The elastic net regularized logistic regression model has been used to perform a longitudinal study in eating disorders, and the authors declared that elastic net regularized logistic regression model can promote the prediction of eating disorders and can screen important risk markers [125]. A penalized multiple logistic regression with adaptive elastic net has been used to find predictive biomarkers for preterm birth [126]. Additionally, the multinomial logistic regression model has been applied to predict the discharge status after liver transplantation [101].
4.4.2. Network Construction
Similar to the penalized linear regression, penalized logistic regression models can be also used to realize network construction [127,128,129]. In 2008, Park et al. developed a new logistic regression model with penalization, and the model was applied to infer gene–gene and gene–environment interactions [128]. They illustrated that the proposed model can not only concretely characterize interaction structures among genes, but also has additional advantages when tackling discrete factors [128]. In 2017, Zhou et al. proposed a dynamic logistic regression method [127]. They observed a time series of network structures. Then, the dynamic logistic regression model can dynamically predict future links by exploring the network structure of the past [127]. A novel conditional MLE method was also proposed to reduce computational burden. Liu et al. developed a new method to reconstruct network structures with binary-state dynamics. In the algorithm, the knowledge of the original dynamical processes was assumed to be unknown [129]. In the proposed algorithm, the transition probabilities of binary dynamical processes were modeled via a logistic regression model, and the original dynamical processes can be simulated via parameter estimations in the regression model [129]. The proposed algorithm can not only infer network structures, but also can estimate dynamical processes of networked systems [129].
5. Performances of Different Models in a RNA-Seq Dataset for Breast Cancer
5.1. Dataset, Models and Simulation Settings
The breast cancer RNA-seq dataset was downloaded from TCGA, which contains the expression of 19,420 genes in 230 samples [130]. Among the 230 samples, 119 samples are for patients with breast cancer, while the remaining 111 samples serve as normal controls. For simplicity, we first performed differential expression analysis, and only considered DEGs in the subsequent regression models. By setting and , 4606 genes were retained.
Based on the gene expression data matrix X and the vector y, which characterizes the type of each sample, we can establish penalized linear or logistic regression models (see Section 3 and Section 4). The linear regression models only rely on the gene expression data X. For simplicity, we took gene BRCA1 as the response variable and the other 4605 genes as covariates in the linear regression models. The penalized logistic regression models rely on X and y. LASSO, elastic net, ridge regression and adaptive LASSO will be considered and compared in both of the two types of models. In the adaptive LASSO, the inverse of the absolute values of the OLS estimations are considered as the weights. The four types of models are solved by using the glmnet package in Matlab. For linear regression models, we consider the mean square errors (MSEs) to evaluate the accuracy of models, while for logistic regression models, we consider the score [54,81]. The score is defined as the harmonic mean of precision and recall [81], which can evaluate the performance of a classification model. For each simulation setting, we randomly extracted 50% of samples as the training set, and the remaining samples were used as the testing set. Totally, 100 simulation runs were performed and averaged for each case, and genes that were selected at least in 80 simulation runs were retained.
5.2. Performances of Different Penalized Regression Models
The boxplots of MSEs for different penalized linear regression models and the boxplots of scores for different logistic regression models are shown in Figure 2. The finally selected informative genes from each type of models are shown in Table 2 and Table 3. From the linear regression models, 19, 24, 946, and 19 informative genes were screened by LASSO, elastic net, ridge regression and adaptive LASSO, respectively (Table 2), whereas the four logistic regression models finally selected 24, 82, 3295, and 24 informative genes.
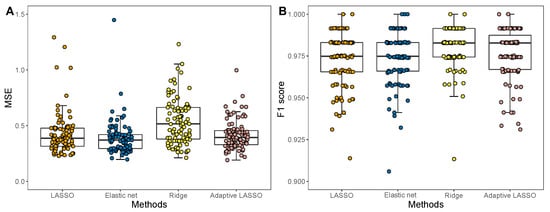
Figure 2.
Accuracy of different penalized linear and logistic regression models in the breast cancer dataset. (A) Boxplots of MSEs for each penalized linear regression models. (B) Boxplots of score for each penalized logistic regression models.

Table 2.
Informative genes that were selected from the breast cancer dataset based on linear regression models with LASSO, elastic net, adaptive LASSO and ridge regression. Genes that are simultaneously screened by the four methods are shown in bold. Since the results from the ridge regression are not sparse, we only show some commonly selected genes by the four methods.

Table 3.
Informative genes that are selected from the breast cancer dataset based on logistic regression models with LASSO, elastic net, adaptive LASSO and ridge regression. Genes that were simultaneously screened by the four methods are shown in bold. Since the results from the ridge regression are not sparse, we only show some commonly selected genes from using the four methods.
Among the four linear regression models, LASSO and adaptive LASSO are the most sparse, but their average MSEs are all slightly higher than the elastic net. The elastic net has the smallest average MSE value, while the average MSE of the ridge regression is the highest. In fact, since the ridge regression is not sparse, the finally obtained model is always overfitted. Therefore, the ridge regression has the highest average MSE among the four methods.
For the penalized logistic regression models, it shows that the ridge regression has very high score. This indicates that the logistic regression model with ridge regression tends to have good classification accuracy. Our results reveal that though the ridge regression couldn’t generate a sparse solution, it tends to have good performance in sample classification. However, since extensive features are selected in the ridge regression, its real-world applications are limited. The adaptive LASSO penalized logistic regression model only selects 24 genes, but it has comparative score with the ridge regression, therefore, the adaptive LASSO penalized logistic regression model may be the best choice to perform sample classification.
Comparing between the finally selected gene sets (genes in bold) from the linear and the logistic regression models, no genes are commonly selected by the two types of models. This can be explained as follows. The finally selected genes from the linear regression models are linearly correlated with BRCA1, while the selected genes from the logistic regression model mainly play roles in distinguishing between patients and normal controls. The finally selected genes from the two kinds of models play different roles, and they explain the dataset from different perspectives.
Except for the above analysis, one can also consider and compare the results from the other penalization methods. Moreover, the finally selected genes can be also further explored through GO and KEGG pathway enrichment analysis, and their biological functions in breast cancer can be also experimentally determined. Finally, we mention that the obtained results can be used to construct gene co-expression networks. For example, in the linear regression models, since gene BRCA1 has been treated as the response variable, therefore, we can deem that all the finally selected genes are co-expressed with BRCA1. Due to space limitation, no more details will be given.
6. Future Directions and Conclusions
This paper reviews some recent advances on penalized regression models and their applications in biological data. Both linear and logistic regression models with various penalization approaches are discussed. Algorithms for some models are introduced and applications of various penalized regression models using biological data have been discussed in detail. The penalized regression models provide effective tools to explore biological data.
Although great advances have been achieved over recent decades, there are also some interesting issues to be further explored. The first issue is to propose some novel penalization methods to more concretely select informative genes, such as those incorporating a priori knowledge. Extensive works on some diseases have provided much useful knowledge; to better understand the disease from biological data, it is important to incorporate the existing a priori information. Secondly, applications of penalized regression models should be further extended, especially developing effective models for ultra-high dimensional biological data. Gene expression data in RNA-seq often contain tens of thousands of genes and tens to hundreds of samples. Dealing with such ultra-high dimensional data is still a challenge in ultra-high-dimensional statistics [4]. Thirdly, the interpretability of the selected results by penalized regression models needs to be further enhanced. Most of the linear and logistic regression models neglect the correlations among genes, which assume that genes are independent of each other. The selected genes are always involved in different biological pathways, and it is hard biologically interpret the obtained results. In fact, genes play their functions via complex regulatory networks or signaling networks [5]. It is interesting to develop models that consider the correlations among genes. In fact, the group penalized algorithms [44], the network constrained penalization [53] and the pairwise structured penalization [54] are all efforts to solve the mentioned problems. Especially, the network-constrained penalization encourages the selection of genes in the same pathways, which helps to explain the mechanisms of certain phenotypes. Fourthly, effective numerical simulation algorithms are still in great demand. Although researchers have developed many optimization algorithms [5], such as OLS estimation, gradient descent algorithm, Newton’s method, Newton–Raphson algorithm, stochastic gradient descent [131], the least angle regression, stepwise regression, coordinate descent algorithms, coordinate gradient descent method [132], blockwise coordinate descent algorithms, iteratively reweighted least square, alternating direction method of multipliers (ADMM) [133] and so on, novel efficient algorithms for high-dimensional biological data are still in great demand. Fifthly, except for gene selection and sample classification, applications of regression models in network construction should also be further explored. Actually, both linear and logistic regression models have been applied to detect gene interactions [88,90,91,128,129]. However, since the regression approaches only consider the linear correlation among expression profiles of genes, and gene expression profiles are highly affected by noise (measurement error, instrument error, varied gene expression abundance due to copy number variations, etc.), the reliability and practicality of the inferred interactions are still to be enhanced. Finally, gene expression profiles are highly nonlinear or oscillate with time [5,27,134]; however, the penalized linear and logistic regression models both assume linear relationships among variables. Therefore, it is intriguing to develop methods that consider such nonlinearity.
As a summary, both theories and applications of penalized regression models have been extensively investigated, and great advances on the related theories have been achieved over recent decades. Besides the mentioned works in this review, there are also many other related works [135,136,137,138], but due to space limitations and the limited knowledge of the authors, this review can not cover all of the works in this topic.
Author Contributions
Conceptualization, P.W.; methodology, P.W.; data curation, S.C. and S.Y.; writing—original draft preparation, P.W., S.C. and S.Y.; writing—review and editing, P.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China under Grant 61773153, by the Natural Science Foundation of Henan Province under Grant 202300410045, in part by the Program for Science & Technology Innovation Talents in Universities of Henan Province under Grant 20HASTIT025.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, Z.; Gerstein, M.; Snyder, M. RNA-seq: A revolutionary tool for transcriptomics. Nat. Rev. Genet. 2009, 10, 57–63. [Google Scholar] [CrossRef]
- Reuter, J.; Spacek, D.V.; Snyder, M.P. High-throughput sequencing technologies. Mol. Cell 2015, 58, 586–597. [Google Scholar] [CrossRef]
- Mayer, B. Bioinformatics for Omics Data: Methods and Protocols; Humana Press: New York, NY, USA, 2011; Volume 719. [Google Scholar]
- Fan, J.; Han, F.; Liu, H. Challenges of big data analysis. Natl. Sci. Rev. 2014, 1, 293–314. [Google Scholar] [CrossRef]
- Lü, J.; Wang, P. Modeling and Analysis of Bio-Molecular Networks; Springer: Singapore, 2020. [Google Scholar]
- Li, W.; Li, J. Modeling and analysis of RNA-seq data: A review from a statistical perspective. Quant. Biol. 2018, 6, 195–209. [Google Scholar] [CrossRef]
- Ritchie, M.D.; Holzinger, E.R.; Li, R.; Pendergrass, S.A.; Kim, D. Methods of integrating data to uncover genotype-phenotype interactions. Nat. Rev. Genet. 2015, 16, 85–97. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Yang, C.; Chen, H.; Luo, L.; Leng, Q.; Li, S.; Han, Z.; Li, X.; Song, C.; Zhang, X.; et al. Exploring transcriptional factors reveals crucial members and regulatory networks involved in different abiotic stresses in Brassica napus L. BMC Plant Biol. 2018, 18, 202. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Yang, C.; Chen, H.; Song, C.; Zhang, X.; Wang, D. Transcriptomic basis for drought-resistance in Brassica napus L. Sci. Rep. 2017, 7, 40532. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Yang, C.; Chen, H.; Wang, P.; Wang, P.; Song, C.; Zhang, X.; Wang, D. Multi-gene co-transformation can improve comprehensive resistance to abiotic stresses in B. napus L. Plant Sci. 2018, 274, 410–419. [Google Scholar] [CrossRef]
- Wang, P.; Wang, D.; Lü, J. Controllability analysis of a gene network for Arabidopsis thaliana reveals characteristics of functional gene families. IEEE/ACM Trans. Comput. Biol. Bioinform. 2019, 16, 912–924. [Google Scholar] [CrossRef] [PubMed]
- Wang, P. Statistical identification of important nodes in biological systems. J. Syst. Sci. Complex. 2021, 34, 1454–1470. [Google Scholar] [CrossRef] [PubMed]
- Jain, A.K. Data clustering: 50 years beyond K-means. Pattern. Recogn. Lett. 2010, 31, 651–666. [Google Scholar] [CrossRef]
- Alon, U.; Barkaie, N.; Notterman, D.A.; Gish, K.; Ybarra, S.; Mack, D.; Levine, A.J. Broad patterns of gene expression revealed by clustering analysis of tumor and normal colon tissues probed by oligonucleotide arrays. Proc. Natl. Acad. Sci. USA 1999, 96, 6745–6750. [Google Scholar] [CrossRef] [PubMed]
- Golub, T.; Slonim, D.; Tamayo, P.; Huard, C.; Gaasenbeek, M.; Mesirov, J.P.; Coller, H.; Loh, M.L.; Downing, J.R.; Caligiuri, M.A. Molecular classification of cancer: Class discovery and class prediction by gene expression monitoring. Science 1999, 286, 513–536. [Google Scholar] [CrossRef] [PubMed]
- Araveeporn, A. The higher-order of adaptive LASSO and elastic net methods for classification on high dimensional data. Mathematics 2021, 9, 1091. [Google Scholar] [CrossRef]
- Bühlmann, P.L.; Geer, S.V.D. Statistics for High-Dimensional Data: Methods, Theory and Applications; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Wang, P. Network biology: Recent advances and challenges. Gene Protein Dis. 2022, 1, 101. [Google Scholar] [CrossRef]
- Jeong, H.; Mason, S.P.; Barabási, A.L.; Oltvai, Z.N. Lethality and centrality in protein networks. Nature 2001, 411, 41–42. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Li, Y. Discovering disease-genes by topological features in human protein-protein interaction network. Bioinformatics 2006, 22, 2800–2805. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Lü, J.; Yu, X. Identification of important nodes in directed biological networks: A network motif approach. PLoS ONE 2014, 9, e106132. [Google Scholar] [CrossRef]
- Wang, P.; Yu, X.; Lü, J. Identification and evolution of structurally dominant nodes in protein-protein interaction networks. IEEE Trans. Biomed. Circ. Syst. 2014, 8, 87–97. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Li, W.; Zeng, M.; Zheng, R.; Li, M. Network-based methods for predicting essential genes or proteins: A survey. Brief. Bioinform. 2020, 21, 566–583. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Chen, Y.; Lü, J.; Wang, Q.; Yu, X. Graphical features of functional genes in human protein interaction network. IEEE Trans. Biomed. Circ. Syst. 2016, 10, 707–720. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.; Jiang, R.; Zhang, M.; Li, S. Network-based global inference of human disease genes. Mol. Syst. Biol. 2008, 4, 189. [Google Scholar] [CrossRef] [PubMed]
- Hou, L.; Chen, M.; Zhang, C.; Cho, J.; Zhao, H. Guilt by rewiring: Gene prioritization through network rewiring in genome wide association studies. Hum. Mol. Genet. 2014, 23, 2780–2790. [Google Scholar] [CrossRef]
- Wang, P.; Wang, D. Gene differential co-expression networks based on RNA-seq data: Construction and its applications. IEEE/ACM Trans. Comput. Biol. Bioinform. 2021; early access. [Google Scholar] [CrossRef]
- Hudson, N.J.; Reverter, A.; Dalrymple, B.P. A differential wiring analysis of expression data correctly identifies the gene containing the causal mutation. PLoS Comput. Biol. 2009, 5, e1000382. [Google Scholar] [CrossRef]
- Meier, L.; Geer, S.V.D.; Bühlmann, P.L. The group LASSO for logistic regression. J. R. Stat. Soc. B 2008, 70, 53–71. [Google Scholar] [CrossRef]
- Guyon, I.; Elisseeff, A. An introduction to variable and feature selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar]
- Ingolia, N.T.; Ghaemmaghami, S.; Newman, J.R.S.; Weissman, J.S. Genome-wide analysis in vivo of translation with nucleotide resolution using ribosome profiling. Science 2009, 324, 218–223. [Google Scholar] [CrossRef]
- Wang, W.Y.S.; Barratt, B.J.; Clayton, D.J.; Todd, J.A. Genome-wide association studies: Theoretical and practical concerns. Nat. Genet. 2005, 6, 109–118. [Google Scholar] [CrossRef]
- Easton, D.F.; Pooley, K.A.; Dunning, A.M.; Pharoah, P.D.P.; Thompson, D.; Ballinger, D.G.; Struewing, J.P.; Morrison, J.; Field, H.; Luben, R.; et al. Genome-wide association study identifies novel breast cancer susceptibility loci. Nature 2007, 447, 1087–1093. [Google Scholar] [CrossRef]
- Wellcome Trust Case Control Consortium. Genome-wide association study of 14,000 cases of seven common diseases and 3000 shared controls. Nature 2007, 447, 661–678. [Google Scholar] [CrossRef] [PubMed]
- Schizophrenia Psychiatric Genome-Wide Association Study (GWAS) Consortium. Genome-wide association study identifies five new schizophrenia loci. Nat. Genet. 2011, 43, 969–976. [Google Scholar] [CrossRef] [PubMed]
- Frank, I.E.; Friedman, J.H. A statistical view of some chemometrics regression tools. Technometrics 1993, 35, 109–148. [Google Scholar] [CrossRef]
- Fu, W. Penalized regressions: The bridge versus the LASSO. J. Comput. Graph. Stat. 1998, 7, 397–416. [Google Scholar]
- Hoerl, A.E.; Kennard, R.W. Ridge regression: Biased estimation for nonorthogonal problems. Technometrics 1970, 12, 55–67. [Google Scholar] [CrossRef]
- Hoerl, A.E.; Kennard, R.W. Ridge regression: Applications to nonorthogonal problems. Technometrics 1970, 12, 69–82. [Google Scholar] [CrossRef]
- Xu, Z.; Zhang, H.; Wang, Y.; Chang, X.; Liang, Y. ℓ1/2 regularization. Sci. China Inform. Sci. 2010, 53, 1159–1169. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the LASSO. J. R. Stat. Soc. B 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Zou, H. The adaptive LASSO and its oracle properties. J. Am. Stat. Assoc. 2006, 101, 1418–1429. [Google Scholar] [CrossRef]
- Zou, H.; Hastie, T. Regularization and variable selection via the elastic net. J. R. Stat. Soc. B 2005, 67, 301–320. [Google Scholar] [CrossRef]
- Yuan, M.; Lin, Y. Model selection and estimation in regression with grouped variables. J. R. Stat. Soc. B 2006, 68, 49–67. [Google Scholar] [CrossRef]
- Fan, J.; Li, R. Variable selection via nonconcave penalized likelihood and its oracle properties. J. Am. Stat. Assoc. 2001, 96, 1348–1361. [Google Scholar] [CrossRef]
- Mortazavi, A.; Williams, B.A.; Mccue, K.; Schaeffer, L.; Wold, B. Mapping and quantifying mammalian transcriptomes by RNA-seq. Nat. Methods 2008, 5, 621–628. [Google Scholar] [CrossRef]
- Trapnell, C.; Pachter, L.; Salzberg, S.L. Tophat: Discovering splice junctions with RNA-seq. Bioinformatics 2009, 25, 1105–1111. [Google Scholar] [CrossRef] [PubMed]
- Li, B.; Dewey, C.N. RSEM: Accurate transcript quantification from RNA-seq data with or without a reference genome. BMC Bioinform. 2011, 12, 323. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Zhu, Y.; Zhu, C. Adaptive bridge estimation for high-dimensional regression models. J. Inequal. Appl. 2016, 2016, 258. [Google Scholar] [CrossRef]
- Zou, H.; Zhang, H. On the adaptive elastic-net with a diverging number of parameters. Ann. Stat. 2009, 37, 1733–1751. [Google Scholar] [CrossRef]
- Tibshirani, R.; Saunders, M.; Rosset, S.; Zhu, J.; Knight, K. Sparsity and smoothness via the fused LASSO. J. R. Stat. Soc. B 2005, 67, 91–108. [Google Scholar] [CrossRef]
- Huang, J.; Ma, S.; Xie, H. A group bridge approach for variable selection. Biometrika 2009, 96, 339–355. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Li, H. Network-constrained regularization and variable selection for analysis of genomic data. Bioinformatics 2008, 24, 1175–1182. [Google Scholar] [CrossRef]
- Liu, C.; Wong, H. Structured penalized logistic regression for gene selection in gene expression data analysis. IEEE/ACM Trans. Comput. Biol. Bioinform. 2019, 16, 312–321. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Y.; He, Y.; Zhang, H. Variable selection with prior information for generalized linear models via the prior LASSO method. J. Am. Stat. Assoc. 2016, 111, 355–376. [Google Scholar] [CrossRef]
- Münch, M.M.; Peeters, C.F.W.; Van Der Vaart, A.W.; Van De Wiel, M.A. Adaptive group-regularized logistic elastic net regression. Biostatistics 2019, 22, 723–737. [Google Scholar] [CrossRef]
- Guo, J.; Hu, J.; Jing, B.; Zhang, Z. Spline-LASSO in high-dimensional linear regression. J. Am. Stat. Assoc. 2016, 111, 288–297. [Google Scholar] [CrossRef]
- Song, Q.; Liang, F. High-dimensional variable selection with reciprocal ℓ1-regularization. J. Am. Stat. Assoc. 2015, 110, 1607–1620. [Google Scholar] [CrossRef]
- Simon, N.; Friedman, J.; Hastie, T.; Tibshirani, R. A sparse-group LASSO. J. Comput. Graph. Stat. 2013, 22, 231–245. [Google Scholar] [CrossRef]
- Detmer, F.J.; Slawski, M. A note on coding and standardization of categorical variables in (sparse) group LASSO regression. J. Stat. Plan. Inference 2020, 206, 1–11. [Google Scholar] [CrossRef]
- Liu, J.; Huang, J.; Ma, S.; Wang, K. Incorporating group correlations in genome-wide association studies using smoothed group LASSO. Biostatistics 2013, 14, 205–219. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C. Nearly unbiased variable selection under minimax concave penalty. Ann. Stat. 2013, 38, 894–942. [Google Scholar] [CrossRef]
- Huang, J.; Breheny, P.; Ma, S. A selective review of group selection in high dimensional models. Stat. Sci. 2013, 27, 481–499. [Google Scholar] [CrossRef] [PubMed]
- Bondell, H.D.; Reich, B.J. Simultaneous regression shrinkage, variable selection, and supervised clustering of predictors with OSCAR. Biometrics 2008, 64, 115–123. [Google Scholar] [CrossRef]
- Wang, H.H.; Lengerich, B.J.; Aragam, B.; Xing, E. Precision LASSO: Accounting for correlations and linear dependencies in high-dimensional genomic data. Bioinformatics 2019, 35, 1181–1187. [Google Scholar] [CrossRef]
- Zeng, C.; Thomas, D.C.; Lewinger, J.P. Incorporating prior knowledge into regularized regression. Bioinformatics 2021, 37, 514–521. [Google Scholar] [CrossRef] [PubMed]
- Sun, Q.; Zhou, W.; Fan, J. Adaptive huber regression. J. Am. Stat. Assoc. 2020, 115, 254–265. [Google Scholar] [CrossRef]
- Huang, Z.; Lin, B.; Feng, F.; Pang, Z. Efficient penalized estimating method in the partially varying-coefficient single-index model. J. Multivar. Anal. 2013, 114, 189–200. [Google Scholar] [CrossRef]
- Srebro, N.; Shraibman, A. Rank, trace-norm and max-norm. In International Conference on Computational Learning Theory, Proceedings of the 18th Annual Conference on Learning Theory, COLT 2005, Bertinoro, Italy, 27–30 June 2005; Auer, P., Meir, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 545–560. [Google Scholar]
- Friedman, J.; Hastie, T.; Hofling, H.; Tibshirani, R. Pathwise coordinate optimization. Ann. Appl. Stat. 2007, 1, 302–332. [Google Scholar] [CrossRef]
- Efron, B.; Hastie, T.; Johnstone, I.; Tibshirani, R. Least angle regression. Ann. Stat. 2004, 32, 407–499. [Google Scholar] [CrossRef]
- Friedman, J.; Hastie, T.; Tibshirani, R. Regularization paths for generalized linear models via coordinate descent. J. Stat. Softw. 2010, 33, 1–22. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Zhao, L.; Ji, J.; Ma, B.; Zhao, Z.; Wu, M.; Zheng, W.; Zhang, Z. Temporal grading index of functional network topology predicts pain perception of patients with chronic back pain. Front. Neurol. 2022, 13, 899254. [Google Scholar] [CrossRef] [PubMed]
- Yuan, R.; Chen, S.; Wang, Y. Computational probing the methylation sites related to EGFR inhibitor-responsive genes. Biomolecules 2021, 11, 1042. [Google Scholar] [CrossRef]
- Walco, J.P.; Mueller, D.A.; Lakha, S.; Weavind, L.M.; Clifton, J.C.; Freundlich, R.E. Etiology and timing of postoperative rapid response team activations. J. Med. Syst. 2021, 45, 82. [Google Scholar] [CrossRef]
- Richie-Halford, A.; Yeatman, J.; Simon, N.; Rokem, A. Multidimensional analysis and detection of informative features in human brain white matter. PLoS Comput. Biol. 2021, 17, e1009136. [Google Scholar] [CrossRef]
- Stamey, T.A.; Kabalin, J.N.; McNeal, J.E.; Johnstone, I.M.; Freiha, F.; Redwine, E.A.; Yang, N. Prostate specific antigen in the diagnosis and treatment of adenocarcinoma of the prostate. II. Radical prostatectomy treated patients. J. Urol. 1989, 141, 1076–1083. [Google Scholar] [CrossRef]
- Qin, Y.; Li, C.; Shi, X.; Wang, W. MLP-based regression prediction model for compound bioactivity. Front. Bioeng. Biotechnol. 2022, 10, 946329. [Google Scholar] [CrossRef]
- Yang, T.; Wang, J.; Sun, Q.; Hibar, D.P.; Jahanshad, N.; Liu, L.; Wang, Y.; Zhan, L.; Thompson, P.M.; Ye, J. Detecting genetic risk factors for Alzheimer’s disease in whole genome sequence data via LASSO screening. In Proceedings of the 2015 IEEE 12th International Symposium on Biomedical Imaging (ISBI), Brooklyn, NY, USA, 16–19 April 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 985–989. [Google Scholar]
- Godbole, S.; Labaki, W.W.; Pratte, K.A.; Hill, A.; Moll, M.; Hastie, A.T.; Peters, S.P.; Gregory, A.; Ortega, V.E.; DeMeo, D.; et al. A metabolomic severity score for airflow obstruction and emphysema. Metabolites 2022, 12, 368. [Google Scholar] [CrossRef]
- Chen, S.; Wang, P. Gene selection from biological data via group LASSO for logistic regression model: Effects of different clustering algorithms. In Proceedings of the 40th Chinese Control Conference, Shanghai, China, 26–28 July 2021; pp. 6374–6379. [Google Scholar]
- Hosmer, D.W.; Lemeshow, S.; Sturdivant, R.X. Applied Logistic Regression, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Horvath, S.; Zhang, B.; Carlson, M.; Lu, K.V.; Zhu, S.; Felciano, R.M.; Laurance, M.F.; Zhao, W.; Qi, S.; Chen, Z.; et al. Analysis of oncogenic signaling networks in glioblastoma identifies ASPM as a molecular target. Proc. Natl. Acad. Sci. USA 2006, 103, 17402–17407. [Google Scholar] [CrossRef]
- Aycheh, H.M.; Seong, J.K.; Shin, J.H.; Na, D.L.; Kang, B.; Seo, S.W.; Sohn, K.A. Biological brain age prediction using cortical thickness data: A large scale cohort study. Front. Aging Neurosci. 2018, 10, 252. [Google Scholar] [CrossRef]
- Frost, H.R.; Amos, C.I. Gene set selection via LASSO penalized regression (SLPR). Nucleic Acids Res. 2017, 45, e114. [Google Scholar] [CrossRef]
- Tharmaratnam, K.; Sperrin, M.; Jaki, T.; Reppe, S.; Frigessi, A. Tilting the LASSO by knowledge-based post-processing. BMC Bioinform. 2016, 17, 344. [Google Scholar] [CrossRef]
- Curtis, C.; Shah, S.P.; Chin, S.F.; Turashvili, G.; Rueda, O.M.; Dunning, M.J.; Speed, D.; Lynch, A.G.; Samarajiwa, S.; Yuan, Y.; et al. The genomic and transcriptomic architecture of 2000 breast tumours reveals novel subgroups. Nature 2012, 486, 346–352. [Google Scholar] [CrossRef]
- Roy, G.G.; Geard, N.; Verspoor, K.; He, S. PoLoBag: Polynomial LASSO bagging for signed gene regulatory network inference from expression data. Bioinformatics 2020, 36, 5187–5193. [Google Scholar]
- Gao, T.; Yan, G. Autonomous inference of complex network dynamics from incomplete and noisy data. Nat. Comput. Sci. 2022, 2, 160–168. [Google Scholar] [CrossRef]
- Finkle, J.D.; Wu, J.; Bagheri, N. Windowed Granger causal inference strategy improves discovery of gene regulatory networks. Proc. Natl. Acad. Sci. USA 2018, 115, 2252–2257. [Google Scholar] [CrossRef]
- Han, X.; Shen, Z.; Wang, W.; Di, Z. Robust reconstruction of complex networks from sparse data. Phys. Rev. Lett. 2015, 114, 028701. [Google Scholar] [CrossRef]
- Erdem, C.; Nagle, A.M.; Casa, A.J.; Litzenburger, B.C.; Wang, Y.; Taylor, D.L.; Lee, A.V.; Lezon, T.R. Proteomic screening and LASSO regression reveal differential signaling in insulin and insulin-like growth factor I (IGF1) pathways. Mol. Cell. Proteom. 2016, 15, 3045–3057. [Google Scholar] [CrossRef]
- Xu, S.; Zhang, C.; Wang, P.; Zhang, J. Variational Bayesian weighted complex network reconstruction. Inform. Sci. 2020, 521, 291–306. [Google Scholar] [CrossRef]
- Hang, Z.; Dai, P.; Jia, S.; Yu, Z. Network structure reconstruction with symmetry constraint. Chaos Solitons Fractals 2020, 139, 110287. [Google Scholar] [CrossRef]
- Yuan, M.; Lin, Y. Model selection and estimation in the Gaussian graphical model. Biometrika 2007, 94, 19–35. [Google Scholar] [CrossRef]
- Friedman, J.; Hastie, T.; Tibshirani, R. Sparse inverse covariance estimation with the graphical LASSO. Biostatistics 2008, 9, 432–441. [Google Scholar] [CrossRef]
- Cai, T.; Liu, W.; Luo, X. A constrained ℓ1 minimization approach to sparse precision matrix estimation. J. Am. Stat. Assoc. 2011, 106, 594–607. [Google Scholar] [CrossRef]
- Shevade, S.K.; Keerthi, S.S. A simple and efficient algorithm for gene selection using sparse logistic regression. Bioinformatics 2003, 19, 2246–2253. [Google Scholar] [CrossRef]
- Liao, J.; Chin, K.V. Logistic regression for disease classification using microarray data: Model selection in a large p and small n case. Bioinformatics 2007, 23, 1945–1951. [Google Scholar] [CrossRef]
- Lee, K.; Ahn, H.; Moon, H.; Kodell, R.L.; Chen, J.J. Multinomial logistic regression ensembles. J. Biopharm. Stat. 2013, 23, 681–694. [Google Scholar] [CrossRef]
- Hashimoto, E.M.; Ortega, E.M.M.; Cordeiro, G.M.; Suzuki, A.K.; Kattan, M.W. The multinomial logistic regression model for predicting the discharge status after liver transplantation: Estimation and diagnostics analysis. J. Appl. Stat. 2019, 47, 2159–2177. [Google Scholar] [CrossRef]
- McCullagh, P.; Nelder, J.A. Generalized Linear Models, 2nd ed.; Chapman & Hall: New York, NY, USA, 1990. [Google Scholar]
- Long, J.S. Regression Models for Categorical and Limited Dependent Variables; SAGE Publications: Thousand Oaks, CA, USA, 1997; pp. 1–328. [Google Scholar]
- Dobson, A.J.; Barnett, A.G. An Introduction to Generalized Linear Models, 3rd ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2008; pp. 1–320. [Google Scholar]
- Hedeker, D. A mixed-effects multinomial logistic regression model. Stat. Med. 2003, 22, 1433–1446. [Google Scholar] [CrossRef]
- Fagerland, M.W.; Hosmer, D.W.; Bofin, A.M. Multinomial goodness-of-fit tests for logistic regression models. Stat. Med. 2008, 27, 4238–4253. [Google Scholar] [CrossRef]
- Agresti, A. Multicategory logit models. In An Introduction to Categorical Data Analysis; Agresti, A., Ed.; Wiley-Interscience: New York, NY, USA, 1996; pp. 286–287. [Google Scholar]
- Allwein, E.L.; Schapire, R.E.; Singer, Y. Reducing multiclass to binary: A unifying approach for margin classifiers. J. Mach. Learn. Res. 2000, 1, 113–141. [Google Scholar]
- Green, P.J. Iteratively reweighted least squares for maximum likelihood estimation, and some robust and resistant alternatives. J. R. Stat. Soc. B 1984, 46, 149–192. [Google Scholar] [CrossRef]
- Kim, Y.; Kim, J.; Kim, Y. Blockwise sparse regression. Stat. Sin. 2006, 16, 375–390. [Google Scholar]
- Zhu, J.; Hastie, T. Classification of gene microarrays by penalized logistic regression. Biostatistics 2004, 5, 427–443. [Google Scholar] [CrossRef]
- Lin, H.; Wang, C.; Liu, P.; Holtkamp, D.J. Construction of disease risk scoring systems using logistic group LASSO: Application to porcine reproductive and respiratory syndrome survey data. J. Appl. Stat. 2013, 40, 736–746. [Google Scholar] [CrossRef]
- Zhang, B.; Chai, H.; Yang, Z.; Liang, Y.; Chu, G.; Liu, X. Application of ℓ1/2 regularization logistic method in heart disease diagnosis. Bio-Med. Mater. Eng. 2014, 24, 3447–3454. [Google Scholar] [CrossRef] [PubMed]
- Torang, A.; Gupta, P.; Klinke, D.J. An elastic-net logistic regression approach to generate classifiers and gene signatures for types of immune cells and T helper cell subsets. BMC Bioinform. 2019, 20, 433. [Google Scholar] [CrossRef] [PubMed]
- Tirosh, I.; Izar, B.; Prakadan, S.M.; Wadsworth, M.H.; Treacy, D.; Trombetta, J.J.; Rotem, A.; Rodman, C.; Lian, C.; Murphy, G.; et al. Dissecting the multicellular ecosystem of metastatic melanoma by single-cell RNA-seq. Science 2016, 352, 189–196. [Google Scholar] [CrossRef]
- Chung, W.; Eum, H.H.; Lee, H.O.; Lee, K.M.; Lee, H.B.; Kim, K.T.; Ryu, H.S.; Kim, S.; Lee, J.E.; Park, Y.H.; et al. Single-cell RNA-seq enables comprehensive tumor and immune cell profiling in primary breast cancer. Nat. Commun. 2017, 8, 15081. [Google Scholar] [CrossRef]
- Wu, Y.; Ren, P.; Chen, R.; Xu, H.; Xu, J.; Zeng, L.; Wu, D.; Jiang, W.; Tang, N.; Liu, X. Detection of functional and structural brain alterations in female schizophrenia using elastic net logistic regression. Brain Imaging Behav. 2021, 16, 281–290. [Google Scholar] [CrossRef] [PubMed]
- Ansari, M.S.; Jain, D.; Harikumar, H.; Rana, S.; Gupta, S.; Budhiraja, S.; Venkatesh, S. Identification of predictors and model for predicting prolonged length of stay in dengue patients. Health Care Manag. Sci. 2021, 24, 786–798. [Google Scholar] [CrossRef]
- Cui, X.; Xiao, R.; Liu, X.; Qiao, H.; Zheng, X.; Zhang, Y.; Du, J. Adaptive LASSO logistic regression based on particle swarm optimization for Alzheimer’s disease early diagnosis. Chemom. Intell. Lab. 2021, 215, 104316. [Google Scholar] [CrossRef]
- Yang, Z.; Yin, S.; Ren, Q.; Lu, D.; Tang, T.; Li, Y.; Sun, Y.; Mo, H.; Yin, T.; Yi, Z.; et al. BAHD1 serves as a critical regulator of breast cancer cell proliferation and invasion. Breast Cancer 2022, 29, 516–530. [Google Scholar] [CrossRef] [PubMed]
- Bierne, H.; Tham, T.N.; Batsche, E.; Dumay, A.; Leguillou, M.; Kerneis-Golsteyn, S.; Regnault, B.; Seeler, J.S.; Muchardt, C.; Feunteun, J.; et al. Human BAHD1 promotes heterochromatic gene silencing. Proc. Natl. Acad. Sci. USA 2009, 106, 13826–13831. [Google Scholar] [CrossRef] [PubMed]
- Tang, G.; Qi, L.; Sun, Z.; Liu, J.; Lv, Z.; Chen, L.; Huang, B.; Zhu, S.; Liu, Y.; Li, Y. Evaluation and analysis of incidence and risk factors of lower extremity venous thrombosis after urologic surgeries: A prospective two-center cohort study using LASSO-logistics regression. Int. J. Surg. 2021, 89, 105948. [Google Scholar] [CrossRef] [PubMed]
- Liang, Y.; Liu, C.; Luan, X.; Leung, K.S.; Chan, T.M.; Xu, Z.; Zhang, H. Sparse logistic regression with a ℓ1/2 penalty for gene selection in cancer classification. BMC Bioinform. 2013, 14, 198. [Google Scholar] [CrossRef]
- Zhang, W.; Wan, Y.; Allen, G.I.; Pang, K.; Anderson, M.L.; Liu, Z. Molecular pathway identification using biological network-regularized logistic models. BMC Genom. 2013, 14 (Suppl. 8), S7. [Google Scholar] [CrossRef] [PubMed]
- Haynos, A.F.; Wang, S.B.; Lipson, S.; Peterson, C.B.; Mitchell, J.E.; Halmi, K.A.; Agras, W.S.; Crow, S.J. Machine learning enhances prediction of illness course: A longitudinal study in eating disorders. Psychol. Med. 2020, 51, 1–11. [Google Scholar] [CrossRef]
- Aung, M.T.; Yu, Y.; Ferguson, K.K.; Cantonwine, D.E.; Zeng, L.; McElrath, T.F.; Pennathur, S.; Mukherjee, B.; Meeker, J.D. Prediction and associations of preterm birth and its subtypes with eicosanoid enzymatic pathways and inflammatory markers. Sci. Rep. 2019, 9, 17049. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Huang, D.; Wang, H. A dynamic logistic regression for network link prediction. Sci. China Math. 2017, 60, 165–176. [Google Scholar] [CrossRef]
- Park, M.Y.; Hastie, T. Penalized logistic regression for detecting gene interactions. Biostatistics 2008, 9, 30–50. [Google Scholar] [CrossRef] [PubMed]
- Liu, Q.; Ma, C.; Xiang, B.; Chen, H.; Zhang, H. Inferring network structure and estimating dynamical process from binary-state data via logistic regression. IEEE Trans. Syst. Man. Cyber. Syst. 2021, 51, 4639–4649. [Google Scholar] [CrossRef]
- Ciriello, G.; Gatza, M.L.; Beck, A.H.; Wilkerson, M.D.; Rhie, S.K.; Pastore, A.; Zhang, H.; McLellan, M.; Yau, C.; Kandoth, C.; et al. Comprehensive molecular portraits of invasive lobular breast cancer. Cell 2015, 163, 506–519. [Google Scholar] [CrossRef] [PubMed]
- Theodoridis, S. Machine Learning: A Bayesian and Optimization Perspective, 1st ed.; Academic Press: New York, NY, USA, 2015. [Google Scholar]
- Tseng, P.; Yun, S. A coordinate gradient descent method for nonsmooth separable minimization. Math. Program. 2009, 117, 387–423. [Google Scholar] [CrossRef]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trend. Mach. Learn. 2011, 3, 1–122. [Google Scholar]
- Wang, P.; Zhang, Y.; Lü, J.; Yu, X. Functional characteristics of additional positive feedback in genetic circuits. Nonlinear Dyn. 2015, 79, 397–408. [Google Scholar] [CrossRef]
- Wang, W.; Liang, J.; Liu, R.; Song, Y.; Zhang, M. A robust variable selection method for sparse online regression via the elastic net penalty. Mathematics 2022, 10, 2985. [Google Scholar] [CrossRef]
- Patil, A.R.; Kim, S. Combination of ensembles of regularized regression models with resampling-based LASSO feature selection in high dimensional data. Mathematics 2020, 8, 110. [Google Scholar] [CrossRef]
- Li, J.; Dong, W.; Meng, D. Grouped gene selection of cancer via adaptive sparse group LASSO based on conditional mutual information. IEEE/ACM Trans. Comput. Biol. Bioinform. 2018, 15, 2028–2038. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Wang, Y.; Jiang, T.; Xiao, H.; Song, X. Grouped gene selection and multi-classification of acute leukemia via new regularized multinomial regression. Gene 2018, 667, 18–24. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).