Abstract
In recent decades there has been an increasing interest in Elliptic curve cryptography (ECC) and, especially, the Elliptic Curve Digital Signature Algorithm (ECDSA) in practice. The rather recent developments of emergent technologies, such as blockchain and the Internet of Things (IoT), have motivated researchers and developers to construct new cryptographic hardware accelerators for ECDSA. Different types of optimizations (either platform dependent or algorithmic) were presented in the literature. In this context, we turn our attention to ECC and propose a new method for generating ECDSA moduli with a predetermined portion that allows one to double the speed of Barrett’s algorithm. Moreover, we take advantage of the advancements in the Artificial Intelligence (AI) field and bring forward an AI-based approach that enhances Schoof’s algorithm for finding the number of points on an elliptic curve in terms of implementation efficiency. Our results represent algorithmic speed-ups exceeding the current paradigm as we are also preoccupied by other particular security environments meeting the needs of governmental organizations.
Keywords:
elliptic curve; elliptic curve cryptography; ECDSA; artificial intelligence; Schoof’s algorithm; Barrett’s algorithm; modular reduction MSC:
11T71; 94A60; 68P25; 14H52; 14G15; 68T01
1. Introduction
Elliptic curve cryptographic (ECC) was initially proposed in [1,2] as an alternative to the already established public key cryptographic schemes. As a side note, the credit for the first use of elliptic curves in a cryptology related context is given to Lenstra for his factorization algorithm [3]. ECC has received an increasing amount of attention in time not only for the high level provable security offered, but especially due to a desired property concerning the implementation efficiency: the cryptographic keys are significantly shorter compared to, e.g., the case of RSA [4].
For more than a decade now, ECC has become a central piece for the Blockchain technology. To be more specific, the Elliptic Curve Digital Signature Algorithm (ECDSA) [5] is widely adopted in the construction of cryptocurrency and, implicitly, blockchains. Thus, there has been a justified hype with respect to efficient implementations of ECDSA and other ECC schemes in recent years, especially using Field Programmable Gate Arrays (FPGAs) [6,7,8,9,10,11,12,13,14]. Hence, FPGA-based hardware accelerators represent the main applied research topic when dealing with (permissioned) blockchains. To underline the importance of the subject, we have to mention that the main FPGA technology producer, Xilinx [15], organized a competition in 2021 [16], which encouraged R&D representants to propose, among other topics, blockchain-related projects [17].
Nonetheless, ECC grew compelling for another important emergent technology, i.e., the Internet of Things (IoT) [18]. Again, the interest for (hardware) optimized implementations of ECC algorithms is clearly shown in theory and practice [19,20,21,22,23,24,25,26,27,28,29,30,31]. Microprocessor, ASIC, and FPGA-based accelerators are proposed. Alongside hardware-specific optimizations, these cryptographic cores make use of different customary algorithmic improvements from the literature, mainly related to modular arithmetic.
Motivated by all the above and following the work of Géraud et al. from [32], this paper aims at building the foundation for new techniques of optimizing the implementation of ECDSA. As in the case of most public-key cryptosystems, the basic arithmetic operation used in ECC is the modular reduction. [32] describes a method allowing to double the speed of Barrett’s algorithm [33] by using specific RSA moduli with a predetermined portion. The result is then applied in order to generate DSA [34] parameters. As an extension, our article presents a technique for generating ECDSA moduli with a predetermined portion that allows one to double the speed of Barrett’s algorithm, a widely adopted efficient technique for performing modular reduction in a costly reduced manner. We also provide the reader with mathematical proof of our algorithm.
Moreover, we target a more general type of optimization suitable not only for ECDSA, but for various ECC algorithms. Thus, we propose an artificial intelligence (AI) based approach that enhances the speed of Schoof’s algorithm for finding the number of points on an elliptic curve [35]. Schoof’s method is the first deterministic polynomial time algorithm for counting points on elliptic curves defined over finite fields. The result represented, undoubtedly, a breakthrough in terms of designing ECC algorithms.
While the first result we propose is rather particular and can be applied for a certain digital signature scheme (ECDSA), the latter can be of general interest in terms of ECC algorithms. We underline that the AI-optimized variant of Schoof’s algorithm is rather a proof of concept for a future series of results, with respect to this research direction.
We stress that all the related works regarding the ECC implementation optimizations [6,7,8,9,10,11,12,13,19,20,21,22,23,24,25,26,27,28,29,30,31] are targetting either specific curves (e.g., NIST P-256 [5], Secp256k1), curves over binary fields , or curves over prime fields . Note that our studies are different from the previously mentioned results, as we point out in Section 1.1.
Nonetheless, our methods can also be combined with already established algorithmic improvements to obtain even better implementation timings.
1.1. Specific Supplementary Motivation
The common practice when using ECC is to have specific curves [5,36] rather than choose them every time when the algorithm is run in order to ease computations (by applying dedicated formulae for point addition and scalar multiplication). Nonetheless, speeding-up ECDSA in the general case can be advantageous, e.g., either for cryptographic implementations, requiring a higher level of security than the standard one, or simply for proprietary cryptographic algorithms (of course, given that a step consisting of checking the security of the generated curve is performed.). Such needs are customary, especially for governmental organizations. Moreover, in the aforementioned example, implementations for resource constrained devices and cryptographic hardware may be of great interest. Thus, when proposing our results, we do not seek to compare them with existing targeted ECC implementations in terms of speed, as we consider performing an initial costly step: the parameter generation.
In addition to the above, we believe that our AI-based strategy will benefit from the rapid advances in the field of AI in the near future.
1.2. Structure of the Paper
In Section 2, we introduce the notations and briefly describe Barrett’s algorithm for modular reduction, Schoof’s algorithm for point counting on elliptic curves, and ECDSA. The main results are discussed in Section 3, namely the algorithm for generating the ECDSA parameters and the method for finding the number of points of an elliptic curve. Details regarding the straightforward, unoptimized implementations of the previously mentioned algorithms are presented in Section 4. We conclude and provide the reader with future work ideas in Section 5. Moreover, we recall ECDSA in Appendix A and Schoof’s algorithm in Appendix B.
2. Preliminaries
2.1. Notations
Throughout this paper, we denote by NextPrime the smallest prime p, such that . represents the cardinality of the set S. We let P be the bit-length of p, such that . The value of P is fixed from now onwards. The binary shift-to-the-right of x by y positions is further denoted by .
2.2. Barrett’s Algorithm
Let d and m be integer numbers. Barrett’s algorithm (Algorithm 1) only uses two bit-shifts and one multiplication to produce an approximate value of the quotient obtained when d is divided by m. This approximation is denoted by and it satisfies the following inequality
which means that the whole loop is not repeated more than two times. The bit-lengths of d and m are represented by D and M. Algorithm 1 also requires a quantity that is denoted by L and which represents the maximal bit-length of the numbers that can be reduced. Barrett’s algorithm works as long as the condition is satisfied. In most cases, these constants can be chosen such that , provided that the reduction is performed after every operation. The constant k is computed only once, since it does not depend on the value of d. Further details regarding Algorithm 1 can be found in [33].
| Algorithm 1: Barrett’s algorithm for modular reduction. |
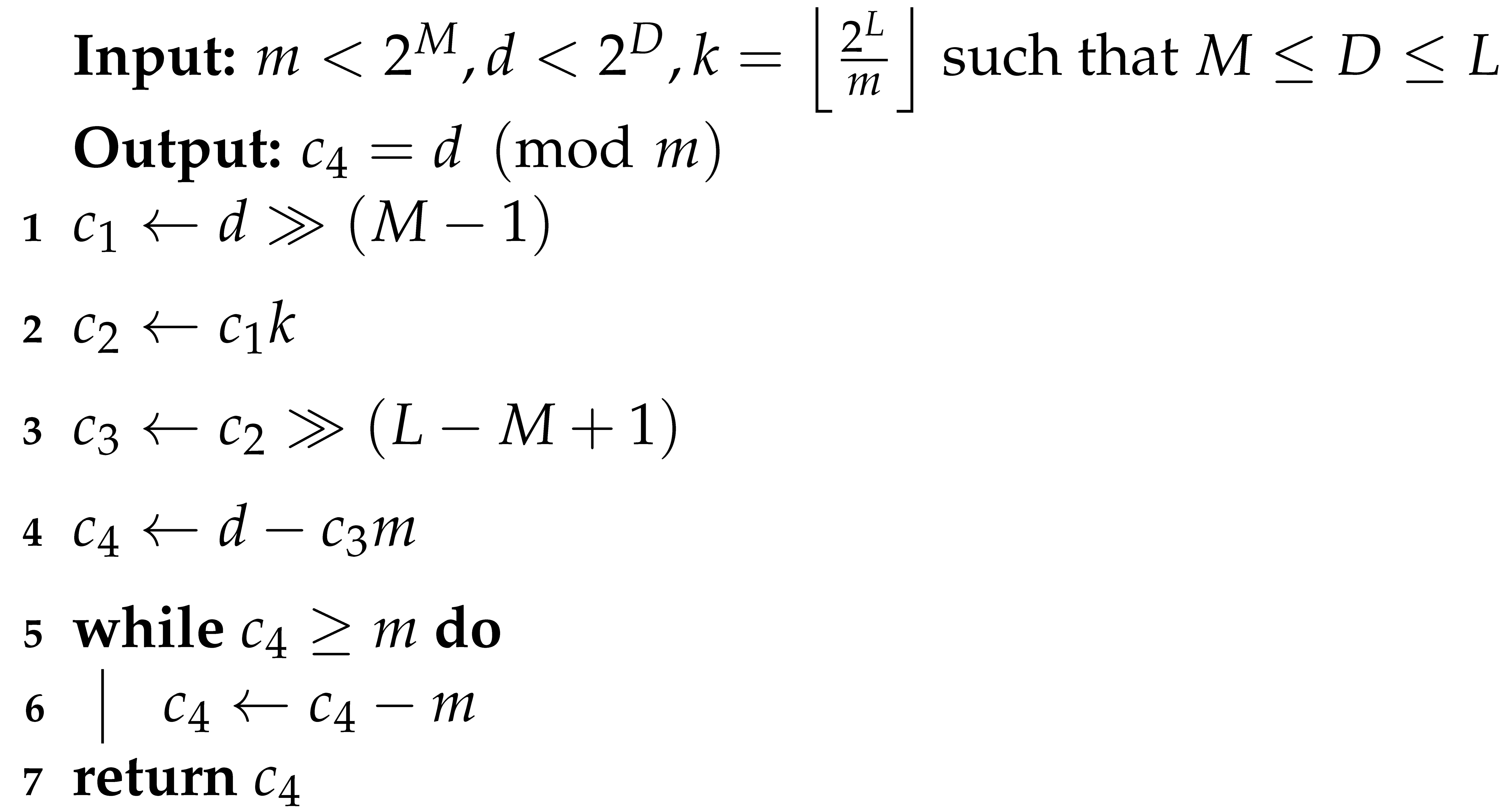 |
2.3. Elliptic Curves in Cryptography
2.3.1. Schoof’s Algorithm
The elliptic curves considered are of the form and are defined over a finite field , where p is prime. An important result, which will be used throughout this paper, is the following theorem.
Theorem 1
(Hasse). The number of points n of an elliptic curve defined over a finite field of size p satisfies the inequality
In [35], Schoof published the first deterministic and polynomial-time algorithm that computes the order of an elliptic curve, which is defined over a finite field. This algorithm starts off by using Theorem 1, which provides an interval of possible values for the order of the elliptic curve. That specific interval has the width .
Since the order can be written as , where t is the trace of the Frobenius endomorphism [37], the problem of finding the order reduces to that of finding the value of t. The next step involves computing the value of t modulo for some primes, such that their product is greater than . Finally, the Chinese Remainder Theorem [37] produces the value of t, which is needed for finding the order.
The details of Schoof’s algorithm are included in Appendix A as Algorithm A4.
2.3.2. ECDSA
ECDSA [5] is a digital signature scheme based on cyclic groups of elliptic curves defined over finite fields. Its security relies on the Elliptic Curve Discrete Logarithm Problem [38]. Details about setting-up the parameters of ECDSA, generating a signature and verifying it are included in Appendix A.
3. Main Results
3.1. Double-Speed Barrett for ECDSA
For the setup of ECDSA, two prime numbers p and n are required: p represents the size of the finite field and n is the order of the group , since we are only considering the case when the order of this group is prime. Note that both the multiplications performed in Algorithm 1 are multiplications by constants, namely k and n.
Our aim is to generate the primes p and n such that their leading bits do not have to be computed. Moreover, we want this to happen also for the associated constants and The idea of Algorithm 2 is that if we choose the prime p in a convenient way, then we can control the most significant bits of n.
| Algorithm 2: Generator for Barrett-compatible ECDSA parameters. |
Input: the bit-length of the prime p, which has to be even and large Output: the parameters needed for ECDSA
|
Lemma 1.
Consider the notations used in Algorithm 2. Let . Then and satisfy the following inequalities:
- 1.
- ;
- 2.
- ;
- 3.
- ;
- 4.
- .
Proof.
- Using the inequality and Line 6 of Algorithm 2, we obtain that .
- From Theorem 1 we have that . Let . For the left side of the inequality, i.e., , we obtain thatThus,For the right side of the inequality, i.e., , we know from Line 1 that . Therefore, we get .
- Using Line 2 of Algorithm 2, we can deduce thatHence,
- Similarly, using Line 2 of Algorithm 2, we obtain thatTherefore,
□
Remark 1.
In Line 6 of Algorithm 2, we do not allow the distance between α and the next prime p to be too large. Additionally, we choose α in a specific way so that we can control p’s size. This implies that the probability of the first U bits of p being different than the first U bits of α is negligible. We performed experiments with the value , and the success rate was .
Example 1.
This example illustrates Algorithm 2. For the values , , and , we get:
- 0xbba46de2b4b53e20b97d41941c01a6b0
- 0x80000000000000000000000000000002bba46de2b4b53e20b97d41941c01a6b0
- 0x80000000000000000000000000000002bba46de2b4b53e20b97d41941c01a6ef
- 0x80000000000000000000000000000001b97deb5c74f4115fd2d9ec6ae5cb520f
- 0x1fffffffffffffffffffffffffffffff5116e48752d2b077d1a0af9af8ff9647f
- 0x1fffffffffffffffffffffffffffffff91a08528e2c2fba80b4984e5468d2b7db
3.2. Enhancing Schoof’s Algorithm Using AI
Our aim is to modify Schoof’s algorithm by replacing Hasse’s interval with another one containing the order, such that the width of the new interval is smaller.
In order to obtain such a result, we can use a neural network that takes input triplets of the form and returns as output elements given by
where we denote by that the estimate of the actual order . Here we use the sigmoid activation function for the output layer to ensure that the output is in the appropriate range. The labels used for training the neural network are written as
The elements of the training, validation, and test sets will be written in the form where instead of ∗, we will have the superscripts , and t, respectively. These three sets will have the cardinal numbers equal to , and , respectively.
At training time, we choose to use as loss function the mean squared logarithmic error, since we want this to work well for large primes. This function is given by
Let us denote by the average distance between the actual order and the estimate of the order, which is computed on the validation set,
Our approach is a probabilistic one, since we need to assume that the order n satisfies the inequality
This leads to the following result involving t,
Notice that in the above inequality, we have doubled in order to increase the probability that our assumption is true. Hence, if we manage to determine the value of , then we can find t by replacing in the formula , and thus we know the order of the group. The benefit of using the estimate given by the neural network is that Schoof’s algorithm can be applied for an interval of width equal to instead of one of width equal to This means that if the neural network is good at estimating the order, i.e., , then this approach will be faster than the standard one.
Remark 2.
Since our algorithm is probabilistic, after obtaining a value of ϵ, which is significantly lower than instead of assuming that n lies in the interval , we can assume that it lies in an interval of greater width, for example . By doing this, we are able to increase the success probability of the algorithm.
Remark 3.
The difference between Schoof’s algorithm and our proposed technique is that we choose the set of primes from Line 1 of Appendix B, such that the product of the elements is greater than . All the steps that follow remain unchanged.
4. Implementation
4.1. GitHub Implementation
We refer the reader to [39] for the source code representing the implementation of our proposed results.
Note that for simplicity, we overlooked the initial part of Algorithm 2 (i.e., from Line 1 to Line 6) in our implementation.
4.2. Implementation Results
We ran the code for our algorithm on a standard laptop using Ubuntu 20.04.5 LTS OS, with the following specifications: Intel Core i3-1005G1 with 2 cores and 8 Gigabytes of RAM. The programming language we used for implementing our algorithms was Python, and the AI library we chose was TensorFlow.
4.2.1. AI-Based Speed-Up
Our AI-based technique can speed up the search for an elliptic curve of prime order. This speed-up depends initially on the model architecture and then on the accuracy of the AI-model. Within the current section, we report our (proof of concept) results.
To achieve our proof of concept goal, in our implementation we initially considered primes p of length 32 bits. Thus, we generated 60,000 elliptic curves of the form by means of Schoof’s algorithm. Based on these examples, we trained, validated, and tested the neural network model we chose. This network was composed of 7 dense hidden layers with the number of units decreasing from 512 to 8. Note that decreasing the number of units, as stated before, is a straightforward technique used in AI algorithms. The reason we decided to have 7 hidden layers was to obtain the best compromise in terms of error rate and code optimization (especially with respect to time complexity). We provide the reader with a graphical representation of the relationship between the number of neural network layers and the error rate of our proposed algorithm in Figure 1. Note that the error rate stabilizes at , starting with the use of 7 layers.
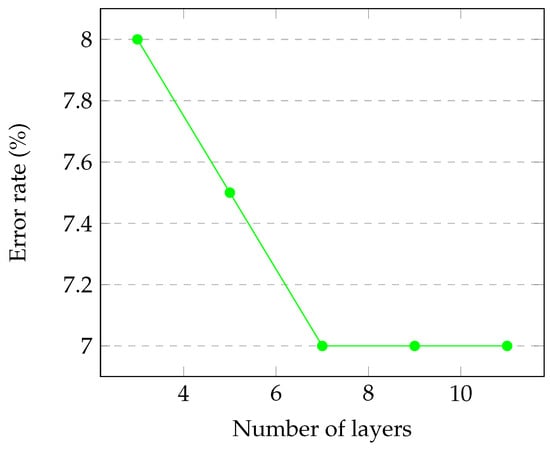
Figure 1.
The relationship between the number of neural network layers and the error rate of our proposed algorithm.
Hence, using the previously described neural network, we managed to replace Hasse’s interval with another interval, with the width approximately smaller than the original one. In this case, the probability that the order n satisfies Equation (1) was , which was also the success rate of our probabilistic algorithm. The obtained probability was computed by finding the number of testing examples, which satisfied Equation (1).
We provide the reader with a graphical representation of the relationship between the number of neural network layers and the reduced Hasse interval of our proposed algorithm in Figure 2. Note that the percent by which the width of our reduced Hasse’s interval is smaller than the original one stabilizes right after 7 layers at . Note that the next value considered after 7 is 9 given that the AI models work better in the case of an odd number of layers.
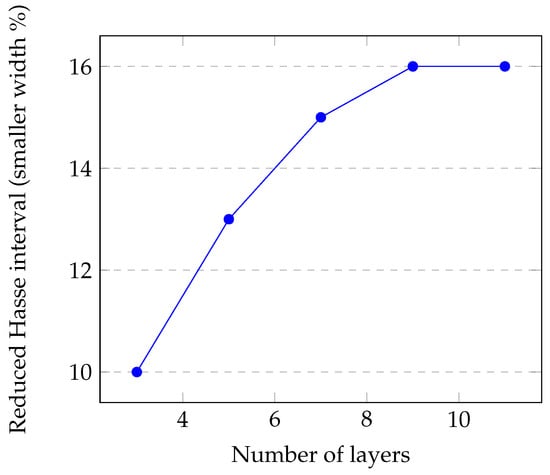
Figure 2.
The relationship between the number of neural network layers and the reduced Hasse interval.
Thus, given the results presented in Figure 1 and Figure 2, we chose to use 7 layers in our implementation as a trade-off between accuracy and time complexity. Table 1 shows that the difference between the timing of the 7 layers implementation version and the 9 layers version is significant (the latter is slower) and clearly sustains our choice of parameters.

Table 1.
Timing comparison between the implementation of our proposed algorithm using 7 and 9 layers, respectively.
Due to the fact that our proposed result is a particular algorithmic improvement, we compare it in terms of efficiency with the original Schoof algorithm (see Remark 3) and provide the reader with precise timings in Table 2. The average timings we report are given for 32, 48, and 64 bits prime numbers. It is straightforward for any other publicly available implementation optimization to be applied in our case too, and, thus, we can obtain the best timings.

Table 2.
Timing comparison between the implementation of our proposed algorithm and the original Schoof algorithm.
4.2.2. Barrett-Based ECDSA Speed-Up
Based on the results in [32], we showed that using Barrett-compatible ECDSA parameters doubles the speed of Barrett’s algorithm when performing the modular reductions required for generating (Algorithm A2) and verifying (Algorithm A3) ECDSA signatures. Thus, in such an optimized ECDSA implementation, the steps including modular reduction are performed two times faster than in a standard ECDSA implementation.
4.2.3. ECDSA Related Works Comparison
The authors of [13] report the fastest implementation of the ECDSA verification algorithm in FPGA compared to the already established results in the literature so far. The majority of papers presenting hardware optimizations for blockchain applications are only discussing the verification algorithm of ECDSA. Nonetheless, we are interested in optimizing the complete ECDSA scheme as our proposed speed-ups can also be applied for the signature generation algorithm (already stated in Section 4.2.2), not only for the verification algorithm.
Given that our FPGA implementation is work in progress, at this point, our target is to make a software implementation comparison of both the signing and the verification ECDSA algorithms. Thus, we considered the fastest (lightweight) ECDSA implementation available online [40] and modified it to include our proposed optimization from Section 3.1. The average time differences we obtained after 100 runs are presented in Table 3. Note that in the implementation at [40], the modular reduction steps are performed in a straightforward manner as opposed to our proposed double-speed Barrett optimization. Hence, the speed-up is obvious both in theory (see Section 4.2.2) and in practice (see Table 3).

Table 3.
Timing comparison between a lightweight ECDSA implementation and our enhanced version of it.
5. Conclusions and Future Work
We briefly described Barrett’s algorithm for modular reduction, Schoof’s algorithm for point counting on elliptic curves, and ECDSA as an example for applying our proposed speed-ups. We presented as main results an algorithm for generating implementation-friendly ECDSA parameters and a method for finding the number of points of an elliptic curve, representing an enhancement of Schoof’s algorithm. We also gave details regarding the unoptimized implementations of the previously mentioned algorithms.
Future Work
We consider that timing comparisons between our enhanced Schoof algorithm and already established implementations of SEA [41] represent an interesting idea to be tackled in the near future.
Next, a valuable idea is looking into more sophisticated AI optimizations for the mathematical computations inside Schoof’s algorithm.
Another interesting research direction is the implementantion of ECDSA in cryptographic hardware while using our proposed optimizations, together with a complexity analysis of other implementations in the literature. We are currently working on such an approach using FPGA-based equipment.
Author Contributions
Conceptualization, D.M. and A.C.M.; formal analysis, D.M. and A.C.M.; project administration, D.M.; resources, D.M. and A.C.M.; software, A.C.M.; supervision, D.M.; validation, D.M. and A.C.M.; writing—original draft, D.M. and A.C.M.; writing—review and editing, D.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to thank George Teşeleanu, Paul Cotan, and Rémi Geraud for their valuable comments.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. ECDSA
| Algorithm A1: ECDSA Setup. |
Input: , defining the elliptic curve over Output:
|
| Algorithm A2: ECDSA Signature. |
Input: Output: the signature generated is the pair
|
| Algorithm A3: ECDSA Verification. |
Input: Output: the signature is valid if and only if the algorithm returns 1
|
Appendix B. Schoof’s Algorithm
| Algorithm A4: Schoof’s Algorithm. |
 |
References
- Miller, V.S. Use of Elliptic Curves in Cryptography. In Advances in Cryptology—CRYPTO’85 Proceedings, Proceedings of the Conference on the Theory and Application of Cryptographic Techniques, Santa Barbara, CA, USA, 19–22 August 1984; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1986; Volume 218, pp. 417–426. [Google Scholar]
- Koblitz, N. Elliptic Curve Cryptosystems. Math. Comput. 1987, 48, 203–209. [Google Scholar] [CrossRef]
- Lenstra, H.W. Factoring Integers with Elliptic Curves. Ann. Math. 1987, 126, 649–673. [Google Scholar] [CrossRef]
- Rivest, R.L.; Shamir, A.; Adleman, L.M. A Method for Obtaining Digital Signatures and Public-Key Cryptosystems. Commun. ACM 1978, 21, 120–126. [Google Scholar] [CrossRef]
- Kerry, C.F.; Romine, C. FIPS PUB 186-4 Federal Information Processing Standards Publication Digital Signature Standard (DSS). 2013. Available online: https://nvlpubs.nist.gov/nistpubs/FIPS/NIST.FIPS.186-4.pdf (accessed on 24 September 2022).
- Güneysu, T.; Paar, C. Ultra High Performance ECC over NIST Primes on Commercial FPGAs. In Cryptographic Hardware and Embedded Systems—CHES’08, Proceedings of the 10th International Workshop, Washington, DC, USA, 10–13 August 2008; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2008; Volume 5154, pp. 62–78. [Google Scholar]
- Gövem, B.; Järvinen, K.; Aerts, K.; Verbauwhede, I.; Mentens, N. A Fast and Compact FPGA Implementation of Elliptic Curve Cryptography Using Lambda Coordinates. In Progress in Cryptology—AFRICACRYPT 2016, Proceedings of the 8th International Conference on Cryptology in Africa, Fes, Morocco, 13–15 April 2016; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2016; Volume 9646, pp. 63–83. [Google Scholar]
- Sghaier, A.; Zeghid, M.; Massoud, C.; Mahchout, M. Design And Implementation of Low Area/Power Elliptic Curve Digital Signature Hardware Core. Electronics 2017, 6, 46. [Google Scholar] [CrossRef]
- Tachibana, S.; Araki, S.; Kajihara, S.; Azuchi, S.; Nakajo, Y.; Shoda, H. FPGA implementation of ECDSA for Blockchain. In Proceedings of the 2019 IEEE International Conference on Consumer Electronics—Taiwan (ICCE-TW), Yilan, Taiwan, 20–22 May 2019; pp. 1–2. [Google Scholar]
- Javaid, H.; Yang, J.; Santoso, N.; Upadhyay, M.; Mohan, S.; Hu, C.; Brebner, G. Blockchain Machine: A Network-Attached Hardware Accelerator for Hyperledger Fabric. arXiv 2021, arXiv:2104.06968. [Google Scholar]
- Sau, S.; Baidya, P.; Paul, R.; Mandal, S. Binary Field Point Multiplication Implementation in FPGA Hardware. In Proceedings of the Intelligent and Cloud Computing, Kyoto, Japan, 17–19 December 2021; Springer: Singapore, 2021; pp. 387–394. [Google Scholar]
- Awaludin, A.M.; Larasati, H.T.; Kim, H. High-Speed and Unified ECC Processor for Generic Weierstrass Curves over GF(p) on FPGA. Sensors 2021, 21, 1451. [Google Scholar] [CrossRef] [PubMed]
- Agrawal, R.; Yang, J.; Javaid, H. Efficient FPGA-based ECDSA Verification Engine for Permissioned Blockchains. arXiv 2021, arXiv:2112.02229. [Google Scholar]
- Available online: https://www.xilinx.com/products/intellectual-property/1-175rk99.html (accessed on 24 September 2022).
- Available online: https://www.xilinx.com (accessed on 24 September 2022).
- Available online: https://www.xilinx.com/developer/adaptive-computing-challenge/contest-2021.html (accessed on 24 September 2022).
- Available online: https://www.hackster.io/contests/xilinxadaptivecomputing2021 (accessed on 24 September 2022).
- Poschmann, A. Lightweight Cryptography—Cryptographic Engineering for a Pervasive World. Ph.D. Thesis, Ruhr University, Bochum, Germany, 2009; pp. 1–174. [Google Scholar]
- Liu, Z.; Seo, H.; Großschädl, J.; Kim, H. Efficient Implementation of NIST-Compliant Elliptic Curve Cryptography for Sensor Nodes. In Proceedings of the ICICS’13, Beijing, China, 20–22 November 2013; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 2013; Volume 8233, pp. 302–317. [Google Scholar]
- Dhillon, P.K.; Kalra, S. Elliptic curve cryptography for real time embedded systems in IoT networks. In Proceedings of the 5th International Conference on Wireless Networks and Embedded Systems (WECON), Rajpura, India, 14–16 October 2016; pp. 1–6. [Google Scholar]
- Knežević, M.; Nikov, V.; Rombouts, P. Low-Latency ECDSA Signature Verification—A Road Toward Safer Traffic. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2016, 24, 3257–3267. [Google Scholar] [CrossRef]
- Liu, Z.; Huang, X.; Hu, Z.; Khan, M.K.; Seo, H.; Zhou, L. On Emerging Family of Elliptic Curves to Secure Internet of Things: ECC Comes of Age. IEEE Trans. Depend. Secur. Comput. 2017, 14, 237–248. [Google Scholar] [CrossRef]
- Ji, J.H.; Kima, H. ASIC implementation for an ECC processor. IDEC J. Integr. Circuits Syst. 2018, 4, 1–5. [Google Scholar]
- Kudithi, T.; Sakthivel, R. High-performance ECC processor architecture design for IoT security applications. J. Supercomput. 2018, 75, 447–474. [Google Scholar] [CrossRef]
- Hu, X.; Zheng, X.; Zhang, S.; Cai, S.; Xiong, X. A Low Hardware Consumption Elliptic Curve Cryptographic Architecture over GF(p) in Embedded Application. Electronics 2018, 7, 104. [Google Scholar] [CrossRef]
- Salarifard, R.; Bayat-Sarmadi, S. An Efficient Low-Latency Point-Multiplication Over Curve25519. IEEE Trans. Circuits Syst. I Regul. Pap. 2019, 66, 3854–3862. [Google Scholar] [CrossRef]
- Lara-Nino, C.A.; Diaz-Perez, A.; Morales-Sandoval, M. Lightweight elliptic curve cryptography accelerator for internet of things applications. Ad Hoc Netw. 2020, 103, 102159. [Google Scholar] [CrossRef]
- Park, D.; Chang, N.S.; Lee, S.; Hong, S. Fast Implementation of NIST P-256 Elliptic Curve Cryptography on 8-Bit AVR Processor. Appl. Sci. 2020, 10, 8816. [Google Scholar] [CrossRef]
- Di Matteo, S.; Baldanzi, L.; Crocetti, L.; Nannipieri, P.; Fanucci, L.; Saponara, S. Secure Elliptic Curve Crypto-Processor for Real-Time IoT Applications. Energies 2021, 14, 4676. [Google Scholar] [CrossRef]
- Simon Francia, A.; Solis-Lastra, J.; Papa Quiroz, E.A. Elliptic Curves Cryptography for Lightweight Devices in IoT Systems. In Proceedings of the Emerging Research in Intelligent Systems, Quito, Ecuador, 14–18 June 2021; Springer: Berlin/Heidelberg, Germany, 2021; pp. 71–82. [Google Scholar]
- Kieu-Do-Nguyen, B.; Pham-Quoc, C.; Tran, N.T.; Pham, C.K.; Hoang, T.T. Low-Cost Area-Efficient FPGA-Based Multi-Functional ECDSA/EdDSA. Cryptography 2022, 6, 25. [Google Scholar] [CrossRef]
- Géraud, R.; Maimuţ, D.; Naccache, D. Double-Speed Barrett Moduli. In New Codebreakers—Essays Dedicated to David Kahn on the Occasion of His 85th Birthday; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2016; Volume 9100, pp. 148–158. [Google Scholar]
- Barrett, P. Implementing the Rivest Shamir and Adleman Public Key Encryption Algorithm on a Standard Digital Signal Processor. In Proceedings of the CRYPTO’86, Santa Barbara, CA, USA, 11–15 August 1986; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 1987; Volume 263, pp. 311–323. [Google Scholar]
- Hoffstein, J.; Pipher, J.; Silverman, J. An Introduction to Mathematical Cryptography; Undergraduate Texts in Mathematics; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Schoof, R. Elliptic Curves Over Finite Fields and the Computation of Square Roots mod p. Math. Comput. 1985, 44, 483–494. [Google Scholar]
- Bernstein, D.J. Curve25519: New Diffie-Hellman Speed Records. In Proceedings of the PKC’06; Lecture Notes in Computer Science, New York, NY, USA, 24–26 April 2006; Springer: Berlin/Heidelberg, Germany, 2006; Volume 3958, pp. 207–228. [Google Scholar]
- Washington, L.C. Elliptic Curves: Number Theory and Cryptography, 2nd ed.; Chapman & Hall/CRC: Boca Raton, FL, USA, 2008. [Google Scholar]
- Katz, J.; Lindell, Y. Introduction to Modern Cryptography; Chapman and Hall/CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Available online: https://github.com/cryptocrew601/schoof (accessed on 24 September 2022).
- Available online: https://github.com/starkbank/ecdsa-python (accessed on 24 September 2022).
- Dewaghe, L. Remarks on the Schoof-Elkies-Atkin Algorithm. Math. Comput. 1998, 67, 1247–1252. [Google Scholar] [CrossRef][Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).