A Super-Twisting Extended State Observer for Nonlinear Systems
Abstract
1. Introduction
2. Problem Formulation
3. Main Results
3.1. Stability Analysis of STESO
3.2. Closed-Loop Stability Analysis of STESO-Based Controller
4. Simulation Analysis
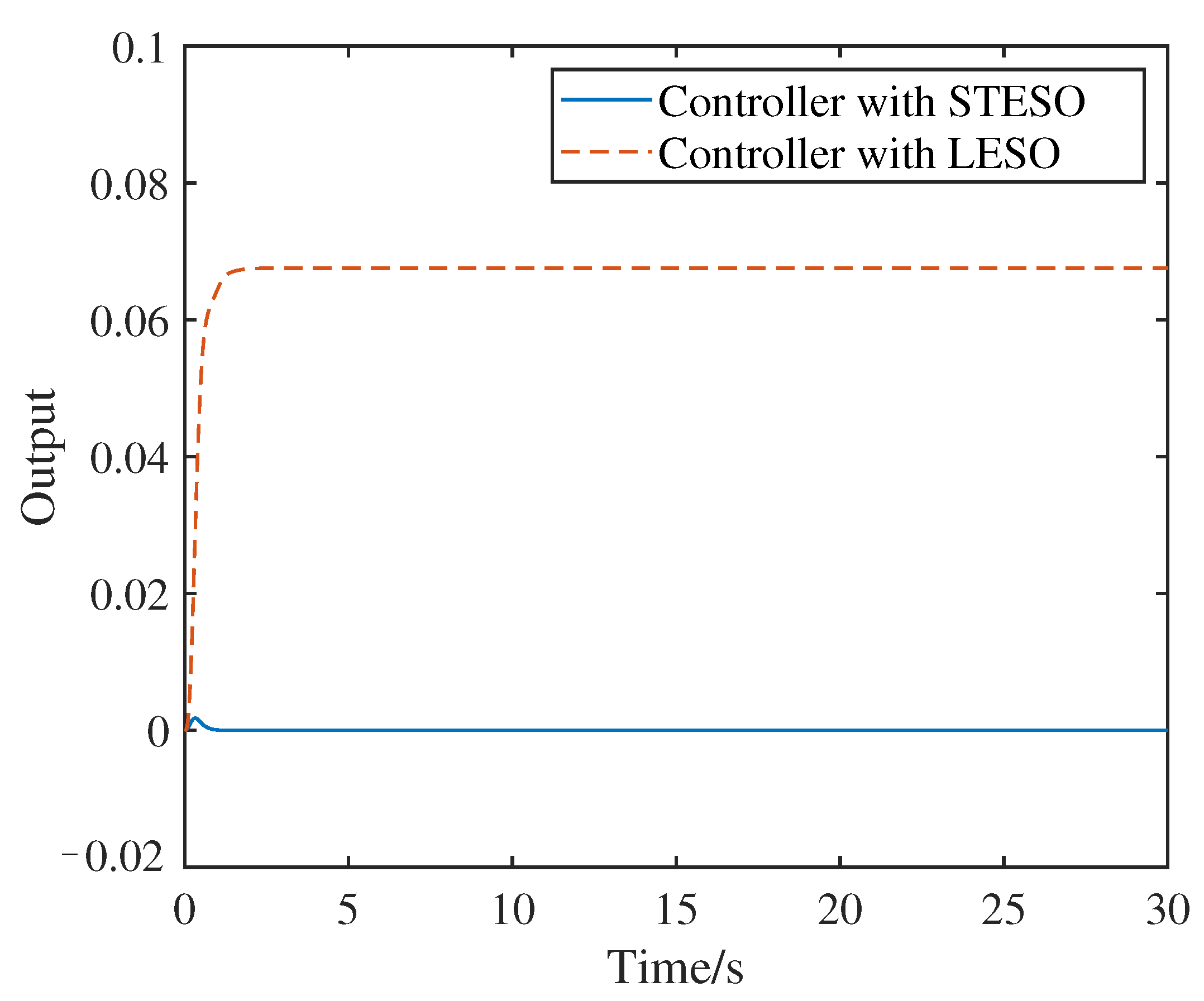
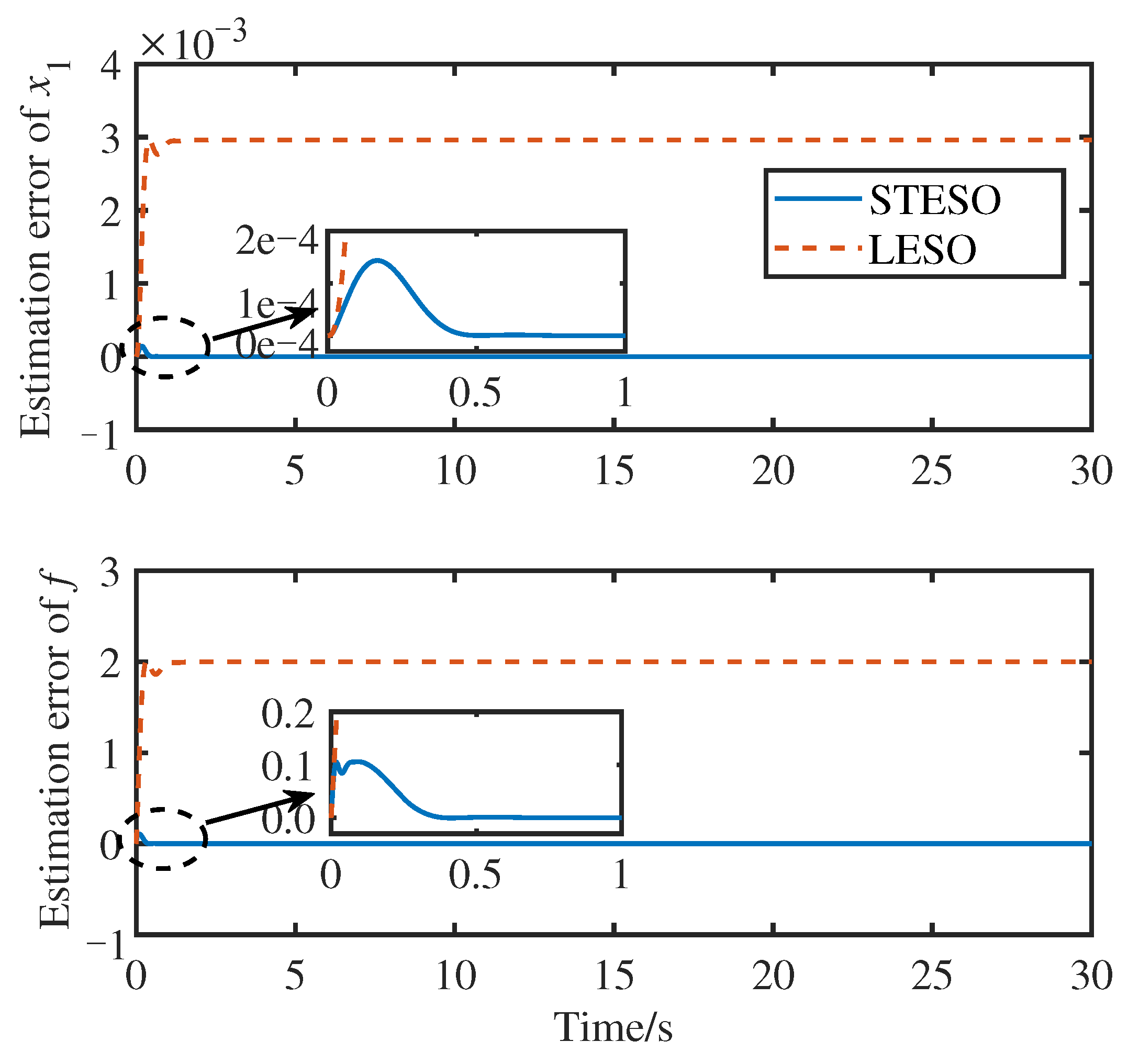
4.1. Ramp Disturbance
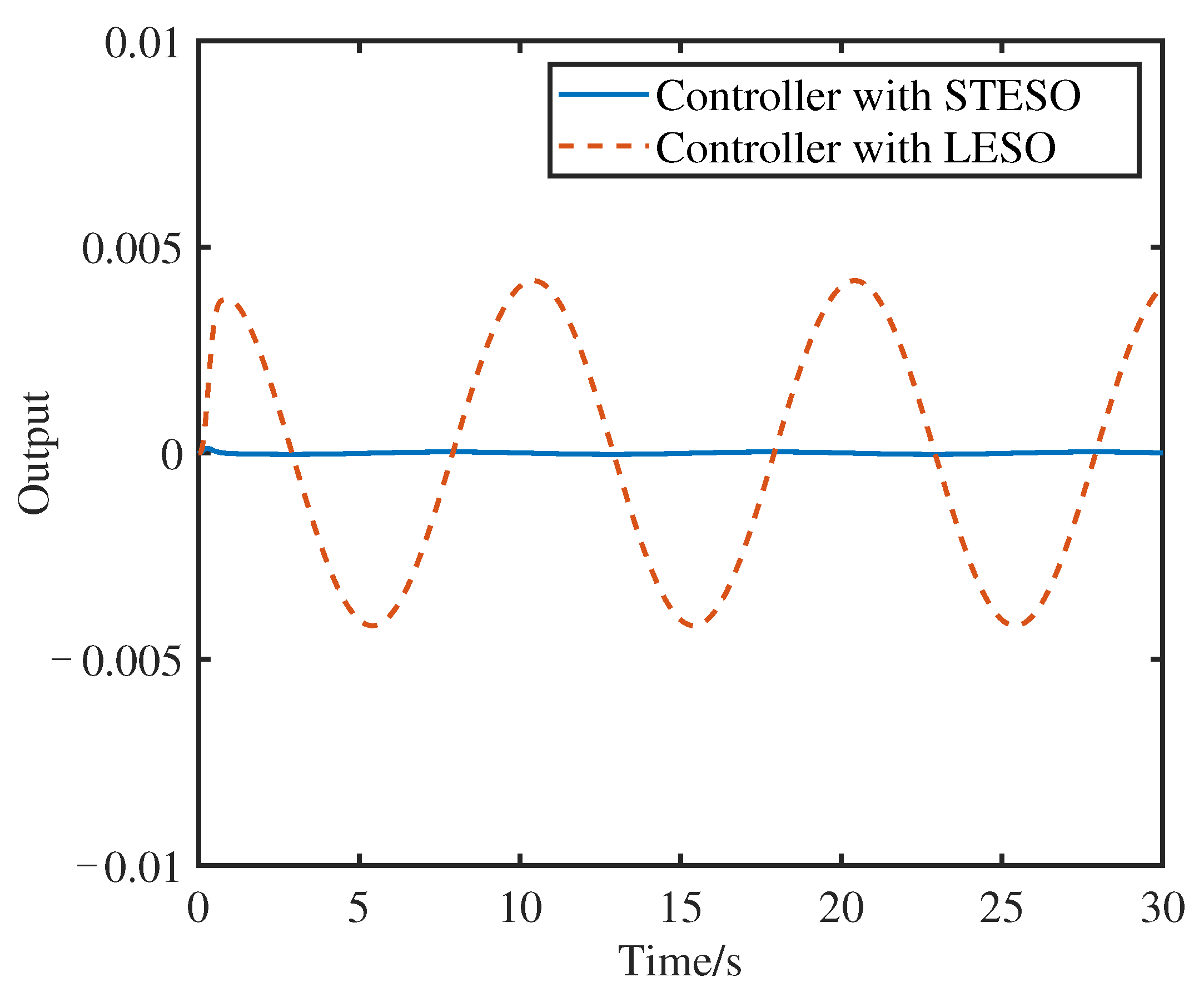
4.2. Sinusoidal Disturbance
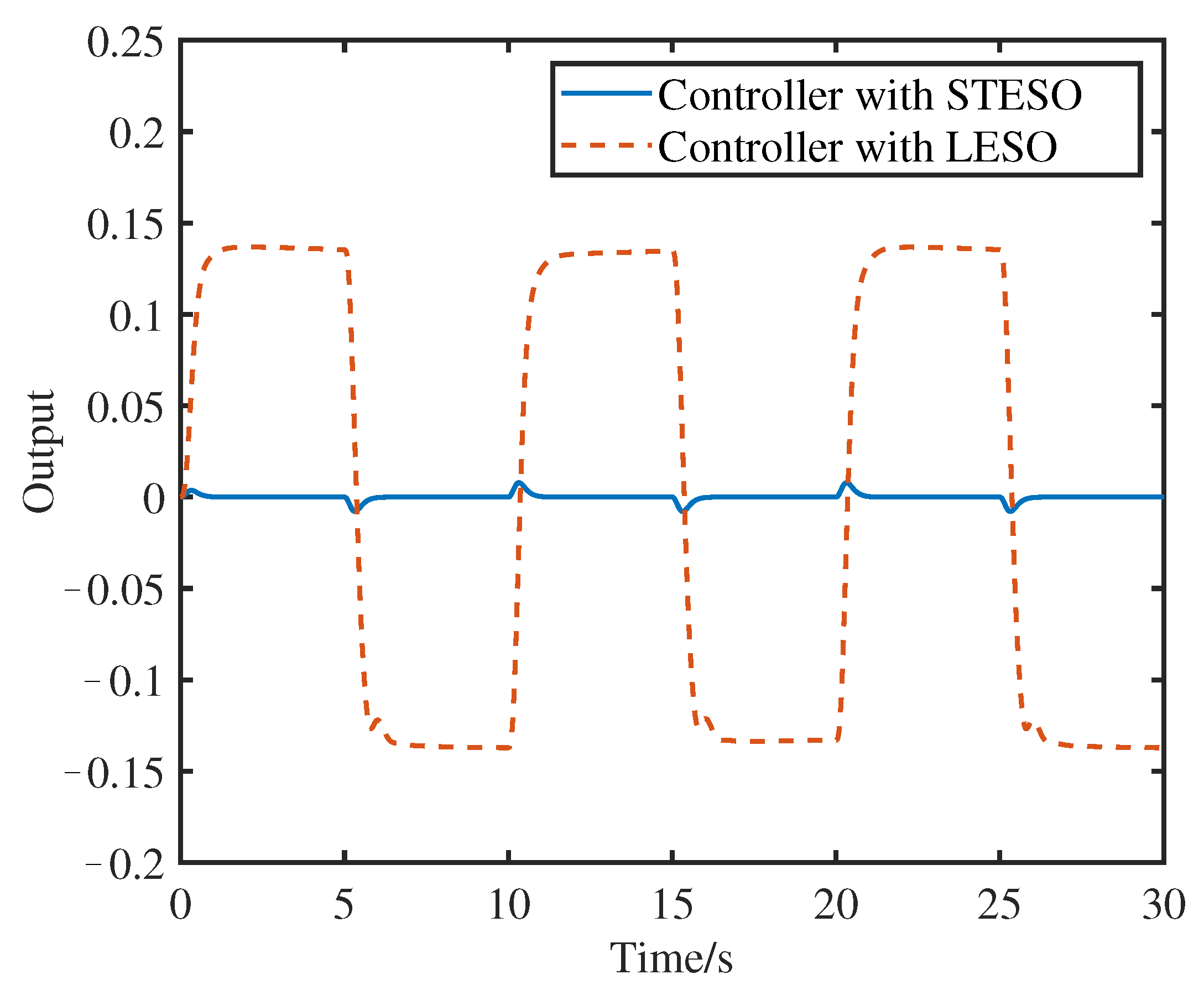
4.3. Robustness Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Xie, L.; Guo, L. How much uncertainty can be dealt with by feedback? IEEE Trans. Autom. Control 2000, 45, 2203–2217. [Google Scholar]
- Gao, Z. On the centrality of disturbance rejection in automatic control. ISA Trans. 2014, 53, 850–857. [Google Scholar] [CrossRef]
- Chen, W.; Yang, J.; Guo, L.; Li, S. Disturbance-Observer-Based Control and Related Methods—An Overview. IEEE Trans. Ind. Electron. 2016, 63, 1083–1095. [Google Scholar] [CrossRef]
- Han, J. From PID to Active Disturbance Rejection Control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Gao, Z. Scaling and bandwidth parameterization based controller tuning. In Proceedings of the American Control Conference, Denver, CO, USA, 4–6 June 2003; pp. 4989–4996. [Google Scholar]
- Guo, B.; Zhao, Z. On the convergence of an extended state observer for nonlinear systems with uncertainty. Syst. Control. Lett. 2011, 60, 420–430. [Google Scholar] [CrossRef]
- Xue, W.; Huang, Y. Performance analysis of active disturbance rejection tracking control for a class of uncertain LTI systems. ISA Trans. 2015, 50, 133–154. [Google Scholar] [CrossRef]
- Zhou, R.; Tan, W. Analysis and Tuning of General Linear Active Disturbance Rejection Controllers. IEEE Trans. Ind. Electron. 2019, 66, 5497–5507. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, Z.; Sun, M. Trajectory tracking control for a quadrotor unmanned aerial vehicle based on dynamic surface active disturbance rejection control. Trans. Inst. Meas. Control 2020, 42, 2198–2205. [Google Scholar] [CrossRef]
- Ran, M.; Wang, Q.; Dong, C. Active disturbance rejection consensus control of uncertain high-order nonlinear multi-agent systems. Trans. Inst. Meas. Control 2016, 42, 604–617. [Google Scholar] [CrossRef]
- Sun, L.; Zhang, Y.; Li, D.; Lee, K. Tuning of Active Disturdance Rejection Control with application to power plant furnace regulation. Control Eng. Pract. 2019, 92, 104122.1–104122.10. [Google Scholar] [CrossRef]
- Xie, H.; Li, S.; Song, K.; He, G. Model-based Decoupling Control of VGT and EGR with Active Disturbance Rejection in Diesel Engines. IFAC Proc. Vol. 2013, 46, 282–288. [Google Scholar] [CrossRef]
- Qiu, D.; Sun, M.; Wang, Z.; Wang, Y.; Chen, Z. Practical Wind-Disturbance Rejection for Large Deep Space Observatory Antenna. IEEE Trans. Control Syst. Technol. 2014, 22, 1983–1990. [Google Scholar] [CrossRef]
- Yoo, D.; Yau, S.S.; Gao, Z. On convergence of the linear extended state observer. In Proceedings of the 2006 IEEE Conference on Computer Aided Control System Design, 2006 IEEE International Conference on Control Applications, 2006 IEEE International Symposium on Intelligent Control, Munich, Germany, 4–6 October 2006; pp. 1645–1650. [Google Scholar]
- Yoo, D.; Yau, S.; Gao, Z. Optimal fast tracking observer bandwidth of the linear extended state observer. Int. J. Control 2007, 80, 102–111. [Google Scholar] [CrossRef]
- Yang, X.; Huang, Y. Capabilities of extended state observer for estimating uncertainties. In Proceedings of the American Control Conference, St. Louis, MO, USA, 10–12 June 2009; pp. 3700–3705. [Google Scholar]
- Zheng, Q.; Gao, L.; Gao, Z. On stability analysis of active disturbance rejection control for nonlinear time-varying plants with unknown dynamics. In Proceedings of the 2007 46th IEEE Conference on Decision and Control, New Orleans, LA, USA, 12–14 December 2007; pp. 3501–3506. [Google Scholar]
- Zheng, Q.; Gao, Z. Active disturbance rejection control: Between the formulation in time and the understanding in frequency. Control Theory Technol. 2016, 14, 250–259. [Google Scholar] [CrossRef]
- Shao, S.; Gao, Z. On the conditions of exponential stability in active disturbance rejection control based on singular perturbation analysis. Int. J. Control 2017, 98, 2085–2097. [Google Scholar] [CrossRef]
- Ran, M.; Wang, Q.; Dong, C. Stabilization of a class of nonlinear systems with actuator saturation via active disturbance rejection control. Automatica 2016, 63, 302–310. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, Y.; Sun, M.; Sun, Q. Convergence and stability analysis of active disturbance rejection control for first-order nonlinear dynamic systems. Trans. Inst. Meas. Control 2019, 41, 2064–2076. [Google Scholar] [CrossRef]
- Shtessel, Y.; Fridman, L.; Zinober, A. Higher order sliding modes. Int. J. Robust Nonlinear Control 2008, 18, 381–384. [Google Scholar] [CrossRef]
- Levant, A. Sliding Order and Sliding Accuracy in Sliding Mode Control. Int. J. Control 1993, 58, 1247–1263. [Google Scholar] [CrossRef]
- Defoort, M.; Nollet, F.; Floquet, T.; Perruquetti, W. A Third-Order Sliding-Mode Controller for a Stepper Motor. IEEE Trans. Ind. Electron. 2009, 56, 3337–3346. [Google Scholar] [CrossRef]
- Haghighi, D.; Mobayen, S. Design of an adaptive super-twisting decoupled terminal sliding mode control scheme for a class of fourth-order systems. ISA Trans. 2011, 75, 216–225. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Sun, M.; Chen, Z.; Sun, Q. Super-twisting sliding mode control for aircraft at high angle of attack based on finite-time extended state observer. Int. J. Control 2020, 99, 2785–2799. [Google Scholar] [CrossRef]
- Salgado, I.; Chairez, I.; Moreno, J.; Fridman, L.; Poznyak, A. Generalized Super-Twisting Observer for Nonlinear Systems. IFAC Proc. Vol. 2011, 44, 14353–14358. [Google Scholar] [CrossRef]
- Zong, Q.; Dong, Q.; Wang, F.; Tian, B. Super twisting sliding mode control for a flexible air-breathing hypersonic vehicle based on disturbance observer. Sci. China Ser. F Inf. Sci. 2015, 58, 1–15. [Google Scholar] [CrossRef]
- Chalanga, A.; Kamal, S.; Fridman, L.; Bandyopadhyay, B.; Moreno, J. Implementation of Super-Twisting Control: Super-Twisting and Higher Order Sliding-Mode Observer-Based Approaches. IEEE Trans. Ind. Electron. 2016, 63, 3677–3685. [Google Scholar] [CrossRef]
- Bhat, S.; Bernstein, D. Finite-time stability of continuous autonomous systems. SIAM J. Control Optim. 2000, 38, 751–766. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Tan, P.; Liu, J.; Chen, Z. A Super-Twisting Extended State Observer for Nonlinear Systems. Mathematics 2022, 10, 3584. https://doi.org/10.3390/math10193584
Li Y, Tan P, Liu J, Chen Z. A Super-Twisting Extended State Observer for Nonlinear Systems. Mathematics. 2022; 10(19):3584. https://doi.org/10.3390/math10193584
Chicago/Turabian StyleLi, Yi, Panlong Tan, Junjie Liu, and Zengqiang Chen. 2022. "A Super-Twisting Extended State Observer for Nonlinear Systems" Mathematics 10, no. 19: 3584. https://doi.org/10.3390/math10193584
APA StyleLi, Y., Tan, P., Liu, J., & Chen, Z. (2022). A Super-Twisting Extended State Observer for Nonlinear Systems. Mathematics, 10(19), 3584. https://doi.org/10.3390/math10193584





