Deriving Fuzzy Weights from the Consistent Fuzzy Analytic Hierarchy Process
Abstract
:1. Introduction
2. The Problem Description
3. Literature Review for the Consistent Issue of the FAHP
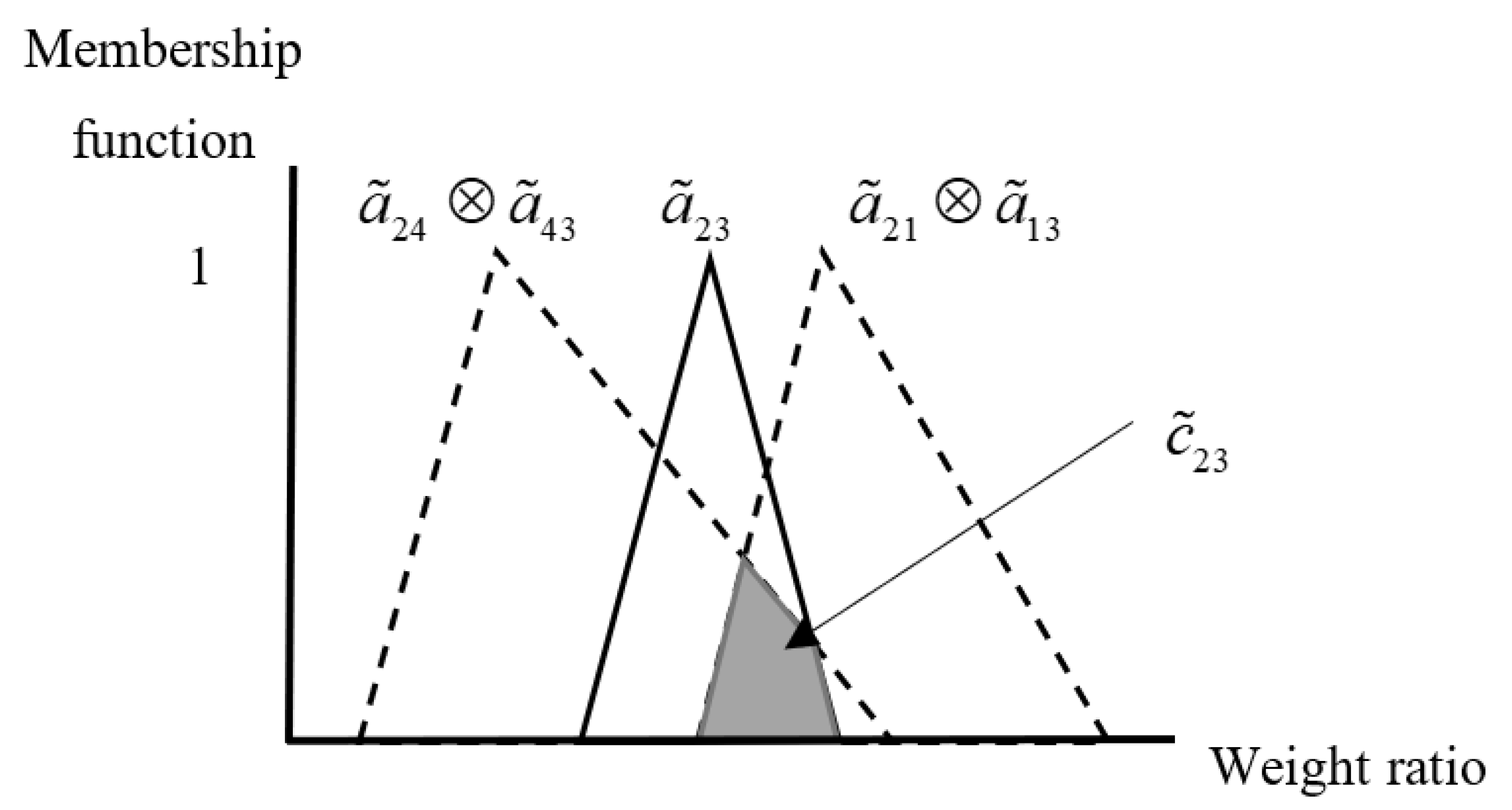
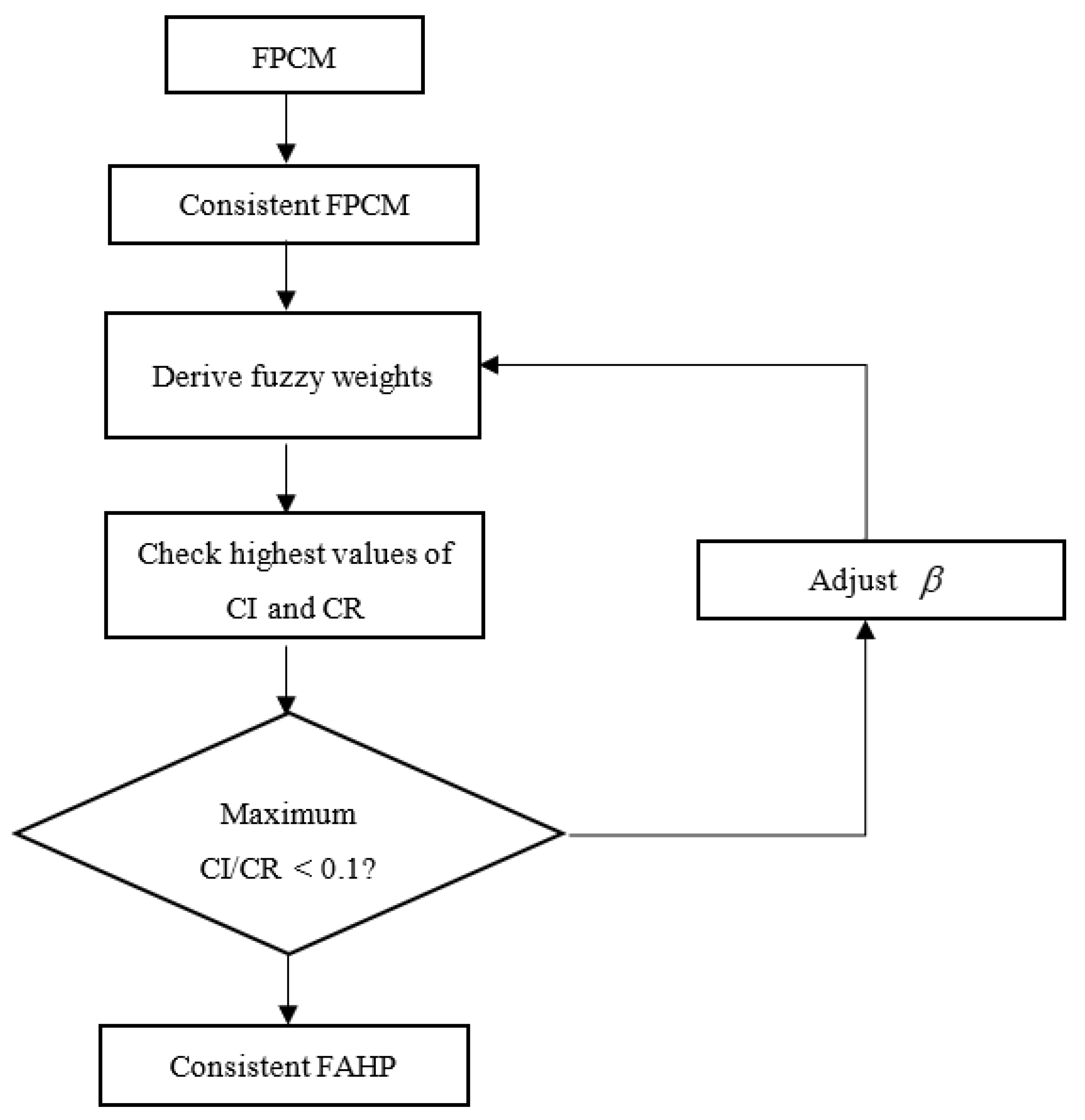
4. The Proposed Method
5. Numerical Example
6. Discussion
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Cui, D.; Zhang, X. Application of Gray Analytic Hierarchy Process in Project Risk Evaluation. In Proceedings of the 2009 International Conference on Artificial Intelligence and Computational Intelligence, Shanghai, China, 7–8 November 2009; Volume 4, pp. 592–594. [Google Scholar]
- Li, H.; Zhang, C.; Zhao, D. Stock Investment Value Analysis Model Based on AHP and Gray Relational Degree. Manag. Sci. Eng. 2011, 4, 1–6. [Google Scholar] [CrossRef]
- Liu, Y.-L.; Wang, X.-L. The Risk Evaluation of Construction Programme Based on Gray-AHP Method. In Proceedings of the 2009 International Workshop on Intelligent Systems and Applications, Wuhan, China, 23–24 May 2009; pp. 1–4. [Google Scholar]
- Guo, X.; Kapucu, N. Assessing social vulnerability to earthquake disaster using rough analytic hierarchy process method: A case study of Hanzhong City, China. Saf. Sci. 2020, 125, 104625. [Google Scholar] [CrossRef]
- Liu, Z.; Ma, R.; Wang, H. Assessing urban resilience to public health disaster using the rough analytic hierarchy process method: A regional study in China. J. Saf. Sci. Resil. 2022, 3, 93–104. [Google Scholar] [CrossRef]
- Meshram, S.G.; Singh, V.P.; Kahya, E.; Sepehri, M.; Meshram, C.; Hasan, M.A.; Islam, S.; Duc, P.A. Assessing erosion prone areas in a watershed using interval rough-analytical hierarchy process (IR-AHP) and fuzzy logic (FL). Stoch. Environ. Res. Risk Assess. 2022, 36, 297–312. [Google Scholar] [CrossRef]
- Mikhailov, L.; Tsvetinov, P. Evaluation of services using a fuzzy analytic hierarchy process. Appl. Soft Comput. 2004, 5, 23–33. [Google Scholar] [CrossRef]
- Emrouznejad, A.; Ho, W. Fuzzy Analytic Hierarchy Process; CRC Press: Boca Raton, FL, USA, 2017; ISBN 978-1-4987-3248-2. [Google Scholar]
- Xu, Z.; Liao, H. Intuitionistic Fuzzy Analytic Hierarchy Process. IEEE Trans. Fuzzy Syst. 2014, 22, 749–761. [Google Scholar] [CrossRef]
- Saaty, T.L. There is no mathematical validity for using fuzzy number crunching in the analytic hierarchy process. J. Syst. Sci. Syst. Eng. 2006, 15, 457–464. [Google Scholar] [CrossRef]
- Saaty, T.L.; Tran, L.T. On the invalidity of fuzzifying numerical judgments in the Analytic Hierarchy Process. Math. Comput. Model. 2007, 46, 962–975. [Google Scholar] [CrossRef]
- Wang, Y.-M.; Luo, Y.; Hua, Z. On the extent analysis method for fuzzy AHP and its applications. Eur. J. Oper. Res. 2008, 186, 735–747. [Google Scholar] [CrossRef]
- Naveed, Q.N.; Qureshi, M.R.N.; Alsayed, A.O.; Muhammad, A.; Sanober, S.; Shah, A. Prioritizing barriers of E-Learning for effective teaching-learning using fuzzy analytic hierarchy process (FAHP). In Proceedings of the 2017 4th IEEE International Conference on Engineering Technologies and Applied Sciences (ICETAS), Salmabad, Bahrain, 29 November–1 December 2017; pp. 1–8. [Google Scholar]
- Çebi, A.; Karal, H. An Application of Fuzzy Analytic Hierarchy Process (FAHP) for Evaluating Students’ Project. Educ. Res. Rev. 2017, 12, 120–132. [Google Scholar]
- Nagpal, R.; Mehrotra, D.; Bhatia, P.K.; Bhatia, A. FAHP Approach to Rank Educational Websites on Usability. Int. J. Comput. Digit. Syst. 2015, 4, 251–260. [Google Scholar] [CrossRef]
- Chirra, S.; Kumar, D. Analysis of supply chain issues under sales promotional schemes using FAHP. Int. J. Logist. Syst. Manag. 2018, 31, 224–248. [Google Scholar] [CrossRef]
- Jianwei, Z.; Minjie, Z.; Liwei, Z. Risk Evaluation of the Logistics Ecological Environment System Based on FAHP. Procedia Eng. 2011, 15, 381–385. [Google Scholar] [CrossRef]
- Lyu, H.-M.; Sun, W.-J.; Shen, S.-L.; Zhou, A.-N. Risk Assessment Using a New Consulting Process in Fuzzy AHP. J. Constr. Eng. Manag. 2020, 146, 04019112. [Google Scholar] [CrossRef]
- Mosadeghi, R.; Warnken, J.; Tomlinson, R.; Mirfenderesk, H. Comparison of Fuzzy-AHP and AHP in a spatial multi-criteria decision making model for urban land-use planning. Comput. Environ. Urban Syst. 2015, 49, 54–65. [Google Scholar] [CrossRef]
- Krejčí, J.; Pavlačka, O.; Talašová, J. A fuzzy extension of Analytic Hierarchy Process based on the constrained fuzzy arithmetic. Fuzzy Optim. Decis. Mak. 2017, 16, 89–110. [Google Scholar] [CrossRef]
- Salo, A.A. On fuzzy ratio comparisons in hierarchical decision models. Fuzzy Sets Syst. 1996, 84, 21–32. [Google Scholar] [CrossRef]
- Leung, L.C.; Cao, D. On consistency and ranking of alternatives in fuzzy AHP. Eur. J. Oper. Res. 2000, 124, 102–113. [Google Scholar] [CrossRef]
- Ohnishi, S.; Dubois, D.; Prade, H.; Yamanoi, T. A Fuzzy Constraint-Based Approach to the Analytic Hierarchy Process. In Uncertainty and Intelligent information Systems; WORLD SCIENTIFIC: Singapore, 2008; pp. 217–227. ISBN 978-981-279-234-1. [Google Scholar]
- Saaty, T.L. The Analytic Hierarchy Process; Mcgraw Hill: New York, NY, USA, 1980; Volume 70. [Google Scholar]
- Huang, J.-J. Consistent Fuzzy Analytic Hierarchy Process by Considering Fuzzy Input and Output Data. In Proceedings of the 2016 Joint 8th International Conference on Soft Computing and Intelligent Systems (SCIS) and 17th International Symposium on Advanced Intelligent Systems (ISIS), Sapporo, Japan, 25–28 August 2016; pp. 564–569. [Google Scholar]
- Saaty, T.L.; Vargas, L.G. Comparison of eigenvalue, logarithmic least squares and least squares methods in estimating ratios. Math. Model. 1984, 5, 309–324. [Google Scholar] [CrossRef]
- Tone, K. Two Technical Notes on the AHP Based on Geometric Mean Method. Proc. ISAHP 1996, 96, 375–381. [Google Scholar]
- Crawford, G.; Williams, C. A note on the analysis of subjective judgment matrices. J. Math. Psychol. 1985, 29, 387–405. [Google Scholar] [CrossRef]
- Aguarón, J.; Moreno-Jiménez, J.M. The geometric consistency index: Approximated thresholds. Eur. J. Oper. Res. 2003, 147, 137–145. [Google Scholar] [CrossRef]
- Stein, W.E.; Mizzi, P.J. The harmonic consistency index for the analytic hierarchy process. Eur. J. Oper. Res. 2007, 177, 488–497. [Google Scholar] [CrossRef]
- Alonso, J.A.; Lamata, M.T. Consistency in the analytic hierarchy process: A new approach. Int. J. Uncertain. Fuzziness Knowl.-Based Syst. 2006, 14, 445–459. [Google Scholar] [CrossRef]
- Aguarón, J.; Escobar, M.T.; Moreno-Jiménez, J.M.; Turón, A. The Triads Geometric Consistency Index in AHP-Pairwise Comparison Matrices. Mathematics 2020, 8, 926. [Google Scholar] [CrossRef]
- Csutora, R.; Buckley, J.J. Fuzzy hierarchical analysis: The Lambda-Max method. Fuzzy Sets Syst. 2001, 120, 181–195. [Google Scholar] [CrossRef]
- Xia, M.; Chen, J. Studies on Interval Multiplicative Preference Relations and Their Application to Group Decision Making. Group Decis. Negot. 2015, 24, 115–144. [Google Scholar] [CrossRef]
- Gogus, O.; Boucher, T.O. Strong transitivity, rationality and weak monotonicity in fuzzy pairwise comparisons. Fuzzy Sets Syst. 1998, 94, 133–144. [Google Scholar] [CrossRef]
- Wang, Z.-J. A note on “A goal programming model for incomplete interval multiplicative preference relations and its application in group decision-making”. Eur. J. Oper. Res. 2015, 247, 867–871. [Google Scholar] [CrossRef]
- Kubler, S.; Derigent, W.; Voisin, A.; Robert, J.; Le Traon, Y.; Viedma, E.H. Measuring inconsistency and deriving priorities from fuzzy pairwise comparison matrices using the knowledge-based consistency index. Knowl.-Based Syst. 2018, 162, 147–160. [Google Scholar] [CrossRef]
- Wang, Y.-M.; Chin, K.-S. An eigenvector method for generating normalized interval and fuzzy weights. Appl. Math. Comput. 2006, 181, 1257–1275. [Google Scholar] [CrossRef]
- van Laarhoven, P.J.M.; Pedrycz, W. A fuzzy extension of Saaty’s priority theory. Fuzzy Sets Syst. 1983, 11, 229–241. [Google Scholar] [CrossRef]
- Ahmed, F.; Kilic, K. Fuzzy Analytic Hierarchy Process: A performance analysis of various algorithms. Fuzzy Sets Syst. 2019, 362, 110–128. [Google Scholar] [CrossRef]
- Buckley, J.J. Fuzzy hierarchical analysis. Fuzzy Sets Syst. 1985, 17, 233–247. [Google Scholar] [CrossRef]
- Helmy, S.E.; Eladl, G.H.; Eisa, M. Fuzzy analytical hierarchy process (FAHP) using geometric mean method to select best processing framework adequate to bit data. J. Theor. Appl. Inf. Technol. 2021, 9, 207–226. [Google Scholar]
- Ju, Y.; Wang, A.; Liu, X. Evaluating emergency response capacity by fuzzy AHP and 2-tuple fuzzy linguistic approach. Expert Syst. Appl. 2012, 39, 6972–6981. [Google Scholar] [CrossRef]
- Wang, T.; Chen, Y. Some Issues on Consistency of Fuzzy Analytic Hierarchy Process. In Proceedings of the 2006 International Conference on Machine Learning and Cybernetics, Dalian, China, 13–16 August 2006; pp. 1818–1822. [Google Scholar]
| C1 | C2 | C3 | |
|---|---|---|---|
| Weights | 0.6833 | 0.1998 | 0.1169 |
| CI | 0.0123 | ||
| CR | 0.0212 | ||
| C1 | C2 | C3 | |
|---|---|---|---|
| Weights | [0.614, 0.6833, 0.732] | [0.138, 0.1998, 0.268] | [0.088, 0.1169, 0.174] |
| CI | [0.000, 0.098] | ||
| CR | [0.000, 0.170] | ||
| C1 | C2 | C3 | Max CI | Max CR | |
|---|---|---|---|---|---|
| The Proposed | [0.632, 0.686] | [0.143, 0.222] | [0.111, 0.167] | 0.000 | 0.000 |
| Without transitivity | [0.614, 0.732] | [0.138, 0.268] | [0.088, 0.174] | 0.098 | 0.170 |
| Weights | C1 | C2 | C3 | C4 |
|---|---|---|---|---|
| The proposed (β = 0) | [0.2727, 0.4167] | [0.1428, 0.2353] | [0.1579, 0.2727] | [0.2000, 0.3333] |
| Max CI | 0.00 | Max CR | 0.00 | |
| The proposed (β = 0.02) | [0.2548, 0.4167] | [0.1389, 0.2476] | [0.1532, 0.2818] | [0.1993, 0.3521] |
| Max CI | 0.0356 | Max CR | 0.0396 | |
| The proposed (β = 0.04) | [0.2482, 0.4167] | [0.1373, 0.2524] | [0.1512, 0.2852] | [0.1989, 0.3594] |
| Max CI | 0.0485 | Max CR | 0.0538 | |
| The proposed (β = 0.06) | [0.2433, 0.4167] | [0.1361, 0.2559] | [0.1497, 0.2877] | [0.1986, 0.3648] |
| Max CI | 0.0577 | Max CR | 0.0641 | |
| The proposed (β = 0.08) | [0.2393, 0.4167] | [0.1351, 0.2589] | [0.1483, 0.2898] | [0.1983, 0.3692] |
| Max CI | 0.0651 | Max CR | 0.0723 | |
| The proposed (β = 0.10) | [0.2359, 0.4167] | [0.1342, 0.2615] | [0.1471, 0.2915] | [0.1980, 0.3730] |
| Max CI | 0.0713 | Max CR | 0.0792 | |
| Without transitivity | [0.2470, 0.4247] | [0.1305, 0.3121] | [0.1154, 0.2915] | [0.1644, 0.3892] |
| Max CI | 0.1143 | Max CR | 0.1270 | |
| Gogus & Boucher [35] | [0.2727, 0.4167] | [0.1428, 0.2353] | [0.1579, 0.2727] | [0.2000, 0.3333] |
| Max CI | 0.00 | Max CR | 0.00 | |
| Wang [36] | [0.2727, 0.4167] | [0.1322, 0.2553] | [0.1333, 0.2727] | [0.2000, 0.3333] |
| Max CI | 0.0392 | Max CR | 0.0426 | |
| Kubler et al. [37] | 0.332 | 0.186 | 0.220 | 0.262 |
| Max CI | 0 | Max CR | 0 |
| Weights | C1 | C2 | C3 | Max CI | Max CR |
|---|---|---|---|---|---|
| The proposed (β = 0) | [0.1176, 0.1250] | [0.1765, 0.1875] | [0.1765, 0.1875] | 0.0000 | 0.0000 |
| C4 | C5 | C6 | |||
| [0.1765, 0.1875] | [0.1250, 0.1765] | [0.1765, 0.1875] | |||
| C1 | C2 | C3 | |||
| The proposed (β = 1) | [0.0898, 0.1356] | [0.1261, 0.2090] | [0.1231, 0.2319] | 0.0298 | 0.0241 |
| C4 | C5 | C6 | |||
| [0.1169, 0.2382] | [0.1035, 0.2380] | [0.1429, 0.2715] | |||
| C1 | C2 | C3 | |||
| Gogus & Boucher [35] | [0.1176, 0.1176] | [0.1765, 0.1765] | [0.1765, 0.1765] | 0.0000 | 0.0000 |
| C4 | C5 | C6 | |||
| [0.1765, 0.1765] | [0.1765, 0.1765] | [0.1765, 0.1765] | |||
| C1 | C2 | C3 | |||
| Wang [36] | [0.1176, 0.1176] | [0.1765, 0.1765] | [0.1765, 0.1765] | 0.0000 | 0.0000 |
| C4 | C5 | C6 | |||
| [0.1765, 0.1765] | [0.1765, 0.1765] | [0.1765, 0.1765] | |||
| C1 | C2 | C3 | |||
| Without transitivity | [0.084, 0.180] | [0.120, 0.228] | [0.107, 0.270] | 0.2350 | 0.1895 |
| C4 | C5 | C6 | |||
| [0.095, 0.291] | [0.101, 0.317] | [0.075, 0.294] | |||
| Wang & Chen [42] | C1 | C2 | C3 | ||
| [0.06, 0.21] | [0.09, 0.26] | [0.11, 0.31] | 0.4598 | 0.3708 | |
| C4 | C5 | C6 | |||
| [0.10, 0.37] | [0.08, 0.32] | [0.12, 0.35] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, C.-Y.; Huang, J.-J. Deriving Fuzzy Weights from the Consistent Fuzzy Analytic Hierarchy Process. Mathematics 2022, 10, 3499. https://doi.org/10.3390/math10193499
Chen C-Y, Huang J-J. Deriving Fuzzy Weights from the Consistent Fuzzy Analytic Hierarchy Process. Mathematics. 2022; 10(19):3499. https://doi.org/10.3390/math10193499
Chicago/Turabian StyleChen, Chin-Yi, and Jih-Jeng Huang. 2022. "Deriving Fuzzy Weights from the Consistent Fuzzy Analytic Hierarchy Process" Mathematics 10, no. 19: 3499. https://doi.org/10.3390/math10193499
APA StyleChen, C.-Y., & Huang, J.-J. (2022). Deriving Fuzzy Weights from the Consistent Fuzzy Analytic Hierarchy Process. Mathematics, 10(19), 3499. https://doi.org/10.3390/math10193499






