Splitting Methods for Semi-Classical Hamiltonian Dynamics of Charge Transfer in Nonlinear Lattices
Abstract
:1. Introduction
1.1. Coupling of Electric Charge and Lattice Vibrations
1.2. Intrinsic Localized Modes without Charge
1.3. Nonlinear Lattice Excitations Transporting Charge
1.4. Existing and Proposed Numerical Methods
1.5. Outline
2. Semi-Classical Hamiltonian Dynamics
2.1. The Lattice Hamiltonian
2.1.1. The On-Site Potential
2.1.2. The Interaction Potential
2.2. The Charge Hamiltonian
2.2.1. The Wave Function and the Charge Probability
2.2.2. The Evolution of the Wave Function: The Schrödinger Equation
2.2.3. The Local Charge Energy
2.2.4. The Charge Transition Matrix
2.2.5. Dynamical Equations for the Charge Probability Amplitude
2.3. The Coupled Hamiltonian
2.4. Rotational Invariance and Redefinition of the Charge Local-Energy Origin
2.5. Scaled Hamiltonian Equations
2.6. Canonical Hamiltonian Equations
2.6.1. Hamiltonian Equations in Real Form
2.6.2. Conservation Laws and Properties of the Semi-Classical Hamiltonian Dynamics
2.7. Model Example: Frenkel–Kontorova with Lennard–Jones Interaction Coupled to a Charge
2.7.1. Lattice Classical Hamiltonian for the Model Example
2.7.2. Coupling to an Electric Charge in the Model Example
2.7.3. Hamiltonian Equations for the Model Example
3. Analysis of the Linearized Equations
3.1. Linearization of Lattice Forces
3.2. The Lattice Dispersion Relation
3.3. The Charge Dispersion Relation
3.4. The Charge Equilibrium States
3.5. Semi-Coupled Lattice–Charge Dispersion Relation
4. Structure-Preserving Splitting Methods
4.1. Splitting of Lattice–Charge Dynamics
4.2. Semi-Implicit Methods with Exact Charge Probability Conservation
4.3. Explicit Splitting Methods
5. Numerical Results
5.1. Approximation Order and Convergence
5.2. Numerical Accuracy of Conserved Quantities
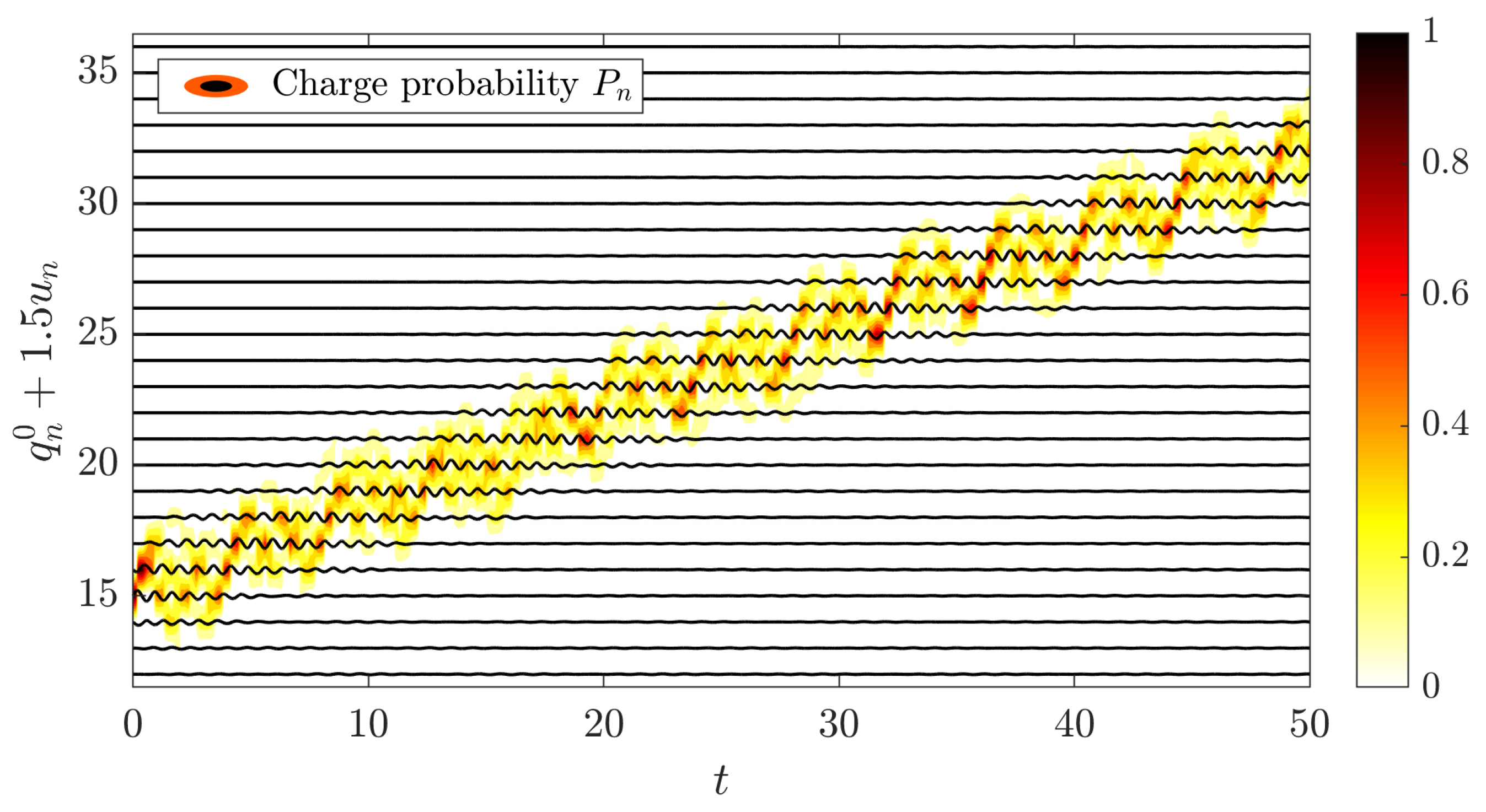
5.3. Charge Transfer by Mobile Discrete Breathers
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Exact Flow Maps
Appendix A.2. Semi-Implicit Numerical Methods
| , | |
| , | |
| , | |
| , | |
Appendix A.3. Explicit Numerical Methods
References
- Landau, L.D. Electron motion in crystal lattices. Phys. Z. Sowjetunion 1933, 3, 664. [Google Scholar]
- Pekar, S.I. Local quantum states of electrons in an ideal ion crystal. J. Phys. USSR 1946, 10, 341. (In German) [Google Scholar]
- Landau, L.D.; Pekar, S.I. Effective mass of a polaron. Zh. Eksp. Teor. Fiz. 1948, 18, 419–423, English translation: Ukr. J. Phys., Special Issue: 2008, 53, 71–74. [Google Scholar]
- Alexandrov, A.S. Polarons in Advanced Materials; Springer Series in Materials Science; Springer: Dordrecht, The Netherlands, 2007. [Google Scholar]
- Ashcroft, N.W.; Mermim, N.D. Solid State Physics, 1st ed.; Cengage Learning: Boston, MA, USA, 1976. [Google Scholar]
- Holstein, T. Studies of polaron motion: Part I. The molecular-crystal model. Ann. Phys. 1959, 8, 325–342. [Google Scholar] [CrossRef]
- Holstein, T. Studies of polaron motion: Part II. The “small” polaron. Ann. Phys. 1959, 8, 343–389. [Google Scholar] [CrossRef]
- Braun, O.M.; Kivshar, Y.S. Nonlinear dynamics of the Frenkel-Kontorova model. Phys. Rep. 1998, 1–2, 1–108. [Google Scholar] [CrossRef]
- Braun, O.M.; Kivshar, Y.S. The Frenkel-Kontorova Model; Springer: Berlin, Germany, 2004. [Google Scholar]
- Davydov, A.S. Solitons in Molecular Systems; Mathematics and Its Applications; Springer Dordrecht: Dordrecht, The Netherlands, 1985. [Google Scholar]
- Sievers, A.J.; Takeno, S. Intrinsic Localized Modes in Anharmonic Crystals. Phys. Rev. Lett. 1988, 61, 970–973. [Google Scholar] [CrossRef]
- Archilla, J.F.R.; Doi, Y.; Kimura, M. Pterobreathers in a model for a layered crystal with realistic potentials: Exact moving breathers in a moving frame. Phys. Rev. E 2019, 100, 022206. [Google Scholar] [CrossRef]
- Bajārs, J.; Archilla, J.F.R. Frequency-momentum representation of moving breathers in a two dimensional hexagonal lattice. Physica D 2022, 441, 133497. [Google Scholar] [CrossRef]
- Aubry, S. Breathers in nonlinear lattices: Existence, linear stability and quantization. Physica D 1997, 103, 201–250. [Google Scholar] [CrossRef]
- Kalosakas, G.; Aubry, S. Polarobreathers in a generalized Holstein model. Physica D 1998, 113, 228–232. [Google Scholar] [CrossRef]
- Cuevas, J.; Kevrekidis, P.G.; Frantzeskakis, D.J.; Bishop, A.R. Existence of bound states of a polaron with a breather in soft potentials. Phys. Rev. B 2006, 74, 064304. [Google Scholar] [CrossRef]
- Hennig, D. Electron-vibron-breather interaction. Phys. Rev. E 2000, 62, 2846–2857. [Google Scholar] [CrossRef] [PubMed]
- Velarde, M. From polaron to solectron: The addition of nonlinear elasticity to quantum mechanics and its possible effect upon electric transport. J. Comput. Appl. Math. 2010, 233, 1432–1445. [Google Scholar] [CrossRef]
- Ros, O.G.C.; Cruzeiro, L.; Velarde, M.G.; Ebeling, W. On the possibility of electric transport mediated by long living intrinsic localized solectron modes. Eur. Phys. J. B 2011, 80, 545–554. [Google Scholar]
- Cruzeiro-Hansson, L.; Eilbeck, J.C.; Marín, J.L.; Russell, F.M. Breathers in systems with intrinsic and extrinsic nonlinearities. Physica D 2000, 142, 101–112. [Google Scholar] [CrossRef]
- Archilla, J.F.R.; Jiménez, N.; Sánchez-Morcillo, V.J.; García-Raffi, L.M. (Eds.) Quodons in Mica: Nonlinear Localized Travelling Excitations in Crystals; Springer Series in Materials Science; Springer: Cham, Switzerland, 2015; Volume 221. [Google Scholar]
- De Moura, F. Numerical evidence of electron–soliton dynamics in Fermi–Pasta–Ulam disordered chains. Physica D 2013, 253, 66–72. [Google Scholar] [CrossRef]
- Archilla, J.F.R.; Zolotaryuk, Y.; Kosevich, Y.A.; Doi, Y. Nonlinear waves in a model for silicate layers. Chaos 2018, 28, 083119. [Google Scholar] [CrossRef]
- Archilla, J.F.R.; Russell, F.M. On the charge of quodons. Lett. Mater. 2016, 6, 3–8. [Google Scholar] [CrossRef]
- Russell, F.M.; Archilla, J.F.R.; Frutos, F.; Medina-Carrasco, S. Infinite charge mobility in muscovite at 300 K. EPL 2017, 120, 46001. [Google Scholar] [CrossRef]
- Russell, F.M.; Russell, A.W.; Archilla, J.F.R. Hyperconductivity in fluorphlogopite at 300 K and 1.1 T. EPL 2019, 127, 16001. [Google Scholar] [CrossRef]
- Russell, F.M.; Archilla, J.F.R. Ballistic charge transport by mobile nonlinear excitations. Phys. Status Solidi RRL 2022, 16, 2100420. [Google Scholar] [CrossRef]
- Russell, F.M.; Archilla, J.F.R.; Medina-Carrasco, S. Localized Waves in Silicates. What Do We Know from Experiments? In 13th Chaotic Modeling and Simulation International Conference; Skiadas, C., Dimotikalis, Y., Eds.; Springer: Berlin, Germany, 2021; pp. 721–734. [Google Scholar]
- MacKay, R.S.; Aubry, S. Proof of existence of breathers for time-reversible or Hamiltonian networks of weakly coupled oscillators. Nonlinearity 1994, 7, 1623–1643. [Google Scholar] [CrossRef]
- Aubry, S. Discrete Breathers: Localization and transfer of energy in discrete Hamiltonian nonlinear systems. Physica D 2006, 216, 1–30. [Google Scholar] [CrossRef]
- Flach, S.; Gorbach, A. Discrete breathers—Advances in theory and applications. Phys. Rep. 2008, 467, 1–116. [Google Scholar] [CrossRef]
- Marín, J.L.; Russell, F.M.; Eilbeck, J.C. Breathers in cuprate-like lattices. Phys. Lett. A 2001, 281, 21–25. [Google Scholar] [CrossRef]
- Dou, Q.; Cuevas, J.; Eilbeck, J.C.; Russell, F.M. Breathers and kinks in a simulated crystal experiment. Discrete Cont. Dyn. Ser. S 2011, 4, 1107–1118. [Google Scholar] [CrossRef]
- Bajārs, J.; Eilbeck, J.C.; Leimkuhler, B. Nonlinear propagating localized modes in a 2D hexagonal crystal lattice. Physica D 2015, 301-302, 8–20. [Google Scholar] [CrossRef]
- Bajārs, J.; Eilbeck, J.C.; Leimkuhler, B. Two-dimensional mobile breather scattering in a hexagonal crystal lattice. Phys. Rev. E 2021, 103, 022212. [Google Scholar] [CrossRef]
- Leimkuhler, B.; Matthews, C. Molecular Dynamics: With Deterministic and Stochastic Numerical Methods; Springer: Berlin, Germany, 2015. [Google Scholar]
- Hairer, E.; Lubich, C.; Wanner, G. Geometric Numerical Integration: Structure-Preserving Algorithms for Ordinary Differential Equations; Springer Science & Business Media: Berlin, Germany, 2006. [Google Scholar]
- Blanes, S.; Casas, F.; Murua, A. Splitting and composition methods in the numerical integration of differential equations. Boletin de la Sociedad Espanola de Matematica Aplicada 2008, 45, 89–145. [Google Scholar]
- Yoshida, H. Construction of higher order symplectic integrators. Phys. Lett. A 1990, 150, 262–268. [Google Scholar] [CrossRef]
- Suzuki, M. General theory of higher-order decomposition of exponential operators and symplectic integrators. Phys. Lett. A 1992, 165, 387–395. [Google Scholar] [CrossRef]
- Cohen-Tannoudji, C.; Diu, B.; Laloe, F. Quantum Mechanics, Vol. 1: Basic Concepts, Tools, and Applications, 2nd ed.; Wiley-VCH: Weinheim, Germany, 2019. [Google Scholar]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bajārs, J.; Archilla, J.F.R. Splitting Methods for Semi-Classical Hamiltonian Dynamics of Charge Transfer in Nonlinear Lattices. Mathematics 2022, 10, 3460. https://doi.org/10.3390/math10193460
Bajārs J, Archilla JFR. Splitting Methods for Semi-Classical Hamiltonian Dynamics of Charge Transfer in Nonlinear Lattices. Mathematics. 2022; 10(19):3460. https://doi.org/10.3390/math10193460
Chicago/Turabian StyleBajārs, Jānis, and Juan F. R. Archilla. 2022. "Splitting Methods for Semi-Classical Hamiltonian Dynamics of Charge Transfer in Nonlinear Lattices" Mathematics 10, no. 19: 3460. https://doi.org/10.3390/math10193460
APA StyleBajārs, J., & Archilla, J. F. R. (2022). Splitting Methods for Semi-Classical Hamiltonian Dynamics of Charge Transfer in Nonlinear Lattices. Mathematics, 10(19), 3460. https://doi.org/10.3390/math10193460








