Local H∞ Control for Continuous-Time T-S Fuzzy Systems via Generalized Non-Quadratic Lyapunov Functions

Abstract

This paper further develops a relaxed method to reduce conservatism in $H\infty$ feedback control for continuous-time T-S fuzzy systems via a generalized non-quadratic Lyapunov function. Different from the results of some exisiting works, the generalized $H\infty$ state feedback controller is designed. The relaxed stabilization conditions are obtained by applying Finsler’s lemma with the homogenous polynomial multipliers, and the $H\infty$ performance is acquired by solving an optimization problem. In addition, the proposed method could be expanded to handle other control problems for fuzzy systems. Two examples are given to show the validity of the proposed results.

1. Introduction

Owing to its better approximation properties, the Takagi–Sugeno (T-S) system [1] has attracted much attention from different communities. The system comprises a set of linear models and normalized membership functions (MFs).

The analysis and synthesis of fuzzy systems have been widely studied, such as stability analysis [2,3,4,5], observer design [6,7], filter [8,9,10], etc. Due to some limitations of the proposed methods in the existing results, researchers are seeking new methods to obtain better results, such as larger domain of attraction or stability region, and better $H\infty$ or $H_2$ performance. To reduce conservatism, many methods usually focus on the form of Lyapunov functions (LFs), the structure of slack variables and analysis of MFs and its derivatives.

Considering the drawbacks of common quadratic LFs, the complex LFs such as the fuzzy Lyapunov functions (FLFs) [11], the non-quadratic Lyapunov functions (NQLFs) [12], the line-integral FLFs [13], and homogeneous polynomial Lyapunov functions (HPLFs) [14], the homogeneous polynomial non-quadratic Lyapunov functions (HPNQLFs) [15] were proposed successively to further reduce the conservatism of stability conditions. For instance, Ref. [12] proposed new relaxed linear matrix inequality (LMI) conditions based on NQLFs. Ref. [14] first provided local asymptotic stability conditions and obtained different estimations of the attraction domain by using HPLFs. Ref. [15] gave the asymptotically necessary and sufficient stability conditions for discrete-time fuzzy systems via non-parallel distributed compensation law (NPDCL) with HPNQLFs. In addition, Ref. [12] designed an NPDCL to outperform previous results. By using the multi-indexed matrix approach, a homogeneous polynomial nonparallel distribution compensator (HPNQDC) was designed in [16], but the Lyapunov matrix used is linearly dependent on MFs. Ref. [17] further generalized previous HPNQDC and enlarged the stabilization region. Based on congruence transformation and Polya’s theorem, inner and outer slack variables were introduced in [18,19,20,21] to obtain a less conservative conclusion. Therefore, the design of a generalized control law for the local $H\infty$ performance of continuous-time T-S fuzzy system is worthy of investigation.

On the other hand, due to the general dependence of LFs on MFs, the time derivative of MFs (TDMFs) must be discussed in the proof process. Usually, there are several ways to deal with the TDMFs: (1) Assuming the upper or lower bounds of TDMF; (2) Finding LMI conditions to guarantee the upper bounds of TDMF hold; (3) Designing the line-integral FLFs; (4) Using a switching idea for the TDMFs. By exploring the upper bounds and properties of TDMFs, Ref. [22] proposed relaxed stability conditions. Considering the lower bounds of TDMF, Ref. [3] provided sufficient conditions to minimize the peak-to-peak level performance of the T-S fuzzy model. However, they overlooked the fact that the TDMFs involved $\dot{x}$ including the control law to be solved, which might be difficult to support in practice. Refs. [23,24,25] proposed the LMI conditions that guaranteed that the boundary of TDMF hold, but ignored disturbance. The line-integral FLFs designed in [13] could abstain from TDMFs, but the Lyapnov matrix structure had to be limited, which might bring about conservatism. Ref. [26] proposed a switching idea by discussing the property of TDMFs, while designing robust methods to commendably incorporate the boundary information of MFs is complex. Therefore, effective methods to manage the TDMFs remain to be explored.

From the above discussions, this paper considers the design of a generalized control law for local $H\infty$ control of continuous-time T-S fuzzy systems to further reduce the conservatism of existing results. The contributions of this paper are as follows:

(1)

The generalized NQLFs and NPCL depending on multi-index MFs are designed, including that found in [27] and double-fuzzy-summation in [20] as a special case, and more variables are introduced to reduce the conservatism.

(2)

The new LMIs conditions, which reduce the adjusted parameters to be calculated [7] and avoid redundant restrictions such as LFs matrices, slack variables in [23,28], are obtained to bound the time derivatives of MFs with disturbance.

(3)

The extended stabilization conditions for $H\infty$ performance are obtained by polynomial technology. As q increases, conservatism of obtained conditions will reduce, and the proposed method can be generalized to handle other cases, such as output feedback controller design [5], finite-time annular domain stability [29], mean-square strong stability [30].

2. Problem Statement and Preliminaries

2.1. The T-S Fuzzy System

The T-S fuzzy system (1) in ${\mathbb{C}}_x$ (${\mathbb{C}}_x=\{x:|x_i|\le {\theta }_{xi},i=1,2,\cdots ,n\}$) can be obtained by applying the local approximation method.

$$\begin{array}{ccc}\hfill \dot{x}\left(t\right)& =& \sum _{i=1}^r{h}_i\left(x\left(t\right)\right)(A_{i}x\left(t\right)+B_{1i}\omega \left(t\right)+B_{2i}u\left(t\right))\hfill \\ & =& A_{h}x\left(t\right)+B_{1h}\omega \left(t\right)+B_{2h}u\left(t\right),\hfill \\ \hfill z\left(t\right)& =& \sum _{i=1}^r{h}_i\left(x\left(t\right)\right)(C_{1i}x\left(t\right)+D_{1i}\omega \left(t\right)+D_{2i}u\left(t\right))\hfill \\ & =& C_{1h}x\left(t\right)+D_{1h}\omega \left(t\right)+D_{2h}u\left(t\right),\hfill \\ \hfill y\left(t\right)& =& \sum _{i=1}^r{h}_i\left(x\left(t\right)\right)C_{2i}x\left(t\right)=C_{2h}x\left(t\right).\hfill \end{array}$$

(1)

where the state $x\left(t\right)\in R^{n\times 1}$, the measured output $y\left(t\right)\in R^{n_y\times 1}$, the external disturbance $\omega \left(t\right)\in R^{n_w\times 1}$, the control input $u\left(t\right)\in R^{n_u\times 1}$ and the controlled output $z\left(t\right)\in R^{n_z\times 1}$. $A_i\in R^{n\times n}$, $B_{1i}\in R^{n\times n_{\omega }}$, $B_{2i}\in R^{n\times n_u}$, $C_{1i}\in R^{n_z\times n}$, $C_{2i}\in R^{n_y\times n}$, $D_{1i}\in R^{n_{{}_z}\times n_{\omega }}$, $D_{2i}\in R^{n_z\times n_u}$ and $D_{3i}\in R^{n_y\times n_{\omega }}$. $h_i\left(x\right)$ is the normalised MF satisfying ${\sum }_{i=1}^r{h}_i\left(x\left(t\right)\right)=1$.

The objective of this paper is to design a controller $u\left(t\right)$ such that the system (1) with $\omega =0$ is locally asymptotically stable, and guarantees ${\int }_0^{t}z{\left(t\right)}^{T}z\left(t\right)dt\le {\gamma }^2{\int }_0^t\omega {\left(t\right)}^T\omega \left(t\right)dt$ ($t>0$) under zero initial conditions.

2.2. Notations and Properties

$\mathbb{N}$ denotes the natural numbers set. $n!$ denotes factorial, i.e., $n!=n(n-1)\cdots \left(2\right)\left(1\right)$ for $n\in \mathbb{N}$ with $0!=1$. For any $\mathsf{\Phi }\in R^{n\times n}$, $He\left(\mathsf{\Phi }\right)=\mathsf{\Phi }+{\mathsf{\Phi }}^T$. $x\left(t\right)$, $h\left(x\right(t\left)\right)$ are replaced, respectively, by x, h for convenience. ${\mathsf{\Omega }}_h={\sum }_{i=1}^r{h}_i{\mathsf{\Omega }}_i$, ${\mathsf{\Omega }}_{hh}={\sum }_{i=1}^r{\sum }_{j=1}^r{h}_i{h}_j{\mathsf{\Omega }}_{ij}$. $diag\{a_1,\dots ,a_n\}=\left[\begin{array}{ccc}{a}_1& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & a_n\end{array}\right]$.

Based on the multi-index notations proposed in [19], that is, ${\mathbb{I}}_q=\{{\mathbf{i}}_q=(i_1,i_2,\dots ,i_q)\in {\mathbb{N}}^q\mid 1\le i_k\le r\}$, ${\mathbb{I}}_q^{+}=\{{\mathbf{i}}_q\in {\mathbb{I}}_q\mid i_1\le i_2\le \dots \le i_q\}$.

The notation of ${\mathbf{i}}_q/i_k$ (${\mathbf{i}}_q\in {\mathbb{I}}_q^{+}$,$1\le k\le r$) in [31] is recommended as follows:

$${\mathbf{i}}_q/i_k=\left\{\begin{array}{cc}{i}_1\dots i_{k-1}{i}_{k+1}\dots i_p,\hfill & \mathrm{if}{i}_k\in {\mathbf{i}}_q;\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(2)

For instance, if $i_1{i}_2{i}_2\in {\mathbb{I}}_3^{+}$, $k\in \{1,2,3,4\}$, $i_1,i_2\ne i_3$, $i_1,i_2\ne i_4$, then $i_1{i}_2{i}_2/i_1=i_2{i}_2$, $i_1{i}_2{i}_2/i_2=i_1{i}_2$, $i_1{i}_2{i}_2/i_3=0$, $i_1{i}_2{i}_2/i_4=0$.

The form of MFs for a product is expressed:

$$h_{{\mathbf{i}}_q}=\prod _{l=1}^q{h}_{i_l}=h_{i_1}{h}_{i_2}\cdots h_{i_q}=h_1^{q_1}{h}_2^{q_2}\cdots h_r^{q_r},$$

(3)

where ${\sum }_{i=1}^r{q}_i=q$.

According to the convex sum property of MFs, one has

$$1=\sum _{i=1}^r{h}_i={(\sum _{i=1}^r{h}_i)}^q=\sum _{{\mathbf{i}}_q\in {\mathbb{I}}_q^{+}}{g}_{{\mathbf{i}}_q}{h}_{{\mathbf{i}}_q},$$

(4)

where $g_{{\mathbf{i}}_q}=\frac{q!}{q_1!q_2!\cdots q_r!}$, ${\sum }_{i=1}^r{q}_i=q$. For example, as $r=2$, $q=4$, if $i_1=i_2=1$, $i_3=i_4=2$, $h_1{h}_1{h}_2{h}_2=h_1^2{h}_2^2$ or $i_1=1$, $i_2=i_3=i_4=2$, $h_1{h}_2{h}_2{h}_2=h_1{h}_2^3$, one gets $g_{1122}=\frac{4!}{2!2!}=6$ ($q_1=2$, $q_2=2$) or $g_{1222}=\frac{4!}{1!3!}=4$ ( $q_1=1$, $q_2=3$).

The q-dimensional fuzzy summations of matrices are defined as follows:

$$\begin{array}{ccc}& & {\mathsf{\Omega }}_{\mathbf{h}}=\sum _{{\mathbf{i}}_q\in {\mathbb{I}}_q}{h}_{{\mathbf{i}}_q}{\mathsf{\Omega }}_{{\mathbf{i}}_q}=\sum _{i_1=1}^r\cdots \sum _{i_q=1}^r{h}_{i_1}\cdots h_{i_q}{\mathsf{\Omega }}_{i_1\dots i_q}\hfill \\ & & {\mathsf{\Omega }}_{{\mathbf{h}}^{+}}=\sum _{{\mathbf{i}}_q\in {\mathbb{I}}_q^{+}}{h}_{{\mathbf{i}}_q}{\mathsf{\Omega }}_{{\mathbf{i}}_q}=\sum _{i_1=1}^r\cdots \sum _{i_q=i_{q-1}}^r{h}_{i_1}\cdots h_{i_q}{\mathsf{\Omega }}_{i_1\dots i_q}\hfill \end{array}$$

To facilitate the formula derivation, the following lemma and several properties are cited.

Lemma 1 (Finsler’s Lemma [18]).

Let $\zeta \in {\mathbb{R}}^n$, $\mathsf{\Theta }\in {\mathbb{R}}^{n\times n}$, $\mathsf{\Phi }\in {\mathbb{R}}^{m\times n}$, $rank\left(\mathsf{\Phi }\right)<n$, then ${\zeta }^T\mathsf{\Theta }\xi <0$, $\forall \zeta \ne 0$, such that $\mathsf{\Phi }\zeta =0$, if and only if one of the following conditions holds:

(1)

${\mathsf{\Phi }}_{\perp }^T\mathsf{\Theta }{\mathsf{\Phi }}_{\perp }<0$, where ${\mathsf{\Phi }}_{\perp }$ satisfies $\mathsf{\Phi }{\mathsf{\Phi }}_{\perp }=0$, and $\mathsf{\Phi }{\mathsf{\Phi }}^T+{\mathsf{\Phi }}_{\perp }^T{\mathsf{\Phi }}_{\perp }>0$;

(2)

$\exists \mu \in \mathbb{R}$: $\mathsf{\Theta }-\mu {\mathsf{\Phi }}^T\mathsf{\Phi }<0$;

(3)

$\exists V\in {\mathbb{R}}^{m\times n}$: $\mathsf{\Theta }+V\mathsf{\Phi }+{\mathsf{\Phi }}^T{V}^T<0$.

Property 1 ([18]).

The following inequalities are equivalent:

(1)

Find symmetric matrix $X=X^T$, such that $T+A^T{X}^T+XA<0$.

(2)

Find symmetric matrix $X=X^T$, $R_1$, $R_2$, such that

$$\left[\begin{array}{cc}T+A^T{R}_1^T+R_{1}A& \mathit{(}*\mathit{)}\\ X-R_1^T+X^{T}A& -R_2-R_2^T\end{array}\right]<0.$$

(5)

Property 2 ([32]).

Considering matrices $\mathsf{\Phi }={\mathsf{\Phi }}^T$ and $\mathsf{\Psi }={\mathsf{\Psi }}^T$ with suitable dimensions, if $\mathsf{\Phi }+\mu \mathsf{\Psi }<0$ and $\mathsf{\Phi }-\mu \mathsf{\Psi }<0$, then $\mathsf{\Phi }+\dot{h}\mathsf{\Psi }<0$ holds for any $\dot{h}$ and μ satisfying $|\dot{h}|\le \mu (\mu >0)$.

Property 3 ([19]).

Let ${\mathsf{\Omega }}_{{\mathbf{i}}_q}$, ${\mathbf{i}}_q\in {\mathbb{I}}_q^{+}$ be the matrices of proper dimensions. Then, ${\mathsf{\Omega }}_{{\mathbf{h}}_q}<0$ holds if

$${\mathsf{\Omega }}_{{\mathbf{i}}_q}<0.$$

(6)

3. Main Results

Theorem 1.

If given ${\mu }_j>0$, $\parallel \frac{\partial h_j}{\partial x}\parallel \le {\sigma }_j$, $j\in {\mathbb{I}}_1$, $\parallel \omega \parallel \le \delta$, there exist symmetric matrices $P_{{\mathbf{i}}_q}>0$, (${\mathbf{i}}_q\in {\mathbb{I}}_q$) and $M_{{\mathbf{i}}_{q+1}}$ (${\mathbf{i}}_{q+1}\in {\mathbb{I}}_{q+1}^{+}$), matrices $F_{{\mathbf{i}}_q}$, $L_{{\mathbf{i}}_q}^{l_1{l}_2}$ and $G_{{\mathbf{i}}_q}^{l_1{l}_2}$ (${\mathbf{i}}_q\in {\mathbb{I}}_q^{+}$) ($l_1,l_2=1,2,3$), such that

$$\begin{array}{c}\hfill {\mathsf{\Omega }}_{{\mathbf{i}}_{q+1}}^{\left(1\right)}=\left[\begin{array}{cccccc}{\mathsf{\Omega }}_{11}& {\mathsf{\Omega }}_{12}& {\mathsf{\Omega }}_{13}& {\mathsf{\Omega }}_{14}& {\mathsf{\Omega }}_{15}& {\mathsf{\Omega }}_{16}\\ \ast & {\mathsf{\Omega }}_{22}& {\mathsf{\Omega }}_{23}& {\mathsf{\Omega }}_{24}& {\mathsf{\Omega }}_{25}& {\mathsf{\Omega }}_{26}\\ \ast & \ast & {\mathsf{\Omega }}_{33}& {\mathsf{\Omega }}_{34}& {\mathsf{\Omega }}_{35}& {\mathsf{\Omega }}_{36}\\ \ast & \ast & \ast & {\mathsf{\Omega }}_{44}& {\mathsf{\Omega }}_{45}& {\mathsf{\Omega }}_{46}\\ \ast & \ast & \ast & \ast & {\mathsf{\Omega }}_{55}& {\mathsf{\Omega }}_{56}\\ \ast & \ast & \ast & \ast & \ast & {\mathsf{\Omega }}_{66}\end{array}\right]<0,\end{array}$$

(7)

$$\begin{array}{c}\hfill {\mathsf{\Omega }}_{{\mathbf{i}}_{q+1}}^{\left(2\right)}=\left[\begin{array}{ccc}\sum _{i=1}^r{P}_{\mathcal{P}({\mathbf{i}}_{q+1}/i_k)}& 0& (\ast )\\ 0& I& (\ast )\\ \sum _{i_{{}_k}=1}^q({\epsilon }_x{A}_{i_k}{P}_{\overline{\mathbf{i}}}+{\epsilon }_x{B}_{2i_k}{F}_{\overline{\mathbf{i}}})& B_{1i_k}& g_{{\mathbf{i}}_{q+1}}\frac{{\alpha }^2{\mu }_j^2}{\rho {\sigma }_j^2}\end{array}\right]>0,\end{array}$$

(8)

where $\overline{\mathbf{i}}={\mathbf{i}}_{q+1}/i_k$,

$$\begin{array}{c}{\mathsf{\Omega }}_{11}=\sum _{i_k=1}^{q}He(L_{\overline{\mathbf{i}}}^{11}{A}_{i_k}^T+B_{2i_k}{F}_{\overline{\mathbf{i}}})\pm \sum _{j=1}^r{\mu }_j{\overline{\mathsf{\Omega }}}_{{\mathbf{i}}_{q+1}}^j,\hfill \\ {\overline{\mathsf{\Omega }}}_{{\mathbf{i}}_{q+1}}^j=\sum _{j=1}^r\sum _{{\mathbf{j}}_q\in \mathcal{P}({\mathbf{i}}_{q+1}/j)}(P_{j\dots j_q}+\cdots +P_{j_1\dots j})+M_{{\mathbf{i}}_{q+1}},\hfill \\ {\mathsf{\Omega }}_{12}=\sum _{i_k=1}^q(g_{\overline{\mathbf{i}}}{B}_{1i_k}+A_{i_k}{L}_{\overline{\mathbf{i}}}^{{21}^T}),\hfill \\ {\mathsf{\Omega }}_{13}=\sum _{i_k=1}^q(F_{\overline{\mathbf{i}}}^T{D}_{2i_k}^T+L_{\overline{\mathbf{i}}}^{11}{C}_{1i_k}^T+A_{i_k}{L}_{\overline{\mathbf{i}}}^{{31}^T}),\hfill \\ {\mathsf{\Omega }}_{14}=\sum _{i_k=1}^q(P_{\mathcal{P}(\overline{\mathbf{i}})}-L_{\overline{\mathbf{i}}}^{11}+A_{i_k}{G}_{{\overline{\mathbf{i}}}_k}^{11}),\hfill \\ {\mathsf{\Omega }}_{15}=\sum _{i_k=1}^q(-L_{\overline{\mathbf{i}}}^{12}+A_{i_k}{G}_{\overline{\mathbf{i}}}^{12}),{\mathsf{\Omega }}_{16}=\sum _{i_k=1}^q(-L_{\overline{\mathbf{i}}}^{13}+A_{i_k}{G}_{\overline{\mathbf{i}}}^{13}),\hfill \\ {\mathsf{\Omega }}_{22}=-g_{{\mathbf{i}}_{q+1}}{\gamma }^2,{\mathsf{\Omega }}_{23}=\sum _{i_k=1}^q(D_{1i_k}^T+L_{\overline{\mathbf{i}}}^{21}{C}_{1i_k}^T),\hfill \\ {\mathsf{\Omega }}_{24}=-\sum _{i_k=1}^q{L}_{\overline{\mathbf{i}}}^{21},{\mathsf{\Omega }}_{25}=g_{{\mathbf{i}}_{q+1}}I-\sum _{i_k=1}^q{L}_{\overline{\mathbf{i}}}^{22},\hfill \\ {\mathsf{\Omega }}_{26}=-\sum _{i_k=1}^q{L}_{\overline{\mathbf{i}}}^{23},{\mathsf{\Omega }}_{33}=\sum _{i_k=1}^{q}He(L_{\overline{\mathbf{i}}}^{31}{C}_{1i_k}^T)-g_{{\mathbf{i}}_{q+1}}I,\hfill \\ {\mathsf{\Omega }}_{34}=\sum _{i_k=1}^q(-L_{\overline{\mathbf{i}}}^{31}+C_{1i_k}{G}_{\overline{\mathbf{i}}}^{11}),\hfill \\ {\mathsf{\Omega }}_{35}=\sum _{i_k=1}^q(-L_{\overline{\mathbf{i}}}^{32}+C_{1i_k}{G}_{\overline{\mathbf{i}}}^{12}),\hfill \\ {\mathsf{\Omega }}_{36}=g_{{\mathbf{i}}_{q+1}}I-\sum _{i_k=1}^q(L_{\overline{\mathbf{i}}}^{33}+C_{1i_k}{G}_{\overline{\mathbf{i}}}^{13}),\hfill \\ {\mathsf{\Omega }}_{44}=\sum _{i_k=1}^{q}He(-G_{\overline{\mathbf{i}}}^{11}),{\mathsf{\Omega }}_{45}=\sum _{i_k=1}^q(-G_{\overline{\mathbf{i}}}^{12}-G_{\overline{\mathbf{i}}}^{{21}^T}),\hfill \\ {\mathsf{\Omega }}_{46}=\sum _{i_k=1}^q(-G_{\overline{\mathbf{i}}}^{13}-G_{\overline{\mathbf{i}}}^{{31}^T}),{\mathsf{\Omega }}_{55}=\sum _{i_k=1}^{q}He(-G_{\overline{\mathbf{i}}}^{22}),\hfill \\ {\mathsf{\Omega }}_{56}=\sum _{i_k=1}^q(-G_{\overline{\mathbf{i}}}^{23}-G_{\overline{\mathbf{i}}}^{{32}^T}),{\mathsf{\Omega }}_{66}=\sum _{i_k=1}^{q}He(-G_{\overline{\mathbf{i}}}^{33}).\hfill \end{array}$$

then, the closed-loop system (1) in ${\mathsf{\Omega }}_x(:=\{x:x^T{P}_{{\mathbf{h}}_q}^{-1}x\le \rho \})$ is locally asymptotically stable with a disturbance attenuation level $\gamma$ under the controller (9)

$$u\left(t\right)=F_{{\mathbf{h}}_q^{+}}{P}_{{\mathbf{h}}_q}^{-1}x.$$

(9)

Proof. 

Designing the generalized NQLF candidate as

$$V\left(x\right)=x^T{P}_{{\mathbf{h}}_q}^{-1}x,$$

(10)

and letting $\mathsf{\Gamma }=\dot{V}\left(x\right)+z^{T}z-{\gamma }^2{\omega }^T\omega$, we get

$$\begin{array}{c}\hfill \mathsf{\Gamma }={\eta }^T\left[\begin{array}{cc}{\mathsf{\Lambda }}_1& P^{-1}{B}_{1h}+{\overline{C}}^T{D}_{1h}\\ (\ast )& -{\gamma }^2+D_{1h}^T{D}_{1h}\end{array}\right]\eta ,\end{array}$$

(11)

where ${\mathsf{\Lambda }}_1=He(P_{{\mathbf{h}}_q}^{-1}\overline{A})+{\dot{P}}_{{\mathbf{h}}_q}^{-1}+{\overline{C}}^T\overline{C}$, ${\eta }^T=\left[\begin{array}{cc}{x}^T& {\omega }^T\end{array}\right]$, $\overline{A}=A_h+B_{2h}{F}_{{\mathbf{h}}_q^{+}}{P}_{{\mathbf{h}}_q}^{-1}$, $\overline{C}=C_{1h}+D_{2h}{F}_{{\mathbf{h}}_q^{+}}{P}_{{\mathbf{h}}_q}^{-1}$. □

On one hand, $\mathsf{\Gamma }\le 0$ is guaranteed by the following formula:

$$\left[\begin{array}{ccc}He(P_{{\mathbf{h}}_q}^{-1}\overline{A})+{\dot{P}}_{{\mathbf{h}}_q}^{-1}& P_{{\mathbf{h}}_q}^{-1}{B}_{1h}& \overline{C}\\ B_{1h}^T{P}_{{\mathbf{h}}_q}^{-1}& -{\gamma }^2& D_{1h}^T\\ \overline{C}& D_{1h}& -I\end{array}\right]<0.$$

(12)

Multiplying left and right by $diag\{P_{{\mathbf{h}}_q},I,I\}$ and using the relation ${\dot{P}}_{{\mathbf{h}}_q}^{-1}=-P_{{\mathbf{h}}_q}^{-1}{\dot{P}}_{{\mathbf{h}}_q}{P}_{{\mathbf{h}}_q}^{-1}$, Equation (12) is transformed into

$$\begin{array}{c}\hfill \left[\begin{array}{ccc}He(\overline{A}{P}_{{\mathbf{h}}_q})-{\dot{P}}_{{\mathbf{h}}_q}& B_{1h}& P_{{\mathbf{h}}_q}\overline{C}\\ B_{1h}^T& -{\gamma }^2& D_{1h}^T\\ \overline{C}{P}_{{\mathbf{h}}_q}& D_{1h}& -I\end{array}\right]<0.\end{array}$$

(13)

Starting from the characteristics where ${\sum }_{j=1}^r{\dot{h}}_j=0$, thus ${\sum }_{j=1}^r{\dot{h}}_j{M}_{{\mathbf{h}}_{q+1}^{+}}=0$ for any symmetric matrix $M_{{\mathbf{h}}_{q+1}^{+}}$ with suitable size, adding ${\sum }_{j=1}^r{\dot{h}}_j{M}_{{\mathbf{h}}_{q+1}^{+}}$ to (13) and using Property 2, we get

$$\begin{array}{c}\hfill \left[\begin{array}{ccc}He(\overline{A}{P}_{{\mathbf{h}}_q})\pm {\mathsf{\Omega }}^j& B_{1h}& P_{{\mathbf{h}}_q}{\overline{C}}^T\\ B_{1h}^T& -{\gamma }^2& D_{1h}^T\\ \overline{C}{P}_{{\mathbf{h}}_q}& D_{1h}& -I\end{array}\right]<0,\end{array}$$

(14)

where ${\mathsf{\Omega }}^j={\sum }_{j=1}^r{\dot{h}}_j(P_{{\mathbf{h}}_q}^j+M_{{\mathbf{h}}_{q+1}^{+}})$.

Then, Equation (14) is transformed in to

$$\begin{array}{c}\hfill Q+{\mathsf{\Lambda }}_2^T\widehat{P}+\widehat{P}{\mathsf{\Lambda }}_2<0\end{array}$$

(15)

where

$$\begin{array}{c}Q=\left[\begin{array}{ccc}He(B_{2h}{F}_{{\mathbf{h}}_q^{+}})-\mathsf{\Omega }& B_{1h}& {(F_{{\mathbf{h}}_q^{+}})}^T{D}_{2h}^T\\ \ast & -{\gamma }^2& D_{1h}^T\\ \ast & \ast & -I\end{array}\right],\hfill \\ \widehat{P}=\left[\begin{array}{ccc}{P}_{{\mathbf{h}}_q}& 0& 0\\ 0& I& 0\\ 0& 0& I\end{array}\right],{\mathsf{\Lambda }}_2^T=\left[\begin{array}{ccc}{A}_h& 0& 0\\ 0& 0& 0\\ C_{1h}& 0& 0\end{array}\right].\hfill \end{array}$$

Applying Property 1 to (15), one gets

$$\begin{array}{c}\hfill {\mathsf{\Omega }}_{{\mathbf{h}}_{q+1}}=\left[\begin{array}{cccccc}{\overline{\mathsf{\Omega }}}_{11}& {\overline{\mathsf{\Omega }}}_{12}& {\overline{\mathsf{\Omega }}}_{13}& {\overline{\mathsf{\Omega }}}_{14}& {\overline{\mathsf{\Omega }}}_{15}& {\overline{\mathsf{\Omega }}}_{16}\\ \ast & -{\gamma }^2& {\overline{\mathsf{\Omega }}}_{23}& {\overline{\mathsf{\Omega }}}_{24}& {\overline{\mathsf{\Omega }}}_{25}& {\overline{\mathsf{\Omega }}}_{26}\\ \ast & \ast & {\overline{\mathsf{\Omega }}}_{33}& {\overline{\mathsf{\Omega }}}_{34}& {\overline{\mathsf{\Omega }}}_{35}& {\overline{\mathsf{\Omega }}}_{36}\\ \ast & \ast & \ast & {\overline{\mathsf{\Omega }}}_{44}& {\overline{\mathsf{\Omega }}}_{45}& {\overline{\mathsf{\Omega }}}_{46}\\ \ast & \ast & \ast & \ast & {\overline{\mathsf{\Omega }}}_{55}& {\overline{\mathsf{\Omega }}}_{56}\\ \ast & \ast & \ast & \ast & \ast & {\overline{\mathsf{\Omega }}}_{66}\end{array}\right]<0,\end{array}$$

(16)

where

$$\begin{array}{c}{\overline{\mathsf{\Omega }}}_{11}=He(L_{{\mathbf{h}}_q^{+}}^{11}{A}_h^T+B_{2h}{F}_{{\mathbf{h}}_q^{+}})\pm {\mathsf{\Omega }}^j,{\overline{\mathsf{\Omega }}}_{12}=B_{1h}+A_h{L}_{{\mathbf{h}}_q^{+}}^{{21}^T},\hfill \\ {\overline{\mathsf{\Omega }}}_{13}=F_{{\mathbf{h}}_q^{+}}^T{D}_{2h}^T+L_{{\mathbf{h}}_q^{+}}^{11}{C}_{1h}^T+A_h{L}_{{\mathbf{h}}_q^{+}}^{{31}^T},{\overline{\mathsf{\Omega }}}_{14}=P_{{\mathbf{h}}_q}-L_{{\mathbf{h}}_q^{+}}^{11}+A_h{G}_{{\mathbf{h}}_q^{+}}^{11},\hfill \\ {\overline{\mathsf{\Omega }}}_{15}=-L_{{\mathbf{h}}_q^{+}}^{12}+A_h{G}_{{\mathbf{h}}_q^{+}}^{12},{\overline{\mathsf{\Omega }}}_{16}=-L_{{\mathbf{h}}_q^{+}}^{13}+A_h{G}_{{\mathbf{h}}_q}^{13},\hfill \\ {\overline{\mathsf{\Omega }}}_{23}=D_{1h}^T+L_{{\mathbf{h}}_q^{+}}^{21}{C}_{1h}^T,{\overline{\mathsf{\Omega }}}_{24}=-L_{{\mathbf{h}}_q^{+}}^{21},{\overline{\mathsf{\Omega }}}_{25}=I-L_{{\mathbf{h}}_q^{+}}^{22},\hfill \\ {\overline{\mathsf{\Omega }}}_{26}=-L_{{\mathbf{h}}_q^{+}}^{23},{\overline{\mathsf{\Omega }}}_{33}=-I+He(L_{{\mathbf{h}}_q^{+}}^{31}{C}_{1h}^T),\hfill \\ {\overline{\mathsf{\Omega }}}_{34}=-L_{{\mathbf{h}}_q^{+}}^{31}+C_{1h}{G}_{{\mathbf{h}}_q^{+}}^{11},{\overline{\mathsf{\Omega }}}_{35}=-L_{{\mathbf{h}}_q^{+}}^{32}+C_{1h}{G}_{{\mathbf{h}}_q^{+}}^{12},\hfill \\ {\overline{\mathsf{\Omega }}}_{36}=I-L_{{\mathbf{h}}_q^{+}}^{33}+C_{1h}{G}_{{\mathbf{h}}_q^{+}}^{13},{\overline{\mathsf{\Omega }}}_{44}=He(-G_{{\mathbf{h}}_q^{+}}^{11}),\hfill \\ {\overline{\mathsf{\Omega }}}_{45}=-G_{{\mathbf{h}}_q^{+}}^{12}-G_{{\mathbf{h}}_q^{+}}^{{21}^T},{\overline{\mathsf{\Omega }}}_{46}=-G_{{\mathbf{h}}_q^{+}}^{13}-G_{{\mathbf{h}}_q^{+}}^{{31}^T},\hfill \\ {\overline{\mathsf{\Omega }}}_{55}=He(-G_{{\mathbf{h}}_q^{+}}^{22}),{\overline{\mathsf{\Omega }}}_{56}=-G_{{\mathbf{h}}_q^{+}}^{23}-G_{{\mathbf{h}}_q^{+}}^{{32}^T}.{\overline{\mathsf{\Omega }}}_{66}=He(-G_{{\mathbf{h}}_q^{+}}^{33}),\hfill \end{array}$$

According to Property 2, (16) is warranted by (7) with $|{\dot{h}}_j|\le {\mu }_j$.

On the other hand, we discuss $|{\dot{h}}_j|\le {\mu }_j$. Let

$$|{\dot{h}}_j|=|{(\frac{\partial h_j}{\partial x})}^T{\epsilon }_x(A_{h}x+B_{2h}{F}_{{\mathbf{h}}_q^{+}}{P}_{{\mathbf{h}}_q}^{-1}x+B_{1h}\omega )|\le {\mu }_j.$$

(17)

Notation: If h contains all state x, then ${\epsilon }_x$ is the unit matrix. If h only contains a part of state, for instance, $x={[x_1,x_2,x_3,x_4]}^T$, h depends on $x_1,x_3$, then ${\epsilon }_x=diag\{1,0,1,0\}$.

For (17), one has

$${\eta }^T{\Delta }^T\frac{\partial h_j}{\partial x}{(\frac{\partial h_j}{\partial x})}^T\Delta \eta <{\mu }_j^2,$$

(18)

where $\Delta ={\epsilon }_x[A_h+B_{2h}{F}_{{\mathbf{h}}_q^{+}}{P}_{{\mathbf{h}}_q}^{-1},B_{1h}]$, $\eta =[x;\omega ]$.

It is known that ${(\frac{\partial h_j}{\partial x})}^T\frac{\partial h_j}{\partial x}\le {\sigma }_j^2\iff \frac{\partial h_j}{\partial x}{(\frac{\partial h_j}{\partial x})}^T\le {\sigma }_j^{2}I$ and ${\eta }^{T}diag\{P_{{\mathbf{h}}_q}^{-1},I\}\eta \le \rho +{\delta }^2$. Equation (18) is guaranteed by

$$\frac{(\rho +{\delta }^2){\sigma }_j^2}{{\alpha }^2{\mu }_j^2}{\Delta }^T\Delta -diag\{P_{{\mathbf{h}}_q}^{-1},I\}<0,$$

(19)

Utilizing Schur complement to (19) and multiplying left and right by $diag\{P_{{\mathbf{h}}_q},I\}$, one has

$$\left[\begin{array}{ccc}{P}_{{\mathbf{h}}_q}& \ast & \ast \\ 0& I& \ast \\ {\epsilon }_x(A_h{P}_{{\mathbf{h}}_q}+B_{2h}{F}_{{\mathbf{h}}_q^{+}})& B_{1h}& \frac{{\alpha }^2{\mu }_j^2}{\rho {\sigma }_j^2}\end{array}\right]>0.$$

(20)

Therefore, if (7) and (8) hold, we have $\mathsf{\Gamma }<0$, which means ${\int }_0^{\infty }{z}^{T}zdt\le {\gamma }^2{\int }_0^{\infty }{\omega }^T\omega dt$. The proof is completed.

Remark 1.

TDMFs in [20,23] were bounded without disturbance and some assumed conditions such as matrix P ($P_i>\frac{{\lambda }_x^2+{\lambda }_k^2}{2{\beta }_k}I$ ) and the free variable S ($S_h=P_h$) in [28,33] were limited. This paper eliminates these restrictions or assumptions.

Remark 2.

Due to ${(\frac{\partial h_j}{\partial x})}^T\frac{\partial h_j}{\partial x}\le {\sigma }_j^2$ being restricted, Theorem 1 means a local result. The Lyapunov level ${\mathsf{\Omega }}_x$($x^T{P}_{{\mathbf{h}}_q}^{-1}x\le \rho$) is an estimated region for $H_{\infty }$ performance, which must be contained in ${\mathsf{\Theta }}_x$. Applying the Lagrange multiplier method, we get

$$\left[\begin{array}{cc}\frac{{\lambda }_{xi}^2}{\rho }& e_i{P}_{{\mathbf{h}}_q}\\ P_{{\mathbf{h}}_q}{e}_i^T& P_{{\mathbf{h}}_q}\end{array}\right]\ge 0$$

(21)

Thus, according to Property 3, conditions (22) guarantee (21).

$$\left[\begin{array}{cc}{g}_{{\mathbf{i}}_q}\frac{{\lambda }_{xi}^2}{\rho }& e_i{P}_{\mathcal{P}\left({\mathbf{i}}_q\right)}\\ \ast & P_{\mathcal{P}\left({\mathbf{i}}_q\right)}\end{array}\right]\ge 0,i=1,2,\dots ,n$$

(22)

Remark 3.

There are two parameters ${\mu }_j$ and ρ in Theorem 1 to be searched. By solving the following optimization problem, one can get $H\infty$ performance with given ${\mu }_j$ and ρ.

$$\begin{array}{ccc}& & \underset{P_{\mathcal{P}\left({\mathbf{i}}_q\right)}>0,F_{{\mathbf{i}}_q},L_{{\mathbf{i}}_q},G_{{\mathbf{i}}_q},{\mu }_j,\alpha }{min}\gamma \hfill \\ & & s.t.\left(7\right),\left(8\right),\left(22\right)\hfill \end{array}$$

(23)

Compared with the methods in [28,33], if $|{\dot{h}}_j|\le {\mu }_j$ is decomposed, that is,

$$\begin{array}{ccc}\hfill |{(\frac{\partial h_j}{\partial x})}^T{\epsilon }_x(A_h+B_{2h}{F}_{{\mathbf{h}}_q^{+}}{P}_{{\mathbf{h}}_q}^{-1})x|& \le & \alpha {\mu }_j\hfill \end{array}$$

(24)

$$\begin{array}{ccc}\hfill |{(\frac{\partial h_j}{\partial x})}^T{\epsilon }_x{B}_{1h}\omega |& \le & (1-\alpha ){\mu }_j\hfill \end{array}$$

(25)

then (8) will be substituted with (26) and (27).

Corollary 1.

Given ${\mu }_j>0$, $\parallel \frac{\partial h_j}{\partial x}\parallel \le {\sigma }_j$, $j\in {\mathbb{I}}_1$, $\parallel \omega \parallel \le \delta$, $\alpha \in (0,1)$, if (7), (26), (27) and (22) hold,

$$\begin{array}{c}\hfill {\mathsf{\Omega }}_{{\mathbf{i}}_{q+1}}^{\left(2\right)}=\left[\begin{array}{cc}\sum _{i=1}^r{P}_{\mathcal{P}({\mathbf{i}}_{q+1}/i)}& (\ast )\\ {\mathsf{\Omega }}_{21}^{\left(2\right)}& g_{{\mathbf{i}}_{q+1}}\frac{{\alpha }^2{\mu }_j^2}{\rho {\sigma }_j^2}\end{array}\right]>0,\end{array}$$

(26)

$$\begin{array}{c}\hfill \left[\begin{array}{cc}\frac{{(1-\alpha )}^2{\mu }_j^2}{{\delta }^2}& (\ast )\\ {\epsilon }_x{B}_{1i_k}& \frac{1}{{\sigma }_j^2}\end{array}\right]>0,\end{array}$$

(27)

Then, the closed-loop system (1) in ${\mathsf{\Omega }}_x(:=\{x:x^T{P}_{{\mathbf{h}}_q}^{-1}x\le \rho \})$ is locally asymptotically stable with a disturbance attenuation level $\gamma$ under the controller (9).

Proof. 

The proof is similar to that of Theorem 1, and is thus omitted here. □

4. Simulation Example

All the experiments were performed on a computer with an Intel(R) Core(TM)i5-7200U CPU @ 2.50 GHz 2.70 GHz, 12 GB(RAM), using Matlab2017a.

Example 1.

Considering the following nonlinear system form [33].

$$\left\{\begin{array}{cc}\hfill {\dot{x}}_1& =-6x_1-4.33x_2+7.59x_{1}si{n}^2(x_1)-2.96x_{2}si{n}^2(x_1)\hfill \\ \hfill & +(si{n}^2(x_1)-2.06co{s}^2(x_1))u+(0.1+0.01co{s}^2(x_1))\omega \hfill \\ \hfill {\dot{x}}_2& =x_{1}si{n}^2(x_1)+5x_2-5si{n}^2(x_1)x_2-co{s}^2(x_1)u\hfill \\ \hfill & +(0.01si{n}^2\left(x_1\right)+0.03)\omega \hfill \end{array}\right.$$

(28)

The above system is expressed as a T-S fuzzy system with two rules in the ${\mathbb{C}}_x=\{x:|x_i|\le \frac{\pi }{2},i=1,2\}$. One gets the system matrices:

$$\begin{array}{c}{A}_1=\left[\begin{array}{cc}1.59& -7.29\\ 1& 0\end{array}\right],A_2=\left[\begin{array}{cc}-6& -4.33\\ 0& 5\end{array}\right],B_{11}=\left[\begin{array}{c}0.01\\ 0.04\end{array}\right],B_{12}=\left[\begin{array}{c}0.011\\ 0.03\end{array}\right],\hfill \\ B_{21}=\left[\begin{array}{c}1\\ 0\end{array}\right],B_{22}=\left[\begin{array}{c}-2.06\\ -1\end{array}\right],C_{11}=C_{12}=\left[\begin{array}{cc}1& 2\end{array}\right],D_{11}=D_{12}=D_{21}=D_{22}=0,\hfill \\ h_1=si{n}^2\left(x_1\right),h_2=1-h_1.\hfill \end{array}$$

Since $\frac{\partial h_1}{\partial x}=2sin(x_1)cos(x_1)$ and $\frac{\partial h_2}{\partial x}=-2sin(x_1)cos(x_1)$, thus

$${(\frac{\partial h_1}{\partial x})}^T\frac{\partial h_1}{\partial x}\le 1,{(\frac{\partial h_2}{\partial x})}^T\frac{\partial h_2}{\partial x}\le 1,$$

one has ${\sigma }_i^2=1$.

The external disturbance signal $\omega \left(t\right)=\{\begin{array}{c}sin\left(t\right),5\le t\le 15 \mathrm{s}\\ 0,\mathrm{else}\end{array}$. The parameters required by Theorem 1 in the region ${\mathsf{\Omega }}_x$($x^T{P}_{{\mathbf{h}}_q}^{-1}x\le \rho =1$) are as follows: ${\sigma }_i^2=1,{\lambda }_{x_i}^2=\frac{{\pi }^2}{4}$, ${\delta }^2=1$, ${\mu }_i=1000$.

All results are solved by function $minx$ in Matlab Toolbox. The minimal $\gamma$ obtained are shown in

Table 1. Minimum $H\infty$ performance $\gamma$.

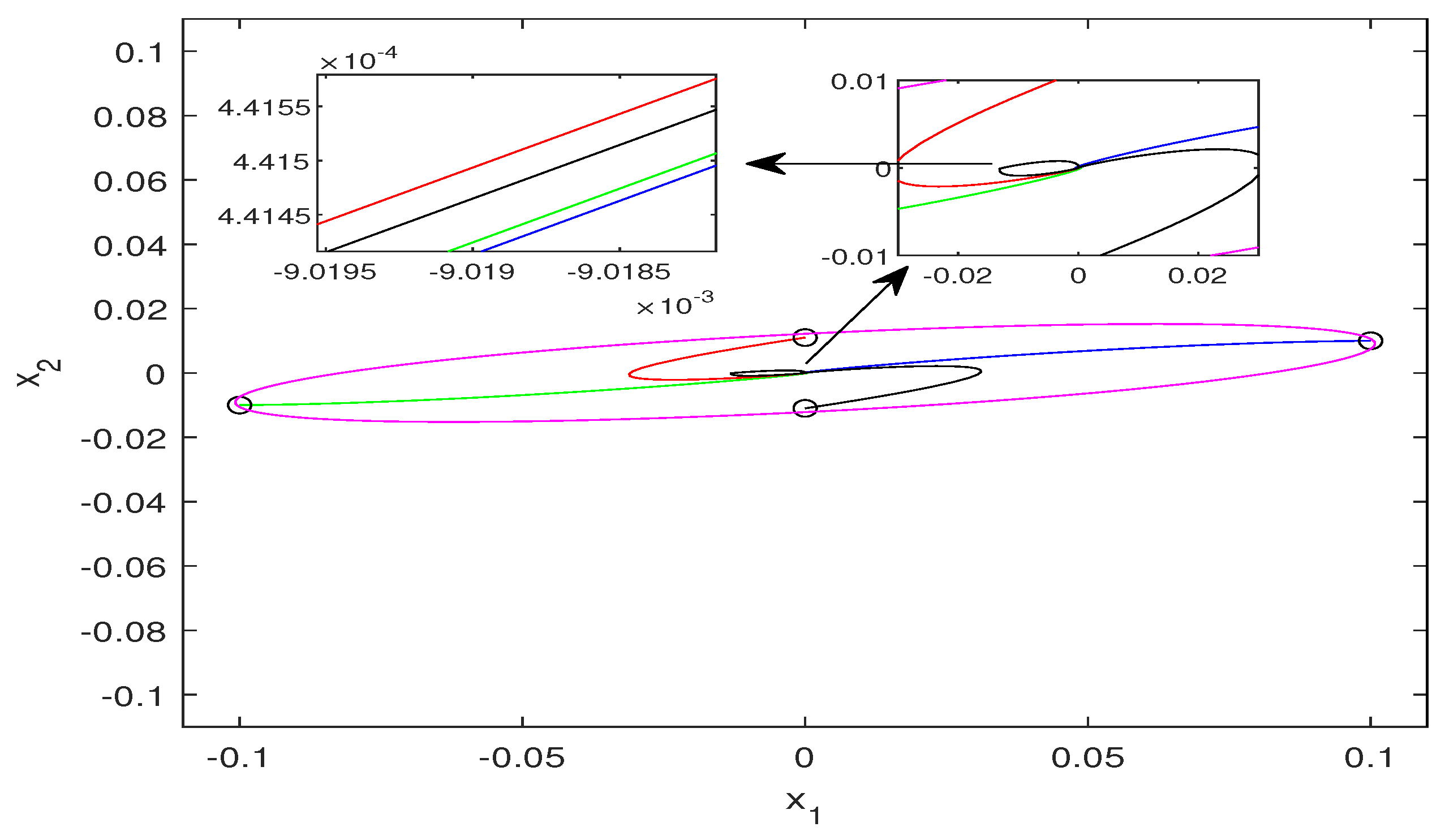
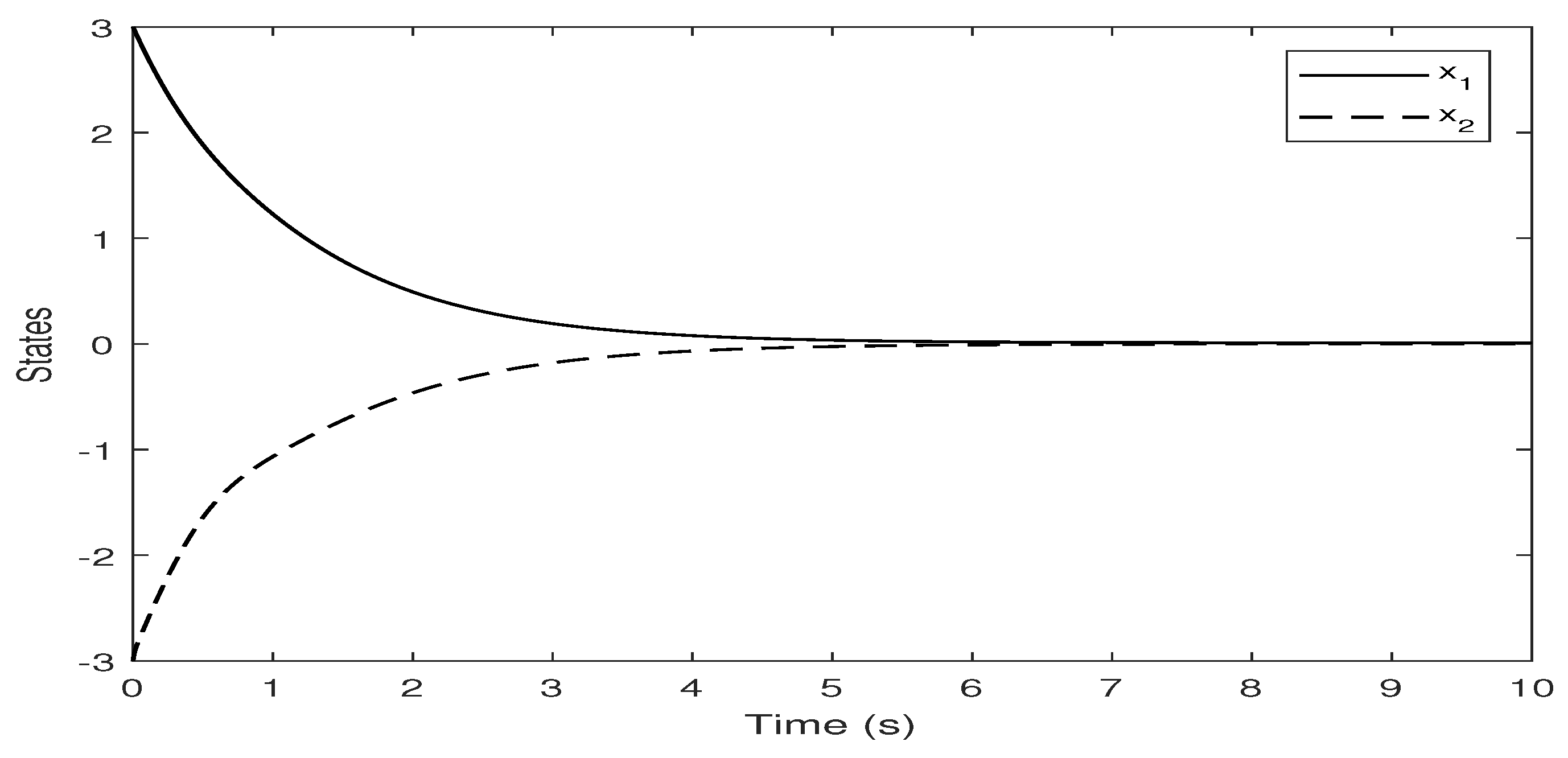
Methods	$\mathit{\gamma }$	Computational Time
[23]	–
[34] (Theorem 1)	0.1896	0.2015 s
[33] (Theorem 1)	0.0483	1.4590 s
[27] (Theorem 1)	0.0434	0.3305 s
Corollary 1 (q = 1)	0.0511	0.4590 s
Corollary 1 (q = 2)	0.0409	0.9586 s
Corollary 1 (q = 3)	0.0345	1.6205 s
Theorem 1 (q = 1)	0.0506	0.5160 s
Theorem 1 (q = 2)	0.0407	1.0272 s
Theorem 1 (q = 3)	0.0338	2.2055 s

under different methods. Notice, a line indicates that SeDuMi solver is unable to converge to a solution.

This clearly shows that the Theorem 1 proposed in this paper is less conservative than other methods. Moreover, as q increases, better results are obtained.

On the other hand, when systems include unknown parameters, such as $B_{22}=\left[\begin{array}{c}-2.06+\lambda \\ -1\end{array}\right]$, we compare the minimal $\gamma$ with the different $\lambda$ shown in

Table 2. Minimum $H\infty$ performance $\gamma$ with different $\lambda$.

Methods	$\mathit{\lambda }$ = 0.1	$\mathit{\lambda }$ = 0.2	$\mathit{\lambda }$ = 0.3	$\mathit{\lambda }$ = 0.4	$\mathit{\lambda }$ = 0.7	$\mathit{\lambda }$ = 1
Corollary 1 (q = 1)	0.0538	0.0567	0.0598	0.0630	0.0742	0.0878
Corollary 1 (q = 2)	0.0391	0.0374	0.0359	0.344	0.0307	0.0281
Corollary 1 (q = 3)	0.0334	0.0323	0.0313	0.0304	0.0280	0.0260
Theorem 1 (q = 1)	0.0506	0.0480	0.0457	0.0414	0.0361	0.0332
Theorem 1 (q = 2)	0.0387	0.0368	0.0350	0.0334	0.0294	0.0271
Theorem 1 (q = 3)	0.0327	0.0317	0.0307	0.0298	0.0275	0.0259

. Although the minimal $\gamma$ increases with the parameter $\lambda$, Theorem 1’s results are better than other ones under the same parameter $\lambda$.

When $\lambda =1$ and $q=3$, one gets $\gamma =0.0259$ and the gain matrices as follow.

$$\begin{array}{c}{P}_{111}=\left[\begin{array}{cc}1.4172& -1.3062\\ -1.3062& 1.2039\end{array}\right],F_{111}={\left[\begin{array}{c}-13.5716\\ 10.4026\end{array}\right]}^T,\hfill \\ P_{112}=\left[\begin{array}{cc}0.0001& -0.0044\\ -0.0044& 1.4004\end{array}\right],F_{112}={\left[\begin{array}{c}-48.4813\\ 22.6372\end{array}\right]}^T,\hfill \\ P_{122}=\left[\begin{array}{cc}7.0579& 3.9604\\ 3.9604& 2.2224\end{array}\right],F_{122}={\left[\begin{array}{c}51.1398\\ 55.7751\end{array}\right]}^T,\hfill \\ P_{222}=\left[\begin{array}{cc}2.4673& 1.0802\\ 1.0802& 0.4736\end{array}\right],F_{222}={\left[\begin{array}{c}-3.3849\\ 5.5163\end{array}\right]}^T.\hfill \end{array}$$

Choosing the initial four points

$$\begin{array}{c}{x}_0^{\left(1\right)}={\left[\begin{array}{cc}0.1& 0.01\end{array}\right]}^T,x_0^{\left(2\right)}={\left[\begin{array}{cc}-0.1& -0.01\end{array}\right]}^T,\hfill \\ x_0^{\left(3\right)}={\begin{array}{cc}0& -0.011\end{array}}^T,x_0^{\left(4\right)}={\left[\begin{array}{cc}0& 0.011\end{array}\right]}^T,\hfill \end{array}$$

four trajectory curves in the domain of attraction ${\mathsf{\Omega }}_x$ are shown in Figure 1, which are asymptotically driven to the origin under the controller. Therefore, this shows that the designed controller is effective.

Example 2.

The state equation of motion for the inverted pendulum controlled by a separately excited direct current (DC) motor from [35].

$$\left\{\begin{array}{cc}\hfill {\dot{x}}_1\left(t\right)& =x_2\left(t\right),\hfill \\ \hfill {\dot{x}}_2\left(t\right)& =\frac{g}{l}sin{x}_1\left(t\right)+\frac{N{K}_1}{m{l}^2}{x}_3\left(t\right)+\omega ,\hfill \\ \hfill 0& =-N{K}_2{x}_2\left(t\right)-\overline{R}{x}_3\left(t\right)+u,\hfill \end{array}\right.$$

(29)

where $x_1\in [-\pi \pi ]$ denotes the angle, $x_2$ denotes the angular velocity, $x_3$ represents the current of the DC motor, u is the control input voltage. The parameter values of the system are $m=1$ kg, $l=1$ m, $g=9.8$ m/s², $N=10$, $K_2=0.1$ Vs/rad, $K_1=0.1$ Nm/A and $0.6\mathsf{\Omega }\le \overline{R}\le 3.5\mathsf{\Omega }$.

Equation (29) can be converted to

$$\left\{\begin{array}{cc}\hfill {\dot{x}}_1\left(t\right)& =x_2\left(t\right),\hfill \\ \hfill {\dot{x}}_2\left(t\right)& =\frac{g}{l}sin{x}_1\left(t\right)-\frac{N^2{K}_1{K}_2}{m{l}^2\overline{R}}{x}_2\left(t\right)+\frac{N{K}_1}{m{l}^2\overline{R}}u+\omega .\hfill \end{array}\right.$$

(30)

We consider $z=x_1+x_2$. Applying local approximation method, the T-S fuzzy model (1) is given with $A_1=\left[\begin{array}{cc}0& 1\\ 9.8& -\frac{5}{3}\end{array}\right]$, $A_2=\left[\begin{array}{cc}0& 1\\ 0& -\frac{5}{3}\end{array}\right]$, $B_{21}=\left[\begin{array}{c}0\\ \frac{5}{3}\end{array}\right]$, $B_{22}=\left[\begin{array}{c}0\\ \frac{5}{3}\end{array}\right]$, $B_{11}=\left[\begin{array}{c}0\\ 1\end{array}\right]$, $B_{12}=\left[\begin{array}{c}0\\ 1\end{array}\right]$, $C_{11}=\left[\begin{array}{cc}1& 1\end{array}\right]$, $C_{12}=\left[\begin{array}{cc}1& 1\end{array}\right]$, $D_{11}=D_{12}=D_{21}=D_{22}=0$. $h_1=\frac{sin\left(x_1\right)+1}{2},$$h_2=1-h_1$ defined in the compact set $\mathbb{C}=\{x:|x_1|\le \pi ,|x_2|\le \pi \}$.

Since $\frac{\partial h_1}{\partial x}={\left[\begin{array}{cc}\frac{cos\left(x_1\right)}{2}& 0\end{array}\right]}^T$ and $\frac{\partial h_2}{\partial x}={\left[\begin{array}{cc}-\frac{cos\left(x_1\right)}{2}& 0\end{array}\right]}^T$, thus ${(\frac{\partial h_1}{\partial x})}^T\frac{\partial h_1}{\partial x}\le \frac{1}{4}$, ${(\frac{\partial h_2}{\partial x})}^T\frac{\partial h_2}{\partial x}\le \frac{1}{4}$, one has ${\mu }_i^2=\frac{1}{4}$. Selecting ${\sigma }_i^2=\frac{1}{4}$, ${\lambda }_x^2=2{\pi }^2$, $\rho =1$.

Here, we consider that the derivative of MFs (${\mu }_1={\mu }_2$) in Theorem 1 affects the conservativeness of the different method. The results are shown in

Table 3. Minimum $H\infty$ performance $\gamma$ with different ${\mu }_i$.

Methods	$\mathit{\mu }$ = 1	$\mathit{\mu }$ = 10	$\mathit{\mu }$ = 100	$\mathit{\mu }$ = 1000
[23] (Theorem 1)	–	$1.6751\times {10}^{-5}$	$7.2367\times {10}^{-6}$	$3.1836\times {10}^{-6}$
[33] (Theorem 1)	–	$1.7001\times {10}^{-5}$	$8.7385\times {10}^{-6}$	$4.0402\times {10}^{-6}$
[27] (Theorem 1)	–	$2.866\times {10}^{-5}$	$2.7622\times {10}^{-5}$	$2.7572\times {10}^{-5}$
Theorem 1 (q = 1)	$1.5039\times {10}^{-5}$	$2.1596\times {10}^{-5}$	$2.1523\times {10}^{-5}$	$2.1224\times {10}^{-5}$
Theorem 1 (q = 2)	$2.5539\times {10}^{-5}$	$1.5306\times {10}^{-5}$	$6.3759\times {10}^{-6}$	$2.6786\times {10}^{-6}$

. It can be seen that [23,27,33] cannot converge to a solution when $\mu =1$, but Theorem 1 can. Moreover, as ${\mu }_i$ increases, $\gamma$ decreases, and Theorem 1’s results with $q=2$ are better than other ones under the same parameter $\mu$.

Choosing $q=2$, $\mu =100$, we get $\gamma =6.3759\times {10}^{-6}$ and control gain matrixes as follow:

$$\begin{array}{c}{P}_{11}={10}^6\times \left[\begin{array}{cc}6.8474& -6.7747\\ -6.7747& 6.8257\end{array}\right],F_{11}={10}^5\times {\left[\begin{array}{c}-5.6759\\ 6.5064\end{array}\right]}^T,\hfill \\ P_{12}={10}^6\times \left[\begin{array}{cc}7.1174& -6.9996\\ -6.9996& 7.0022\end{array}\right],F_{12}={10}^6\times {\left[\begin{array}{c}0.5910\\ -9.8859\end{array}\right]}^T,\hfill \\ P_{22}={10}^6\times \left[\begin{array}{cc}6.9380& -6.8626\\ -6.8626& 6.9128\end{array}\right],F_{22}={10}^6\times {\left[\begin{array}{c}-0.0242\\ -7.6379\end{array}\right]}^T.\hfill \end{array}$$

From the starting point $x_0={[3,-3]}^T$, the response trajectories of the states, Lyapunov function and control input are shown in Figure 2, Figure 3 and Figure 4, respectively. Therefore, the closed-loop system (30) is locally asymptotically stable with disturbance attenuation level $\gamma$ under the controller (9).

5. Conclusions

This paper has presented the local $H\infty$ control for continuous-time T-S fuzzy systems via generalized nonquadratic Lyapunov functions. Using polynomial technology, relaxed LMIs conditions satisfying $H\infty$ performance are obtained, which are easily solved by the optimization problem. The simulation examples provided show the validity of the proposed method.

Furthermore, the method proposed in this paper could be generalized to handle problems regarding output feedback controllers, filters or observers. Now, our group is considering the output feedback controller design for nonlinear systems, finite-time boundedness, finite-time annular domain stability and mean-square strong stability for stochastic systems using our method.