Entropy Analysis in MHD CNTS Flow Due to a Stretching Surface with Thermal Radiation and Heat Source/Sink
Abstract
1. Introduction
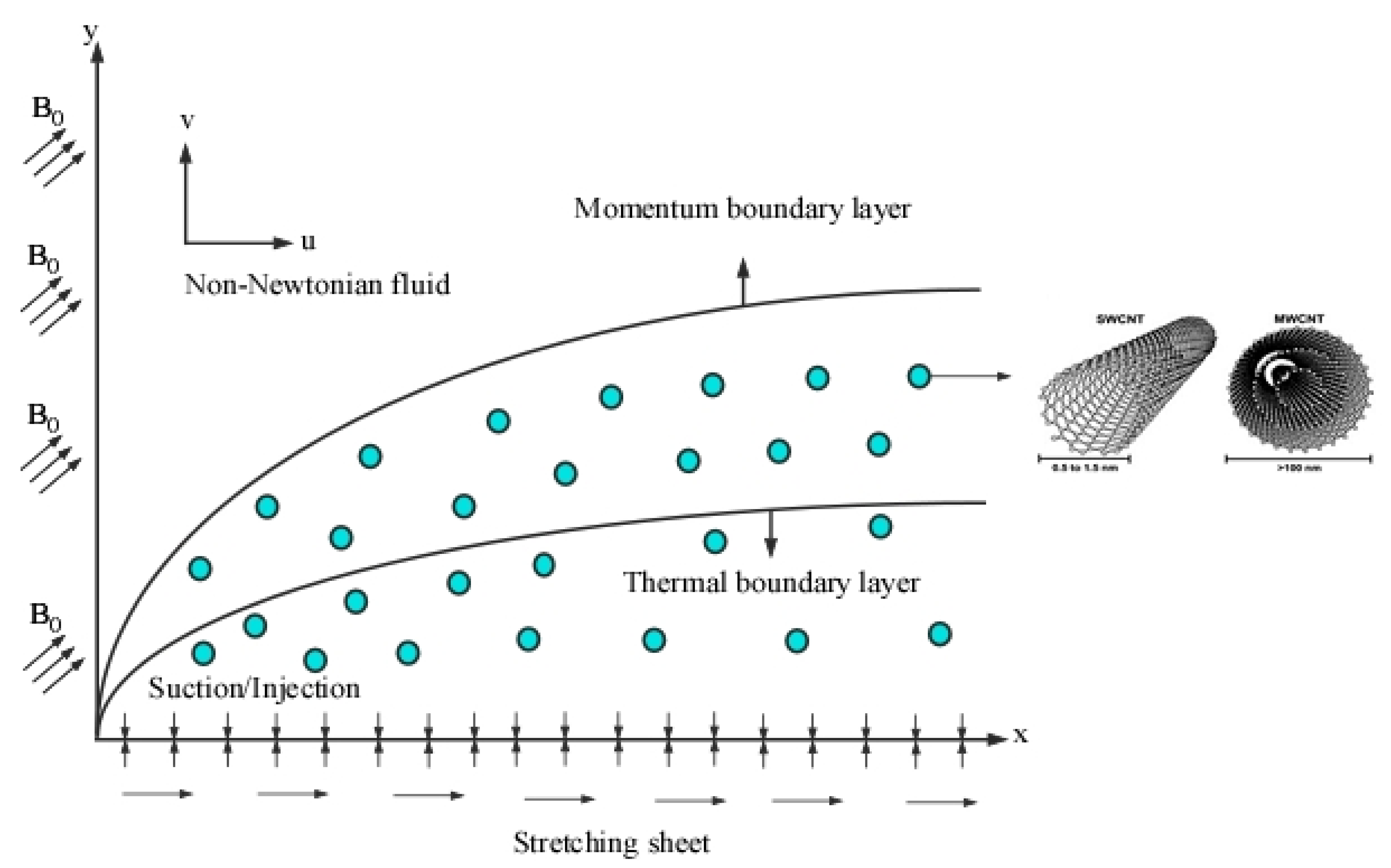
2. Mathematical Analysis and Solution
3. Analytical Solution for Energy Equation
4. Entropy Generation Analysis
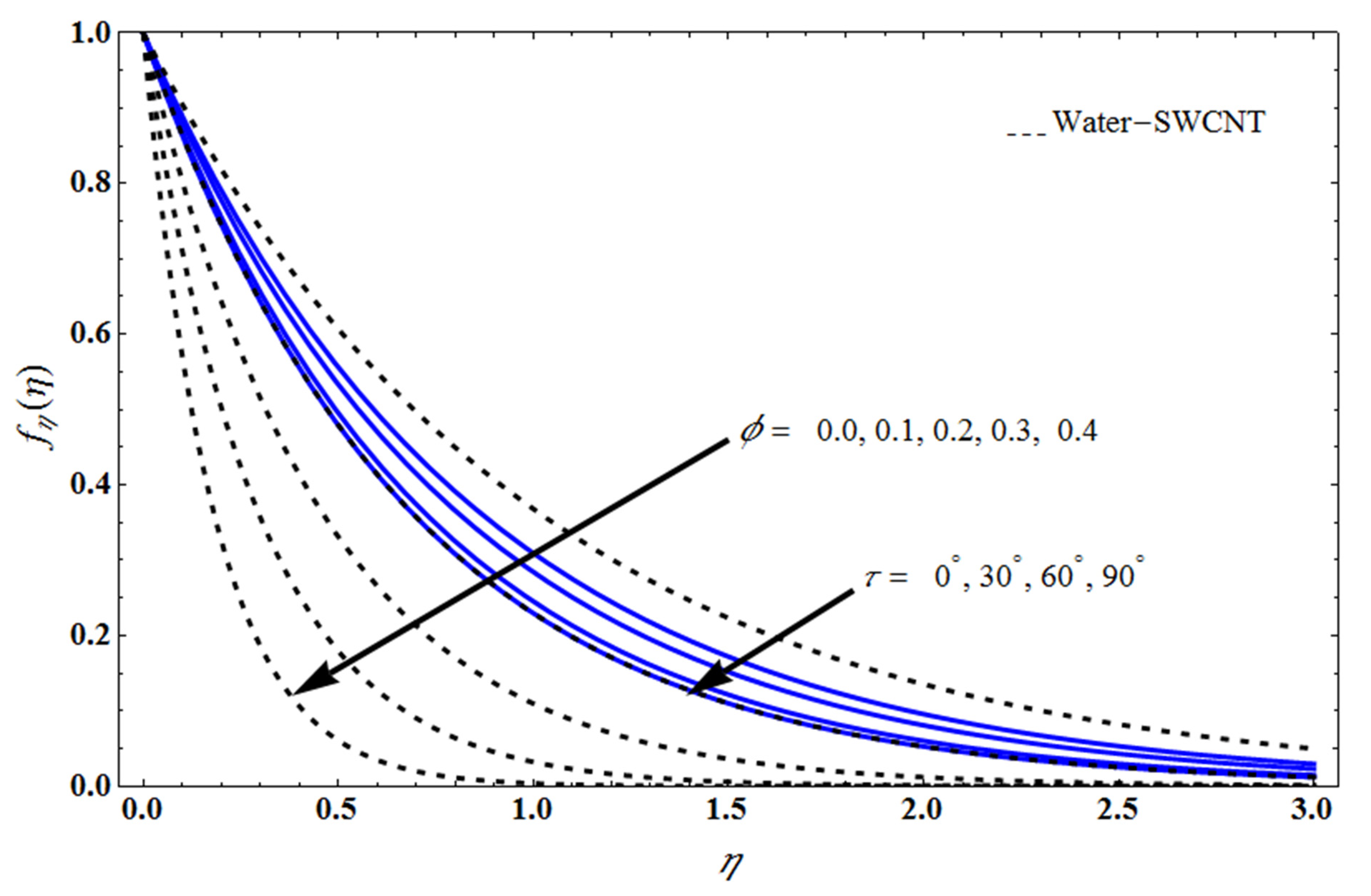
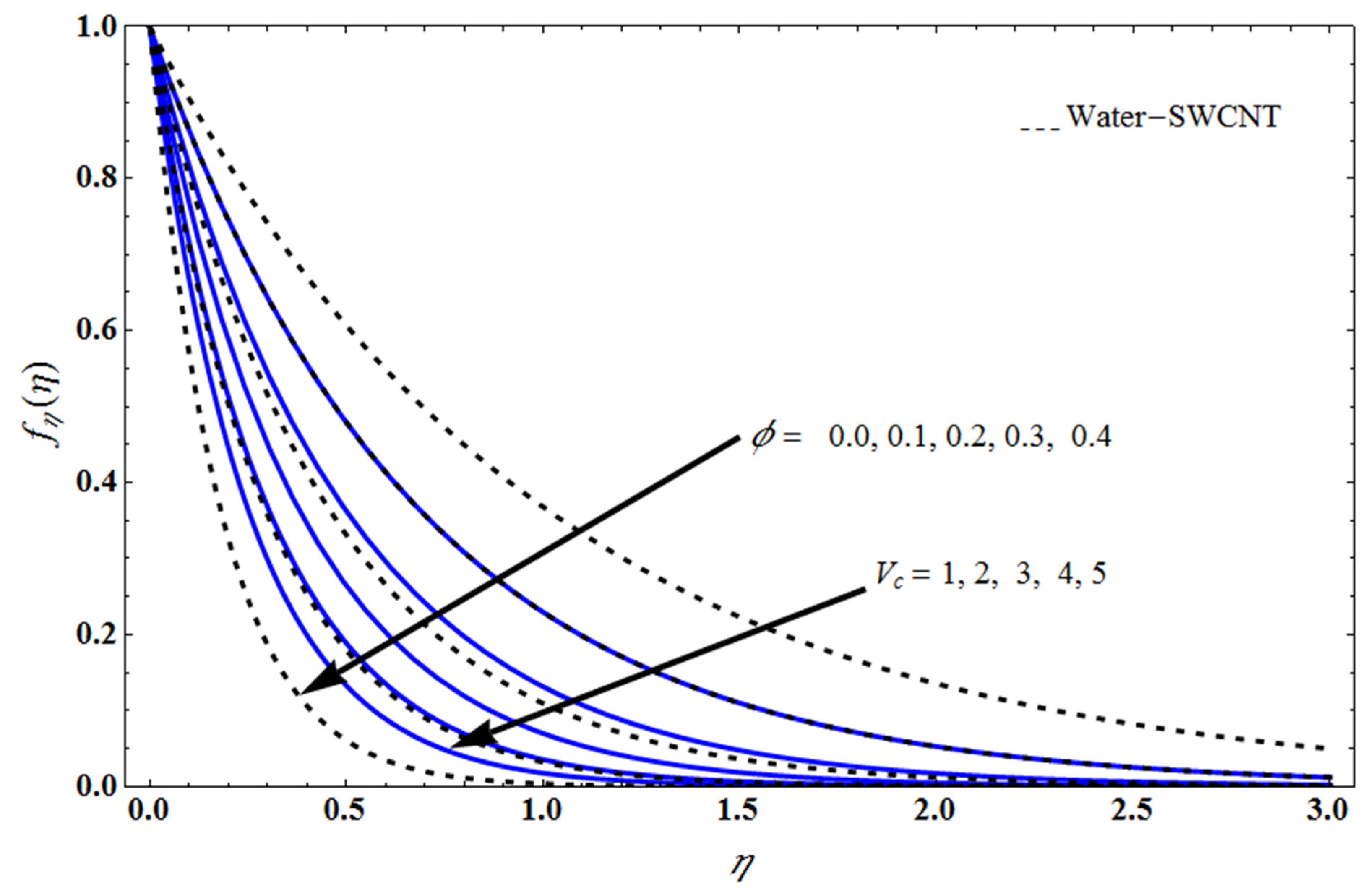
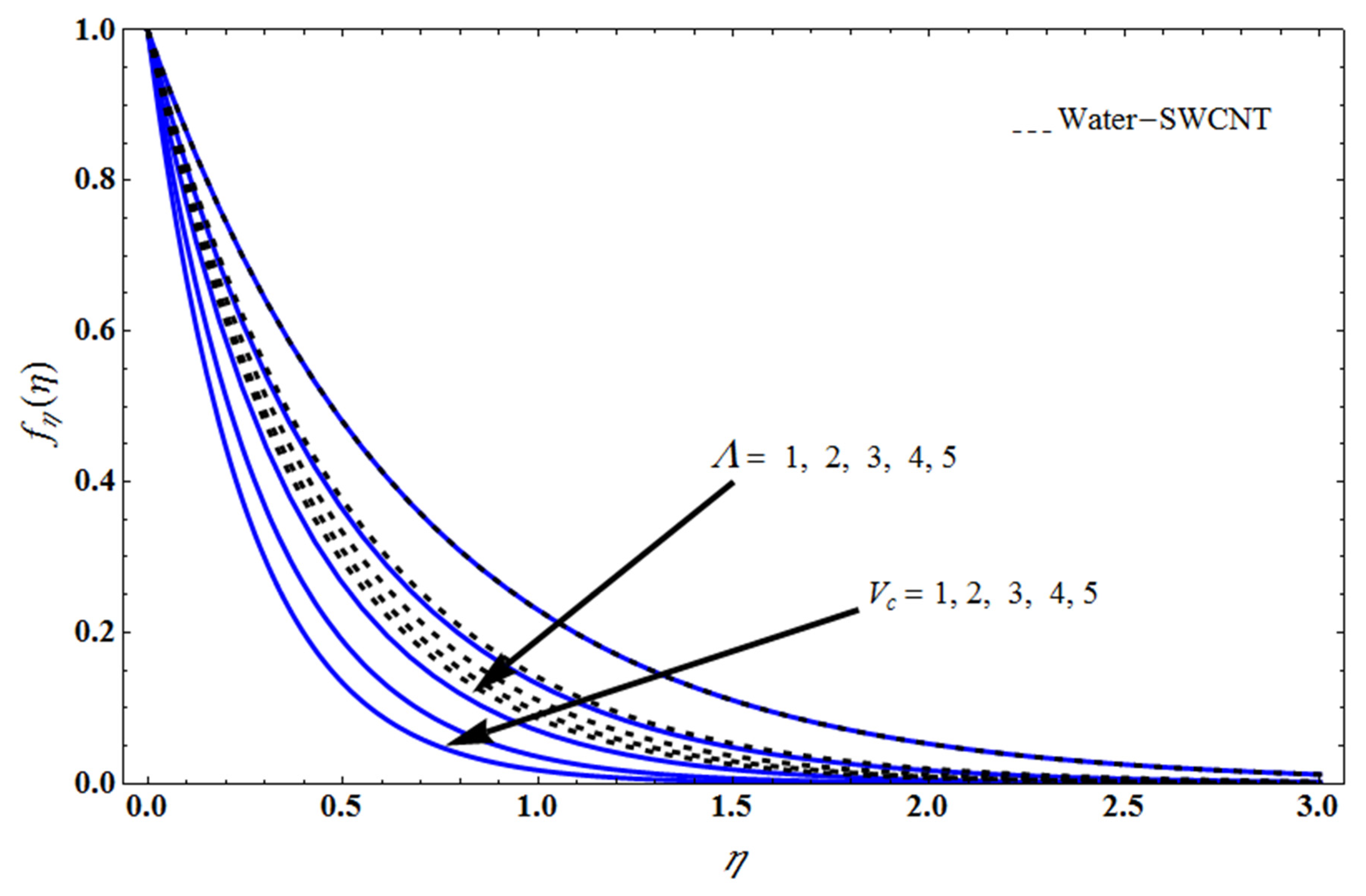
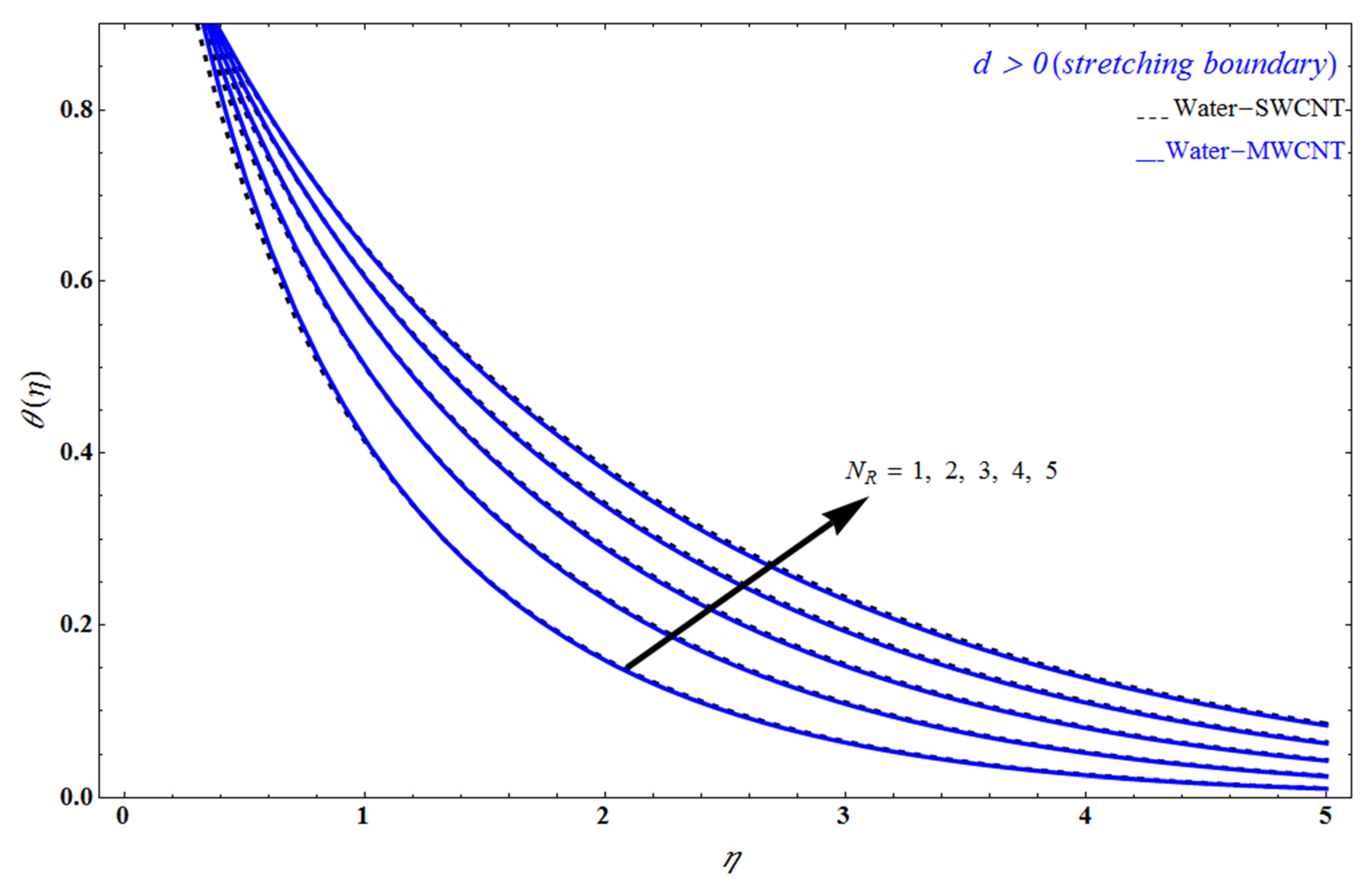
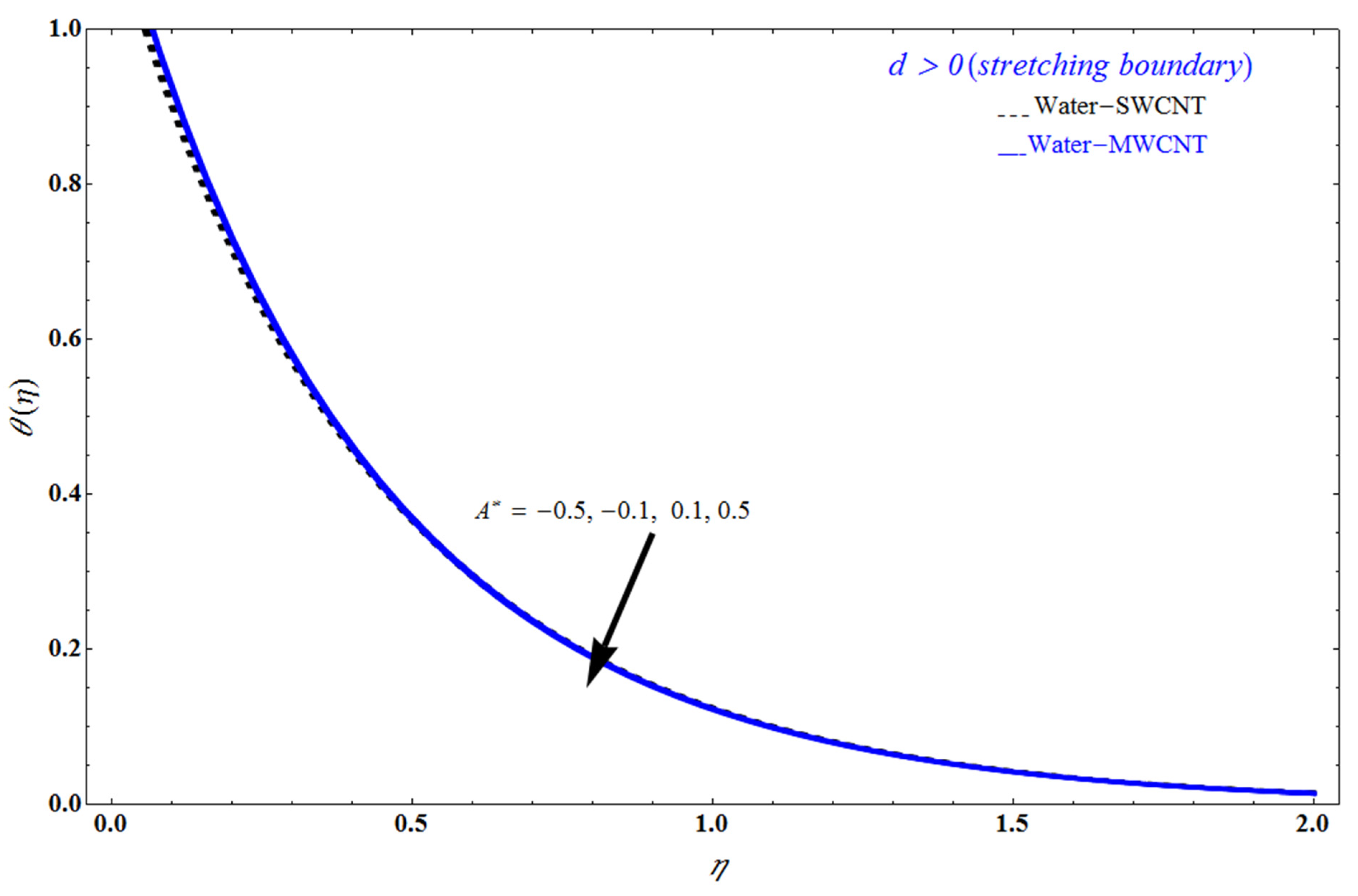
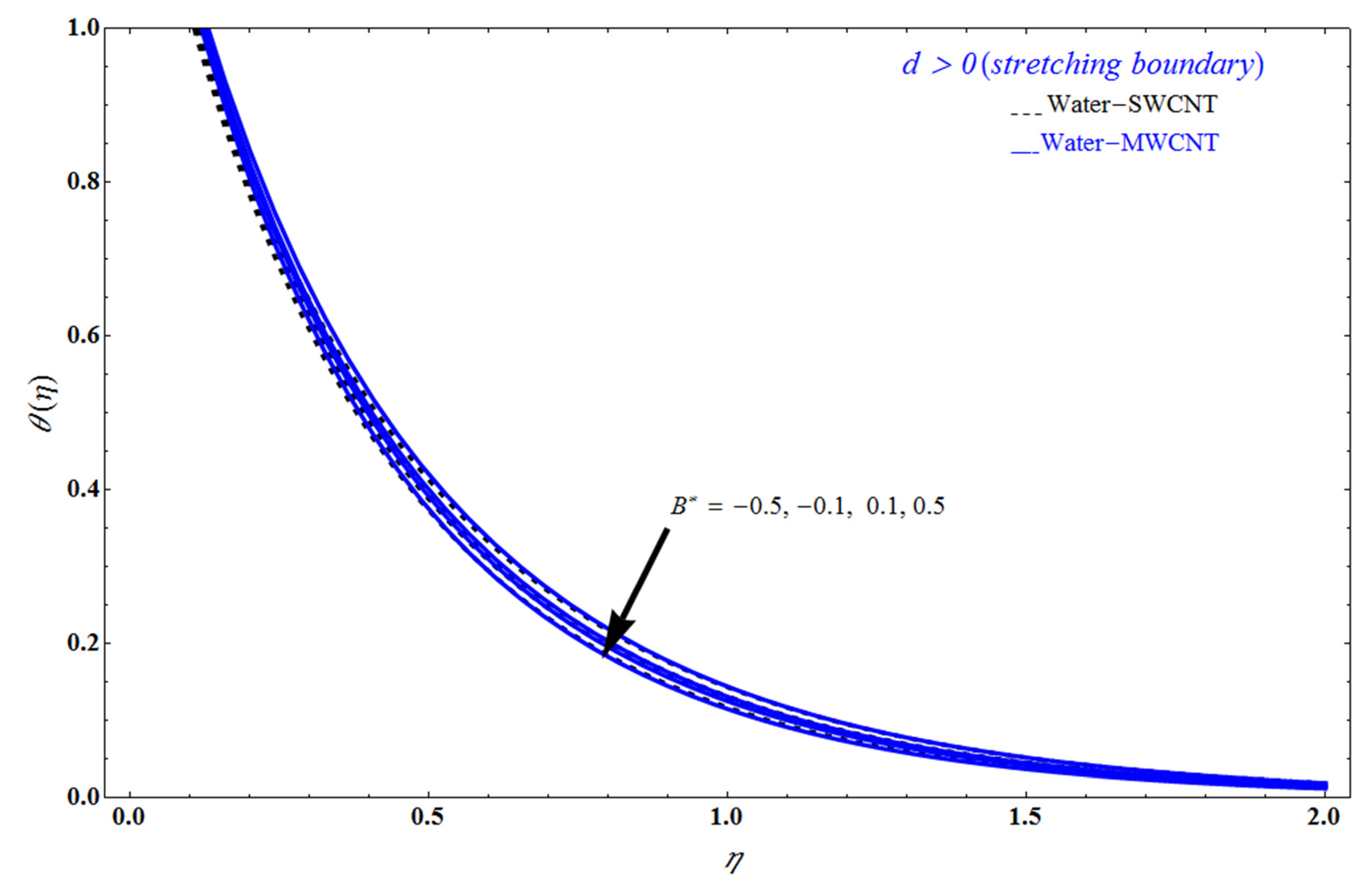
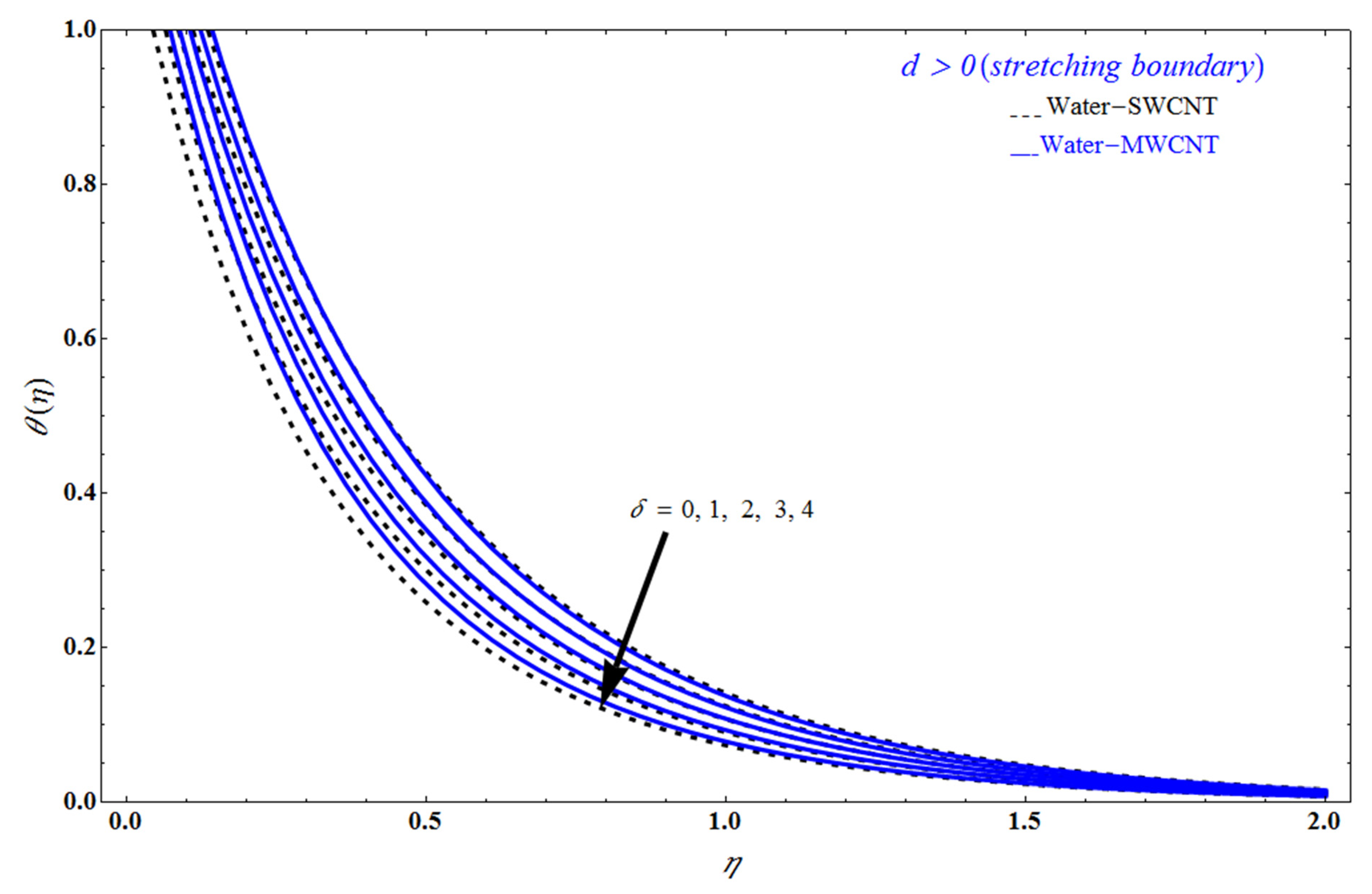
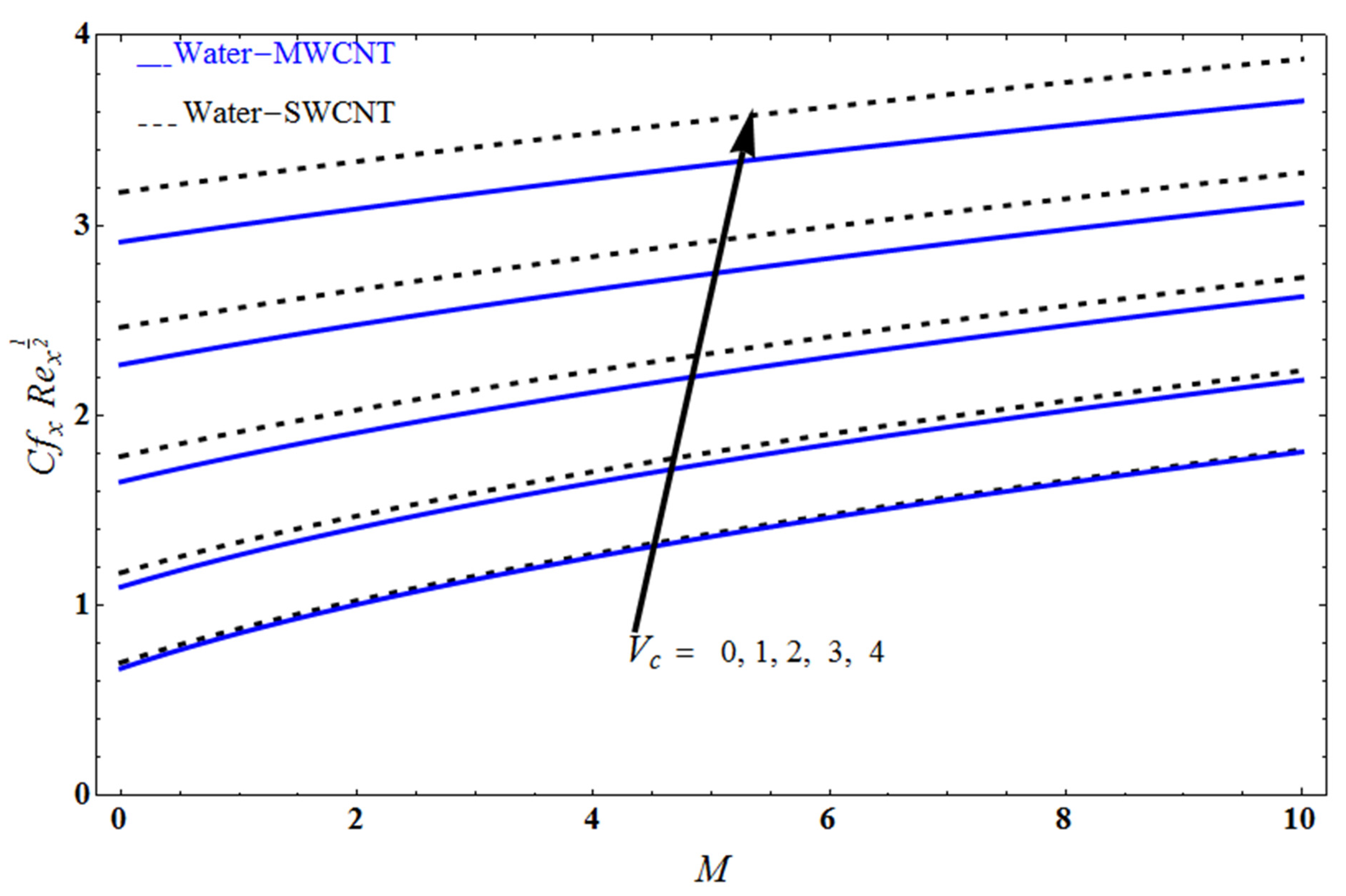
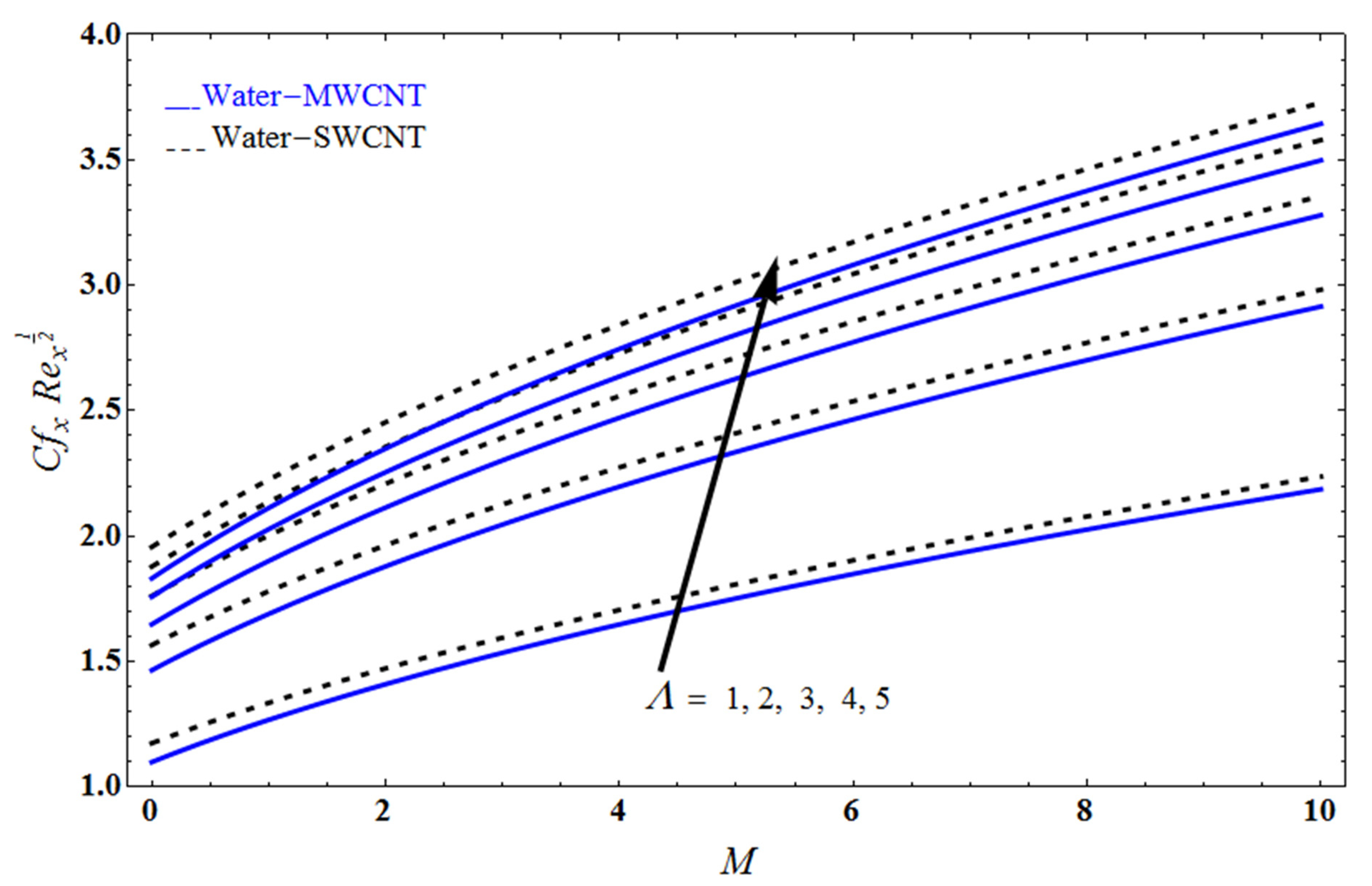
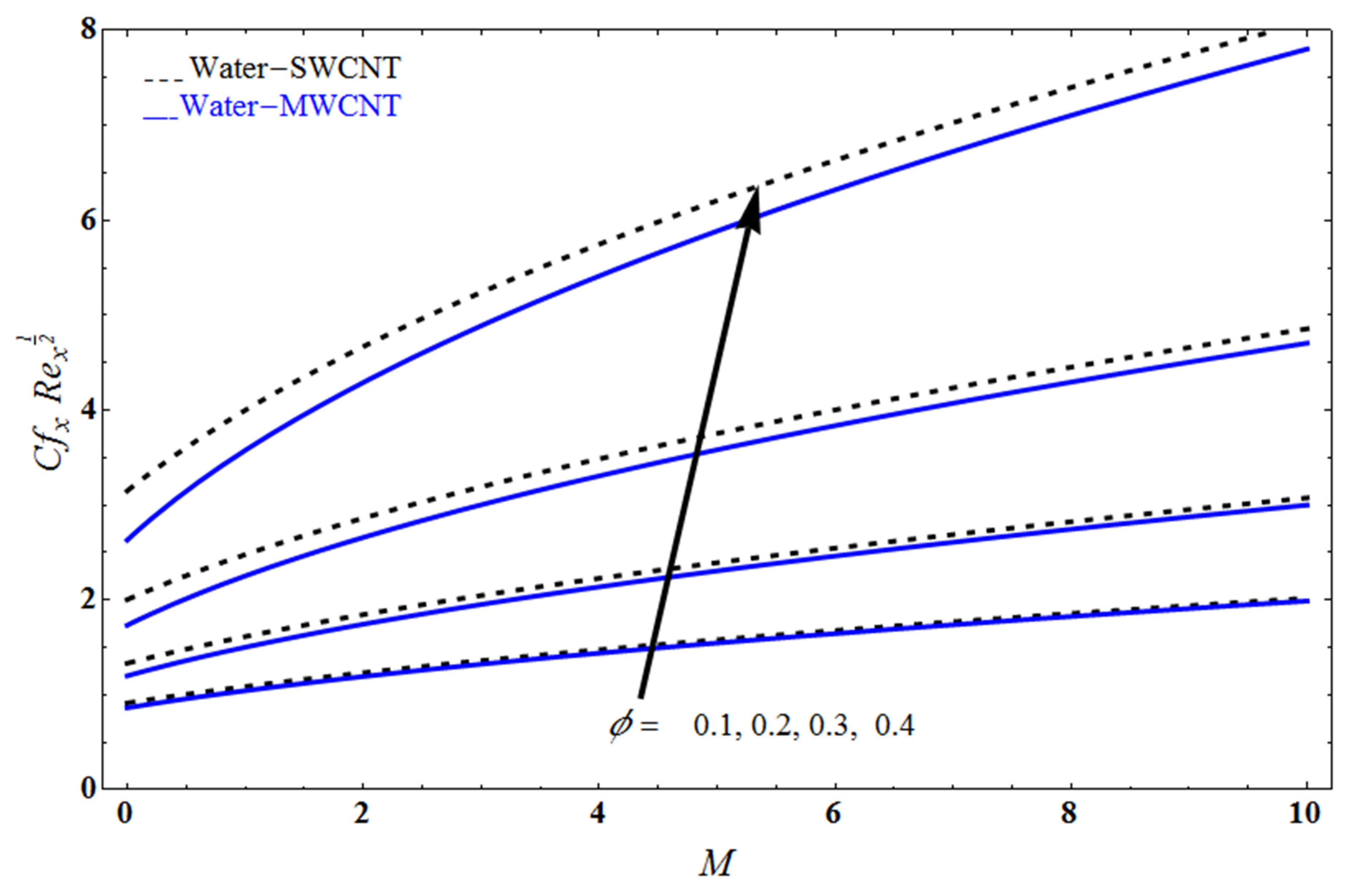
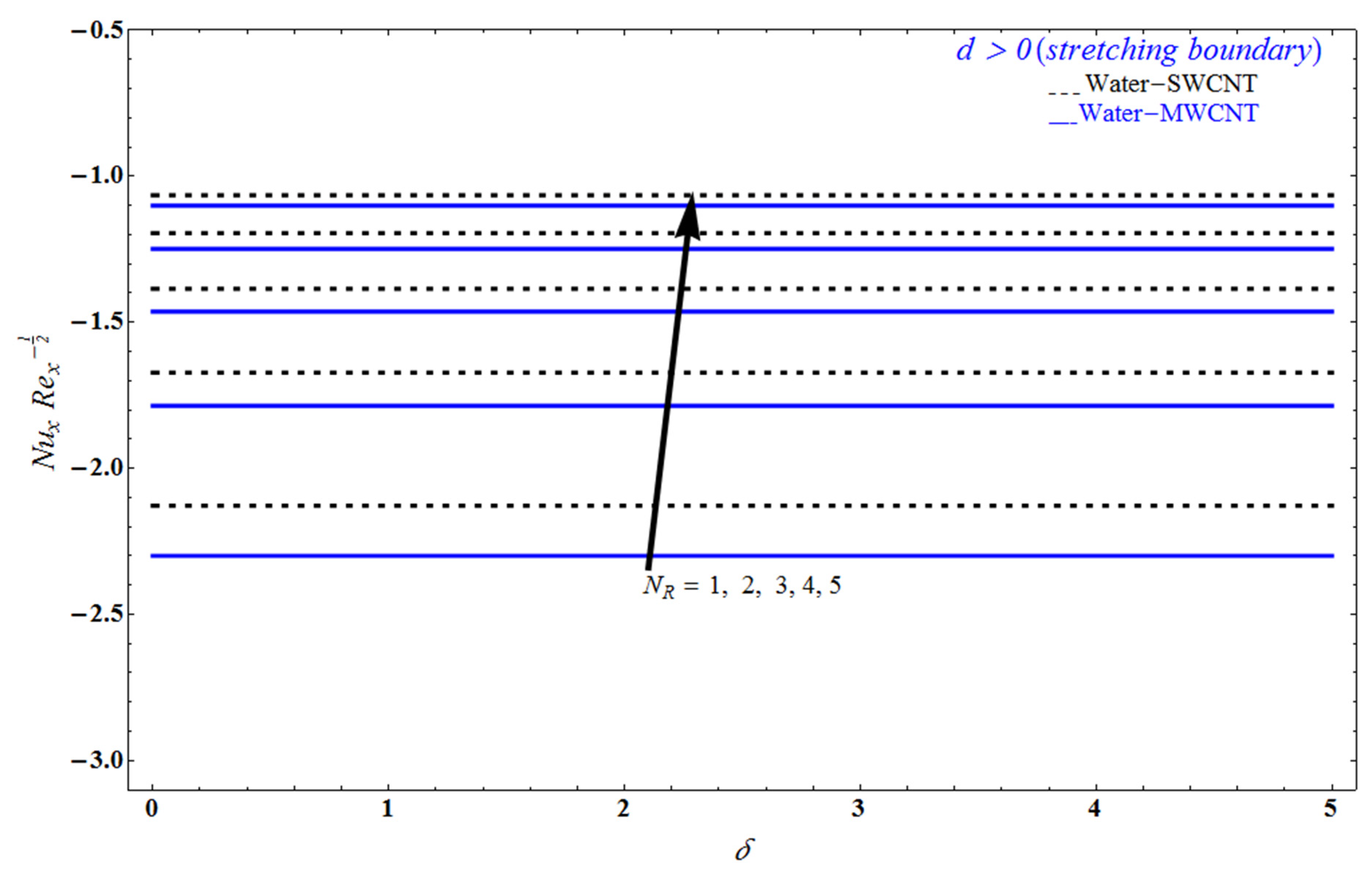
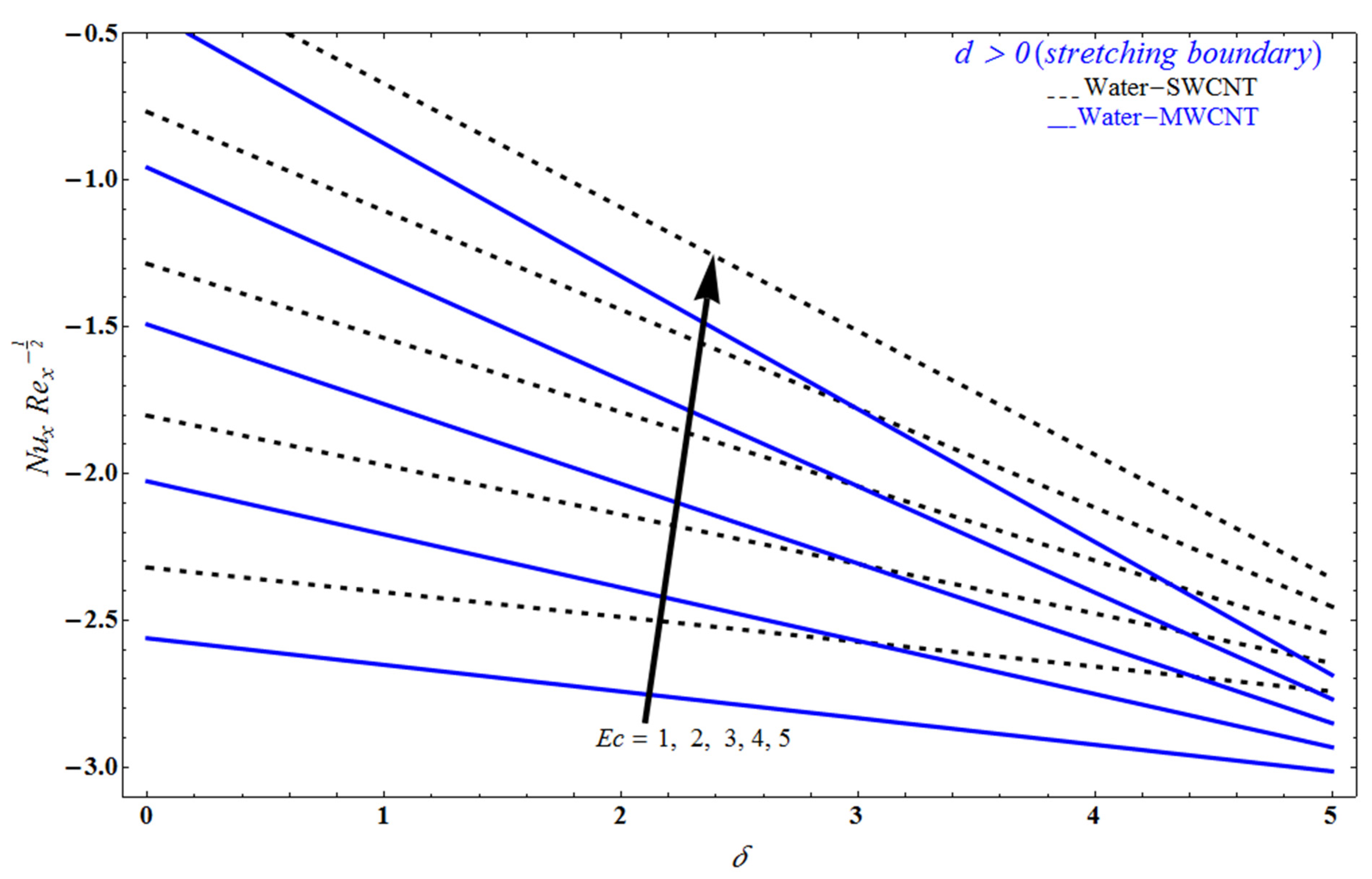
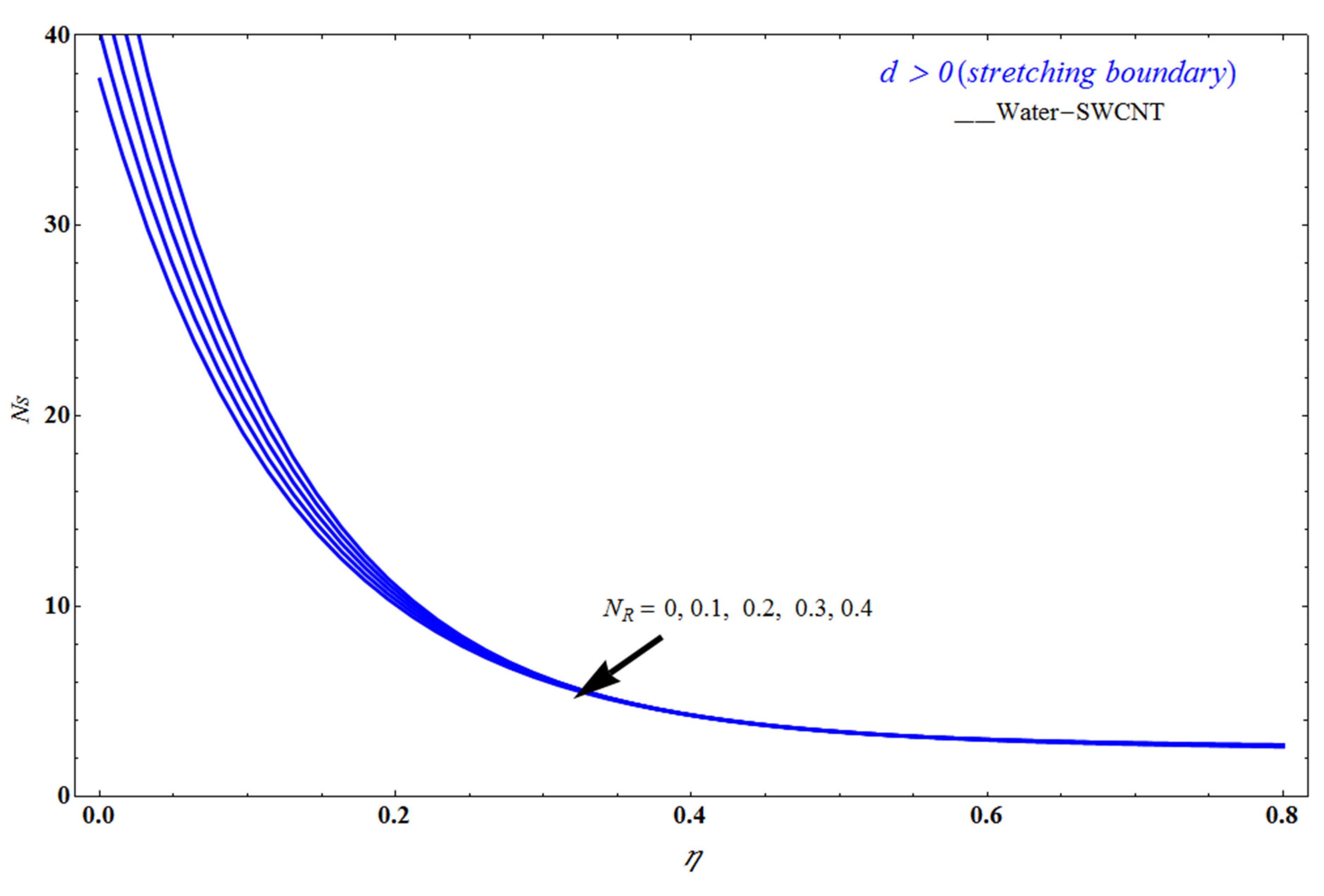
5. Result and Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| List of Symbols | Definitions | SI Units |
| a | constants | [s−1] |
| non-uniform heat production | [-] | |
| non-uniform heat absorption | [-] | |
| strength of magnetic field | [W m−2] | |
| non-uniform heat production | [-] | |
| non-uniform heat absorption | [-] | |
| constant | [-] | |
| CP | specific heat at constant pressure | [J K−1 kg−1] |
| d | stretching parameter | [-] |
| f | similarity variable | [-] |
| mean absorption coefficient | [m−2] | |
| elastic parameter | [-] | |
| M | Hartmann number | [-] |
| Pr | Prandtl number | [-] |
| radiative heat flux | [J s−1 m−2] | |
| heat flux at the wall | [J s−1 m−2] | |
| non-uniform heat generation/absorption | [-] | |
| constant | [-] | |
| radiation number | [-] | |
| local Reynolds number | [-] | |
| T | temperature | [K] |
| ambient temperature | [K] | |
| surface temperature | [K] | |
| u, v | velocity component | [m s−1] |
| VC | suction/injection | [m s−1] |
| x, y | coordinate along the sheet | [m] |
| Greek symbols | ||
| α | thermal diffusivity | [m2 s−1] |
| solution domain | [-] | |
| Casson fluid | [-] | |
| elastic deformation | [-] | |
| Brinkman number | [-] | |
| dimensionless temperature difference | [-] | |
| thermal conductivity | [mol m−3] | |
| kinematic viscosity | [] | |
| similarity variable | [-] | |
| dynamic viscosity | [] | |
| density | [] | |
| Stefan-Boltzmann constant | [] | |
| inclined angle | [rad] | |
| volume fraction of nanoparticle | [-] | |
| Subscript | ||
| f | base fluid | [-] |
| nf | nano fluid | [-] |
| w | wall condition | [-] |
| For from the sheet | [-] | |
| Abbreviations | ||
| B. Cs | boundary conditions | [-] |
| CNTs | carbon nanotubes | [-] |
| SWCNT | single-wall CNTs | [-] |
| MWCNT | multi-wall CNTs | [-] |
| MHD | magnetohydrodynamics | [-] |
| EG | Entropy generation | [-] |
References
- Fisher, E.G. Extrusion of Plastics, 3rd ed.; Newnes-Butterworld: London, UK, 1976; Volume 16, pp. 52–53. [Google Scholar]
- Nandy, S.K. MHD Stagnation-Point Flow of Casson Fluid and Heat Transfer over a Stretching Sheet with Thermal Radiation. J. Thermodyn. 2013, 9, 169674. [Google Scholar]
- Mabood, F.; Das, K. Outlining the impact of melting on MHD Casson fluid flow past a stretching sheet in a porous medium with radiation. Heliyon 2019, 5, e01216. [Google Scholar] [CrossRef] [PubMed]
- Crane, L.J. Flow past a stretching plate. Z. Angew. Math. Phys. 1990, 21, 645–647. [Google Scholar] [CrossRef]
- Andersson, H.; Bech, K.; Dandapat, B. Magnetohydrodynamic flow of a power-law fluid over a stretching sheet. Int. J. Non-Linear Mech. 1992, 27, 929–936. [Google Scholar] [CrossRef]
- Andersson, H.I. MHD flow of a viscoelastic fluid past a stretching surface. Acta Mech. 1992, 95, 227–230. [Google Scholar] [CrossRef]
- Fang, T.; Zhang, J. Closed-form exact solutions of MHD viscous flow over a shrinking sheet. Commun. Non-Linear Sci. Numer. Simul. 2009, 14, 2853–2857. [Google Scholar] [CrossRef]
- Abolbashari, M.H.; Freidoonimehr, N.; Nazari, F.; Rashidi, M.M. Analytical modeling of entropy generation for Casson nano-fluid flow induced by a stretching surface. Adv. Powder Technol. 2015, 26, 542–552. [Google Scholar] [CrossRef]
- Souayeh, B.; Reddy, M.G.; Sreenivasulu, P.; Poornima, T.; Rahimi-Gorji, M.; Alarifi, I.M. Comparative analysis on non-linear radiative heat transfer on MHD Casson nanofluid past a thin needle. J. Mol. Liq. 2019, 284, 163–174. [Google Scholar] [CrossRef]
- Hakeem, A.A.; Renuka, P.; Ganesh, N.V.; Kalaivanan, R.; Ganga, B. Influence of inclined Lorentz forces on boundary layer flow of Casson fluid over an impermeable stretching sheet with heat transfer. J. Magn. Magn. Mater. 2016, 401, 354–361. [Google Scholar] [CrossRef]
- Aly, E.H.; Pop, I. MHD flow and heat transfer near stagnation point over a stretching/shrinking surface with partial slip and viscous dissipation: Hybrid nanofluid versus nanofluid. Powder Technol. 2020, 367, 192–205. [Google Scholar] [CrossRef]
- Aly, E.H.; Ebaid, A. MHD Marangoni boundary layer problem for hybrid nanofluids with thermal radiation. Int. J. Numer. Methods Heat Fluid Flow 2020, 31, 897–913. [Google Scholar] [CrossRef]
- Anusha, T.; Mahabaleshwar, U.S.; Sheikhnejad, Y. An MHD of Nanofluid Flow Over a Porous Stretching/Shrinking Plate with Mass Transpiration and Brinkman Ratio. Transp. Porous Media 2021, 142, 333–352. [Google Scholar] [CrossRef]
- Kumaran, G.; Sandeep, N. Thermophoresis and Brownian moment effects on parabolic flow of MHD Casson and Williamson fluids with cross diffusion. J. Mol. Liq. 2017, 233, 262–269. [Google Scholar] [CrossRef]
- Iijima, S. Helical microtubules of graphitic carbon. Nature 1991, 354, 56–58. [Google Scholar] [CrossRef]
- Khan, W.; Culham, R.; Haq, R.U. Heat Transfer Analysis of MHD Water Functionalized Carbon Nanotube Flow over a Static/Moving Wedge. J. Nanomater. 2015, 2015, 1–13. [Google Scholar] [CrossRef]
- Anuar, N.S.; Norfifah, B.; Norihan, M.A.; Haliza, R. Mixed Convection Flow and Heat Transfer of Carbon Nanotubes over an Exponentially Stretching/Shrinking Sheet with Suction and Slip Effect. J. Adv. Res. Fluid Mech. Therm. Sci. 2019, 59, 232–242. [Google Scholar]
- Khan, W.A.; Khan, Z.H.; Rahi, M. Fluid flow and heat transfer of carbon nanotubes along a flat plate with Navier slip boundary. Appl. Nanosci. 2014, 4, 633–641. [Google Scholar] [CrossRef]
- Shalini, J.; Manjeet, K.; Amit, P. Unsteady MHD chemically reacting mixed convection nano-fluids flow past an inclined pours stretching sheet with slip effect and variable thermal radiation and heat source. Sci. Direct 2018, 5, 6297–6312. [Google Scholar]
- Yana, S.R.; Mohsen, I.; Mikhali, A.S.; Ioan, I.; Hakan, F.; Oztope, M.A. Inclined Lorentz force impact on convective-radiative heat exchange of micropolar nanofluid inside a porous enclosure with tilted elliptical heater. Int. Commun. Heat Mass Transf. 2020, 117, 104762. [Google Scholar] [CrossRef]
- Mukhopadhyay, S.; Vajravelu, K. Diffusion of chemically reactive species in Casson fluid flow over an unsteady permeable stretching surface. J. Hydrodyn. 2013, 25, 591–598. [Google Scholar] [CrossRef]
- Sankar, D.; Lee, U. Two-fluid Casson model for pulsatile blood flow through stenosed arteries: A theoretical model. Commun. Non-Linear Sci. Numer. Simul. 2010, 15, 2086–2097. [Google Scholar] [CrossRef]
- Sneha, K.N.; Mahabaleshwar, U.S.; Chan, A.; Hatami, M. Investigation of radiation and MHD on non-Newtonian fluid flow over a stretching/shrinking sheet with CNTs and mass transpiration. Waves Random Complex Media 2022, 11, 1–20. [Google Scholar] [CrossRef]
- Bejan, A. The Method of Entropy Generation Minimization. In Energy and the Environment; Springer: Dordrecht, The Netherlands, 1999; pp. 11–22. [Google Scholar] [CrossRef]
- Khan, M.I.; Hafeez, M.; Hayat, T.; Khan, M.I.; Alsaedi, A. Magnetorotating flow of hybrid nanofluid with entropy generation. Comput. Methods Programs Biomed. 2020, 183, 105093. [Google Scholar] [CrossRef] [PubMed]
- Shafee, A.; Haq, R.U.; Sheikholeslami, M.; Herki, J.A.A.; Nguyen, T.K. An entropy generation analysis for MHD water based Fe3O4 ferrofluid through a porous semi annulus cavity via CVFEM. Int. Commun. Heat Mass Transf. 2019, 108, 104295. [Google Scholar] [CrossRef]
- Jamshed, W.; Aziz, A. Cattaneo–christov based study of tio 2-cuo/eg casson hybrid nanofluid flow over a stretching surface with entropy generation. Appl. Nanosci. 2018, 8, 685–698. [Google Scholar] [CrossRef]
- Sindhu, S.; Gireesha, B. Entropy generation analysis of hybrid nanofluid in a microchannel with slip flow, convective boundary and nonlinear heat flux. Int. J. Numer. Methods Heat Fluid Flow 2019, 3, 53–74. [Google Scholar] [CrossRef]
- Khan, M.I.; Qayyum, S.; Kadry, S.; Khan, W.A.; Abbas, S.Z. Irreversibility Analysis and Heat Transport in Squeezing Nanoliquid Flow of Non-Newtonian (Second-Grade) Fluid Between Infinite Plates with Activation Energy. Arab. J. Sci. Eng. 2020, 45, 4939–4947. [Google Scholar] [CrossRef]
- Mumraiz, S.; Ali, A.; Awais, M.; Shutaywi, M.; Shah, Z. Entropy generation in electrical magnetohydrodynamic flow of Al2O3/Cu-H2O hybrid nanofluid with non-uniform heat flux. J. Therm. Anal. Calorim. 2021, 143, 2135–2148. [Google Scholar] [CrossRef]
- Reddy, P.B.A. Biomedical aspects of entropy generation on electromagnet hydrodynamic blood flow of hybrid nanofluid with nonlinear thermal radiation and non-uniform heat source/sink. Eur. Phys. J. Plus 2020, 135, 852. [Google Scholar] [CrossRef]
- Hayat, T.; Tamoor, M.; Khan, M.I.; Alsaedi, A. Numerical simulation for nonlinear radiative flow by convective cylinder. Results Phys. 2016, 6, 1031–1035. [Google Scholar] [CrossRef]
- Sneha, K.N.; Mahabaleshwar, U.S.; Bennacer, R.; Ganaoui, M.E. Darcy Brinkman Equations for Hybrid Dusty Nanofluid Flow with Heat Transfer and Mass Transpiration. Computation 2021, 9, 118. [Google Scholar] [CrossRef]
- Vishalakshi, A.B.; Mahabaleshwar, U.S.; Sarris, I.E. An MHD Fluid Flow over a Porous Stretching/Shrinking Sheet with Slips and Mass Transpiration. Micromachines 2022, 13, 116. [Google Scholar] [CrossRef] [PubMed]
- Xue, Q.Z. Model for thermal conductivity of carbon nanotube-based composites. Phys. B Condens. Matter 2005, 368, 302–307. [Google Scholar] [CrossRef]
- Anuar, N.S.; Bachok, N.; Turkyilmazoglu, M.; Arifin, N.M.; Rosali, H. Analytical and stability analysis of MHD deforming vertical surface in carbon nanotubes. Alex. Eng. J. 2020, 59, 497–507. [Google Scholar] [CrossRef]
- Ali, L.; Ali, B.; Ghori, M.B. Melting effect on Cattaneo–Christov and thermal radiation features for aligned MHD nanofluid flow comprising microorganisms to leading edge: FEM approach. Comput. Math. Appl. 2022, 109, 260–269. [Google Scholar] [CrossRef]
- Ali, L.; Ali, B.; Liu, X.; Iqbal, T.; Zulqarnain, R.M.; Javid, M. A comparative study of unsteady MHD Falkner–Skan wedge flow for non-Newtonian nanofluids considering thermal radiation and activation energy. Chin. J. Phys. 2022, 77, 1625–1638. [Google Scholar] [CrossRef]
- Ali, L.; Ali, B.; Liu, X.; Ahmed, S.; Shah, M.A. Analysis of bio-convective MHD Blasius and Sakiadis flow with Cattaneo-Christov heat flux model and chemical reaction. Chin. J. Phys. 2022, 77, 1963–1975. [Google Scholar] [CrossRef]
- Ali, L.; Liu, X.; Ali, B.; Abdal, S.; Zulqarnain, R.M. Finite element analysis of unsteady MHD Blasius and Sakiadis flow with radiation and thermal convection using Cattaneo-Christov heat flux model. Phys. Scr. 2021, 96, 125219. [Google Scholar] [CrossRef]
- Siddheshwar, P.; Mahabaleswar, U. Effects of radiation and heat source on MHD flow of a viscoelastic liquid and heat transfer over a stretching sheet. Int. J. Non-Linear Mech. 2005, 40, 807–820. [Google Scholar] [CrossRef]
- Mahabaleshwar, U.S.; Anusha, T.; Sakanaka, P.H.; Bhattacharyya, S. Impact of inclined Lorentz force and Schmidt number on chemically reactive Newtonian fluid flow on a stretchable surface when Stefan blowing and thermal radiation are significant. Arab. J. Sci. Eng. 2021, 46, 12427–12443. [Google Scholar] [CrossRef]
- Pavlov, K.B. Magnetohydrodynamic flow of an incompressible viscous liquid caused by deformation of plane surface. Magn. Gidrodin. 1974, 4, 146–147. [Google Scholar]
- Siddheshwar, P.G.; Chan, A.; Mahabaleswar, U.S. Suction-induced magnetohydrodynamics of a viscoelastic fluid over a stretching surface within a porous medium. IMA J. Appl. Math. 2014, 79, 445–458. [Google Scholar] [CrossRef]





| Properties | SWCNT | MWCNT | H2O |
|---|---|---|---|
| 425 | 796 | 997 | |
| 2600 | 1600 | 4179 | |
| 6600 | 3000 | 0.613 | |
| 48,000,000 | 38,000,000 | 0.05 | |
| ------------ | ------------ |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sneha, K.N.; Mahabaleshwar, U.S.; Sharifpur, M.; Ahmadi, M.H.; Al-Bahrani, M. Entropy Analysis in MHD CNTS Flow Due to a Stretching Surface with Thermal Radiation and Heat Source/Sink. Mathematics 2022, 10, 3404. https://doi.org/10.3390/math10183404
Sneha KN, Mahabaleshwar US, Sharifpur M, Ahmadi MH, Al-Bahrani M. Entropy Analysis in MHD CNTS Flow Due to a Stretching Surface with Thermal Radiation and Heat Source/Sink. Mathematics. 2022; 10(18):3404. https://doi.org/10.3390/math10183404
Chicago/Turabian StyleSneha, K. N., U. S. Mahabaleshwar, Mohsen Sharifpur, Mohammad Hossein Ahmadi, and Mohammed Al-Bahrani. 2022. "Entropy Analysis in MHD CNTS Flow Due to a Stretching Surface with Thermal Radiation and Heat Source/Sink" Mathematics 10, no. 18: 3404. https://doi.org/10.3390/math10183404
APA StyleSneha, K. N., Mahabaleshwar, U. S., Sharifpur, M., Ahmadi, M. H., & Al-Bahrani, M. (2022). Entropy Analysis in MHD CNTS Flow Due to a Stretching Surface with Thermal Radiation and Heat Source/Sink. Mathematics, 10(18), 3404. https://doi.org/10.3390/math10183404







