Nonlinear Bending of Sandwich Plates with Graphene Nanoplatelets Reinforced Porous Composite Core under Various Loads and Boundary Conditions
Abstract
:1. Introduction
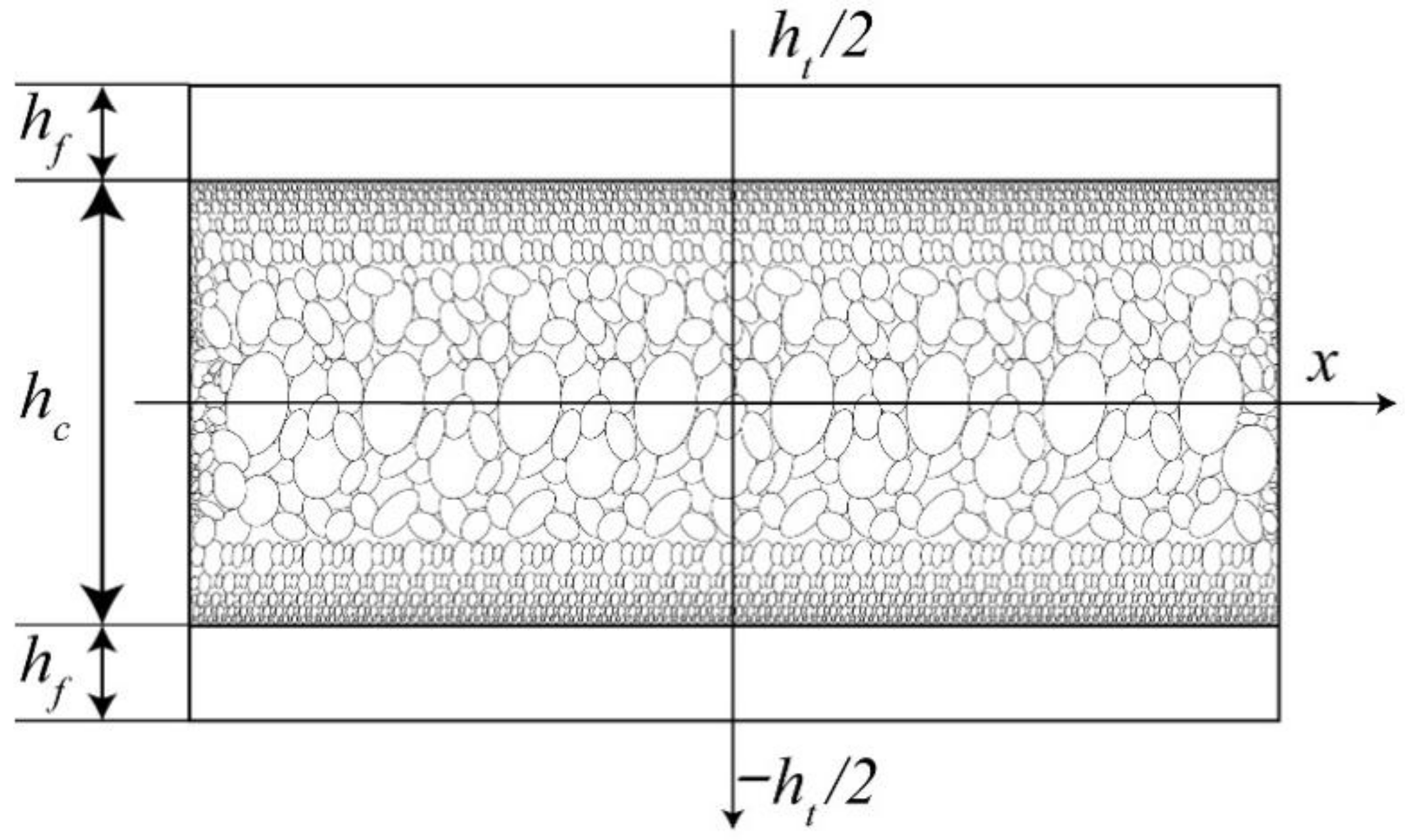
2. Characteristic Material Parameters
3. Theoretical Formulation
4. Finite Element Discretization
5. Numerical Results and Analysis
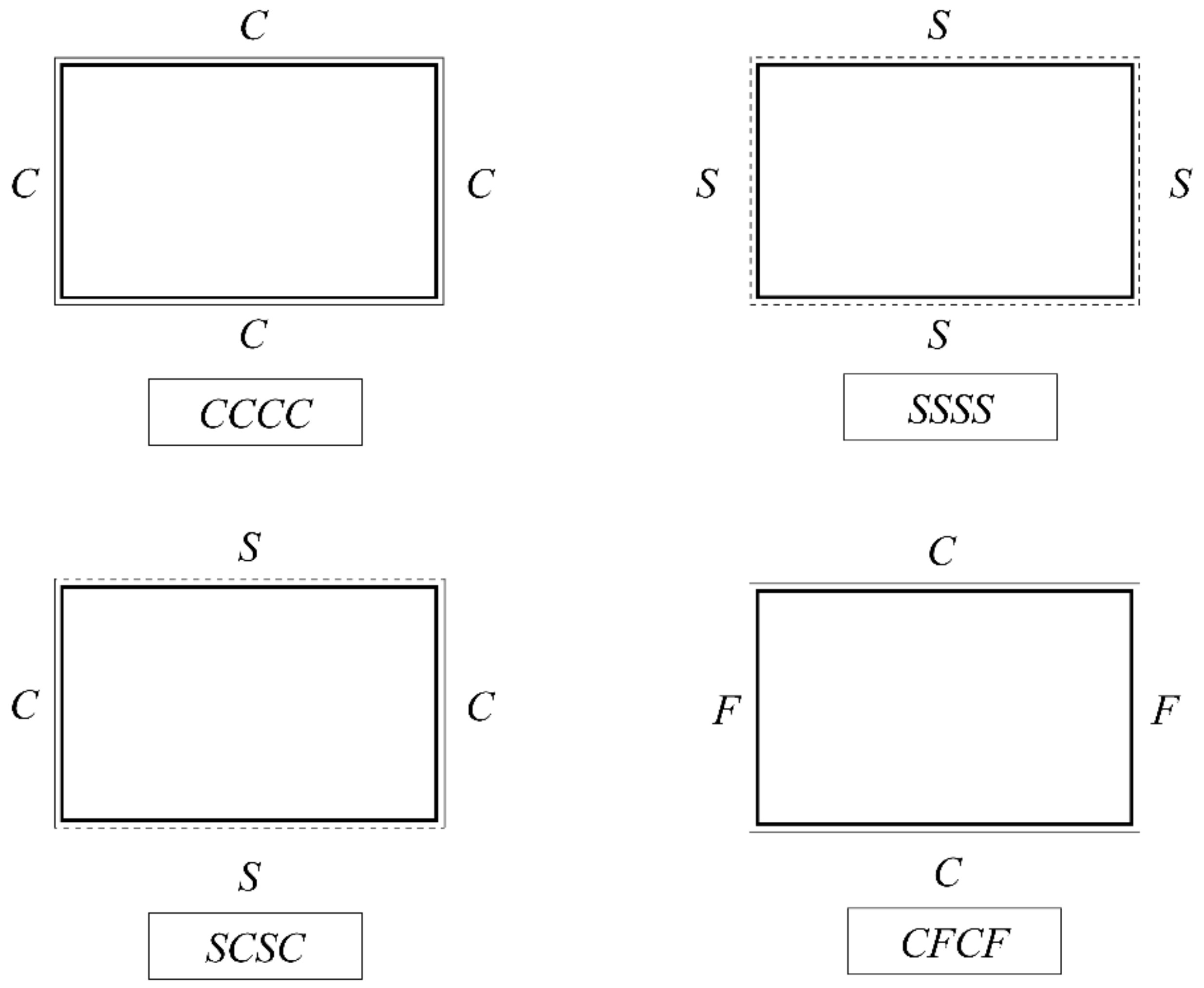
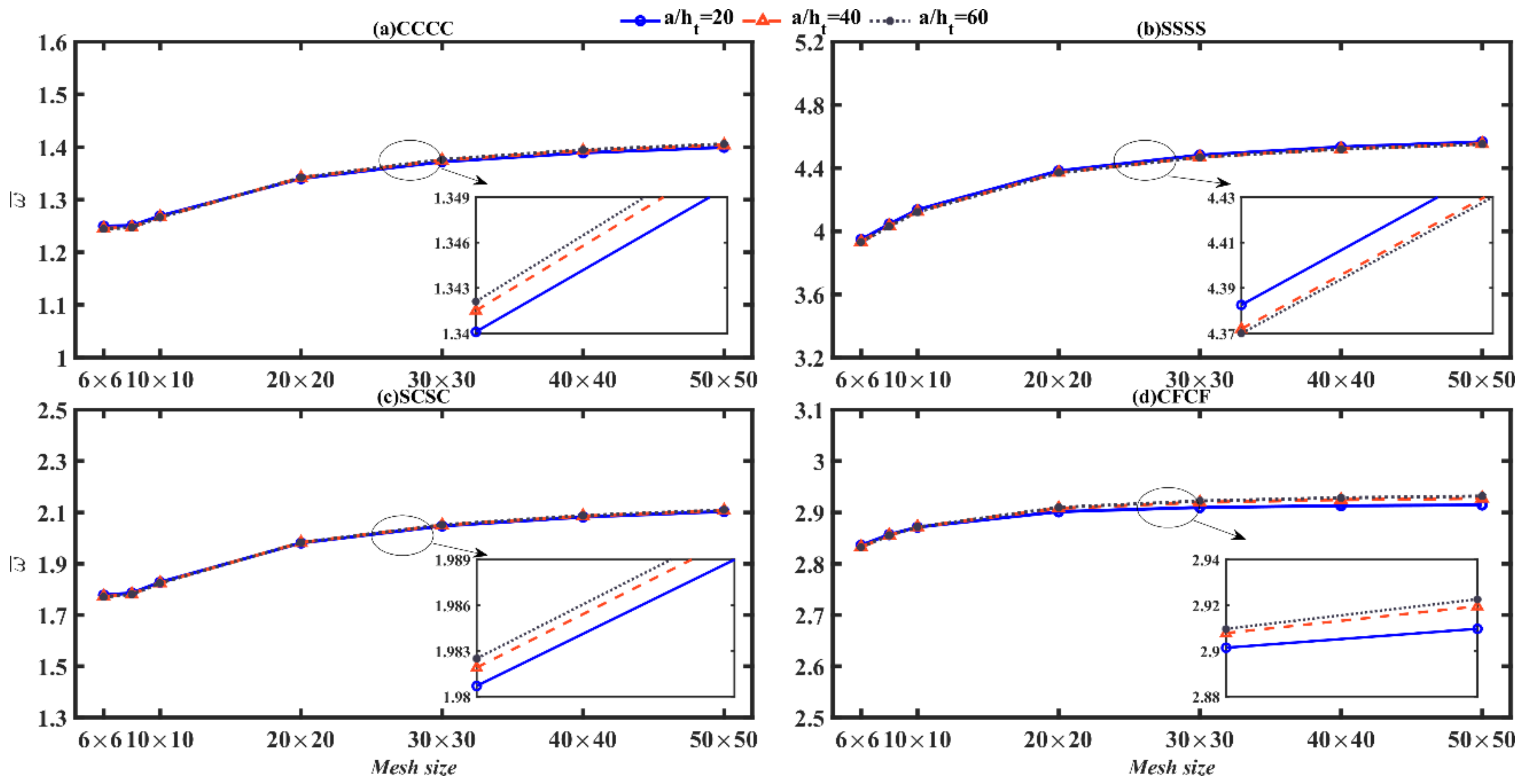
5.1. Parameters and Validation
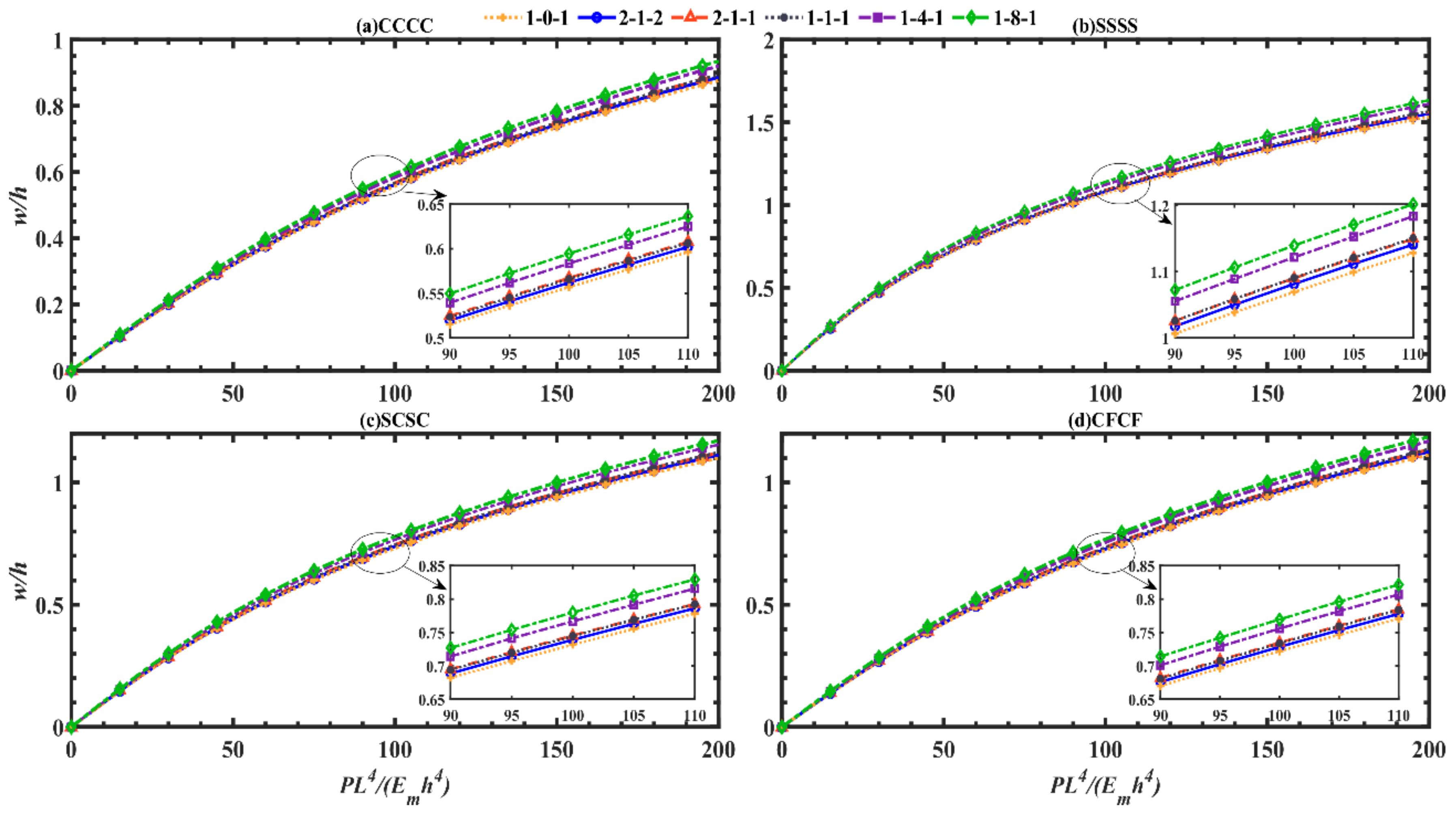
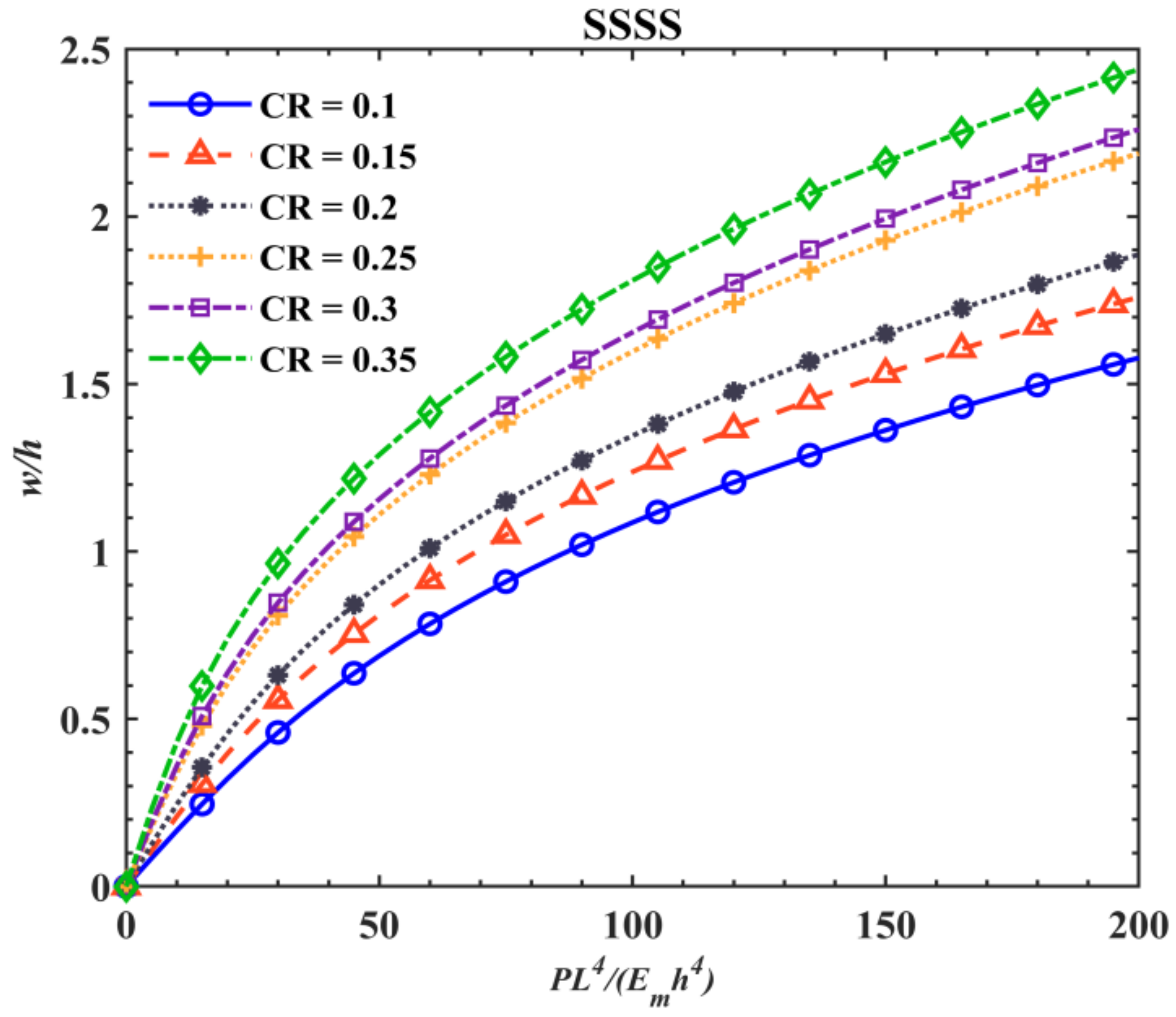
5.2. Nonlinear Bending Analysis of Sandwich Plates with GNRPC Core
6. Conclusions
- (1)
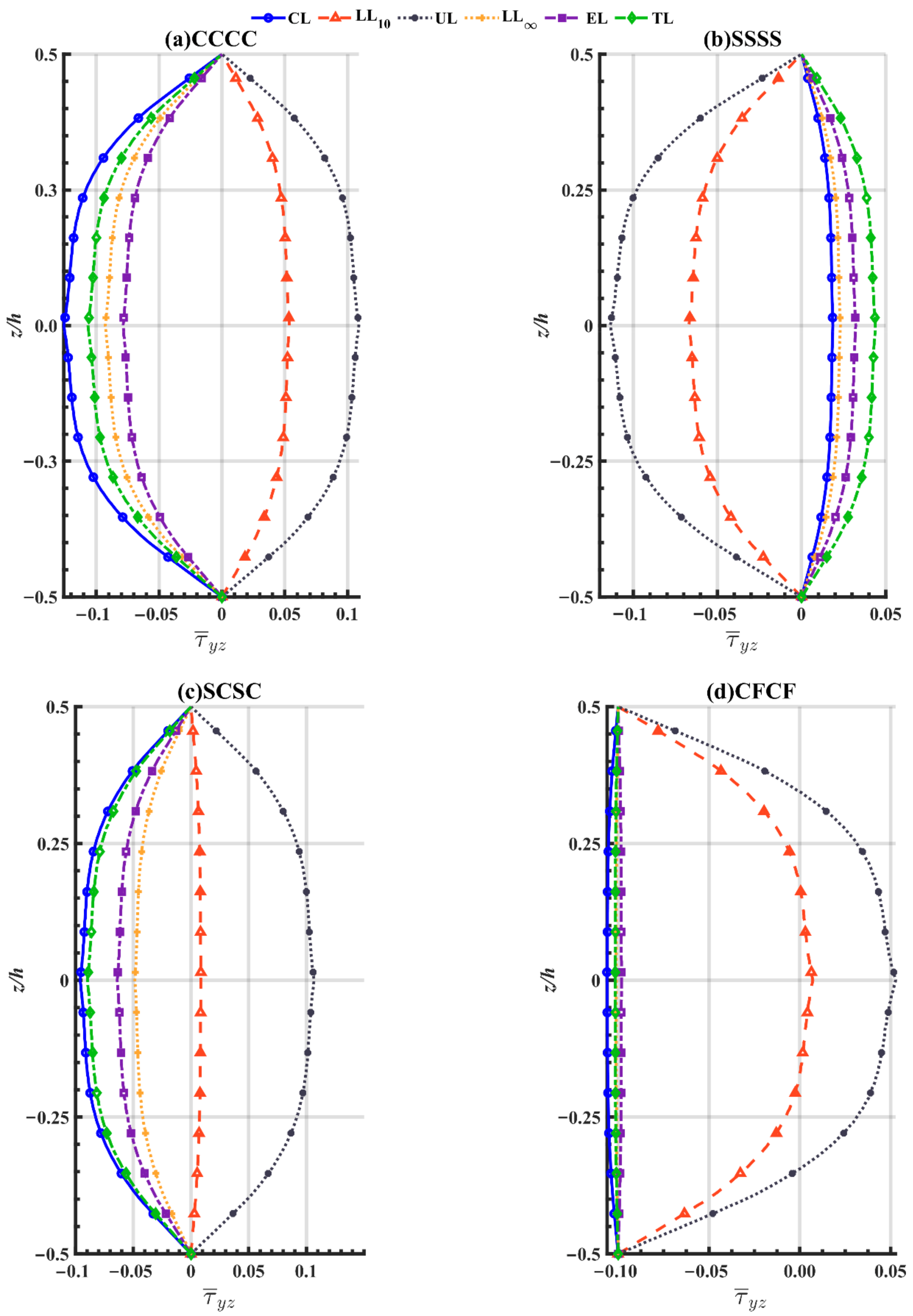
- The adopted higher order theory can significantly improve the simulation of the transverse deflection and different stresses in the thickness direction.
- (2)
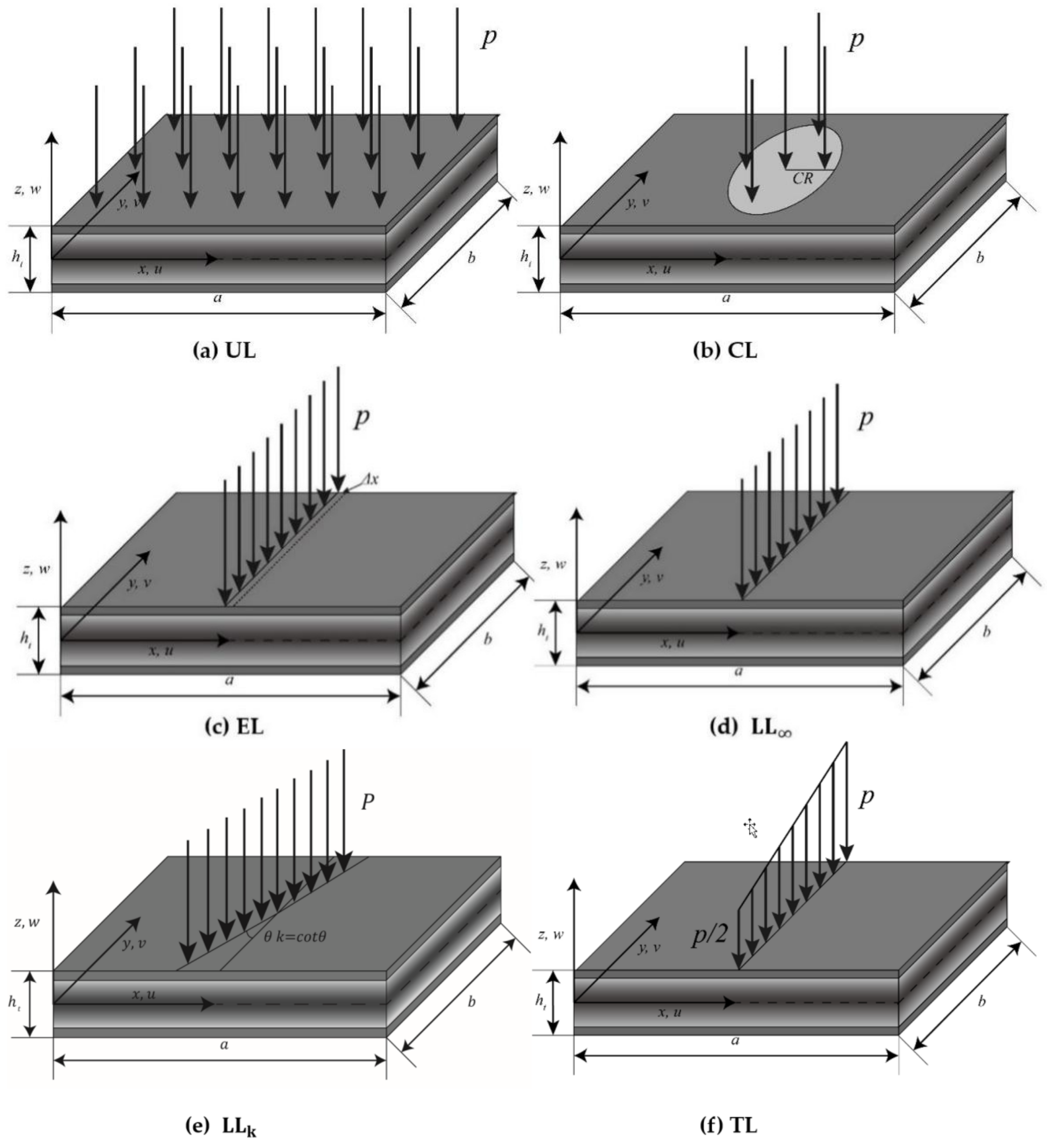
- All six types of loads have similar mechanical behaviors. According to the dimensionless central deformation caused by them, six load types are sorted with a descending order UL, , CL with CR = 0.1 m, , TL, EL for CCCC as well as CFCF boundary conditions and UL, , , CL with CR = 0.1 m, TL, EL for SSSS and SCSC boundary conditions.
- (3)
- The dimensionless central deflection is maximum for the UL and minimum for the EL compared to other examined four different types of load.
- (4)
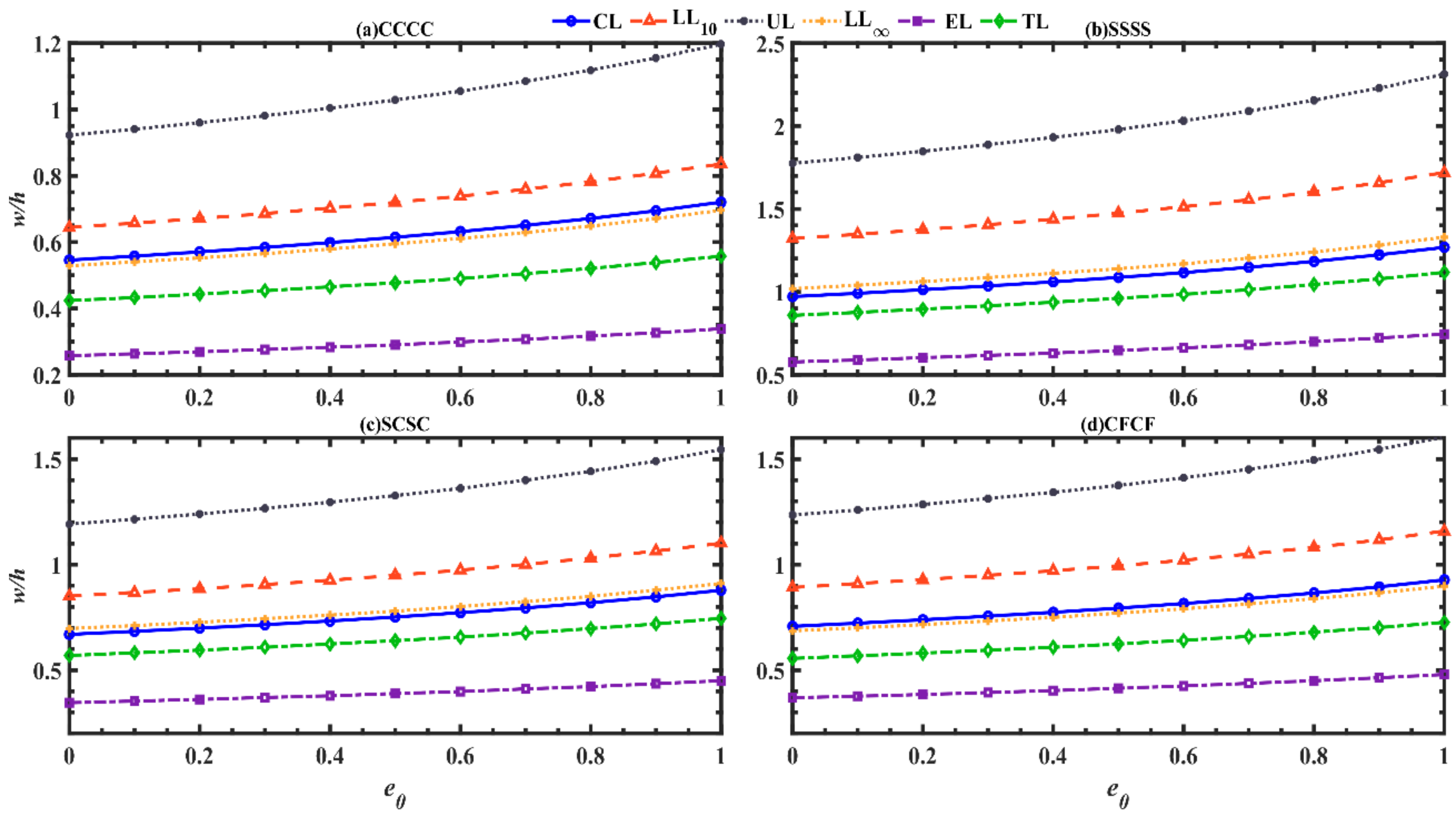
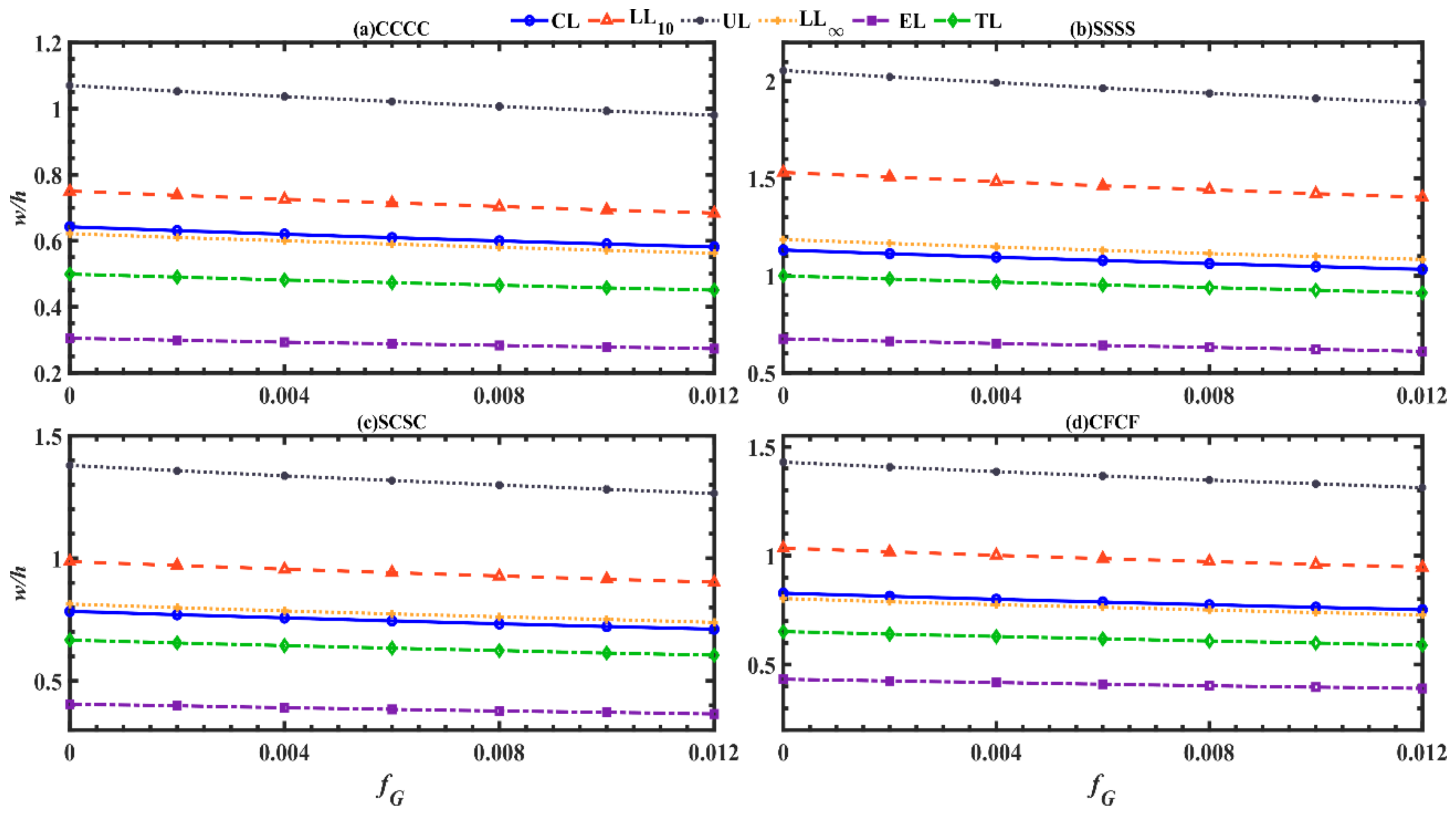
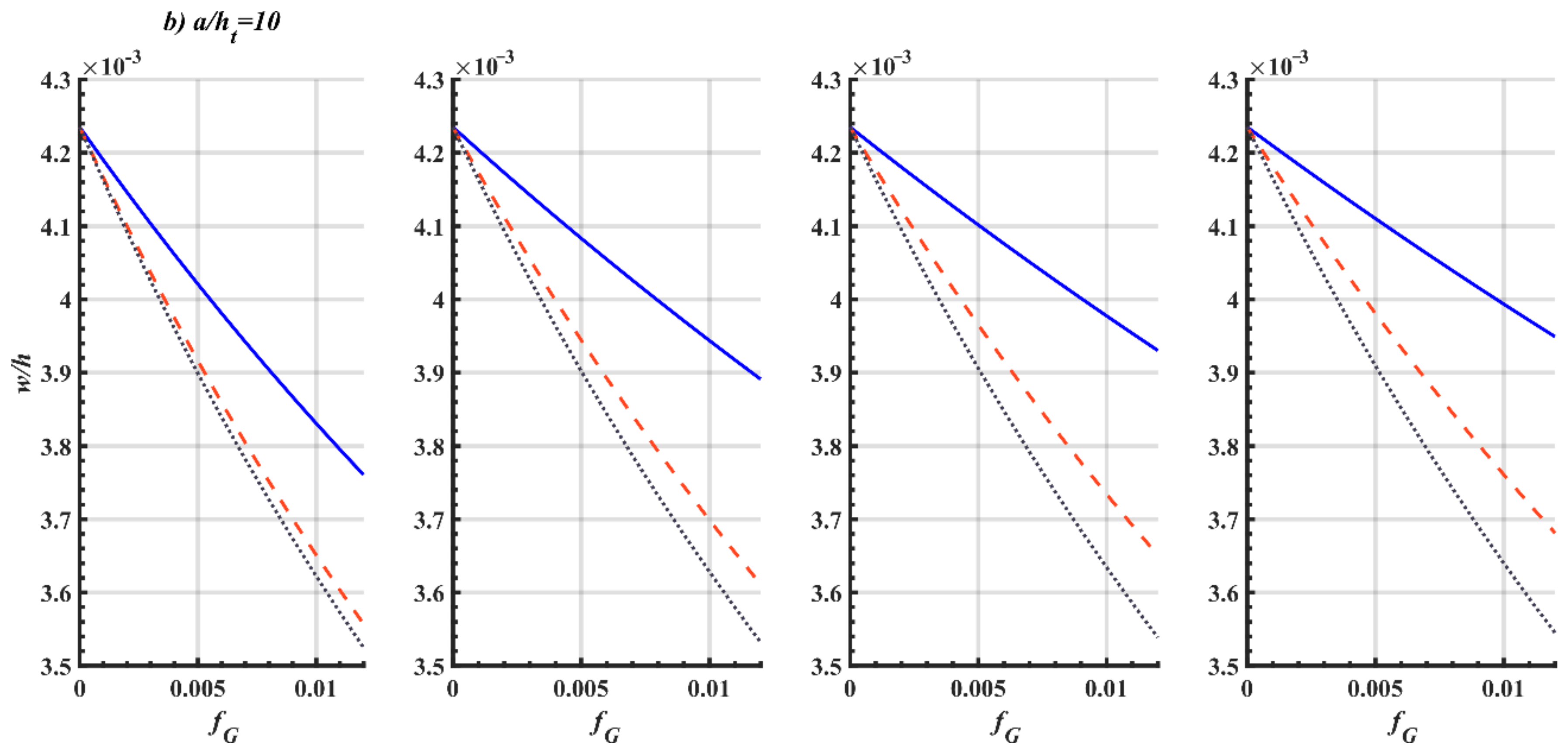
- Under the same boundary conditions, the dimensionless central nonlinear bending deflection increases with the enhancement of porosity coefficient, GPLs aspect ratio, thickness of porous core layer. However, it shows a reverse trend for the GPLs weight fraction, GPLs length-to-thickness ratio.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Lefebvre, L.P.; Banhart, J.; Dunand, D.C. Porous metals and metallic foams: Current status and recent developments. Adv. Eng. Mater. 2008, 10, 775–787. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Ye, C.; Zu, J.W. Nonlinear vibration of metal foam cylindrical shells re-inforced with graphene platelets. Aerosp. Sci. Technol. 2019, 85, 359–370. [Google Scholar] [CrossRef]
- Yaghoobi, H.; Taheri, F. Analytical solution and statistical analysis of buckling capacity of sand- wich plates with uniform and non-uniform porous core reinforced with graphene nanoplatelets. Compos. Struct. 2020, 252, 112700. [Google Scholar] [CrossRef]
- Rafiee, M.A.; Rafiee, J.; Wang, Z.; Song, H.H.; Yu, Z.Z.; Koratkar, N. Enhanced mechanical properties of nanocomposites at low graphene content. ACS Nano 2009, 3, 3884–3890. [Google Scholar] [CrossRef]
- Yang, J.; Wu, H.L.; Kitipornchai, S. Buckling and postbuckling of functionally graded multilayer graphene platelet-reinforced composite beams. Compos. Struct. 2017, 161, 111–118. [Google Scholar] [CrossRef]
- Guo, H.L.; Cao, S.Q.; Yang, T.Z.; Chen, Y.S. Vibration of laminated composite quadrilateral plates reinforced with graphene nanoplatelets using the element-free IMLS-Ritz method. Int. J. Mech. Sci. 2018, 142–143, 610–621. [Google Scholar] [CrossRef]
- Mao, J.J.; Zhang, W. Linear and nonlinear free and forced vibrations of graphene reinforced piezoelectric composite plate under external voltage excitation. Compos. Struct. 2018, 203, 551–565. [Google Scholar] [CrossRef]
- Wang, A.W.; Chen, H.Y.; Hao, Y.X.; Zhang, W. Vibration and bending behavior of functionally graded nanocomposite doubly-curved shallow shells reinforced by graphene nanoplatelets. Results Phys. 2018, 9, 550–559. [Google Scholar] [CrossRef]
- Fu, T.; Chen, Z.B.; Yu, H.Y.; Wang, Z.L.; Liu, X.X. An analytical study of sound transmission through corrugated core FGM sandwich plates with porous material. Compos. Part B Eng. 2018, 151, 161–172. [Google Scholar] [CrossRef]
- Zeng, S.; Wang, B.; Wang, K.F. Nonlinear vibration of piezoelcetric sandwich nanoplates with functionally graded porous core with consideration of flexoelectric effect. Compos. Struct. 2019, 207, 340–351. [Google Scholar] [CrossRef]
- Yu, Y.; Shen, H.S.; Wang, H.; Hui, D. Postbuckling of sandwich plates with graphene-reinforced composite face sheets in thermal environments. Compos. Part B Eng. 2018, 135, 72–83. [Google Scholar] [CrossRef]
- Allam, M.N.M.; Radwan, A.F.; Sobhy, M. Hygrothermal deformation of spinning FG graphene sandwich cylindrical shells having an auxetic core. Eng. Struct. 2022, 251, 11343. [Google Scholar] [CrossRef]
- Arefi, M.; Najafitabar, F. Buckling and free vibration analyses of a sandwich beam made of a soft core with FG-GNPs reinforced composite face-sheets using Ritz Method. Thin-Walled Struct. 2021, 158, 107200. [Google Scholar] [CrossRef]
- Nguyen, N.V.; Nguyen, X.H.; Nguyen, T.N.; Kang, J.; Lee, J. A comprehensive analysis of auxetic honeycomb sandwich plates with graphene nanoplatelets reinforcement. Compos. Struct. 2021, 259, 113213. [Google Scholar] [CrossRef]
- Aydogdu, M. A new shear deformation theory for laminated composite plates. Compos. Struct. 2009, 89, 94–101. [Google Scholar] [CrossRef]
- Li, C.; Shen, H.S.; Yang, J.; Wang, H. Low-velocity impact response of sandwich plates with GRC face sheets and FG auxetic 3D lattice cores. Eng. Anal. Bound. Elem. 2021, 132, 335–344. [Google Scholar] [CrossRef]
- Yadav, A.; Amabili, M.; Panda, S.K.; Dey, T. Nonlinear analysis of cylindrical sandwich shells with porous core and CNT reinforced face-sheets by higher-order thickness and shear deformation theory. Eur. J. Mech. A Solids 2021, 90, 104366. [Google Scholar] [CrossRef]
- Karimiasl, M.; Alibeigloo, A. Nonlinear free and forced vibration analysis of sandwich cylindrical panel with auxetic core and GPLRC facing sheets in hygrothermal environment. Thin-Walled Struct. 2022, 175, 109164. [Google Scholar] [CrossRef]
- Safaei, B.; Moradi-Dastjerdi, R.; Behdinan, K.; Chu, F. Critical buckling temperature and force in porous sandwich plates with CNT-reinforced nanocomposite layers. Aerosp. Sci. Technol. 2019, 91, 175–185. [Google Scholar] [CrossRef]
- Tao, C.; Dai, T. Isogeometric analysis for postbuckling of sandwich cylindrical shell panels with graphene platelet reinforced functionally graded porous core. Compos. Struct. 2021, 260, 113258. [Google Scholar] [CrossRef]
- Chen, X.H.; Shen, H.S. Thermo-mechanical postbuckling analysis of sandwich cylindrical panels with functionally graded auxetic GRMMC core supported by elastic foundations. Ocean. Eng. 2022, 247, 110661. [Google Scholar] [CrossRef]
- Chen, X.H.; Shen, H.S.; Xiang, Y. Thermo-mechanical postbuckling analysis of sandwich cylindrical shells with functionally graded auxetic GRMMC core surrounded by an elastic medium. Thin-Walled Struct. 2022, 171, 108755. [Google Scholar] [CrossRef]
- Twinkle, C.M.; Pitchaimani, J. Static stability and vibration behavior of graphene platelets reinforced porous sandwich cylindrical panel under non-uniform edge loads using semi-analytical approach. Compos. Struct. 2022, 280, 114837. [Google Scholar] [CrossRef]
- Li, Q.Y.; Wu, D.; Chen, X.J.; Liu, L.; Yu, Y.G.; Gao, W. Nonlinear vibration and dynamic buckling analyses of sandwich functionally graded porous plate with graphene platelet reinforcement resting on Winkler–Pasternak elastic foundation. Int. J. Mech. Sci. 2018, 148, 596–610. [Google Scholar] [CrossRef]
- Zhu, C.S.; Fang, X.Q.; Liu, J.X.; Nie, G.Q. Smart control of large amplitude vibration of porous piezoelectric conical sandwich panels resting on nonlinear elastic foundation. Compos. Struct. 2020, 246, 112384. [Google Scholar] [CrossRef]
- Polit, O.; Anant, C.; Anirudh, B.; Ganapathi, M. Functionally graded graphene reinforced porous nanocomposite curved beams: Bending and elastic stability using a higher-order model with thickness stretch effect. Compos. Part B Eng. 2019, 166, 310–327. [Google Scholar] [CrossRef]
- Zenkour, A. A simple four-unknown refined theory for bending analysis of functionally graded plates. Appl. Math. Model. 2013, 37, 9041–9051. [Google Scholar] [CrossRef]
- Ferreira, A.J.M. Matlab Codes for Finite Element Analysis: Solids and Structures; Springer: Dordrecht, The Netherlands, 2009. [Google Scholar]
- Walter, G. Numerical Analysis, 2nd ed.; Springer: New York, NY, USA, 2012. [Google Scholar]
- Wang, A.W.; Chen, H.Y.; Zhang, W. Nonlinear transient response of doubly curved shallow shells reinforced with graphene nanoplatelets subjected to blast loads considering thermal effects. Compos. Struct. 2019, 225, 111063. [Google Scholar] [CrossRef]
- Choe, J.C.; Huang, Q.; Yang, J.; Hu, H. An efficient approach to investigate the post-buckling behaviors of sandwich structures. Compos. Struct. 2018, 201, 377–388. [Google Scholar] [CrossRef]
- Yu, K.; Hu, H.; Tang, H.Y.; Giunta, G.; Potier-Ferry, M.; Belouettar, S. A novel two-dimensional finite element to study the instability phenomena of sandwich plates. Comput. Methods Appl. Mech. Eng. 2015, 283, 1117–1137. [Google Scholar] [CrossRef]
- Song, M.T.; Yang, J.; Kitipornchai, S. Bending and buckling analyses of functionally graded polymer composite plates reinforced with graphene nanoplatelets. Compos. Part B Eng. 2018, 134, 106–113. [Google Scholar] [CrossRef]
- Nguye-Xuan, H.; Tran, L.V.; Nguyen-Thoi, T.; Vu-Do, H.C. Analysis of functionally graded plates using an edge-based smoothed finite element method. Compos. Struct. 2011, 93, 3019–3039. [Google Scholar] [CrossRef]
- Gilhooley, D.F.; Batra, R.C.; Xiao, J.R.; McCarthy, M.A.; Gillespie, J.W. Analysis of thick functionally graded plates by using higher-order shear and normal deformable plate theory and MLPG method with radial basis functions. Compos. Struct. 2007, 80, 539–552. [Google Scholar] [CrossRef]
- Lee, Y.Y.; Zhao, X.; Liew, K.M. Thermoelastic analysis of functionally graded plates using the element-free kp-Ritz method. Smart Mater. Struct. 2009, 18, 035007. [Google Scholar] [CrossRef]






| Material | Young’s Modulus | Poisson’s Ratio | Density |
|---|---|---|---|
| ()-1 |
| Element Number | ||||
|---|---|---|---|---|
| 0 | 0.5 | 1 | 2 | |
| 0.1752 | 0.2392 | 0.2834 | 0.3296 | |
| 0.1750 | 0.2390 | 0.2830 | 0.3292 | |
| 0.1749 | 0.2389 | 0.2829 | 0.3291 | |
| 0.1749 | 0.2389 | 0.2828 | 0.3290 | |
| 0.1749 | 0.2388 | 0.2828 | 0.3290 | |
| Method | ||||
|---|---|---|---|---|
| 0 | 0.5 | 1 | 2 | |
| Present | 0.1752 | 0.2392 | 0.2834 | 0.3296 |
| Ref. [32] | 0.1717 | 0.2319 | 0.2716 | 0.3121 |
| Ref. [33] | 0.1703 | 0.2232 | 0.2522 | 0.2827 |
| Ref. [34] | 0.1671 | 0.2505 | 0.2905 | 0.3280 |
| Ref. [35] | 0.1722 | 0.2403 | 0.2811 | 0.3221 |
| Ansys | 0.1541 | 0.2594 | 0.2793 | 0.3013 |
| Boundary Conditions | Method | ||||
|---|---|---|---|---|---|
| 0 | 0.5 | 1 | 2 | ||
| CCCC | Present | 0.0692 | 0.0938 | 0.1113 | 0.1308 |
| Ref. [34] | 0.0731 | 0.1073 | 0.1253 | 0.1444 | |
| Ref. [35] | 0.0773 | 0.1034 | 0.1207 | 0.1404 | |
| SCSC | Present | 0.0941 | 0.1282 | 0.1522 | 0.1783 |
| Ref. [34] | 0.1017 | 0.1501 | 0.1751 | 0.2008 | |
| Ref. [35] | 0.1073 | 0.1447 | 0.1701 | 0.1953 | |
| SFSF | Present | 0.5177 | 0.6830 | 0.7795 | 0.8805 |
| Ref. [34] | 0.5019 | 0.7543 | 0.8708 | 0.9744 | |
| Ref. [35] | 0.5061 | 0.7029 | 0.8214 | 0.9423 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, X.; Wang, A.; Jiang, P.; Wu, S.; Sun, Y. Nonlinear Bending of Sandwich Plates with Graphene Nanoplatelets Reinforced Porous Composite Core under Various Loads and Boundary Conditions. Mathematics 2022, 10, 3396. https://doi.org/10.3390/math10183396
Fan X, Wang A, Jiang P, Wu S, Sun Y. Nonlinear Bending of Sandwich Plates with Graphene Nanoplatelets Reinforced Porous Composite Core under Various Loads and Boundary Conditions. Mathematics. 2022; 10(18):3396. https://doi.org/10.3390/math10183396
Chicago/Turabian StyleFan, Xudong, Aiwen Wang, Pengcheng Jiang, Sijin Wu, and Ying Sun. 2022. "Nonlinear Bending of Sandwich Plates with Graphene Nanoplatelets Reinforced Porous Composite Core under Various Loads and Boundary Conditions" Mathematics 10, no. 18: 3396. https://doi.org/10.3390/math10183396
APA StyleFan, X., Wang, A., Jiang, P., Wu, S., & Sun, Y. (2022). Nonlinear Bending of Sandwich Plates with Graphene Nanoplatelets Reinforced Porous Composite Core under Various Loads and Boundary Conditions. Mathematics, 10(18), 3396. https://doi.org/10.3390/math10183396






