Abstract
The seagull optimization algorithm (SOA), a well-known illustration of intelligent algorithms, has recently drawn a lot of academic interest. However, it has a variety of issues including slower convergence, poorer search accuracy, the single path for pursuing optimization, and the simple propensity to slip into local optimality. This paper suggests a multi-mechanism seagull optimization algorithm (GEN−SOA) that incorporates the generalized opposition-based, adaptive nonlinear weights, and evolutionary boundary constraints to address these demerits further. These methods are balanced and promoted the population variety and the capability to conduct global and local search. Compared with SOA, PSO, SCA, SSA, and BOA on 12 well-known test functions, the experimental results demonstrate that GEN-SOA has a higher accuracy and faster convergence than the other five algorithms, and it can find the global optimal solution beyond the local optimum. Furthermore, to verify the capability of GEN−SOA to solve practical problems, this paper applied GEN−SOA to solve two standard engineering optimization design problems including a welding optimization and a pressure vessel optimization, and the experimental results showed that it has significant advantages over SOA.
Keywords:
seagull optimization algorithm; nonlinear weights; evolutionary boundary constraints; opposition-based learning MSC:
68W50
1. Introduction
With the widespread popularity of computers in recent years, machine learning and algorithmic learning research have become an important resource for the development of the computer field and society at large. Nowadays, more and more scholars have been inspired by capturing the behavioral characteristics of plants and animals in nature and trying to simulate the behavioral characteristics or natural laws of certain types of plants and animals in nature to synthesize and propose many new population intelligence optimization algorithms to search and capture the optimal solutions to complex optimization problems in a certain spatial range.
Thus, it can be seen that the group intelligence optimization algorithm is a class of bionic algorithm that mimics the behaviors of organisms in nature. In recent years, due to its easy-to-implement process, relatively simple structure, and considerable effect, it has gained great momentum and widespread attention and has become a practical intelligence technology with rapid development. Typically, academics use multiple types of engineering optimization problems such as welding design optimization problems to determine whether the manufacturing costs required for welding applications can be minimized; pressure vessel optimization problems to determine whether the total cost of materials, forming, and welding for cylindrical vessels can be minimized; and compression spring optimization problems to determine the effectiveness of various algorithms by using those types of engineering optimization problems as a medium for algorithm performance testing. As far as we know, the more intensively studied swarm intelligence algorithms are: bat algorithm (BA) [1], particle swarm optimization (PSO) [2], whale optimization algorithm (WOA) [3], sine cosine algorithm (SCA) [4], grey wolf optimization (GWO) [5], butterfly optimization algorithm (BOA) [6], seagull optimization algorithm (SOA) [7], etc.
Among them, SOA is a new population intelligent optimization algorithm proposed by Gaurav Dhiman, Vijay Kumar, and other research scholars in 2019. The main characteristic advantage of this algorithm is that its overall construction composition is relatively simple, and the global search ability and local search ability are strong, which not only meets the overall requirements of the swarm intelligent optimization algorithm, but also has good results in solving some industrial production problems and classification optimization problems. However, although the seagull optimization algorithm is one of the most popular representatives of group intelligence optimization algorithms today, the basic seagull optimization algorithm still has some shortcomings. For example, the single action route of the seagull movement often leads to a lack of algorithm diversity, which causes the algorithm to fall into the local optimum in the late iteration or affects and reduces the convergence rate of the algorithm in the late iteration. In order to make the seagull algorithm in practical application achieve the optimal ideal effect, the initial seagull optimization algorithm should take appropriate strategies or necessary measures to increase the algorithm diversity, improve the ability to jump out of the local optimum, etc., so that the seagull optimization algorithm is improved in all aspects of the systematic improvement.
2. Related Work Overview
2.1. Status of Research
Since the development of intelligent optimization algorithms, the pace of the development of optimization design research is accelerating and has become widely popular in production life and other fields in countries around the world. Because traditional optimization algorithms are often ineffective and bring only weak benefits and low efficiency in production life, intelligent optimization algorithms have gradually been applied to many production life fields and have become an important research direction.
Among them, the seagull optimization algorithm, one of the popular algorithms in bionic metaheuristics, has been widely studied by scientists and related scholars at home and abroad, and various improvements have been made to the migration behavior and attack behavior of the seagull optimization algorithm to obtain more optimization strategies and better optimization effects.
2.1.1. Traditional Research Advances
Since Gaurav Dhiman and Vijay Kumar, two distinguished scholars, first proposed the underlying theory of the seagull optimization algorithm and its application to large-scale industrial engineering problems in 2018, it has triggered a large number of local research scholars to introduce new strategy models and construction methods based on the seagull optimization algorithm to enhance the optimization strength of the algorithm.
To address the slight shortcomings of the original seagull algorithm, Gaurav Dhiman, Krishna Kant Singh, Mukesh Soni, and Atulya Nagar proposed MoSOA [8], based on the basic development, which is a new multi-objective seagull global optimization algorithm for extensions to multi-objective problems. This multi-objective seagull global optimization algorithm introduces the concept of dynamic archiving, which gives it the property of caching non-dominated optimal solutions (Pareto solutions) and uses the roulette wheel selection method to select an effective archiving solution by simulating the migration behavior and attack behavior of seagulls. In the same year, a new optimization algorithm, EMoSOA [9], was proposed by Gaurav Dhiman, Krishna Kant Singh, Adam Slowik, and other research scholars. This algorithm is a new evolutionary multi-objective seagull global optimization algorithm proposed on the basis of the original MoSOA. In the EMoSOA algorithm, the authors not only introduced the concept of dynamic archiving, but also used the lattice mechanism and genetic operators to cache the non-dominated solutions (Pareto solutions) and used the roulette wheel method to find the best solution. In addition, along with the proposed multi-objective global optimization algorithm, the researchers used the proposed EMoSOA algorithm to verify four real-world engineering design problems, which optimizes the seagull optimization algorithm in multi-objective real-world problems and enhances the versatility and convergence of the seagull algorithm.
Meanwhile, in addition to the successive proposals of MoSOA and EMoSOA, Ahmed A. Ewees et al. [10] experimentally found that the global optimization search space of the seagull optimization algorithm varied linearly, which means that the global search capability cannot be fully utilized on SOA. They proposed an improved seagull optimization algorithm, ISOA, using Lévy flight and genetic operators. The algorithm can perform large spatial jumps by Lévy flight to make the search escape from the local optimal solution, while genetic operators can balance the weights between global survey and local search to speed up the optimization search process.
2.1.2. Recent Research Advances
In recent years, as young scholars have been studying swarm intelligence optimization algorithms, it is not difficult to find that the shortcomings of the optimization process are exposed due to the structural characteristics of the algorithm itself. For example, it is known that the randomization of parameters and the random initialization of the algorithm can affect the performance of the algorithm itself, and the population diversity can indirectly affect the algorithm and make it fall into local optimality. Therefore, scholars have tried to introduce different optimization strategies and improvement measures to optimize and improve the seagull algorithm, expecting to provide a systematic solution to the basic problems such as easily falling into a local optimum and poor diversity. To address the lack of convergence speed and find the optimal solution for the algorithm, Mao et al. [11] proposed an adaptive t-distribution seagull algorithm (ISOA) integrating improved logistics chaos and a sine cosine operator, and Wang et al. [12] also proposed a seagull optimization algorithm (CtSOA) based on chaos mapping with improved t-distribution variance. The former uses modified logistics chaos mapping to initialize the population and introduces a sine cosine operator to optimize the algorithm to coordinate the local and global search capabilities, while the latter introduces tent mapping to enable the initial seagull population to be uniformly distributed in the search space and uses t-distribution variation to balance the exploration and exploitation capabilities of the algorithm. Qin et al. [13] tried to improve the calculation of the value of the additional variable A and hoped to achieve an effect where the position of the seagull could be adjusted while using a nonlinear decreasing inertia weight to calculate the value of A. They expected to enhance the global search ability by introducing the random index value and Lévy flight strategy to greatly increase the randomness of the seagull flight to obtain a nonlinear inertia weight-based seagull optimization algorithm (I−SOA). In contrast, Wang et al. [14] first proposed a seagull optimization algorithm (GSCSOA) integrating golden sine guidance and the Sigmoid continuum, using the Sigmoid function as a nonlinear convergence factor for the seagull search process and using the golden sine mechanism to guide the population position update and improve the global and local search capability of the algorithm. Zhang et al. [15] proposed a new chaotic seagull optimization algorithm (MESOA) with multi-directional spiral search because it was considered that the seagull optimization algorithm would have a relatively single optimal path and optimal solution in the process of finding the optimal path and optimal solution, and the accuracy of the search needs to be improved. First, in order to make the gulls more uniform in distribution and closer to the target individuals in action, it uses chaotic sequences as a new strategy for population initialization; second, to increase the diversity of the algorithm, it solves the problem of a single flight path by increasing the spiral flight directions that the gulls can choose, which in turn logically increases the diversity of the algorithm.
3. Seagull Optimization Algorithm
Seagulls are a highly intelligent group of animals that exist on Earth and are now distributed around the globe in a variety of species and sizes. Seagulls are seasonal migratory birds that migrate according to seasonal climate changes to obtain sufficient food sources. The main idea of the seagull optimization algorithm is to simulate the migratory and aggressive behaviors of the seagulls themselves and to find the optimal solution by constantly updating the seagull positions.
3.1. Biological Characteristics
Seagulls are the most common seabirds in most coastal cities; they basically live in groups and use their intelligence to search for prey and attack them. Seagulls have two very important characteristic behaviors: one is migratory behavior and the other is aggressive behavior. Migration, as the name suggests, refers to the movement of animals from one place to another by their specific way of moving according to the alternation of climate, with the intention to seek sufficient food sources to maintain their energy supply. During the migration process, seagulls mainly fly in flocks, with each seagull in a different position on the way to avoid collisions between individuals. In a seagull group, each seagull can move in the direction of the best position, thus changing its position; at the same time, the gulls will carry out the necessary attack behavior to find food, and in the attack process, the seagull group will keep moving in a spiral form as a flight norm.
3.2. Biomathematical Modeling
Through the biological characteristics of the seagull population, an individual seagull is randomly selected and its migratory behavior and aggression are specified, described, and implemented using the following mathematical model.
3.2.1. Migration Behavior
The algorithm simulates how the seagull population moves from one location to another during the migration process. During this phase, individual seagulls should satisfy three conditions:
(1) Collision avoidance: In order to avoid collisions with neighbors (other seagulls), the algorithm calculates the new position of an individual gull by using an additional variable . The variable is the control to avoid collisions between neighboring seagulls.
As shown in Equations (1) and (2), indicates the new position obtained by the seagull movement, and this search position will not conflict with other seagull positions. indicates the current position of the seagull. denotes the number of iterations of the algorithm at the current time, and represents the largest number of iterations of the algorithm in operation. is an additional variable defined to avoid collisions with neighbors (other seagulls). is a hyperparameter defined by the algorithm and the value of this parameter is fixed to 2, so that the value of decreases linearly from 2 to 0 as the number of iterations is superimposed.
(2) Move in the direction of the best neighbor: To avoid overlapping with other seagulls, individual seagulls will move in the direction of their best neighbor.
where denotes the direction of the best seagull and denotes the location direction of the best neighbor (seagull). The above is a random number in the range , can disrupt the algorithm’s execution by performing its own random updates within the range of values chosen, preventing the algorithm from falling into a local optimum during execution. is another random number based on the value of , and the value of is used to weigh the global or local search of the algorithm.
(3) Approach to the best seagull’s location: After moving to the direction of the best neighbor, the individual seagull will move to the global optimal direction and finally reach a new location.
where combines the conditions for seagulls to avoid collision and move to the optimal individual, which can be expressed as another new position reached by the seagull, and also the distance between the current seagull and the optimal seagull.
3.2.2. Attacking Behavior
Seagulls are a class of highly intelligent creatures that are adept at using their history and experience in the search process. In the process of migration, due to the need for a long period to hunt and often carry out attack behavior, when seagulls attack their prey, they will first rely on their wings and their weight to maintain a high degree of stability, followed by a specific spiral motion behavior in flight, constantly changing their flight speed and angle of attack. When a seagull attacks, its motion in the three-dimensional plane is described as follows.
where refers to the flight radius of the spiral flight when the seagull performs the attack behavior, is a random number within the interval , while and are constants that define the shape of the spiral, usually defining the value of both to be 1, and is denoted as the base of the natural logarithm.
Above, is an updated expression based on a combination of migratory and attack behaviors to determine the final seagull search location.
4. Design of the Proposed Seagull Optimization Algorithm
4.1. Adaptive Nonlinear Weighting Strategy
In 2018, He et al. [16] proposed an improved whale optimization algorithm (EWOA) for a series of problems as the whale optimization algorithm is more likely to fall into local optimum, slow convergence speed, and low accuracy of the optimization search. In the above optimization algorithm, the authors combined the idea of using adaptive inertia weights in the particle swarm optimization algorithm to guide the population’s search for optimality, and introduced the adaptive strategy into the update formula of whale position for the first time, which was used to balance the adaptive ability of the algorithm’s global survey and local exploration. Meanwhile, in 2020, Zhao et al. [17] proposed a new nonlinear weighted adaptive whale optimization algorithm (NWAWOA) on top of the basic performance based on the whale optimization algorithm. The above new whale optimization algorithm not only solves the problems of convergence speed and optimization-seeking accuracy to a certain extent, but more importantly, it also provides a wide range of optimization strategies in the field of intelligent algorithms.
It is well-known that there are many important additional variables in the seagull optimization algorithm. These additional variables or update parameters not only make biological individuals behave in a way to avoid collision with other individuals, but the additional variables and corresponding parameters of the seagull optimization algorithm are also very important to coordinate the global survey and local exploration process of the algorithm compared to other metaheuristic optimization algorithms.
Thus, if we want to speed up the algorithm and improve its searchability, it is a good choice to try to give different weights to the algorithm in the updating process. The size of the weights for the seagull optimization algorithm is pivotal. When the weight value is larger, the algorithm converges faster, to a certain extent, to expand its own search range; when the weight value is small, the search range is reduced and the search accuracy is greatly improved to constantly approach the optimal individual search for the optimal solution. At the same time, it is not difficult to see that the traditional seagull optimization algorithm in the setting of additional parameters linearly decreases with the increase in the number of iterations, which will lead to the seagull in the search for neighboring positions, the update of the optimal position, and the process of determining the optimal solution being the corresponding deviation from the actual problem of nonlinear factors, reducing the accuracy of the algorithm in the resulting implementation results.
Therefore, in this paper, the nonlinear weights were subsequently introduced in the traditional seagull optimization algorithm, and the nonlinear weights were fused in Equation (10) to update the final seagull’s search position and make adaptations, as shown in the following expressions:
In this paper, is the range of , and ; is a constant; and is the best result according to many experiments. As a result, the weights were introduced into Equation (10), and the formula is shown in Equation (13).
In practical problem-solving applications, the search process is often carried out step-by-step with a non-linear search trend. To improve the search capability of the algorithm in a certain space and to avoid falling into problems such as local optimization, the process of changing the introduced nonlinear weights is shown in Figure 1.
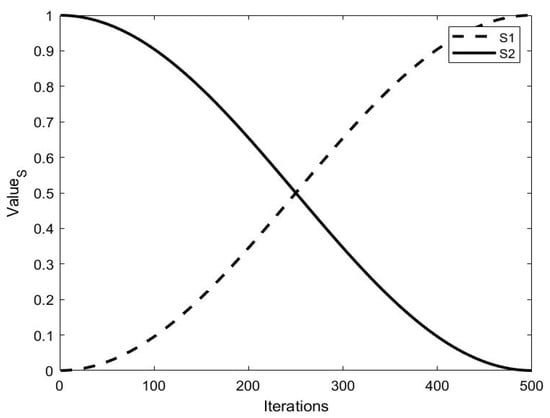
Figure 1.
The trend of the nonlinear weights with the number of iterations.
It can be seen from Figure 1 that exhibited a nonlinear increment with an increasing number of generations in the range of the maximum number of iterations, prompting the population to conduct a broader global survey in the early stage and leading the population as a whole to move sufficiently toward the optimal position. In contrast, showed a nonlinear decrease in the range of the maximum number of iterations with an increase in the number of generations so that it enhanced the concentration of the seagull population to carry out the local search in the later stage and greatly accelerated the convergence speed of the algorithm. In summary, the introduction of nonlinear weights not only balances the coordination of the algorithm in global surveying and local exploration, but also accelerates the algorithm’s own global and local search ability, which makes the search accuracy qualitatively improved in essence. Moreover, because of the specific spiral attack of each seagull, it will largely collide with the optimal individual during the spiral flight. For this reason, the introduction of nonlinear weights optimization can help the individual seagull behavior to maintain relative asynchrony and subsequently enhance the search accuracy again.
4.2. Evolutionary Boundary Constraint Handling Strategy
The essence of an optimization algorithm is to achieve the maximum optimization effect based on the algorithmic strategy, and a powerful algorithm is only one of the important components to achieving satisfactory results in a real sense. Another important component is how to properly handle constraints and limitations. From the perspective of optimization algorithm implementation, the boundary constraints of the corresponding algorithm are an important basis for achieving correct or even optimal results. Of course, the seagull optimization algorithm is no exception, as a new star of the population intelligence optimization algorithm, and this paper will also introduce a new boundary constraint handling strategy to improve the traditional seagull optimization algorithm.
A simple and effective evolutionary scheme for handling boundary constraints was first proposed by Gandomi [18] and other scholars in 2012, while in 2018, Zhao [19] proposed a firefly algorithm based on perturbation and boundary constraint handling mechanisms to overcome the shortcomings of the firefly optimization algorithm, in which an effective boundary constraint handling mechanism was employed to deal with the boundary constraints.
Among them, evolutionary boundary constraints processing means that when an individual crosses the boundary during the execution of the algorithm, a new solution is generated at that time, using the optimal solution of the current run and the corresponding boundary conditions, and the main processing mechanism of this process is as follows:
In Equation (14), denote the lower and upper boundaries of the -th individual, respectively; denotes the location of the transgressing seagull; denotes the location of the optimal seagull; and represents the random number in the interval . The processing of evolutionary boundary constraints has exceptional benefits and is highly adaptable. The boundary determination process is focused on the real-time update using the current optimal position, allowing the generated solution to be based on the optimal solution rather than an arbitrary random solution. The use of this strategy can significantly speed up the algorithm’s convergence and improve the algorithm’s optimization effect.
4.3. Opposition-Based Learning and Generalized Opposition-Based Learning
4.3.1. Opposition-Based Learning
Opposition-based learning is an optimization strategy proposed by Tizhooshs [20] in 2005, which has been widely used in intelligent computing in recent years due to its powerful optimization mechanism and has been applied in various intelligent optimization algorithms. The central idea of the opposition-based learning strategy is to select a feasible solution at random, compute the inverse solution to which it belongs, and select the better solution to become the next generation of individuals. However, the opposition-based learning strategy not only benefits from its good theoretical idea, but Tizhooshs also found through extensive research that the probability that the backward solution is closer to the global optimum than the current solution is as much as 50%, which means that the applied algorithm can be significantly improved in terms of population diversity and also greatly avoids the situation where the algorithm falls into the local optimum.
Thus, an opposition-based learning strategy was introduced into the metaheuristic algorithm to expand the current search range by calculating the inverse solution of the current solution to be able to find a more suitable candidate solution for the given problem, which effectively improves the accuracy and precision of the algorithm to find the best solution.
- (Definition 1): Opposite number
Suppose there exists any real number , where , then the opposite number obtained by reversing is
In addition, if the opposite number is found and the conceptual theory of multidimensional space is provided, the opposite point’s definition can be deduced
- (Definition 2): Opposite point.
Suppose that a target individual of dimension D is a point in the current search space, where , then the opposite point , which is expressed in the following form:
Collectively, for the opposition-based learning [21] strategy, the objects targeted by the basic definition are mostly general individuals, while the updated objects appearing in the algorithm update are mostly biological populations. If the algorithm takes into account choosing the best individuals to create the next generation population from a population perspective, it will still be able to indirectly obtain the opposite population through the generated opposite individuals, speeding up the algorithm’s convergence.
4.3.2. Generalized Opposition-Based Learning
Generalized opposition-based learning is an optimization strategy proposed by introducing a region transformation model based on opposition-based learning.
Among them, opposition-based learning is comparable to the generalized opposition-based learning strategy in that the search space of both is , and the principles and methods of implementation are largely the same. However, the current solution for the actual problem of the algorithm is the defined interval given by the problem; obviously, the search area formed by the candidate solutions is shrinking in the process of continuous search, and if the algorithm can converge to the global optimal solution in the iterative process, then the search area of the candidate solutions will eventually converge to the point . It can be seen that as the search area keeps shrinking, if the opposite solution is continuously generated in the original definition interval, the resulting opposite solution will fall out of the search area easily due to the definition interval, which will lead to a much lower convergence rate. Thus, in order to enhance the self-adaptive capability of the algorithm in practice, a dynamic generalized opposition-based learning strategy will be introduced to improve the convergence speed and operational accuracy of the algorithm in actual operation.
where is the number of populations; is the resulting dimension; is the number of iterations; and is the random number on the interval . The is the component of the solution of the current population in dimensions, is the opposite solution of in the search space, is the minimum in the j-dimensional search space, and represents the maximum value in the -dimensional search space.
4.4. GEN−SOA Algorithm Description
To address the shortcomings and defects of the initial seagull optimization algorithm, this paper proposed a seagull optimization algorithm that integrates nonlinear weights and evolutionary boundary processing mechanisms, and on this basis, a new seagull optimization algorithm (GEN−SOA) was generated by incorporating a generalized opposition-based learning strategy. The basic seagull optimization algorithm uses a random initialization method to arbitrarily select individuals in the initial population selection, which leads to an increase in the uncertainty of the algorithm in the optimization-seeking phase from the beginning and easily leads to a decrease in the diversity of the seagull population. Therefore, in this paper, after a large number of experimental comparative studies, a generalized opposition-based learning strategy was introduced to the seagull optimization algorithm, in which the optimal position of each generation of the seagull population is learned by generalized opposition-based learning and the corresponding inverse optimal solution is obtained. Meanwhile, the opposite population is sorted by the size of the requested fitness value, and the better seagull is selected as the new generation of individuals, and its fitness value is taken out and updated. Moreover, this can also substantially improve the population quality of the seagull optimization algorithm.
The generalized opposition-based learning optimization not only improves the diversity of the seagull population and accelerates the chance of the optimal individuals approaching the optimal solution in the search space, but also lays the necessary foundation for the improvement in local exploration. Second, in order to improve the operational accuracy and convergence speed of the seagull optimization algorithm in actual operation, the generalized opposition-based learning introduced in this paper can update the search boundary in time and keep the search boundary where the individuals are dynamically updated, improving the operational accuracy and convergence speed of the seagull optimization algorithm in actual operation.
In addition, this paper introduced nonlinear weights and evolutionary boundary constraint mechanisms. The application of nonlinear weights can optimize and improve the integrated mathematical formulation model of the seagull migration and predation process so that the seagull can adapt within the effective range in the process of determining the optimal position and maximizing the algorithm to achieve real-time tilt between global survey and local exploration. At the same time, to improve the algorithm execution efficiency and result accuracy, this paper focused on the important restriction significance of the position boundary to the gull’s search for the optimal. To prevent individuals from transgressing the search boundary in the process of finding the optimal, the evolutionary boundary constraint processing mechanism was introduced based on the original optimal position and was used to enhance the accuracy of the search for the optimal, improve the convergence speed of the algorithm, and provide the necessary guarantee to find the optimal solution.
In summary, the specific implementation steps and the diagram of the process of GEN−SOA are shown below:
Step 1: Initialize the population , initialize the parameters and , set the values , is taken randomly in , and is taken randomly in .
Step 2: Calculate the fitness value of each individual seagull in the population, find the position of the seagull with the best fitness value , and record the optimal solution at this time.
Step 3: The new position reached by the individual seagull is calculated from Equations (1), (3), and (5).
Step 4: From Equations (6)–(9) and (13), the final seagull search and attack positions are calculated.
Step 5: Equation (14) determines whether the location of the seagull is out of bounds, and if it is out of bounds, the position is updated according to the corresponding conditions.
Step 6: Update the position of the resulting best seagull and update the corresponding fitness value.
Step 7: From Equations (17) and (18), the opposite solution is generated by generalized opposition-based learning on the basis of the original population optimal solution , and choose the solution that retains the better fitness value of the two and update the optimal solution .
Step 8: If the end condition is met, the program is ready to end and output the result, otherwise skip to Step 2.
Step 9: At the end of the program execution, the optimal value and the optimal solution are output.
The diagram of the GEN−SOA process is shown in Figure 2 below:
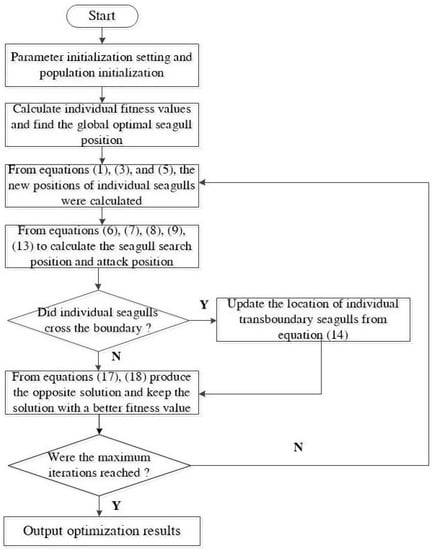
Figure 2.
A schematic diagram of the GEN−SOA process.
4.5. Summary of Optimization
This part mainly introduces the specific optimization mechanism of GEN−SOA in detail compared to the traditional seagull optimization algorithm, in which three main optimization mechanisms are introduced, namely: nonlinear weights, evolutionary boundary constraints, and generalized opposition-based learning. Through the auxiliary optimization of the above three mechanisms, resulting in GEN−SOA to a greater extent on the convergence speed of the algorithm, the accuracy of the optimal value and the algorithm in the global survey and local search of the balance of coordination were significantly improved, and the optimization effect was significant.
5. Experimental Simulation and Result Analysis
5.1. Simulation Experiment Environment and Parameter Setting
The experimental environment was as follows: A 64-bit Windows 10 operating system, Intel Core i5-8265U CPU, 8 GB memory, 1.8 GHz main frequency, and the experimental software by MATLAB R2018b were responsible for the execution of the algorithmic operations.
In the experimental parameter settings, in order to fully demonstrate the feasibility and accuracy of the GEN−SOA algorithm and to ensure the fairness of the algorithm results, all of the test data and test methods in the unified algorithm including the number of populations were set to 30, and the maximum number of iterations was the same as 500 generations in the simulation experiments. To avoid the influence of random deviation in the algorithm execution, all experiments were executed independently 30 times, the mean, variance, maximum, and minimum values of the obtained results were kept, and the best results of the independent experiments were taken for comparison experiments to ensure the accuracy of the experiments to the maximum extent. Thus, in this paper, GEN-SOA was implemented with , , the original definition of parameter , and the constants .
5.2. Test Functions
To verify the optimization effect of GN−SOA, 12 benchmark test functions derived from the seagull optimization algorithm theory and its applications for large-scale industrial engineering problems were used in this paper for the simulation and comparison experiments, and the obtained experimental results were statistically analyzed. The following are the 12 benchmark functions: F1 is Sphere, F2 is Schwefel 2.22, F3 is Schwefel 1.2, F4 is Schwefel 2. 21, F5 is Rosenbrock, F6 is Step, F7 is Quartic, F8 is Rastrigin, F9 is Ackley, F10 is Griewank, F11 is Penalized, and F12 is Kowalik, where F1−F7 is the single-peaked test function, F8−F11 is the multi-peak test function, and F12 is the multi-peak test function with fixed dimensions.
5.3. Simulation Results Analysis
The experimental data obtained from the comparison of the above simulation experiments by running tests are shown statistically in Table 1 and Table 2, Table 1 is a comparison of the GEN−SOA and SOA operation results, Table 2 is A comparison of the results of different algorithm operations (Table 1). The results of the six optimization algorithms presented in Table 1 and Table 2 include the optimal values obtained from the algorithm execution, the average values of 30 independent runs, and the standard deviation. The optimal values and average values recorded in Table 1 and Table 2 reflect the convergence speed and optimization accuracy of the algorithms during the basic runs, while the statistics of the standard deviations recorded can generally reflect the stability of the algorithm execution.

Table 1.
A comparison of the GEN−SOA and SOA operation results.

Table 2.
A comparison of the results of different algorithm operations.
5.3.1. GEN−SOA Compared with SOA
First, the optimized GEN-SOA was compared with the conventional SOA. For the single-peaked test function F1−F7, the convergence of the test algorithm during the execution could be determined by the unique global optimal solution based on the basic characteristics of the single-peaked test function. In contrast to the multi-peaked test function F8−F12, the multi-peaked test function could better verify the ability of the algorithm to perform global surveys. For the deterministic analysis, the results of the GEN−SOA and SOA experiments are shown in Table 1.
From the experimental results in Table 1, it can be seen that the GEN−SOA algorithm outperformed the SOA algorithm to a large extent in the execution of the test functions F1−F12. For the single-peak test functions F1−F4 and multi-peak test functions F8, F10, the optimal results of GEN−SOA reached the theoreticalf the test functions, and for the fixed-dimensional multi-peak test function F12, a optimal value olthough the difference between the two values under the comparison of the optimal values was not significant, the global weighting by nonlinear weighting for the average of 30 independent runs of the 12 test functions, the GEN−SOA algorithm had a smaller average value than the SOA algorithm, and the difference in value was at least 10 times; meanwhile, for the stability of the two algorithms, by comparing the standard deviations obtained from the test experiments, we found that the GEN−SOA algorithm had a smaller average value than the SOA algorithm. The standard deviation of the GEN−SOA algorithm was higher than that of the SOA algorithm, and the magnitude difference of F11 was at least 10 times higher than that of the SOA algorithm.
In summary, the experimental results of the table and the analysis of the function convergence graph showed that the GEN−SOA algorithm had good convergence in the range of the maximum number of iterations and could improve the optimization-seeking accuracy through multi-mechanism optimization and find the theoretical optimal value within a certain number of generations.
5.3.2. Comparison of GEN−SOA with Other Optimization Algorithms
To verify that GEN−SOA had a more outstanding performance in finding the best performance and could grasp enough competitiveness in the core area of optimization algorithms, PSO was chosen as one of the representatives of classical intelligent algorithms in this paper, while SCA, SSA, and BOA were chosen for the comparison experiments to measure the effectiveness of the seagull optimization algorithm in finding the best performance in new areas. Additionally, from the perspective of experimental intuitiveness, this paper took the optimal values of F1−F12 test functions for the SOA algorithm along with all control algorithms, with the mean and standard deviation shown in the statistics in Table 2, and plotted the convergence curves of each test function for convergence analysis. The convergence curves of the six optimization algorithms are shown in Figure 3.
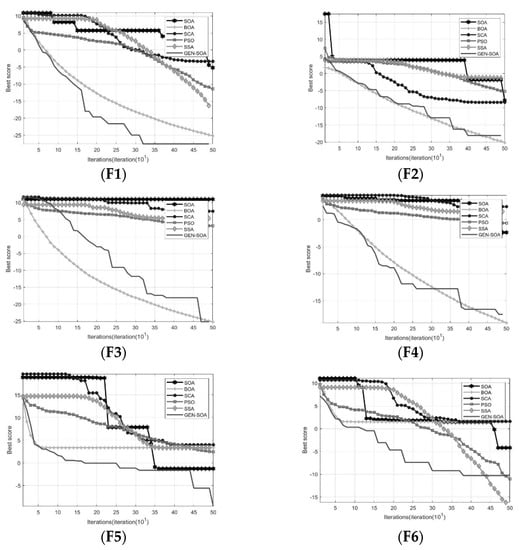
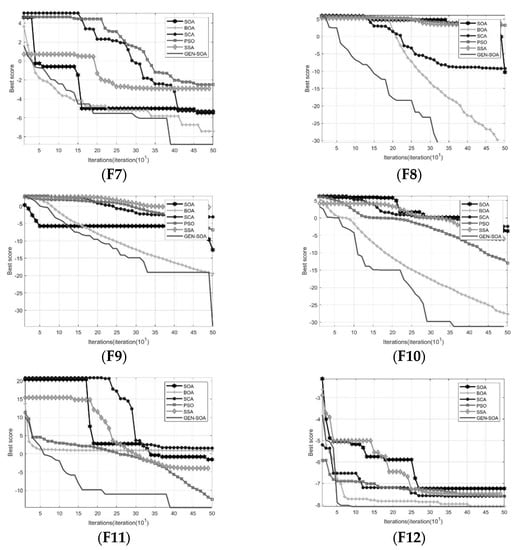
Figure 3.
The convergence curves of the six optimization algorithms.
(1) Algorithm accuracy analysis
For the experimental single-peak test functions F1−F7, SCA and SOA had weaker execution capability in terms of seeking accuracy compared to other optimization algorithms, while BOA and GEN-SOA were slightly better in terms of seeking the accuracy capability. For F1−F4, GEN-SOA could find the theoretical optimum within the maximum iteration range, while the convergence speed of BOA was also comparable to GEN-SOA in the first four test functions, and was on average nearly eight orders of magnitude or higher in numerical accuracy. For the test function F5, GEN−SOA remained the smallest in terms of optimal values, at which point the seagull characteristic behavior with that possessed by SOA helped the algorithm to improve the late local search ability and accelerate the convergence speed of the algorithm in the late stage. For F6, although SSA and PSO achieved smaller optimal values, thanks to the introduction of nonlinear weights and the restriction update of the boundary constraint, it helped GEN−SOA to present fast convergence on the global search in the early stage, with good global survey ability. For F7, it can be found that GEN−SOA had good global search ability with BOA and SOA in the early stage, but through general backward learning, could select better population individuals to update the optimal position in the late stage of the algorithm, which enhanced its local search ability to obtain the optimal value and the minimum mean, and showed better searchability. However, for the multi-peak test function F8−F12, GEN−SOA found the theoretical optimal values on the functions F8 and F12, and although the BOA algorithm was slightly deficient in the evaluation parameters compared with the F12 test function, in general, GEN−SOA still had excellent searchability.
(2) Algorithm convergence analysis
From the algorithm convergence graph, it can be seen that for the test functions F1−F12, the global optima of the GEN−SOA algorithm all converged and fell at a high rate, and the algorithm had significant superiority in the coordination ability of global survey and local search, as shown by the example that the test functions F5 and F9 are still able to find the optimal values at a later stage by strong local search values. For the test functions F1, F7, F8, F10, and F11, GEN−SOA converged to the optimal value in about 350 generations, and was the optimization algorithm with the fastest convergence speed and the smallest convergence accuracy, while the test function F12 showed the strongest convergence, converging to the optimal value in 50 generations. The strongest convergence was shown in the test function F12, which converged to the optimal value of the algorithm and the global minimum in 50 generations, demonstrating the stable global search capability of the GEN−SOA algorithm.
Comprehensive analysis showed that GEN−SOA retained the characteristic advantages of traditional spiral search based on the SOA algorithm, and this paper ensured the effectiveness and accuracy of the optimal position by updating the optimal position with the introduced nonlinear weights and keeping dynamic monitoring in the position update, while the multi-mechanism seagull optimization algorithm updated the optimal position adaptation value of each generation in reverse order to obtain the optimal solution. The GEN−SOA algorithm not only had outstanding search ability and convergence accuracy compared with other algorithms, but the participation of multiple mechanisms ensures that the GEN−SOA algorithm also has a unique strategy for finding the optimal position.
5.4. Performance Testing of GEN-SOA
To practically verify the optimization effect of GEN−SOA on the premise that the previous algorithm achieved excellent convergence effect and optimization-seeking ability, this paper used two standard engineering optimization design problems to verify GEN−SOA and SOA by example. The population size was set to 30, and the maximum number of iterations was 500 for both.
The welding design optimization problem focuses on minimizing the required manufacturing cost in welding applications using optimization algorithms. The variables to be optimized for this problem mainly include the thickness of the weld , the length of the connected part of the reinforcement , the height of the bar , and the thickness of the bar . According to the above constraints, the mathematical model of the problem can be obtained as shown in Equations (20) and (21).
On the other hand, the pressure vessel optimization design problem minimizes the cylindrical vessel’s total materials, forming and welding costs, and this problem also has four main optimization variables including the shell thickness , top thickness , inner radius , and the length of the cylindrical part, ignoring the top . Again, the mathematical model of this problem can be obtained from the above constraints, as shown in Equation (22).
In this paper, GEN−SOA was verified by applying GEN−SOA and traditional SOA to the pressure vessel optimization problem and the welding design optimization problem as examples. The effect of the pressure vessel optimization problem is shown in Figure 4, and the effect of the welding design optimization problem is shown in Figure 5. It is clear that GEN−SOA not only had significant advantages in the accuracy and convergence speed of the preceding analysis, but it also outperformed traditional SOA in the following two standard engineering optimization problems.
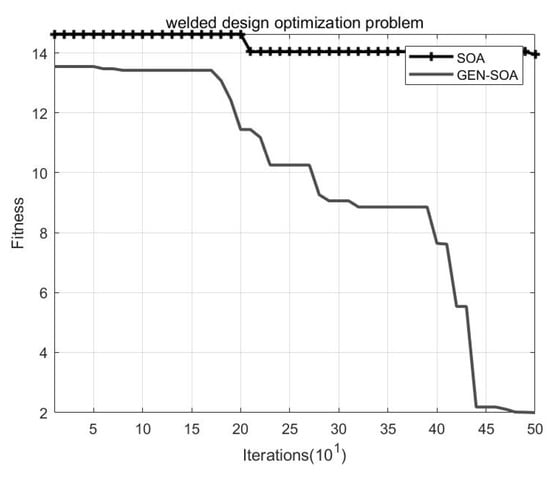
Figure 4.
The welded design.
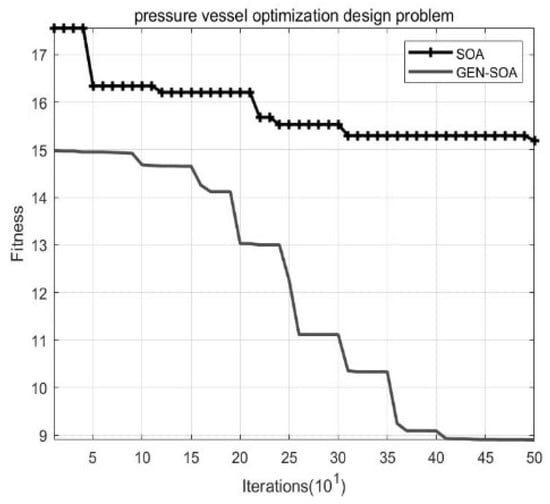
Figure 5.
The pressure vessel.
5.5. Summary of Experiment
In this part, simulation experiments were conducted on GEN−SOA, and the results were analyzed. In this simulation experiment, 12 benchmark test functions with different characteristics were used to verify the performance of GEN−SOA. Among them, the performance of GEN−SOA was compared with the above five optimization algorithms of SOA, BOA, SCA, PSO, and SSA, and by comparing the optimal values obtained from the execution of the six optimization algorithms, the mean and standard deviation of 30 independent runs, combined with the convergence curve in Figure 3, showed that the optimization effect of GEN−SOA was outstanding in the evaluation indices of algorithm accuracy and convergence speed. This paper also used two standard engineering optimization design problems to verify GEN−SOA and traditional SOA by example and found that GEN−SOA also had more outstanding optimization effects than SOA in performance testing.
6. Conclusions
In this paper, we proposed an improved seagull optimization algorithm (GEN−SOA) through extensive learning experiments to address the problems of slow convergence, low search accuracy, and easy fall into the local optimality of the seagull optimization algorithm. At the same time, this paper also stimulated the GEN−SOA algorithm by 12 standard test functions, and the data comparison based on the obtained experimental results showed that the GEN−SOA algorithm had high accuracy in finding the optimal value, fast convergence, and could find the global optimal value beyond the local optimal, which can make up for the shortcomings and defects of the seagull optimization algorithm to the maximum extent. However, to a certain extent, the GEN−SOA algorithm also has some shortcomings in the execution process. The algorithm can be further optimized in subsequent improvement research to reduce the mean and standard deviation values, thereby improving the algorithm’s stability.
In summary, the above research not only shows that the GEN−SOA algorithm had superior performance but also showed that the algorithm had certain research significance. In the future, this paper will continue to focus the research results obtained from GEN−SOA on some engineering optimization design problems, and we will expect GEN−SOA to achieve excellent optimization results in other problems such as compression spring design.
Author Contributions
Conceptualization, X.L., G.L. and P.S.; formal analysis, X.L.; methodology, X.L.; project administration, X.L.; writing—original draft, X.L.; writing—review & editing, G.L. and P.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the National Natural Science Foundation of China (Nos. 61862032, 62041702), the Science and Technology Plan Projects of Jiangxi Provincial Education Department (No. GJJ200424), the Ministry of Education Humanities and Social Sciences Planning Project (20YJA870010), the Jiangxi Provincial Social Sciences Planning Project (19TQ05, 21GL12), and the Jiangxi Provincial Higher Education Humanities and Social Sciences Planning Project (TQ20105).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data supporting the results of this study can be obtained from the corresponding corresponding author upon reasonable request.
Conflicts of Interest
The authors declare that they have no known competing financial interest or personal relationships that could have appeared to influence the work reported in this paper.
References
- Yang, X.S. A new metaheuristic bat-inspired algorithm. In Nature Inspired Cooperative Strategies for Optimization (NICSO 2010); Springer: Berlin/Heidelberg, Germany, 2010; pp. 65–74. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November 1995–1 December 1995; IEEE: Piscataway, NJ, USA, 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A sine cosine algorithm for solving optimization problems. Knowl.-Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Emary, E.; Zawbaa, H.M.; Hassanien, A.E. Binary grey wolf optimization approaches for feature selection. Neurocomputing 2016, 172, 371–381. [Google Scholar] [CrossRef]
- Arora, S.; Singh, S. Butterfly optimization algorithm: A novel approach for global optimization. Soft Comput. 2019, 23, 715–734. [Google Scholar] [CrossRef]
- Dhiman, G.; Kumar, V. Seagull optimization algorithm: Theory and its applications for large-scale industrial engineering problems. Knowl.-Based Syst. 2019, 165, 169–196. [Google Scholar] [CrossRef]
- Dhiman, G.; Singh, K.K.; Soni, M.; Nagar, A.; Dehghani, M.; Slowik, A.; Kaur, A.; Sharma, A.; Houssein, E.H.; Cengiz, K. MOSOA: A new multi-objective seagull optimization algorithm. Expert Syst. Appl. 2021, 167, 114150. [Google Scholar] [CrossRef]
- Dhiman, G.; Singh, K.K.; Slowik, A.; Chang, V.; Yildiz, A.R.; Kaur, A.; Garg, M. EMoSOA: A new evolutionary multi-objective seagull optimization algorithm for global optimization. Int. J. Mach. Learn. Cybern. 2021, 12, 571–596. [Google Scholar] [CrossRef]
- Ewees, A.A.; Mostafa, R.R.; Ghoniem, R.M.; Gaheen, M.A. Improved seagull optimization algorithm using Lévy flight and mutation operator for feature selection. Neural Comput. Appl. 2022, 34, 7437–7472. [Google Scholar] [CrossRef]
- Mao, Q.-H.; Wang, Y.-G. Adaptive T-distribution Seagull Optimization Algorithm Combining Improved Logistics Chaos and Sine-Cosine Operator. J. Chin. Comput. Syst. 2022, 1–9. Available online: http://kns.cnki.net/kcms/detail/21.1106.TP.20211019.1549.006.html (accessed on 22 March 2022).
- Wang, J.; Qin, J. Improved seagull optimization algorithm based on chaotic map and t-distributed mutation strategy. Appl. Res. Comput. 2022, 39, 170–176+182. [Google Scholar] [CrossRef]
- Qin, W.-N.; Zhang, D.-M.; Yin, D.-X.; Cai, P.-C. Seagull Optimization Algorithm Based on Nonlinear Inertia Weight. J. Chin. Comput. Syst. 2022, 43, 10–14. [Google Scholar]
- Wang, N.; He, Q. Seagull optimization algorithm combining golden sine and sigmoid continuity. Appl. Res. Comput. 2022, 39, 157–162+169. [Google Scholar] [CrossRef]
- Zhang, B.-J.; He, Q.; Dai, S.-L.; Du, N.-S. Multi-directional Exploring Seagull Optimization Algorithm Based On Chaotic Map. J. Chin. Comput. Syst. 2022, 1–10. [Google Scholar]
- He, Q.; Wei, K.Y.; Xu, Q.S. Anenhanced whale optimization algorithm for the problems of functions optimization. Microelectron. Comput. 2019, 36, 72–77. [Google Scholar]
- Zhao, C.-W.; Huang, B.-Z.; Yan, Y.-G.; Dai, W.-C.; Zhang, J. An Adaptive Whale Optimization Algorithm of Nonlinear Inertia Weight. Comput. Technol. Dev. 2020, 30, 7–13. [Google Scholar]
- Gandomi, A.H.; Yang, X.S. Evolutionary boundary constraint handling scheme. Neural Comput. Appl. 2012, 21, 1449–1462. [Google Scholar] [CrossRef]
- Zhao, P. Firefly Algorithm Based on Perturbed and Boundary Constraint Handling Scheme. Henan Sci. 2018, 36, 652–656. [Google Scholar]
- Tizhoosh, H.R. Opposition-based learning: A new scheme for machine intelligence. In Proceedings of the International Conference on Computational Intelligence for Modelling, Control and Automation and International Conference on Intelligent Agents, Web Technologies and Internet Commerce (CIMCA-IAWTIC’06), Vienna, Austria, 28–30 November 2005; IEEE: Piscataway, NJ, USA, 2005; Volume 1, pp. 695–701. [Google Scholar]
- Wang, H. A framework of population-based stochastic search algorithm with generalized opposition-based learning. J. Nanchang Inst. Technol. 2012, 31, 1–6. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).