Abstract
The efficiency of track utilization is one of the important factors for train operation in marshalling stations, and it can not only affect the turnover efficiency of trains, but also determine the capacity of railway stations. This paper presents an optimization method for track utilization in the arrival yard of a marshalling station considering Arrival and Break-up Coordination Operation (ABCO). The interaction between the push operation of trains and track utilization efficiency is investigated. First, the case of crossing the running route for shunting locomotives is analyzed. Whether the shunting route crosses or not can greatly affect the duration of trains occupying tracks in the station. Then, a nonlinear integer programming model (NLPM) is established based on the above analysis. The ultimate goal is to minimize the number of crossovers of the shunting route by adding a constraint condition for ensuring traffic safety. A track assignment algorithm based on ABCO for solving the NLPM is proposed. Train operations in the downlink arrival yard of station A are simulated with the proposed method. The results after applying the optimization method show that the average duration of trains on the tracks is reduced by 49.1%, and the degree to which tracks utilization is balanced is also significantly improved. The proposed method optimizes and extends the current achievements that have been reported in the literature.
Keywords:
tracks utilization optimization method; marshalling station; arrival and break-up coordination operation; nonlinear integer programming model; track assignment algorithm MSC:
90B20
1. Introduction
Planning tracks utilization together with coupling of shunting locomotives, pushing and other operations in the marshalling station are important components in the arrival and break-up operation system [1]. The planning mainly includes two elements: (1) tracks for the arrival of trains in the station; (2) the duration for which tracks are occupied, and this is closely related to other operations in the system. Once tracks for trains arriving in the station are determined, the shunting and running routes can be determined accordingly. However, when the shunting route is crossing, this can not only disturb the balance of shunting locomotive pushing operations, and thus increase the shunting locomotive occupied duration, but also delay the time when the tracks become free for subsequent trains waiting for shunting coupling. Therefore, determining the tracks for arriving trains and considering the coordination of the various operations in the system are of great significance, and it can increase the continuity between operations and further improve the robustness of tracks utilization planning [2].
Tracks utilization in the arrival yard of a marshalling station can be affected by many factors, and relevant models are complicated to construct, since most of them are NP-hard problems [3,4]. Investigations to optimize the planning of tracks utilization have been conducted by many researchers but without considering the interactions with other operations in the system. The related research can be classified briefly as sorting problems [5], graph theory problems [6] and 0–1 programming problems [7], which can be solved by a branch and bound algorithm [8] or heuristic algorithm [9,10,11]. The analysis of application for single- and double-track railway arrivals was first conducted by Carey et al. [12,13,14]. Nikbakhsh et al. [15] analyzed the operations in a railway station with fixed equipment resources, and the problem related to the application of arrivals was solved using a simulated annealing algorithm. However, only arrival tracks were determined and, the occupied duration was set as a fixed value. In practice, a variable occupied duration can have an influence on the track’s utilization efficiency.
Variable occupied duration time due to delayed train arrivals and departures has been taken into account by several researchers [16,17]. Partha et al. [18] established a mixed integer programming model to describe the tracks assignment problem considering factors caused by delayed train arrivals. Peng et al. [19] determined the best adjustment planning for tracks utilization with the goal of restoring both station and train operation order. D’ariano [20] and Caprara et al. [21] investigated a method for adjustment of tracks assignment planning under the condition of random disturbance. Though variable duration time due to train delay has been considered, the interactions with other operations in the system were ignored, although these can also cause changes in the duration time.
As the complexities of the problems increase, a majority of researchers are engaged in improving the robustness of the arrival scheme of trains. Krate [22] proposed the idea that the substance of robustness optimization of operations in railway station is a problem of “dualism”, which is constantly being weighed, based on which a dual-objective optimization model is proposed. With the object in the robustness optimization model of maximum time span of two consecutive trains, Thijs Dewidle [23] obtained time slack by adjusting the trains occupied duration on equipment in railway stations. Sofie [24] established a linear integer programming model (LPM) by limiting the number of assignments for complex station lines under no time constraint condition.
In this work, the interactions of various operations, such as shunting locomotive operations and track utilization in the system, are considered. A nonlinear integer programming-based optimization model considering the arrival and break-up coordination operation (ABCO) in marshalling stations is established. Then, a track assignment algorithm is adopted to solve this nonlinear integer programming model (NLPM). Finally, we utilize the proposed track utilization optimization method to simulate the downlink trains in marshalling station A. The efficiency of the proposed track utilization optimization method is demonstrated to verify its effectiveness for practical application.
2. Problem Description
As mentioned above, existing research related to tracks utilization in marshalling stations can be improved mainly in two areas: (1) the shortcomings of the fixed occupied duration time value; (2) ignorance of operations interactions in the system. Both these factors can have a huge influence on the efficiency of tracks utilization in a marshalling station.
First is the issue of the fixed occupied duration time, which has drawbacks in two respects. A long-fixed duration time will reduce the tracks utilization efficiency in the marshalling station, while on the contrary, a short-fixed time value will cause the trains controller to fail to vacate tracks on time, which can then result in the need to adjust the arrival tracks of subsequent trains. Secondly, the interactions with other operations in the system also have an influence on the tracks utilization. Two specific main operations, namely the pushing operation by the previous shunting locomotive and the returning operation by the following shunting locomotive, can be affected by the crossovers of train running routes [25].
An arrival yard in a marshalling station with a double pushing and single sliding hump operation mode is used to illustrate the interactions between the two main operations mentioned above, as shown in Figure 1. When two trains designated A and B arrive one after the other and are connected to tracks numbered 3 and 4 on the same side of the pushing line, the following situations will occur. After the disassembly of train A, the shunting locomotive, which is coupled with A, returns to the arrival yard in the marshalling station. However, the return route is occupied by train B since it has entered the hump through the pushing line. Thus, the shunting locomotive will have to wait some time for the disassembly of train B in the no-slip line. In this case, not only does the idle time of the shunting locomotive increase, but also the connection between these two shunting locomotive operations is broken, which reduces the operation efficiency of the hump. In the case that A and B are connected to tracks 3 and 6 on both sides of the pushing line, the situations mentioned above can be avoided. While train B is being disassembled, the shunting locomotive coupled with A returns to the arrival yard through the opposite pushing line at the same time. Thus, the connection between the two pushing operations (pre-pushing and continuous pushing) of shunting locomotives is closer. In other words, it is critical to arrange arriving trains on both sides of the pushing line in the tracks, as this then has the potential to improve the efficiency of the tracks utilization in the marshalling station.
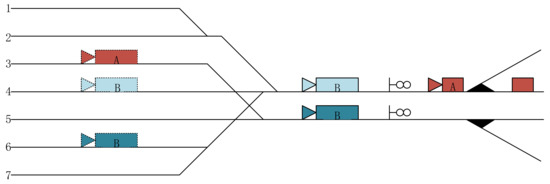
Figure 1.
Schematic diagram of adjacent trains connected to different tracks.
In this work, the optimization of tracks utilization in the arrival yard of a marshalling station aims to obtain the most reasonable track allocation scheme. The ultimate goal is to minimize crossovers of shunting locomotive routes and further to reduce the train’s dwell time on the tracks, as well as to achieve balanced tracks utilization. We consider the station yard layouts, personnel and equipment configuration and hump operation modes, and we assume that the down (up) trains enter the corresponding arrival yard of the marshalling station on time. The constraint conditions are to meet the requirement of ensuring the safety of train operations and the fixed utilization scheme of arrival tracks. A system simulation method is needed to obtain the exact time that each train occupies the track, so as to arrange the receiving track for subsequent arrival trains [26].
3. Nonlinear Integer Programming Model
In order to provide a good illustration and analysis of the abovementioned problem, the variables involved in this model are defined in this section as listed in Table 1.

Table 1.
Symbol description.
3.1. Symbol Description
Since the fixed utilization rules for the arrival tracks have been specified according to the length of trains, the types of operations in the station and the matching of corresponding tracks [27], as well as tracks utilization, should aim to meet the rules for the arrival tracks. A parameter is set as the weight of the track occupied with train . When the value is equal to 1, it means that track can be occupied by train and also meet the fixed utilization rules for arrival tracks; when the value is 10, it means that track can be occupied by train but does not conform to the rules, and when is taken as 100, it means that track cannot be occupied by train .
Considering the problem analysis in Section 2, we take the middle of two pushing lines as the central axis line, so the arrival yard is divided into two parts, namely the up and down half areas. When two trains arrive one after the other and are connected to tracks in the same half area, crossovers occur between the shunting locomotive routes of these two trains. This can be expressed with symbols as when or and , where and ; otherwise, .
A queuing theory is adopted here to illustrate the operations status in the marshalling station. Operations carried out by trains can be regarded as a queuing system that includes four subsystems: a train inspection queuing system, a shunting locomotive pushing queuing system, a pushing line queuing system and a hump disassembly queuing system, as shown in Figure 2. In each subsystem, trains are regarded as “customers” and equipment such as tracks, train inspection teams, shunting locomotives, pushing lines and the hump are regarded as “service desks”.
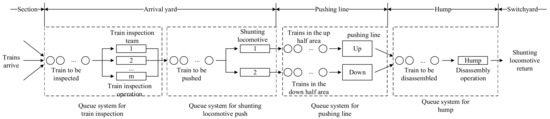
Figure 2.
Schematic diagram of each queuing system in marshalling station.
The earliest available time of each “service desk” , , , is time-dependent. When the service in the service desk starts, the corresponding time variable is updated to infinity. When the service in the service desk ends, the corresponding time variable is updated to the end time.
3.2. Objective Function of Tracks Utilization
The minimum time for which the tracks are occupied with trains and the most balanced utilization are often taken as the objective function for tracks operation planning optimization [28,29,30]. The total occupied duration time of trains can be calculated as
In order to avoid the frequent occupation of some tracks and long-term idleness of other tracks, the arrival tracks should be utilized in a balanced manner. The balance degree β of arrival tracks utilization can be measured from the total occupied time. The value of variance of the occupied duration time can show the balance degree. The parameter β can be expressed as
The two objectives mentioned above are related to the crossovers of shunting locomotive routes. The fewer the crossovers of shunting locomotive routes, the better the continuity of operation. The shorter the waiting time of trains, the less the occupied duration time. Meanwhile, the crossovers of shunting locomotive routes can also reflect whether or not the tracks utilization is balanced. Therefore, the objective function of the optimization model here is to select a more direct index, which is the minimum number of crossovers of shunting locomotive routes, as shown in Equation (3).
3.3. Constraint Condition of Tracks Utilization
Tracks utilization in the arrival yard of a marshalling station is exclusive. When a track has been occupied by a train, then the track cannot be connected to other trains until the occupying train leaves.
A train can only occupy one arrival track until its departure. It cannot switch to other arrival tracks half-way through.
During peak hours, arrival tracks are utilized frequently. When the interval between two trains occupying the same arrival track is too close, accidents are likely to occur. Therefore, the requirement for a minimum safety interval must be satisfied when receiving consecutive trains on the same arrival track.
Restrictions are imposed by the fixed utilization rules for the arrival tracks. For example, a freight train cannot stay on a passenger train track, and an out of gauge freight train can only stay on a specific track.
To sum up, the arrival tracks utilization optimization model constructed here aims to minimize the crossovers of shunting locomotive routes and to utilize the arrival tracks in a balanced manner, together with full consideration of ensuring operation safety and the fixed utilization rules for the arrival tracks.
4. Track Assignment Algorithm Design
In order to solve the nonlinear integer programming model mentioned in Section 3, a system simulation method with tracks assignment rules was designed to assign the tracks available for trains to be disassembled when arriving in the arrival yard of the station, the detailed designing of this algorithm which is Algorithm 1 named “Track Assignment” is shown in Section 4.1. Specific track for each arrival train has been determined with the solution of Algorithm 1, then activities such as trains entering the arrival yard, inspection of arriving trains, coupling with a shunting locomotive, entering the pushing line and disassembly operation are simulated as shown in Figure 2 with Algorithm 2 named “Trains Movement Simulation” which is introduced with details in Section 4.2. A simulation clock is set for each train, so that the trains converted after separating from the leading locomotive can use this clock. Meanwhile, status values are set for the service desk, including the shunting locomotive, pushing line and hump. Then, the clock and status values can be updated in the simulation system by using an event step method. The entire framework of the proposed system simulation method is shown in Figure 3.
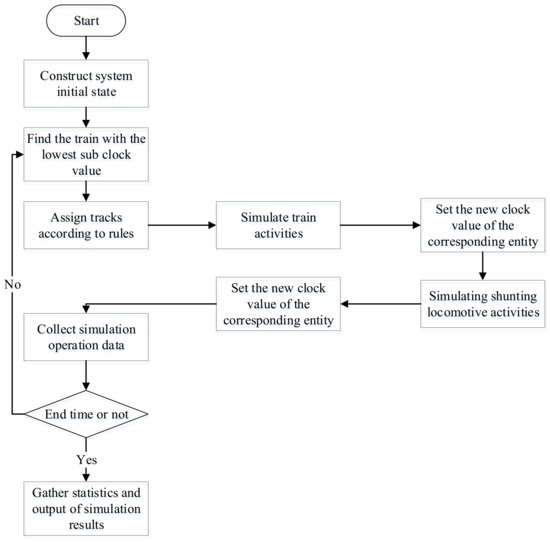
Figure 3.
The framework for the system simulation method.
Having satisfied the requirements of the arrival tracks utilization rules, the trains are alternately assigned to free tracks in the up and down half areas of the arrival yard. A track nearest to the pushing line is selected to satisfy the requirement to shorten the traveling distance of arriving trains. This can not only balance the utilization of arrival tracks, but also reduce route crossovers during shunting locomotive operation. When trains arrive in the yard of the marshalling station, three different situations, together with the corresponding tracks assignment rules, are as follows:
First situation: When a train arrives, there are free tracks in the arrival yard that meet the fixed utilization planning of arrival tracks.
Rule: Compare the number of tracks in the up and down half areas that meet the above situation. If the number of tracks in the up half of the arrival yard is larger than or equal to that of tracks in the down half, we assign the track with the largest index in the up half to receive the train. Otherwise, the track with the lowest index in the down half area is assigned.
Second situation: Free tracks are available in the current arrival yard but do not match the fixed utilization scheme of arrival tracks, even though tracks can still be occupied.
Rule: Compare the number of tracks in the up and down half areas that meet the second situation. If the number of tracks in the up half of the arrival yard is larger than or equal to that in the down half, the tracks assignment rule is the same as the one in the first situation.
Third situation: There are only free tracks that cannot be occupied or no free tracks in the current arrival yard.
Rule: The train must wait outside the station until there is an available track.
The initial state of the system is to set the sub-clock for each arrival train as its scheduled arrival time and the sub-clocks of each track, train inspection team, shunting locomotive, pushing line and hump as the planned start time, that is as , , , .
4.1. Tracks Assignment according to Rules
An algorithm is designed to uniformly assign arrival trains to tracks which locate on both sides of the pushing line, the detailed flow is shown as following,
| Algorithm 1 Track Assignment |
| 1: Initialize a trains set L, tracks set D, empty set K,W |
| 2: for each train i do |
| 3: check each track j |
| 4: if and then |
| 5: Add j to K |
| 6: end if |
| 7: end for |
| 8: if then |
| 9: check each track j |
| 10: if and then |
| 11: Add j to K |
| 12: end if |
| 13: end if |
| 14: if then |
| 15: Add i to W |
| 16: else |
| 17: compare the number of intersections between set and sets and |
| 18: if then |
| 19: select track sj with the largest median value of |
| 20: else |
| 21: select track sj with the smallest median value of |
| 22: end if |
| 23: end if |
| 24: return the track sj |
4.2. A Sub-Algorithm for the Simulation of Trains Movement
Trains are the key parts in the operation system, so it is of significance to simulate relevant technical operation links. The main steps for adjusting the arrival activities of transfer trains are as follows:
| Algorithm 2 Trains Movement Simulation |
| 1: Initialize track which is available for the train according Algorithm 1, set flag = 0 |
| 2: update |
| 3: for each train inspection team a do |
| 4: if then |
| 5: update |
| 6: set flag=1 |
| 7: end if |
| 8: break |
| 9: end for |
| 10: if flag == 0 then |
| 11: set |
| 12: end if |
| 13: for each shunting locomotive b do |
| 14: Compare the sub-clock of train and sub-clock of shunting locomotive |
| 15: if then |
| 16: |
| 17: set flag2 = 1 |
| 18: end if |
| 19: break |
| 20: end for |
| 21: if flag == 0 then |
| 22: set |
| 23: |
| 24: end if |
| 25: Check the half area of track where train is located |
| 26: if then |
| 27: |
| 28: |
| 29: |
| 30: else |
| 31: |
| 32: |
| 33: |
| 34: end if |
| 35: if then |
| 36: |
| 37: |
| 38: else |
| 39: |
| 40: |
| 41: end |
The condition of the shunting locomotive returning is considered when trains enter the pushing line. Therefore, the sub-clock of the pushing line is delayed by 10 min compared with that of the hump. In fact, shunting locomotive drivers only consider whether the pushing line is occupied or not for them entering, which increases the waiting time of the shunting locomotive. Therefore, we change the update method of the pushing line sub-clock when simulating the dispatcher’s arrival tracks occupation scheme in step 8. That is, if , we update the pushing line sub-clock ; otherwise, , where is the value before updating, and the others are the same as in the above model.
4.3. A Sub-Algorithm for the Simulation of Shunting Locomotive Activities
When the shunting locomotive is coupled with the train, it acts as a whole train. After the train is disassembled, the shunting locomotive will return to the end of the arrival yard from the hump through the pushing line and the track, and then, it continues to be coupled with the next train. The returning time of the shunting locomotive has an impact on vacating the track and improving the pick-up efficiency during busy periods in the arrival yard. An algorithm which is Algorithm 3 and named “Shunting Locomotive Simulation” is designed to show this simulation process as follows:
| Algorithm 3 Shunting Locomotive Simulation |
| 1: Initialize the hump sub-clock and pushing line sub-clock in the half area. |
| 2: if then |
| 3: |
| 4: else |
| 5: update |
| 6: end if |
| 7: select the track which is the closest to the pushing line and free |
| 8: update |
| 9: update |
| 10: End |
5. Method Verification and Application
There are 12 main marshalling stations in China, and we take one of them as an example and named station A to have an analysis. The layout of the station contains two directions, three levels and seven yards, as shown in Figure 4. The mode of hump operation is double pushing and single sliding. Since the up and down shunting operation systems are independent of each other, the down arrival yard is selected to verify the proposed method and can be viewed as a practical application.
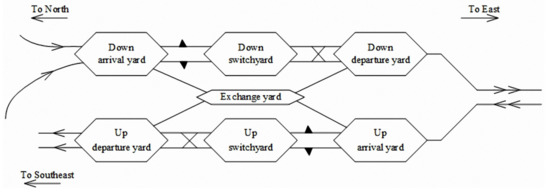
Figure 4.
Layout of station A.
The down arrival yard includes 15 tracks, where tracks numbered 1 and 2 are used for passenger trains and are not available for freight trains. Tracks 9 and 10, which are located in the center of the arrival yard, are connected to the pushing line. Tracks 12 to 15 are only available for the North to the South downlink arrival trains according to the fixed utilization scheme of arrival tracks.
The track assignment algorithm is adopted to assign tracks to arrival trains and compared with the assignment scheme of arrival tracks in the station. The simulation results are shown in Table 2.

Table 2.
Schedule of station tracks occupied by trains.
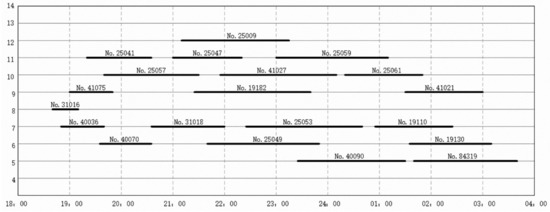
Figure 5.
Improved arrival and departure track arrangement scheme.
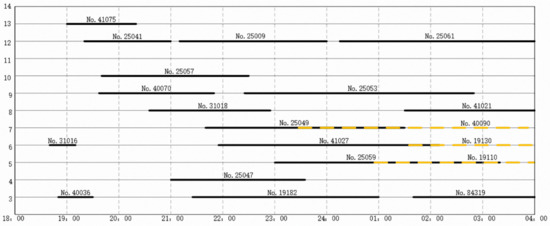
Figure 6.
Arrival and departure track arrangement scheme before improvement.
From these two figures, one can see that compared with the assignment scheme, the tracks utilization scheme calculated with the proposed model and method has the following advantages: Firstly, the duration time for which the arrival tracks are occupied by trains is effectively reduced. The average duration time calculated by the proposed method is 98.8 min, while it is 194.2 min without adopting the model, which is an improvement of 49.1%. Secondly, more balanced utilization of the arrival tracks is obtained. The variance, which can reflect the degree of balance, is reduced from 201.4 to 141.9. Finally, the carrying capacity of the arrival tracks is improved. All the arriving trains that are scheduled before 4:00 a.m. early the next day are connected in time and complete all operations by using the proposed method. However, the same cannot be achieved with the assignment utilization scheme, and some trains still occupy the arrival tracks the next day. Adjustments must be made for trains connecting to the arrival tracks.
6. Conclusions
In this work, the optimization method of arrival tracks utilization in a marshalling station under the double pushing and single sliding mode was proposed. A track assignment algorithm solution to the established model was designed. It was found that the traditional algorithms that are usually applied to arrival tracks in passenger stations are not applicable for tracks assignment in a marshalling station. Finally, the advantage of the proposed method was verified by the data in the downlink arrival yard of station A. The simulation results generated by the proposed method show advantages in effectively reducing the duration time of trains occupying the arrival tracks and improving the carrying capacity of the station A.
The proposed method shows advantages over the current practical scheme; however, a limitation occurs since it is mainly applicable and effective for a marshalling station with the double pushing and single running humps mode problem. It can be slightly modified for other mode problems if one wishes; for example, it is a good attempt to set different train inspection and disassembly times according to various train formation contents to improve the system simulation algorithm in the proposed method.
Author Contributions
The authors confirm their contributions to the paper as follows: study conception and design: W.C., W.Y.; data collection: W.Y.; analysis and interpretation of results: W.Y., G.Z.; draft manuscript preparation: W.Y., G.Z. All authors reviewed the results and approved the final version of the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research is supported by the Fundamental Research Funds for the Central Universities of Central South University (Grant No. 2022ZZTS0647) and the open funding from Rail Data Research and Application Key Laboratory of Hunan Province at Central South University (Grant No. 502401004).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
I sincerely thank the staff of station A who provided data support for this paper. Furthermore, I thank my classmates for their encouragement and support.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses or interpretation of data; in the writing of the manuscript or in the decision to publish the results.
References
- Zhou, W.; Yang, X.; Qin, J.; Deng, L. Optimizing the long-term operating plan of railway marshalling station for capacity utilization analysis. Sci. World J. 2014, 2014, 251315. [Google Scholar] [CrossRef] [PubMed]
- Hu, Z.-A.; Pu, Z.; Li, B.-W.; Wang, P. Research on the Minimum Organized Number of Train Wagons Considering Dual Benefits in a Railway Marshalling Station. In Proceedings of the CICTP 2019, Nanjing, China, 6–8 July 2019; pp. 2900–2911. [Google Scholar]
- Garey, M.R.; Johnson, D.S.; Sethi, R. The Complexity of Flowshop and Job Shop Scheduling. Math. Oper. Res. 1976, 1, 117–129. [Google Scholar] [CrossRef]
- Gilg, B.; Klug, T.; Martienssen, R.; Paat, J.; Schlechte, T.; Schulz, C.; Seymen, S.; Tesch, A. Conflict-free railway track assignment at depots. J. Rail. Transp. Plan Manag. 2018, 8, 16–28. [Google Scholar] [CrossRef]
- Wenquan Li; Wei Wang; Shihui Cheng. Scheduling Model and Algorithm of Using Up and Down Lines on Railway Marshalling Station. Syst. Eng.-Theory Pract. 2000, 2000, 75–78. [Google Scholar]
- Jie Xu; Wen Du; Jun Wen; Zhijie Liang. The Genetic Based Algorithms Optimization Plan of Using the Arrival and Departure Track at Railway Sectional Station. China Railw. Sci. 2003, 2003, 112–117. [Google Scholar]
- Lei Li; Bingmou Li. Algorithm and Model of Arrival-Departure Lines in Marshalling Station Based on Hybrid Algorithm. J. Transp. Eng. Inf. 2008, 2008, 86–90. [Google Scholar]
- Chunong Xie; Xinhua Li. Optimization Research for Utilization of Arrival and Departure Tracks in Railroad Passenger Station. China Rail. Sci. 2004, 25, 130–133. [Google Scholar]
- Baoshan, W.; Lixin, H.; Haidong, L. Optimized utilization of arrival and departure tracks in dedicated passenger lines. J. Transp. Syst. Eng. Inf. Technol. 2012, 12, 105–110. [Google Scholar]
- Feng, Z.; Cao, C.; Liu, Y.; Zhou, Y. A multiobjective optimization for train routing at the high-speed railway station based on tabu search algorithm. Math. Probl. Eng. 2018, 2018, 8394397. [Google Scholar] [CrossRef]
- Kang, L.; Lu, Z.; Meng, Q. Stochastic schedule–based optimization model for track allocations in large railway stations. J. Transp. Eng. Part A Syst. 2019, 145, 04019001. [Google Scholar] [CrossRef]
- Malachy, C. Extending a train pathing model from one-way to two-way track. Pergamon 1994, 28, 395–400. [Google Scholar]
- Malachy, C.; Lockwood, D. A Model, Algorithms and Strategy for Train Pathing. J. Oper. Res. Soc. 1995, 46, 998–1005. [Google Scholar]
- Malachy, C.; Sinead, C. Scheduling and platforming trains at busy complex stations. Transp. Res. Part A 2003, 37, 195–224. [Google Scholar]
- Nikbakhsh, J.; Hamid, R.S.; Sajjad, N. Using simulated annealing for determination of the capacity of yard stations in a railway industry. Appl. Soft Comput. J. 2010, 11, 1–9. [Google Scholar]
- Ma, L.; Guo, J. Robust stage plan for a railway marshalling station. In Proceedings of the 2014 IEEE International Conference on System Science and Engineering (ICSSE), Shanghai, China, 11–13 July 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 195–200. [Google Scholar]
- Schasfoort, B.; Gkiotsalitis, K.; Eikenbroek, O.; van Berkum, E. A dynamic model for real-time track assignment at railway yards. J. Rail Transp. Plan. Manag. 2020, 14, 100198. [Google Scholar] [CrossRef]
- Chakroborty, P.; Vikram, D. Optimum assignment of trains to platforms under partial schedule compliance. Transp. Sci. 2008, 42, 169–184. [Google Scholar] [CrossRef]
- Qiyuan, P.; Jia, N.; Gongyuan, L. Model and Algorithm for Train Platform Scheme Rescheduling at Large High-speed Railway Station. J. China Railw. Soc. 2019, 41, 10–19. [Google Scholar]
- D’Ariano, A.; Corman, F.; Pacciarelli, D.; Pranzo, M. Reordering and Local Rerouting Strategies to Manage Train Traffic in Real Time. Transp. Sci. 2008, 42, 405–419. [Google Scholar] [CrossRef]
- Caprara, A.; Galli, L.; Toth, P. Solution of the Train Platforming Problem. Transp. Sci. 2011, 45, 246–257. [Google Scholar] [CrossRef]
- Kratz, A. A. A Bicriteria Approach for Robust Timetabling. In Robust and Online Large-Scale Optimization; Springer: Berlin/Heidelberg, Germany, 2009; p. 119. [Google Scholar]
- Dewilde, T.; Sels, P.; Cattrysse, D.; Vansteenwegen, P. Robust railway station planning: An interaction between routing, timetabling and platforming. J. Rail Transp. Plan. Manag. 2013, 3, 68–77. [Google Scholar] [CrossRef]
- Sofie, B.; Pieter, V. Robust routing and timetabling in complex railway stations. Transp. Res. Part B 2017, 101, 228–244. [Google Scholar]
- Stanić, M.; Stojić, G.; Tanackov, I.; Aleksić, D. Model for the optimization of technology and capacity in marshalling station. In Proceedings of the 20th International Scientific Conference “TRANSPORT” 2011, Sofia, Bulgaria, 4–5 November 2011. [Google Scholar]
- Bažant, M.; Kavička, A. Artificial neural network as a support of platform track assignment within simulation models reflecting passenger railway stations. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2009, 223, 505–515. [Google Scholar] [CrossRef]
- Hu, Z.A.; Zou, Z.F.; Jia, Y.Z.; Li, B.W. Arrival and Departure Track Utilization Adjustment Plan for Passenger Station Considering Fluctuation of Train Arrival Time. In Proceedings of the CICTP 2019, Nanjing, China, 6–8 July 2019; pp. 2912–2923. [Google Scholar]
- Meng, X.; Wang, Y.; Xiang, W.; Jia, L. An integrated model for train rescheduling and station track assignment. IET Intell. Transp. Syst. 2021, 15, 17–30. [Google Scholar] [CrossRef]
- Zhang, Y.; Song, R.; He, S.; Li, H.; Guo, X. Optimization of classification track assignment considering block sequence at train marshaling yard. J. Adv. Transp. 2018, 2018, 3802032. [Google Scholar] [CrossRef]
- Huang, J.; Guang, X. A Research on Optimization of Arrival and Departure Tracks in Marshalling Yard for the Last Trains with Flexibility and Overlapped Time Windows. Rail. Transp. Econ. 2019, 41, 23–29. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).