Efficiency-Enhancing Horizontal Mergers in Spatial Competition with Network Externalities

Abstract

We study horizontal mergers in a network products market with a three-firm model of spatial competition, where two merged firms become compatible at the expense of product differentiation. We consider two different approaches to modeling rational expectations: responsive and passive. The results show that the merger may reduce industry competition, since the merger-related compatibility enlarges the network scales for insiders and amplifies product differentiation between the insiders and the outsider; therefore, the proposed merger may benefit all firms, raise consumer surplus, and enhance social welfare, i.e., the merger is Pareto-improving.

1. Introduction

In industries such as telecommunications, mergers and acquisitions (M&A) have been persistently observed since the 1990s. The existence of network externalities is a very obvious character in these industries, which means that the value a user derives from purchasing a good increases with the network scale. In these industries, it is also commonly observed that products of different firms can be compatible as a result of mergers [1]. However, there is a drawback regarding compatibility, since consumers perceive compatible products as closer substitutes, i.e., choosing to be compatible is renouncing some product differentiation [2,3,4]. In this paper, we study the incentives of firms to merge, the merger’s influences on the profitability of the outsider, and how welfare varies because of the merger; where the product exerts direct network externalities, the product differentiation of the merging firms is weakened to some extent because of merger-related compatibility.

The extant literature suggests that horizontal mergers may result in a merger paradox, referring to the fact that firms should have no incentives to merge, if a great majority of firms in the industry participate, whereas the outsiders always benefit from mergers [5]. This seems to be in contrast with real-life observations, therefore, a growing part of the literature is devoted to identifying alternative models for privately beneficial mergers, e.g., ref. [6] deems that firms have incentives to merge for a broad range of parameters, if the cost function depends on the output and fraction of capital stock; ref. [7] demonstrates that mergers are beneficial, if firms provide differentiated products and compete in price; ref. [8] shows that mergers may be beneficial even in the absence of dramatic cost synergies with free entry; ref. [9] finds that there is a range of R&D technology, for which a merger is profitable for any number of firms to engage in; and ref. [10] shows that the presence of a strategic tax policy increases the incentive for a horizontal merger, compared to a situation with no tax policy.

Even if the profitability of the merged firms is increased, there is a consensus that market concentration caused by M&A reduces consumer surplus and harms social welfare; therefore, from an antitrust and competition policy perspective, the merger should not be allowed. In a special model, which assumes consumers are spread along an infinite line that has many firms, ref. [11] points out that a horizontal merger between two firms can enhance efficiency, if the spacing between them is much closer compared to the spacing between other firms. However, these studies seldom consider the role of network externalities, except for [1,12]. The former develops a three-firm Cournot model, in which each firm provides a horizontally differentiated product with network externalities, and the level of compatibility between merging firms improves compared to the premerger case (i.e., merger-related network compatibility effect). The author finds that the proposed merger should be allowed from the perspective of a consumer surplus standard, if the degree of the merger-related network compatibility effect is sufficiently large. The latter studies the incentives of horizontally differentiated oligopoly firms to merge and the post-merger welfare outcomes under merger-cost-saving and network effects, showing that an insider of the merger is better off than an outsider, unless both cost-savings and network effects are too low; this means mergers can enhance consumer surplus and total welfare, if cost savings and network effects are high enough.

In reality, consumers perceive compatible products as closer substitutes in a network products market. Based on this observation, a three-firm circular city model is developed, where the products of the merging firms become compatible and the locations of insiders get closer. Furthermore, we consider two different approaches to modeling rational expectations: responsive and passive. The model with a responsive expectation implicitly assumes that agents are capable of perfectly computing the effect of price changes for all firms, i.e., expectations adjust perfectly to match the realized demands for all prices [13]. Conversely, the model with a passive expectation assumes that agents hold their expectation of total demand as fixed, irrespective of firms’ price choices. In equilibrium, consumers should act in a manner to fulfill those expectations, i.e., the expectations are required to be fulfilled [14,15]. We show that, in both scenarios, a merger enlarges the network scale for insiders due to compatibility and amplifies product differentiation between the insiders and the outsider; therefore, it may benefit all firms and simultaneously raise consumer surplus and social welfare, even without cost synergies [16] or firm-entry [8].

In the next section, we develop a horizontally differentiated three-firm circular city model with network externalities. Next, we analyze the equilibrium with a responsive expectation and with a passive expectation in Section 3 and Section 4, respectively, and we reveal the condition for firms to merge and the impact on welfare. At last, we summarize our main results and make some further discussions.

2. Model

Consider a three-firm spatial model with horizontal product differentiation, where consumers of mass one are uniformly distributed along a unit circular city. Three firms with products that exert network externalities are initially located equidistantly from each other along the city, and all of them are incompatible with each other before the merger.

We assume that the merging firms are firms 1 and 2 (the “insiders”), which are originally located at $z_1=1/3$ and $z_2=2/3$, respectively. After the merger, the insiders can adopt a common standard and be compatible with each other, resulting in the loss of some amount of product differentiation [2,3], i.e., their locations become closer in the product space. We assume the merged firms are located at $z_1=1/3+a$ and $z_2=2/3-a$, respectively, where parameter $a$ measures the loss in production differentiation, with $0<a<1/6$, as shown in Figure 1. In other words, the merger-related synergies offer less-differentiated products but may generate a larger network compared to the premerger case. We assume firm 3 (the “outsider”) is always fixed at $z_3=0$, regardless of premerger or merger status, and is always incompatible with the other two firms. For the sake of simplifying the analyses, we assume the production costs of all firms are zero.

The indirect utility a consumer located at $z$ derives from purchasing product $i$ is

$$U_i\left(z\right)=v-p_i+\theta y_i^e-\left|z-z_i\right|$$

(1)

where $v$ is the basic utility that is sufficiently large, $p_i$ is the price of product $i$, $\theta$ is the measure of network externalities, and $y_i^e$ is consumer’s expectation of the network size of product $i$, with $i=1,2,3$.

The timing of the game is as follows. Firstly, firms 1 and 2 determine whether to merge or not. Secondly, all firms set prices $p_i$ simultaneously. We look for subgame-perfect equilibria through backward induction.

In this paper, we solve the equilibrium of the model with two expectations: responsive and passive. Following the method of backward induction, we first derive the equilibrium in the cases of premerger and horizontal merger, respectively, then analyze the incentives for the insiders to merge. Furthermore, we will analyze the profitability for the outsider, investigate the influences of the merger on welfare, and summarize the policy implications.

3. Analysis of Equilibrium with Responsive Expectation

In this scenario, consumers’ expectation about the network size of product $i$ always matches realized network size [13], i.e., $y_i^e=y_i$ for any given price $p_i$, $i=1,2,3$. To guarantee that the second order conditions hold and all firms exist in the market in both premerger and merger cases, we assume that $0<\theta <\left(4+3a\right)/9$. It is worth noting that the tipping point emerges if the intensity of network externality is too large, i.e., the outsider will be squeezed out of the market and only the insiders remain in the market, which will not be allowed from the perspective of the antitrust authority. Therefore, we do not consider this an extreme case in this paper, with a responsive expectation or with a passive expectation.

3.1. Premerger

In the premerger case, let $z_{i,j}$ denote the location of the indifferent consumer between good $i$ and good $j$: $i,j=1,2,3$, and $i\ne j$. Since all firms are incompatible, given the prices set by all firms, the network sizes of each product are $y_1=z_{1,2}-z_{3,1}$, $y_2=z_{2,3}-z_{1,2}$, and $y_3=z_{3,1}+1-z_{2,3}$. The locations of the indifferent consumers satisfy the following equations

$$\left\{\begin{array}{l}v-p_3+\theta \left(z_{3,1}+1-z_{2,3}\right)-z_{3,1}=v-p_1+\theta \left(z_{1,2}-z_{3,1}\right)-\left(1/3-z_{3,1}\right)\hfill \\ v-p_1+\theta \left(z_{1,2}-z_{3,1}\right)-\left(z_{1,2}-1/3\right)=v-p_2+\theta \left(z_{2,3}-z_{1,2}\right)-\left(2/3-z_{1,2}\right)\hfill \\ v-p_2+\theta \left(z_{2,3}-z_{1,2}\right)-\left(z_{2,3}-2/3\right)=v-p_3+\theta \left(z_{3,1}+1-z_{2,3}\right)-\left(1-z_{2,3}\right)\hfill \end{array}\right.,$$

(2)

which yield

$$z_{3,1}=\frac{1}{6}-\frac{p_3-p_1}{2-3\theta },z_{1,2}=\frac{1}{2}-\frac{p_1-p_2}{2-3\theta },z_{2,3}=\frac{5}{6}-\frac{p_2-p_3}{2-3\theta }.$$

(3)

Therefore, the demand functions of firms are

$$d_1=z_{1,2}-z_{3,1},d_2=z_{2,3}-z_{1,2},d_3=z_{3,1}+1-z_{2,3}.$$

(4)

The aim of every firm under premerger is to maximize its profit, ${\mathsf{\Pi }}_i=p_i{d}_i$. By differentiating ${\mathsf{\Pi }}_i$, with respect to $p_i$, we obtain the following lemma.

Lemma 1.

In the premerger case, the equilibrium prices and demands are

$$p_i^{\ast }=\frac{1}{3}-\frac{\theta }{2},d_i^{\ast }=\frac{1}{3},$$

the equilibrium profits, consumer surplus, and social welfare are

$${\mathsf{\Pi }}_i^{\ast }=\frac{1}{9}-\frac{\theta }{6},C{S}^{\ast }=v+\frac{5\theta }{6}-\frac{5}{12},S{W}^{\ast }=v+\frac{\theta }{3}-\frac{1}{12},i=1,2,3.$$

Proof of Lemma 1.

From the first order condition of the profit function ${\mathsf{\Pi }}_i$, with respect to price $p_i$, we obtain the equilibrium prices $p_i^{\ast }$. By substituting $p_i^{\ast }$ into Equation (3), the indifferent consumers’ locations are

$$z_{3,1}^{\ast }=1/6, z_{1,2}^{\ast }=1/2 \mathrm{and} z_{2,3}^{\ast }=5/6.$$

By substituting $p_i^{\ast }$ into Equation (4), equilibrium demands $d_i^{\ast }$ are obtained. Firm $i$’s optimal profit ${\mathsf{\Pi }}_i^{\ast }$ is equal to $p_i^{\ast }{d}_i^{\ast }$. Due to symmetry, consumer surplus and social welfare are

$$C{S}^{\ast }=v-p_i^{\ast }+\theta d_i^{\ast }-6\times {\displaystyle {\int }_0^{z_{3,1}^{\ast }}zdz} \mathrm{and} S{W}^{\ast }=C{S}^{\ast }+{\displaystyle \sum _{i=1}^3{\mathsf{\Pi }}_i^{\ast }}.$$

It is easy to check that the second-order condition of optimality is satisfied. □

3.2. Horizontal Merger

In the merger case, ${\tilde{z}}_{i,j}$ denotes the location of the indifferent consumer between good $i$ and good $j$: $i,j=1,2,3$, and $i\ne j$. Since the insiders become compatible, given the prices set by all firms, the network sizes of the firms are ${\tilde{y}}_1={\tilde{y}}_2={\tilde{z}}_{2,3}-{\tilde{z}}_{3,1}$, and ${\tilde{y}}_3={\tilde{z}}_{3,1}+1-{\tilde{z}}_{2,3}$. The locations of the indifferent consumers satisfy the following equations

$$\begin{array}{c}\hfill \left\{\begin{array}{c}v-{\tilde{p}}_3+\theta \left({\tilde{z}}_{3,1}+1-{\tilde{z}}_{2,3}\right)-{\tilde{z}}_{3,1}=v-{\tilde{p}}_1+\theta \left({\tilde{z}}_{1,2}-{\tilde{z}}_{3,1}\right)-\left(1/3+a-{\tilde{z}}_{3,1}\right)\hfill \\ v-{\tilde{p}}_1+\theta \left({\tilde{z}}_{1,2}-{\tilde{z}}_{3,1}\right)-\left({\tilde{z}}_{1,2}-\left(1/3+a\right)\right)=v-{\tilde{p}}_2+\theta \left({\tilde{z}}_{2,3}-{\tilde{z}}_{1,2}\right)-\left(2/3-a-{\tilde{z}}_{1,2}\right),\hfill \\ v-{\tilde{p}}_2+\theta \left({\tilde{z}}_{2,3}-{\tilde{z}}_{1,2}\right)-\left({\tilde{z}}_{2,3}-\left(2/3-a\right)\right)=v-{\tilde{p}}_3+\theta \left({\tilde{z}}_{3,1}+1-{\tilde{z}}_{2,3}\right)-\left(1-{\tilde{z}}_{2,3}\right)\hfill \end{array}\right.\end{array}$$

(5)

which yield

$$\begin{array}{c}{\tilde{z}}_{3,1}=\frac{\left(1-\theta \right){\tilde{p}}_1+\theta {\tilde{p}}_2-{\tilde{p}}_3}{2\left(1-2\theta \right)}+\frac{1+3\left(a-\theta \right)}{6\left(1-2\theta \right)}, {\tilde{z}}_{1,2}=\frac{1}{2}-\frac{{\tilde{p}}_1-{\tilde{p}}_2}{2},\\ {\tilde{z}}_{2,3}=\frac{5-3\left(a+3\theta \right)}{6\left(1-2\theta \right)}-\frac{\theta {\tilde{p}}_1+\left(1-\theta \right){\tilde{p}}_2-{\tilde{p}}_3}{2\left(1-2\theta \right)}.\end{array}$$

(6)

Therefore, the demand functions of the firms are

$${\tilde{d}}_1={\tilde{z}}_{1,2}-{\tilde{z}}_{3,1},{\tilde{d}}_2={\tilde{z}}_{2,3}-{\tilde{z}}_{1,2},{\tilde{d}}_3={\tilde{z}}_{3,1}+1-{\tilde{z}}_{2,3}.$$

(7)

The aim of the insiders is to maximize the joint profit, $\tilde{\mathsf{\Pi }}={\tilde{\mathsf{\Pi }}}_1+{\tilde{\mathsf{\Pi }}}_2$, while the aim of the outsider is to maximize profit ${\tilde{\mathsf{\Pi }}}_3$, where ${\tilde{\mathsf{\Pi }}}_i={\tilde{p}}_i{\tilde{d}}_i$, and $i=1,2,3$. By differentiating $\tilde{\mathsf{\Pi }}$, with respect to ${\tilde{p}}_1$ and ${\tilde{p}}_2$, and differentiating ${\tilde{\mathsf{\Pi }}}_3$, with respect to ${\tilde{p}}_3$, we obtain the following lemma.

Lemma 2.

In the merger case, the equilibrium prices and demands are

$${\tilde{p}}_1^{\ast }={\tilde{p}}_2^{\ast }=\frac{5-3a}{9}-\theta , {\tilde{p}}_3^{\ast }=\frac{4+3a}{9}-\theta ,$$

$${\tilde{d}}_1^{\ast }={\tilde{d}}_2^{\ast }=\frac{5-3a-9\theta }{18\left(1-2\theta \right)}, {\tilde{d}}_3^{\ast }=\frac{4+3a-9\theta }{9\left(1-2\theta \right)};$$

the equilibrium profits, consumer surplus, and social welfare are

$${\tilde{\mathsf{\Pi }}}_1^{\ast }={\tilde{\mathsf{\Pi }}}_2^{\ast }=\frac{{\left(5-3a-9\theta \right)}^2}{162\left(1-2\theta \right)},{\tilde{\mathsf{\Pi }}}_3^{\ast }=\frac{{\left(4+3a-9\theta \right)}^2}{81\left(1-2\theta \right)},$$

$${\widetilde{CS}}^{\ast }=v+\frac{6{\theta }^3}{{\left(1-2\theta \right)}^2}-\frac{\left(151-12a+144a^2\right){\theta }^2}{18{\left(1-2\theta \right)}^2}+\frac{\left(35-6a+72a^2\right)\theta }{9{\left(1-2\theta \right)}^2}-\frac{193-48a+630a^2}{324{\left(1-2\theta \right)}^2},$$

$${\widetilde{SW}}^{\ast }=v+\frac{2{\theta }^3}{{\left(1-2\theta \right)}^2}-\frac{\left(43-12a+144a^2\right){\theta }^2}{18{\left(1-2\theta \right)}^2}+\frac{\left(71-42a+612a^2\right)\theta }{81{\left(1-2\theta \right)}^2}-\frac{29-24a+558a^2}{324{\left(1-2\theta \right)}^2}.$$

Proof of Lemma 2.

From the first-order conditions of $\tilde{\mathsf{\Pi }}={\tilde{\mathsf{\Pi }}}_1+{\tilde{\mathsf{\Pi }}}_2$, with respect to ${\tilde{p}}_1$ and ${\tilde{p}}_2$, and the first-order condition of ${\tilde{\mathsf{\Pi }}}_3$, with respect to ${\tilde{p}}_3$, we obtain the equilibrium prices ${\tilde{p}}_i^{\ast }$. By substitution of ${\tilde{p}}_i^{\ast }$ into Equation (6), the indifferent consumers’ locations are

$${\tilde{z}}_{3,1}^{\ast }=\frac{4+3a-9\theta }{18\left(1-2\theta \right)}, {\tilde{z}}_{1,2}^{\ast }=\frac{1}{2} \mathrm{and} {\tilde{z}}_{2,3}^{\ast }=\frac{14-3a-27\theta }{18\left(1-2\theta \right)}.$$

By the substitution of ${\tilde{p}}_i^{\ast }$ into Equation (7), equilibrium demands ${\tilde{d}}_i^{\ast }$ are obtained. Firm $i$’s optimal profit ${\tilde{\mathsf{\Pi }}}_i^{\ast }$ is equal to ${\tilde{p}}_i^{\ast }{\tilde{d}}_i^{\ast }$. The consumer surplus is

$$\begin{array}{c}{\widetilde{CS}}^{\ast }=2\times {\displaystyle {\int }_{{\tilde{z}}_{3,1}^{\ast }}^{{\tilde{z}}_{1,2}^{\ast }}\left[v-{\tilde{p}}_1^{\ast }+\theta \left({\tilde{d}}_1^{\ast }+{\tilde{d}}_1^{\ast }\right)-\left|z-\left(1/3+a\right)\right|\right]}dz+2\times {\displaystyle {\int }_0^{{\tilde{z}}_{3,1}^{\ast }}\left[v-{\tilde{p}}_3^{\ast }+\theta {\tilde{d}}_3^{\ast }-z\right]}dz\\ =v+\frac{6{\theta }^3}{{\left(1-2\theta \right)}^2}-\frac{\left(151-12a+144a^2\right){\theta }^2}{18{\left(1-2\theta \right)}^2}+\frac{\left(35-6a+72a^2\right)\theta }{9{\left(1-2\theta \right)}^2}-\frac{193-48a+630a^2}{324{\left(1-2\theta \right)}^2},\end{array}$$

and the social welfare is

$$\begin{array}{c}{\widetilde{SW}}^{\ast }={\widetilde{CS}}^{\ast }+{\displaystyle \sum _{i=1}^3{\tilde{\mathsf{\Pi }}}_i^{\ast }}\\ =v+\frac{2{\theta }^3}{{\left(1-2\theta \right)}^2}-\frac{\left(43-12a+144a^2\right){\theta }^2}{18{\left(1-2\theta \right)}^2}+\frac{\left(71-42a+612a^2\right)\theta }{81{\left(1-2\theta \right)}^2}-\frac{29-24a+558a^2}{324{\left(1-2\theta \right)}^2}.\end{array}$$

It is easy to check that the second-order condition of optimality is satisfied. □

3.3. Comparison and Results

By comparing Lemmas 1 and 2, we investigate how the merger influences firms’ profits, consumer surplus, and social welfare, if consumers form a responsive expectation.

Proposition 1.

(1) The merger lowers the insiders’ profits, if $\theta >1/6$ and $a>5/3-3\theta -\sqrt{\left(2-3\theta \right)\left(1-2\theta \right)}$; otherwise, the merger increases the insiders’ profits. (2) The merger lowers the outsider’s profit, if $\theta >{\theta }_1(a)$; otherwise, the merger increases the outsider’s profit. (3) The merger reduces consumer surplus, if $\theta <{\theta }_2(a)$; otherwise, the merger increases consumer surplus. (4) The merger harms social welfare, if $\theta <{\theta }_3(a)$; otherwise, the merger enhances social welfare.

Proof of Proposition 1.

(1)

For the merging firms 1 and 2,

$$\Delta {\mathsf{\Pi }}_M\equiv {\tilde{\mathsf{\Pi }}}_i^{\ast }-{\mathsf{\Pi }}_i^{\ast }=\frac{9a^2-6\left(5-9\theta \right)a+27{\theta }^2-27\theta +7}{162\left(1-2\theta \right)}, i=1,2.$$

Obviously, $\Delta {\mathsf{\Pi }}_M$ is a quadratic function, with respect to $a$ ($0<a<1/6$), and the sign of $\Delta {\mathsf{\Pi }}_M$ depends on the numerator. Let $\Delta {\mathsf{\Pi }}_M<0$, which leads to

$$5/3-3\theta -\sqrt{\left(2-3\theta \right)\left(1-2\theta \right)}<a<5/3-3\theta +\sqrt{\left(2-3\theta \right)\left(1-2\theta \right)}.$$

For $0<a<1/6$ and $0<\theta <(4+3a)/9$, note that $5/3-3\theta +\sqrt{\left(2-3\theta \right)\left(1-2\theta \right)}>1/6$ and $5/3-3\theta -\sqrt{\left(2-3\theta \right)\left(1-2\theta \right)}<(>)1/6\iff \theta >(<)1/6$. We have

$$\Delta {\mathsf{\Pi }}_M<0 \mathrm{iff} \theta >1/6 \mathrm{and} a>5/3-3\theta -\sqrt{\left(2-3\theta \right)\left(1-2\theta \right)},$$

and $\Delta {\mathsf{\Pi }}_M>0$ otherwise.

(2)

For the outsider firm 3,

$$\Delta {\mathsf{\Pi }}_O\equiv {\tilde{\mathsf{\Pi }}}_3^{\ast }-{\mathsf{\Pi }}_3^{\ast }=\frac{108{\theta }^2-27\left(3+4a\right)\theta +14+48a+18a^2}{162\left(1-2\theta \right)}.$$

Let $\Delta {\mathsf{\Pi }}_O>0$, we obtain

$$0<\theta <{\theta }_1\left(a\right) \mathrm{or} \theta >\frac{3}{8}+\frac{a}{2}+\frac{1}{72}\sqrt{57-360a+432a^2},$$

where ${\theta }_1\left(a\right)=\frac{3}{8}+\frac{a}{2}-\frac{1}{72}\sqrt{57-360a+432a^2}$. It is easy to check that the right inequality violates the assumption that $0<\theta <\left(4+3a\right)/9$, thus it is eliminated.

(3)

The differences of the consumer surpluses and social welfares are

$$\begin{array}{c}\Delta CS={\widetilde{CS}}^{\ast }-C{S}^{\ast }\\ =\frac{8{\theta }^3}{3{\left(1-2\theta \right)}^2}-\frac{\left(61-12a+144a^2\right){\theta }^2}{18{\left(1-2\theta \right)}^2}+\frac{\left(25-12a+144a^2\right)\theta }{18{\left(1-2\theta \right)}^2}-\frac{29-24a+315a^2}{162{\left(1-2\theta \right)}^2},\end{array}$$

$$\begin{array}{c}\Delta SW={\widetilde{SW}}^{\ast }-S{W}^{\ast }\\ =\frac{2{\theta }^3}{3{\left(1-2\theta \right)}^2}-\frac{\left(13-12a+144a^2\right){\theta }^2}{18{\left(1-2\theta \right)}^2}+\frac{\left(17-42a+612a^2\right)\theta }{81{\left(1-2\theta \right)}^2}-\frac{1-12a+279a^2}{162{\left(1-2\theta \right)}^2}.\end{array}$$

The unique real solutions to $\Delta CS=0$ and $\Delta SW=0$ are denoted as ${\theta }_2={\theta }_2\left(a\right)$ and ${\theta }_3={\theta }_3\left(a\right)$, respectively. Here, ${\theta }_2\left(a\right)$ and ${\theta }_3\left(a\right)$ are uniquely determined by

$$432{\theta }^3-9\left(61-12a+144a^2\right){\theta }^2+9\left(25-12a+144a^2\right)\theta -29+24a-315a^2=0,$$

and

$$108{\theta }^3-9\left(13-12a+144a^2\right){\theta }^2+2\left(17-42a+612a^2\right)\theta -1+12a-279a^2=0,$$

respectively. It is easy to check that ${\theta }_2\left(a\right)$ is always larger than ${\theta }_3\left(a\right)$, for $0<a<1/6$. Furthermore, $\Delta CS>0$, if $\theta >{\theta }_2\left(a\right)$, and $\Delta SW>0$, if $\theta >{\theta }_3\left(a\right)$. □

When consumers form a responsive expectation, the influences of a merger on the profits of the firms and welfare is shown clearly in Figure 2 and

Table 1. Effects of merger with responsive expectation.

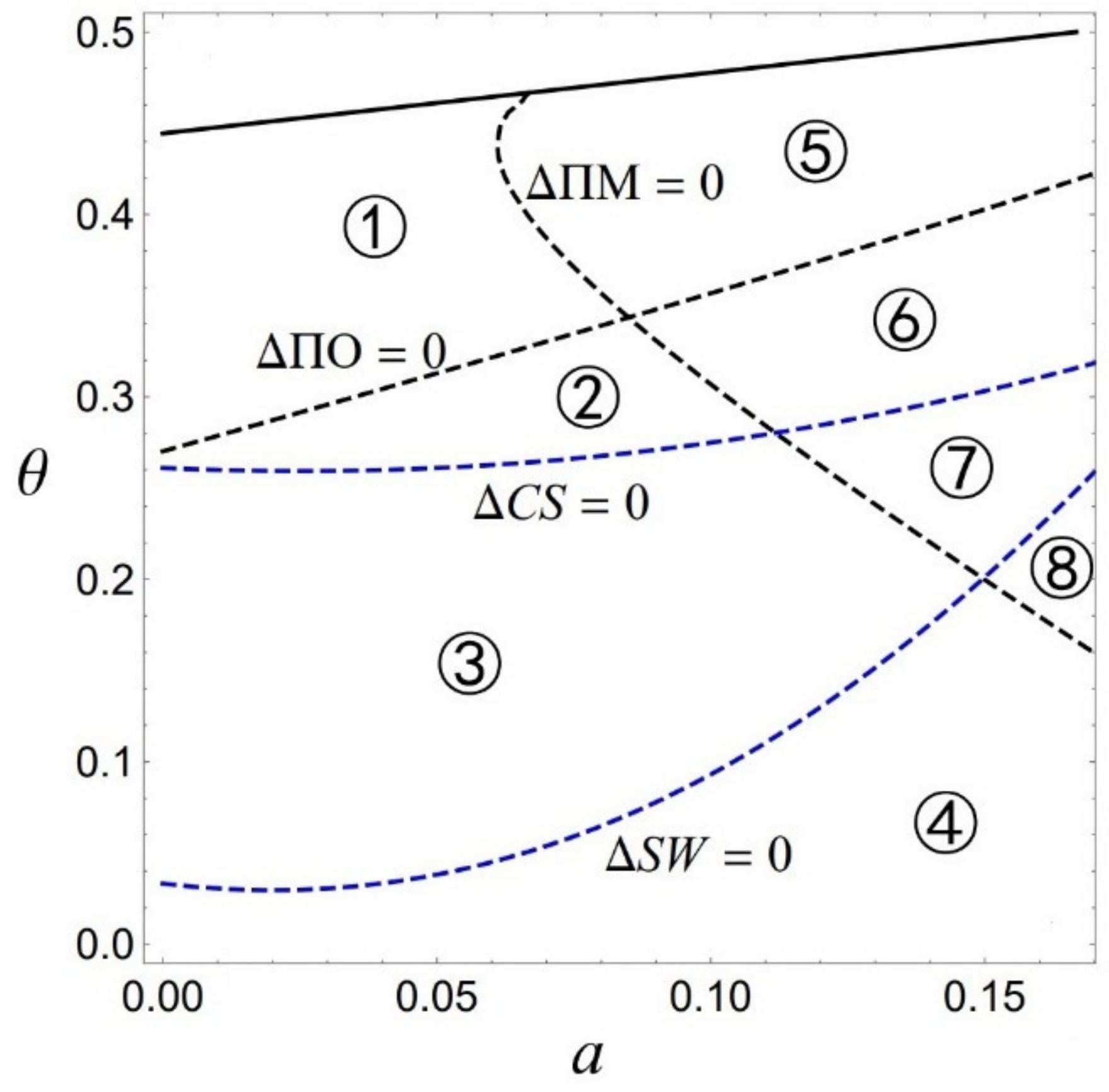
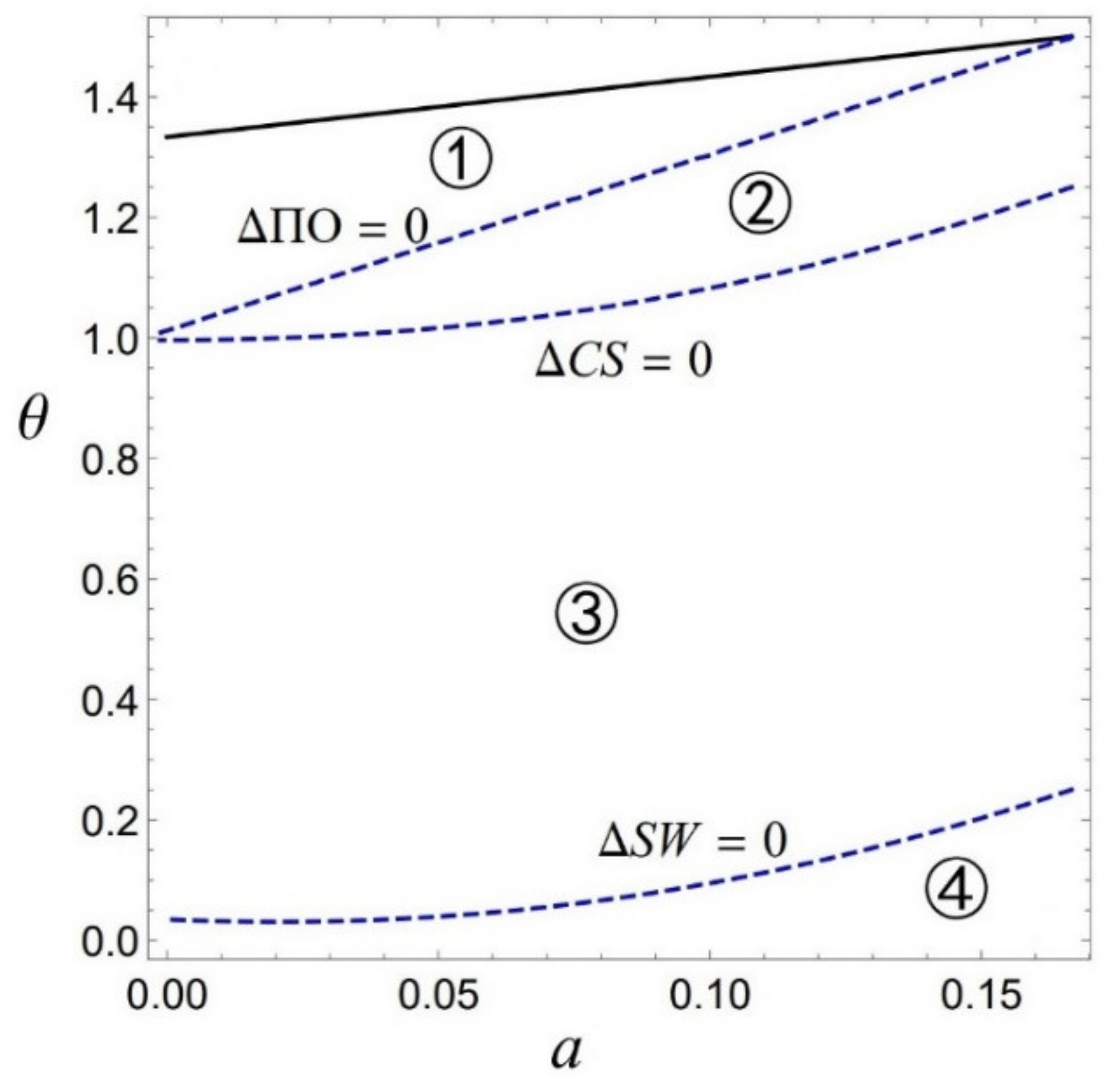
	Advantage (+)	Disadvantage (−)
Profits of the insiders	①, ②, ③, ④	⑤, ⑥, ⑦, ⑧
Profit of the outsider	②, ③, ④, ⑥, ⑦, ⑧	①, ⑤
Consumer surplus	①, ②, ⑤, ⑥	③, ④, ⑦, ⑧
Social welfare	①, ②, ③, ⑤, ⑥, ⑦	④, ⑧

.

The impact of the merger on insiders’ profits can be explained as follows. Above all, let us consider the case when $a=\theta =0$. Since firms 1 and 2 are now cooperating divisions of the merged firm, they do not compete for the consumers located between them anymore; thus, they have incentives to raise the prices of products 1 and 2. Though this may lead to the loss of some consumers, the increased prices chosen by the merged firm will induce firm 3 to likewise set a higher price. Such a response reduces the loss of market share that the merged firm actually suffers; in other words, the increase in prices makes all the firms more profitable.

In this paper, we assume network externalities ($\theta >0$) exist, and the merger leads to a loss of product differentiation ($a>0$). In fact, the renouncement of product differentiation due to the merger will reduce the attractiveness of the merged firms; thus, the merger lowers both the prices and the demands for the insiders ($\partial {\tilde{p}}_i^{\ast }/\partial a<0$ and $\partial {\tilde{d}}_i^{\ast }/\partial a<0$). Therefore, it tends to reduce the profit for the merging firms, which can be called the differentiation renouncing effect. On the other hand, when network externalities exist, all firms have motivations to take advantage of the network externalities to attract more consumers; therefore, they will choose to lower prices. The merger creates larger network scales for the merging firms, which means the insiders are likely to benefit more. However, the price reduction is much greater for the merging case ($\left|\partial {\tilde{p}}_i^{\ast }/\partial \theta \right|=1>\left|\partial p_i^{\ast }/\partial \theta \right|=1/2$) and reduces the profits of the merging firms accordingly, which can be called the price competition effect. Both the differentiation renouncing effect and the price competition effect will lower the insiders’ profits, if the intensity of the network effect (i.e., $\theta$) and the loss in differentiation (i.e., $a$) are relatively large; otherwise, the insiders’ profits will increase.

Proposition 1(2) shows that the impact of a merger on the outsider’s profit is ambiguous too. On one hand, the merger helps alleviate market competition between firms, which is good news for the outsider; in addition, the merger leads to a loss of product differentiation, which also benefits the outsider ($\partial {\tilde{p}}_3^{\ast }/\partial a>0$, $\partial {\tilde{d}}_3^{\ast }/\partial a>0$). On the other hand, the existence of network externalities will enhance competition; therefore, both the price and the demand for the outsider ($\partial ({\tilde{p}}_3^{\ast }-p_3^{\ast })/\partial \theta <0$, $\partial ({\tilde{d}}_3^{\ast }-d_3^{\ast })/\partial \theta <0$) will be reduced, which tends to reduce the outsider’s profit. When the intensity of the network effect is weak, the first factor plays a major role; thus, the profit of the outsider will increase. Otherwise, when $\theta$ is large, the effect of the merger exacerbating competition plays a major role, which harms the outsider.

Next, there are three factors that act upon consumer surplus: transport costs, network externalities, and prices. First, before the merger, each consumer buys products from firms that are closest to them, but the merger leads to uneven market distribution, thus increasing transport costs. Second, the merged firms are compatible with each other, which enlarges the network consumers can enjoy. At last, when $\theta$ is small, the effect of alleviating competition plays a major role, i.e., the merger leads to rising equilibrium prices. When $\theta$ is small (i.e., $\theta <{\theta }_2(a)$), the increase in the network effect is dominated by the rise of prices and the increase in transportation costs; therefore, the merger hurts consumer surplus. However, the increase in the network effect takes a major role, if $\theta$ is relatively large (i.e., $\theta >{\theta }_2(a)$), which enhances consumer surplus.

At last, social welfare merely depends on transport costs and network externalities. If $\theta$ is small (i.e., $\theta <{\theta }_3(a)$), the increase in network externalities is relatively weak and is dominated by the increase in transport costs, so the merger reduces social welfare. However, if $\theta$ is large, the increase in network externalities is more than that of transport costs, so the merger is socially beneficial.

In stage 1, the insiders have an incentive to merge, if $(a,\theta )$ falls into Region ①, ②, ③, or ④. The following proposition discusses the welfare effects of the merger.

Proposition 2.

(1) When$(a,\theta )$falls into Region ①, the outsider will oppose the merger, but it raises consumer surplus and social welfare. (2) When$(a,\theta )$falls into Region ②, the merger is Pareto-improving. (3) When$(a,\theta )$falls into Region ③, the merger benefits all firms but reduces consumer surplus and enhances social welfare. (4) When$(a,\theta )$falls into Region ④, the merger benefits all firms but reduces consumer surplus and social welfare.

Proof of Proposition 2.

The proof is derived directly from Table 1. □

Proposition 2 has the following policy implications, for the antitrust authorities, on merger control. If consumer surplus is taken as the criteria, the proposed merger should be approved when the intensity of the network effect is strong (Region ①, ②). If social welfare is used as the standard, Region ③ should also be included. Though a legal action may be taken by the outsider, since it is unprofitable for them when the intensity of the network effect is extremely strong (Region ①), the antitrust authorities should reject this claim. It is noteworthy that the merger is Pareto-improving if the intensity of the network effect is relatively strong (Region ②); in this case, all firms benefit, and the welfare rises.

4. Extension: Analysis of Equilibrium with Passive Expectation

In this scenario, consumers’ expectations about the network sizes are fixed, i.e., consumers do not adjust their expectations in response to any changes in prices set by the firms, and the expectations are required to be fulfilled in equilibrium [14,15]. To guarantee that the second-order conditions hold and that all firms exist in the market in both the premerger and merger cases, we assume $\theta <4/3+a$. In this section, we continue to use the same notations as above.

4.1. Premerger

Since all firms are incompatible, and consumers form passive expectations $y_i^e$, the locations of the indifferent consumers satisfy the following equations

$$\left\{\begin{array}{l}v-p_3+\theta y_3^e-z_{3,1}=v-p_1+\theta y_1^e-\left(1/3-z_{3,1}\right)\hfill \\ v-p_1+\theta y_1^e-\left(z_{1,2}-1/3\right)=v-p_2+\theta y_2^e-\left(2/3-z_{1,2}\right)\hfill \\ v-p_2+\theta y_2^e-\left(z_{2,3}-2/3\right)=v-p_3+\theta y_3^e-\left(1-z_{2,3}\right)\hfill \end{array}\right.,$$

(8)

which yield

$$\begin{array}{c}{z}_{3,1}=\frac{1}{6}+\frac{p_1-p_3}{2}-\frac{\theta }{2}\left(y_1^e-y_3^e\right), z_{1,2}=\frac{1}{2}-\frac{p_1-p_2}{2}+\frac{\theta }{2}\left(y_1^e-y_2^e\right),\\ z_{2,3}=\frac{5}{6}-\frac{p_2-p_3}{2}+\frac{\theta }{2}\left(y_2^e-y_3^e\right).\end{array}$$

(9)

Therefore, the demand functions of the firms are

$$d_1=z_{1,2}-z_{3,1},d_2=z_{2,3}-z_{1,2},d_3=z_{3,1}+1-z_{2,3}.$$

(10)

By differentiating ${\mathsf{\Pi }}_i$, with respect to $p_i$, we obtain

$$\begin{array}{c}{p}_1=\frac{1}{3}+\frac{\theta }{5}\left(2y_1^e-y_2^e-y_3^e\right), p_2=\frac{1}{3}+\frac{\theta }{5}\left(-y_1^e+2y_2^e-y_3^e\right),\\ p_3=\frac{1}{3}+\frac{\theta }{5}\left(-y_1^e-y_2^e+2y_3^e\right).\end{array}$$

(11)

First, bringing Formula (11) into (9) and, next, substituting (9) into (10), we derive the demand of firm $i$

$$\begin{array}{c}{d}_1=\frac{1}{3}+\frac{\theta }{5}\left(2y_1^e-y_2^e-y_3^e\right), d_2=\frac{1}{3}+\frac{\theta }{5}\left(-y_1^e+2y_2^e-y_3^e\right),\\ d_3=\frac{1}{3}+\frac{\theta }{5}\left(-y_1^e-y_2^e+2y_3^e\right).\end{array}$$

(12)

At the equilibrium, $y_i^e$ equals to $d_i$. Therefore, we obtain that

$$y_i^{e,\ast }=\frac{1}{3}, i=1,2,3.$$

We have the following lemma.

Lemma 3.

In the premerger case, the equilibrium prices and demands are

$$p_i^{\ast }=\frac{1}{3}, d_i^{\ast }=\frac{1}{3};$$

the equilibrium profits, consumer surplus, and social welfare are

$${\mathsf{\Pi }}_i^{\ast }=\frac{1}{9}, C{S}^{\ast }=v+\frac{\theta }{3}-\frac{5}{12}, S{W}^{\ast }=v+\frac{\theta }{3}-\frac{1}{12}, i=1,2,3.$$

4.2. Horizontal Merger

In the merger case, the locations of the indifferent consumers satisfy the following equations

$$\left\{\begin{array}{l}v-{\tilde{p}}_3+\theta {\tilde{y}}_3^e-{\tilde{z}}_{3,1}=v-{\tilde{p}}_1+\theta \left({\tilde{y}}_1^e+{\tilde{y}}_2^e\right)-\left(1/3+a-{\tilde{z}}_{3,1}\right)\hfill \\ v-{\tilde{p}}_1+\theta \left({\tilde{y}}_1^e+{\tilde{y}}_2^e\right)-\left({\tilde{z}}_{1,2}-\left(1/3+a\right)\right)=v-{\tilde{p}}_2+\theta \left({\tilde{y}}_1^e+{\tilde{y}}_2^e\right)-\left(2/3-a-{\tilde{z}}_{1,2}\right)\hfill \\ v-{\tilde{p}}_2+\theta \left({\tilde{y}}_1^e+{\tilde{y}}_2^e\right)-\left({\tilde{z}}_{2,3}-\left(2/3-a\right)\right)=v-{\tilde{p}}_3+\theta {\tilde{y}}_3^e-\left(1-{\tilde{z}}_{2,3}\right)\hfill \end{array}\right.,$$

(13)

which yield

$$\begin{array}{c}{\tilde{z}}_{3,1}=\frac{1}{6}+\frac{a}{2}+\frac{{\tilde{p}}_1-{\tilde{p}}_3}{2}-\frac{\theta }{2}\left({\tilde{y}}_1^e-{\tilde{y}}_3^e\right), {\tilde{z}}_{1,2}=\frac{1}{2}-\frac{{\tilde{p}}_1-{\tilde{p}}_2}{2}+\frac{\theta }{2}\left({\tilde{y}}_1^e-{\tilde{y}}_2^e\right),\\ {\tilde{z}}_{2,3}=\frac{5}{6}-\frac{a}{2}-\frac{{\tilde{p}}_2-{\tilde{p}}_3}{2}+\frac{\theta }{2}\left({\tilde{y}}_2^e-{\tilde{y}}_3^e\right).\end{array}$$

(14)

Therefore, the demand functions of the firms are

$${\tilde{d}}_1={\tilde{z}}_{1,2}-{\tilde{z}}_{3,1},{\tilde{d}}_2={\tilde{z}}_{2,3}-{\tilde{z}}_{1,2},{\tilde{d}}_3={\tilde{z}}_{3,1}+1-{\tilde{z}}_{2,3}.$$

(15)

By differentiating $\tilde{\mathsf{\Pi }}={\tilde{\mathsf{\Pi }}}_1+{\tilde{\mathsf{\Pi }}}_2$, with respect to ${\tilde{p}}_1$ and ${\tilde{p}}_2$, and differentiating ${\tilde{\mathsf{\Pi }}}_3$, with respect to ${\tilde{p}}_3$, we obtain that

$$\begin{array}{c}{\tilde{p}}_1=\frac{5}{9}-\frac{a}{3}+\frac{\theta }{12}\left(5{\tilde{y}}_1^e-{\tilde{y}}_2^e-4{\tilde{y}}_3^e\right), {\tilde{p}}_2=\frac{5}{9}-\frac{a}{3}+\frac{\theta }{12}\left(-{\tilde{y}}_1^e+5{\tilde{y}}_2^e-4{\tilde{y}}_3^e\right),\\ {\tilde{p}}_3=\frac{4}{9}+\frac{a}{3}+\frac{\theta }{6}\left(-{\tilde{y}}_1^e-{\tilde{y}}_2^e+2{\tilde{y}}_3^e\right).\end{array}$$

(16)

Bringing formula (16) into (14) and, further, substituting (14) into (15), we derive the demand functions

$$\begin{array}{c}{\tilde{d}}_1=\frac{5}{18}-\frac{a}{6}+\frac{\theta }{24}\left(11{\tilde{y}}_1^e-7{\tilde{y}}_2^e-4{\tilde{y}}_3^e\right), {\tilde{d}}_2=\frac{5}{18}-\frac{a}{6}+\frac{\theta }{24}\left(-7{\tilde{y}}_1^e+11{\tilde{y}}_2^e-4{\tilde{y}}_3^e\right),\\ {\tilde{d}}_3=\frac{4}{9}+\frac{a}{3}+\frac{\theta }{6}\left(-{\tilde{y}}_1^e-{\tilde{y}}_2^e+2{\tilde{y}}_3^e\right).\end{array}$$

(17)

At the equilibrium, ${\tilde{y}}_1^e+{\tilde{y}}_2^e$ ($i=1,2$) is equal to ${\tilde{d}}_1+{\tilde{d}}_2$, and ${\tilde{y}}_3^e$ is equal to ${\tilde{d}}_3$. Therefore, we have

$${\tilde{y}}_1^{e,\ast }={\tilde{y}}_2^{e,\ast }=\frac{5-3a-3\theta }{3\left(3-2\theta \right)}, {\tilde{y}}_3^{e,\ast }=\frac{4+3a-3\theta }{3\left(3-2\theta \right)}.$$

The following lemma holds.

Lemma 4.

In the merger case, the equilibrium prices and demands are

$${\tilde{p}}_1^{\ast }={\tilde{p}}_2^{\ast }=\frac{5-3a-3\theta }{3\left(3-2\theta \right)}, {\tilde{p}}_3^{\ast }=\frac{4+3a-3\theta }{3\left(3-2\theta \right)},$$

$${\tilde{d}}_1^{\ast }={\tilde{d}}_2^{\ast }=\frac{5-3a-3\theta }{6\left(3-2\theta \right)}, {\tilde{d}}_3^{\ast }=\frac{4+3a-3\theta }{3\left(3-2\theta \right)};$$

the equilibrium profits, consumer surplus, and social welfare are

$${\tilde{\mathsf{\Pi }}}_1^{\ast }={\tilde{\mathsf{\Pi }}}_2^{\ast }=\frac{{\left(5-3a-3\theta \right)}^2}{18{\left(3-2\theta \right)}^2}, {\tilde{\mathsf{\Pi }}}_3^{\ast }=\frac{{\left(4+3a-3\theta \right)}^2}{9{\left(3-2\theta \right)}^2},$$

$${\widetilde{CS}}^{\ast }=v-\frac{193-420\theta +302{\theta }^2-72{\theta }^3}{36{\left(3-2\theta \right)}^2}+\frac{2\left(2-3\theta +{\theta }^2\right)a}{3{\left(3-2\theta \right)}^2}-\frac{\left(35-48\theta +16{\theta }^2\right)a^2}{2{\left(3-2\theta \right)}^2},$$

$${\widetilde{SW}}^{\ast }=v-\frac{29-204\theta +230{\theta }^2-72{\theta }^3}{36{\left(3-2\theta \right)}^2}+\frac{2\left(1-3\theta +{\theta }^2\right)a}{3{\left(3-2\theta \right)}^2}-\frac{\left(31-48\theta +16{\theta }^2\right)a^2}{2{\left(3-2\theta \right)}^2}.$$

4.3. Comparison and Results

By comparing Lemmas 3 and 4, we investigate how the merger influences firms’ profits, consumer surplus, and social welfare, if consumers form a passive expectation.

Proposition 3.

(1) The merger always raises the insiders’ profits, and the merger raises the outsider’s profit only if$\theta <1+3a$; otherwise, it reduces the profit of the outsider. (2) The merger reduces consumer surplus, if$\theta <{\theta }_4(a)$, otherwise, it raises consumer surplus; the merger harms social welfare, if$\theta <{\theta }_5(a)$, otherwise, it enhances social welfare.

Proof of Proposition 3.

For the insiders,

$${\tilde{\mathsf{\Pi }}}_i^{\ast }-{\mathsf{\Pi }}_i^{\ast }=\frac{{\left(5-3a-3\theta \right)}^2}{18{\left(3-2\theta \right)}^2}-\frac{1}{9}=\frac{{\theta }^2+\left(18a-6\right)\theta +9a^2-30a+7}{18{\left(3-2\theta \right)}^2}, i=1,2.$$

Solving the inequality ${\theta }^2+\left(18a-6\right)\theta +9a^2-30a+7>0$, we obtain $\theta <3-9a-\sqrt{2}\left(1-6a\right)$ or $\theta >3-9a+\sqrt{2}\left(1-6a\right)$. Combining the non-negative condition $\theta <\frac{4}{3}+a$ and considering that $0<a<\frac{1}{6}$ and ${\tilde{\mathsf{\Pi }}}_i^{\ast }-{\mathsf{\Pi }}_i^{\ast }>0$ always holds, $i=1,2$.

For the outsider,

$${\tilde{\mathsf{\Pi }}}_3^{\ast }-{\mathsf{\Pi }}_3^{\ast }=\frac{{\left(4+3a-3\theta \right)}^2}{9{\left(3-2\theta \right)}^2}-\frac{1}{9}=\frac{\left(1-\theta +3a\right)\left(7-5\theta +3a\right)}{9{\left(3-2\theta \right)}^2}$$

${\tilde{\mathsf{\Pi }}}_3^{\ast }-{\mathsf{\Pi }}_3^{\ast }>0$, if (i) $1-\theta +3a>0$ and $7-5\theta +3a>0$ or (ii) $1-\theta +3a<0$ and $7-5\theta +3a<0$. Combining the non-negative condition $\theta <\frac{4}{3}+a$ and considering that $0<a<\frac{1}{6}$ and ${\tilde{\mathsf{\Pi }}}_3^{\ast }-{\mathsf{\Pi }}_3^{\ast }>0$, if $\theta <1+3a$, and ${\tilde{\mathsf{\Pi }}}_3^{\ast }-{\mathsf{\Pi }}_3^{\ast }<0$, if $1+3a<\theta <\frac{4}{3}+a$.

The difference of consumer surpluses is

$$\begin{array}{c}\Delta CS={\widetilde{CS}}^{\ast }-C{S}^{\ast },\\ =\frac{-29+24a-315a^2+\left(66-36a+432a^2\right)\theta -\left(49-12a+144a^2\right){\theta }^2+12{\theta }^3}{18{\left(3-2\theta \right)}^2}.\end{array}$$

We find that $\Delta CS>0$, if $\theta >{\theta }_4\left(a\right)$, and $\Delta CS<0$, if $\theta <{\theta }_4\left(a\right)$, where ${\theta }_4\left(a\right)$ is uniquely determined by $\Delta CS=0$.

The difference of social welfares is

$$\begin{array}{c}\Delta SW={\widetilde{SW}}^{\ast }-S{W}^{\ast },\\ =\frac{-1+12a-279a^2+\left(30-36a+432a^2\right)\theta -\left(37-12a+144a^2\right){\theta }^2+12{\theta }^3}{18{\left(3-2\theta \right)}^2}.\end{array}$$

We find that $\Delta SW>0$, if $\theta >{\theta }_5\left(a\right)$, and $\Delta SW<0$, if $\theta <{\theta }_5\left(a\right)$, where ${\theta }_5\left(a\right)$ is uniquely determined by $\Delta SW=0$. □

It can be found that, with a passive expectation, other conclusions are qualitatively invariant, except for the insiders’ profits, as Figure 3 shows. For the insiders, the merger always increases the profits with a passive expectation, while the impact of the merger on insiders’ profits is ambiguous with a responsive expectation. This is because consumers treat the network size as given in the case of a passive expectation, which reduces the demand elasticity; therefore, the merging firms can gain more competitive advantages and set higher prices, which can always raise the profitability of the insiders.

Proposition 3(1) shows that a merger always benefits the merging firms, while it is profitable for the outsider only if the intensity of the network effect is not too large. For the outsider, the price and the demand increase only if $\theta <1+3a$, or else both decrease, compared to the premerger case. Therefore, the proposed merger benefits the outsider, only when the intensity of the network effect is not too strong.

Next, as with a responsive expectation, when $\theta$ is small (i.e., $\theta <{\theta }_4(a)$), the increase in network effect is dominated by the rise of prices and the increase in transportation costs; therefore, the merger hurts consumer surplus. Moreover, if $\theta$ is small (i.e., $\theta <{\theta }_5(a)$), the increase in network externalities is relatively weak and is dominated by the increase in transport costs, so the merger reduces social welfare. However, if $\theta$ is large, the increase in network externalities is more than that of transport costs, so the merger is socially beneficial.

In stage 1, the insiders always have an incentive to merge. The following proposition discusses the welfare effects of the merger.

Proposition 4.

(1) When$(a,\theta )$falls into Region ①, the outsider will oppose the merger, but it raises consumer surplus and social welfare. (2) When$(a,\theta )$falls into Region ②, the merger is Pareto-improving. (3) When$(a,\theta )$falls into Region ③, the merger benefits all firms but reduces consumer surplus and enhances social welfare. (4) When$(a,\theta )$falls into Region ④, the merger benefits all firms but reduces consumer surplus and social welfare.

Proof of Proposition 4.

The proof is derived directly from

Table 2. Effects of merger with passive expectation.

	Advantage (+)	Disadvantage (−)
Profits of the insiders	①, ②, ③, ④	Null
Profit of the outsider	②, ③, ④	①
Consumer surplus	①, ②	③, ④
Social welfare	④, ②, ③	④

. □

5. Conclusions

We examine the influence of a merger in a network products market, with a three-firm spatial model. The incentive for the merger is subject to both the network externalities and the loss of product differentiation caused by merger-related compatibility. We find that, for the insiders, the merger lowers the insiders’ profits, if the network effect is strong enough, and the renouncement of the product differentiation is large enough with a responsive expectation, while the merger is always beneficial to the insiders with a passive expectation. For the outsider, with both responsive and passive expectations, the merger lowers the outsider’s profit only if the intensity of the network effect is not large enough, because the effect of the merger exacerbating competition plays a major role, which is unprofitable to the outsider if the network effect is strong. Concerning consumer surplus and social welfare, the merger reduces consumer surplus and harms social welfare, if the intensity of the network effect is weak. Obviously, the merger may benefit all firms and simultaneously raise consumer surplus and social welfare, when the intensity of the network effect is not too large and the renouncement of product differentiation due to merger-related compatibility is not too heavy. Therefore, a merger may be Pareto-improving in the presence of merger-related compatibility.

In this study, in order to focus on the relationship between the merging decision and renunciation of product differentiation due to compatibility, we just consider a simple model, e.g., we assume the production costs for all three firms are zero. However, in reality, the merging firms may benefit from cost-savings, as [12] suggests. Extending our analysis to consider the situation of production cost saving is valuable, so it should be studied in the future. Moreover, we assume that the intensity of the network effect is invariable after the merger; however, ref. [1] points out that the insider may enjoy a stronger network externality if the merger takes place. This extension also remains for future research.