Abstract
In this paper, we introduce the notion of n-tilting (resp. n-cotilting) objects in functor categories and give some characterizations of n-tilting objects and n-tilting classes (resp. n-cotilting objects and n-cotilting classes).
MSC:
18A25; 18G10
1. Introduction
Tilting theory traces its history back to the fundamental work in [1], and later, was generalized by Brenner and Butler in [2]. The notion of tilting modules over finite dimensional algebras and the beginning of the extensive study of tilting theory and tilted algebras are principally due to Happel and Ringel [3], Bongartz [4], and others. After that, some results of tilting theory in module categories were obtained by many authors, see [5,6,7,8,9,10,11,12,13,14,15,16,17,18].
As a higher dimensional generalization of tilting modules of a projective dimension over arbitrary rings, Bazzoni gave in [8] a characterization of n-tilting (resp. n-cotilting) modules in module categories over arbitrary rings, which provided an equivalent condition for a module to be tilting. Then, Wei in [17] characterized n-tilting modules in arbitrary module categories. Angeleri Hügel and Coelho characterized the classes induced by generalized tilting modules in terms of the existence of -preenvelopes in [5].
Let be a skeletally small preadditive category. By (resp. ) we denote the functor category whose objects are additive contravariant (resp. covariant) functors from to the category Ab of abelian groups and morphisms as the natural transformations between two such functors. If , we write (or for short) for the class of natural transformations from T to U. The induced cohomological group will be denoted by . Functor categories are of interest in category theory, especially in representation theory of algebra and homological algebra (e.g., [19,20,21,22,23,24,25,26]). The reasons are as follows: on the one hand, many common categories are in fact functor categories, most results coming from functor categories are widely applicable; on the other hand, by applying the well-known Yoneda Lemma, every category can be embeded in a functor category, so that we often obtain our desired properties in the original category by studying the associated functor categories.
Based on the references above, some natural questions arise:
Question A. How can we define the tilting and cotilting objects in the functor categories felicitously?
Question B. Are the characterizations in the functor categories as good as those of the tilting objects in classical tilting theory?
The aim of this paper is to solve these questions for which we introduce the notions of n-tilting (resp. n-cotilting) objects and n-tilting (resp. n-cotilting) classes in the functor category and then provide some of their characterizations.
The paper is organized as follows. In Section 2, we give provide some preliminaries and terminology. Based on the result of Mitchell [27], we introduce the notions of n-tilting (resp. n-cotilting) objects and n-tilting (resp. n-cotilting) classes in the functor category and then study some of their basic properties. In Section 3, we give our main results, namely some characterizations of tilting objects and tilting classes in the functor category . The following are Theorems 1 and 2, respectively.
Theorem 1.
Let . Then,
(1) T is n-tilting if and only if ;
(2) U is n-cotilting if and only if .
Theorem 2.
Let be a class of objects. Then, the following assertions are equivalent.
(1) is n-tilting.
(2) is coresolving, special preenveloping, and closed under direct sums and direct summands and .
2. Preliminaries
In this section, is an abelian category. For a subcategory of , we always mean a full and additive subcategory closed under isomorphisms and direct summands.
Definition 1
([11], Definition 2.2.8, see also [28], Definition 16). Let be an abelian category with enough projective and injective objects. A subcategory of is resolving if it is closed under extensions, kernels of epimorphisms and contains the projective objects in . Dually, is coresolving if it is closed under extensions and cokernels of monomorphisms and contains the injective objects in .
Assume that has enough projective and injective objects. For every subcategory of , we set
and
A pair () of subcategories in is called a cotorsion pair if and ([11], Definition 2.2.1). For every subcategory , is resolving and is coresolving.
Note that if is resolving, then ; if is coresolving, then A pair () is called a hereditary cotorsion pair if and A cotorsion pair () is hereditary if and only if is resolving if and only if is coresolving ([11], Lemma 2.2.10).
A concept very useful when dealing with cotorsion pairs is the notion of approximations via precovers and preenvelopes defined by Enochs in [29] as a generalization of the notion of right and left approximations introduced by Auslander and Smalø [30] in representation theory of finite dimensional algebras. We recall now these definitions.
Let be a class of objects in . Following [29,30], we say that a morphism in is a -precover of A if , and, for any morphism with , there is a morphism such that . A -precover is said to be a -cover of A if every endomorphism such that is an isomorphism. A -precover is said to be special if it is an epimorphism and . Dually, we have the definitions of a -preenvelope, a -envelope, and a special -preenvelope. -covers (-envelopes) may not exist in general, but if they exist, they are unique up to isomorphisms.
A class is said to be precovering, covering, special precovering (preenveloping, enveloping, special preenveloping), respectively, if every object in admits a -precover, a -cover, a special -precover (a -preenvelope, a -envelope, a special -preenvelope) respectively.
A cotorsion pair () is said to be complete if every object in admits a special -precover and a special -preenvelope. In fact, by ([11], Proposition 1.1), a cotorsion pair () in is complete if and only if is special precovering and if and only if is special preenveloping.
In this sequel, we mainly work on the functor category , where is a skeletally small preadditive category. Note that the category admits arbitrary coproducts; products and the direct products are exact, and it satisfies Grothendieck’s AB5 condition, that is, it has exact filtered limits.
Let be a class of additive contravariant functors from to Ab. We denote by (resp. ) the subcategory consisting of all additive contravariant functors isomorphic to direct summands of direct sums (resp. direct products) of elements of . If with , then we shall denote these subcategories by and , respectively.
Given an object , we write for the subcategory of all M-generated objects in , that is, those objects X admitting an epimorphism with . The subcategory of M-cogenerated objects, that is, those objects X admitting a monomorphism with , is denoted by .
The following lemma is useful in this paper, it is cited from ([5], Proposition 1.1), see also [31]. Here, we talk about a similar version in functor categories, and give the proof for the reader’s convenience.
Lemma 1.
Let . Then, is precovering, and is preenveloping.
Proof.
For any , let ; then, the codiagonal map induced by all homomorphisms is an -precover. Dually, for the diagonal map is a -preenvelope. □
Following Mitchell [27], one has that is an abelian category with a projective generator and an injective cogenerator. Using it, we give the following definitions.
Definition 2.
An object is said to be n-tilting provided that:
(T1) ;
(T2) for each and for every cardinal λ;
(T3) there exists a long exact sequence
where P is a projective generator in , and for every .
In this case, the associated class is called the n-tilting class induced by T. Clearly, () is a hereditary cotorsion pair in , called the n-tilting cotorsion pair induced by T.
Dually, we have the following definition.
Definition 3.
An object is said to be n-cotilting provided that:
(C1) ;
(C2) for each and for every cardinal λ;
(C3) there exists a long exact sequence
where Q is an injective cogenerator in , and for every .
In this case, the class is called the n-cotilting class induced by U. Clearly, () is a hereditary cotorsion pair in , called the n-cotilting cotorsion pair induced by U.
Definition 4.
(1) Let . We write
In particular, .
(2) Let . We write
In particular, .
Lemma 2.
Let .
(1) If T satisfies the conditions (T2) and (T3), then .
(2) If U satisfies the conditions (C2) and (C3), then .
Proof
(1) Consider the following sequence given by the condition (T3):
with P a projective generator and for every . Clearly, we have that by (T2). Notice that is resolving, we infer that for each . Let . There exists some cardinal , such that is epic. Consider the pushout diagram:
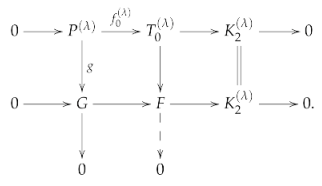

Since , the second row splits, so G is a direct summand of F. Since , and . This implies that .
The proof of (2) is the dual. □
Lemma 3.
Let .
(1) If T satisfies the condition (T2) and , then
(i) for each , there exists a short exact sequence
with and ;
(ii) every map with and factors through . In particular, we have = .
(2) If U satisfies the condition (C2), and , then
(i) for each , there exists a short exact sequence
with and ;
(ii) every map with and factors through . In particular, we have = .
Proof.
We only prove (1), and (2) is dual.
(i) Let . By Lemma 1, there exists an -precover with . Clearly, g is an epimorphism, since . We claim that belongs to . Indeed, we observe that because is an epimorphism, and (by (T2)). For , consider the sequence
Since , we obtain for . So .
(ii) Let be a map with and . By (i), there exists a short exact sequence
with , we obtain f factors through g as required, since . For , we observe that for , its identity map id factors through , and so . The other inclusion follows directly from the condition (T2). □
Proposition 1.
(1) Let . If T is n-tilting, then . In particular, is closed under direct sums. Moroever, , for every .
(2) Let . If U is n-cotilting, then . In particular, is closed under direct products. Moroever, , for every .
Proof.
We only prove (1), and (2) is dual.
Let T be an n-tilting object in . We first claim that . In fact, for any , by Lemma 3(1), there exists an exact infinite sequence of the form
with . So, by adding suitable direct sums of copies of T to , we obtain the following sequence of the form
for some cardinals , that is, . The other inclusion follows directly from dimension shifting. Clearly, is closed under direct sums by the claim. Next we prove the “MOROEVER”, and then we complete the proof. Note that for every . Conversely, suppose ; that is, there exists an exact sequence
for some cardinals . Let for each . By dimension shifting, , for each , and we obtain , since . Hence, by the claim. □
The following lemma is important for the main results in Section 3, it is cited from ([11], Theorem 3.2.1). Here, we give a similar version in functor categories. We leave the details of the proof for the reader.
Lemma 4.
Let be a set of objects in . Then, is special preenveloping.
Recall from [7] that for a subcategory , we denote by the subcategory of whose objects are the C for which there is some nonnegative integer n and an exact sequence
with in . Dually, we denote by the subcategory of whose objects are the C for which there are some nonnegative integer n and an exact sequence
with in .
For a fixed nonnegative integer n, we use (resp. ) to denote the subcategory consisting of all objects in with projective (resp. injective) dimensions at most n.
Proposition 2.
Let and n be a nonnegative integer.
(1) If , then , and .
(2) If , then , and .
Proof.
We only prove (2), and (1) is the dual.
Let . Consider the long exact sequence
with projective. Since , we have that for all ; that is, , and so . Let . We obtain for each , since . By the former argument, X is arbitrary, and we infer that . □
Lemma 5
([32], Theorem 1.1). Let be closed under extensions, and . Suppose there exists, for each , a short exact sequence
with and . Then, for each , there exists short exact sequences
with and .
Lemma 6.
Let be an n-cotilting object. Then, is special precovering.
Proof.
Put , and (by Lemma 3(2)). It follows from Lemma 3(2) that, for each , there exists a short exact sequence
with and . By Lemma 5, for each (by Proposition 2(2)), we obtain a short exact sequence
with and . Notice that ; we infer that . So, f is a special -precover, as required. □
3. Main Results
In this section, we will give some characterizations of tilting objects and tilting classes in the functor category . The dual versions for cotilting are also true. We first show that the converse of Proposition 1 holds. Here, we need the following lemma.
Lemma 7.
Let .
(1) Assume that . Then, T satisfies (T1) and (T2).
(2) Assume that . Then, U satisfies (C1) and (C2).
Proof.
We only prove (1), and (2) is dual.
Let (). Clearly, (T2) holds, since for every cardinal . We prove that . For any , we consider an injective resolution of H:
Let for . By Lemma 3(1), there exists a cardinal and an exact sequence
with for every . We claim that for every .
We proceed with the proof by induction on m. If , notice that , and we have . We assume that the claim is true for (). Then, we have two exact sequences
Consider the following pullback diagram:
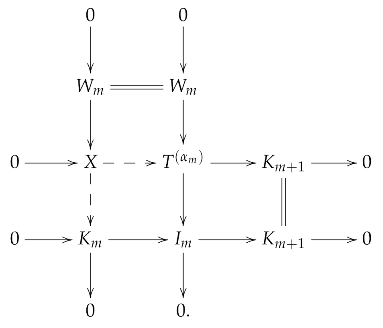

To prove , it suffices to check . Consider the second column
with and . By Lemma 3(1) and the Horseshoe Lemma, it is not hard to prove that .
So, in particular, . By dimension shifting, we obtain ; that is, , since H is arbitrary. □
Now we give the main results in this paper.
Theorem 1.
Let . Then,
(1) T is n-tilting if and only if ;
(2) U is n-cotilting if and only if .
Proof.
We only prove (1), and (2) is dual.
The necessity is trivial by Proposition 1(1). For the sufficiency, let (). Then, (T1) and (T2) follow from Lemma 7(1).
Next, we show that T satisfies (T3). Since (by (T1)), there exists a projective resolution of T
with the syzygies . Take ; then, . So, by Lemma 4, there exists a -preenvelope for every . By Lemma 3(1), f factors through a map with ; hence, g is an -preenvelope for every since (by (T2)). From (ii) of Lemma 3(1), we infer that all homomorphisms with and factor through and therefore factor through g. In particular, this applies to any monomorphism with I injective, showing that g is a monomorphism. We claim that . In fact, for any we have that is an epimorphism, and , which implies ; that is, . Notice that is coresolving, we obtain . Let us now take , where P is a projective generator in . Iterating the above construction, we obtain an exact sequence
with , and all cokernels in . So, we infer that for all ; hence, by Lemma 3(1), and the above sequence gives the one required in condition (T3). □
Proposition 3.
Let T be an n-tilting -module and U an n-cotilting -module. Then,
(1) the n-tilting cotorsion pair () is complete, and ;
(2) the n-cotilting cotorsion pair () is complete, and .
Proof.
(1) Let
be a projective resolution of T with the syzygies . Take ; then, . Clearly, the cotorsion pair () is complete by Lemma 4. Notice that , and the second part follows from Proposition 2(1).
(2) The first part follows from Lemma 6 and the second part follows from Proposition 2(2). □
The following result, due to Angeleri Hügel and Coelho [5], is proved for module categories over rings, see also Trlifaj [11]. Here, we give the counterpart in functor categories.
Theorem 2.
Let be a class of objects. Then, the following assertions are equivalent.
(1) is n-tilting.
(2) is coresolving, special preenveloping, closed under direct sums and direct summands, and .
Proof.
(1)⇒(2) Let be an n-tilting class, that is, there exists an n-tilting object T such that . This follows from Proposition 3(1) and Proposition 1(1).
(2)⇒(1) First, , since is coresolving.
Let P be a projective generator in . Because is special preenveloping, there exists a short exact sequence
with and . We have , since . By induction, we obtain short exact sequences
with and for any i. Since , we have ; then, the sequence
splits. So, we can assume that and form the long exact sequence
with for all . Put . We will prove that T is n-tilting. Clearly, (T1) holds since , and the long exact sequence above gives (T3). Since is closed under direct sums, for each cardinal , and (T2) holds.
Next, we show that . First, we observe that since . Conversely, suppose . Since is special preenveloping, repeatedly, it follows from the former argument that there exists an exact sequence of finite length
with for all , and . Since , and is coresolving, we infer that for all . We claim that . So splits, and by induction, splits; that is, since is closed under direct summands.
Proof of the claim: suppose . We observe that . Notice that T is n-tilting, by Lemma 3(1), it is easy to show that there exists a long exact sequence
with for all . Since is closed under direct sums and direct summands, , and we infer that since is coresolving; then, the sequence
splits. So . □
Corollary 1.
Let be a cotorsion pair in . Then, the following assertions are equivalent.
(1) is an n-tilting cotorsion pair.
(2) is complete and hereditary, and is closed under direct sums.
Proof.
Easy. □
Using Lemma 3(2), Propositions 1(2) and 3(2), we can obtain the dual versions of Theorem 2 and Corollary 1. We leave the details of the proof for the reader.
Theorem 3.
Let be a class of objects. Then, the following assertions are equivalent.
(1) is n-cotilting.
(2) is resolving, special precovering, closed under direct products and direct summands, and .
Corollary 2.
Let be a cotorsion pair in . Then, the following assertions are equivalent.
(1) is an n-cotilting cotorsion pair.
(2) is complete and hereditary, and is closed under direct products.
Author Contributions
Writing—original draft preparation, J.W. and T.Z.; writing—review and editing, J.W. and T.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by NSFC (11901341, 11971225) and the project ZR2019QA015 supported by Shandong Provincial Natural Science Foundation.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors thank the referees for the helpful suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bernstein, I.N.; Gelfand, I.M.; Ponomarev, V.A. Coxeter functors and Gabriel’s theorem. Usp. Mat. Nauk 1973, 28, 19–33. [Google Scholar]
- Brenner, S.; Butler, M. Generalizations of the Bernstein-Gelfand-Ponomarev refection functors. In Proceedings of the Second International Conference on Representations of Algebras, LNM 832. Ottawa, ON, Canada, 13–25 August 1979; Springer: Berlin, Germany, 1980; pp. 103–169. [Google Scholar]
- Happel, D.; Ringel, C.M. Tilted algebras. Trans. Am. Math. Soc. 1982, 274, 399–443. [Google Scholar]
- Bongartz, K. Tilted algebras. In Proceedings of the Third International Conference on Representations of Algebras, LNM 903. Puebla, Mexico, 4–8 August 1980; Springer: Berlin, Germany, 1981; pp. 26–38. [Google Scholar]
- Angeleri Hügel, L.; Coelho, F.U. Infinitely generated tilting modules of finite projective dimension. Forum Math. 2001, 13, 239–250. [Google Scholar]
- Angeleri Hügel, L.; Tonolo, A.; Trlifaj, J. Tilting preenvelopes and cotilting precovers. Algebr. Represent. Theory 2001, 4, 155–170. [Google Scholar] [CrossRef]
- Auslander, M.; Reiten, I. Applications of Contravariantly Finite Subcategories. Adv. Math. 1991, 86, 111–152. [Google Scholar]
- Bazzoni, S. A characterization of n-cotilting and n-tilting modules. J. Algebra 2004, 273, 359–372. [Google Scholar]
- Colby, R.R.; Fuller, K.R. Tilting, cotilting and serially tilted rings. Commun. Algebra 1990, 18, 1585–1615. [Google Scholar]
- Colby, R.R.; Trlifaj, J. Tilting modules and tilting torsion theories. J. Algebra 1995, 178, 614–634. [Google Scholar]
- Göbel, R.; Trlifaj, J. Approximations and Endomorphism Algebras of Modules; De Gruyter: Berlin, Germany, 2006; Volume 41. [Google Scholar]
- Huang, Z. Generalized tilting modules with finite injective dimension. J. Algebra 2007, 311, 619–634. [Google Scholar]
- Miyashita, Y. Tilting modules of finite projective dimension. Math. Z. 1986, 193, 113–146. [Google Scholar]
- Smalø, S. Torsion theories and tilting modules. Bull. Lond. Math. Soc. 1984, 16, 518–522. [Google Scholar]
- Šťovíček, J. All n-cotilting modules are pure-injective. Proc. Am. Math. Soc. 2006, 134, 1891–1897. [Google Scholar]
- Wei, J. Equivalences and the tilting theory. J. Algebra 2005, 283, 584–595. [Google Scholar]
- Wei, J. n-star modules and n-tilting modules. J. Algebra 2005, 283, 711–722. [Google Scholar]
- Wei, J.; Huang, Z.; Tong, W.; Huang, J. Tilting modules of finite projective dimension and a generalization of *-modules. J. Algebra 2003, 268, 404–418. [Google Scholar]
- Asadollahi, J.; Hafezi, R.; Vahed, R. On the recollements of functor categories. Appl. Categor. Struct. 2016, 24, 331–371. [Google Scholar]
- Asadollahi, J.; Hafezi, R.; Vahed, R. Derived equivalences of functor categories. J. Pure Appl. Algebra 2019, 223, 1073–1096. [Google Scholar]
- Mao, L. On covers and envelopes in some functor categories. Commun. Algebra 2013, 41, 1655–1684. [Google Scholar]
- Mao, L. On strongly flat and Ω-Mittag-Leffler objects in the category ((R−mod)op,Ab). Mediterr. J. Math. 2013, 10, 655–676. [Google Scholar]
- Mao, L.; Ding, N. On covers and envelopes under Hom and tensor functors. Commun. Algebra 2015, 43, 4334–4349. [Google Scholar]
- Martínez-Villa, R.; Ortiz-Morales, M. Tilting theory and functor categories I: Classical tilting. Appl. Categor. Struct. 2014, 22, 595–646. [Google Scholar]
- Martínez-Villa, R.; Ortiz-Morales, M. Tilting theory and functor categories II: Generalized tilting. Appl. Categor. Struct. 2013, 21, 311–348. [Google Scholar]
- Martínez-Villa, R.; Ortiz-Morales, M. Tilting theory and functor categories III: The maps category. Int. J. Algebra 2011, 5, 529–561. [Google Scholar]
- Mitchell, B. Rings with several objects. Adv. Math. 1972, 8, 1–161. [Google Scholar]
- Tan, L.; Liu, L. Resolution dimension relative to resolving subcategories in extriangulated categories. Mathematics 2021, 9, 980. [Google Scholar]
- Enochs, E.E. Injective and flat covers, envelopes and resolvents. Israel J. Math. 1981, 39, 33–38. [Google Scholar]
- Auslander, M.; Smalø, S. Preprojective modules over artin algebras. J. Algebra 1980, 66, 61–122. [Google Scholar]
- Rada, J.; Saorín, M. Rings characterized by (pre)envelopes and (pre)covers of their modules. Commun. Algebra 1998, 26, 899–912. [Google Scholar]
- Auslander, M.; Buchweitz, R. The homological theory of maximal Cohen-Macaulay approximations. Mem. Soc. Math. Fr. Suppl. Nouv. Ser. 1989, 38, 5–37. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).