Performance Analysis of Picking Routing Strategies in the Leaf Layout Warehouse
Abstract
:1. Introduction
- For non-traditional warehouse layouts, most of the current research is focused on the V-shaped layout [19,20,21] and fishbone layout [22,23,24,25,26,27], and less research is conducted on the leaf layout [28]. Therefore, we select the leaf layout as the research object in this paper to enrich the study of the routing strategy in the picking operation in non-traditional layout warehouses;
- There is no effective and efficient method to calculate the travel distance between any two storage locations to be visited in the leaf layout warehouse;
- The existing routing strategies in the leaf layout warehouse only have four applications: the S-shape, the return, the midpoint, and the largest gap, and more routing strategies need to be explored and extended.
- By focusing on the leaf warehouse layout, this paper develops the distance equation between any two storage locations to be visited in the picking operation of the leaf layout warehouse to meet the construction of walking distance models of heuristic routing strategies for different numbers of locations to be visited in order picking operations, which is one of the innovations of our work;
- We construct walking distance models corresponding to the three picking routing strategies of the leaf layout: the S-shape, the return, and the composite, in which the composite strategy of the leaf layout proposed by our work is also one of the innovative points of this paper.
- In this paper, the cuckoo search algorithm is introduced to solve and calculate the walking distance of the composite strategy in leaf layout warehouses for experiments, and the effectiveness of the cuckoo search algorithm is also proved based on the comparison of the numerical experimental results of the three routing strategies while demonstrating the selection of the routing strategy under different numbers of storage locations to be visited in the picking operation in leaf layout warehouses.
2. Literature Review
2.1. Warehouse Layouts
2.2. Routing Strategies
2.3. S/R Operations
2.4. Research Gaps and Novelties
- Compared with the traditional layout, the non-traditional layouts mainly include the fishbone layout, the Flying-V layout, the chevron layout, the leaf layout, etc. Among them, there are relatively more studies on the fishbone layout and the Flying-V layout, and there is a lack of studies on the chevron layout and the leaf layout;
- The existing studies on S/R operation strategies in non-traditional layout warehouses in the literature mainly apply the single-command strategy to unit-load warehouses, focus mostly on the fishbone and Flying-V layouts, and fewer scholars have studied the multi-command strategy in the leaf layout warehouse;
- Few studies have examined the effect of the number of storage locations to be visited in picking operations in non-traditional layout warehouses on the selection of routing strategies.
- Developing a new heuristic routing strategy in the leaf layout: the composite strategy;
- Exploring the distance equation between any two storage locations to be visited for the three heuristic path strategies, the S-shape, the return, and the composite, in the leaf layout warehouse, and based on the construction of walking distance models for the three routing strategies for different numbers of storage locations to be visited. We introduced the cuckoo search algorithm to numerically experiment and solve them;
- Evaluating three heuristic strategies by comparing them under different demand scales and storage assignments commonly used in warehouses.
3. Problem Description and Model Construction
3.1. Notations and Assumptions
3.1.1. Notations
3.1.2. Assumptions
- The shelves in the warehouse are composed of unit storage locations with equal length and width, and the shelf height is not considered [28];
- There is no shortage of goods in the warehouse, the goods at each storage location can meet the picking demand, and the picker or equipment can complete each batch of picking list at one time [18];
- The picking operation runs along the picking aisle’s center line, and the picking operation of shelves on both sides can be completed from the picking aisle’s center line [28];
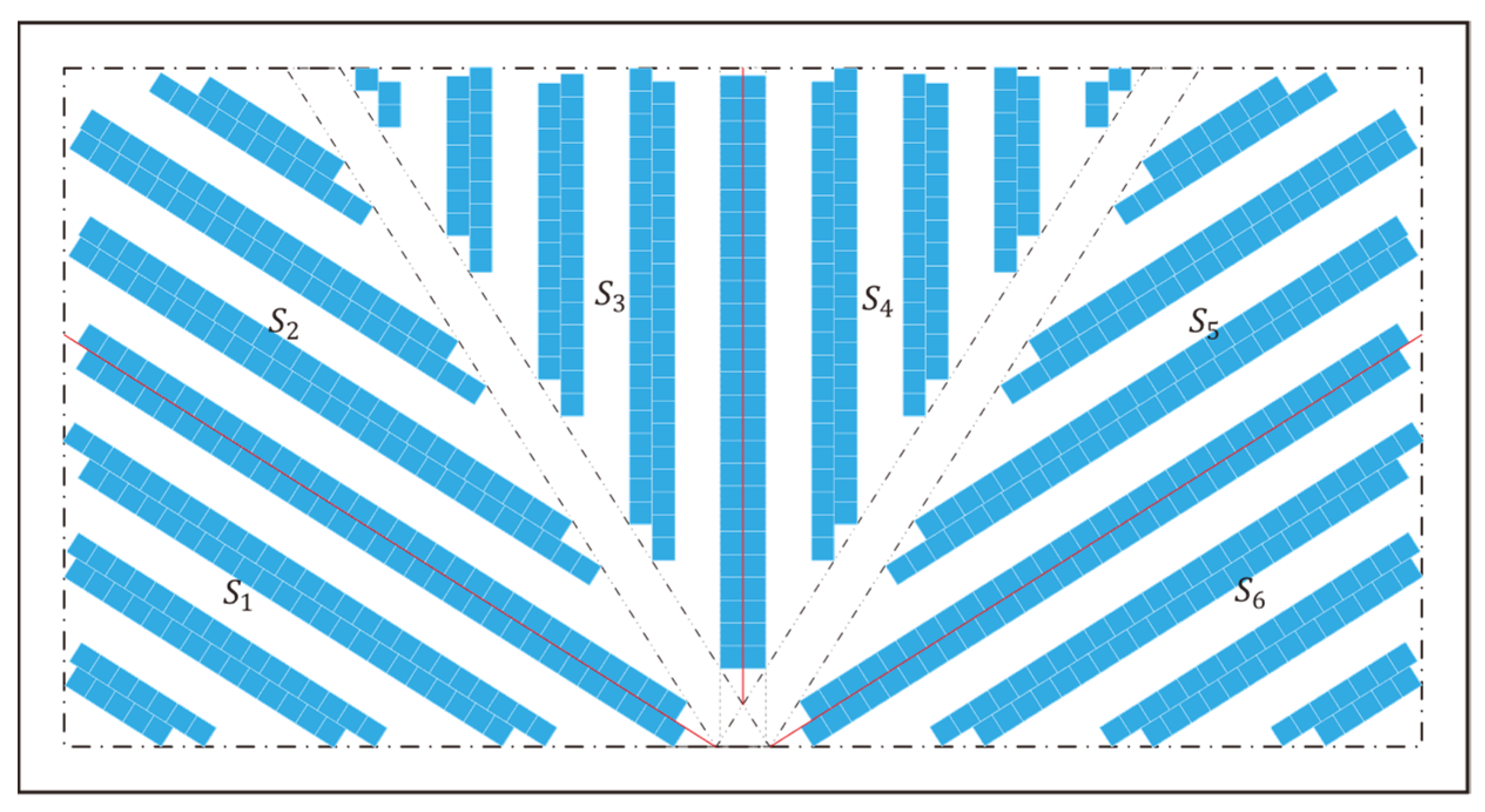
3.2. Problem Description
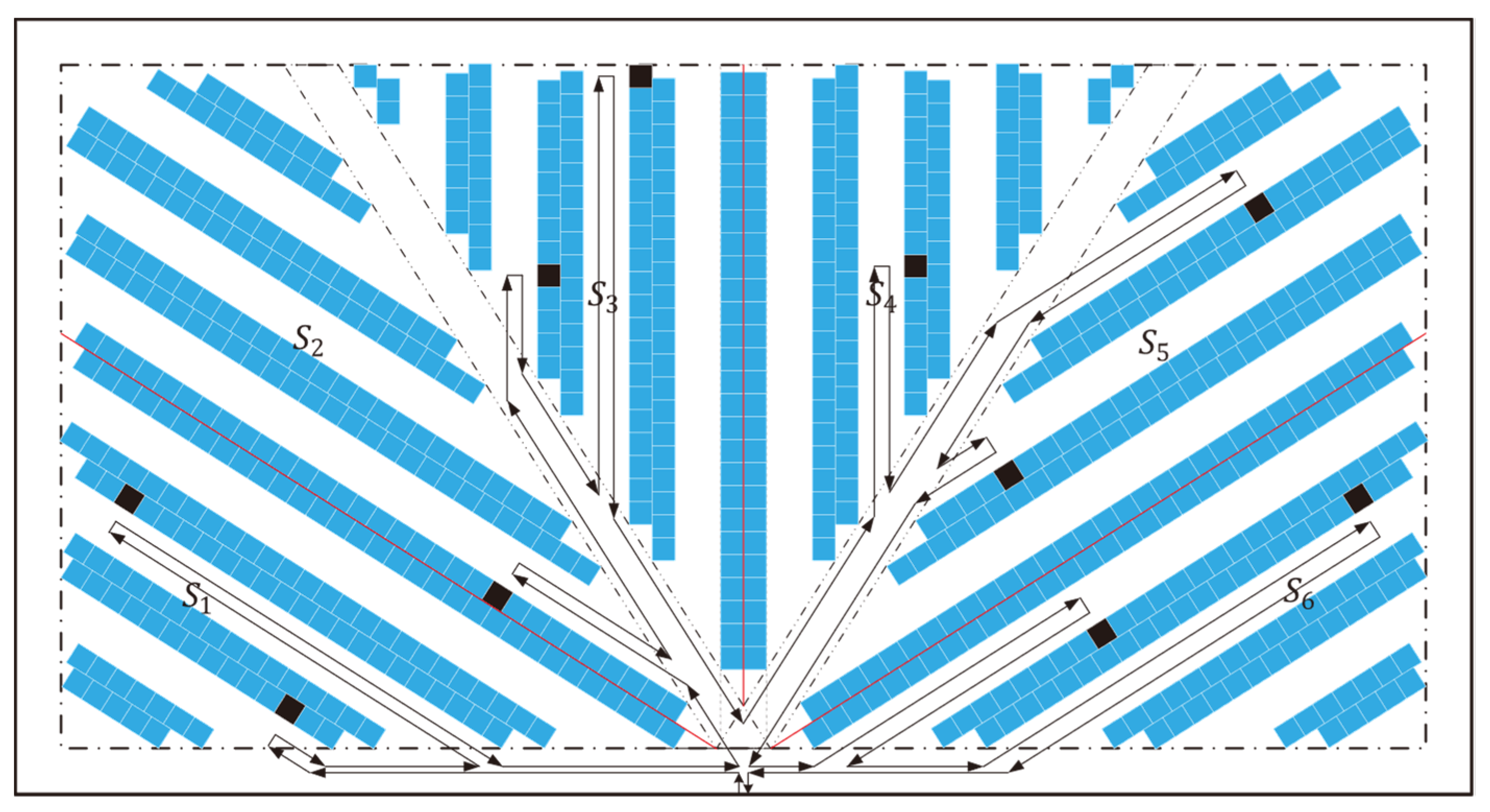
3.3. Walking Distance Model of the Return Strategy
3.4. Walking Distance Model of the S-Shape Strategy
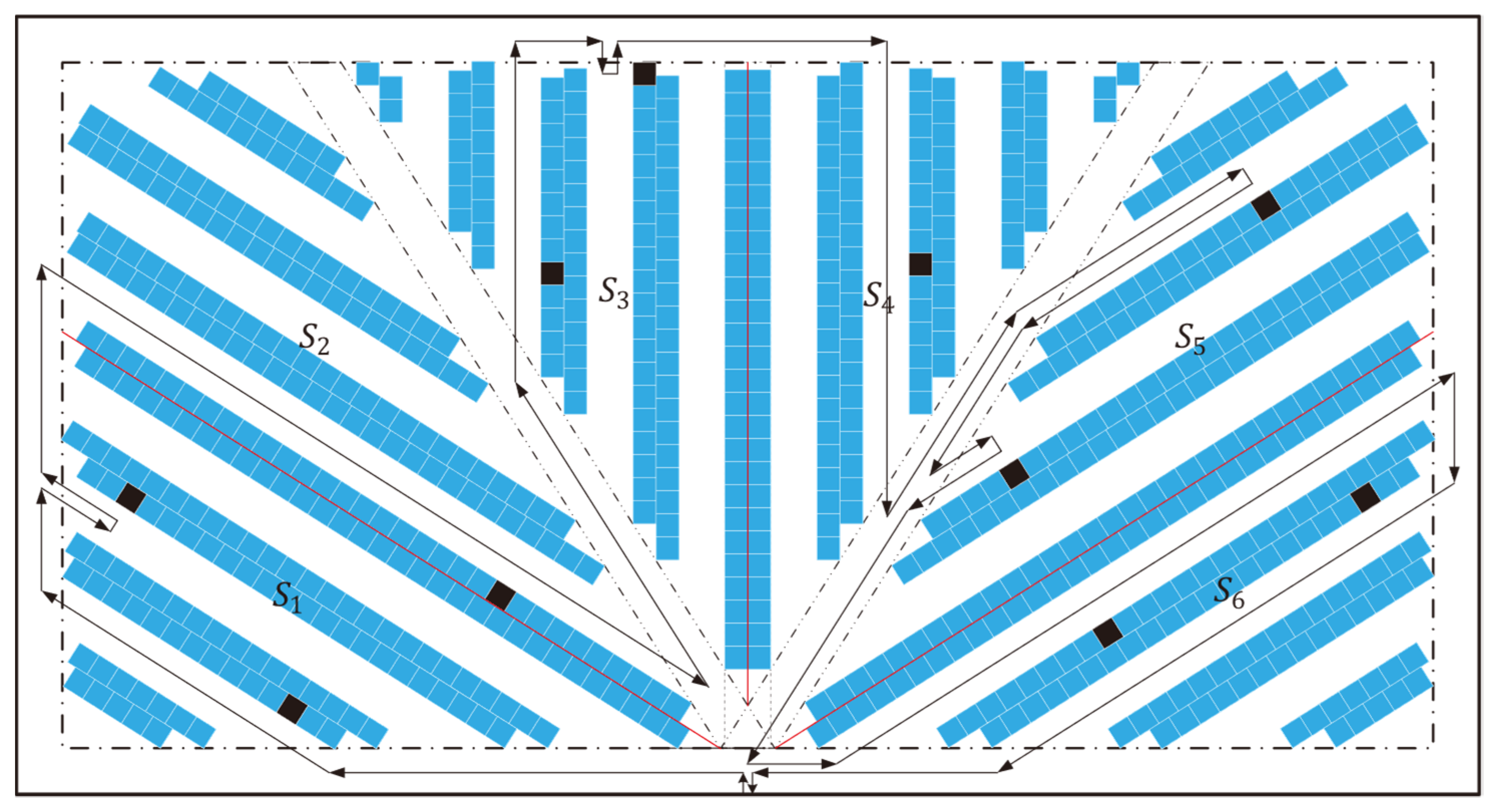
3.5. Walking Distance Model of the Composite Strategy
- It is the same as the S-shape strategy when is even and is the same as in Equation (16);
- It is the same as the S-shape strategy when is odd and is the same as in Equation (23).
- It is the same as the S-shape strategy when is even and is the same as in Equation (16);
- It is the same as the S-shape strategy when is odd and is the same as in Equation (24);
- Via the corresponding picking aisles in areas and , and from the diagonal cross-aisle to visit the picking aisle to complete the picking operation on the location ,
- Via the corresponding picking aisle in area and the back aisle, and from the back aisle or the right aisle to visit the picking aisle to complete the picking operation on the location ,
- Via the back aisle and the corresponding picking aisle in area , and from the diagonal cross-aisle to visit the picking aisle to complete the picking operation on the location ,
- It is the same as the S-shape strategy when is even and is the same as in Equation (16);
- It is the same as the S-shape strategy when is odd and is the same as in Equation (25).
- It is the same as the S-shape strategy when is odd and is the same as in Equation (27);
- It is the same as the S-shape strategy when is even and is the same as in Equation (26).
- It is the same as the S-shape strategy when is odd and is the same as in Equation (28);
- It is the same as the S-shape strategy when is even and is the same as in Equation (15).
- It is the same as the S-shape strategy when is odd and is the same as in Equation (29);
- It is the same as the S-shape strategy when is even and is the same as in Equation (26).
- It is the same as the S-shape strategy when is even and is the same as in Equation (16);
- It is the same as the S-shape strategy when is odd and is the same as in Equation (30);
- Via the diagonal cross-aisle, visit the picking aisle in area , the back aisle, and from the back aisle to the picking aisle to complete the picking operation on the location .
- It is the same as the S-shape strategy when is even and is the same as in Equation (26);
- It is the same as the S-shape strategy when is odd and is the same as in Equation (31);
- Via the left aisle, visit the picking aisle in area , the diagonal cross-aisle, and from the diagonal cross-aisle to the picking aisle to complete the picking operation on the location .
- It is the same as the S-shape strategy when is even and is the same as in Equation (26);
- It is the same as the S-shape strategy when is odd and is the same as in Equation (32);
- Via the left aisle, visit the picking aisle in area , the diagonal cross-aisle, and from the diagonal cross-aisle to the picking aisle to complete the picking operation on the location , and is the same as in Equation (38).
- Via the bottom aisle, visit the picking aisle in area the right aisle, and from the right or back aisle to visit the picking aisle to complete the picking operation on the location .
- Via the left aisle, visit the picking aisle in area , the picking aisle in area , the right aisle, and from the right or back aisle to the picking aisle to complete the picking operation on the location ,
- Via the left aisle, visit the back aisle, the diagonal cross-aisle, and from the diagonal cross-aisle to the picking aisle to complete the picking operation on the location ,
4. Results and Analysis
| Algorithm 1: CS algorithm to solve the walking distance of composite routing strategy. |
| 1: begin 2: Set up the nest: , 3: Calculate the initial fitness value: 4: while termination conditions not met 5: A new solution is generated by Lévy flight 6: Calculate the fitness of the new solution 7: Select the current optimal solution 8: if 9: Update current optimal solution 10: end 11: Find, and replace the inferior solution according to probability 12: Save the optimal solution 13: end 14: end |
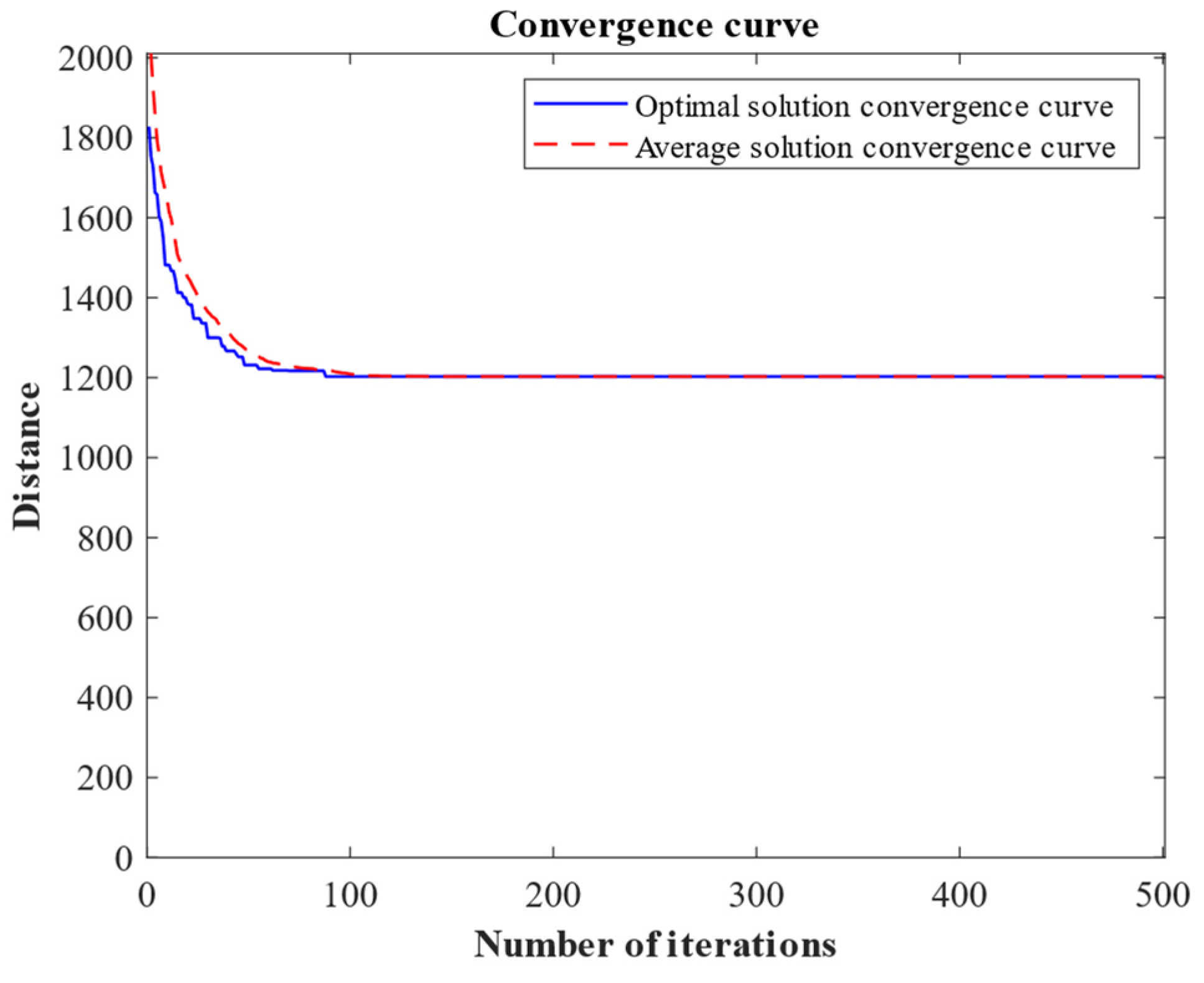
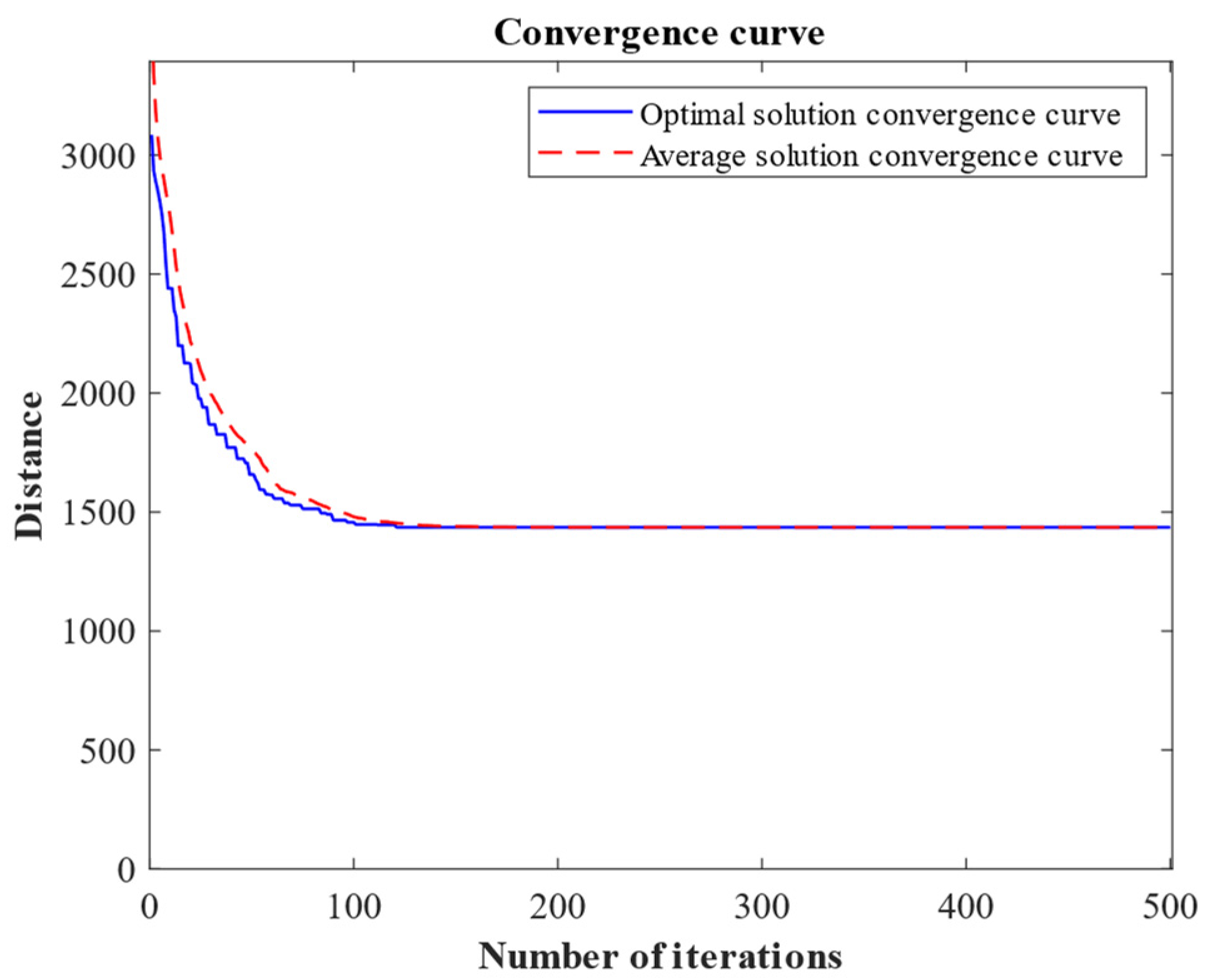
4.1. Numeric Results
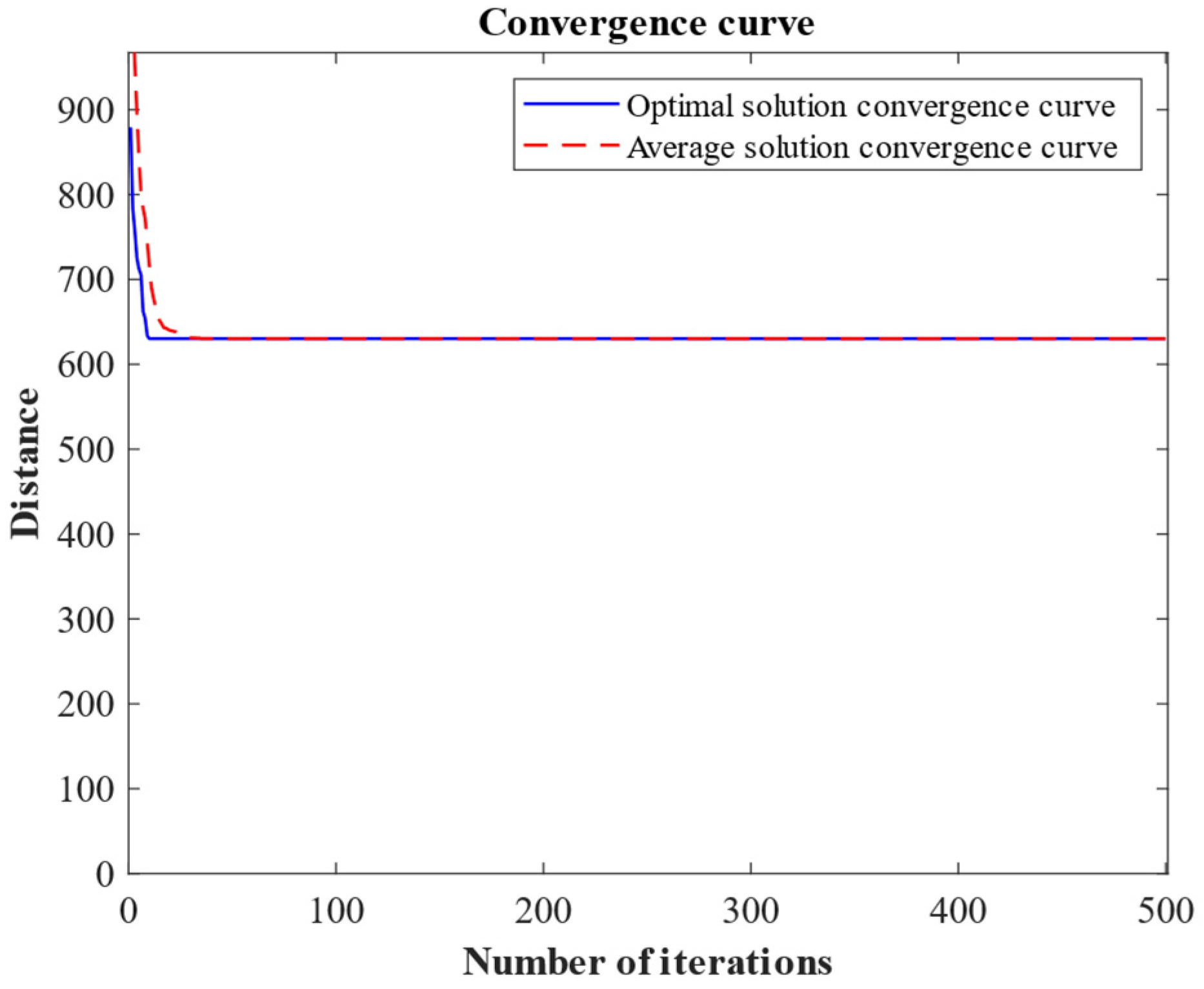
4.2. Analysis of Numeric Results
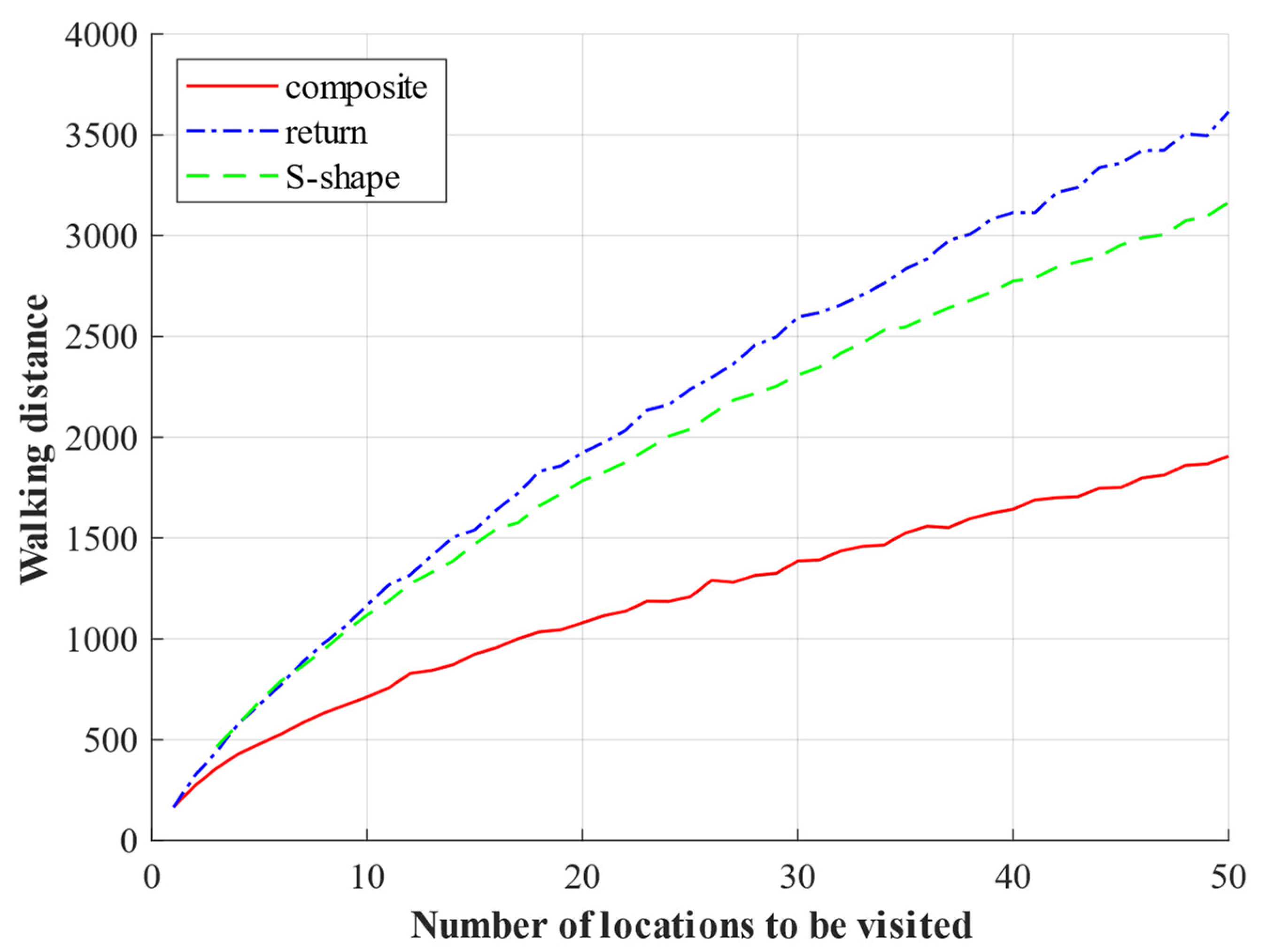
- The walking distance generated by the composite strategy is better than the S-shape strategy and the return strategy in the picking process;
- Compared with the S-shape strategy, the composite strategy provides better results than the return strategy, and the average proportion of optimization is higher than 40%;
- When the number of locations to be visited increases, the optimization effect of the composite strategy improves when compared to the S-shape strategy and the return strategy.
- When the order contains a small number of locations to be visited, the walking distance generated by the return strategy in the picking process is better than the S-shape strategy;
- With the increase in the number of locations to be visited in the order (the number of locations to be visited is greater than 7), the walking distance generated by the S-shape strategy is better than the return strategy.
4.3. Analysis of Storage Loss
- As shown in Table 13, at a certain width of the picking aisle, the wider the shelf, the larger the storage location, which leads to more loss of the storage area.
- As shown in Table 14, when the shelf width and the size of the storage location are certain, the wider the picking aisle, the higher the storage area loss rate.
- As shown in Table 15, when the ratio of the picking aisle width to the shelf width is certain, the loss rate of the storage area increases gradually with the increase of both the picking aisle width and the shelf width.
5. Conclusions
5.1. Theoretical Contributions
5.2. Managerial and Operational Implications
- High customer satisfaction and low operational costs are the keys to gaining a competitive advantage for e-commerce companies, in which the non-conventional layout design of the warehouse and routing strategies both have an impact on the efficiency and cost of picking operations. We took the leaf warehouse layout design as the research object, of which three heuristic routing strategies, the S-shape, the return, and the composite, were studied and compared, and we found that the composite strategy had advantages over both the S-shape strategy and the return strategy, and the advantage over the return strategy was higher than 40%. Therefore, in the leaf layout warehouse, the use of the composite strategy was more helpful for companies to improve their competitiveness compared to the other two routing strategies.
- E-commerce sales were mainly affected by promotions and seasonal fluctuations, and consumer demand curves and order sizes were similarly subject to change, which can create significant challenges for warehouse picking operations. Our work shows that when the number of storage locations to be visited in picking operations is high, i.e., during the peak sales season, and for simplicity, the S-shape strategy can achieve better results in practice, while during the low sales season, when order sizes are small and fewer locations need to be visited, the return strategy is simpler and easier to implement.
- In addition, according to the results of Liu et al. [18], compared to the chevron layout, the composite strategy can achieve better results in the leaf layout, which also brings more options for the warehouse layout of e-commerce enterprises. However, at the same time, due to the design of the cross-aisle, the number of storage locations in the leaf layout was less than that of the chevron layout warehouse. Therefore, when choosing a warehouse layout for e-commerce companies, it is necessary to consider the balance between the number of storage locations and picking efficiency in the adopted layout design.
5.3. Future Research
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ma, Z.; Wu, G.; Ji, B.; Wang, L.; Luo, Q.; Chen, X. A Novel Scattered Storage Policy Considering Commodity Classification and Correlation in Robotic Mobile Fulfillment Systems. IEEE Trans. Autom. Sci. Eng. 2022, 1–14. [Google Scholar] [CrossRef]
- Ali, S.S.; Kaur, R. Exploring the Impact of Technology 4.0 Driven Practice on Warehousing Performance: A Hybrid Approach. Mathematics 2022, 10, 1252. [Google Scholar] [CrossRef]
- Masae, M.; Glock, C.H.; Grosse, E.H. Order Picker Routing in Warehouses: A Systematic Literature Review. Int. J. Prod. Econ. 2020, 224, 107564. [Google Scholar] [CrossRef]
- Mou, S. Integrated Order Picking and Multi-Skilled Picker Scheduling in Omni-Channel Retail Stores. Mathematics 2022, 10, 1484. [Google Scholar] [CrossRef]
- Tompkins, J.A. Facilities Planning; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2010; ISBN 978-0-470-44404-7. [Google Scholar]
- De Koster, R.; Le-Duc, T.; Roodbergen, K.J. Design and control of warehouse order picking: A literature review. Eur. J. Oper. Res. 2007, 182, 481–501. [Google Scholar] [CrossRef]
- Li, X.; Hua, G.; Huang, A.; Sheu, J.-B.; Cheng, T.C.E.; Huang, F. Storage assignment policy with awareness of energy consumption in the Kiva mobile fulfilment system. Transp. Res. Part E Logist. Transp. Rev. 2020, 144, 102158. [Google Scholar] [CrossRef]
- Liang, J.; Wu, Z.; Zhu, C.; Zhang, Z.-H. An estimation distribution algorithm for wave-picking warehouse management. J. Intell. Manuf. 2022, 33, 929–942. [Google Scholar] [CrossRef]
- Hu, X.; Chuang, Y.-F. E-commerce warehouse layout optimization: Systematic layout planning using a genetic algorithm. Electron. Commer. Res. 2022, 1–18. [Google Scholar] [CrossRef]
- Derpich, I.; Sepúlveda, J.M.; Barraza, R.; Castro, F. Warehouse Optimization: Energy Efficient Layout and Design. Mathematics 2022, 10, 1705. [Google Scholar] [CrossRef]
- Gue, K.R.; Meller, R.D. The Aisle Design Problem. In Progress in Material Handling Research; College Industry Council on Material Handling Education (CICMHE): Charlotte, NC, USA, 2006. [Google Scholar]
- Gue, K.R.; Meller, R.D. Aisle configurations for unit-load warehouses. IIE Trans. 2009, 41, 171–182. [Google Scholar] [CrossRef]
- Pohl, L.M.; Meller, R.D.; Gue, K.R. A New Aisle Design for Dual-Command Travel. In Proceedings of the 2010 Industrial Engineering Research Conference, Cancun, Mexico, 6–9 June 2010; pp. 1–6. [Google Scholar]
- Gue, K.R.; Ivanović, G.; Meller, R.D. A unit-load warehouse with multiple pickup and deposit points and non-traditional aisles. Transp. Res. Part E Logist. Transp. Rev. 2012, 48, 795–806. [Google Scholar] [CrossRef]
- Meller, R.D.; Gue, K.R. The Application of New Aisle Designs for Unit-Load Warehouses. In Proceedings of the NSF Engineering Research and Innovation Conference, Honolulu, HI, USA, 22–25 June 2009; pp. 1–8. [Google Scholar]
- Öztürkoğlu, Ö. New Warehouse Designs: Angled Aisles and Their Effects on Travel Distance. Ph.D. Thesis, Auburn University, Auburn, AL, USA, 2011. [Google Scholar]
- Özturkoglu, Ö.; Gue, K.R.; Meller, R.D. Optimal unit-load warehouse designs for single-command operations. IIE Trans. 2012, 44, 459–475. [Google Scholar] [CrossRef]
- Liu, H.; Wang, F.; Zhao, J.; Yang, J.; Tan, C.; Zhou, L. Performance Analysis of Picking Path Strategies in Chevron Layout Warehouse. Mathematics 2022, 10, 395. [Google Scholar] [CrossRef]
- Zhou, L.; Fan, X.; Wang, J.; Wang, S.; Cao, N.; Wu, M. A Random Classified-Storage Picking Path Model for V-Type Storage Layout. Complexity 2020, 2020, e8784910. [Google Scholar] [CrossRef]
- Accorsi, R.; Bortolini, M.; Ferrari, E.; Gamberi, M.; Pilati, F. Class-Based Storage Warehouse Design with Diagonal Cross-Aisle. LogForum 2018, 14, 17650. [Google Scholar] [CrossRef]
- Bortolini, M.; Faccio, M.; Ferrari, E.; Gamberi, M.; Pilati, F. Design of diagonal cross-aisle warehouses with class-based storage assignment strategy. Int. J. Adv. Manuf. Technol. 2019, 100, 2521–2536. [Google Scholar] [CrossRef]
- Çelik, M.; Süral, H. Order picking under random and turnover-based storage policies in fishbone aisle warehouses. IIE Trans. 2014, 46, 283–300. [Google Scholar] [CrossRef]
- Cardona, L.F.; Rivera, L.; Martínez, H.J. Analytical study of the Fishbone Warehouse layout. Int. J. Logist. Res. Appl. 2012, 15, 365–388. [Google Scholar] [CrossRef]
- Pohl, L.M.; Meller, R.D.; Gue, K.R. Optimizing fishbone aisles for dual-command operations in a warehouse. Nav. Res. Logist. 2009, 56, 389–403. [Google Scholar] [CrossRef]
- Cardona, L.F.; Soto, D.F.; Rivera, L.; Martínez, H.J. Detailed design of fishbone warehouse layouts with vertical travel. Int. J. Prod. Econ. 2015, 170, 825–837. [Google Scholar] [CrossRef]
- Zhou, L.; Guo, J.; Zhu, J. Fishbone Layout Design and Analysis of Storage Area in Distribution Center. Manage. World 2014, 5, 184–185. [Google Scholar]
- Zhou, L.; Zhao, J.; Liu, H.; Wang, F.; Yang, J.; Wang, S. Stochastic models of routing strategies under the class-based storage policy in fishbone layout warehouses. Sci. Rep. 2022, 12, 12876. [Google Scholar] [CrossRef] [PubMed]
- Masae, M.; Glock, C.H.; Vichitkunakorn, P. A method for efficiently routing order pickers in the leaf warehouse. Int. J. Prod. Econ. 2021, 234, 108069. [Google Scholar] [CrossRef]
- Caron, F.; Marchet, G.; Perego, A. Optimal layout in low-level picker-to-part systems. Int. J. Prod. Res. 2000, 38, 101–117. [Google Scholar] [CrossRef]
- Öztürkoğlu, Ö.; Gue, K.R.; Meller, R.D. A constructive aisle design model for unit-load warehouses with multiple pickup and deposit points. Eur. J. Oper. Res. 2014, 236, 382–394. [Google Scholar] [CrossRef]
- Bortolini, M.; Faccio, M.; Gamberi, M.; Manzini, R. Diagonal cross-aisles in unit load warehouses to increase handling performance. Int. J. Prod. Econ. 2015, 170, 838–849. [Google Scholar] [CrossRef]
- Gharehgozli, A.H.; Yu, Y.; Zhang, X.; de Koster, R. Polynomial Time Algorithms to Minimize Total Travel Time in a Two-Depot Automated Storage/Retrieval System. Transp. Sci. 2017, 51, 19–33. [Google Scholar] [CrossRef]
- Zhou, S.; Gong, Y.; de Koster, R. Designing self-storage warehouses with customer choice. Int. J. Prod. Res. 2016, 54, 3080–3104. [Google Scholar] [CrossRef]
- Li, J.; Moghaddam, M.; Nof, S.Y. Dynamic storage assignment with product affinity and ABC classification—A case study. Int. J. Adv. Manuf. Technol. 2016, 84, 2179–2194. [Google Scholar] [CrossRef]
- Derhami, S.; Smith, J.S.; Gue, K.R. Space-efficient layouts for block stacking warehouses. IISE Trans. 2019, 51, 957–971. [Google Scholar] [CrossRef]
- Cardona, L.F.; Gue, K.R. How to determine slot sizes in a unit-load warehouse. IISE Trans. 2019, 51, 355–367. [Google Scholar] [CrossRef] [Green Version]
- Charkhgard, H.; Savelsbergh, M. Efficient Algorithms for Travelling Salesman Problems Arising in Warehouse Order Picking. ANZIAM J. 2015, 57, 166–174. [Google Scholar] [CrossRef]
- van Nieuwenhuyse, I.; de Koster, R.B.M. Evaluating order throughput time in 2-block warehouses with time window batching. Int. J. Prod. Econ. 2009, 121, 654–664. [Google Scholar] [CrossRef]
- Ardjmand, E.; Shakeri, H.; Singh, M.; Bajgiran, O.S. Minimizing order picking makespan with multiple pickers in a wave picking warehouse. Int. J. Prod. Econ. 2018, 206, 169–183. [Google Scholar] [CrossRef]
- Zaerpour, N.; de Koster, R.B.M.; Yu, Y. Storage policies and optimal shape of a storage system. Int. J. Prod. Res. 2013, 51, 6891–6899. [Google Scholar] [CrossRef]
- Roodbergen, K.J.; Vis, I.F.A.; Taylor, G.D. Simultaneous determination of warehouse layout and control policies. Int. J. Prod. Res. 2015, 53, 3306–3326. [Google Scholar] [CrossRef]
- Guo, X.; Yu, Y.; de Koster, R.B.M. Impact of required storage space on storage policy performance in a unit-load warehouse. Int. J. Prod. Res. 2016, 54, 2405–2418. [Google Scholar] [CrossRef]
- White, J.A. Optimum Design of Warehouses Having Radial Aisles. AIIE Trans. 1972, 4, 333–336. [Google Scholar] [CrossRef]
- Öztürkoğlu, Ö.; Hoser, D. A discrete cross aisle design model for order-picking warehouses. Eur. J. Oper. Res. 2019, 275, 411–430. [Google Scholar] [CrossRef]
- Kocaman, Y.; Öztürkoğlu, Ö.; Gümüşoğlu, Ş. Aisle designs in unit-load warehouses with different flow policies of multiple pickup and deposit points. Central Eur. J. Oper. Res. 2021, 29, 323–355. [Google Scholar] [CrossRef]
- Mesa, A.; Masel, D.T. A Non-Traditional Warehouse Layout with Multiple Pickup and Deposit Points. In Proceedings of the IIE Annual Conference, Pittsburgh, PA, USA, 20–23 May 2017; pp. 163–168. [Google Scholar]
- Liu, J.; Xiong, F.; Hu, Y. Crossing Aisles Design Approach to Flying-V Warehouse Layout Based on Improved PSO. Oper. Res. Manag. Sci. 2019, 28, 80–88. [Google Scholar]
- Clark, K.A.; Meller, R.D. Incorporating vertical travel into non-traditional cross aisles for unit-load warehouse designs. IIE Trans. 2013, 45, 1322–1331. [Google Scholar] [CrossRef]
- Öztürkoğlu, Ö. Effects of Varying Input and Output Points on New Aisle Designs in Warehouses. In Proceedings of the 2016 IEEE Congress on Evolutionary Computation (CEC), Vancouver, BC, Canada, 24–29 July 2016; pp. 3925–3932. [Google Scholar]
- Zhang, Z.; Wang, Q.; Liang, Y. Twin Leaf Method for Warehouse Internal Layout and Its Aisles Angle Optimization. Systems Eng. 2019, 37, 70–80. [Google Scholar]
- Roodbergen, K.J.; Koster, R. Routing methods for warehouses with multiple cross aisles. Int. J. Prod. Res. 2001, 39, 1865–1883. [Google Scholar] [CrossRef]
- Masae, M.; Glock, C.H.; Vichitkunakorn, P. Optimal order picker routing in the chevron warehouse. IISE Trans. 2020, 52, 665–687. [Google Scholar] [CrossRef]
- Dijkstra, A.S.; Roodbergen, K.J. Exact route-length formulas and a storage location assignment heuristic for picker-to-parts warehouses. Transp. Res. Part E Logist. Transp. Rev. 2017, 102, 38–59. [Google Scholar] [CrossRef]
- Rao, S.S.; Adil, G.K. Class-based storage with exact S-shaped traversal routeing in low-level picker-to-part systems. Int. J. Prod. Res. 2013, 51, 4979–4996. [Google Scholar] [CrossRef]
- Zhu, J.; Guo, J.; Zhou, L.; Zhang, H. Study on the Improvement of the Additional Distance for Sorted-Storage S-Type Manual Order Picking. J. Comput. Theor. Nanosci. 2016, 13, 2639–2644. [Google Scholar] [CrossRef]
- Hsu, C.-M.; Chen, K.-Y.; Chen, M.-C. Batching orders in warehouses by minimizing travel distance with genetic algorithms. Comput. Ind. 2005, 56, 169–178. [Google Scholar] [CrossRef]
- Theys, C.; Bräysy, O.; Dullaert, W.; Raa, B. Using a TSP heuristic for routing order pickers in warehouses. Eur. J. Oper. Res. 2010, 200, 755–763. [Google Scholar] [CrossRef]
- Kulak, O.; Sahin, Y.; Taner, M.E. Joint order batching and picker routing in single and multiple-cross-aisle warehouses using cluster-based tabu search algorithms. Flex. Serv. Manuf. J. 2012, 24, 52–80. [Google Scholar] [CrossRef]
- Pan, J.C.-H.; Wu, M.-H.; Chang, W.-L. A travel time estimation model for a high-level picker-to-part system with class-based storage policies. Eur. J. Oper. Res. 2014, 237, 1054–1066. [Google Scholar] [CrossRef]
- Cheng, C.-Y.; Chen, Y.-Y.; Chen, T.-L.; Yoo, J.J.-W. Using a hybrid approach based on the particle swarm optimization and ant colony optimization to solve a joint order batching and picker routing problem. Int. J. Prod. Econ. 2015, 170, 805–814. [Google Scholar] [CrossRef]
- Chen, T.-L.; Cheng, C.-Y.; Chen, Y.-Y.; Chan, L.-K. An efficient hybrid algorithm for integrated order batching, sequencing and routing problem. Int. J. Prod. Econ. 2015, 159, 158–167. [Google Scholar] [CrossRef]
- Lu, W.; McFarlane, D.; Giannikas, V.; Zhang, Q. An algorithm for dynamic order-picking in warehouse operations. Eur. J. Oper. Res. 2016, 248, 107–122. [Google Scholar] [CrossRef]
- Gómez-Montoya, R.A.; Correa-Espinal, A.A.; Hernández-Vahos, J.D. Picking Routing Problem with K homogenous material handling equipment for a refrigerated warehouse. Rev. Fac. Ing.-Univ. Ant. 2016, 80, 9–20. [Google Scholar] [CrossRef]
- Hong, S.; Kim, Y. A route-selecting order batching model with the S-shape routes in a parallel-aisle order picking system. Eur. J. Oper. Res. 2017, 257, 185–196. [Google Scholar] [CrossRef]
- Scholz, A.; Schubert, D.; Wäscher, G. Order picking with multiple pickers and due dates—Simultaneous solution of Order Batching, Batch Assignment and Sequencing, and Picker Routing Problems. Eur. J. Oper. Res. 2017, 263, 461–478. [Google Scholar] [CrossRef]
- De Santis, R.; Montanari, R.; Vignali, G.; Bottani, E. An adapted ant colony optimization algorithm for the minimization of the travel distance of pickers in manual warehouses. Eur. J. Oper. Res. 2018, 267, 120–137. [Google Scholar] [CrossRef]
- Bódis, T.; Botzheim, J. Bacterial Memetic Algorithms for Order Picking Routing Problem with Loading Constraints. Expert Syst. Appl. 2018, 105, 196–220. [Google Scholar] [CrossRef]
- Zhou, L.; Li, Z.; Shi, N.; Liu, S.; Xiong, K. Performance Analysis of Three Intelligent Algorithms on Route Selection of Fishbone Layout. Sustainability 2019, 11, 1148. [Google Scholar] [CrossRef]
- Diefenbach, H.; Glock, C.H. Ergonomic and economic optimization of layout and item assignment of a U-shaped order picking zone. Comput. Ind. Eng. 2019, 138, 106094. [Google Scholar] [CrossRef]
- Yang, P.; Zhao, Z.; Guo, H. Order batch picking optimization under different storage scenarios for e-commerce warehouses. Transp. Res. Part E Logist. Transp. Rev. 2020, 136, 101897. [Google Scholar] [CrossRef]
- Sebo, J.; Busa, J., Jr. Comparison of Advanced Methods for Picking Path Optimization: Case Study of Dual-Zone Warehouse. Int. J. Simul. Model. 2020, 19, 410–421. [Google Scholar] [CrossRef]
- Amorim-Lopes, M.; Guimarães, L.; Alves, J.; Almada-Lobo, B. Improving picking performance at a large retailer warehouse by combining probabilistic simulation, optimization, and discrete-event simulation. Int. Trans. Oper. Res. 2021, 28, 687–715. [Google Scholar] [CrossRef]
- Pohl, L.M.; Meller, R.D.; Gue, K.R. Turnover-based storage in non-traditional unit-load warehouse designs. IIE Trans. 2011, 43, 703–720. [Google Scholar] [CrossRef]
- Jiang, M.; Feng, D.; Zhao, Y.; Yu, M. Optimization of logistics warehouse layout based on the improved Fishbone layout. Syst. Eng. Theory Pract. 2013, 33, 2920–2929. [Google Scholar]
- Mesa, A. A Methodology to Incorporate Multiple Cross Aisles in a Non-Traditional Warehouse Layout. Master’s Thesis, Ohio University, Athens, OH, USA, 2016. [Google Scholar]
- Accorsi, R.; Bortolini, M.; Gamberi, M.; Manzini, R.; Pilati, F. Multi-objective warehouse building design to optimize the cycle time, total cost, and carbon footprint. Int. J. Adv. Manuf. Technol. 2017, 92, 839–854. [Google Scholar] [CrossRef]
- Bortolini, M.; Galizia, F.G.; Gamberi, M.; Gualano, F. Integration of single and dual command operations in non-traditional warehouse design. Int. J. Adv. Manuf. Technol. 2020, 111, 2461–2473. [Google Scholar] [CrossRef]
- Kurniawati, D.A.; Handoko, A.; Piplani, R.; Rosdiahti, R. Optimized distribution of halal products using tabu search. J. Islam. Mark. 2022; ahead-of-print. [Google Scholar] [CrossRef]
- Xing, L.; Liu, Y.; Li, H.; Wu, C.-C.; Lin, W.-C.; Chen, X. A Novel Tabu Search Algorithm for Multi-AGV Routing Problem. Mathematics 2020, 8, 279. [Google Scholar] [CrossRef]
- Konstantakopoulos, G.D.; Gayialis, S.P.; Kechagias, E.P.; Papadopoulos, G.A.; Tatsiopoulos, I.P. An algorithmic approach for sustainable and collaborative logistics: A case study in Greece. Int. J. Inf. Manag. Data Insights 2021, 1, 100010. [Google Scholar] [CrossRef]


| Research Points | Storage Policy | Routing Strategy | Model/Method | |
|---|---|---|---|---|
| Öztürkoğlu et al. [17] | Optimal layout | Random | Single-command | Expected walking distance model |
| Öztürkoğlu [49] | I/O points | Random | Single-command | Warehouse network model |
| Zhang et al. [50] | Twin leaf | Single-command | Expected walking distance model | |
| Masae et al. [28] | Routing | Random, turnover-based | Optimal, midpoint, S-shape, largest gap, return | Eulerian graph, dynamic programming |
| Warehouse Layout | S/R Operations | |
|---|---|---|
| Gue et al. [12] | Fling-V, fishbone | Single |
| Pohl et al. [24] | Fishbone | Single |
| Pohl et al. [73] | Fishbone | Single, dual |
| Öztürkoğlu et al. [17] | Chevron, leaf, butterfly | Single |
| Gue et al. [14] | Fling-V | Single |
| Cardona et al. [23] | Fishbone | Single |
| Clark et al. [48] | Fling-V, fishbone | Single |
| Jiang et al. [74] | Fishbone | Single |
| Öztürkoğlu et al. [30] | Chevron | Single |
| Bortolini et al. [31] | V-shaped | Single |
| Mesa [75] | Diamond | Single |
| Öztürkoğlu et al. [49] | Leaf | Single |
| Accorsi et al. [76] | V-shaped | Single |
| Bortolini et al. [21] | V-shaped | Single |
| Zhang et al. [50] | Twin leaf | Single |
| Bortolini et al. [77] | V-shaped | Integration of single and dual |
| Kocaman et al. [45] | Chevron | Single |
| Warehouse Layout | Routing Strategy, or S/R Operations | Model/Method | |
|---|---|---|---|
| Zhou et al. [19] | V-shaped | Return, S-shape | Travel distance model, stochastic |
| Öztürkoğlu et al. [17] | Chevron, leaf, butterfly | Single-command | Expected walking distance model |
| Accorsi et al. [20] | V-shaped | Single-command | Access time model |
| Bortolini et al. [21] | V-shaped | Single-command | Analytic model |
| Masae et al. [52] | Chevron | Optimal, S-shape, midpoint, largest gap | Graph theory, dynamic programming |
| Masae et al. [28] | Leaf | Optimal, return, S-shape, midpoint, largest gap | Eulerian graph, dynamic programming |
| Zhou et al. [27] | Fishbone | S-shape, return | Travel distance model, stochastic |
| Liu et al. [18] | Chevron | S-shape, return, composite | Analytic model |
| Our work | Leaf | S-shape, return, composite | Analytic model |
| Notations | Descriptions |
|---|---|
| The length and width of the right-half warehouse (excluding the aisle width around the warehouse). | |
| The widths of the shelf, the aisle, and the storage location. | |
| The angle of the shelf and picking aisle in the lower right warehouse | |
| The angle of the diagonal cross-aisle in the right-half warehouse | |
| Six picking areas divided by , and the central cross-aisle. | |
| The parallel line of passing through the top right vertex of the warehouse. | |
| The total walking distance to complete a picking operation. | |
| The th and th storage locations to be visited . | |
| The distance from the th storage location to the th storage location. | |
| Indicates whether to select the route from location to location . | |
| The coordinate of any location to be visited. | |
| The serial number of the picking area. | |
| The picking aisle where the location to be visited is located. | |
| The side of the location to be visited in the picking aisle. | |
| The location to be visited on the or side in the picking aisle. | |
| The distance from the I/O point to the first visited location. | |
| The distance from the last visited location to the I/O point. | |
| The route from the I/O point to the first visited location. | |
| The route from the last visited location to the I/O point. | |
| The number of goods to be picked. | |
| The number of storage locations to be visited. | |
| The coordinates of the first, the th, and the th locations to be visited. | |
| The distance from the I/O point to . | |
| The walking distance from the I/O point to the diagonal cross-aisle or the front aisle. | |
| The walking distance in the diagonal cross-aisle or front aisle. | |
| The walking distance from the diagonal cross-aisle or front aisle to the th or th storage location. | |
| The walking distance in the picking aisle to be visited. | |
| The length of picking aisle or . | |
| The notations to judge the specific position of picking aisle or . | |
| The remaining distance in picking aisle except or except . | |
| The mapping distance of the picking aisle or in the central cross-aisle when it is below . | |
| The mapping distance of the picking aisle or in the front aisle when it is above . |
| Coordinates | No. | Coordinates | No. | Coordinates | No. | Coordinates | No. |
|---|---|---|---|---|---|---|---|
| (0,0,0,0) | 0 | (2,6,0,75) | 3 | (3,2,0,28) | 6 | (6,2,0,83) | 9 |
| (5,8,1,29) | 1 | (3,7,0,16) | 4 | (3,14,0,1) | 7 | (2,1,1,110) | 10 |
| (5,2,1,71) | 2 | (4,4,0,23) | 5 | (4,8,0,38) | 8 | — | — |
| Coordinates | No. | Coordinates | No. | Coordinates | No. | Coordinates | No. |
|---|---|---|---|---|---|---|---|
| (0,0,0,0) | 0 | (4,9,1,29) | 6 | (1,8,1,26) | 12 | (5,12,1,4) | 18 |
| (2,6,1,76) | 1 | (2,4,0,19) | 7 | (2,2,1,62) | 13 | (5,8,1,29) | 19 |
| (6,8,0,9) | 2 | (3,3,1,55) | 8 | (5,8,0,5) | 14 | (3,3,0,11) | 20 |
| (4,1,1,10) | 3 | (4,3,0,35) | 9 | (1,7,0,45) | 15 | — | — |
| (6,3,0,4) | 4 | (4,4,0,23) | 10 | (2,1,0,49) | 16 | — | — |
| (5,7,0,21) | 5 | (2,4,0,68) | 11 | (6,1,1,10) | 17 | — | — |
| Coordinates | No. | Coordinates | No. | Coordinates | No. | Coordinates | No. |
|---|---|---|---|---|---|---|---|
| (0,0,0,0) | 0 | (4,4,0,23) | 8 | (4,3,1,42) | 16 | (6,8,1,11) | 24 |
| (3,7,0,55) | 1 | (5,7,0,53) | 9 | (4,9,0,19) | 17 | (6,7,0,32) | 25 |
| (5,8,1,29) | 2 | (1,8,1,26) | 10 | (2,4,0,68) | 18 | (6,5,1,60) | 26 |
| (5,12,1,4) | 3 | (5,7,0,9) | 11 | (6,8,1,14) | 19 | (6,3,0,4) | 27 |
| (5,2,1,3) | 4 | (2,6,1,76) | 12 | (4,5,1,48) | 20 | (2,2,1,91) | 28 |
| (1,3,0,46) | 5 | (2,10,0,32) | 13 | (6,11,0,16) | 21 | (6,4,1,73) | 29 |
| (1,9,1,5) | 6 | (1,1,1,92) | 14 | (4,10,0,8) | 22 | (3,7,1,19) | 30 |
| (4,3,1,16) | 7 | (3,1,1,82) | 15 | (5,7,0,21) | 23 | — | — |
| Coordinates | No. | Coordinates | No. | Coordinates | No. | Coordinates | No. |
|---|---|---|---|---|---|---|---|
| (0,0,0,0) | 0 | (6,9,1,31) | 11 | (3,14,0,1) | 22 | (6,4,1,47) | 33 |
| (2,10,0,32) | 1 | (2,4,0,68) | 12 | (3,9,0,23) | 23 | (1,7,0,45) | 34 |
| (5,1,1,16) | 2 | (3,12,1,8) | 13 | (1,2,0,15) | 24 | (4,12,1,13) | 35 |
| (5,7,0,9) | 3 | (6,8,0,25) | 14 | (3,1,1,82) | 25 | (2,4,0,19) | 36 |
| (4,7,1,24) | 4 | (4,9,1,29) | 15 | (3,7,1,31) | 26 | (6,8,0,9) | 37 |
| (6,7,0,32) | 5 | (1,9,1,5) | 16 | (4,3,1,42) | 27 | (1,13,0,7) | 38 |
| (2,8,1,42) | 6 | (2,1,1,24) | 17 | (4,8,0,38) | 28 | (2,6,0,77) | 39 |
| (5,7,0,53) | 7 | (2,2,1,25) | 18 | (4,7,1,18) | 29 | (1,2,1,75) | 40 |
| (6,8,0,47) | 8 | (5,12,1,4) | 19 | (5,8,1,29) | 30 | — | — |
| (5,12,1,11) | 9 | (5,1,1,94) | 20 | (3,3,0,11) | 31 | — | — |
| (3,7,0,16) | 10 | (6,11,0,16) | 21 | (2,1,0,66) | 32 | — | — |
| Number of Locations | Routing Strategy | CPU Running Time | Distance | Optimized Proportion | ||
|---|---|---|---|---|---|---|
| to S-Shape | to Return | to Composite | ||||
| 10 | S-shape | 0.170682 | 1180.4058 | 0.00% | 9.96% | −87.29% |
| return | 0.139839 | 1310.9619 | −11.06% | 0.00% | −108.01% | |
| composite | 3.876069 | 630.2524 | 46.61% | 51.92% | 0.00% | |
| 20 | S-shape | 0.220125 | 1831.4547 | 0.00% | −10.32% | −52.27% |
| return | 0.164067 | 1660.1804 | 9.35% | 0.00% | −38.03% | |
| composite | 3.231893 | 1202.7395 | 34.33% | 27.55% | 0.00% | |
| 30 | S-shape | 0.239186 | 2369.2273 | 0.00% | 11.93% | −62.72% |
| return | 0.175856 | 2690.1585 | −13.55% | 0.00% | −84.76% | |
| composite | 4.420893 | 1456.0361 | 38.54% | 45.88% | 0.00% | |
| 40 | S-shape | 0.231844 | 2541.5162 | 0.00% | 14.62% | −56.50% |
| return | 0.231118 | 2976.7253 | −17.12% | 0.00% | −83.30% | |
| composite | 4.792556 | 1623.9958 | 36.10% | 45.44% | 0.00% | |
| Orders | 1 | 2 | 3 | 4 | 5 | |
| 10 | S-shape | 1180.4058 | 1150.3016 | 1109.7596 | 1056.5574 | 1072.8256 |
| return | 1310.9619 | 1327.9820 | 1170.8092 | 1336.0670 | 943.3111 | |
| composite | 630.2524 | 797.9164 | 795.3686 | 585.9644 | 791.4205 | |
| 20 | S-shape | 1831.4547 | 1590.7011 | 2012.4419 | 1783.7113 | 1892.3519 |
| return | 1660.1804 | 1747.4264 | 1852.1397 | 1792.9413 | 2017.2153 | |
| composite | 1202.7395 | 977.0313 | 1183.2679 | 1056.9142 | 1137.5424 | |
| 30 | S-shape | 2369.2273 | 1959.3428 | 2321.9254 | 2691.2847 | 2369.3568 |
| return | 2690.1585 | 2163.4744 | 2716.2634 | 2885.6680 | 2886.8075 | |
| composite | 1456.0361 | 999.5249 | 1297.6445 | 1492.6086 | 1421.8737 | |
| 40 | S-shape | 2541.5162 | 2524.2810 | 2570.8561 | 2754.9982 | 2920.5409 |
| return | 2976.7253 | 2962.3912 | 2887.1379 | 3091.3559 | 2992.8084 | |
| composite | 1623.9958 | 1364.7088 | 1700.6997 | 1660.9445 | 1568.4643 | |
| Orders | 6 | 7 | 8 | 9 | 10 | |
| 10 | S-shape | 1086.0787 | 851.4957 | 1034.5959 | 1020.0817 | 1153.3554 |
| return | 1459.9661 | 1016.7349 | 1428.8193 | 1074.5994 | 1095.0887 | |
| composite | 799.5363 | 649.7566 | 627.4810 | 682.9333 | 761.3741 | |
| 20 | S-shape | 1801.2077 | 1825.5588 | 1662.3446 | 1804.1432 | 1761.4635 |
| return | 1686.1954 | 1910.6276 | 1986.7992 | 2250.8594 | 1829.9145 | |
| composite | 1254.7663 | 1040.5726 | 1192.2926 | 1036.7237 | 1181.0978 | |
| 30 | S-shape | 2289.9545 | 2364.2413 | 2320.6033 | 2118.5214 | 2059.3743 |
| return | 2488.5332 | 2726.7524 | 2549.8209 | 2054.9456 | 2425.8369 | |
| composite | 1228.4882 | 1298.9774 | 1419.1072 | 1420.8772 | 1084.4516 | |
| 40 | S-shape | 2728.6124 | 2594.4353 | 2592.3312 | 2937.5072 | 2678.2096 |
| return | 2863.1707 | 3103.1463 | 3233.6603 | 3279.1435 | 3299.7715 | |
| composite | 1694.2977 | 1557.3505 | 1534.8450 | 1718.7293 | 1698.7772 | |
| Group | Composite to S-Shape | Composite to Return | ||||||
|---|---|---|---|---|---|---|---|---|
| 10 | 20 | 30 | 40 | 10 | 20 | 30 | 40 | |
| <20% | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 20–30% | 4 | 1 | 0 | 0 | 0 | 2 | 0 | 0 |
| 30–40% | 4 | 5 | 4 | 6 | 5 | 3 | 1 | 0 |
| 40–50% | 2 | 4 | 6 | 4 | 1 | 4 | 3 | 8 |
| >50% | 0 | 0 | 0 | 0 | 3 | 1 | 6 | 2 |
| Total | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 |
| Leaf Layout | Traditional Layout | Leaf Layout vs. Traditional Layout | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Number of Aisles | Number of Storage Locations | Number of Aisles | Number of Storage Locations | Storage Location Loss | Storage Area Loss | Loss Rate | |||
| 1 | 1 | 0.5 | 166 | 38,918 | 100 | 40,000 | 1082 | 270.5 | 2.705% |
| 1 | 2 | 1 | 112 | 12,778 | 68 | 13,400 | 622 | 622 | 4.642% |
| 2 | 1 | 0.5 | 112 | 25,644 | 68 | 26,800 | 1156 | 289 | 4.313% |
| 2 | 2 | 1 | 84 | 9460 | 50 | 10,000 | 540 | 540 | 5.400% |
| 2 | 4 | 2 | 54 | 3056 | 34 | 3300 | 244 | 976 | 7.394% |
| 4 | 2 | 1 | 56 | 6158 | 34 | 6600 | 442 | 442 | 6.697% |
| 4 | 4 | 2 | 42 | 2238 | 26 | 2500 | 262 | 1048 | 10.480% |
| Loss Rate | ||||
|---|---|---|---|---|
| 1 | 1 | 0.5 | 2.705% | |
| 1 | 2 | 1 | 4.642% | |
| 2 | 1 | 0.5 | 4.313% | |
| 2 | 2 | 1 | 5.400% | |
| 2 | 4 | 2 | 7.394% | |
| 4 | 2 | 1 | 6.697% | |
| 4 | 4 | 2 | 10.480% | |
| Loss Rate | ||||
|---|---|---|---|---|
| 1 | 1 | 0.5 | 2.705% | |
| 2 | 1 | 0.5 | 4.313% | |
| 1 | 2 | 1 | 4.642% | |
| 2 | 2 | 1 | 5.400% | |
| 4 | 2 | 1 | 6.697% | |
| 2 | 4 | 2 | 7.394% | |
| 4 | 4 | 2 | 10.480% | |
| Loss Rate | ||||
|---|---|---|---|---|
| 1 | 1 | 0.5 | 2.705% | |
| 2 | 2 | 1 | 5.400% | |
| 4 | 4 | 2 | 10.480% | |
| 1 | 2 | 1 | 4.642% | |
| 2 | 4 | 2 | 7.394% | |
| 2 | 1 | 0.5 | 4.313% | |
| 4 | 2 | 1 | 6.697% | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, L.; Liu, H.; Zhao, J.; Wang, F.; Yang, J. Performance Analysis of Picking Routing Strategies in the Leaf Layout Warehouse. Mathematics 2022, 10, 3149. https://doi.org/10.3390/math10173149
Zhou L, Liu H, Zhao J, Wang F, Yang J. Performance Analysis of Picking Routing Strategies in the Leaf Layout Warehouse. Mathematics. 2022; 10(17):3149. https://doi.org/10.3390/math10173149
Chicago/Turabian StyleZhou, Li, Huwei Liu, Junhui Zhao, Fan Wang, and Jianglong Yang. 2022. "Performance Analysis of Picking Routing Strategies in the Leaf Layout Warehouse" Mathematics 10, no. 17: 3149. https://doi.org/10.3390/math10173149
APA StyleZhou, L., Liu, H., Zhao, J., Wang, F., & Yang, J. (2022). Performance Analysis of Picking Routing Strategies in the Leaf Layout Warehouse. Mathematics, 10(17), 3149. https://doi.org/10.3390/math10173149







