Asymptotic Behavior for the Discrete in Time Heat Equation

Abstract

In this paper, we investigate the asymptotic behavior and decay of the solution of the discrete in time N-dimensional heat equation. We give a convergence rate with which the solution tends to the discrete fundamental solution, and the asymptotic decay, both in $L^p\left({\mathbb{R}}^N\right).$ Furthermore, we prove optimal $L^2$-decay of solutions. Since the technique of energy methods is not applicable, we follow the approach of estimates based on the discrete fundamental solution which is given by an original integral representation and also by MacDonald’s special functions. As a consequence, the analysis is different to the continuous in time heat equation and the calculations are rather involved.

1. Introduction

The linear heat equation $u_t=\Delta u$ is one of the most studied problems in the theory of partial differential equations. It was introduced by J. Fourier (see [1]) to model several diffusion phenomena. Since then, it has been applied in the study of different processes in many mathematical areas such as PDEs, functional analysis, harmonic analysis, probability, among others. The nature of this problem is well known and we will not further explain it.

One of the aspects of interest, see [2,3,4], is the large-time behavior of solutions of the heat problem

$$\left\{\begin{array}{c}{u}_t(t,x)=\Delta u(t,x),t>0,x\in {\mathbb{R}}^N,\hfill \\ u(0,x)=f\left(x\right),\hfill \end{array}\right.$$

(1)

where the Laplacian operator $\Delta$ is taken on the spatial variable(s) $x$. If $f\in L^1\left({\mathbb{R}}^N\right),$ the solution of (1) on $L^p\left({\mathbb{R}}^N\right)$ is $u\left(t\right)=G_t\ast f,$ where ∗ denotes the classical convolution on ${\mathbb{R}}^N$ and

$$G_t\left(x\right)=\frac{1}{{\left(4\pi t\right)}^{N/2}}{e}^{-\frac{{\left|x\right|}^2}{4t}},t>0,x\in {\mathbb{R}}^N,$$

is the heat kernel. It is known that integrating over all of ${\mathbb{R}}^N$, we get that the total mass of solutions is conserved for all time, that is,

$${\int }_{{\mathbb{R}}^N}u(t,x)dx={\int }_{{\mathbb{R}}^N}u(0,x)dx.$$

This fact leads us to think that the total mass of solutions should have importance in the asymptotic behavior of solutions. Indeed, it is well known that if $M={\int }_{{\mathbb{R}}^N}u(0,x)dx$ then

$$t^{\frac{N}{2}(1-1/p)}{\parallel u(t,·)-M{G}_t(·)\parallel }_p\to 0,\mathrm{as}t\to \infty ,$$

(2)

for $1\le p\le \infty ,$ where ${\parallel ·\parallel }_p$ is the classical norm on $L^p\left({\mathbb{R}}^N\right)$. The previous estimate shows that the difference on $L^p\left({\mathbb{R}}^N\right)$ between the solution $u(t,·)$ and $M{G}_t(·)$ decays to zero like $o\left(\frac{1}{t^{\frac{N}{2}(1-1/p)}}\right)$ as t goes to infinity.

It is also known that the p-norms of the solution vanish as $t\to \infty$ for $p>1.$ This fact is known the fact of the p-energy not being conservative. More precisely,

$${\parallel u(t,·)\parallel }_p\le \frac{C_p{\parallel f\parallel }_q}{t^{\frac{N}{2}(1/q-1/p)}}{,\parallel \nabla u(t,·)\parallel }_p\le \frac{C_p{\parallel f\parallel }_q}{t^{\frac{N}{2}(1/q-1/p)+1/2}},{\parallel \Delta u(t,·)\parallel }_p\le \frac{C_p{\parallel f\parallel }_q}{t^{\frac{N}{2}(1/q-1/p)+1}},$$

for $f\in L^q\left({\mathbb{R}}^N\right),1\le q\le p\le \infty .$

One can consider the first moment as the vector quantity ${\int }_{{\mathbb{R}}^n}xu(t,x)dx.$ It can be seen that such moment is also conserved in time for the solution of (1) whenever $(1+|x\left|\right)f\in L^1\left({\mathbb{R}}^N\right),$ that is,

$${\int }_{{\mathbb{R}}^N}xu(t,x)dx={\int }_{{\mathbb{R}}^N}xf\left(x\right)dx.$$

To prove the previous identity it is enough to use that $u(t,x)=(G_t\ast f)\left(x\right)$ and that ${\int }_{{\mathbb{R}}^N}{x}_j{G}_t\left(x\right)dx=0$ for all $j=1,\cdots ,N.$ Moreover, under such assumption, for each $1\le p\le \infty$ there is $C>0$ such that

$$t^{\frac{N}{2}(1-1/p)+1/2}{\parallel u(t,·)-M{G}_t(·)\parallel }_p\le C,\mathrm{for}\mathrm{all}t>0,$$

see, for example, equation (1.11) in [5]. However, if ${(1+|x|}^2)f\in L^1\left({\mathbb{R}}^N\right)$ observe that

$${\int }_{{\mathbb{R}}^N}{\left|x\right|}^{2}u(0,x)dx={\int }_{{\mathbb{R}}^N}{\left|x\right|}^{2}f\left(x\right)dx,$$

and integrating by parts, we obtain

$${\int }_{{\mathbb{R}}^N}{\left|x\right|}^2{u}_t(t,x)dx={\int }_{{\mathbb{R}}^N}{\left|x\right|}^2\Delta u(t,x)dx=2N{\int }_{{\mathbb{R}}^N}f\left(x\right)dx,$$

where we have used that ${\int }_{{\mathbb{R}}^N}{x}_i^2\frac{{\partial }^2}{\partial x_j^2}u(t,x)dx=0$ for $i\ne j.$ Thus,

$${\int }_{{\mathbb{R}}^N}{\left|x\right|}^{2}u(t,x)dx={\int }_{{\mathbb{R}}^N}{\left|x\right|}^{2}f\left(x\right)dx+2Nt{\int }_{{\mathbb{R}}^N}f\left(x\right)dx,$$

and the second-order moment is not conservative. In fact, it is known that only integral quantities conserved by the solutions of (1) are the mass and the first moment.

This type of large-time asymptotic results have been also studied for several diffusion problems. For example, in [5,6,7,8,9], the authors studied large-time behavior and other asymptotic estimates for the solutions of different diffusion problems in ${\mathbb{R}}^N,$ and similar aspects are studied for open bounded domains in [7,10]. Estimates for heat kernels on manifolds have been also studied in [11,12,13]. In [14], the author obtains Gaussian upper estimates for the heat kernel associated to the sub-Laplacian on a Lie group, and also for its first-order time and space derivatives.

On the other hand, finite differences, sometimes also called discrete derivatives, were introduced some centuries ago, and they have been used along the literature in different mathematical problems, mainly in approximation of derivatives for the numerical solution of differential equations and partial differential equations. The most knowing ones are the forward, backward and central differences (the forward and backward differences are associated to the Euler, explicit and implicit, numerical methods). We denote them in the following way: let $h>0,$ for a function u defined on the mesh ${\mathbb{Z}}_h:=\{nh:n\in \mathbb{Z}\}$ we write

$${\delta }_{\mathrm{right}}u\left(nh\right):=\frac{u\left(\right(n+1\left)h\right)-u\left(nh\right)}{h},{\delta }_{\mathrm{left}}u\left(nh\right):=\frac{u\left(nh\right)-u\left(\right(n-1\left)h\right)}{h},$$

and

$${\delta }_{c}u\left(nh\right):=\left(\frac{{\delta }_{\mathrm{right}}+{\delta }_{\mathrm{left}}}{2}\right)u\left(nh\right)=\frac{u\left(\right(n+1\left)h\right)-u\left(\right(n-1\left)h\right)}{2h}.$$

In the last years, and taking as a guide the paper [15], several authors have been working in the context of partial difference–differential equations (see [16,17,18,19,20,21]) from a specific point of view; in these papers, the approach is focused on mathematical analysis, more precisely, harmonic analysis, functional analysis and fractional differences. Particularly in [16], it is shown that the operators ${\delta }_{\mathrm{right}}$ and ${\delta }_{\mathrm{left}}$ generate Markovian $C_0$-semigroups on ${\ell }^p\left(\mathbb{Z}\right).$ Additionally, in [18], the authors study harmonic properties of the solution of the heat problem on one-dimensional graphs (the mesh ${\mathbb{Z}}_h$), and the wave equation on graphs is studied in [21]. An abstract approach for discrete in time Cauchy problems is given in [20]. Furthermore, non-local problems in the discrete framework appear in [17,19].

Motivated by the importance of the classical heat problem (1) and the knowing of the numerical approximations of the solutions of evolution problems, we consider the first-order Cauchy problem for the heat equation in discrete time

$$\left\{\begin{array}{c}{\delta }_{\mathrm{left}}u(nh,x)=\Delta u(nh,x)+g(nh,x),n\in \mathbb{N},x\in {\mathbb{R}}^N,\hfill \\ u(0,x)=f\left(x\right),\hfill \end{array}\right.$$

(3)

with $h>0,$ where $\Delta$ is the classical Laplacian on $L^p\left({\mathbb{R}}^N\right)$ (taken on the spatial variable(s) x), u is defined on ${\mathbb{N}}_0^h\times {\mathbb{R}}^N$, with ${\mathbb{N}}_0^h:=\{nh:n\in {\mathbb{N}}_0\}$, f is defined on ${\mathbb{R}}^N$ and g is defined on ${\mathbb{N}}^h\times {\mathbb{R}}^N,$ with ${\mathbb{N}}^h:=\{nh:n\in \mathbb{N}\}.$

Along the paper, we study asymptotic behavior and decay of the solution of (3). For that purpose, we need to know properties of the fundamental solution of the homogeneous problem associated to (3) (when $g=0$). In fact, one of the key points to obtaining such asymptotic properties is an integral representation of the fundamental solution for the associated homogeneous equation. Furthermore, we describe explicitly this solution in terms of MacDonald’s functions which arise naturally from the integral representation of the solution. This representation is quite original and allows to study the decay of solutions for the problem (3) when the initial datum belongs to p-integrable Lebesgue spaces. Moreover, both the integral representation and the explicit expression via MacDonald’s functions allow to give a quantitative rate at which the solution converges to M times the fundamental solution, where M will denote, as in the continuous case, the initial mass of solution. The techniques used to obtain our results differs to the continuous case because we have to deal with the integral representation and asymptotic properties of MacDonald’s special functions. We also note to the reader that obtaining the relation $t=nh,$ the asymptotics of $G_t$ will be similar to ${\mathcal{G}}_{n,h}$ as $t\to \infty$ or equivalently $n\to \infty ,$ where ${\mathcal{G}}_{n,h}$ will denote the fundamental solution of the homogeneous problem associated to (3).

One can think about the possibility of studying similar problems to (3) but considering the discrete derivatives ${\delta }_{\mathrm{right}}$ or ${\delta }_c.$ However, as we explain in Remark 2, the fundamental solutions to that problem do not have good properties.

The paper is organized as follows. Section 2 is focused on the fundamental solution of the homogeneous problem associated with (3). We introduce an integral representation (5) and the explicit expression via MacDonald’s functions (6). We deduce basic properties, we calculate its gradient and Laplacian, and we see that the mass and the first moment of solutions of the homogeneous problem are conservative in discrete time $nh,$ and not the second moment. Furthermore, some pictures of the continuous and discrete Gaussian kernels, with their corresponding comments, are stated. In Section 3, we give pointwise estimates (Theorem 1) and $L^p$ asymptotic upper bounds (Theorem 2) for the fundamental solution ${\mathcal{G}}_{n,h},$ and we use such estimates to prove in Section 4 that the p-energies of solutions of (3) are dissipative (Theorems 3 and 4). Section 5 is the main part of the paper; we prove the asymptotic behavior for the discrete in time heat problem (Theorem 5). In Section 6, we succeed in proving optimal $L^2$-decay estimates for the solution of the homogeneous problem associated to (3) (Theorem 6). The proof is based on Fourier analysis techniques. Finally, we include an Appendix (Appendix A) where we show some basic properties of Gamma and MacDonald’s functions, and a technical result about integrability.

2. The Discrete Gaussian Fundamental Solution

In this section, we study the fundamental solution for the homogeneous discrete in time heat initial value problem on the Lebesgue $L^p\left({\mathbb{R}}^N\right)$ spaces. Let $h>0,$ we consider

$$\left\{\begin{array}{c}{\delta }_{\mathrm{left}}u(nh,x)=\Delta u(nh,x),n\in \mathbb{N},x\in {\mathbb{R}}^N,\hfill \\ u(0,x)=f\left(x\right),\hfill \end{array}\right.$$

(4)

where u and f are functions defined on ${\mathbb{N}}_0^h\times {\mathbb{R}}^N$ and ${\mathbb{R}}^N$, respectively. Formally, one can write the solution in the following way

$$u(nh,x)=\frac{1}{h^n}{(1/h-\Delta )}^{-n}f\left(x\right),n\in \mathbb{N},x\in {\mathbb{R}}^N,$$

whenever the resolvent operator ${(1/h-\Delta )}^{-1}$ has sense. It is well known that the Laplacian operator $\Delta$ associated with the standard heat equation in continuous time on $L^p\left({\mathbb{R}}^N\right)$ for $1\le p\le \infty$ generates the Gaussian semigroup

$$T\left(t\right)f\left(x\right)={\int }_{{\mathbb{R}}^N}{G}_t(x-y)f\left(y\right)dy=(G_t\ast f)\left(x\right),$$

where ∗ denotes the classical convolution on ${\mathbb{R}}^N$ and $G_t\left(x\right)$ is the convolution kernel which is given by

$$G_t\left(x\right)=\frac{1}{{\left(4\pi t\right)}^{N/2}}{e}^{-\frac{{\left|x\right|}^2}{4t}},t>0,x\in {\mathbb{R}}^N.$$

From semigroup theory (see Chapter 3, Corollary 1.11 (equation (1.16) ) in [22]), we obtain

$$\begin{array}{c}\hfill \frac{1}{h^n}{(1/h-\Delta )}^{-n}f(·)=\frac{1}{h^n\Gamma \left(n\right)}{\int }_0^{\infty }{e}^{-t/h}{t}^{n-1}T\left(t\right)f(·)dt.\end{array}$$

Hence,

$$\begin{array}{cc}\hfill u(nh,·)& =\frac{1}{h^n}{(1/h-\Delta )}^{-n}f(·)\hfill \\ \hfill & =\frac{1}{h^n\Gamma \left(n\right)}{\int }_0^{\infty }{e}^{-t/h}{t}^{n-1}(G_t\ast f)(·)dt:=({\mathcal{G}}_{n,h}\ast f)(·),f\in L^p\left({\mathbb{R}}^N\right),\hfill \end{array}$$

where

$${\mathcal{G}}_{n,h}\left(x\right)=\frac{1}{h^n\Gamma \left(n\right)}{\int }_0^{\infty }{e}^{-t/h}{t}^{n-1}{G}_t\left(x\right)dt,n\in \mathbb{N},x\in {\mathbb{R}}^N\backslash \left\{0\right\}.$$

(5)

Remark 1.

Note that fixed a positive number $t>0,$ the approximants ${(1-\frac{t}{n}\Delta )}^{-n}$ given by the Post-Widder inversion formula (see Chapter III, Section 5, Corollary 5.5 in [22]) allow to approximate the Gaussian $C_0$-semigroup $G_t\ast f$ as $n\to \infty .$ That is, for $f\in L^p\left({\mathbb{R}}^N\right),$

$$\parallel G_t\ast f-{(1-\frac{t}{n}\Delta )}^{-n}{f\parallel }_p\to 0,n\to \infty ,$$

uniformly for t in compact intervals. Writing $h=t/n,$ the previous convergence shows that the Gaussian semigroup can be approximated by the solutions of the discrete in time problems (4), i.e., ${(1-\frac{t}{n}\Delta )}^{-n}f={\mathcal{G}}_{n,h}\ast f,$ as the mesh $h\to 0.$

Remark 2.

It is easy to see that if we consider the forward difference ${\delta }_{\mathrm{right}}$ on (4), then formally, the solution of the problem would be $u(nh,·)=\frac{1}{h^n}{(1/h+\Delta )}^{n}f(·),$ which is not defined (bounded) on $L^p\left({\mathbb{R}}^N\right).$

Additionally, for the central difference ${\delta }_{\mathrm{c}}$, the fundamental solution would be given by

$${\int }_0^{\infty }{J}_n(t/h)G_t\left(x\right)dt,$$

where $J_n$ are the Bessel functions of the first kind. In this case, it is not difficult to prove that the solution is bounded on $L^p\left({\mathbb{R}}^N\right),$ however, it does not have as good properties as ${\mathcal{G}}_{n,h}$ satisfies, for example, the contractivity on $L^1\left({\mathbb{R}}^N\right).$

These are the main reasons we consider the discrete in time heat problem with the backward difference ${\delta }_{\mathrm{left}}.$

Now, we will see the explicit expression of the fundamental solution ${\mathcal{G}}_{n,h}$ in terms of special functions. By [23] (p. 363 (9)), we have

$$\begin{array}{cc}\hfill {\mathcal{G}}_{n,h}\left(x\right)& =\frac{1}{h^n\Gamma \left(n\right){\left(4\pi \right)}^{N/2}}{\int }_0^{\infty }{e}^{-(t/h+|x{|}^2/4t)}{t}^{n-N/2-1}dt\hfill \\ \hfill & =\frac{2}{\Gamma \left(n\right){\left(4\pi h\right)}^{N/2}}{\left(\frac{\left|x\right|}{2\sqrt{h}}\right)}^{n-N/2}{K}_{n-N/2}\left(\frac{\left|x\right|}{\sqrt{h}}\right),n\in \mathbb{N},x\in {\mathbb{R}}^N\backslash \left\{0\right\}.\hfill \end{array}$$

(6)

Here, the functions $K_{\nu }$ denote the Bessel functions of imaginary argument, also called MacDonald’s functions or modified cylinder functions (see Appendix A). Observe that the identity has no pointwise sense for $x=0$ if $n-N/2\le 0.$ In fact, for that values $n-N/2\le 0$, taking $\left|x\right|\to 0$ in (6) and using (P4), (P6) and (P8) of Appendix A one obtains ${\mathcal{G}}_{n,h}\left(x\right)\to \infty .$ For the case $n-N/2>0,$ by (P4), we have ${\mathcal{G}}_{n,h}\left(x\right)\to \frac{\Gamma (n-N/2)}{\Gamma \left(n\right){\left(4\pi h\right)}^{N/2}}$ as $\left|x\right|\to 0.$

Remark 3.

The Gaussian kernel satisfies the semigroup property on time, $G_t\ast G_s=G_{t+s}$. Since ${\mathcal{G}}_{n,h}$ is given by natural powers of the resolvent operator of the Laplacian, it satisfies the discrete semigroup property. Indeed, we also can prove that property using the expression (5) as follows,

$$\begin{array}{cc}\hfill ({\mathcal{G}}_{n,h}\ast {\mathcal{G}}_{m,h})\left(x\right)& =\frac{1}{h^{n+m}\Gamma \left(n\right)\Gamma \left(m\right)}{\int }_{{\mathbb{R}}^N}\left({\int }_0^{\infty }{\int }_0^{\infty }{e}^{-\frac{t+s}{h}}{t}^{n-1}{s}^{m-1}{G}_t(x-y)G_s\left(y\right)dsdt\right)dy\hfill \\ \hfill & =\frac{1}{h^{n+m}\Gamma \left(n\right)\Gamma \left(m\right)}{\int }_0^{\infty }\left({\int }_0^{\infty }{e}^{-\frac{t+s}{h}}{t}^{n-1}{s}^{m-1}{G}_{t+s}\left(y\right)ds\right)dt\hfill \\ \hfill & =\frac{1}{h^{n+m}\Gamma \left(n\right)\Gamma \left(m\right)}{\int }_0^{\infty }\left({\int }_t^{\infty }{e}^{-\frac{\sigma }{h}}{t}^{n-1}{(\sigma -t)}^{m-1}{G}_{\sigma }\left(x\right)d\sigma \right)dt\hfill \\ \hfill & =\frac{1}{h^{n+m}\Gamma \left(n\right)\Gamma \left(m\right)}{\int }_0^{\infty }{e}^{-\frac{\sigma }{h}}{G}_{\sigma }\left(x\right)\left({\int }_0^{\sigma }{t}^{n-1}{(\sigma -t)}^{m-1}dt\right)d\sigma \hfill \\ \hfill & =\frac{1}{h^{n+m}\Gamma \left(n\right)\Gamma \left(m\right)}{\int }_0^{\infty }{e}^{-\frac{\sigma }{h}}{G}_{\sigma }\left(x\right){\sigma }^{m+n-1}B(n,m)d\sigma ={\mathcal{G}}_{n+m,h}\left(x\right).\hfill \end{array}$$

Here, $B(n,m)$ is the Beta function.

In the following, we denote

$$p_{n,h}\left(t\right)=:\frac{1}{h^n\Gamma \left(n\right)}{e}^{-t/h}{t}^{n-1},n\in \mathbb{N}.$$

Then, we can write

$${\mathcal{G}}_{n,h}\left(x\right)={\int }_0^{\infty }{p}_{n,h}\left(t\right)G_t\left(x\right)dt,x\ne 0.$$

(7)

The above integral representation is a discretization formula for the Gaussian semigroup. The case $h=1$ was treated in [20] for a general $C_0$-semigroup on an abstract context.

Next, we refer to the function ${\mathcal{G}}_{n,h}$ as the fundamental solution for the problem (4). The following proposition states some basic properties of it.

Proposition 1.

The function ${\mathcal{G}}_{n,h}$ satisfies:

(i) 

${\displaystyle {\mathcal{G}}_{n,h}\left(x\right)>0,n\in \mathbb{N},x\ne 0;}$

(ii) 

${\displaystyle {\int }_{{\mathbb{R}}^N}{\mathcal{G}}_{n,h}\left(x\right)dx=1,n\in \mathbb{N}}$;

(iii) 

${\displaystyle \mathcal{F}\left({\mathcal{G}}_{n,h}\right)\left(\xi \right)=\frac{1}{{(1+h|\xi |}^2{)}^n},n\in \mathbb{N},\xi \in {\mathbb{R}}^N;}$

(iv) 

${\displaystyle \frac{{\mathcal{G}}_{n,h}\left(x\right)-{\mathcal{G}}_{n-1,h}\left(x\right)}{h}}=\Delta {\mathcal{G}}_{n,h}\left(x\right),n\ge 2,x\ne 0;$

(v) 

${\displaystyle {\int }_{{\mathbb{R}}^N}{\left|x\right|}^2{\mathcal{G}}_{n,h}\left(x\right)dx=2Nnh,n\in \mathbb{N}.}$

Proof. 

(i) It is clear by (7). (ii) Note that ${\int }_0^{\infty }{p}_{n,h}\left(t\right)dt=1$ and ${\int }_{{\mathbb{R}}^N}{G}_t\left(x\right)dx=1,$ then the result follows from the Fubini’s theorem. (iii) It is known that $\mathcal{F}\left(G_t\right)\left(\xi \right)=e^{-{t\left|\xi \right|}^2}$, for $\xi \in {\mathbb{R}}^N,$ then by (7) one obtains

$$\mathcal{F}\left({\mathcal{G}}_{n,h}\right)\left(\xi \right)={\int }_0^{\infty }{p}_{n,h}\left(t\right)\mathcal{F}\left(G_t\right)\left(\xi \right)dt=\frac{1}{{(1+h|\xi |}^2{)}^n}.$$

(iv) First of all, observe that $\frac{d}{dt}{p}_{n,h}\left(t\right)=-\frac{1}{h}(p_{n,h}\left(t\right)-p_{n-1,h}\left(t\right))$ for $n\ge 2.$ Then, integrating by parts, we obtain

$$\begin{array}{cc}\hfill \frac{{\mathcal{G}}_{n,h}\left(x\right)-{\mathcal{G}}_{n-1,h}\left(x\right)}{h}& ={\int }_0^{\infty }{p}_{n,h}\left(t\right)\frac{\partial }{\partial t}{G}_t\left(x\right)dt\hfill \\ \hfill & ={\int }_0^{\infty }{p}_{n,h}\left(t\right)\Delta G_t\left(x\right)dt\hfill \\ \hfill & =\Delta {\mathcal{G}}_{n,h}\left(x\right),x\ne 0,\hfill \end{array}$$

where we have used that ${lim}_{t\to 0^{+}}{p}_n\left(t\right)G_t\left(x\right)=0$ and ${lim}_{t\to \infty }{p}_n\left(t\right)G_t\left(x\right)=0.$ (v) It follows easily by the second moment of $G_t\left(x\right)$ and the representation (5).  □

Remark 4.

Observe that one can prove the above properties via the expression (6) given by the MacDonald’s function. For example, from (P1) of Appendix A we get the positivity of the fundamental solution. Furthermore, by [23] (p. 668 (16)), it follows

$$\begin{array}{cc}\hfill {\int }_{{\mathbb{R}}^N}{\mathcal{G}}_{n,h}\left(x\right)dx& =\frac{2}{\Gamma \left(n\right){\left(4\pi h\right)}^{1/2}}{\int }_{{\mathbb{R}}^N}{\left(\frac{\left|x\right|}{2\sqrt{h}}\right)}^{n-N/2}{K}_{n-N/2}\left(\frac{\left|x\right|}{\sqrt{h}}\right)dx\hfill \\ \hfill & =\frac{2^{1+\frac{N}{2}-n}}{\Gamma \left(n\right){\left(4\pi h\right)}^{1/2}{h}^{\frac{n}{2}-\frac{N}{4}}}\left(\frac{N{\pi }^{N/2}}{\Gamma (\frac{N}{2}+1)}{\int }_0^{\infty }{r}^{n-N/2}{K}_{n-N/2}\left(\frac{r}{\sqrt{h}}\right)dr\right)\hfill \\ \hfill & =\frac{\frac{N}{2}\Gamma \left(\frac{N}{2}\right)h^{\frac{N}{2}+\frac{N}{4}}}{h^{\frac{N}{2}+\frac{N}{4}}\Gamma (\frac{N}{2}+1)}=1.\hfill \end{array}$$

We also note that by $\frac{\partial \left|x\right|}{\partial x_j}=\frac{x_j}{\left|x\right|}$ and (P2) of Appendix A, we obtain

$$\frac{\partial }{\partial x_j}{\mathcal{G}}_{n,h}\left(x\right)=\frac{-2}{\Gamma \left(n\right){\left(4\pi h\right)}^{N/2}\sqrt{h}}\frac{x_j}{\left|x\right|}{\left(\frac{\left|x\right|}{2\sqrt{h}}\right)}^{n-N/2}{K}_{n-N/2-1}\left(\frac{\left|x\right|}{\sqrt{h}}\right),$$

(8)

and then derivating once more in the previous expression and taking into account (P3) and (P7) (with $\nu =n-\frac{N}{2}-1$) of Appendix A, we have

$$\begin{array}{cc}\hfill \frac{{\partial }^2}{\partial x_j^2}{\mathcal{G}}_{n,h}\left(x\right)& =-\frac{1}{h\Gamma \left(n\right){\left(4\pi h\right)}^{N/2}}{\left(\frac{\left|x\right|}{2\sqrt{h}}\right)}^{n-\frac{N}{2}-1}{K}_{n-\frac{N}{2}-1}\left(\frac{\left|x\right|}{\sqrt{h}}\right)\hfill \\ \hfill & +\frac{x_j^2}{h}\frac{1}{2h\Gamma \left(n\right){\left(4\pi h\right)}^{N/2}}{\left(\frac{\left|x\right|}{2\sqrt{h}}\right)}^{n-\frac{N}{2}-2}{K}_{n-\frac{N}{2}}\left(\frac{\left|x\right|}{\sqrt{h}}\right)\hfill \\ \hfill & +N\frac{x_j^2}{h}\frac{1}{4h\Gamma \left(n\right){\left(4\pi h\right)}^{N/2}}{\left(\frac{\left|x\right|}{2\sqrt{h}}\right)}^{n-\frac{N}{2}-3}{K}_{n-\frac{N}{2}-1}\left(\frac{\left|x\right|}{\sqrt{h}}\right)\hfill \\ \hfill & -2(n-1)\frac{x_j^2}{h}\frac{1}{4h\Gamma \left(n\right){\left(4\pi h\right)}^{N/2}}{\left(\frac{\left|x\right|}{2\sqrt{h}}\right)}^{n-\frac{N}{2}-3}{K}_{n-\frac{N}{2}-1}\left(\frac{\left|x\right|}{\sqrt{h}}\right).\hfill \end{array}$$

Now, since ${\sum }_{j=1}^N\frac{x_j^2}{h}={\left(\frac{\left|x\right|}{\sqrt{h}}\right)}^2$, we obtain

$$\Delta {\mathcal{G}}_{n,h}\left(x\right)=\frac{{\mathcal{G}}_{n,h}\left(x\right)-{\mathcal{G}}_{n-1,h}\left(x\right)}{h}.$$

Finally, observe that the mean square displacement can be also calculated in the following way; using (6), a change of variables and [23] (p. 668 (16)), we have

$$\begin{array}{cc}\hfill {\int }_{{\mathbb{R}}^N}{\left|x\right|}^2{\mathcal{G}}_{n,h}\left(x\right)dx& =\frac{2}{\Gamma \left(n\right){\left(4\pi h\right)}^{N/2}{\left(2\sqrt{h}\right)}^{N-1/2}}{\int }_{{\mathbb{R}}^N}{\left|x\right|}^{n-N/2+2}{K}_{n-N/2}\left(\frac{\left|x\right|}{\sqrt{h}}\right)dx\hfill \\ \hfill & =\frac{2}{\Gamma \left(n\right){\left(4\pi h\right)}^{N/2}{\left(2\sqrt{h}\right)}^{N-1/2}}\left(\frac{N{\pi }^{N/2}}{\Gamma (\frac{N}{2}+1)}{\int }_0^{\infty }{r}^{n+\frac{N}{2}+1}{K}_{n-N/2}\left(\frac{r}{\sqrt{h}}\right)dr\right)\hfill \\ \hfill & =2Nnh.\hfill \end{array}$$

Remark 5.

Note that by Proposition 1 (ii), we have that the total mass of solution of (4) is conservative in the discrete time $nh,$ that is,

$${\int }_{{\mathbb{R}}^N}u(nh,x)dx={\int }_{{\mathbb{R}}^N}f\left(x\right)dx.$$

Moreover, the first moment is also conservative: if $(1+|x\left|\right)f\in L^1\left({\mathbb{R}}^N\right)$ one gets

$${\int }_{{\mathbb{R}}^N}x(u(nh,x)-u((n-1)h,x))dx=h{\int }_{{\mathbb{R}}^N}x\Delta u(nh,x)dx=0,$$

and so ${\int }_{{\mathbb{R}}^N}xu(nh,x)dx={\int }_{{\mathbb{R}}^N}xf\left(x\right)dx.$ However, as in the continuous case holds, by Proposition 1 (v), it follows that if ${(1+|x|}^2)f\in L^1\left({\mathbb{R}}^N\right)$, the second-order moment is

$${\int }_{{\mathbb{R}}^N}{\left|x\right|}^{2}u(nh,x)dx={\int }_{{\mathbb{R}}^N}{\left|x\right|}^{2}f\left(x\right)dx+2Nnh{\int }_{{\mathbb{R}}^N}f\left(x\right)dx.$$

To finish this section, we show some pictures of the fundamental solution of (4). We have used Mathematica to make them. The objective is that the reader visualizes the convergence of ${\mathcal{G}}_{n,h}$ to $G_t$ as the mesh $h\to 0.$

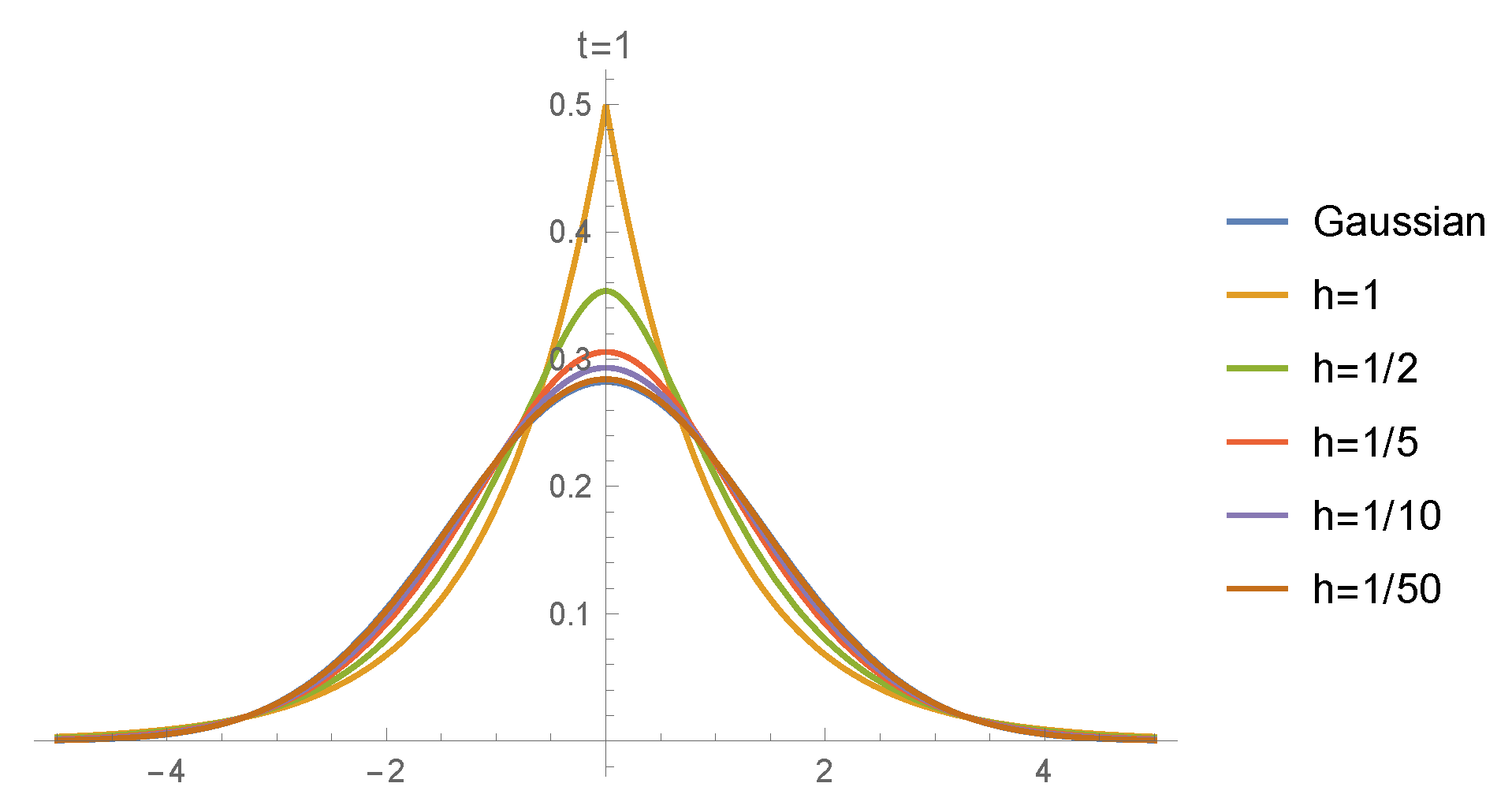
Figure 1 shows, in the one-dimensional case ($N=1$), the Gauss kernel $G_1$ and the fundamental solutions of the discrete problems for several values of $h.$ As we have mentioned, the approximants in the Post-Wider inversion formula (which are given by the fundamental solutions in the discrete setting) converge to the Gaussian semigroup as $h\to 0$ writing $t=nh.$ Therefore, for the different values of $h,$ we choose n such that $nh=1.$ For example, for $h=1/2$, we have represented the fundamental solution ${\mathcal{G}}_{2,1/2}.$ Furthermore, observe that for $N=1$ the fundamental solution ${\mathcal{G}}_{n,h}\left(x\right)$ is defined on the whole real line since $n-N/2>0$ for all $n\in \mathbb{N}.$ However, by (8), and (P6) and (P4) of Appendix A, we obtain

$${\mathcal{G}}_{1,h}^{\prime }\left(x\right)=C_h\frac{x}{{\left|x\right|}^{1/2}}{K}_{-1/2}\left(\frac{\left|x\right|}{\sqrt{h}}\right)=C_h\frac{x}{{\left|x\right|}^{1/2}}{K}_{1/2}\left(\frac{\left|x\right|}{\sqrt{h}}\right)\sim -C_h\frac{x}{\left|x\right|},\left|x\right|\to 0,$$

where $C_h$ is a positive constant depending on h (the symbol ∼ denotes that both functions are equivalent in the limit, in this case, as $\left|x\right|\to 0$). This shows that ${\mathcal{G}}_{1,h}$ is not derivable in $x=0$ (see Figure 1 for $h=1$).

Figure 1. Behavior of Gauss kernel $G_1$.

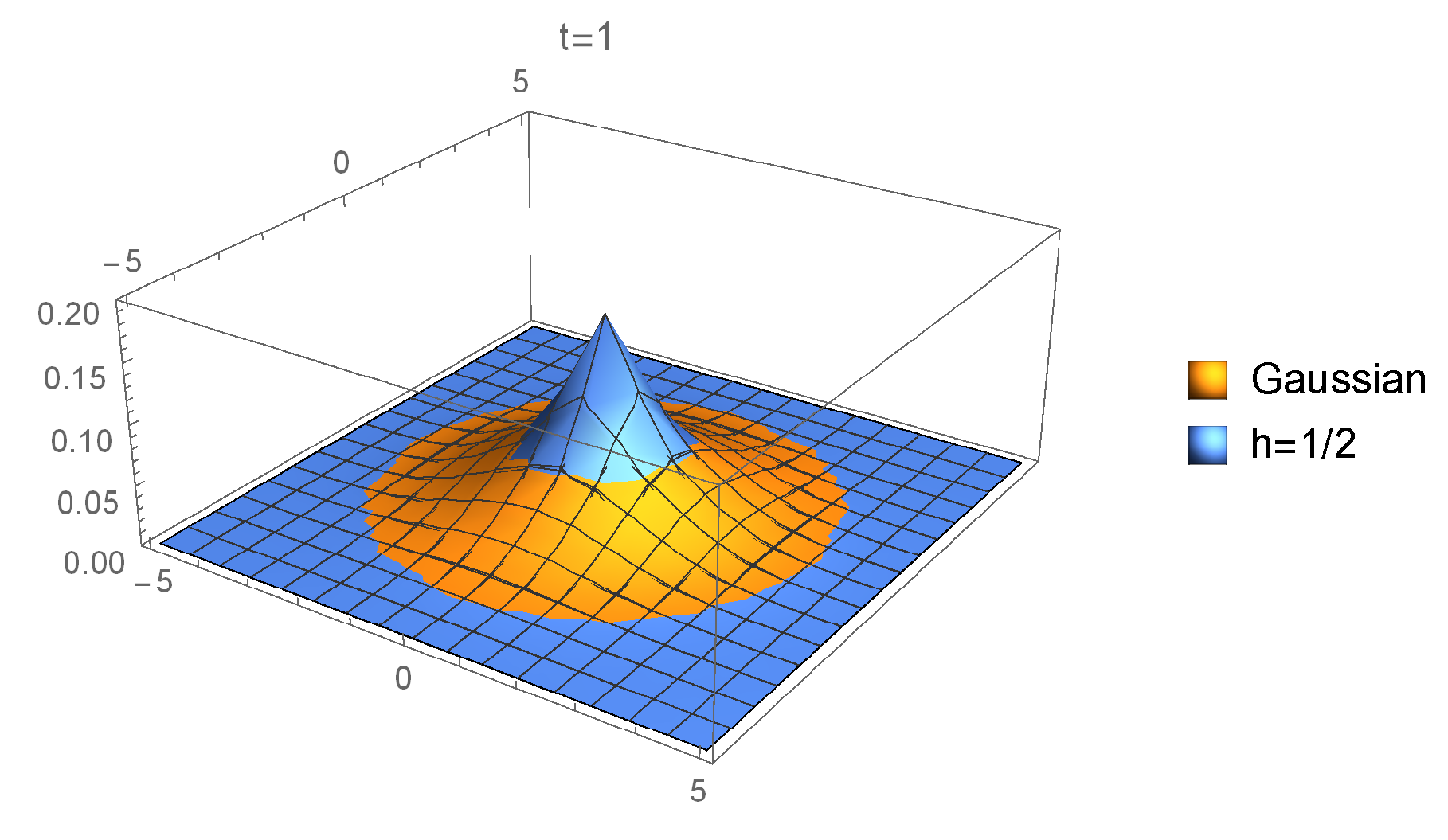
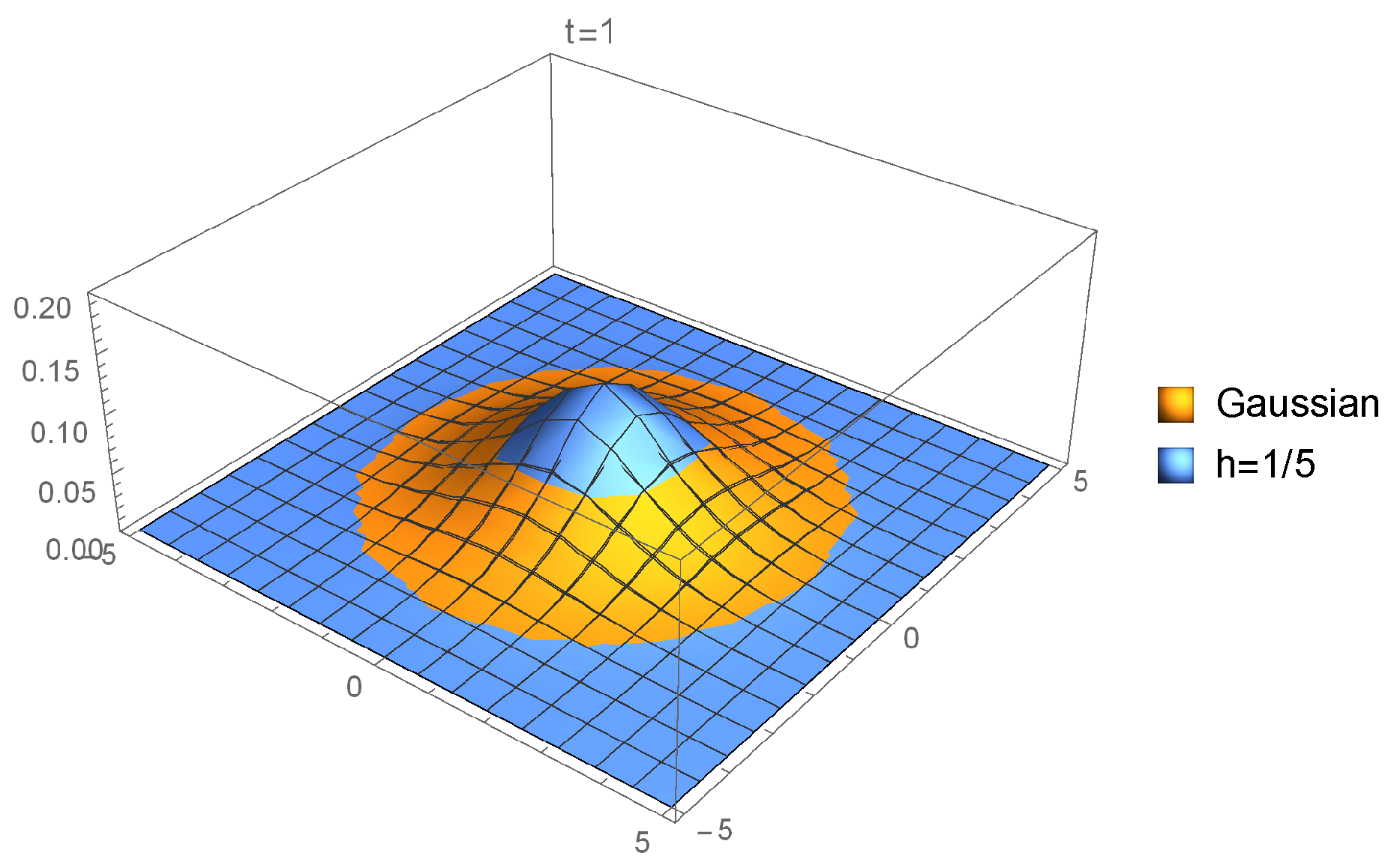
Figure 2, Figure 3 and Figure 4 show several approximants to the Gaussian $G_1$ in the two-dimensional case ($N=2$). In Figure 2, we observe that ${\mathcal{G}}_{1,1}\left(x\right)\to +\infty$ taking $x\to 0,$ as we have commented previously (since $n-N/2=0$ for $n=1,N=2$).

Figure 2. Comparison of ${\mathcal{G}}_{1,1}$ with $G_1$ near $x=0$.

Figure 3. Comparison of ${\mathcal{G}}_{2,1/2}$ with $G_1$ near $x=0$.

Figure 4. Comparison of ${\mathcal{G}}_{n,h}$ with $G_1$ as h decrease.

In Figure 3 we glimpse that ${\mathcal{G}}_{2,1/2}\left(x\right)$ is well defined for $x=0,$ but it is not differentiable (since $n-N/2=1$). Finally, Figure 4 shows, not only as the approximation improves as h decreases, but also that the function is smoother.

3. Estimates for the Fundamental Solution

In this section, we present pointwise and p-norm estimates for the fundamental solution of (4). In the following, we will assume that the step size h of the mesh will be fixed because our main aim is to study asymptotic results when the discrete time n goes to infinity. Therefore, the constants that will appear along the manuscript could depend on such h (as well as on p), although we do not indicate it. We use the variable constant convention, in which $C>0$ denotes a constant which may not be the same from line to line.

Theorem 1.

There exists a positive constant C (independent on x and n) in each next case such that

(i) 

$$|{\mathcal{G}}_{n,h}\left(x\right)|\le \frac{C}{{\left(nh\right)}^{N/2}},\mathrm{for}\frac{{\left|x\right|}^2}{nh}\le 1\mathrm{and}n-N/2>0,$$

and

$$|{\mathcal{G}}_{n,h}\left(x\right)|\le C\frac{nh}{{\left|x\right|}^{N+2}},\mathrm{for}\frac{{\left|x\right|}^2}{nh}\ge 1.$$

(ii) 

$$|\nabla {\mathcal{G}}_{n,h}\left(x\right)|\le C\frac{\left|x\right|}{{\left(nh\right)}^{N/2+1}},\mathrm{for}\frac{{\left|x\right|}^2}{nh}\le 1\mathrm{and}n-N/2>1,$$

and

$$|\nabla {\mathcal{G}}_{n,h}\left(x\right)|\le C\frac{nh}{{\left|x\right|}^{N+3}},\mathrm{for}\frac{{\left|x\right|}^2}{nh}\ge 1.$$

(iii) 

$$\left|\frac{{\mathcal{G}}_{n,h}\left(x\right)-{\mathcal{G}}_{n-1,h}\left(x\right)}{h}\right|\le \frac{C}{{\left(nh\right)}^{N/2+1}},\mathrm{for}\frac{{\left|x\right|}^2}{nh}\le 1\mathrm{and}n-N/2>1,$$

and

$$\left|\frac{{\mathcal{G}}_{n,h}\left(x\right)-{\mathcal{G}}_{n-1,h}\left(x\right)}{h}\right|\le \frac{C}{{\left|x\right|}^{N+2}},\mathrm{for}\frac{{\left|x\right|}^2}{nh}\ge 1.$$

Proof. 

(i) By (6), (P4) of Appendix A and (A1) we have that there is a positive constant C such that whenever $\frac{{\left|x\right|}^2}{nh}\le 1\mathrm{and}n-N/2>0,$ it follows

$$|{\mathcal{G}}_{n,h}\left(x\right)|\le C\frac{\Gamma (n-N/2)}{\Gamma \left(n\right){\left(4\pi h\right)}^{N/2}}\le C\frac{1}{{\left(nh\right)}^{N/2}}.$$

Along the proof, we will use that

$$e^{-\frac{\left|x\right|}{\sqrt{h}}}\le \frac{k!h^{k/2}}{{\left|x\right|}^k},k\in {\mathbb{N}}_0.$$

(9)

By (P5) of Appendix A there is $C>0$ such that if $\frac{{\left|x\right|}^2}{nh}\ge 1,$ taking $k=n+N+1$ in (9), it follows

$$|{\mathcal{G}}_{n,h}\left(x\right)|\le C\frac{n^{3N/4+5/4}}{2^n}\frac{nh}{{\left|x\right|}^{N+2}}\le C\frac{nh}{{\left|x\right|}^{N+2}}.$$

(ii) Note that Equation (8) implies that

$$|\nabla {\mathcal{G}}_{n,h}\left(x\right)|=\frac{2}{\Gamma \left(n\right){\left(4\pi h\right)}^{N/2}\sqrt{h}}{\left(\frac{\left|x\right|}{2\sqrt{h}}\right)}^{n-N/2}{K}_{n-N/2-1}\left(\frac{\left|x\right|}{\sqrt{h}}\right).$$

(10)

From (P4) of Appendix A and (A1) there is $C>0$ such that if $\frac{{\left|x\right|}^2}{nh}\le 1\mathrm{and}n-N/2>1,$ we have

$$|\nabla {\mathcal{G}}_{n,h}\left(x\right)|\le C\frac{\Gamma (n-N/2-1)\left|x\right|}{\Gamma \left(n\right)h^{N/2+1}}\le C\frac{\left|x\right|}{{\left(nh\right)}^{N/2+1}}.$$

On the other hand, by (10) and (P5) of Appendix A, there is $C>0$ such that if $\frac{{\left|x\right|}^2}{nh}\ge 1,$ taking $k=n+N+2$ in (9), we obtain

$$|\nabla {\mathcal{G}}_{n,h}\left(x\right)|\le C\frac{hn(n+1)(n+2)(n+3)}{2^n{\left|x\right|}^4}\le C\frac{nh}{{\left|x\right|}^4}.$$

(iii) Applying (P3) and (P2) of Appendix A in turn, it follows that

$$\begin{array}{cc}\hfill \frac{{\mathcal{G}}_{n,h}\left(x\right)-{\mathcal{G}}_{n-1,h}\left(x\right)}{h}& =\frac{-{2\left|x\right|}^{n-N/2-1}}{\Gamma \left(n\right){\left(4\pi \right)}^{N/2}{h}^{N/2+1/2}{\left(2\sqrt{h}\right)}^{n-N/2}}\hfill \\ \hfill & \times \left(N{K}_{n-N/2-1}\left(\frac{\left|x\right|}{\sqrt{h}}\right)-\frac{\left|x\right|}{\sqrt{h}}{K}_{n-N/2-2}\left(\frac{\left|x\right|}{\sqrt{h}}\right)\right)\hfill \\ \hfill & =:\left(I\right)+\left(II\right).\hfill \end{array}$$

By (P4) of Appendix A and (A1), there is $C>0$ such that for $\frac{{\left|x\right|}^2}{nh}\le 1\mathrm{and}n-N/2>1,$

$$\left|\left(I\right)\right|\le C\frac{\Gamma (n-N/2-1)}{\Gamma \left(n\right)h^{N/2+1}}\le C\frac{1}{{\left(nh\right)}^{N/2+1}},$$

and

$$\left|\left(II\right)\right|\le C\frac{{\left|x\right|}^2}{{\left(nh\right)}^{N/2+2}}\le \frac{C}{{\left(nh\right)}^{N/2+1}}.$$

Note that from the part (i), we have there is $C>0$ such that for $\frac{{\left|x\right|}^2}{nh}\ge 1,$

$$|{\mathcal{G}}_{n,h}\left(x\right)|,|{\mathcal{G}}_{n-1,h}\left(x\right)|\le C\frac{h{n}^{3N/4+9/4}}{2^n{\left|x\right|}^{N+2}}.$$

Then

$$\left|\frac{{\mathcal{G}}_{n,h}\left(x\right)-{\mathcal{G}}_{n-1,h}\left(x\right)}{h}\right|\le C\frac{1}{{\left|x\right|}^{N+2}}.$$

 □

Now, we present the asymptotic decay of the fundamental solution ${\mathcal{G}}_{n,h}$ in Lebesgue and Sobolev spaces.

Theorem 2.

Let $1\le p\le \infty$ and $n\in \mathbb{N}.$ Then ${\mathcal{G}}_{n,h}\in L^p\left({\mathbb{R}}^N\right)$ if and only if $n-\frac{N}{2}(1-1/p)>0,$ and then

$$\parallel {\mathcal{G}}_{n,h}{\parallel }_p\le C_p{\displaystyle \frac{1}{{\left(nh\right)}^{\frac{N}{2}(1-1/p)}}}.$$

Furthermore,

(i) 

if $n-\frac{N}{2}(1-1/p)>1/2,$ then

$$\parallel \nabla {\mathcal{G}}_{n,h}{\parallel }_p\le C{\displaystyle \frac{1}{{\left(nh\right)}^{\frac{N}{2}(1-1/p)+1/2}}}.$$

(ii) 

if $n-\frac{N}{2}(1-1/p)>1,$ then

$${∥{\displaystyle \frac{{\mathcal{G}}_{n,h}-{\mathcal{G}}_{n-1,h}}{h}}∥}_p\le C{\displaystyle \frac{1}{{\left(nh\right)}^{\frac{N}{2}(1-1/p)+1}}}.$$

Here, C is a constant independent of h and n.

Proof. 

It is well known (see p. 334 (3.326) in [23]) that there exists $C>0$ (independent of t) such that $\left|\right|G_t{\left|\right|}_p=C\frac{1}{t^{\frac{N}{2}(1-\frac{1}{p})}},$ $\parallel \nabla G_t{\parallel }_p=C\frac{1}{t^{\frac{N}{2}(1-\frac{1}{p})+1/2}}$ and $\parallel \frac{\partial }{\partial t}{G}_t{\parallel }_p\le C\frac{1}{t^{\frac{N}{2}(1-\frac{1}{p})+1}}$ for $t>0$.

Note that by (7), then one arrives at

$$\parallel {\mathcal{G}}_{n,h}{\parallel }_p\le \frac{C}{h^n\Gamma \left(n\right)}{\int }_0^{\infty }{e}^{\frac{-t}{h}}{t}^{n-\frac{N}{2}(1-\frac{1}{p})-1}dt=C\frac{\Gamma (n-\frac{N}{2}(1-\frac{1}{p}))}{h^{\frac{N}{2}(1-\frac{1}{p})}\Gamma \left(n\right)}\le \frac{C}{{\left(nh\right)}^{\frac{N}{2}(1-\frac{1}{p})}},$$

if $n-\frac{N}{2}(1-1/p)>0,$ where we have applied (A1). The boundedness of items (i) and (ii) follows in a similar way.

Now, we prove that if $n-\frac{N}{2}(1-1/p)\le 0,$ then ${\mathcal{G}}_{n,h}\notin L^p\left({\mathbb{R}}^N\right).$ We distinguish two cases under assumption $n\le \frac{N}{2}(1-1/p).$

First, if $n=\frac{N}{2},$ which only could happen if $p=\infty .$ In that case, by (6) and (P8) of Appendix A, we have ${\mathcal{G}}_{n,h}\left(x\right)\sim C_{n,h}log\left(\frac{2\sqrt{h}}{\left|x\right|}\right)$ as $\left|x\right|\to 0,$ and then ${\mathcal{G}}_{n,h}\notin L^{\infty }\left({\mathbb{R}}^N\right).$

Secondly, consider $n<\frac{N}{2}.$ In that case, by (6), and (P4) and (P6) of Appendix A, we have ${\mathcal{G}}_{n,h}\left(x\right)\sim C_{n,h}\frac{1}{{\left|x\right|}^{N-2n}}$ as $\left|x\right|\to 0,$ and then ${\mathcal{G}}_{n,h}\notin L^p\left({\mathbb{R}}^N\right)$ (it is enough to use spherical coordinates to prove the divergence of the integral at zero).  □

4. Asymptotic ${\mathit{L}}^{\mathit{p}}$-${\mathit{L}}^{\mathit{q}}$ Decay

Let $h>0,$ and the time mesh ${\mathbb{N}}_0^h$. Now, we consider the non-homogeneous problem

$$\left\{\begin{array}{c}{\delta }_{\mathrm{left}}u(nh,x)=\Delta u(nh,x)+g(nh,x),n\in \mathbb{N},x\in {\mathbb{R}}^N,\hfill \\ u(0,x)=f\left(x\right),\hfill \end{array}\right.$$

(11)

where $u,f,g$ are functions defined on ${\mathbb{N}}_0^h\times {\mathbb{R}}^N,$ ${\mathbb{R}}^N$ and ${\mathbb{N}}^h\times {\mathbb{R}}^N$, respectively.

Formally, from (11), one arrives at

$$u(nh,x)=({\mathcal{G}}_{n,h}\ast f)\left(x\right)+h\sum _{j=1}^n({\mathcal{G}}_{j,h}\ast g((n-j+1)h,·))\left(x\right),n\in \mathbb{N},x\in {\mathbb{R}}^N.$$

(12)

The expression (12) gives a classical solution of (11) on $L^p\left({\mathbb{R}}^N\right)$ ($1\le p\le \infty$) whenever $f,g(nh,·)\in L^p\left({\mathbb{R}}^N\right),$ for $n\in \mathbb{N},$ since ${\mathcal{G}}_{n,h}\in L^1\left({\mathbb{R}}^N\right)$ for all $n\in \mathbb{N}.$ For convenience, we write the classical solution as $u(nh,x)=u_{\mathfrak{c}}(nh,x)+u_{\mathfrak{p}}(nh,x),$ where

$$u_{\mathfrak{c}}(nh,x)=({\mathcal{G}}_{n,h}\ast f)\left(x\right)$$

(13)

and

$$u_{\mathfrak{p}}(nh,x)=h\sum _{j=1}^n({\mathcal{G}}_{n-j+1,h}\ast g(jh,·))\left(x\right).$$

(14)

Next, let us present a result about the $L^p$-$L^q$ asymptotic decay for $u_{\mathfrak{c}}.$

Theorem 3.

Let $1\le q\le p\le \infty$ and $f\in L^q\left({\mathbb{R}}^N\right).$ If $n-\frac{N}{2}(1/q-1/p)>0$, then $u_{\mathfrak{c}}(nh,·)\in L^p\left({\mathbb{R}}^N\right),$ and

$$\parallel u_{\mathfrak{c}}{(nh,·)\parallel }_p\le C{\displaystyle \frac{1}{{\left(nh\right)}^{\frac{N}{2}(1/q-1/p)}}}{\parallel f\parallel }_q.$$

Furthermore,

(i) 

$\parallel \nabla u_{\mathfrak{c}}{(nh,·)\parallel }_p\le C{\displaystyle \frac{1}{{\left(nh\right)}^{\frac{N}{2}(1/q-1/p)+1/2}}}{\parallel f\parallel }_q,n-\frac{N}{2}(1/q-1/p)>1/2.$

(ii) 

$\parallel {\delta }_{\mathrm{left}}{u}_{\mathfrak{c}}{(nh,·)\parallel }_p\le C{\displaystyle \frac{1}{{\left(nh\right)}^{\frac{N}{2}(1/q-1/p)+1}}}{\parallel f\parallel }_q,n-\frac{N}{2}(1/q-1/p)>1.$

Here, $C>0$ is a constant independent on h and n.

Proof. 

Take $r\ge 1$ such that $1+1/p=1/q+1/r,$ and applying Young’s inequality, we get

$$\parallel u_{\mathfrak{c}}{(nh,·)\parallel }_p=\parallel {\mathcal{G}}_{n,h}{\ast f\parallel }_p\le \parallel {\mathcal{G}}_{n,h}{\parallel }_r{\parallel f\parallel }_q.$$

The results follows from Theorem 2. Items (ii) and (iii) are similar by items (ii) and (iii) of Theorem 2.  □

Now, assuming certain conditions on the function g, we obtain an asymptotic behavior for $u_{\mathfrak{p}},$ given by (14).

Theorem 4.

Let $1\le q\le p\le \infty ,$ and $g(nh,·)\in L^q\left({\mathbb{R}}^N\right)$ for each $n\in \mathbb{N},$ such that there are $\gamma >0$ and a positive constant K independent on $n\in \mathbb{N}$ such that

$${\parallel g(nh,·)\parallel }_q\le \frac{K}{n^{\gamma }}.$$

If $\frac{1}{q}-\frac{1}{p}<2/N$, then $u_{\mathfrak{p}}(nh,·)\in L^p\left({\mathbb{R}}^N\right)$ for all $n\in \mathbb{N}.$ Furthermore,

(i) 

If $\gamma \ne 1$, then

$$\parallel u_{\mathfrak{p}}{(nh,·)\parallel }_p\le C\frac{{\left(nh\right)}^{1-min\{1,\gamma \}}}{{\left(nh\right)}^{\frac{N}{2}(1/q-1/p)}}.$$

(ii) 

If $\gamma =1,$

$$\parallel u_{\mathfrak{p}}{(nh,·)\parallel }_p\le C\frac{lognh}{{\left(nh\right)}^{\frac{N}{2}(1/q-1/p)}}.$$

Here, $C>0$ is a constant independent on n.

Proof. 

Let $r\ge 1$ such that $1+1/p=1/q+1/r.$ Note that by Theorem 2, we have ${\mathcal{G}}_{j,h}\in L^r\left({\mathbb{R}}^N\right)$ for all $j\in \mathbb{N}.$ Therefore, by Young’s inequality and Theorem 2, one obtains for each $n\in \mathbb{N}$ that

$$\begin{array}{cc}\hfill \parallel u_{\mathfrak{p}}{(nh,·)\parallel }_p& \le h\sum _{j=1}^n\parallel {\mathcal{G}}_{n-j+1,h}{\parallel }_r{\parallel g(jh,·)\parallel }_q\le Ch\sum _{j=1}^n\frac{1}{{\left((n-j+1)h\right)}^{\frac{N}{2}(1/q-1/p)}}\frac{1}{{\left(jh\right)}^{\gamma }}\hfill \\ \hfill & =Ch\left(\sum _{j=1}^{[n/2]}+\sum _{j=[n/2]+1}^n\right)\frac{1}{{\left((n-j+1)h\right)}^{\frac{N}{2}(1/q-1/p)}}\frac{1}{{\left(jh\right)}^{\gamma }}=:I_1+I_2.\hfill \end{array}$$

On one hand, for $1\le j\le [n/2]$ we have $n/2\le n-j+1,$ which in turn implies that

$$I_1\le C\frac{1}{{\left(nh\right)}^{\frac{N}{2}(1/q-1/p)}}\sum _{j=1}^{[n/2]}\frac{1}{{\left(jh\right)}^{\gamma }}\le C\frac{{\left(nh\right)}^{1-min\{1,\gamma \}}}{{\left(nh\right)}^{\frac{N}{2}(1/q-1/p)}},\gamma \ne 1,$$

and $I_1\le C\frac{lognh}{{\left(nh\right)}^{\frac{N}{2}(1/q-1/p)}}$ when $\gamma =1.$

On the other hand,

$$I_2\le C\frac{1}{{\left(nh\right)}^{\gamma }}\sum _{j=1}^n\frac{1}{{\left(jh\right)}^{\frac{N}{2}(1/q-1/p)}}\le C\frac{{\left(nh\right)}^{1-\frac{N}{2}(1/q-1/p)}}{{\left(nh\right)}^{\gamma }}.$$

 □

5. Large-Time Behavior of Solutions

In the following, we study the asymptotic behavior of solution of (11), more precisely we will prove as the solution $u_{\mathfrak{c}}+u_{\mathfrak{p}}$ converges asymptotically to a linear combination of the mass of the initial data f and the mass of the non-homogeneity $g.$ Moreover, we will be able to state the rate of the convergence. Along the section, we will assume the following:

(a)

$f\in L^1\left({\mathbb{R}}^N\right)$.

(b)

There exists $\gamma >1$ such that

$${\parallel g(jh,·)\parallel }_1\le C\frac{1}{j^{\gamma }},j\in \mathbb{N}.$$

Set also

$$M_{\mathfrak{c}}={\int }_{{\mathbb{R}}^N}f\left(x\right)dx,M_{\mathfrak{p}}=\sum _{j=1}^{\infty }{\int }_{{\mathbb{R}}^N}g(jh,x)dx.$$

Next, we consider the intervals $I_N$ (depending on $N\in \mathbb{N}$) of values of p, for which the following result will be valid. We define

$$I_N:=\left\{\begin{array}{cc}[1,\infty ],\hfill & N=1.\hfill \\ [1,\infty )\hfill & ,N=2.\hfill \\ [1,\frac{N}{N-2})\hfill & N\ge 3.\hfill \end{array}\right.$$

Taking into account the previous notation, we present the next theorem.

Theorem 5.

Let $1\le p\le \infty .$ Assume the conditions $\left(a\right)$–$\left(b\right),$ and let $u_{\mathfrak{c}}$ and $u_{\mathfrak{p}}$ given by (13) and (14), respectively. If $p\in I_N,$ then $u(nh,·)\in L^p\left({\mathbb{R}}^N\right)$ for all $n\in \mathbb{N}.$

(i) 

Furthermore,

$${\left(nh\right)}^{\frac{N}{2}(1-\frac{1}{p})}{\parallel u_{\mathfrak{c}}(nh,·)-M_{\mathfrak{c}}{\mathcal{G}}_{n,h}(·)\parallel }_p\to 0,asn\to \infty ,$$

and

$${\left(nh\right)}^{\frac{N}{2}(1-\frac{1}{p})}{\parallel u_{\mathfrak{p}}(nh,·)-h{M}_{\mathfrak{p}}{\mathcal{G}}_{n,h}(·)\parallel }_p\to 0,asn\to \infty .$$

(ii) 

Suppose, in addition, that $\left|x\right|f\in L^1\left(\mathbb{R}\right),$ then there exists $K_{p,f}>0$ such that

$${\left(nh\right)}^{\frac{N}{2}(1-\frac{1}{p})}{\parallel u_{\mathfrak{c}}(nh,·)-M_{\mathfrak{c}}{\mathcal{G}}_{n,h}(·)\parallel }_p\le K_{p,f}{\left(nh\right)}^{-1/2}.$$

Proof. 

Note that by Theorems 3 and 4, we have that $u_{\mathfrak{c}}(nh,·),u_{\mathfrak{p}}(nh,·)\in L^p\left({\mathbb{R}}^N\right)$ when $\frac{N}{2}(1-1/p)<1,$ that is, when $p\in I_N.$

We start proving the assertion $\left(ii\right)$. Next, we can assume that n is large enough. Since $f,\left|x\right|f\in L^1\left({\mathbb{R}}^N\right),$ by Decomposition Lemma A1 there exists $\varphi \in L^1({\mathbb{R}}^N;{\mathbb{R}}^N)$ such that

$$f=M_{\mathfrak{c}}{\delta }_0+div\varphi$$

in the distributional sense, and

$${\parallel \varphi \parallel }_1\le C{\int }_{{\mathbb{R}}^N}\left|x\right|\left|f\left(x\right)\right|dx<\infty .$$

Then,

$$\begin{array}{cc}\hfill u_{\mathfrak{c}}(nh,x)& =({\mathcal{G}}_{n,h}\ast (M_{\mathfrak{c}}{\delta }_0+div\varphi (·)))\left(x\right)\hfill \\ \hfill & =M_{\mathfrak{c}}{\mathcal{G}}_{n,h}\left(x\right)+(\nabla {\mathcal{G}}_{n,h}\ast \varphi )\left(x\right),\hfill \end{array}$$

which implies (n large enough such that $n>\frac{N}{2}(1-1/p)+1/2$)

$$\parallel u_{\mathfrak{c}}(nh,·)-M_{\mathfrak{c}}{\mathcal{G}}_{n,h}{(·)\parallel }_p\le C\parallel \nabla {\mathcal{G}}_{n,h}{\parallel }_p{\parallel \left|x\right|f(·)\parallel }_1\le K_{p,f}{\displaystyle \frac{1}{{\left(nh\right)}^{\frac{N}{2}(1-1/p)+1/2}}},$$

where we have used part $\left(i\right)$ of Theorem 2. This implies

$$\parallel {\mathcal{G}}_{n,h}\ast f-M_{\mathfrak{c}}{\mathcal{G}}_{n,h}{\parallel }_p\le K_{p,f}{\displaystyle \frac{1}{{\left(nh\right)}^{\frac{N}{2}(1-1/p)+\frac{1}{2}}}}.$$

(15)

To prove the first part of assertion $\left(i\right)$, we choose a sequence $\left({\eta }_j\right)\subset C_0^{\infty }\left({\mathbb{R}}^N\right)$ such that ${\int }_{{\mathbb{R}}^N}{\eta }_j\left(x\right)dx=M_{\mathfrak{c}}$ for all $j,$ and ${\eta }_j\to f$ in $L^1\left({\mathbb{R}}^N\right)$. For each j, by Theorem 2 and (15) we get

$$\begin{array}{cc}\hfill \parallel u_{\mathfrak{c}}(nh,·)-M_{\mathfrak{c}}{\mathcal{G}}_{n,h}{(·)\parallel }_p& =\parallel {\mathcal{G}}_{n,h}\ast f-M_{\mathfrak{c}}{\mathcal{G}}_{n,h}{\parallel }_p\hfill \\ \hfill & \le \parallel {\mathcal{G}}_{n,h}\ast (f-{\eta }_j){\parallel }_p+{\parallel {\mathcal{G}}_{n,h}\ast {\eta }_j-M_{\mathfrak{c}}{\mathcal{G}}_{n,h}\parallel }_p\hfill \\ \hfill & \le \parallel {\mathcal{G}}_{n,h}{\parallel }_p\parallel f-{\eta }_j{\parallel }_1+{\parallel {\mathcal{G}}_{n,h}\ast {\eta }_j-M_{\mathfrak{c}}{\mathcal{G}}_{n,h}\parallel }_p\hfill \\ \hfill & \le C_p{\displaystyle \frac{1}{{\left(nh\right)}^{\frac{N}{2}(1-1/p)}}}{\parallel f-{\eta }_j\parallel }_1+K_{p,{\eta }_j}{\displaystyle \frac{1}{{\left(nh\right)}^{\frac{N}{2}(1-1/p)+\frac{1}{2}}}}.\hfill \end{array}$$

It follows that

$${\left(nh\right)}^{\frac{N}{2}(1-1/p)}\parallel u_{\mathfrak{c}}(nh,·)-M_{\mathfrak{c}}{\mathcal{G}}_{n,h}{(·)\parallel }_p\le C_p{\parallel f-{\eta }_j\parallel }_1+K_{p,{\eta }_j}\frac{1}{{\left(nh\right)}^{\frac{1}{2}}},$$

which implies

$$\underset{n\to \infty }{lim\; sup}{\left(nh\right)}^{\frac{N}{2}(1-1/p)}\parallel u_{\mathfrak{c}}(nh,·)-M_{\mathfrak{c}}{\mathcal{G}}_{n,h}{(·)\parallel }_p\le C_p{\parallel f-{\eta }_j\parallel }_1.$$

The assertion follows by letting $j\to \infty$.

Next, let us prove the second part of $\left(i\right)$. We can write

$$M_{\mathfrak{p}}=\sum _{j=1}^n{\int }_{{\mathbb{R}}^N}g(jh,x)+\sum _{j=n+1}^{\infty }{\int }_{{\mathbb{R}}^N}g(jh,x)dx.$$

It follows from Theorem 2 that

$$\begin{array}{cc}\hfill & {\left(nh\right)}^{\frac{N}{2}(1-\frac{1}{p})}{∥{\mathcal{G}}_{n,h}(·)\sum _{j=n+1}^{\infty }{\int }_{{\mathbb{R}}^N}g(jh,x)dx∥}_p\hfill \\ \hfill & \le {\left(nh\right)}^{\frac{N}{2}(1-\frac{1}{p})}\parallel {\mathcal{G}}_{n,h}{\parallel }_p\sum _{j=n+1}^{\infty }{\int }_{{\mathbb{R}}^N}\left|g(jh,x)\right|dx\to 0,n\to \infty .\hfill \end{array}$$

Therefore, it is enough to show the following

$${\left(nh\right)}^{\frac{N}{2}(1-\frac{1}{p})}{∥h\sum _{j=1}^n({\mathcal{G}}_{n-j+1,h}\ast g(jh,·))(·)-h{\mathcal{G}}_{n,h}(·)\sum _{j=1}^n{\int }_{{\mathbb{R}}^N}g(jh,y)dy∥}_p\to 0,n\to \infty .$$

Ir order to prove the assertion, we fix $0<\delta <\frac{1}{10}.$ In particular, this implies that $0<\delta <{\displaystyle \frac{1}{5}}<{\displaystyle \frac{1}{2}}$ and

$$\frac{\delta }{1-\delta }<\frac{1}{4}.$$

Next, we decompose the set $\{1,2,3,\dots ,n\}\times {\mathbb{R}}^N$ into two parts

$${\Omega }_1:=\{1,2,\dots ,\lceil n\delta \rceil \}\times \{y\in {\mathbb{R}}^N:\left|y\right|\le {\left(\delta nh\right)}^{1/2}\},$$

$${\Omega }_2:=\{1,2,\dots ,n\}\times {\mathbb{R}}^N\backslash {\Omega }_1.$$

Let us start with the set ${\Omega }_1$. By the integral form of the Minkowski inequality, we obtain

$$\begin{array}{cc}\hfill & {∥{\sum \int }_{\begin{array}{c}(j,y)\in {\Omega }_1\end{array}}(h{\mathcal{G}}_{n-j+1,h}(·-y)-h{\mathcal{G}}_{n,h}(·))g(jh,y)dy∥}_p\hfill \\ \hfill & \le h{\sum \int }_{(j,y)\in {\Omega }_1}\parallel {\mathcal{G}}_{n-j+1,h}(·-y)-{\mathcal{G}}_{n,h}{(·)\parallel }_p\left|g(jh,y)\right|dy.\hfill \end{array}$$

Note that in this set, the following inequalities hold:

$$n\ge n-j+1\ge n(1-\delta )>\frac{n}{2},$$

(16)

where the second inequality follows from $\delta n-\lceil \delta n\rceil \ge -1.$ Now, when $(j,y)\in {\Omega }_1,$ we consider the following subsets over ${\mathbb{R}}^N$

$$A=\{x\in {\mathbb{R}}^N:|x-y|\le 2{\left(\delta nh\right)}^{1/2}\},B:=\{x\in {\mathbb{R}}^N{:|x-y|>2\left(\delta nh\right)}^{1/2}\},$$

and we write the p-norm over ${\Omega }_1$ in the following way

$$\begin{array}{cc}\hfill \parallel {\mathcal{G}}_{n-j+1,h}(·-y)-{\mathcal{G}}_{n,h}{(·)\parallel }_p& \le {\left({\int }_A{|{\mathcal{G}}_{n-j+1,h}(x-y)-{\mathcal{G}}_{n,h}\left(x\right)|}^{p}dx\right)}^{1/p}\hfill \\ \hfill & +{\left({\int }_B{|{\mathcal{G}}_{n-j+1,h}(x-y)-{\mathcal{G}}_{n,h}\left(x\right)|}^{p}dx\right)}^{1/p}.\hfill \end{array}$$

Let us estimate on ${\Omega }_1$ the part A of the p-norm. First, we write

$$\begin{array}{cc}\hfill {\left({\int }_A{|{\mathcal{G}}_{n-j+1,h}(x-y)-{\mathcal{G}}_{n,h}\left(x\right)|}^{p}dx\right)}^{1/p}& \le {\left({\int }_A{\left|{\mathcal{G}}_{n-j+1,h}(x-y)\right|}^{p}dx\right)}^{1/p}\hfill \\ \hfill & +{\left({\int }_A{\left|{\mathcal{G}}_{n,h}\left(x\right)\right|}^{p}dx\right)}^{1/p}\hfill \\ \hfill & =:I_1+I_2.\hfill \end{array}$$

For $(j,y)\in {\Omega }_1$ and $x\in A$, we have that

$$\begin{array}{c}\hfill \frac{{|x-y|}^2}{(n-j+1)h}\le \frac{4\delta }{(1-\delta )}<1.\end{array}$$

Since we want to estimate the solution for large values of n, we can assume that $n>N$. Thus, (16) implies that $n-j+1>n/2>N/2.$ It follows from Theorem 1 (i) that

$$|{\mathcal{G}}_{n-j+1,h}(x-y)|\le \frac{C}{{\left((n-j+1)h\right)}^{N/2}}.$$

Then,

$$\begin{array}{cc}\hfill {\left(nh\right)}^{\frac{N}{2}(1-\frac{1}{p})}h{I}_1& \le C\frac{{\left(nh\right)}^{\frac{N}{2}(1-\frac{1}{p})}h}{{\left((n-j+1)h\right)}^{N/2}}{\left({\int }_{A}dx\right)}^{1/p}\hfill \\ \hfill & =\frac{C{\left(nh\right)}^{\frac{N}{2}(1-\frac{1}{p})}h{\left(\delta nh\right)}^{N/2p}}{{\left((n-j+1)h\right)}^{N/2}}\le Ch{\delta }^{N/2p},\hfill \end{array}$$

where in the last inequality we have used (16). Analogously, for $(j,y)\in {\Omega }_1$ and $x\in A$, we have

$$\frac{{\left|x\right|}^2}{nh}\le \frac{{\left(\right|x-y|+|y\left|\right)}^2}{nh}\le 9\delta <1,$$

which implies that

$$|{\mathcal{G}}_{n,h}\left(x\right)|\le \frac{C}{{\left(nh\right)}^{N/2}}.$$

Therefore,

$$\begin{array}{c}\hfill {\left(nh\right)}^{\frac{N}{2}(1-\frac{1}{p})}h{I}_2\le Ch{\delta }^{N/2p}.\end{array}$$

Since ${\sum }_{j=1}^{\infty }{\parallel g(jh,·)\parallel }_1<\infty ,$ we get

$$\begin{array}{cc}\hfill & {\left(nh\right)}^{N/2(1-1/p)}h\sum {\int }_{(j,y)\in {\Omega }_1}{\left({\int }_A{|{\mathcal{G}}_{n-j+1,h}(x-y)-{\mathcal{G}}_{n,h}\left(x\right)|}^{p}dx\right)}^{1/p}\left|g(jh,y)\right|dy\hfill \\ \hfill & \le Ch{\delta }^{N/2p}\to 0,\delta \to 0.\hfill \end{array}$$

Now, we consider on ${\Omega }_1$ the part B of the p-norm. We write

$$\begin{array}{cc}\hfill {\left({\int }_B{|{\mathcal{G}}_{n-j+1,h}(x-y)-{\mathcal{G}}_{n,h}\left(x\right)|}^{p}dx\right)}^{1/p}& \le {\left({\int }_B{|{\mathcal{G}}_{n-j+1,h}(x-y)-{\mathcal{G}}_{n-j+1,h}\left(x\right)|}^{p}dx\right)}^{1/p}\hfill \\ \hfill & +{\left({\int }_B{|{\mathcal{G}}_{n-j+1,h}\left(x\right)-{\mathcal{G}}_{n,h}\left(x\right)|}^{p}dx\right)}^{1/p}\hfill \\ \hfill & =:I_3+I_4.\hfill \end{array}$$

First, let us estimate $I_3$. By mean value theorem, there exists $\tilde{x}$ between $x-y$ and x (x denote the integration variable) such that

$$I_3=\left|y\right|{\left({\int }_B{|\nabla {\mathcal{G}}_{n-j+1,h}\left(\tilde{x}\right)|}^{p}dx\right)}^{1/p}.$$

Since $\left|y\right|\le {\left(\delta nh\right)}^{1/2}<\frac{1}{2}|x-y|$, then

$$|\tilde{x}|\ge |x-y|-|\tilde{x}-(x-y)|\ge |x-y|-|y|\ge \frac{|x-y|}{2},$$

(17)

and

$$|\tilde{x}|\le |x-y|+|y|\le |x-y|+\frac{|x-y|}{2}=\frac{3}{2}|x-y|.$$

(18)

Equations (17) and (18) show that $|\tilde{x}|$ and $|x-y|$ are comparable. Furthermore, by (16) and (17), we obtain

$$\frac{|\tilde{x}|}{{\left((n-j+1)h\right)}^{1/2}}\ge \frac{|x-y|}{2{\left((n-j+1)h\right)}^{1/2}}>{\delta }^{1/2}.$$

(19)

Now, we will use the asymptotics of $|\nabla {\mathcal{G}}_{n-j+1,h}\left(\tilde{x}\right)|,$ so we divide $I_3$ in two parts, $I_{31}$ and $I_{32}$ depending on whether $\frac{|\tilde{x}|}{{\left((n-j+1)h\right)}^{1/2}}$ is less or greater than 1, respectively (we are assuming $\delta$ to be small enough).

In $I_{32}$, when $\frac{|\tilde{x}|}{{\left((n-j+1)h\right)}^{1/2}}\ge 1$, by (18) one obtains

$${\left((n-j+1)h\right)}^{1/2}\le |\tilde{x}|\le \frac{3}{2}|x-y|.$$

For this reason, the integration region in $I_{32}$ is contained in $\{x\in {\mathbb{R}}^N:\frac{2}{3}{\left((n-j+1)h\right)}^{1/2}\le |x-y\left|\right\}$. From Theorem 1 (ii), the fact that $\left|y\right|\le {\left(\delta nh\right)}^{1/2},$ (16) and (17), we have

$$\begin{array}{cc}\hfill I_{32}& \le C{\left(\delta nh\right)}^{1/2}{\left({\int }_{|x-y|\ge \frac{2}{3}{\left((n-j+1)h\right)}^{1/2}}{\left(\frac{(n-j+1)h}{|\tilde{x}{|}^{N+3}}\right)}^{p}dx\right)}^{1/p}\hfill \\ \hfill & \le C{\left(\delta nh\right)}^{1/2}{\left({\int }_{|x-y|\ge \frac{2}{3}{\left((n-j+1)h\right)}^{1/2}}{\left(\frac{nh}{{|x-y|}^{N+3}}\right)}^{p}dx\right)}^{1/p}\hfill \\ \hfill & =C{\delta }^{1/2}{\left(nh\right)}^{3/2}{\left((n-j+1)h\right)}^{N/\left(2p\right)-(N+3)/2}\hfill \\ \hfill & \le C{\delta }^{1/2}{\left(nh\right)}^{-N/2(1-1/p)}.\hfill \end{array}$$

Consequently,

$${\left(nh\right)}^{N/2(1-1/p)}h{I}_{32}\le Ch{\delta }^{1/2}.$$

For $I_{31},$ by (19) note that the set of integration is contained in $\{x\in {\mathbb{R}}^N:1\ge \frac{|x-y|}{2{\left((n-j+1)h\right)}^{1/2}}>{\delta }^{1/2}\}.$ Then, from Theorem 1 (ii) (by (16) we can take n large enough, $n>N+2,$ such that $n-j+1>\frac{N}{2}+1$), it follows

$$\begin{array}{cc}\hfill I_{31}& \le C{\left(\delta nh\right)}^{1/2}{\left({\int }_{{\delta }^{1/2}\le \frac{|x-y|}{{\left((n-j+1)h\right)}^{1/2}}\le 1}{\left(\frac{|\tilde{x}|}{{\left((n-j+1)h\right)}^{N/2+1}}\right)}^{p}dx\right)}^{1/p}\hfill \\ \hfill & \le C\frac{{\delta }^{1/2}{\left(nh\right)}^{1/2}}{{\left(nh\right)}^{N/2+1}}{\left({\int }_{{\delta }^{1/2}\le \frac{|x-y|}{{\left((n-j+1)h\right)}^{1/2}}\le 1}{|x-y|}^{p}dx\right)}^{1/p}\hfill \\ \hfill & \le C{\delta }^{1/2}{\left(nh\right)}^{-N/2(1-1/p)}{(1-{\delta }^{(N+p)/2})}^{1/p}\hfill \\ \hfill & \le C{\delta }^{1/2}{\left(nh\right)}^{-N/2(1-1/p)},\hfill \end{array}$$

which is equivalent to

$${\left(nh\right)}^{N/2(1-1/p)}h{I}_{31}\le Ch{\delta }^{1/2}.$$

Next, let us estimate $I_4$. From discrete mean value theorem (see Corollary 2 in [24]), there exist $\tilde{n}\in \{n-j+2,\dots ,n\}$ (whenever $j\ge 2$) and $C>0$ such that

$$I_4\le C(j-1)h{\left({\int }_B{|{\mathcal{G}}_{\tilde{n},h}\left(x\right)-{\mathcal{G}}_{\tilde{n}-1,h}\left(x\right)|}^{p}dx\right)}^p=C(j-1)h{\left({\int }_B{|\Delta {\mathcal{G}}_{\tilde{n},h}\left(x\right)|}^{p}dx\right)}^p.$$

(20)

Recall that in ${\Omega }_1$ we have $n-j+1\le \tilde{n}\le n,$ which implies by (16) that $nh(1-\delta )\le \tilde{n}h\le nh.$ Additionally, in ${\Omega }_1$ and B, we have

$$\left|x\right|=|x+y-y|\ge |x-y|-\left|y\right|\ge {\left(\delta nh\right)}^{1/2},$$

so

$$\tilde{z}:=\frac{\left|x\right|}{{\left(\tilde{n}h\right)}^{1/2}}\ge \frac{\left|x\right|}{{\left(nh\right)}^{1/2}}\ge \frac{{\left(\delta nh\right)}^{1/2}}{{\left(nh\right)}^{1/2}}={\delta }^{1/2},$$

and we have again two cases. We denote by $I_{41}$ and $I_{42}$ depending on whether $\tilde{z}\le 1$ or $\tilde{z}\ge 1$ on the right side of (20).

For $I_{41},$ since $\tilde{z}\le 1$ and $\left|x\right|\ge {\left(\delta nh\right)}^{1/2}$ the set of integration is contained in $\{x\in {\mathbb{R}}^N:{\left(\delta nh\right)}^{1/2}\le |x|\le {\left(nh\right)}^{1/2}\}.$ Then, from Theorem 1 (iii) (by (16) we can take n large enough, $n>N+2,$ such that $\tilde{n}\ge n-j+1>\frac{N}{2}+1$) and the fact that we are in ${\Omega }_1$, we have

$$\begin{array}{cc}\hfill I_{41}& \le C(j-1)h{\left({\int }_{{\left(\delta nh\right)}^{1/2}\le \left|x\right|\le {\left(nh\right)}^{1/2}}\frac{1}{{\left(\tilde{n}h\right)}^{(N/2+1)p}}dx\right)}^{1/p}\hfill \\ \hfill & \le \frac{C\delta nh}{{\left(nh(1-\delta )\right)}^{N/2+1}}{\left({\int }_{{\left(\delta nh\right)}^{1/2}\le \left|x\right|\le {\left(nh\right)}^{1/2}}dx\right)}^{1/p}\hfill \\ \hfill & =\frac{C\delta {(1-{\delta }^{N/2})}^{1/p}{\left(nh\right)}^{-N/2(1-1/p)}}{{(1-\delta )}^{N/2+1}}.\hfill \end{array}$$

Consequently,

$${\left(nh\right)}^{N/2(1-1/p)}h{I}_{41}\le \frac{Ch\delta }{{(1-\delta )}^{N/2+1}}.$$

For $I_{42}$, we have

$$1\le \tilde{z}=\frac{\left|x\right|}{{\left(\tilde{n}h\right)}^{1/2}}\le \frac{\left|x\right|}{{\left(nh(1-\delta )\right)}^{1/2}},$$

which implies that the set of integration is contained in $\{x\in {\mathbb{R}}^N:|x|\ge {\left(nh(1-\delta )\right)}^{1/2}\}.$ Then, by Theorem 1 (iii), we have

$$\begin{array}{cc}\hfill I_{42}& \le C(j-1)h{\left({\int }_{\left|x\right|\ge {\left((1-\delta )nh\right)}^{1/2}}\frac{1}{{\left|x\right|}^{(N+2)p}}dx\right)}^{1/p}\hfill \\ \hfill & =\frac{C\delta {\left(nh\right)}^{-N/2(1-1/p)}}{{(1-\delta )}^{N/2(1-1/p)+1}}.\hfill \end{array}$$

Consequently,

$${\left(nh\right)}^{1/2(1-1/p)}h{I}_{42}\le \frac{Ch\delta }{{(1-\delta )}^{N/2(1-1/p)+1}}.$$

Collecting all above terms over B, we obtain

$$\begin{array}{cc}\hfill & {\left(nh\right)}^{N/2(1-1/p)}h\sum {\int }_{(j,y)\in {\Omega }_1}{\left({\int }_B{|{\mathcal{G}}_{n-j+1,h}(x-y)-{\mathcal{G}}_{n,h}\left(x\right)|}^{p}dx\right)}^{1/p}\left|g(jh,y)\right|dy\hfill \\ \hfill & \le C{\delta }^{\eta }\sum _{j=1}^n{\int }_{{\mathbb{R}}^N}\left|g(jh,y)\right|dy\hfill \end{array}$$

for some positive number $\eta$. The upper bound tends to zero as $\delta \to 0$ uniformly in $nh$.

Now, we consider the set ${\Omega }_2$. Then,

$$\begin{array}{cc}\hfill & {\left(nh\right)}^{N/2(1-1/p)}h\sum {\int }_{(j,y)\in {\Omega }_2}\parallel {\mathcal{G}}_{n-j+1,h}(·-y)-{\mathcal{G}}_{n,h}{(·)\parallel }_p\left|g(jh,y)\right|dy\hfill \\ \hfill & \le {\left(nh\right)}^{N/2(1-1/p)}h\sum {\int }_{(j,y)\in {\Omega }_2}\parallel {\mathcal{G}}_{n-j+1,h}{(·-y)\parallel }_p\left|g(jh,y)\right|dy\hfill \\ \hfill & +{\left(nh\right)}^{N/2(1-1/p)}h\sum {\int }_{(j,y)\in {\Omega }_2}\parallel {\mathcal{G}}_{n,h}{\parallel }_p\left|g(jh,y)\right|dy\hfill \\ \hfill & =:I_5+I_6.\hfill \end{array}$$

By Theorem 2 (i) (the condition $p\in I_N$ implies $1>\frac{N}{2}(1-1/p)$) one gets

$$I_6\le C\sum {\int }_{(j,y)\in {\Omega }_2}\left|g(jh,y)\right|dy.$$

As $n\to \infty$, ${\Omega }_1\to \mathbb{N}\times {\mathbb{R}}^N$. This implies that ${\Omega }_2$ has measure zero, and since ${\sum }_{j=1}^{\infty }{\int }_{{\mathbb{R}}^N}\left|g(jh,y)\right|dy<\infty ,$ then $\sum {\int }_{(j,y)\in {\Omega }_2}\left|g(jh,y)\right|dy\to 0$ as $n\to \infty$. It follows that $I_6\to 0$ as $n\to \infty$.

For $I_5$, we have two possibilities: either $j\le \lceil \delta n\rceil$ or $j>\lceil \delta n\rceil$. Thus, we divide

$${\Omega }_2=\{1,\dots ,\lceil \delta n\rceil \}\times \{y\in {\mathbb{R}}^N{:\left|y\right|>\left(\delta nh\right)}^{1/2}\}\cup \{\lceil \delta n\rceil +1,\dots ,n\}\times {\mathbb{R}}^N.$$

Then,

$$\begin{array}{cc}\hfill I_5& \le {\left(nh\right)}^{N/2(1-1/p)}h\sum _{j=1}^{\lceil \delta n\rceil }{\int }_{{\left|y\right|>\left(\delta nh\right)}^{1/2}}\parallel {\mathcal{G}}_{n-j+1,h}{(·-y)\parallel }_p\left|g(jh,y)\right|dy\hfill \\ \hfill & +{\left(nh\right)}^{N/2(1-1/p)}h\sum _{j=\lceil \delta n\rceil +1}^n{\int }_{{\mathbb{R}}^N}\parallel {\mathcal{G}}_{n-j+1,h}{(·-y)\parallel }_p\left|g(jh,y)\right|dy\hfill \\ \hfill & =:I_{51}+I_{52}.\hfill \end{array}$$

Let us start with $I_{51}$. Recall that for $j\in \{1,\dots ,\lceil \delta n\rceil \}$ the expression (16) holds. Therefore, by Theorem 2 (i) (the condition $p\in I_N$ implies $1>\frac{N}{2}(1-1/p)$) we have that

$$\begin{array}{cc}\hfill I_{51}& \le Ch\sum _{j=1}^{\lceil \delta n\rceil }{\int }_{{\left|y\right|>\left(\delta nh\right)}^{1/2}}\left|g(jh,y)\right|dy\to 0\hfill \end{array}$$

as $n\to \infty .$

Next, for $I_{52},$ again by Theorem 2 (i), $\gamma >1$ and $\frac{N}{2}(1-1/p)\in [0,1)$ we obtain

$$\begin{array}{cc}\hfill I_{52}& \le C{\left(nh\right)}^{N/2(1-1/p)}h\sum _{j=\lceil \delta n\rceil +1}^n{\displaystyle \frac{1}{{\left((n-j+1)h\right)}^{\frac{N}{2}(1-1/p)}}}\frac{1}{j^{\gamma }}\hfill \\ \hfill & \le \frac{C{\left(nh\right)}^{N/2(1-1/p)}h}{{(\lceil \delta n\rceil +1)}^{\gamma }{h}^{\gamma }}\sum _{j=1}^{n-\lceil \delta n\rceil }\frac{1}{{\left(jh\right)}^{\frac{N}{2}(1-1/p)}}\hfill \\ \hfill & \le \frac{Ch{\left(nh\right)}^{N/2(1-1/p)}{(nh-\lceil \delta n\rceil h)}^{1-N/2(1-1/p)}}{{\left(\delta nh\right)}^{\gamma }}\to 0,n\to \infty .\hfill \end{array}$$

 □

6. Optimal ${\mathbf{L}}^{\mathbf{2}}$-Decay for Solutions

In this section, we prove that the decay rate of the solution $u_{\mathfrak{c}}$ of (4) given in Theorem 3 (i) is optimal.

Theorem 6.

Let $u_{\mathfrak{c}}$ be the solution of (4). Assume that $f\in L^1\left({\mathbb{R}}^N\right)\cap L^2\left({\mathbb{R}}^N\right)$ and ${\int }_{{\mathbb{R}}^N}f\left(x\right)dx\ne 0$. Then, there exist $c,C>0$ such that

$$\frac{c}{{\left(nh\right)}^{N/4}}\le {\parallel u_{\mathfrak{c}}(nh,·)\parallel }_2\le \frac{C}{{\left(nh\right)}^{N/4}},nh\ge 1.$$

Proof. 

It is cleat that if $f\in L^2\left({\mathbb{R}}^N\right),$ then $u_{\mathfrak{c}}(nh,·)\in L^2\left({\mathbb{R}}^N\right)$ for all $n\in \mathbb{N}.$ Let $\rho >0,$ we have by Proposition 1 (iii) that

$$\begin{array}{cc}\hfill \parallel u_{\mathfrak{c}}{(nh,·)\parallel }_2^2& =\parallel \mathcal{F}{u}_{\mathfrak{c}}{(n,·)\parallel }_2^2={\int }_{{\mathbb{R}}^N}|\mathcal{F}{\mathcal{G}}_{n,h}{\left(\xi \right)|}^2{\left|\mathcal{F}f\left(\xi \right)\right|}^{2}d\xi \hfill \\ \hfill & \ge {\int }_{\mathcal{B}(0,\rho )}\frac{1}{{(1+h|\xi |}^2{)}^{2n}}{\left|\mathcal{F}f\left(\xi \right)\right|}^{2}d\xi \hfill \\ \hfill & \ge \frac{1}{{(1+h|\rho |}^2{)}^{2n}}{\int }_{\mathcal{B}(0,\rho )}{\left|\mathcal{F}f\left(\xi \right)\right|}^{2}d\xi .\hfill \end{array}$$

(21)

By Plancherel Theorem and the Riemann–Lebesgue Lemma we have that $\mathcal{F}f\in C_0\left({\mathbb{R}}^N\right)\cap L^2\left({\mathbb{R}}^N\right)$. By the Lebesgue differentiation theorem, we may choose ${\rho }_0$ small enough such that

$$\frac{1}{{\rho }^N}{\int }_{\mathcal{B}(0,\rho )}{\left|\mathcal{F}f\left(\xi \right)\right|}^{2}d\xi \ge \frac{1}{2}{\left|\mathcal{F}\left(0\right)\right|}^{2}forall\rho \in (0,{\rho }_0].$$

Substituting the previous inequality in (21), we have that for all $\rho \in (0,{\rho }_0]$

$$\parallel u_{\mathfrak{c}}{(nh,·)\parallel }_2^2\ge \frac{{\rho }^N}{{2(1+h|\rho |}^2{)}^{2n}}{\left|\mathcal{F}\left(0\right)\right|}^2.$$

We choose $\rho :={\displaystyle \frac{{\rho }_0}{{\left(nh\right)}^{1/2}}}$. For large enough n, $nh\ge 1$ then $\rho$ belongs to $(0,{\rho }_0)$. Hence,

$$\begin{array}{cc}\hfill \frac{{\rho }^N}{{(1+h|\rho |}^2{)}^{2n}}& =\frac{{\rho }_0^N}{{\left(nh\right)}^{N/2}{\left(1+{\displaystyle \frac{{\rho }_0^2}{n}}\right)}^{2n}}\hfill \\ \hfill & \ge \frac{{\rho }_0^N}{{\left(nh\right)}^{N/2}{e}^{2{\rho }_0^2}}=\frac{c}{{\left(nh\right)}^{N/2}},nh\ge 1,\hfill \end{array}$$

and then we get the first assertion of the result.

Next, let us prove the upper bound. By Plancherel’s Theorem and the Riemann–Lebesgue Lemma, we have

$$\begin{array}{cc}\hfill \parallel u_{\mathfrak{c}}{(nh,·)\parallel }_2^2& ={\int }_{{\mathbb{R}}^N}\frac{1}{{(1+h|\xi |}^2{)}^{2n}}{\left|\mathcal{F}f\left(\xi \right)\right|}^{2}d\xi \hfill \\ \hfill & \le {\parallel \mathcal{F}f\parallel }_{\infty }^2{\int }_{{\mathbb{R}}^N}\frac{1}{{(1+h|\xi |}^2{)}^{2n}}d\xi \le {\parallel f\parallel }_1^2{\int }_{{\mathbb{R}}^N}\frac{1}{{(1+nh|\xi |}^2{)}^2}d\xi \hfill \\ \hfill & =\frac{{C\parallel f\parallel }_1^2}{{\left(nh\right)}^{N/2}}{\int }_{{\mathbb{R}}^N}\frac{1}{{(1+|\xi |}^2{)}^2}d\xi =\frac{C}{{\left(nh\right)}^{N/2}}.\hfill \end{array}$$

 □