Variable Neighborhood Search Algorithms to Solve the Electric Vehicle Routing Problem with Simultaneous Pickup and Delivery
Abstract
:1. Introduction
- An integer programming model for EVRP-SPD is developed, which is the first time it has been studied in the literature.
- A modified Clark and Wright sparse algorithm is proposed to obtain a feasible initial solution to the problem.
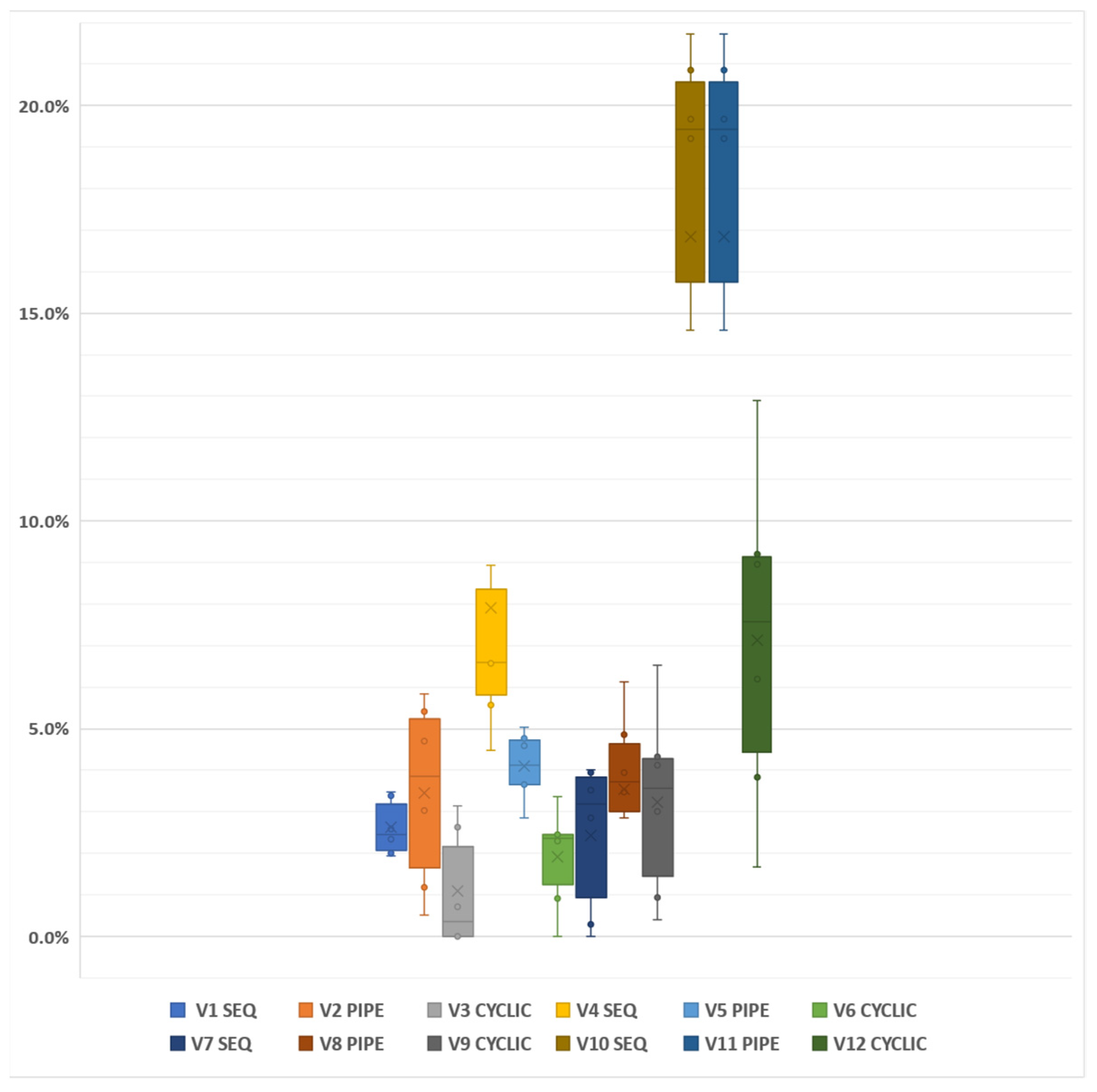
- Different neighborhood structures are extensively tested on the benchmark instances, and the performance of the structures in terms of algorithm speed and efficiency are shown.
- Several VNS variants are investigated, and the results are compared in detail.
2. Literature Review
3. Mathematical Model
| Notation and Sets |
| Parameters |
| Decision Variables |
4. The Proposed Solution Methodology
| Algorithm 1 Modified CW Savings Algorithm for EVRP-SPD |
| 1: Start 2: while There are customers not added to the routes do 3: Create back-forth (BF) tours (depot-customer-depot) 4: if EV charge level insufficient to complete the tour then 5: Add the CS with the lowest cost to the tour 6: if energy constraint is not met then 7: Cancel the tour and remove from tour list 8: Add customer to the list of unvisited customers 9: else 10: Add the tour to the tour list 11: end if 12: else 13: Add the BF tour to the tour list 14: end if 15: end while 16: Create savings list by computing the savings 17: Sort the savings in descending order 18: while the savings list is not empty do 19: Select two BF tours with largest savings 20: if customer(s) have already been added to the current tours then 21: Cancel the merge 22: Remove the relevant customer pair from the savings list 23: else 24: Check remaining capacity of EV 25: if capacity constraint is not met then 26: Cancel the merge 27: Remove the relevant customer pair from the savings list 28: else 29: Check remaining charge level of EV 30: if energy constraint is not met then 31: Add CS to the tour with minimum cost 32: if energy constraint is not met then 33: Cancel the merge 34: Remove the relevant customer pair from the savings list 35: else 36: Merge selected BF tours 37: Update the tour list 38: end if 39: else 40: Merge selected BF tours 41: Update the tour list 42: end if 43: end if 44: end if 45: Update the savings list based on new tour list 46: end while 47: Add customers from the list of unvisited customers to existing tours using the greedy insertion operator 48: End |
| Algorithm 2 VNS Framework |
| 1: Function VNS Variants () 2: Initial Solution 3: while the stopping condition is not fulfilled do 4: 5: while do 6: Shake (); 7: Local Search (); 8: Neighborhood Change: Sequential or Pipe or Cyclic (); 9: if then 10: ; ; 11: end if 12: end while 13: end while 14: Return |
4.1. Construction of the Initial Solution
4.2. Variable Neighborhood Search
4.3. Neighborhood Structures
5. Numerical Investigations
5.1. Implementation
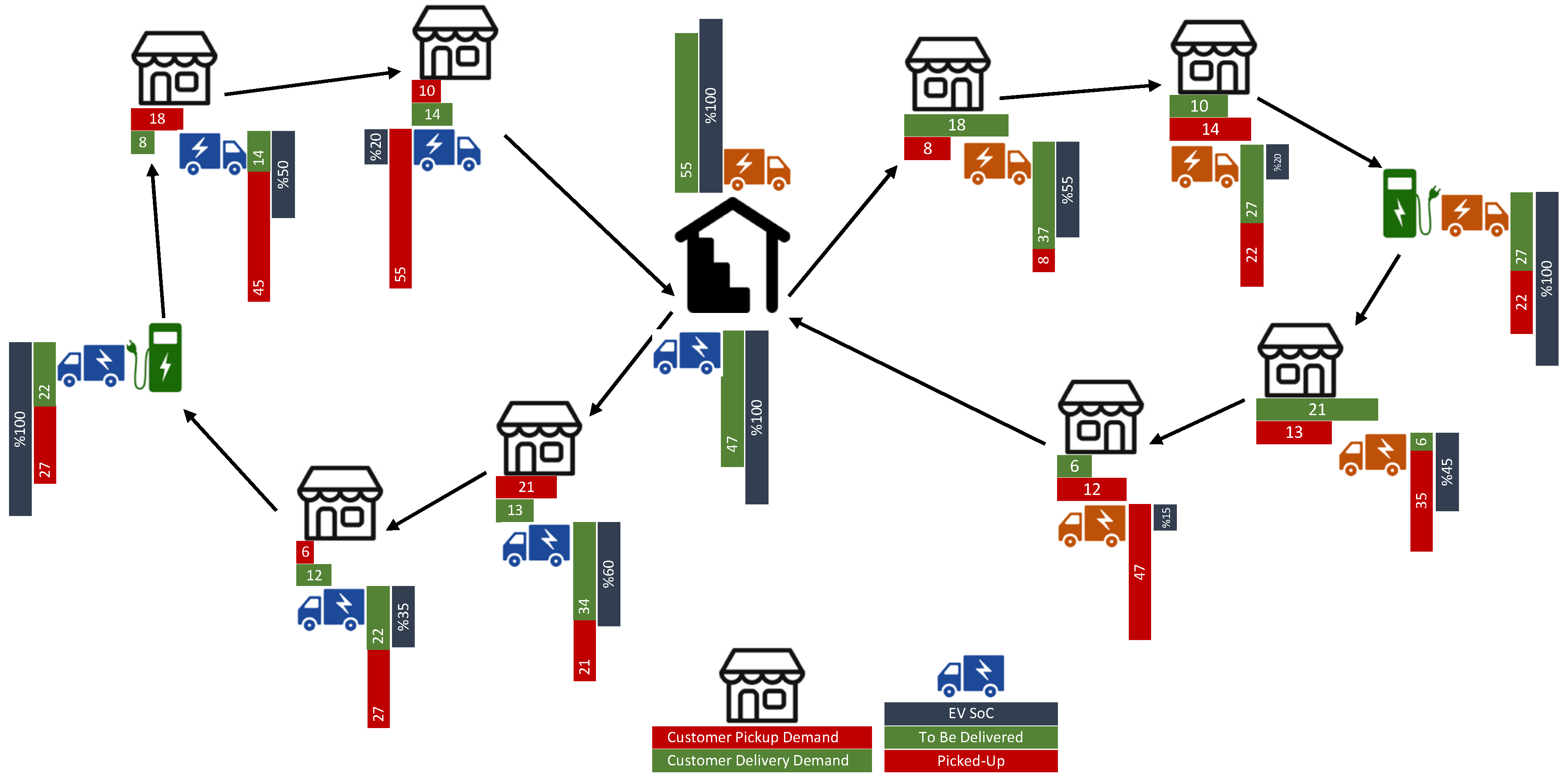
5.2. Generation of EVRP-SPD Instances
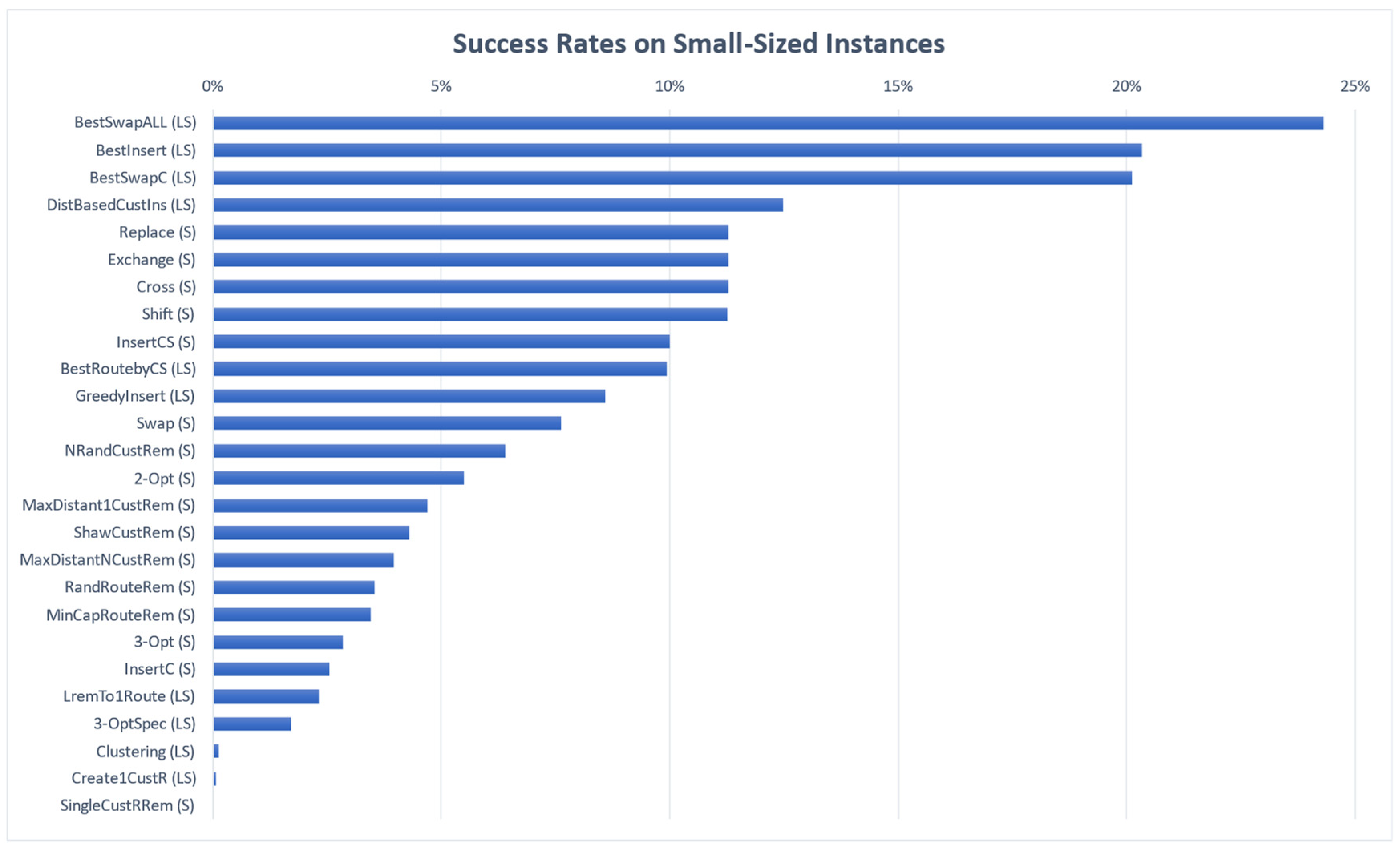
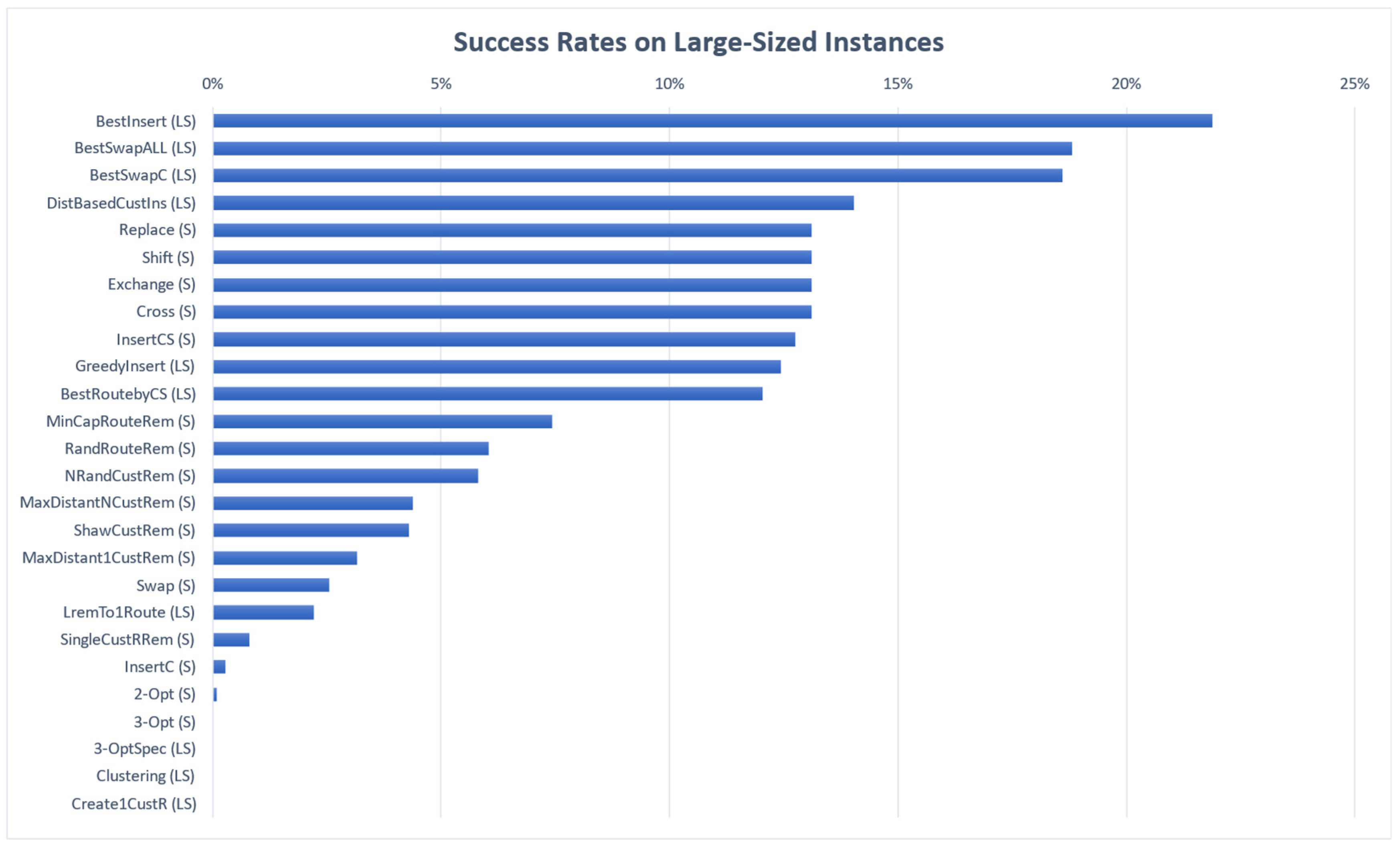
5.3. Neighborhood Structure Tests on Instances
| Algorithm 3 Neighborhood Structure (NS) Performance Test Algorithm |
| 1: Function Fair Performance Comparison 2: Select the set of NS for Shake Phase () 3: Select the set of NS for Local Search Phase () 4: // Initialize No of Success for 5: // Initialize No of Success for 6: // Initialize No of Total Usage for 7: // Initialize No of Total Usage for 8: : Average Success Rate of 9: : Average Success Rate of 10: Initial Solution by Modified CW Savings 11: while the stopping condition is not fulfilled do 12: ; 13: for do 14: Shake (); 15: ; 16: if then 17: ; 18: end if 19: if then 20: ; 21: end if 22: for do 23: Local Search (); 24: ; 25: if then 26: ; 27: end if 28: if then 29: ; 30: end if 31: end for 32: end for 33: end while 34: for do 35: ; 36: end for 37: for do 38: ; 39: end for 40: Return |
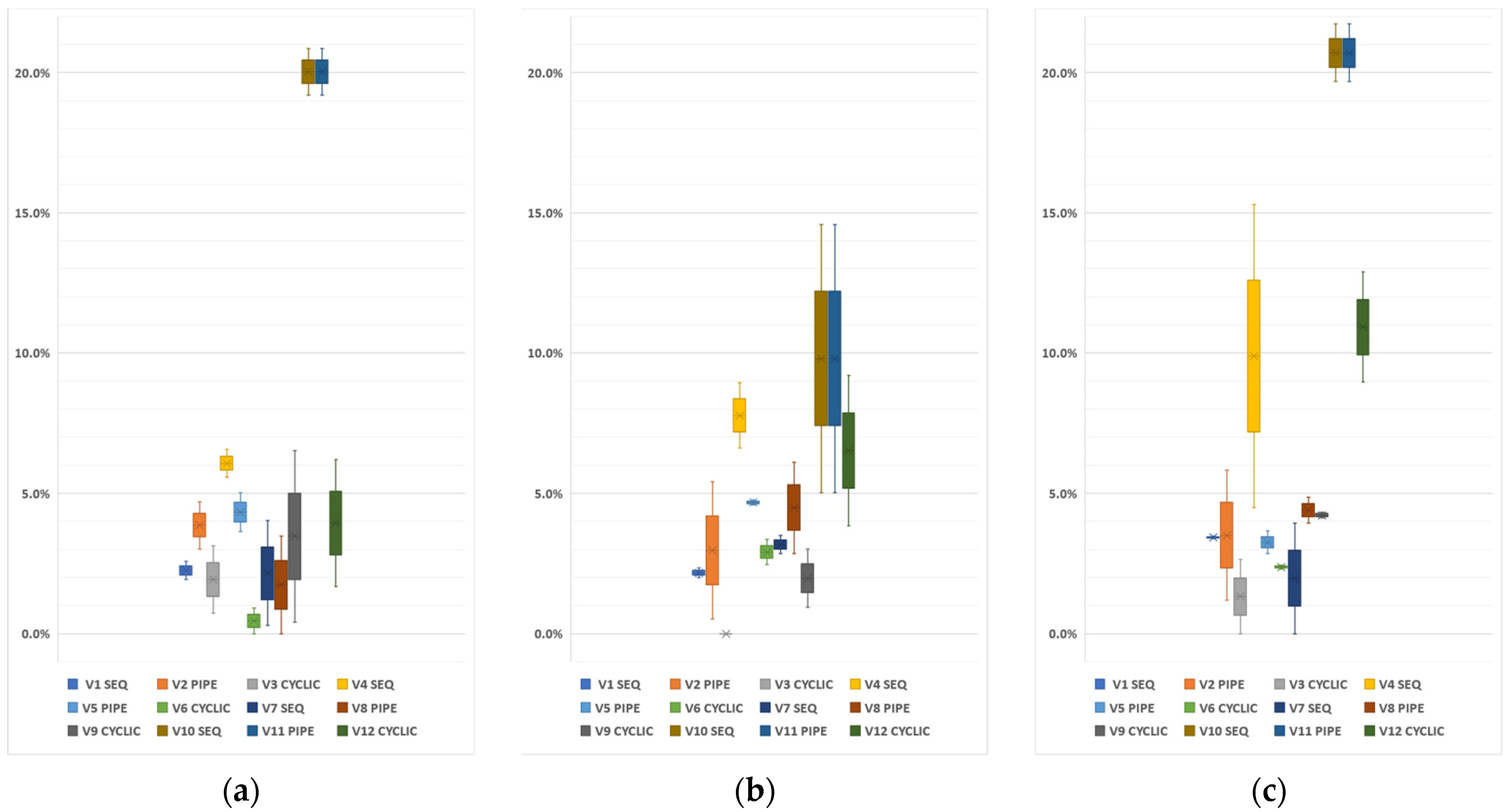
5.4. Numerical Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Schneider, M.; Stenger, A.; Goeke, D. The Electric Vehicle-Routing Problem with Time Windows and Recharging Stations. Transp. Sci. 2014, 48, 500–520. [Google Scholar] [CrossRef]
- Salhi, S.; Nagy, G. A cluster insertion heuristic for single and multiple depot vehicle routing problems with backhauling. J. Oper. Res. Soc. 1999, 50, 1034–1042. [Google Scholar] [CrossRef]
- Dantzig, G.B.; Ramser, J.H. The Truck Dispatching Problem. Manag. Sci. 1959, 6, 80–91. [Google Scholar] [CrossRef]
- Afroditi, A.; Boile, M.; Theofanis, S.; Sdoukopoulos, E.; Margaritis, D. Electric Vehicle Routing Problem with Industry Constraints: Trends and Insights for Future Research. Transp. Res. Procedia 2014, 3, 452–459. [Google Scholar] [CrossRef]
- Schiffer, M.; Walther, G. The electric location routing problem with time windows and partial recharging. Eur. J. Oper. Res. 2017, 260, 995–1013. [Google Scholar] [CrossRef]
- Felipe, Á.; Ortuño, M.T.; Righini, G.; Tirado, G. A heuristic approach for the green vehicle routing problem with multiple technologies and partial recharges. Transp. Res. Part E Logist. Transp. Rev. 2014, 71, 111–128. [Google Scholar] [CrossRef]
- Bruglieri, M.; Pezzella, F.; Pisacane, O.; Suraci, S. A Variable Neighborhood Search Branching for the Electric Vehicle Routing Problem with Time Windows. Electron. Notes Discret. Math. 2015, 47, 221–228. [Google Scholar] [CrossRef]
- Keskin, M.; Catay, B. Partial recharge strategies for the electric vehicle routing problem with time windows. Transp. Res. Part C-Emerg. Technol. 2016, 65, 111–127. [Google Scholar] [CrossRef]
- Desaulniers, G.; Errico, F.; Irnich, S.; Schneider, M. Exact Algorithms for Electric Vehicle-Routing Problems with Time Windows. Oper. Res. 2016, 64, 1388–1405. [Google Scholar] [CrossRef]
- Montoya, A.; Gueret, C.; Mendoza, J.E.; Villegas, J.G. The electric vehicle routing problem with nonlinear charging function. Transp. Res. B Methodol. 2017, 103, 87–110. [Google Scholar] [CrossRef] [Green Version]
- Lin, J.; Zhou, W.; Wolfson, O. Electric Vehicle Routing Problem. Transp. Res. Procedia 2016, 12, 508–521. [Google Scholar] [CrossRef]
- Erdoĝan, S.; Miller-Hooks, E. A Green Vehicle Routing Problem. Transp. Res. Part E Logist. Transp. Rev. 2012, 48, 100–114. [Google Scholar] [CrossRef]
- Kancharla, S.R.; Ramadurai, G. Electric vehicle routing problem with non-linear charging and load-dependent discharging. Expert Syst. Appl. 2020, 160, 113714. [Google Scholar] [CrossRef]
- Strehler, M.; Merting, S.; Schwan, C. Energy-efficient shortest routes for electric and hybrid vehicles. Transp. Res. B Methodol. 2017, 103, 111–135. [Google Scholar] [CrossRef]
- Froger, A.; Mendoza, J.E.; Jabali, O.; Laporte, G. Improved formulations and algorithmic components for the electric vehicle routing problem with nonlinear charging functions. Comput. Oper. Res. 2019, 104, 256–294. [Google Scholar] [CrossRef]
- Keskin, M.; Laporte, G.; Catay, B. Electric Vehicle Routing Problem with Time-Dependent Waiting Times at Recharging Stations. Comput. Oper. Res. 2019, 107, 77–94. [Google Scholar] [CrossRef]
- Koç, Ç.; Jabali, O.; Mendoza, J.E.; Laporte, G. The electric vehicle routing problem with shared charging stations. Int. Trans. Oper. Res. 2019, 26, 1211–1243. [Google Scholar] [CrossRef]
- Goeke, D.; Schneider, M. Routing a mixed fleet of electric and conventional vehicles. Eur. J. Oper. Res. 2015, 245, 81–99. [Google Scholar] [CrossRef]
- Hiermann, G.; Puchinger, J.; Ropke, S.; Hartl, R.F. The Electric Fleet Size and Mix Vehicle Routing Problem with Time Windows and Recharging Stations. Eur. J. Oper. Res. 2016, 252, 995–1018. [Google Scholar] [CrossRef]
- Hiermann, G.; Hartl, R.F.; Puchinger, J.; Vidal, T. Routing a mix of conventional, plug-in hybrid, and electric vehicles. Eur. J. Oper. Res. 2019, 272, 235–248. [Google Scholar] [CrossRef] [Green Version]
- Lu, J.; Chen, Y.N.; Hao, J.K.; He, R.J. The Time-dependent Electric Vehicle Routing Problem: Model and solution. Expert Syst. Appl. 2020, 161, 113593. [Google Scholar] [CrossRef]
- Yang, J.; Sun, H. Battery swap station location-routing problem with capacitated electric vehicles. Comput. Oper. Res. 2015, 55, 217–232. [Google Scholar] [CrossRef]
- Li-Ying, W.; Yuan-Bin, S. Multiple charging station location-routing problem with time window of electric vehicle. J. Eng. Sci. Technol. Rev. 2015, 8, 190–201. [Google Scholar] [CrossRef]
- Hof, J.; Schneider, M.; Goeke, D. Solving the battery swap station location-routing problem with capacitated electric vehicles using an AVNS algorithm for vehicle-routing problems with intermediate stops. Transport. Res. B Methodol. 2017, 97, 102–112. [Google Scholar] [CrossRef]
- Gatica, G.; Ahumada, G.; Escobar, J.W.; Linfati, R. Efficient Heuristic Algorithms for Location of Charging Stations in Electric Vehicle Routing Problems. Stud. Inform. Control 2018, 27, 73–82. [Google Scholar] [CrossRef]
- Zhang, S.; Chen, M.Z.; Zhang, W.Y. A novel location-routing problem in electric vehicle transportation with stochastic demands. J. Clean. Prod. 2019, 221, 567–581. [Google Scholar] [CrossRef]
- Paz, J.C.; Granada-Echeverri, M.; Escobar, J.W. The multi-depot electric vehicle location routing problem with time windows. Int. J. Ind. Eng. Comput. 2018, 9, 123–136. [Google Scholar] [CrossRef]
- Arias, A.; Sanchez, J.D.; Granada, M. Integrated planning of electric vehicles routing and charging stations location considering transportation networks and power distribution systems. Int. J. Ind. Eng. Comput. 2018, 9, 535–550. [Google Scholar] [CrossRef]
- Chen, Y.; Li, D.; Zhang, Z.; Wahab, M.I.M.; Jiang, Y. Solving the battery swap station location-routing problem with a mixed fleet of electric and conventional vehicles using a heuristic branch-and-price algorithm with an adaptive selection scheme. Expert Syst. Appl. 2021, 186, 115683. [Google Scholar] [CrossRef]
- Çalık, H.; Oulamara, A.; Prodhon, C.; Salhi, S. The electric location-routing problem with heterogeneous fleet: Formulation and Benders decomposition approach. Comput. Oper. Res. 2021, 131, 105251. [Google Scholar] [CrossRef]
- Zhao, M.T.; Lu, Y.W. A Heuristic Approach for a Real-World Electric Vehicle Routing Problem. Algorithms 2019, 12, 45. [Google Scholar] [CrossRef]
- Grandinetti, L.; Guerriero, F.; Pezzella, F.; Pisacane, O. A pick-up and delivery problem with time windows by electric vehicles. Int. J. Product. Qual. Manag. 2016, 18, 403–423. [Google Scholar] [CrossRef]
- Yang, S.; Ning, L.; Tong, L.C.; Shang, P. Optimizing electric vehicle routing problems with mixed backhauls and recharging strategies in multi-dimensional representation network. Expert Syst. Appl. 2021, 176, 114804. [Google Scholar] [CrossRef]
- Goeke, D. Granular tabu search for the pickup and delivery problem with time windows and electric vehicles. Eur. J. Oper. Res. 2019, 278, 821–836. [Google Scholar] [CrossRef]
- Ahmadi, S.; Tack, G.; Harabor, D.; Kilby, P. Vehicle Dynamics in Pickup-and-Delivery Problems Using Electric Vehicles. 2021. Available online: https://drops.dagstuhl.de/opus/volltexte/2021/15302/ (accessed on 6 April 2022).
- Ghobadi, A.; Tavakkoli Moghadam, R.; Fallah, M.; Kazemipoor, H. Multi-depot electric vehicle routing problem with fuzzy time windows and pickup/delivery constraints. J. Appl. Res. Ind. Eng. 2021, 8, 1–18. [Google Scholar]
- Soysal, M.; Cimen, M.; Belbag, S. Pickup and delivery with electric vehicles under stochastic battery depletion. Comput. Ind. Eng. 2020, 146, 106512. [Google Scholar] [CrossRef]
- Nolz, P.C.; Absi, N.; Feillet, D.; Seragiotto, C. The consistent electric-Vehicle routing problem with backhauls and charging management. Eur. J. Oper. Res. 2022, 302, 700–716. [Google Scholar] [CrossRef]
- Mladenović, N.; Hansen, P. Variable neighborhood search. Comput. Oper. Res. 1997, 24, 1097–1100. [Google Scholar] [CrossRef]
- Bräysy, O. A Reactive Variable Neighborhood Search for the Vehicle-Routing Problem with Time Windows. INFORMS J. Comput. 2003, 15, 347–368. [Google Scholar] [CrossRef]
- Hemmelmayr, V.C.; Doerner, K.F.; Hartl, R.F. A variable neighborhood search heuristic for periodic routing problems. Eur. J. Oper. Res. 2009, 195, 791–802. [Google Scholar] [CrossRef]
- Polat, O.; Kalayci, C.B.; Kulak, O.; Günther, H.-O. A perturbation based variable neighborhood search heuristic for solving the Vehicle Routing Problem with Simultaneous Pickup and Delivery with Time Limit. Eur. J. Oper. Res. 2015, 242, 369–382. [Google Scholar] [CrossRef]
- Schneider, M.; Stenger, A.; Hof, J. An adaptive VNS algorithm for vehicle routing problems with intermediate stops. OR Spectr. 2015, 37, 353–387. [Google Scholar] [CrossRef]
- Zhu, X.N.; Yan, R.; Huang, Z.C.; Wei, W.C.; Yang, J.Q.; Kudratova, S. Logistic Optimization for Multi Depots Loading Capacitated Electric Vehicle Routing Problem From Low Carbon Perspective. IEEE Access 2020, 8, 31934–31947. [Google Scholar] [CrossRef]
- Paul, A.; Kumar, R.S.; Rout, C.; Goswami, A. A bi-objective two-echelon pollution routing problem with simultaneous pickup and delivery under multiple time windows constraint. OPSEARCH 2021, 58, 962–993. [Google Scholar] [CrossRef]
- Clarke, G.; Wright, J.W. Scheduling of vehicles from a central depot to a number of delivery points. Oper. Res. 1964, 12, 568–581. [Google Scholar] [CrossRef]
- Li, L.; Li, T.; Wang, K.; Gao, S.; Chen, Z.; Wang, L. Heterogeneous fleet electric vehicle routing optimization for logistic distribution with time windows and simultaneous pick-up and delivery service. In Proceedings of the 16th International Conference on Service Systems and Service Management (ICSSSM), Shenzhen, China, 13–15 July 2019. [Google Scholar]
- Salhi, S.; Imran, A.; Wassan, N.A. The multi-depot vehicle routing problem with heterogeneous vehicle fleet: Formulation and a variable neighborhood search implementation. Comput. Oper. Res. 2014, 52, 315–325. [Google Scholar] [CrossRef]
- Wang, L.; Gao, S.; Wang, K.; Li, T.; Li, L.; Chen, Z.Y. Time-Dependent Electric Vehicle Routing Problem with Time Windows and Path Flexibility. J. Adv. Transp. 2020, 2020, 19. [Google Scholar] [CrossRef]
- Hansen, P.; Mladenovic, N.; Todosijevic, R.; Hanafi, S. Variable neighborhood search: Basics and variants. Euro J. Comput. Optim. 2017, 5, 423–454. [Google Scholar] [CrossRef]
- Hansen, P.; Mladenovic, N. Variable neighborhood search: Principles and applications. Eur. J. Oper. Res. 2001, 130, 449–467. [Google Scholar] [CrossRef]
- Hansen, P.; Mladenović, N. Developments of Variable Neighborhood Search. In Essays and Surveys in Metaheuristics; Springer: Berlin/Heidelberg, Germany, 2002; pp. 415–439. [Google Scholar]
- Hansen, P.; Mladenović, N.; Brimberg, J.; Pérez, J.A.M. Variable Neighborhood Search. In Handbook of Metaheuristics; Springer: Berlin/Heidelberg, Germany, 2019; pp. 57–97. [Google Scholar]
- Marinho Diana, R.O.; de Souza, S.R. Analysis of variable neighborhood descent as a local search operator for total weighted tardiness problem on unrelated parallel machines. Comput. Oper. Res. 2020, 117, 104886. [Google Scholar] [CrossRef]
- Mladenović, N.; Dražić, M.; Kovačevic-Vujčić, V.; Čangalović, M. General variable neighborhood search for the continuous optimization. Eur. J. Oper. Res. 2008, 191, 753–770. [Google Scholar] [CrossRef]
- Todosijević, R.; Benmansour, R.; Hanafi, S.; Mladenović, N.; Artiba, A. Nested general variable neighborhood search for the periodic maintenance problem. Eur. J. Oper. Res. 2016, 252, 385–396. [Google Scholar] [CrossRef]
- Kramer, A.; Subramanian, A. A unified heuristic and an annotated bibliography for a large class of earliness–tardiness scheduling problems. J. Sched. 2019, 22, 21–57. [Google Scholar] [CrossRef] [Green Version]
| Paper | SPD | PDP | TW | PD | BSS | MD | DM | ECM | OCM | TM | HEF | PC | CF |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Grandinetti, Guerriero, Pezzella, and Pisacane [32] | ✓ | ✓ | ✓ | ✓ | L | ||||||||
| Lin, Zhou, and Wolfson [11] | ✓ | ✓ | ✓ | ✓ | L | ||||||||
| Goeke [34] | ✓ | ✓ | ✓ | ✓ | L | ||||||||
| Zhao, and Lu [31] | ✓ | ✓ | ✓ | ✓ | ✓ | FT | |||||||
| Soysal, Cimen, and Belbag [37] | ✓ | ✓ | ✓ | ||||||||||
| Ahmadi, Tack, Harabor, and Kilby [35] | ✓ | ✓ | ✓ | ✓ | NL | ||||||||
| Ghobadi, Tavakkoli Moghadam, Fallah, and Kazemipoor [36] | ✓ | ✓ | ✓ | ✓ | FT | ||||||||
| Yang, Ning, Tong, and Shang [33] | ✓ | ✓ | ✓ | ✓ | ✓ | L | |||||||
| Nolz, Absi, Feillet, and Seragiotto [38] | ✓ | ✓ | ✓ | L |
| NCS | BVNS | GVNS | RVNS | RNDVNS | NVNS |
|---|---|---|---|---|---|
| Sequential | (v4) | - | (v1) | (v7) | (v10) |
| Pipe | - | (v5) | (v2) | (v8) | (v11) |
| Cyclic | - | (v6) | (v3) | (v9) | (v12) |
| Name | Applied to | Name | Applied to | ||
|---|---|---|---|---|---|
| Shaking Step | C | CS | Local Search Step | C | CS |
| Swap | ✓ | Best Swap Customer | ✓ | ||
| 2-Opt | ✓ | Best Swap All | ✓ | ✓ | |
| 3-Opt | ✓ | ✓ | Best Insert | ✓ | |
| Insert Customer (C) | ✓ | Best Reverse Route | ✓ | ✓ | |
| Insert Charging Station (CS) | ✓ | ||||
| Replace | ✓ | ||||
| Cross | ✓ | ||||
| Exchange | ✓ | ||||
| Shift | ✓ | ||||
| Shaking Step | Description | C | CS | ||
| Shaw Customer Removal | SeedC (Random), C (Similarity) | ✓ | |||
| Maximum Distant N Customer Removal | N (Random), C (Distance) | ✓ | |||
| N Random Customer Removal | N (Random), C (Random) | ✓ | |||
| Minimum Capacity Route Removal | R (Min Cap) | ✓ | ✓ | ||
| Random Route Removal | R (Random) | ✓ | ✓ | ||
| Maximum Distant One Customer Removal | C (Distance) | ✓ | |||
| Local Search Step | C | CS | |||
| Distance Base Insertion | Distance Change (Calc by Whole Route) | ✓ | |||
| Greedy Customer Insert | Distance Change (Calc by Pred. and Succ. Nodes) | ✓ | |||
| Create a Route from List of Removed | Creates Routes from Single Customers that Cannot be Added to the Same Route | ✓ | |||
| Small-Sized Instances | Large-Sized Instances |
|---|---|
| Shake | Shake |
| Replace | Replace |
| Exchange | Shift |
| Cross | Exchange |
| Shift | Cross |
| InsertCS | InsertCS |
| Swap | MinCapRouteRem |
| NRandCustRem | RandRouteRem |
| 2-Opt | NRandCustRem |
| MaxDistant1CustRem | MaxDistantNCustRem |
| ShawCustRem | ShawCustRem |
| MaxDistantNCustRem | MaxDistant1CustRem |
| RandRouteRem | Swap |
| MinCapRouteRem | SingleCustRRem |
| 3-Opt | InsertC |
| InsertC | |
| Local Search | Local Search |
| BestSwapALL | BestInsert |
| BestInsert | BestSwapALL |
| BestSwapC | BestSwapC |
| BestRoutebyCS | BestRoutebyCS |
| DistBasedCustIns | DistBasedCustIns |
| GreedyInsert | GreedyInsert |
| LremTo1Route | LremTo1Route |
| Reduced VNS | Basic VNS | General VNS | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CPLEX | V1 Seq | V2 Pipe | V3 Cyclic | V4 Seq | V5 Pipe | V6 Cyclic | |||||||||||||||
| Instance | |||||||||||||||||||||
| C101C5 | 208.9 | 1.35 | 0% | 208.9 | 0.05 | 0.00% | 208.9 | 0.03 | 0.00% | 208.9 | 0.05 | 0.00% | 208.9 | 0.16 | 0.00% | 208.9 | 0.16 | 0.00% | 208.9 | 0.13 | 0.00% |
| C103C5 | 154.5 | 1.2 | 0% | 154.5 | 0.17 | 0.00% | 154.5 | 0.17 | 0.00% | 154.5 | 0.2 | 0.00% | 154.5 | 0.7 | 0.00% | 154.5 | 0.34 | 0.00% | 154.5 | 0.36 | 0.00% |
| C206C5 | 201.55 | 1.92 | 0% | 201.55 | 0.03 | 0.00% | 201.55 | 0.03 | 0.00% | 201.55 | 0.03 | 0.00% | 201.55 | 0.08 | 0.00% | 201.55 | 0.06 | 0.00% | 201.55 | 0.08 | 0.00% |
| C208C5 | 158.48 | 1.34 | 0% | 158.48 | 0.06 | 0.00% | 158.48 | 0.08 | 0.00% | 158.48 | 0.08 | 0.00% | 158.48 | 0.06 | 0.00% | 158.48 | 0.06 | 0.00% | 158.48 | 0.09 | 0.00% |
| R104C5 * | 136.69 | 1.75 | 0% | 136.69 | 0 | - | 136.69 | 0 | - | 136.69 | 0 | - | 136.69 | 0 | - | 136.69 | 0 | - | 136.69 | 0 | - |
| R105C5 * | 139.48 | 1.23 | 0% | 139.48 | 0 | - | 139.48 | 0 | - | 139.48 | 0 | - | 139.48 | 0 | - | 139.48 | 0 | - | 139.48 | 0 | - |
| R202C5 | 128.78 | 1.29 | 0% | 128.78 | 1.73 | 0.00% | 128.78 | 0.23 | 0.00% | 128.78 | 0.33 | 0.00% | 128.78 | 0.75 | 0.00% | 128.78 | 0.36 | 0.00% | 128.78 | 0.33 | 0.00% |
| R203C5 | 179.06 | 1.37 | 0% | 179.06 | 0.22 | 0.00% | 179.06 | 0.2 | 0.00% | 179.06 | 0.2 | 0.00% | 179.06 | 16.36 | 0.00% | 179.06 | 6.14 | 0.00% | 179.06 | 6.14 | 0.00% |
| RC105C5 | 208.43 | 1.89 | 0% | 208.43 | 0.13 | 0.00% | 208.43 | 0.13 | 0.00% | 208.43 | 0.23 | 0.00% | 208.43 | 0.75 | 0.00% | 208.43 | 0.41 | 0.00% | 208.43 | 0.34 | 0.00% |
| RC108C5 | 211.53 | 1.36 | 0% | 211.53 | 0.25 | 0.00% | 211.53 | 0.23 | 0.00% | 211.53 | 0.22 | 0.00% | 211.53 | 0.83 | 0.00% | 211.53 | 0.41 | 0.00% | 211.53 | 0.39 | 0.00% |
| RC204C5 | 176.39 | 2.54 | 0% | 176.39 | 3.17 | 0.00% | 179.16 | 1.36 | 1.60% | 176.39 | 0.2 | 0.00% | 179.16 | 1.13 | 1.60% | 179.16 | 0.52 | 1.60% | 179.16 | 0.52 | 1.60% |
| RC208C5 | 167.98 | 2.29 | 0% | 167.98 | 0.02 | 0.00% | 167.98 | 0.02 | 0.00% | 167.98 | 0.02 | 0.00% | 167.98 | 0.06 | 0.00% | 167.98 | 0.05 | 0.00% | 167.98 | 0.05 | 0.00% |
| C101C10 | 260.01 | 4.85 | 0% | 260.01 | 5.67 | 0.00% | 260.01 | 3.13 | 0.00% | 260.01 | 7.36 | 0.00% | 265.75 | 9.52 | 2.20% | 260.01 | 13.96 | 0.00% | 260.01 | 19.95 | 0.00% |
| C104C10 | 239.13 | 3.39 | 0% | 239.13 | 4.98 | 0.00% | 239.13 | 3.71 | 0.00% | 239.13 | 1.53 | 0.00% | 239.13 | 17.08 | 0.00% | 239.13 | 9.12 | 0.00% | 239.13 | 9.42 | 0.00% |
| C202C10 | 214.96 | 4.12 | 0% | 214.96 | 7.2 | 0.00% | 214.96 | 3.57 | 0.00% | 214.96 | 8.73 | 0.00% | 214.96 | 10.72 | 0.00% | 214.96 | 6.03 | 0.00% | 214.96 | 4.54 | 0.00% |
| C205C10 | 224.78 | 4.45 | 0% | 227.08 | 0.79 | 1.00% | 227.08 | 0.73 | 1.00% | 224.78 | 0.36 | 0.00% | 227.08 | 2.66 | 1.00% | 227.08 | 1.73 | 1.00% | 227.08 | 1.08 | 1.00% |
| R102C10 | 220.97 | 19.01 | 0% | 220.97 | 0.74 | 0.00% | 220.97 | 0.72 | 0.00% | 220.97 | 2.44 | 0.00% | 220.97 | 11.1 | 0.00% | 220.97 | 2 | 0.00% | 220.97 | 1.56 | 0.00% |
| R103C10 | 160.41 | 10.35 | 0% | 160.41 | 3.87 | 0.00% | 160.41 | 2.55 | 0.00% | 160.41 | 11.17 | 0.00% | 160.41 | 18.15 | 0.00% | 160.41 | 16.38 | 0.00% | 160.41 | 9.27 | 0.00% |
| R201C10 | 183.11 | 2.36 | 0% | 197.54 | 1.9 | 7.90% | 183.11 | 2.3 | 0.00% | 183.11 | 4.73 | 0.00% | 197.54 | 8.98 | 7.90% | 183.11 | 15.55 | 0.00% | 183.11 | 13.63 | 0.00% |
| R203C10 | 214.9 | 5.43 | 0% | 214.9 | 2.3 | 0.00% | 214.9 | 2.98 | 0.00% | 214.9 | 2.88 | 0.00% | 214.9 | 12.03 | 0.00% | 214.9 | 6.27 | 0.00% | 214.9 | 3.59 | 0.00% |
| RC102C10 | 346.7 | 4.03 | 0% | 346.7 | 1.65 | 0.00% | 346.7 | 5.57 | 0.00% | 346.7 | 4.5 | 0.00% | 354.31 | 6.55 | 2.20% | 346.7 | 8.15 | 0.00% | 346.7 | 7.12 | 0.00% |
| RC108C10 | 317.96 | 6 | 0% | 317.96 | 13.13 | 0.00% | 317.96 | 6.63 | 0.00% | 317.96 | 3.3 | 0.00% | 345.53 | 10.82 | 8.70% | 317.96 | 20.73 | 0.00% | 317.96 | 5 | 0.00% |
| RC201C10 | 246.99 | 5.26 | 0% | 246.99 | 27.07 | 0.00% | 246.99 | 26.49 | 0.00% | 246.99 | 9.78 | 0.00% | 247.26 | 16.97 | 0.10% | 247.26 | 8.67 | 0.10% | 247.26 | 11.8 | 0.10% |
| RC205C10 | 306.82 | 4.14 | 0% | 306.82 | 0.79 | 0.00% | 306.82 | 1.3 | 0.00% | 306.82 | 0.92 | 0.00% | 306.82 | 3.56 | 0.00% | 306.82 | 1.94 | 0.00% | 306.82 | 2.08 | 0.00% |
| C103C15 | 255.68 | 30.81 | 0% | 255.68 | 49.81 | 0.00% | 255.68 | 21.63 | 0.00% | 255.68 | 34.23 | 0.00% | 255.68 | 126.46 | 0.00% | 255.68 | 20.29 | 0.00% | 255.68 | 46.59 | 0.00% |
| C106C15 | 223.84 | 142.65 | 0% | 223.84 | 172.21 | 0.00% | 223.84 | 6.36 | 0.00% | 223.84 | 88.61 | 0.00% | 223.84 | 61.63 | 0.00% | 223.84 | 16.1 | 0.00% | 223.84 | 19.6 | 0.00% |
| C202C15 | 314.62 | 373.2 | 0% | 326.57 | 205.19 | 3.80% | 314.62 | 52.62 | 0.00% | 314.62 | 129.31 | 0.00% | 314.62 | 95.09 | 0.00% | 314.62 | 48.33 | 0.00% | 326.57 | 243.03 | 3.80% |
| C208C15 | 262.5 | 244.4 | 0% | 262.5 | 7.55 | 0.00% | 262.5 | 4.79 | 0.00% | 262.5 | 2.84 | 0.00% | 262.5 | 27.33 | 0.00% | 262.5 | 6.05 | 0.00% | 262.5 | 5.34 | 0.00% |
| R102C15 | 258.59 | 681.12 | 0% | 258.59 | 110.03 | 0.00% | 259.79 | 144.02 | 0.50% | 258.59 | 23.27 | 0.00% | 259.79 | 106.54 | 0.50% | 258.59 | 49.21 | 0.00% | 258.59 | 30.68 | 0.00% |
| R105C15 | 231.96 | 119.88 | 0% | 231.96 | 40.64 | 0.00% | 231.96 | 19.04 | 0.00% | 231.96 | 11.73 | 0.00% | 233.92 | 284.61 | 0.80% | 231.96 | 29.16 | 0.00% | 231.96 | 28.65 | 0.00% |
| R202C15 | 275.04 | 64.31 | 0% | 275.04 | 42.01 | 0.00% | 275.04 | 44.88 | 0.00% | 275.04 | 13.64 | 0.00% | 275.04 | 108.5 | 0.00% | 275.04 | 36.39 | 0.00% | 275.04 | 34.26 | 0.00% |
| R209C15 | 239.7 | 49.6 | 0% | 239.7 | 10.76 | 0.00% | 239.7 | 26.31 | 0.00% | 239.7 | 9.22 | 0.00% | 239.7 | 76.07 | 0.00% | 239.7 | 239.62 | 0.00% | 239.7 | 46.26 | 0.00% |
| RC103C15 | 291.07 | 52.73 | 0% | 291.07 | 22.78 | 0.00% | 291.07 | 22.25 | 0.00% | 291.07 | 9.73 | 0.00% | 291.07 | 62.43 | 0.00% | 291.07 | 35.31 | 0.00% | 291.07 | 34.67 | 0.00% |
| RC108C15 | 330.01 | 1197.23 | 0% | 330.01 | 6.22 | 0.00% | 330.01 | 5.76 | 0.00% | 330.01 | 7.27 | 0.00% | 330.01 | 61.84 | 0.00% | 330.01 | 9.97 | 0.00% | 330.01 | 26.47 | 0.00% |
| RC202C15 | 295.6 | 87 | 0% | 319.32 | 85.21 | 8.00% | 295.6 | 201.46 | 0.00% | 295.6 | 94.69 | 0.00% | 315.22 | 60.75 | 6.60% | 295.6 | 50.44 | 0.00% | 315.22 | 49.43 | 6.60% |
| RC204C15 | 255.68 | 30 | 0% | 255.68 | 51.88 | 0.00% | 255.68 | 16.12 | 0.00% | 255.68 | 29.24 | 0.00% | 255.68 | 118.24 | 0.00% | 255.68 | 14.64 | 0.00% | 255.68 | 40.24 | 0.00% |
| Avg. | 87.94 | 24.45 | 0.60% | 17.43 | 0.10% | 14.25 | 0.00% | 37.18 | 0.90% | 18.74 | 0.10% | 19.52 | 0.40% | ||||||||
| Random VNS | Nested VNS | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CPLEX | V7 Seq | V8 Pipe | V9 Cyclic | V10 Seq | V11 Pipe | V12 Cyclic | |||||||||||||||
| Instance | |||||||||||||||||||||
| C101C5 | 208.90 | 1.35 | 0% | 208.90 | 0.02 | 0.0% | 208.90 | 0.02 | 0.0% | 208.90 | 0.03 | 0.0% | 208.90 | 0.16 | 0.0% | 208.90 | 0.17 | 0.0% | 208.90 | 0.16 | 0.0% |
| C103C5 | 154.50 | 1.20 | 0% | 154.50 | 0.11 | 0.0% | 154.50 | 0.17 | 0.0% | 154.50 | 0.13 | 0.0% | 154.50 | 0.33 | 0.0% | 154.50 | 0.34 | 0.0% | 154.50 | 0.28 | 0.0% |
| C206C5 | 201.55 | 1.92 | 0% | 201.55 | 0.06 | 0.0% | 201.55 | 0.08 | 0.0% | 201.55 | 0.06 | 0.0% | 201.55 | 0.02 | 0.0% | 201.55 | 0.02 | 0.0% | 201.55 | 0.02 | 0.0% |
| C208C5 | 158.48 | 1.34 | 0% | 158.48 | 0.08 | 0.0% | 158.48 | 0.06 | 0.0% | 158.48 | 0.08 | 0.0% | 158.48 | 0.05 | 0.0% | 158.48 | 0.06 | 0.0% | 158.48 | 0.09 | 0.0% |
| R104C5 * | 136.69 | 1.75 | 0% | 136.69 | 0.00 | - | 136.69 | 0.00 | - | 136.69 | 0.00 | - | 136.69 | 0.00 | - | 136.69 | 0.00 | - | 136.69 | 0.00 | - |
| R105C5 * | 139.48 | 1.23 | 0% | 139.48 | 0.00 | - | 139.48 | 0.00 | - | 139.48 | 0.00 | - | 139.48 | 0.00 | - | 139.48 | 0.00 | - | 139.48 | 0.00 | - |
| R202C5 | 128.78 | 1.29 | 0% | 128.78 | 0.39 | 0.0% | 128.78 | 0.38 | 0.0% | 128.78 | 0.36 | 0.0% | 128.78 | 0.39 | 0.0% | 128.78 | 0.42 | 0.0% | 128.78 | 0.38 | 0.0% |
| R203C5 | 179.06 | 1.37 | 0% | 179.06 | 0.05 | 0.0% | 179.06 | 0.03 | 0.0% | 179.06 | 0.05 | 0.0% | 179.06 | 2.39 | 0.0% | 179.06 | 2.52 | 0.0% | 179.06 | 1.80 | 0.0% |
| RC105C5 | 208.43 | 1.89 | 0% | 208.43 | 0.16 | 0.0% | 208.43 | 0.14 | 0.0% | 208.43 | 0.14 | 0.0% | 208.43 | 0.56 | 0.0% | 208.43 | 0.52 | 0.0% | 208.43 | 0.48 | 0.0% |
| RC108C5 | 211.53 | 1.36 | 0% | 211.53 | 0.19 | 0.0% | 211.53 | 0.19 | 0.0% | 211.53 | 0.16 | 0.0% | 211.53 | 0.63 | 0.0% | 211.53 | 0.47 | 0.0% | 211.53 | 0.44 | 0.0% |
| RC204C5 | 176.39 | 2.54 | 0% | 179.16 | 0.59 | 1.6% | 179.16 | 0.53 | 1.6% | 179.16 | 0.55 | 1.6% | 185.16 | 0.28 | 5.0% | 185.16 | 0.27 | 5.0% | 179.16 | 2.41 | 1.6% |
| RC208C5 | 167.98 | 2.29 | 0% | 167.98 | 0.08 | 0.0% | 167.98 | 0.06 | 0.0% | 167.98 | 0.05 | 0.0% | 167.98 | 0.05 | 0.0% | 167.98 | 0.06 | 0.0% | 167.98 | 0.23 | 0.0% |
| C101C10 | 260.01 | 4.85 | 0% | 260.01 | 8.84 | 0.0% | 260.01 | 3.51 | 0.0% | 260.01 | 5.16 | 0.0% | 260.01 | 11.94 | 0.0% | 260.01 | 13.68 | 0.0% | 260.01 | 29.00 | 0.0% |
| C104C10 | 239.13 | 3.39 | 0% | 239.13 | 3.44 | 0.0% | 239.13 | 2.95 | 0.0% | 239.13 | 7.50 | 0.0% | 239.13 | 19.18 | 0.0% | 239.13 | 22.24 | 0.0% | 239.13 | 20.90 | 0.0% |
| C202C10 | 214.96 | 4.12 | 0% | 214.96 | 4.61 | 0.0% | 214.96 | 4.61 | 0.0% | 214.96 | 3.05 | 0.0% | 231.07 | 8.79 | 7.5% | 231.07 | 8.31 | 7.5% | 214.96 | 7.32 | 0.0% |
| C205C10 | 224.78 | 4.45 | 0% | 227.08 | 0.52 | 1.0% | 224.78 | 3.52 | 0.0% | 224.78 | 17.95 | 0.0% | 227.08 | 1.76 | 1.0% | 227.08 | 1.92 | 1.0% | 227.08 | 1.32 | 1.0% |
| R102C10 | 220.97 | 19.01 | 0% | 220.97 | 4.43 | 0.0% | 220.97 | 3.54 | 0.0% | 220.97 | 2.26 | 0.0% | 220.97 | 7.22 | 0.0% | 220.97 | 6.03 | 0.0% | 220.97 | 4.36 | 0.0% |
| R103C10 | 160.41 | 10.35 | 0% | 164.58 | 2.36 | 2.6% | 160.41 | 23.15 | 0.0% | 160.41 | 11.88 | 0.0% | 164.58 | 7.59 | 2.6% | 164.58 | 8.11 | 2.6% | 160.41 | 15.17 | 0.0% |
| R201C10 | 183.11 | 2.36 | 0% | 183.11 | 11.16 | 0.0% | 183.11 | 11.25 | 0.0% | 183.11 | 18.57 | 0.0% | 197.54 | 2.92 | 7.9% | 197.54 | 3.46 | 7.9% | 183.42 | 26.99 | 0.2% |
| R203C10 | 214.90 | 5.43 | 0% | 214.90 | 2.14 | 0.0% | 214.90 | 2.34 | 0.0% | 214.90 | 1.86 | 0.0% | 214.90 | 2.58 | 0.0% | 214.90 | 2.86 | 0.0% | 214.90 | 2.32 | 0.0% |
| RC102C10 | 346.70 | 4.03 | 0% | 346.70 | 6.80 | 0.0% | 346.70 | 5.93 | 0.0% | 346.70 | 5.64 | 0.0% | 354.31 | 2.22 | 2.2% | 354.31 | 1.83 | 2.2% | 346.70 | 18.64 | 0.0% |
| RC108C10 | 317.96 | 6.00 | 0% | 329.93 | 9.41 | 3.8% | 317.96 | 8.42 | 0.0% | 317.96 | 14.75 | 0.0% | 317.96 | 23.79 | 0.0% | 317.96 | 25.74 | 0.0% | 317.96 | 26.44 | 0.0% |
| RC201C10 | 246.99 | 5.26 | 0% | 247.26 | 12.70 | 0.1% | 247.26 | 12.00 | 0.1% | 247.26 | 11.98 | 0.1% | 260.77 | 9.32 | 5.6% | 260.77 | 11.06 | 5.6% | 247.26 | 21.19 | 0.1% |
| RC205C10 | 306.82 | 4.14 | 0% | 306.82 | 1.45 | 0.0% | 306.82 | 1.62 | 0.0% | 306.82 | 1.22 | 0.0% | 306.82 | 7.94 | 0.0% | 306.82 | 9.06 | 0.0% | 306.82 | 2.18 | 0.0% |
| C103C15 | 255.68 | 30.81 | 0% | 255.68 | 30.16 | 0.0% | 255.68 | 30.82 | 0.0% | 255.68 | 23.25 | 0.0% | 255.68 | 206.50 | 0.0% | 255.68 | 206.38 | 0.0% | 255.68 | 57.03 | 0.0% |
| C106C15 | 223.84 | 142.65 | 0% | 223.84 | 35.76 | 0.0% | 223.84 | 95.40 | 0.0% | 223.84 | 93.70 | 0.0% | 227.78 | 30.76 | 1.8% | 227.78 | 30.12 | 1.8% | 223.84 | 222.96 | 0.0% |
| C202C15 | 314.62 | 373.20 | 0% | 314.62 | 40.32 | 0.0% | 314.62 | 68.19 | 0.0% | 314.62 | 63.72 | 0.0% | 334.21 | 203.73 | 6.2% | 334.21 | 205.38 | 6.2% | 314.62 | 252.76 | 0.0% |
| C208C15 | 262.50 | 244.40 | 0% | 262.50 | 5.99 | 0.0% | 262.50 | 6.16 | 0.0% | 262.50 | 5.83 | 0.0% | 262.50 | 17.38 | 0.0% | 262.50 | 4.96 | 0.0% | 262.50 | 5.89 | 0.0% |
| R102C15 | 258.59 | 681.12 | 0% | 259.79 | 48.23 | 0.5% | 259.79 | 22.92 | 0.5% | 259.79 | 36.62 | 0.5% | 259.79 | 158.44 | 0.5% | 259.79 | 157.34 | 0.5% | 259.79 | 54.84 | 0.5% |
| R105C15 | 231.96 | 119.88 | 0% | 231.96 | 46.06 | 0.0% | 231.96 | 18.04 | 0.0% | 231.96 | 10.78 | 0.0% | 234.46 | 102.50 | 1.1% | 234.46 | 101.79 | 1.1% | 231.96 | 32.26 | 0.0% |
| R202C15 | 275.04 | 64.31 | 0% | 275.04 | 220.29 | 0.0% | 275.04 | 155.40 | 0.0% | 275.04 | 109.75 | 0.0% | 276.42 | 221.23 | 0.5% | 276.42 | 221.08 | 0.5% | 275.04 | 59.99 | 0.0% |
| R209C15 | 239.70 | 49.60 | 0% | 239.70 | 21.16 | 0.0% | 239.70 | 32.72 | 0.0% | 239.70 | 30.10 | 0.0% | 247.27 | 38.90 | 3.2% | 247.27 | 38.02 | 3.2% | 239.70 | 90.17 | 0.0% |
| RC103C15 | 291.07 | 52.73 | 0% | 291.07 | 156.43 | 0.0% | 295.95 | 40.17 | 1.7% | 291.07 | 27.88 | 0.0% | 305.49 | 46.14 | 5.0% | 305.49 | 45.55 | 5.0% | 291.07 | 115.49 | 0.0% |
| RC108C15 | 330.01 | 1197.23 | 0% | 330.01 | 12.54 | 0.0% | 330.01 | 32.08 | 0.0% | 330.01 | 34.12 | 0.0% | 332.40 | 104.08 | 0.7% | 332.40 | 104.68 | 0.7% | 330.01 | 48.19 | 0.0% |
| RC202C15 | 295.60 | 87.00 | 0% | 315.22 | 61.14 | 6.6% | 319.32 | 50.38 | 8.0% | 319.32 | 13.65 | 8.0% | 315.22 | 198.38 | 6.6% | 315.22 | 198.12 | 6.6% | 295.60 | 250.79 | 0.0% |
| RC204C15 | 255.68 | 30.00 | 0% | 255.68 | 24.44 | 0.0% | 255.68 | 24.53 | 0.0% | 255.68 | 17.52 | 0.0% | 255.68 | 192.45 | 0.0% | 255.68 | 190.64 | 0.0% | 255.68 | 43.87 | 0.0% |
| Avg. | 87.94 | 21.45 | 0.5% | 18.37 | 0.3% | 15.84 | 0.3% | 45.29 | 1.7% | 45.09 | 1.7% | 39.34 | 0.1% | ||||||||
| Reduced VNS | Basic VNS | General VNS | Random VNS | Nested VNS | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| V1 Seq | V2 Pipe | V3 Cyclic | V4 Seq | V5 Pipe | V6 Cyclic | V7 Seq | V8 Pipe | V9 Cyclic | V10 Seq | V11 Pipe | V12 Cyclic | BFS | |||||||||||||
| Instance | |||||||||||||||||||||||||
| C101_21 | 730.88 | 2.6% | 734.05 | 3.0% | 734.89 | 3.1% | 752.18 | 5.6% | 738.50 | 3.6% | 718.96 | 0.9% | 714.52 | 0.3% | 712.52 | 0.0% | 759.07 | 6.5% | 849.28 | 19.2% | 849.28 | 19.2% | 724.39 | 1.7% | 712.52 |
| C201_21 | 574.00 | 1.9% | 589.58 | 4.7% | 567.14 | 0.7% | 600.12 | 6.6% | 591.40 | 5.0% | 563.09 | 0.0% | 585.73 | 4.0% | 582.67 | 3.5% | 565.36 | 0.4% | 680.57 | 20.9% | 680.57 | 20.9% | 597.98 | 6.2% | 563.09 |
| R101_21 | 842.73 | 2.3% | 868.07 | 5.4% | 823.51 | 0.0% | 878.06 | 6.6% | 861.24 | 4.6% | 843.74 | 2.5% | 847.03 | 2.9% | 847.03 | 2.9% | 848.29 | 3.0% | 943.66 | 14.6% | 943.66 | 14.6% | 899.26 | 9.2% | 823.51 |
| R201_21 | 704.53 | 2.0% | 694.34 | 0.5% | 690.73 | 0.0% | 752.46 | 8.9% | 723.70 | 4.8% | 713.90 | 3.4% | 714.97 | 3.5% | 732.99 | 6.1% | 697.23 | 0.9% | 725.46 | 5.0% | 725.46 | 5.0% | 717.22 | 3.8% | 690.73 |
| RC101_21 | 894.95 | 3.5% | 875.07 | 1.2% | 887.66 | 2.6% | 903.66 | 4.5% | 896.42 | 3.7% | 885.96 | 2.4% | 864.85 | 0.0% | 906.84 | 4.9% | 902.26 | 4.3% | 1052.76 | 21.7% | 1052.76 | 21.7% | 976.32 | 12.9% | 864.85 |
| RC201_21 | 705.77 | 3.4% | 722.44 | 5.8% | 682.65 | 0.0% | 786.99 | 15.3% | 702.12 | 2.9% | 698.37 | 2.3% | 709.56 | 3.9% | 709.56 | 3.9% | 710.73 | 4.1% | 816.95 | 19.7% | 816.95 | 19.7% | 743.82 | 9.0% | 682.65 |
| Avg. | 2.6% | 3.4% | 1.1% | 7.9% | 4.1% | 1.9% | 2.4% | 3.5% | 3.2% | 16.8% | 16.8% | 7.1% | |||||||||||||
| Reduced VNS | General VNS | Best Found Solution | |||||
|---|---|---|---|---|---|---|---|
| V3 Cyclic | V6 Cyclic | ||||||
| Instance | |||||||
| C101_21 | 734.89 | 2185 | 2.2% | 718.96 | 2402.7 | 0.0% | 718.96 |
| C201_21 | 567.14 | 2067 | 0.7% | 563.09 | 2244.5 | 0.0% | 563.09 |
| C204_21 | 585.63 | 2405 | 1.0% | 579.59 | 2356.9 | 0.0% | 579.59 |
| C206_21 | 569.20 | 2288 | 0.0% | 597.46 | 2155.3 | 5.0% | 569.20 |
| C207_21 | 567.76 | 2513 | 0.0% | 599.72 | 1793.2 | 5.6% | 567.76 |
| R101_21 | 823.51 | 2305 | 0.0% | 843.74 | 2395.3 | 2.5% | 823.51 |
| R104_21 | 880.77 | 1222 | 0.0% | 888.24 | 2334.8 | 0.8% | 880.77 |
| R106_21 | 864.58 | 1812 | 0.0% | 886.88 | 2290.6 | 2.6% | 864.58 |
| R107_21 | 856.46 | 2347 | 0.0% | 864.49 | 2363.4 | 0.9% | 856.46 |
| R108_21 | 842.01 | 2291 | 0.0% | 857.77 | 2188.1 | 1.9% | 842.01 |
| R109_21 | 865.47 | 2272 | 1.3% | 854.32 | 1848.1 | 0.0% | 854.32 |
| R110_21 | 880.77 | 1235 | 2.7% | 857.25 | 1834.6 | 0.0% | 857.25 |
| R111_21 | 879.50 | 1596 | 2.0% | 862.00 | 2333.7 | 0.0% | 862.00 |
| R112_21 | 876.19 | 1637 | 2.6% | 854.32 | 1924.6 | 0.0% | 854.32 |
| R201_21 | 690.73 | 2133 | 0.0% | 713.90 | 1687.4 | 3.4% | 690.73 |
| R202_21 | 690.38 | 2247 | 0.0% | 711.74 | 1791.3 | 3.1% | 690.38 |
| R203_21 | 708.41 | 1964 | 0.0% | 713.90 | 2239.7 | 0.8% | 708.41 |
| R204_21 | 698.59 | 1477 | 0.0% | 708.64 | 2282.2 | 1.4% | 698.59 |
| R205_21 | 690.35 | 2425 | 0.0% | 704.02 | 2378.9 | 2.0% | 690.35 |
| R206_21 | 694.54 | 2099 | 0.2% | 692.95 | 2205.3 | 0.0% | 692.95 |
| R207_21 | 701.66 | 1020 | 0.0% | 701.42 | 2265.3 | 0.0% | 701.42 |
| R208_21 | 687.23 | 2283 | 0.0% | 714.12 | 2210.4 | 3.9% | 687.23 |
| R209_21 | 696.17 | 2141 | 0.5% | 692.95 | 2178.9 | 0.0% | 692.95 |
| R210_21 | 708.41 | 1991 | 0.0% | 713.90 | 2166.8 | 0.8% | 708.41 |
| R211_21 | 701.66 | 1031 | 0.2% | 700.53 | 2208.0 | 0.0% | 700.53 |
| RC101_21 | 887.66 | 2404 | 0.2% | 885.96 | 1812.1 | 0.0% | 885.96 |
| RC201_21 | 682.65 | 1767 | 0.0% | 698.37 | 1658.4 | 2.3% | 682.65 |
| RC202_21 | 703.03 | 2187 | 0.0% | 710.30 | 2100.2 | 1.0% | 703.03 |
| RC203_21 | 685.09 | 2305 | 0.0% | 698.37 | 2358.5 | 1.9% | 685.09 |
| RC204_21 | 723.14 | 2341 | 0.0% | 731.65 | 2168.8 | 1.2% | 723.14 |
| RC205_21 | 715.51 | 1828 | 0.0% | 721.60 | 2437.4 | 0.9% | 715.51 |
| RC206_21 | 691.17 | 2402 | 0.0% | 735.66 | 1682.5 | 6.4% | 691.17 |
| RC207_21 | 685.09 | 2309 | 0.0% | 707.51 | 2024.8 | 3.3% | 685.09 |
| RC208_21 | 721.41 | 2100 | 0.0% | 743.13 | 2438.8 | 3.0% | 721.41 |
| Avg. | 0.4% | 1.6% | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yilmaz, Y.; Kalayci, C.B. Variable Neighborhood Search Algorithms to Solve the Electric Vehicle Routing Problem with Simultaneous Pickup and Delivery. Mathematics 2022, 10, 3108. https://doi.org/10.3390/math10173108
Yilmaz Y, Kalayci CB. Variable Neighborhood Search Algorithms to Solve the Electric Vehicle Routing Problem with Simultaneous Pickup and Delivery. Mathematics. 2022; 10(17):3108. https://doi.org/10.3390/math10173108
Chicago/Turabian StyleYilmaz, Yusuf, and Can B. Kalayci. 2022. "Variable Neighborhood Search Algorithms to Solve the Electric Vehicle Routing Problem with Simultaneous Pickup and Delivery" Mathematics 10, no. 17: 3108. https://doi.org/10.3390/math10173108
APA StyleYilmaz, Y., & Kalayci, C. B. (2022). Variable Neighborhood Search Algorithms to Solve the Electric Vehicle Routing Problem with Simultaneous Pickup and Delivery. Mathematics, 10(17), 3108. https://doi.org/10.3390/math10173108







