A Mathematical Study of the (3+1)-D Variable Coefficients Generalized Shallow Water Wave Equation with Its Application in the Interaction between the Lump and Soliton Solutions
Abstract
:1. Introduction
2. Preliminary
Binary Bell Polynomials
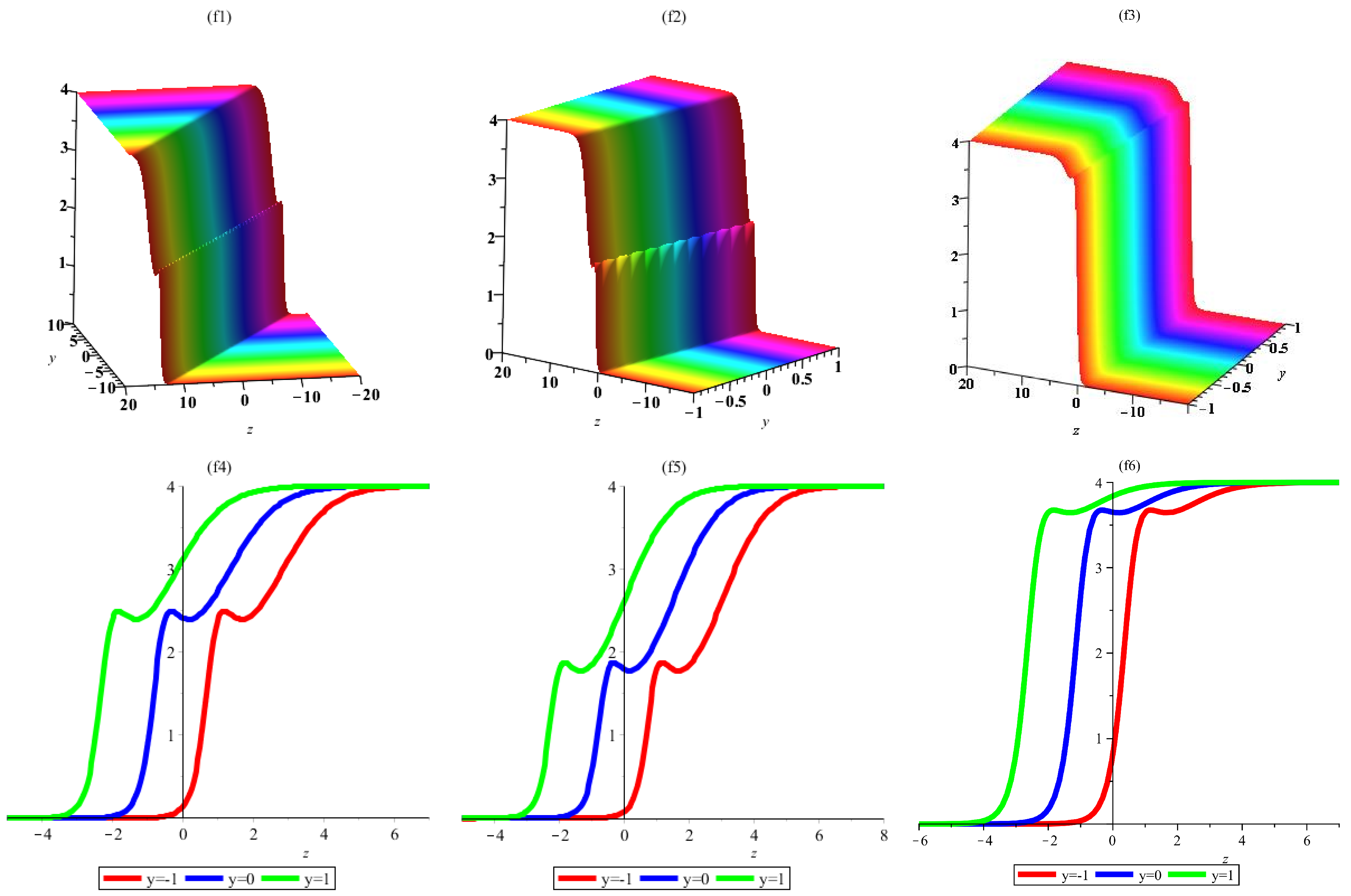
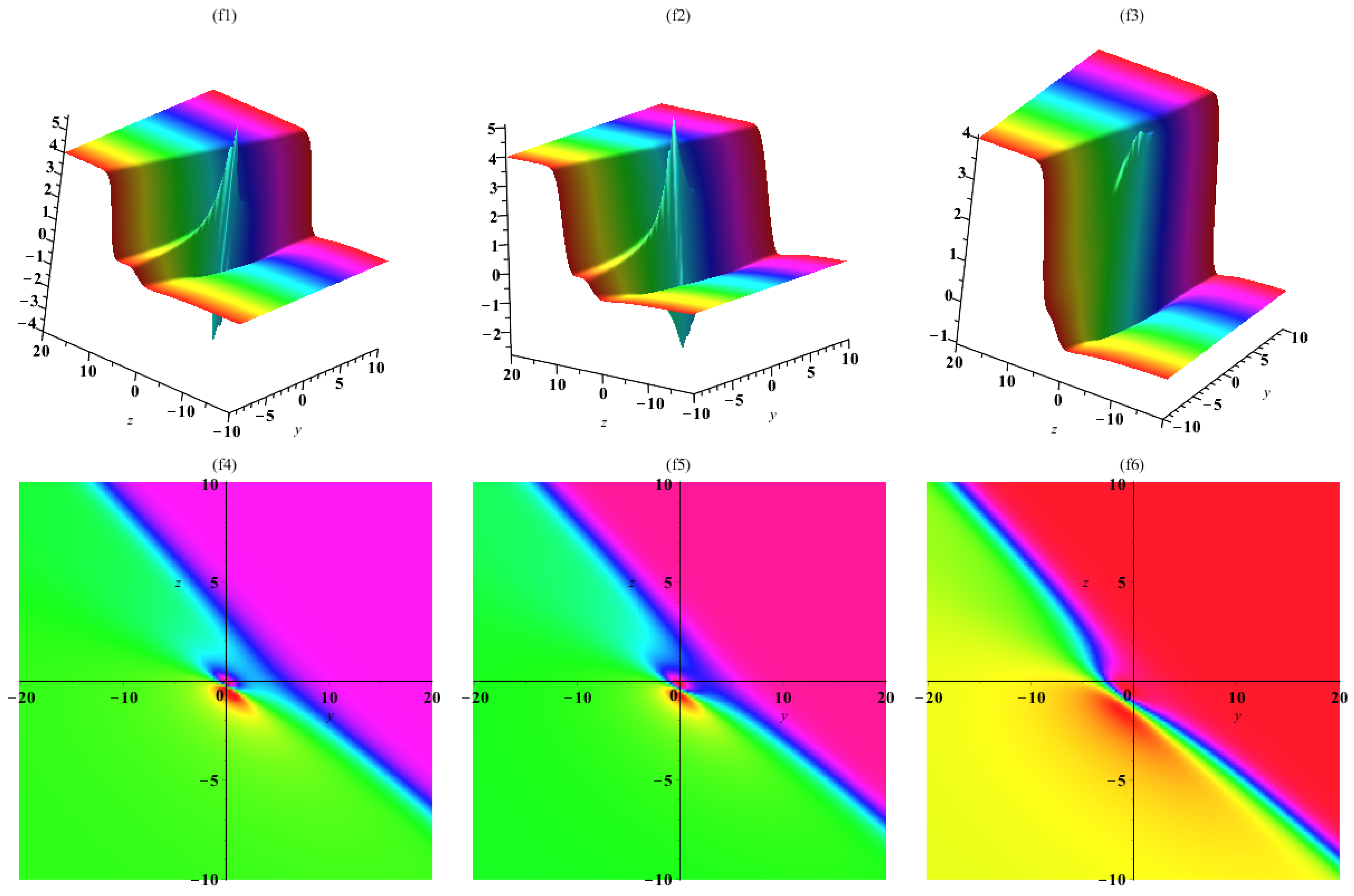
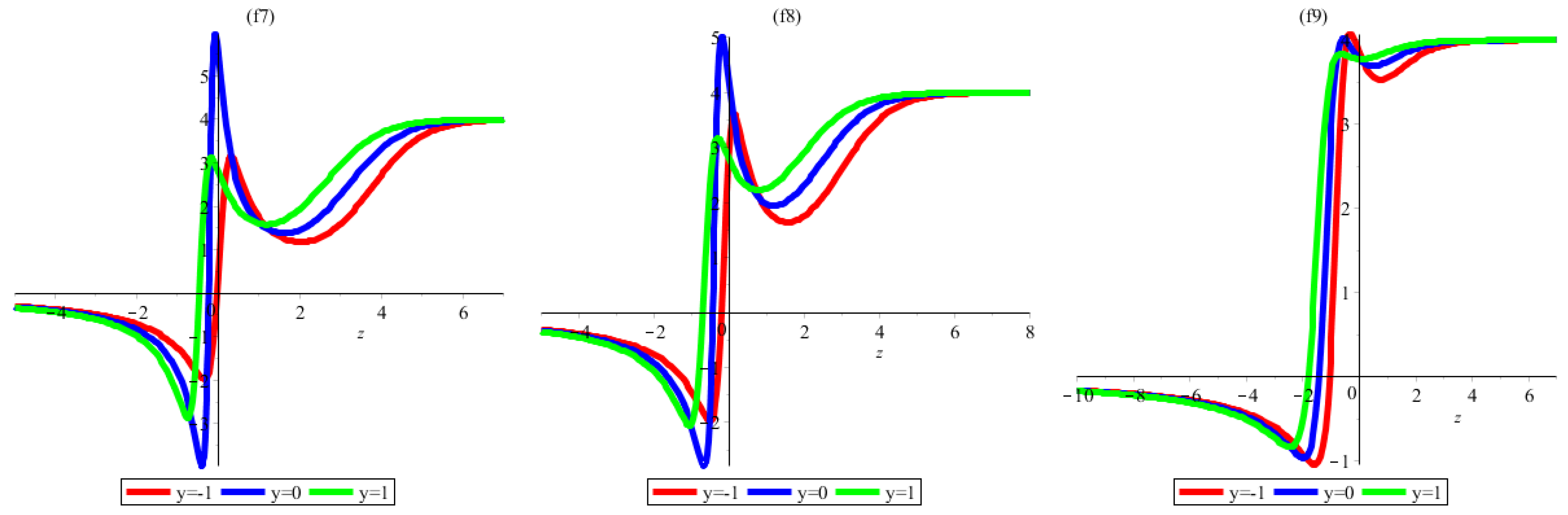
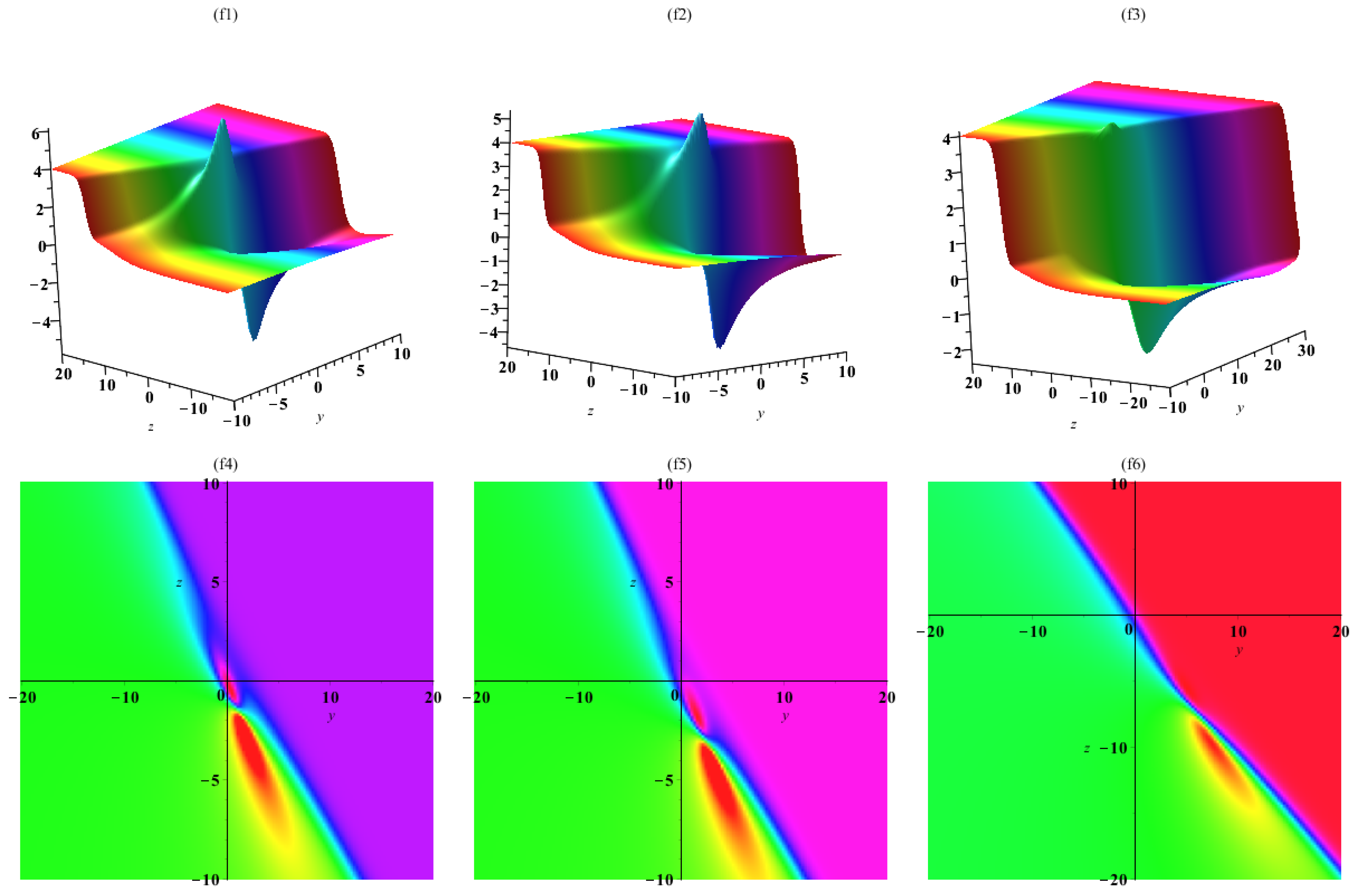
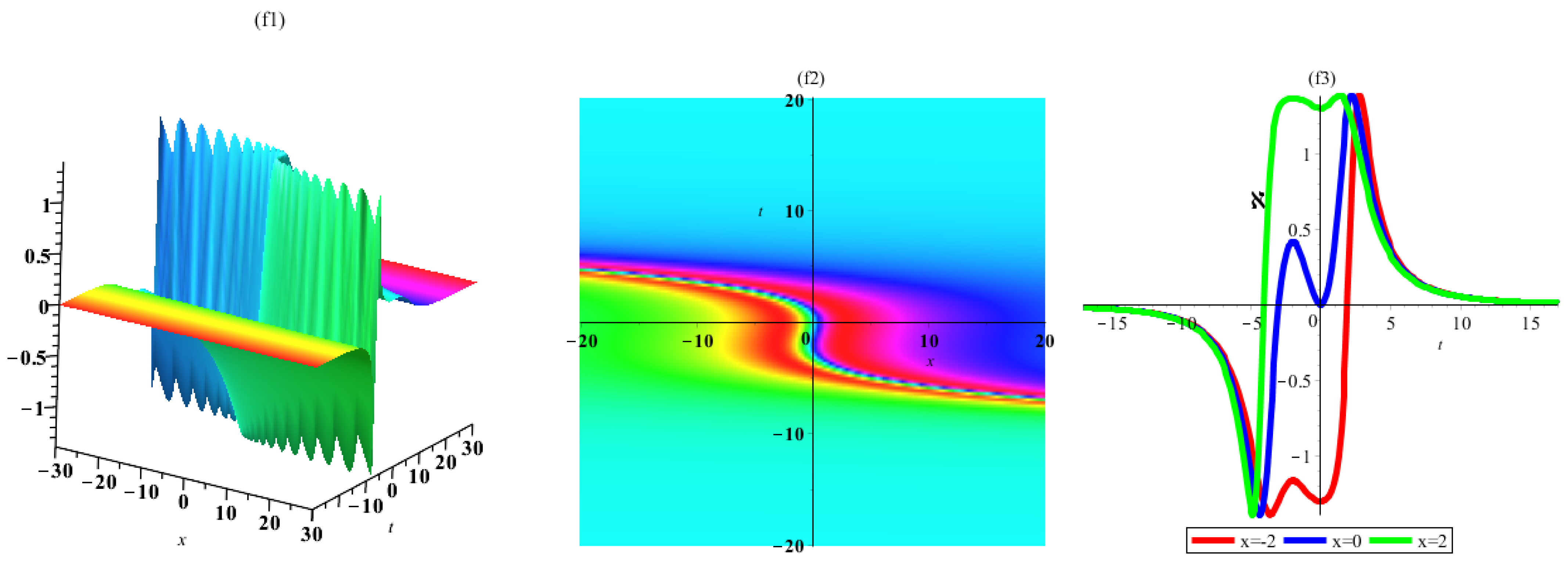
3. Interaction a Lump with One Soliton Solutions
4. Interaction a Lump with Two Soliton Solutions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Randall, D.A. The Shallow Water Equations; Technical Report; Atmospheric Science, Colorado State University: Fort Collins, CO, USA, 2006. [Google Scholar]
- Shinbrot, M. The shallow water equations. J. Eng. Math. 1970, 4, 293–304. [Google Scholar] [CrossRef]
- Klimachkov, D.A.; Petrosyan, A.S. Rossby waves in the magnetic fluid dynamics of a rotating plasma in the shallow-water approximation. J. Exp. Theor. Phys. 2017, 125, 597–612. [Google Scholar] [CrossRef]
- Zayed, E.M.E. Traveling wave solutions for higher dimensional nonlinear evolution equations using the (G’/G) expansion method. J. Appl. Math. Inf. 2010, 28, 383–395. [Google Scholar]
- Tang, Y.N.; Ma, W.X.; Xu, W. Grammian and Pfaffian solutions as well as pfaffianization for a (3+1)-dimensional generalized shallow water equation. Chin. Phys. B 2012, 21, 070212. [Google Scholar] [CrossRef]
- Liu, J.G.; Zhou, L.; He, Y. Multiple soliton solutions for the new (2+1)-dimensional Korteweg-de Vries equation by multiple exp-function method. Appl. Math. Lett. 2018, 80, 71–78. [Google Scholar] [CrossRef]
- Noori, A.W.; Royen, M.J.; Haydary, J. Thin-layer mathematical modeling of apple slices drying, using open sun and cabinet solar drying methods. Int. J. Innov. Sci. Stud. 2021, 4, 43–52. [Google Scholar] [CrossRef]
- Chen, S.; Zhang, J.; Meng, F.; Wang, D.; Wei, Z.; Zhang, W. A Markov Chain Position Prediction Model Based on Multidimensional Correction. Complexity 2021, 2021, 6677132. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, C.; Zhang, X. Rational Localized Waves and Their Absorb-Emit Interactions in the (2+1)-Dimensional Hirota–Satsuma–Ito Equation. Mathematics 2020, 8, 1807. [Google Scholar] [CrossRef]
- Srinivasareddy, S.; Narayana, Y.V.; Krishna, D. Sector Beam Synthesis in Linear Antenna Arrays using Social Group Optimization Algorithm. Natl. J. Antennas Propag. 2021, 3, 6–9. [Google Scholar]
- Wickramasinghe, K. The Use of Deep Data Locality towards a Hadoop Performance Analysis Framework. Int. J. Commun. Comput. Technol. 2020, 8, 5–8. [Google Scholar]
- Xiao, Y.; Fan, E.; Liu, P. Inverse scattering transform for the coupled modified Korteweg–de Vries equation with nonzero boundary conditions. J. Math. Anal. Appl. 2021, 504, 125567. [Google Scholar] [CrossRef]
- Zhou, G.; Zhang, R.; Huang, S. Generalized Buffering Algorithm. IEEE Access 2021, 9, 27140–27157. [Google Scholar] [CrossRef]
- Wen, X.Y.; Xu, X.G. Multiple soliton solutions and fusion interaction phenomena for the (2+1)-dimensional modified dispersive water-wave system. Appl. Math. Comput. 2013, 219, 7730–7740. [Google Scholar] [CrossRef]
- Svilović, S.; Zelić, J. Comparison of Non-Linear and Linear Ho Models Applied for Copper Ions Sorption on Geopolymer. Teh. Glas. 2021, 15, 305–309. [Google Scholar]
- Liu, X.; Zhang, G.; Li, J.; Shi, G.; Zhou, M.; Huang, B.; Yang, W. Deep Learning for Feynman’s Path Integral in Strong-Field Time-Dependent Dynamics. Phys. Rev. Lett. 2020, 124, 113202. [Google Scholar] [CrossRef] [PubMed]
- Cai, L.; Xiong, L.; Cao, J.; Zhang, H.; Alsaadi, F.E. State quantized sampled-data control design for complex-valued memristive neural networks. J. Frankl. Inst. 2020. [Google Scholar] [CrossRef]
- Liu, S.; He, X.; Chan, F.T.S.; Wang, Z. An Extended Multi-Criteria Group Decision-Making Method with Psychological Factors and Bidirectional Influence Relation for Emergency Medical Supplier Selection. Expert Syst. Appl. 2022, 202, 117414. [Google Scholar] [CrossRef]
- Meng, F.; Pang, A.; Dong, X.; Han, C.; Sha, X.; Jing, N.; Na, J. H∞ Optimal Performance Design of an Unstable Plant under Bode Integral Constraint. Complexity 2018, 2018, 4942906. [Google Scholar] [CrossRef]
- Meng, F.; Wang, D.; Yang, P.; Xie, G.; Cutberto, R.; Romero-Melendez, C. Application of Sum of Squares Method in Nonlinear H∞ Control for Satellite Attitude Maneuvers. Complexity 2019, 2019, 5124108. [Google Scholar] [CrossRef]
- Tian, H.; Huang, N.; Niu, Z.; Qin, Y.; Pei, J.; Wang, J. Mapping Winter Crops in China with Multi-Source Satellite Imagery and Phenology-Based Algorithm. Remote Sens. 2019, 11, 820. [Google Scholar] [CrossRef]
- Tan, W.; Zhang, W.; Zhang, J. Evolutionary behavior of breathers and interaction solutions with M-solitons for (2+1)-dimensional KdV system. Appl. Math. Lett. 2020, 101, 106063. [Google Scholar] [CrossRef]
- Chen, S.J.; Lü, X.; Li, M.G.; Wang, F. Derivation and simulation of the M-lump solutions to two (2+1)-dimensional nonlinear equations. Phys. Scr. 2021, 96, 095201. [Google Scholar] [CrossRef]
- Wang, C.; Dai, Z.; Liu, C. Interaction between Kink Solitary Wave and Rogue Wave for (2+1)-Dimensional Burgers Equation. Mediterr. J. Math. 2016, 13, 10871098. [Google Scholar] [CrossRef]
- Sulaiman, T.A.; Yusuf, A.; Abdeljabbar, A.; Alquran, M. Dynamics of lump collision phenomena to the (3+1)-dimensional nonlinear evolution equation. J. Geo. Phys. 2021, 169, 104347. [Google Scholar] [CrossRef]
- Sulaiman, T.A.; Yusuf, A.; Abdeljabbar, A.; Alquran, M. Dynamics of lump solutions to the variable coefficients (2+1)-dimensional Burger’s and Chaffee-infante equations. J. Geo. Phys. 2021, 168, 104315. [Google Scholar] [CrossRef]
- Gang, W.; Manafian, J.; Benli, F.B.; Ilhan, O.A.; Goldaran, R. Modulational instability and multiple rogue wave solutions for the generalized CBSBK equation. Mod. Phys. Lett. B 2021, 35, 2150408. [Google Scholar] [CrossRef]
- Yang, X.Y.; Fan, R.; Li, B. Soliton molecules and some novel interaction solutions to the (2+1)-dimensional B-type Kadomtsev-Petviashvili equation. Phys. Scr. 2020, 95, 045213. [Google Scholar] [CrossRef]
- Ohta, Y.; Yang, J.K. Rogue waves in the Davey-Stewartson I equation. Phys. Rev. E 2012, 86, 036604. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Guo, Q.; Li, B.; Chen, J.C. A new class of nonlinear superposition between lump waves and other waves for Kadomtsev-Petviashvili I equation. Commun. Nonlinear Sci. Num. Simul. 2021, 101, 105866. [Google Scholar] [CrossRef]
- Tao, G.; Manafian, J.; Ilhan, O.A.; Zia, S.M.; Agamalieva, L. Abundant soliton wave solutions for the (3+1)-dimensional variable-coefficient nonlinear wave equation in liquid with gas bubbles by bilinear analysis. Mod. Phys. Lett. B 2022, 36, 2150565. [Google Scholar] [CrossRef]
- Shen, X.; Manafian, J.; Jiang, M.; Ilhan, O.A.; Shafik, S.S.; Zaidi, M. Abundant wave solutions for generalized Hietarinta equation with Hirota’s bilinear operator. Mod. Phys. Lett. B 2022, 36, 2250032. [Google Scholar] [CrossRef]
- Ilhan, O.A.; Abdulazeez, S.T.; Manafian, J.; Azizi, A.; Zeynalli, S.M. Multiple rogue and soliton wave solutions to the generalized KonopelchenkoDubrovskyKaupKupershmidt equation arising in fluid mechanics and plasma physics. Mod. Phys. Lett. B 2021, 35, 2150383. [Google Scholar] [CrossRef]
- Huang, M.; Murad, M.A.S.; Ilhan, O.A.; Manafian, J. One-, two- and three-soliton, periodic and cross-kink solutions to the (2+1) -D variable-coefficient KP equation. Mod. Phys. Lett. B 2020, 34, 2050045. [Google Scholar] [CrossRef]
- Ilhan, O.A.; Manafian, J.; Lakestani, M.; Singh, G. Some novel optical solutions to the perturbed nonlinear Schrdinger model arising in nano-fibers mechanical systems. Mod. Phys. Lett. B 2022, 36, 2150551. [Google Scholar] [CrossRef]
- Seadawy, A.R.; Zahed, H.; Rizvi, S.T.R. Diverse Forms of Breathers and Rogue Wave Solutions for the Complex Cubic Quintic Ginzburg Landau Equation with Intrapulse Raman Scattering. Mathematics 2022, 10, 1818. [Google Scholar] [CrossRef]
- Alruwaili, A.D.; Seadawy, A.R.; Rizvi, S.T.R.; Beinane, S.A.O. Diverse Multiple Lump Analytical Solutions for Ion Sound and Langmuir Waves. Mathematics 2022, 10, 200. [Google Scholar] [CrossRef]
- Feng, B.; Manafian, J.; Ilhan, O.A.; Rao, A.M.; Agadi, A.H. Cross-kink wave, solitary, dark, and periodic wave solutions by bilinear and He’s variational direct methods for the KP-BBM equation. Int. J. Mod. Phys. B 2021, 35, 2150275. [Google Scholar] [CrossRef]
- Zhao, N.; Manafian, J.; Ilhan, O.A.; Singh, G.; Zulfugarova, R. Abundant interaction between lump and k-kink, periodic and other analytical solutions for the (3+1)-D Burger system by bilinear analysis. Int. J. Mod. Phys. B 2021, 35, 2150173. [Google Scholar] [CrossRef]
- Zhang, M.; Xie, X.; Manafian, J.; Ilhan, O.A.; Singh, G. Characteristics of the new multiple rogue wave solutions to the fractional generalized CBS-BK equation. J. Adv. Res. 2022, 38, 131–142. [Google Scholar] [CrossRef]
- Manafian, J.; Lakestani, M. N–lump and interaction solutions of localized waves to the (2+1)-dimensional variable-coefficient Caudrey-Dodd-Gibbon-KoteraSawada equation. J. Geo. Phys. 2020, 150, 103598. [Google Scholar] [CrossRef]
- Zhou, X.; Ilhan, O.A.; Manafian, J.; Singh, G.; Tuguz, N.S. N–lump and interaction solutions of localized waves to the (2+1)–dimensional generalized KDKK equation. J. Geo. Phys. 2021, 168, 104312. [Google Scholar] [CrossRef]
- Wang, W.; Hasanirokh, K.; Manafian, J.; Abotaleb, M.; Yang, Y. Analytical approach for polar magnetooptics in multilayer spin-polarized light emitting diodes based on InAs quantum dots. Opt. Quan. Elec. 2022, 54, 127. [Google Scholar] [CrossRef]
- Manafian, J. Variety interaction solutions comprising lump solitons for a generalized BK equation by trilinear analysis. Eur. Phys. J. Plus 2021, 136, 1097. [Google Scholar] [CrossRef]
- Manafian, J.; Ilhan, O.A.; Avazpour, L.; Alizadeh, A. Localized waves and interaction solutions to the fractional generalized CBS-BK equation arising in fluid mechanics. Adv. Diff. Equ. 2021, 141, 2021. [Google Scholar] [CrossRef]
- Manafian, J.; Jalali, J.; Alizadehdiz, A. Some new analytical solutions of the variant Boussinesq equations. Adv. Diff. Equ. 2018, 50, 80. [Google Scholar] [CrossRef]
- Manafian, J.; Alimirzaluo, E.; Nadjafikhah, M. Conservation laws and exact solutions of the (3+1)-dimensional Jimbo-Miwa equation. Adv. Diff. Equ. 2021, 424, 2021. [Google Scholar] [CrossRef] [PubMed]
- Yang, W.; Lin, Y.; Chen, X.; Xu, Y.; Song, X. Wave mixing and high-harmonic generation enhancement by a two-color field driven dielectric metasurface. Chin. Opt. Lett. 2021, 19, 123202. [Google Scholar] [CrossRef]
- Chen, Z.; Tang, J.; Zhang, X.Y.; So, D.K.C.; Jin, S.; Wong, K. Hybrid Evolutionary-Based Sparse Channel Estimation for IRS-Assisted mmWave MIMO Systems. IEEE Trans. Wireless Commun. 2022, 21, 1586–1601. [Google Scholar] [CrossRef]
- Jiang, Y.; Li, X. Broadband cancellation method in an adaptive co-site interference cancellation system. Int. J. Electron. 2021, 109, 854–874. [Google Scholar] [CrossRef]
- Wang, K.; Wang, H.; Li, S. Renewable quantile regression for streaming datasets. Knowl.-Based Syst. 2022, 235, 107675. [Google Scholar] [CrossRef]
- Meng, Q.; Ma, Q.; Zhou, G. Adaptive Output Feedback Control for Stochastic Uncertain Nonlinear Time-delay Systems. IEEE transactions on circuits and systems. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 3289–3293. [Google Scholar] [CrossRef]
- Qin, X.; Zhang, L.; Yang, L.; Cao, S. Heuristics to sift extraneous factors in Dixon resultants. J. Symb. Comput. 2022, 112, 105–121. [Google Scholar] [CrossRef]
- Xiao, G.; Chen, B.; Li, S.; Zhuo, X. Fatigue life analysis of aero-engine blades for abrasive belt grinding considering residual stress. Eng. Fail. Anal. 2022, 131, 105846. [Google Scholar] [CrossRef]
- Zhang, M.; Chen, Y.; Lin, J. A Privacy-Preserving Optimization of Neighborhood-Based Recommendation for Medical-Aided Diagnosis and Treatment. IEEE Internet Things J. 2021, 8, 10830–10842. [Google Scholar] [CrossRef]
- Liu, J.G.; Zhu, W.H. Breather wave solutions for the generalized shallow water wave equation with variable coefficients in the atmosphere, rivers, lakes and oceans. Comput. Math. Appl. 2019, 78, 848856. [Google Scholar] [CrossRef]
- Liu, J.G.; Zhu, W.H.; He, Y.; Lei, Z.Q. Characteristics of lump solutions to a (3+1)-dimensional variable-coefficient generalized shallow water wave equation in oceanography and atmospheric science. Eur. Phys. J. Plus 2019, 134, 385. [Google Scholar] [CrossRef]
- Zayeda, E.M.E.; Gepreel, K.A. The (G’/G)-expansion method for finding traveling wave solutions of nonlinear partial differential equations in mathematical physics. J. Math. Phys. 2009, 50, 013502. [Google Scholar] [CrossRef]
- Darvishi, M.T.; Najafi, M. Some complexiton type solutions of the (3+1)-dimensional Jimbo-Miwa equation. Int. J. Comput. Math. Sci. 2012, 6, 25–27. [Google Scholar]
- Chen, Y.; Liu, R. Some new nonlinear wave solutions for two (3+1)-dimensional equations. Appl. Math. Comput. 2015, 260, 397–411. [Google Scholar] [CrossRef]
- Huang, Q.M.; Gao, Y.T.; Jia, S.L.; Wang, Y.L.; Deng, G.F. Bilinear backlund transformation, soliton and periodic wave solutions for a (3+1)-dimensional variable-coefficient generalized shallow water wave equation. Nonlinear Dyn. 2017, 87, 2529–2540. [Google Scholar] [CrossRef]
- Huang, Q.M.; Gao, Y.T. Bilinear backlund transformation and dynamic features of the soliton solutions for a variable-coefficient (3+1)-dimensional generalized shallow water wave equation. Mod. Phys. Lett. B 2017, 31, 1750126. [Google Scholar] [CrossRef]
- Ma, W.X. Bilinear equations, Bell polynomials and linear superposition principle. J. Phys. Conf. Ser. 2013, 411, 012021. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, R.; İlhan, O.A.; Manafian, J.; Mahmoud, K.H.; Abotaleb, M.; Kadi, A. A Mathematical Study of the (3+1)-D Variable Coefficients Generalized Shallow Water Wave Equation with Its Application in the Interaction between the Lump and Soliton Solutions. Mathematics 2022, 10, 3074. https://doi.org/10.3390/math10173074
Li R, İlhan OA, Manafian J, Mahmoud KH, Abotaleb M, Kadi A. A Mathematical Study of the (3+1)-D Variable Coefficients Generalized Shallow Water Wave Equation with Its Application in the Interaction between the Lump and Soliton Solutions. Mathematics. 2022; 10(17):3074. https://doi.org/10.3390/math10173074
Chicago/Turabian StyleLi, Ruijuan, Onur Alp İlhan, Jalil Manafian, Khaled H. Mahmoud, Mostafa Abotaleb, and Ammar Kadi. 2022. "A Mathematical Study of the (3+1)-D Variable Coefficients Generalized Shallow Water Wave Equation with Its Application in the Interaction between the Lump and Soliton Solutions" Mathematics 10, no. 17: 3074. https://doi.org/10.3390/math10173074
APA StyleLi, R., İlhan, O. A., Manafian, J., Mahmoud, K. H., Abotaleb, M., & Kadi, A. (2022). A Mathematical Study of the (3+1)-D Variable Coefficients Generalized Shallow Water Wave Equation with Its Application in the Interaction between the Lump and Soliton Solutions. Mathematics, 10(17), 3074. https://doi.org/10.3390/math10173074






