A Novel Early Warning Method for Handling Non-Homogeneous Information
Abstract
1. Introduction
2. Preliminary Knowledge
2.1. Linguistic Terms
2.2. Hesitant Fuzzy Linguistic Term Sets
2.3. Fuzzy TOPSIS Method Based on Alpha-Level Sets
2.4. Related Work
3. Proposed Method
3.1. Problem Definition
3.2. Information Collection
3.3. Information Transformation
3.4. Information Aggregation
3.5. Fuzzy TOPSIS Method Based on Alpha-Level Sets
- Step 1: To judge the intersection relation between and .
- Step 2: When , if , then the status results of belongs to the corresponding status ; if , then the status results of belongs to the corresponding status ; and if there exists and , then the status results of belongs to the corresponding status .
4. Illustrative Example and Comparison
4.1. Illustrative Example
4.1.1. Problem Definition
4.1.2. Information Collection
4.1.3. Information Transformation
4.1.4. Information Aggregation
4.1.5. Fuzzy TOPSIS Method Based on Alpha-Level Sets
4.1.6. Sensitivity Analysis
4.2. Comparisons with Existing Studies
5. Discussion
6. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- World Meteorological Organization. Multi-hazard early warning systems: A checklist. In Proceedings of the Outcome of the first Multi-hazard Early Warning Conference, Cancun, Mexico, 22–23 May 2017. [Google Scholar]
- Al-Zaabi, S.; Al-Zadjali, S. Qualitative analysis of early warning: A case study from Oman. Int. J. Disaster Risk Reduct. 2022, 68, 102731. [Google Scholar] [CrossRef]
- Biansoongnern, S.; Plungkang, B.; Susuk, S. Development of low cost vibration sensor network for early warning system of landslides. Energy Proc. 2016, 89, 417–420. [Google Scholar] [CrossRef]
- Cong, X.H.; Ma, L.; Wang, L.; Šaparauskas, J.; Górecki, J.; Skibniewski, M.J. The early warning system for determining the “not in My Back Yard” of heavy pollution projects based on public perception. J. Clean. Product. 2021, 282, 125398. [Google Scholar] [CrossRef]
- Cremen, G.; Bozzoni, F.; Pistorio, S.; Galasso, C. Developing a risk-informed decision-support system for earthquake early warning at a critical seaport. Reliab. Eng. Syst. Saf. 2022, 218, 108035. [Google Scholar] [CrossRef]
- Kitazawa, K.; Hale, S.A. Social media and early warning systems for natural disasters: A case study of Typhoon Etau in Japan. Int. J. Disaster Risk Reduct. 2021, 52, 101926. [Google Scholar] [CrossRef]
- Vaiciulyte, S.; Novelo-Casanova, D.A.; Husker, A.L.; Garduño-González, A.B. Population response to earthquakes and earthquake early warnings in Mexico. Int. J. Disaster Risk Reduct. 2022, 72, 102854. [Google Scholar] [CrossRef]
- Chen, W.L.; Wang, X.L.; Tong, D.W.; Cai, Z.; Zhu, Y.; Liu, C. Dynamic early-warning model of dam deformation based on deep learning and fusion of spatiotemporal features. Knowl. Based Syst. 2021, 233, 107537. [Google Scholar] [CrossRef]
- Chen, X.L.; Wang, P.H.; Hao, Y.S.; Zhao, M. Evidential KNN-based condition monitoring and early warning method with applications in power plant. Neurocomputing 2018, 315, 18–32. [Google Scholar] [CrossRef]
- Dokas, I.M.; Karras, D.A.; Panagiotakopoulos, D.C. Fault tree analysis and fuzzy expert systems: Early warning and emergency response of landfill operations. Environ. Model. Softw. 2009, 24, 8–25. [Google Scholar] [CrossRef]
- Gao, F.; Li, Q.; Ji, Y.; Ji, S.; Guo, J.; Sun, H.; Zhang, H. EWNet: An early warning classification framework for smart grid based on local-to-global perception. Neurocomputing 2021, 443, 199–212. [Google Scholar] [CrossRef]
- Lin, Z.A.; Shi, Y.C.; Chen, B.; Liu, S.; Ge, Y.; Ma, J.; Lin, Z. Early warning method for power supply service quality based on three-way decision theory and LSTM neural network. Energy Rep. 2022, 8, 537–543. [Google Scholar] [CrossRef]
- Xu, R.H.; Luo, F. Risk prediction and early warning for air traffic controllers’ unsafe acts using association rule mining and random forest. Saf. Sci. 2021, 135, 105125. [Google Scholar] [CrossRef]
- Yan, Z.G.; Wang, X.L.; Fu, Y.C. Study on early warning model of coal mining engineering with fuzzy AHP. Syst. Eng. Proc. 2012, 5, 113–118. [Google Scholar] [CrossRef][Green Version]
- Burchard-Levine, A.; Liu, S.M.; Vince, F.; Li, M.M.; Ostfeld, A. A hybrid evolutionary data driven model for river water quality early warning. J. Environ. Manag. 2014, 143, 8–16. [Google Scholar] [CrossRef]
- Akwango, D.; Obaa, B.B.; Turyahabwe, N.; Baguma, Y.; Egeru, A. Quality and dissemination of information from a drought early warning system in Karamoja sub-region, Uganda. J. Arid Environ. 2017, 145, 69–80. [Google Scholar] [CrossRef]
- Li, D.Y.; Wei, Y.M.; Dong, Z.; Wang, C.; Wang, C. Quantitative study on the early warning indexes of conventional sudden water pollution in a plain river network. J. Clean. Product. 2021, 303, 127067. [Google Scholar] [CrossRef]
- Yang, Z.S.; Wang, J. A new air quality monitoring and early warning system: Air quality assessment and air pollutant concentration prediction. Environ. Res. 2017, 158, 105–117. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.M.; Chen, K.; Weng, Y.; Chen, Z.; Zhang, J.; Hubbard, R. An intelligent early warning system of analyzing Twitter data using machine learning on COVID-19 surveillance in the US. Expert Syst. Applicat. 2022, 198, 116882. [Google Scholar] [CrossRef]
- Li, B.; Wang, E.; Shang, Z.; Liu, X.; Li, Z.; Li, B.; Wang, H.; Niu, Y.; Song, Y. Optimize the early warning time of coal and gas outburst by multi-source information fusion method during the tunneling process. Process Saf. Environ. Protect. 2021, 149, 839–849. [Google Scholar] [CrossRef]
- Pyayt, A.L.; Shevchenko, D.V.; Kozionov, A.P.; Mokhov, I.I.; Lang, B.; Krzhizhanovskaya, V.V.; Sloot, P.M. Combining data-driven methods with finite element analysis for flood early warning systems. Proc. Comput. Sci. 2015, 51, 2347–2356. [Google Scholar] [CrossRef]
- Zhang, Z.X.; Wang, L.; Wang, Y.M. Dynamic early-warning method of emergency event with interval information. Control Decis. 2017, 32, 1306–1312. [Google Scholar]
- Zhang, Z.X.; Wang, L.; Wang, Y.M. Early warning method for emergencies based on linguistic information. China Saf. Sci. J. 2020, 30, 93–100. [Google Scholar]
- Wang, Y.M.; Elhag, T.M.S. Fuzzy TOPSIS method based on alpha level sets with an application to bridge risk assessment. Expert Syst. Appl. 2006, 31, 309–319. [Google Scholar] [CrossRef]
- Zadeh, L. The concept of a linguistic variable and its applications to approximate reasoning. Inf. Sci. 1975, 8, 199–249. [Google Scholar] [CrossRef]
- Yager, R.R. An approach to ordinal decision making. Int. J. Approx. Reason. 1995, 12, 237–261. [Google Scholar] [CrossRef]
- Zimmermann, H.J. Fuzzy Set Theory and Its Applications; Kluwer Academic Publishers: Boston, MA, USA, 1991; pp. 23–26. [Google Scholar]
- Khorshidi, H.A.; Nikfalazar, S. An improved similarity measure for generalized fuzzy numbers and its application to fuzzy risk analysis. Appl. Soft Comput. 2017, 52, 478–486. [Google Scholar] [CrossRef]
- Luo, C.; Ju, Y.B.; Gonzalez, E.; Dong, P.W.; Wang, A.H. The waste-to-energy incineration plant site selection based on hesitant fuzzy linguistic Best-Worst method ANP and double parameters TOPSIS approach: A case study in China. Energy 2020, 211, 118564. [Google Scholar] [CrossRef]
- Yang, J.B.; Wang, Y.M.; Xu, D.L.; Chin, K.S. The evidential reasoning approach for MADA under both probabilistic and fuzzy uncertainties. Eur. J. Oper. Res. 2006, 171, 309–343. [Google Scholar] [CrossRef]
- Rodríguez, R.M.; Martínez, L.; Herrera, F. Hesitant fuzzy linguistic term sets for decision making. IEEE Trans. Fuzzy Syst. 2012, 20, 109–119. [Google Scholar] [CrossRef]
- Liu, P.D.; Shen, M.J.; Teng, F.; Zhu, B.Y.; Geng, Y.S. Double hierarchy hesitant fuzzy linguistic entropy-based TODIM approach using evidential theory. Inf. Sci. 2021, 547, 223–243. [Google Scholar] [CrossRef]
- Montserrat-Adell, J.; Xu, Z.S.; Gou, X.; Agell, N. Free double hierarchy hesitant fuzzy linguistic term sets: An application on ranking alternatives in GDM. Inf. Fusion 2019, 47, 45–59. [Google Scholar] [CrossRef]
- Wang, L.; Labella, Á.; Rodríguez, R.M.; Wang, Y.M.; Martínez, L. Managing non-homogeneous information and experts’ psychological behavior in group emergency decision making. Symmetry 2017, 9, 234. [Google Scholar] [CrossRef]
- Rodríguez, R.M.; Martínez, L.; Herrera, F. A group decision making model dealing with comparative linguistic expressions based on hesitant fuzzy linguistic term sets. Inf. Sci. 2013, 241, 28–42. [Google Scholar] [CrossRef]
- Liu, H.B.; Rodríguez, R.M. A fuzzy envelope for hesitant fuzzy linguistic term set and its application to multicriteria decision making. Inf. Sci. 2014, 258, 220–238. [Google Scholar] [CrossRef]
- Hwang, C.L.; Yoon, K. Multiple Attribute Decision Making: Methods and Applications; Springer: Berlin/Heidelberg, Germany, 1981. [Google Scholar]
- Salih, M.M.; Zaidan, B.B.; Zaidan, A.A.; Ahmed, M.A. Survey on fuzzy TOPSIS state-of-the-art between 2007 and 2017. Comput. Operation. Res. 2019, 104, 207–227. [Google Scholar] [CrossRef]
- Yorulmaz, O.Y.S.K.; Yıldırım, B.F. Robust Mahalanobis distance based TOPSIS to evaluate the economic development of provinces. Operation. Res. Eng. Sci. Theory Appl. 2021, 4, 102–123. [Google Scholar] [CrossRef]
- Ramakrishnan, K.R.; Chakraborty, S. A cloud TOPSIS model for green supplier selection. Facta Universitatis. Ser. Mech. Eng. 2020, 18, 375–397. [Google Scholar] [CrossRef]
- Govil, N.; Sharma, A. Validation of agile methodology as ideal software development process using Fuzzy-TOPSIS method. Adv. Eng. Softw. 2022, 168, 103125. [Google Scholar] [CrossRef]
- Rani, P.; Mishra, A.R.; Mardani, A.; Cavallaro, F.; Alrasheedi, M.; Alrashidi, A. A novel approach to extended fuzzy TOPSIS based on new divergence measures for renewable energy sources selection. J. Clean. Product. 2020, 257, 120352. [Google Scholar] [CrossRef]
- Wang, L.; Rodriguez, R.M.; Wang, Y.M. A dynamic multi-attribute group emergency decision making method considering experts’ hesitation. Int. J. Comput. Intell. Syst. 2018, 11, 163–182. [Google Scholar] [CrossRef]
- Chen, M.F.; Tzeng, G.H. Combining grey relation and TOPSIS concepts for selecting an expatriate host country. Math. Comput. Modell. 2004, 40, 1473–1490. [Google Scholar] [CrossRef]
- Chu, T.C. Facility location selection using fuzzy TOPSIS under group decisions. Int. J. Uncertain. Fuzziness Knowl. Based Syst. 2002, 10, 687–701. [Google Scholar] [CrossRef]
- Wang, T.X. A novel approach of integrating natural language processing techniques with fuzzy TOPSIS for product evaluation. Symmetry 2022, 14, 120. [Google Scholar] [CrossRef]
- Chen, C.T. Extension of the TOPSIS for group decision-making under fuzzy environment. Fuzzy Sets Syst. 2000, 114, 1–9. [Google Scholar] [CrossRef]
- Oussalah, M. On the compatibility between defuzzification and fuzzy arithmetic operations. Fuzzy Sets Syst. 2002, 128, 247–260. [Google Scholar] [CrossRef]
- Wang, Y.M.; Yang, J.B.; Xu, D.L. A preference aggregation method through the estimation of utility intervals. Comput. Oper. Res. 2005, 32, 2027–2049. [Google Scholar] [CrossRef]
- Zhang, Z.X. Research on Emergnecy Early-Warning Method and Emergency Decision Making Method. Ph.D. Thesis, Fuzhou University, Fuzhou, China, 2019. [Google Scholar]
- Kahneman, D.; Tversky, A. Prospect theory: An analysis of decision under risk. Econom. J. Econom. Soc. 1979, 47, 263–291. [Google Scholar] [CrossRef]
- Tversky, A.; Kahneman, D. Advances in prospect theory: Cumulative representation of uncertainty. J. Risk Uncertain. 1992, 5, 297–323. [Google Scholar] [CrossRef]
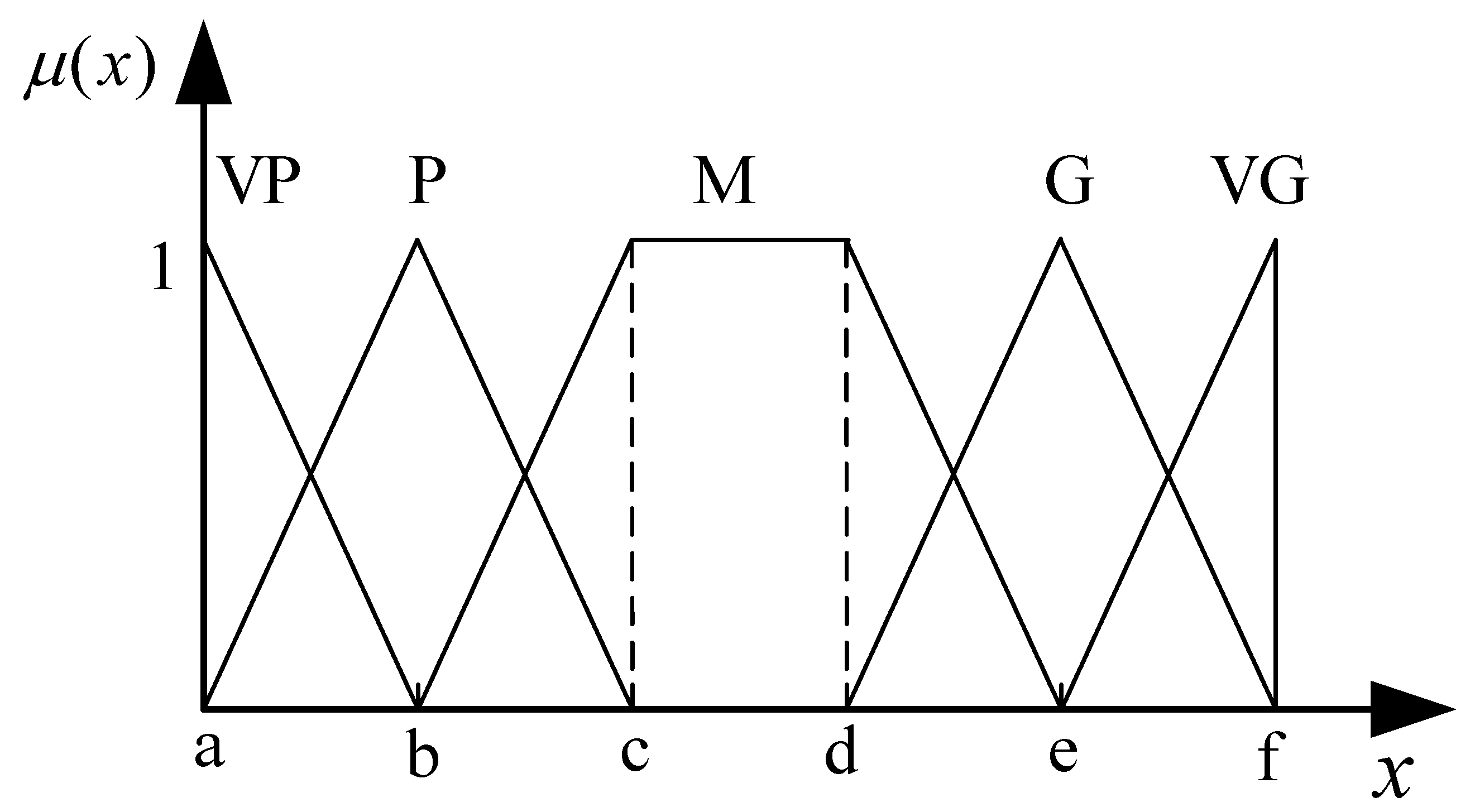


| S | Linguistic Terms | Fuzzy Numbers |
|---|---|---|
| very poor (VP) | ||
| poor (P) | ||
| medium (M) | ||
| good (G) | ||
| very good (VG) |
| Status () | Very Dangerous () | Dangerous () | Fairly Dangerous () | Fairly Safety () | Safety () |
|---|---|---|---|---|---|
| [0, 0.2) | [0.2, 0.4) | [0.4, 0.6) | [0.6, 0.8) | [0.8, 1] |
| Criteria | Description | Information Type |
|---|---|---|
| Rainfall (mm) | The higher the rainfall, the more easily a landslide occurs | I |
| Coverage rate of the forest (%) | The lower the coverage rate of the forest, the more easily a landslide occurs | N |
| Saturated water content of soil (%) | The higher the saturated water content of the soil, the more easily a landslide occurs | N |
| Slope (◦) | The higher the slope, the more easily a landslide occurs | N |
| Influence Degree of Earthquake | The higher the influence degree of an earthquake, the more easily a landslide occurs | |
| Degree of human activity | The higher the degree of human activity, the more easily a landslide occurs | |
| Stability of Geological Structure | The lower the stability of a geological structure, the more easily a landslide occurs |
| Experts | Objects | Criteria | ||||||
|---|---|---|---|---|---|---|---|---|
| [35,55] | 62 | 33 | 35 | M | L | H | ||
| [25,38] | 45 | 26 | 29 | L | L | M | ||
| [20,35] | 33 | 40 | 38 | VL | H | H | ||
| [30,46] | 65 | 38 | 40 | H | H | M | ||
| [18,35] | 55 | 29 | 33 | M | bt M and FH | M | ||
| [23,34] | 42 | 35 | 28 | L | M | H | ||
| [40,50] | 58 | 35 | 33 | bt L and M | M | FH | ||
| [22,35] | 50 | 28 | 36 | M | FH | M | ||
| [25,40] | 44 | 38 | 32 | L | L | M | ||
| [20,38] | 53 | 44 | 37 | M | H | bt M and FH | ||
| [22,38] | 48 | 36 | 31 | H | bt FH and H | H | ||
| [21,44] | 39 | 29 | 30 | At most H | M | H | ||
| [33,45] | 66 | 29 | 38 | L | L | M | ||
| [18,36] | 53 | 33 | 41 | FH | L | L | ||
| [18,24] | 48 | 42 | 26 | M | M | FH | ||
| [23,38] | 50 | 41 | 33 | L | At most H | M | ||
| [16,24] | 49 | 39 | 29 | H | FH | FH | ||
| [20,34] | 45 | 34 | 34 | H | L | FH | ||
| Experts | Criteria Importance | ||||||
|---|---|---|---|---|---|---|---|
| VHI | HI | bt MI and HI | HI | MI | LI | HI | |
| At least HI | HI | MI | VHI | LI | VLI | MI | |
| VHI | MI | HI | bt HI and VHI | LI | LI | VHI | |
| Experts | Objects | Criteria | |||
|---|---|---|---|---|---|
| (0.4872,0.4872,1.0000,1.0000) | (0.9394,0.9394,0.9394,0.9394) | (0.7500,0.7500,0.7500,0.7500) | (0.8537,0.8537,0.8537,0.8537) | ||
| (0.2308,0.2308,0.5641,0.5641) | (0.6818,0.6818,0.6818,0.6818) | (0.5909,0.5909,0.5909,0.5909) | (0.7073,0.7073,0.7073,0.7073) | ||
| (0.1026,0.1026,0.4872,0.4872) | (0.5000,0.5000,0.5000,0.5000) | (0.9091,0.9091,0.9091,0.9091) | (0.9268,0.9268,0.9268,0.9268) | ||
| (0.3590,0.3590,0.7692,0.7692) | (0.9848,0.9848,0.9848,0.9848) | (0.8636,0.8636,0.8636,0.8636) | (0.9756,0.9756,0.9756,0.9756) | ||
| (0.0513,0.0513,0.4872,0.4872) | (0.8333,0.8333,0.8333,0.8333) | (0.6591,0.6591,0.6591,0.6591) | (0.8049,0.8049,0.8049,0.8049) | ||
| (0.1795,0.1795,0.4615,0.4615) | (0.6364,0.6364,0.6364,0.6364) | (0.7955,0.7955,0.7955,0.7955) | (0.6829,0.6829,0.6829,0.6829) | ||
| (0.6154,0.6154,0.8718,0.8718) | (0.8788,0.8788,0.8788,0.8788) | (0.7955,0.7955,0.7955,0.7955) | (0.8049,0.8049,0.8049,0.8049) | ||
| (0.1538,0.1538,0.4872,0.4872) | (0.7576,0.7576,0.7576,0.7576) | (0.6364,0.6364,0.6364,0.6364) | (0.8780,0.8780,0.8780,0.8780) | ||
| (0.2308,0.2308,0.6154,0.6154) | (0.6667,0.6667,0.6667,0.6667) | (0.8636,0.8636,0.8636,0.8636) | (0.7805,0.7805,0.7805,0.7805) | ||
| (0.1026,0.1026,0.5641,0.5641) | (0.8030,0.8030,0.8030,0.8030) | (1.0000,1.0000,1.0000,1.0000) | (1.9024,0.9024,0.9024,0.9024) | ||
| (0.1538,0.1538,0.5641,0.5641) | (0.7273,0.7273,0.7273,0.7273) | (0.8182,0.8182,0.8182,0.8182) | (0.7561,0.7561,0.7561,0.7561) | ||
| (0.1282,0.1282,0.7179,0.7179) | (0.5909,0.5909,0.5909,0.5909) | (0.6591,0.6591,0.6591,0.6591) | (0.7317,0.7317,0.7317,0.7317) | ||
| (0.4359,0.4359,0.7436,0.7436) | (1.0000,1.0000,1.0000,1.0000) | (0.6591,0.6591,0.6591,0.6591) | (0.9268,0.9268,0.9268,0.9268) | ||
| (0.0513,0.0513,0.5128,0.5128) | (0.8030,0.8030,0.8030,0.8030) | (0.7500,0.7500,0.7500,0.7500) | (0.0000,1.0000,1.0000,1.0000) | ||
| (0.0513,0.0513,0.2051,0.2051) | (0.7273,0.7273,0.7273,0.7273) | (0.9545,0.9545,0.9545,0.9545) | (0.6341,0.6341,0.6341,0.6341) | ||
| (0.1795,0.1795,0.5641,0.5641) | (0.7576,0.7576,0.7576,0.7576) | (0.9318,0.9318,0.9318,0.9318) | (0.8049,0.8049,0.8049,0.8049) | ||
| (0.0000,0.0000,0.2051,0.2051) | (0.7424,0.7424,0.7424,0.7424) | (0.8864,0.8864,0.8864,0.8864) | (0.7073,0.7073,0.7073,0.7073) | ||
| (0.1026,0.1026,0.4615,0.4615) | (0.6818,0.6818,0.6818,0.6818) | (0.7727,0.7727,0.7727,0.7727) | (0.8293,0.8293,0.8293,0.8293) | ||
| Experts | Objects | Criteria | ||
|---|---|---|---|---|
| (0.3300,0.5000,0.5000,0.6700) | (0.1700,0.3300,0.3300,0.5000) | (0.6700,0.8300,0.8300,1.0000) | ||
| (0.1700,0.3300,0.3300,0.5000) | (0.1700,0.3300,0.3300,0.5000) | (0.3300,0.5000,0.5000,0.6700) | ||
| (0.0000,0.1700,0.1700,0.3300) | (0.6700,0.8300,0.8300,1.0000) | (0.6700,0.8300,0.8300,1.0000) | ||
| (0.6700,0.8300,0.8300,1.0000) | (0.6700,0.8300,0.8300,1.0000) | (0.3300,0.5000,0.5000,0.6700) | ||
| (0.3300,0.5000,0.5000,0.6700) | (0.3400,0.5000,0.6700,0.8400) | (0.3300,0.5000,0.5000,0.6700) | ||
| (0.1700,0.3300,0.3300,0.5000) | (0.3300,0.5000,0.5000,0.6700) | (0.6700,0.8300,0.8300,1.0000) | ||
| (0.1700,0.3400,0.5000,0.6700) | (0.3300,0.5000,0.5000,0.6700) | (0.5000,0.6700,0.6700,0.8300) | ||
| (0.3300,0.5000,0.5000,0.6700) | (0.5000,0.6700,0.6700,0.8300) | (0.3300,0.5000,0.5000,0.6700) | ||
| (0.1700,0.3300,0.3300,0.5000) | (0.1700,0.3300,0.3300,0.5000) | (0.3300,0.5000,0.5000,0.6700) | ||
| (0.3300,0.5000,0.5000,0.6700) | (0.6700,0.8300,0.8300,1.0000) | (0.3400,0.5000,0.6700,0.8400) | ||
| (0.6700,0.8300,0.8300,1.0000) | (0.5000,0.6700,0.8300,1.0000) | (0.6700,0.8300,0.8300,1.0000) | ||
| (0.0000,0.0000,0.5900,0.8400) | (0.3300,0.5000,0.5000,0.6700) | (0.6700,0.8300,0.8300,1.0000) | ||
| (0.1700,0.3300,0.3300,0.5000) | (0.1700,0.3300,0.3300,0.5000) | (0.3300,0.5000,0.5000,0.6700) | ||
| (0.5000,0.6700,0.6700,0.8300) | (0.5000,0.6700,0.6700,0.8300) | (0.1700,0.3300,0.3300,0.5000) | ||
| (0.3300,0.5000,0.5000,0.6700) | (0.3300,0.5000,0.5000,0.6700) | (0.5000,0.6700,0.6700,0.8300) | ||
| (0.1700,0.3300,0.3300,0.5000) | (0.0000,0.0000,0.5900,0.8400) | (0.3300,0.5000,0.5000,0.6700) | ||
| (0.6700,0.8300,0.8300,1.0000) | (0.5000,0.6700,0.6700,0.8300) | (0.5000,0.6700,0.6700,0.8300) | ||
| (0.6700,0.8300,0.8300,1.0000) | (0.1700,0.3300,0.3300,0.5000) | (0.5000,0.6700,0.6700,0.8300) | ||
| Experts | Transformed Criteria Importance | |||
|---|---|---|---|---|
| (0.6700,0.8300,0.8300,1.0000) | (0.5000,0.6700,0.6700,0.8300) | (0.3400,0.5000,0.6700,0.8400) | (0.5000,0.6700,0.6700,0.8300) | |
| (0.5000,0.8600,0.8600,1.0000) | (0.5000,0.6700,0.6700,0.8300) | (0.3300,0.5000,0.5000,0.6700) | (0.6700,0.8300,0.8300,1.0000) | |
| (0.6700,0.8300,0.8300,1.0000) | (0.3300,0.5000,0.5000,0.6700) | (0.5000,0.3300,0.6700,0.8300) | (0.5000,0.6700,0.8300,1.0000) | |
| Experts | Transformed Criteria Importance | ||
|---|---|---|---|
| (0.3300,0.5000,0.5000,0.6700) | (0.1700,0.3300,0.3300,0.5000) | (0.5000,0.6700,0.6700,0.8300) | |
| (0.1700,0.3300,0.3300,0.5000) | (0.0000,0.1700,0.1700,0.6700) | (0.3300,0.5000,0.5000,0.6700) | |
| (0.1700,0.3300,0.3300,0.5000) | (0.1700,0.3300,0.3300,0.5000) | (0.6700,0.8300,0.8300,1.0000) | |
| Aggregated Information | Criteria | |||
|---|---|---|---|---|
| X | (0.4359,0.5128,0.8718,1.0000) | (0.8788,0.9394,0.9394,1.0000) | (0.6591,0.7348,0.7348,0.7955) | (0.8049,0.8618,0.8618,0.9268) |
| (0.0513,0.1453,0.5214,0.5641) | (0.6818,0.7475,0.7475,0.8030) | (0.5909,0.6591,0.6591,0.7500) | (0.7073,0.8618,0.8618,1.0000) | |
| (0.0513,0.1282,0.4359,0.6154) | (0.5000,0.6313,0.6313,0.7273) | (0.8636,0.9091,0.9091,0.9545) | (0.6341,0.7805,0.7805,0.9268) | |
| (0.1026,0.2137,0.6325,0.7692) | (0.7576,0.8485,0.8485,0.9848) | (0.8636,0.9318,0.9318,1.0000) | (0.8049,0.8943,0.8943,0.9756) | |
| (0.0000,0.0684,0.4188,0.5641) | (0.7273,0.7677,0.7677,0.8333) | (0.6591,0.7879,0.7879,0.8864) | (0.7073,0.7561,0.7561,0.8049) | |
| (0.1026,0.1368,0.5470,0.7179) | (0.5909,0.6364,0.6364,0.6818) | (0.6591,0.7424,0.7424,0.7955) | (0.6829,0.7480,0.7480,0.8293) | |
| W | (0.5000,0.8400,0.8400,1.0000) | (0.3300,0.6133,0.6133,0.8300) | (0.3300,0.5567,0.6133,0.8400) | (0.5000,0.7233,0.7767,1.0000) |
| Aggregated Information | Criteria | ||
|---|---|---|---|
| X | (0.1700,0.3900,0.4433,0.6700) | (0.1700,0.3867,0.3867,0.6700) | (0.3300,0.6667,0.6667,1.0000) |
| (0.1700,0.5000,0.5000,0.8300) | (0.1700,0.4433,0.4433,0.8300) | (0.1700,0.4433,0.4433,0.6700) | |
| (0.0000,0.3333,0.3333,0.6700) | (0.1700,0.5533,0.5533,1.0000) | (0.3300,0.6667,0.6667,1.0000) | |
| (0.1700,0.5533,0.5533,1.0000) | (0.0000,0.5533,0.7500,1.0000) | (0.3300,0.5000,0.5567,0.8400) | |
| (0.3300,0.7200,0.7200,1.0000) | (0.3400,0.6133,0.7233,1.0000) | (0.3300,0.6667,0.6667,1.0000) | |
| (0.0000,0.3867,0.5833,1.0000) | (0.1700,0.4433,0.4433,0.6700) | (0.5000,0.7767,0.7767,1.0000) | |
| W | (0.1700,0.3867,0.3867,0.6700) | (0.0000,0.2767,0.2767,0.5000) | (0.3300,0.6667,0.6667,1.0000) |
| Alpha | ||||||
|---|---|---|---|---|---|---|
| Status | Status | Status | ||||
| 0 | [0.4027,0.9478] | FD | [0.2613,0.8143] | D | [0.2732,0.8792] | D |
| 0.1 | [0.4348,0.9357] | FD | [0.2879,0.7930] | D | [0.2989,0.8589] | D |
| 0.2 | [0.4634,0.9190] | FD | [0.3146,0.7760] | D | [0.3253,0.8357] | D |
| 0.3 | [0.4903,0.9012] | FD | [0.3412,0.7586] | D | [0.3519,0.8106] | D |
| 0.4 | [0.5169,0.8857] | FD | [0.3675,0.7403] | D | [0.3786,0.7845] | D |
| 0.5 | [0.5431,0.8685] | FD | [0.3936,0.7212] | D | [0.4053,0.7578] | FD |
| 0.6 | [0.5688,0.8495] | FD | [0.4192,0.7014] | FD | [0.4317,0.7307] | FD |
| 0.7 | [0.5939,0.8291] | FD | [0.4443,0.6814] | FD | [0.4577,0.7040] | FD |
| 0.8 | [0.6182,0.8074] | FS | [0.4688,0.6611] | FD | [0.4834,0.6772] | FD |
| 0.9 | [0.6416,0.7845] | FS | [0.4925,0.6400] | FD | [0.5085,0.6501] | FD |
| 1 | [0.6647,0.7600] | FS | [0.5160,0.6182] | FD | [0.5332,0.6231] | FD |
| 0.7012 | FS | 0.5551 | FD | 0.5800 | FD | |
| Alpha | ||||||
|---|---|---|---|---|---|---|
| Status | Status | Status | ||||
| 0 | [0.3280,0.9328] | D | [0.3202,0.8591] | D | [0.2880,0.8686] | D |
| 0.1 | [0.3544,0.9176] | D | [0.3409,0.8404] | D | [0.3126,0.8495] | D |
| 0.2 | [0.3808,0.8992] | D | [0.3619,0.8193] | D | [0.3378,0.8277] | D |
| 0.3 | [0.4073,0.8802] | FD | [0.3832,0.7984] | D | [0.3632,0.8046] | D |
| 0.4 | [0.4337,0.8609] | FD | [0.4049,0.7775] | FD | [0.3886,0.7837] | D |
| 0.5 | [0.4599,0.8405] | FD | [0.4267,0.7567] | FD | [0.4137,0.7630] | FD |
| 0.6 | [0.4855,0.8188] | FD | [0.4488,0.7350] | FD | [0.4384,0.7428] | FD |
| 0.7 | [0.5106,0.7961] | FD | [0.4711,0.7128] | FD | [0.4625,0.7229] | FD |
| 0.8 | [0.5349,0.7724] | FD | [0.4935,0.6902] | FD | [0.4860,0.7025] | FD |
| 0.9 | [0.5584,0.7478] | FD | [0.5159,0.6672] | FD | [0.5087,0.6815] | FD |
| 1 | [0.5811,0.7225] | FD | [0.5384,0.6441] | FD | [0.5306,0.6600] | FD |
| 0.6465 | FS | 0.5912 | FD | 0.5880 | FD | |
| Alpha | ||||||
|---|---|---|---|---|---|---|
| Status | Status | Status | ||||
| 0 | [0.3696,0.9093] | D | [0.2512,0.8169] | D | [0.2453,0.8606] | D |
| 0.1 | [0.3992,0.8952] | D | [0.2781,0.7936] | D | [0.2696,0.8376] | D |
| 0.2 | [0.4282,0.8783] | FD | [0.3053,0.7749] | D | [0.295,0.812] | D |
| 0.3 | [0.4564,0.8595] | FD | [0.3324,0.7557] | D | [0.3213,0.7847] | D |
| 0.4 | [0.4817,0.8395] | FD | [0.3594,0.7355] | D | [0.3481,0.7565] | D |
| 0.5 | [0.5065,0.8186] | FD | [0.3863,0.7145] | D | [0.3752,0.7276] | D |
| 0.6 | [0.5307,0.797] | FD | [0.4128,0.693] | FD | [0.4024,0.6985] | FD |
| 0.7 | [0.5539,0.7756] | FD | [0.4389,0.6714] | FD | [0.4294,0.6693] | FD |
| 0.8 | [0.577,0.7535] | FD | [0.4645,0.649] | FD | [0.4563,0.6405] | FD |
| 0.9 | [0.6001,0.7309] | FD | [0.4894,0.6259] | FD | [0.4831,0.6119] | FD |
| 1 | [0.6238,0.7074] | FD | [0.5143,0.6021] | FD | [0.5097,0.5828] | FD |
| 0.6587 | FS | 0.5484 | FD | 0.5508 | FD | |
| Alpha | ||||||
|---|---|---|---|---|---|---|
| Status | Status | Status | ||||
| 0 | [0.3075,0.9376] | D | [0.3211,0.8704] | D | [0.2571,0.8827] | D |
| 0.1 | [0.3364,0.9217] | D | [0.3434,0.8530] | D | [0.2807,0.8640] | D |
| 0.2 | [0.3655,0.9006] | D | [0.3663,0.8326] | D | [0.3057,0.8411] | D |
| 0.3 | [0.3929,0.8789] | D | [0.3896,0.8106] | D | [0.3315,0.816] | D |
| 0.4 | [0.4205,0.8569] | FD | [0.4133,0.7889] | FD | [0.3579,0.7908] | D |
| 0.5 | [0.4479,0.8333] | FD | [0.4372,0.7676] | FD | [0.3845,0.7669] | D |
| 0.6 | [0.4750,0.8082] | FD | [0.4614,0.7458] | FD | [0.4110,0.7438] | FD |
| 0.7 | [0.5017,0.7819] | FD | [0.4857,0.7234] | FD | [0.4373,0.7211] | FD |
| 0.8 | [0.5279,0.7546] | FD | [0.5099,0.7005] | FD | [0.4632,0.6979] | FD |
| 0.9 | [0.5533,0.7264] | FD | [0.5342,0.6772] | FD | [0.4885,0.6738] | FD |
| 1 | [0.5779,0.6975] | FD | [0.5583,0.6536] | FD | [0.5132,0.6490] | FD |
| 0.6366 | FS | 0.602 | FS | 0.5763 | FD | |
| Literature | Information Type | Hesitant Information Considered |
|---|---|---|
| literature [14,21] | Numerical values | No |
| literature [22] | Interval values | No |
| literature [23] | Linguistic terms | No |
| Our proposal | Numerical values, interval values, linguistic terms, hesitant fuzzy linguistic informaiton | Yes |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.-X.; Wang, L.; Wang, Y.-M. A Novel Early Warning Method for Handling Non-Homogeneous Information. Mathematics 2022, 10, 3016. https://doi.org/10.3390/math10163016
Zhang Z-X, Wang L, Wang Y-M. A Novel Early Warning Method for Handling Non-Homogeneous Information. Mathematics. 2022; 10(16):3016. https://doi.org/10.3390/math10163016
Chicago/Turabian StyleZhang, Zi-Xin, Liang Wang, and Ying-Ming Wang. 2022. "A Novel Early Warning Method for Handling Non-Homogeneous Information" Mathematics 10, no. 16: 3016. https://doi.org/10.3390/math10163016
APA StyleZhang, Z.-X., Wang, L., & Wang, Y.-M. (2022). A Novel Early Warning Method for Handling Non-Homogeneous Information. Mathematics, 10(16), 3016. https://doi.org/10.3390/math10163016







