Adaptive Barrier Fast Terminal Sliding Mode Actuator Fault Tolerant Control Approach for Quadrotor UAVs
Abstract
:1. Introduction
- A fast terminal sliding mode control (FTSMC) approach speeds up the convergence rate in both reaching and sliding phases, and fast finite-time robust performance is achieved.
- A design method that provides a barrier function without information about the upper bounds of perturbations and actuator faults makes the quadrotor track the desired trajectory.
- An SMC technique relies on the hyperbolic tangent function in order to achieve the chattering-free responses.
2. Quadrotor Model
3. Adaptive Barrier Fast Terminal Sliding Mode Control
- The multiplication ofandmust be a positive value.
- multiplied bymust be a positive value.
- The terms−1 and−1 should also be positive values.
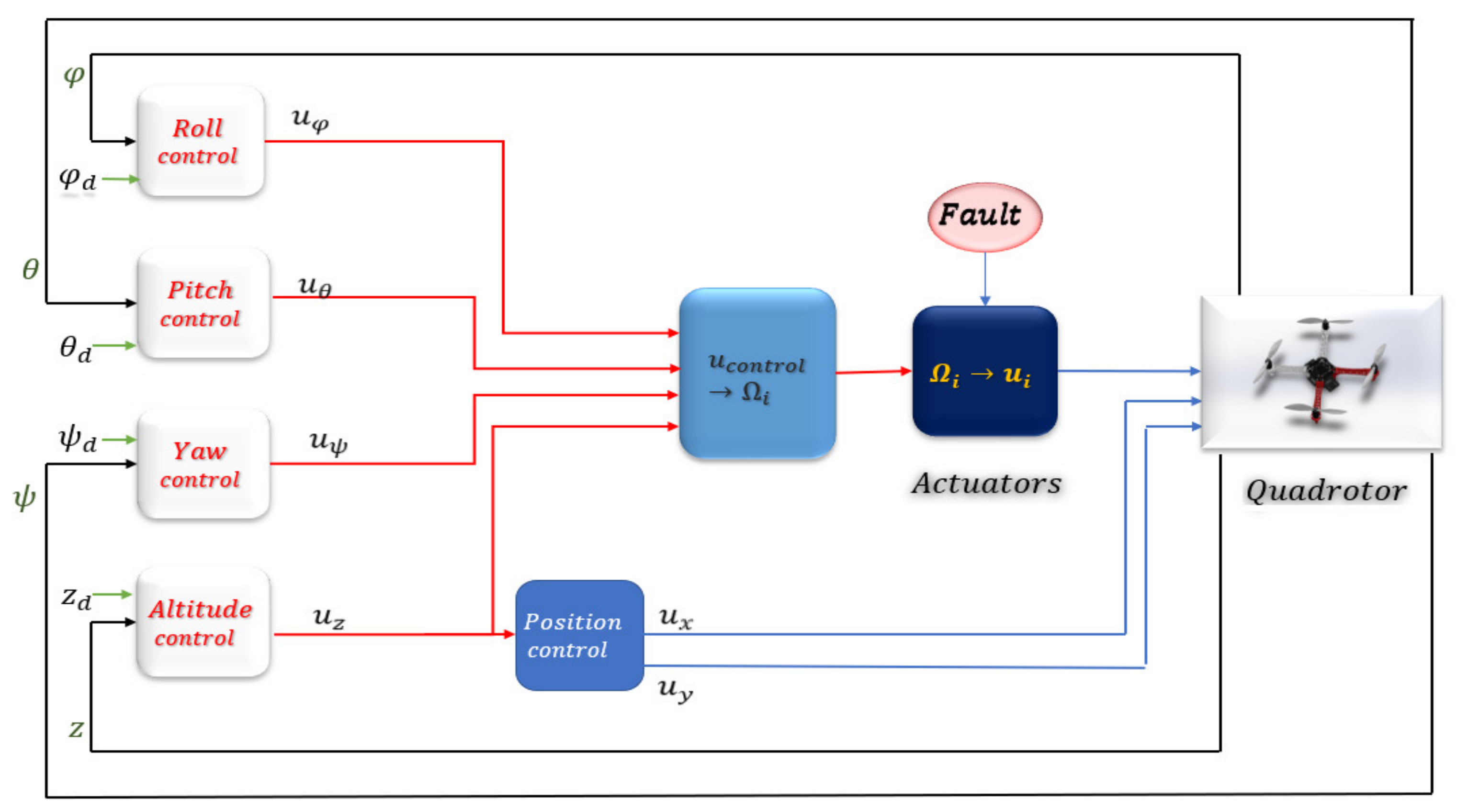
4. Simulation Results
- Input controller;
- Quadrotor actuators;
- General quadrotor system;
- System output.
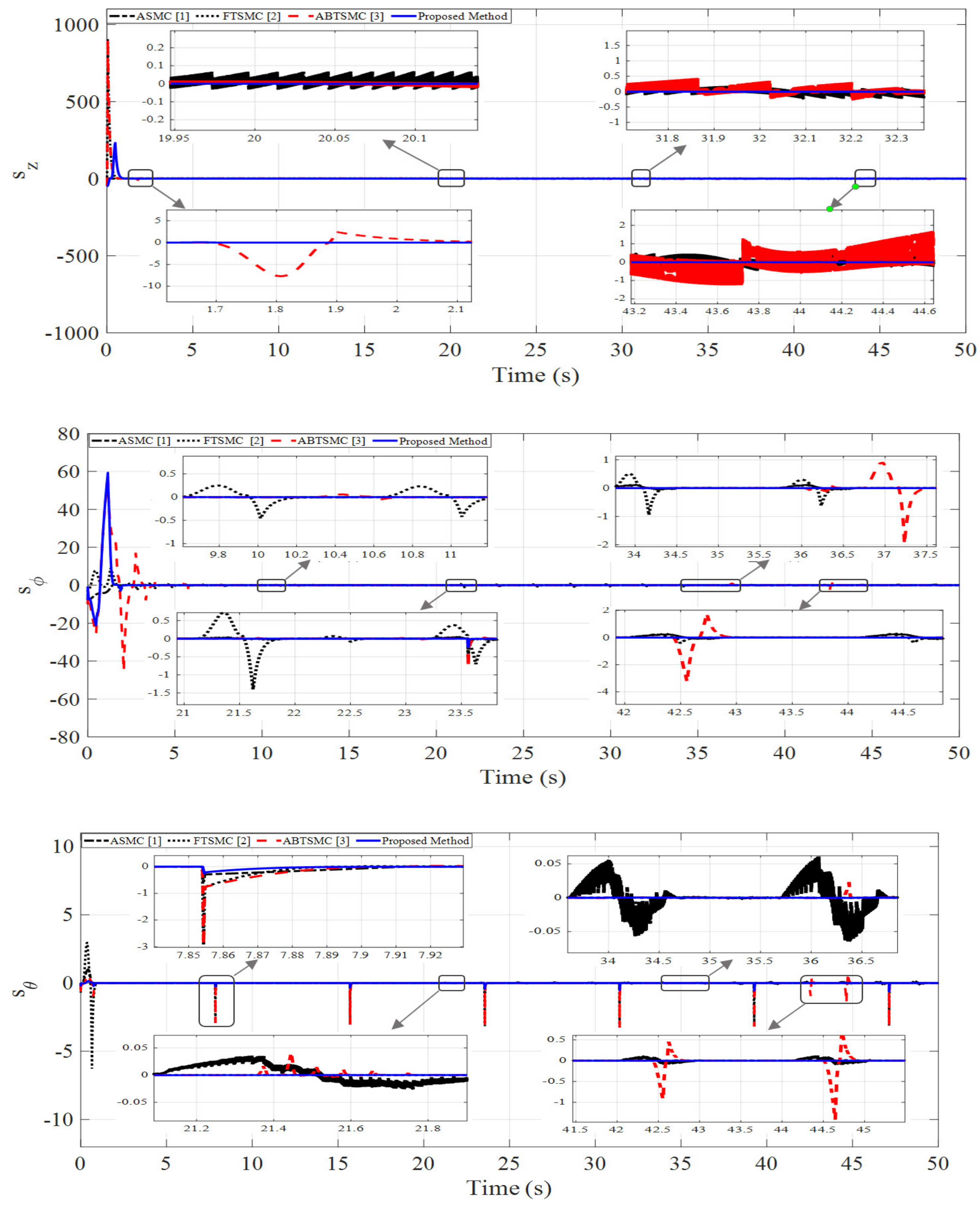
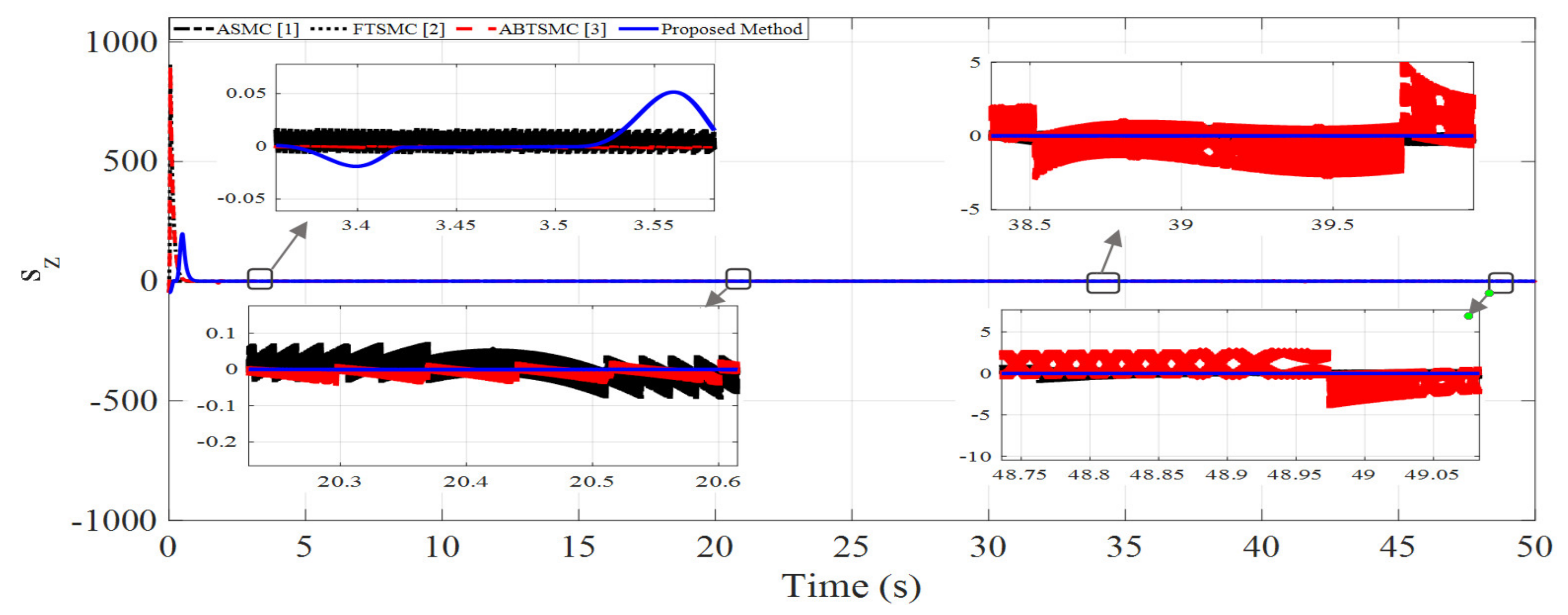
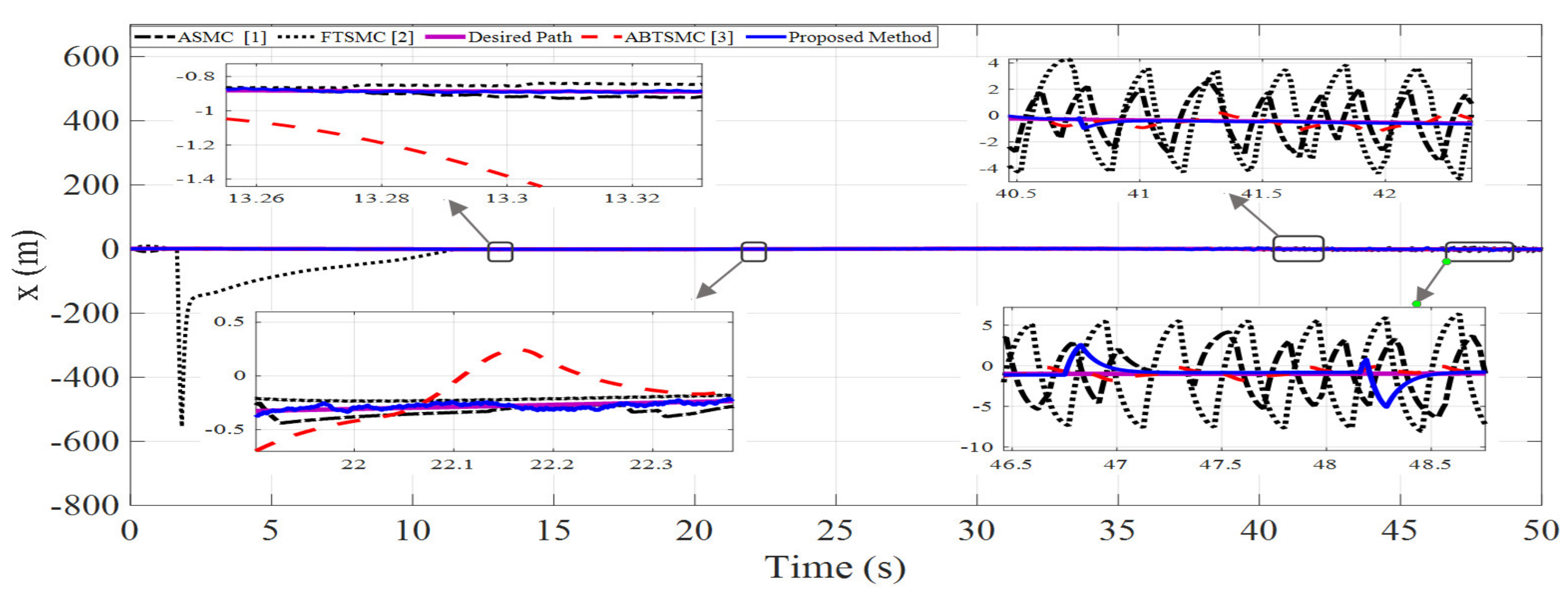
- -
- In the first scenario, 40% of the fault was entered into the system, but in scenario 2, the amount of this fault was 50% in the form of loss of rotor efficiency.
- -
- In the first scenario, the type of sinusoidal fault was intermittent, which sometimes results from cracking of the rotor blades, but the type of fault in the second scenario was a fixed-step function.
- -
- In the first scenario, fault was entered in actuators 2 and 3, but in the second scenario, it was applied to actuators 1 and 2.
5. Conclusions and Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Parameter | Value | Unit | Parameter | Value | Unit |
|---|---|---|---|---|---|
| 9.81 | |||||
| 1 | 0.24 | ||||
References
- Yang, P.; Liu, Z.; Wang, Y.; Li, D. Adaptive sliding mode fault-tolerant control for uncertain systems with time delay. Int. J. Autom. Technol. 2020, 14, 337–345. [Google Scholar] [CrossRef]
- Labbadi, M.; Cherkaoui, M. Robust adaptive nonsingular fast terminal sliding-mode tracking control for an uncertain quadrotor UAV subjected to disturbances. ISA Trans. 2020, 99, 290–304. [Google Scholar] [CrossRef] [PubMed]
- Alattas, K.A.; Mofid, O.; Alanazi, A.K.; Abo-Dief, H.M.; Bartoszewicz, A.; Bakouri, M.; Mobayen, S. Barrier Function Adaptive Nonsingular Terminal Sliding Mode Control Approach for Quad-Rotor Unmanned Aerial Vehicles. Sensors 2022, 22, 909. [Google Scholar] [CrossRef]
- Yang, P.; Wang, Z.; Zhang, Z.; Hu, X. Sliding Mode Fault Tolerant Control for a Quadrotor with Varying Load and Actuator Fault. Actuators 2021, 10, 323. [Google Scholar] [CrossRef]
- Tang, P.; Lin, D.; Zheng, D.; Fan, S.; Ye, J. Observer based finite-time fault tolerant quadrotor attitude control with actuator faults. Aerosp. Sci. Technol. 2020, 104, 105968. [Google Scholar] [CrossRef]
- Drozeski, G.R. A Fault-Tolerant Control Architecture for Unmanned Aerial Vehicles; Georgia Institute of Technology: Atlanta, GA, USA, 2005. [Google Scholar]
- Alkadi, R.; Alnuaimi, N.; Yeun, C.; Shoufan, A. Blockchain Interoperability in Unmanned Aerial Vehicles Networks: State-of-the-art and Open Issues. IEEE Access 2022, 10, 14463–14479. [Google Scholar] [CrossRef]
- Alattas, K.A.; Vu, M.T.; Mofid, O.; El-Sousy, F.F.; Fekih, A.; Mobayen, S. Barrier Function-Based Nonsingular Finite-Time Tracker for Quadrotor UAVs Subject to Uncertainties and Input Constraints. Mathematics 2022, 10, 1659. [Google Scholar] [CrossRef]
- Mofid, O.; Mobayen, S.; Zhang, C.; Esakki, B. Desired tracking of delayed quadrotor UAV under model uncertainty and wind disturbance using adaptive super-twisting terminal sliding mode control. ISA Trans. 2022, 123, 455–471. [Google Scholar] [CrossRef]
- Maddikunta, P.K.R.; Hakak, S.; Alazab, M.; Bhattacharya, S.; Gadekallu, T.R.; Khan, W.Z.; Pham, Q.-V. Unmanned aerial vehicles in smart agriculture: Applications, requirements, and challenges. IEEE Sens. J. 2021, 21, 17608–17619. [Google Scholar] [CrossRef]
- Blanke, M.; Kinnaert, M.; Lunze, J.; Staroswiecki, M.; Schröder, J. Diagnosis and Fault-Tolerant Control; Springer: Berlin/Heidelberg, Germany, 2006; Volume 2. [Google Scholar]
- Sadeghzadeh, I.; Zhang, Y. A review on fault-tolerant control for unmanned aerial vehicles (UAVs). Infotech@ Aerosp. 2011, 2011, 1472. [Google Scholar]
- Najafi, A.; Bustan, D. Multiple actuator fault diagnosis based on parity space for quadrotor system. J. Aeronaut. Eng. 2020, 22, 1–11. [Google Scholar]
- Fekih, A.; Mobayen, S.; Chen, C.-C. Adaptive Robust Fault-Tolerant Control Design for Wind Turbines Subject to Pitch Actuator Faults. Energies 2021, 14, 1791. [Google Scholar] [CrossRef]
- Bustan, D.; Sani, S.H.; Pariz, N. Adaptive fault-tolerant spacecraft attitude control design with transient response control. IEEE/ASME Trans. Mechatron. 2013, 19, 1404–1411. [Google Scholar]
- Zhang, Y.; Guan, Y.; Jiang, Y.; Chen, X. Lmi-based design of robust fault-tolerant controller. In Proceedings of the 2010 3rd International Symposium on Systems and Control in Aeronautics and Astronautics, Harbin, China, 8–10 June 2010; pp. 353–356. [Google Scholar]
- Yang, G.-H.; Ye, D. Adaptive fault-tolerant H∞ control against sensor failures. IET Control Theory Appl. 2008, 2, 95–107. [Google Scholar] [CrossRef]
- Wang, Y.; Jiang, B.; Wu, Z.-G.; Xie, S.; Peng, Y. Adaptive sliding mode fault-tolerant fuzzy tracking control with application to unmanned marine vehicles. IEEE Trans. Syst. Man Cybern. Syst. 2020, 51, 6691–6700. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, J.; Yan, F.; Shen, Y. Adaptive sliding mode fault-tolerant control for type-2 fuzzy systems with distributed delays. Inf. Sci. 2019, 473, 227–238. [Google Scholar] [CrossRef]
- Qinglei, H.; Zhang, Y.; Xing, H.; Bing, X. Adaptive integral-type sliding mode control for spacecraft attitude maneuvering under actuator stuck failures. Chin. J. Aeronaut. 2011, 24, 32–45. [Google Scholar]
- Xu, S.S.-D.; Chen, C.-C.; Wu, Z.-L. Study of nonsingular fast terminal sliding-mode fault-tolerant control. IEEE Trans. Ind. Electron. 2015, 62, 3906–3913. [Google Scholar] [CrossRef]
- Li, Y.; Sun, K.; Tong, S. Observer-based adaptive fuzzy fault-tolerant optimal control for SISO nonlinear systems. IEEE Trans. Cybern. 2018, 49, 649–661. [Google Scholar] [CrossRef]
- Zou, A.-M.; Kumar, K.D. Adaptive fuzzy fault-tolerant attitude control of spacecraft. Control Eng. Pract. 2011, 19, 10–21. [Google Scholar] [CrossRef]
- Jin, X.; Zhao, X.; Yu, J.; Wu, X.; Chi, J. Adaptive fault-tolerant consensus for a class of leader-following systems using neural network learning strategy. Neural Netw. 2020, 121, 474–483. [Google Scholar] [CrossRef] [PubMed]
- Li, X.-J.; Yang, G.-H. Neural-network-based adaptive decentralized fault-tolerant control for a class of interconnected nonlinear systems. IEEE Trans. Neural Netw. Learn. Syst. 2016, 29, 144–155. [Google Scholar] [CrossRef] [PubMed]
- Maciejowski, J.M.; Jones, C.N. MPC fault-tolerant flight control case study: Flight 1862. IFAC Proc. Vol. 2003, 36, 119–124. [Google Scholar] [CrossRef] [Green Version]
- Sun, S.; Dong, L.; Li, L.; Gu, S. Fault-tolerant control for constrained linear systems based on MPC and FDI. Int. J. Inf. Syst. Sci. 2008, 4, 512–523. [Google Scholar]
- Barghandan, S.; Badamchizadeh, M.A.; Jahed-Motlagh, M.R. Improved adaptive fuzzy sliding mode controller for robust fault tolerant of a quadrotor. Int. J. Control Autom. Syst. 2017, 15, 427–441. [Google Scholar] [CrossRef]
- Chen, F.; Zhang, K.; Wang, Z.; Tao, G.; Jiang, B. Trajectory tracking of a quadrotor with unknown parameters and its fault-tolerant control via sliding mode fault observer. Proc. Inst. Mech. Eng. Part I J. Syst. Control. Eng. 2015, 229, 279–292. [Google Scholar] [CrossRef]
- Mallavalli, S.; Fekih, A. Sliding mode-based fault tolerant control designs for quadrotor UAVs-A comparative study. In Proceedings of the 2017 13th IEEE International Conference on Control & Automation (ICCA), Ohrid, Macedonia, 3–6 July 2017; pp. 154–159. [Google Scholar]
- Ullah, S.; Iqbal, K.; Malik, F.M. Fault-Tolerant Sliding Mode Control of a Quadrotor UAV with Delayed Feedback. Int. J. Mech. Eng. Robot. Res. 2020, 9, 1–6. [Google Scholar] [CrossRef]
- Wang, Z.; Yang, P.; Hu, X.; Zhang, Z.; Wen, C. Sliding Mode Fault Tolerant Control of Quadrotor Uav with State Constraints Under Actuator Fault. Int. J. Innov. Comput. Inf. Control. 2021, 17, 639–653. [Google Scholar]
- Aguilar-Ibanez, C.; Moreno-Valenzuela, J.; García-Alarcón, O.; Martinez-Lopez, M.; Acosta, J.Á.; Suarez-Castanon, M.S. PI-type controllers and Σ–Δ modulation for saturated DC-DC buck power converters. IEEE Access 2021, 9, 20346–20357. [Google Scholar] [CrossRef]
- Balcazar, R.; Rubio, J.d.J.; Orozco, E.; Andres Cordova, D.; Ochoa, G.; Garcia, E.; Pacheco, J.; Gutierrez, G.J.; Mujica-Vargas, D.; Aguilar-Ibañez, C. The Regulation of an Electric Oven and an Inverted Pendulum. Symmetry 2022, 14, 759. [Google Scholar] [CrossRef]
- Rubio, J.D.J.; Orozco, E.; Cordova, D.A.; Islas, M.A.; Pacheco, J.; Gutierrez, G.J.; Zacarias, A.; Soriano, L.A.; Meda-Campaña, J.A.; Mujica-Vargas, D. Modified linear technique for the controllability and observability of robotic arms. IEEE Access 2022, 10, 3366–3377. [Google Scholar] [CrossRef]
- Silva-Ortigoza, R.; Hernández-Márquez, E.; Roldán-Caballero, A.; Tavera-Mosqueda, S.; Marciano-Melchor, M.; Garcia-Sanchez, J.R.; Hernández-Guzmán, V.M.; Silva-Ortigoza, G. Sensorless Tracking Control for a “Full-Bridge Buck Inverter–DC Motor” System: Passivity and Flatness-Based Design. IEEE Access 2021, 9, 132191–132204. [Google Scholar] [CrossRef]
- Soriano, L.A.; Rubio, J.d.J.; Orozco, E.; Cordova, D.A.; Ochoa, G.; Balcazar, R.; Cruz, D.R.; Meda-Campaña, J.A.; Zacarias, A.; Gutierrez, G.J. Optimization of sliding mode control to save energy in a SCARA robot. Mathematics 2021, 9, 3160. [Google Scholar] [CrossRef]
- Soriano, L.A.; Zamora, E.; Vazquez-Nicolas, J.; Hernández, G.; Barraza Madrigal, J.A.; Balderas, D. PD control compensation based on a cascade neural network applied to a robot manipulator. Front. NeuroRobot. 2020, 14, 577749. [Google Scholar] [CrossRef]
- Samir, B. Design and Control of Quadrotors with Application to Autonomous Flying. Ph.D. Thesis, Swiss Federal Institute of Technology, Lausanne, Switzerland, 2007. [Google Scholar]
- Eliker, K.; Grouni, S.; Tadjine, M.; Zhang, W. Practical finite time adaptive robust flight control system for quad-copter UAVs. Aerosp. Sci. Technol. 2020, 98, 105708. [Google Scholar] [CrossRef]
- Eliker, K.; Grouni, S.; Tadjine, M.; Zhang, W. Quadcopter nonsingular finite-time adaptive robust saturated command-filtered control system under the presence of uncertainties and input saturation. Nonlinear Dyn. 2021, 104, 1363–1387. [Google Scholar] [CrossRef]
- Ejaz, F.; Hamayun, M.T.; Hussain, S.; Ijaz, S.; Yang, S.; Shehzad, N.; Rashid, A. An adaptive sliding mode actuator fault tolerant control scheme for octorotor system. Int. J. Adv. Robot. Syst. 2019, 16, 1729881419832435. [Google Scholar] [CrossRef] [Green Version]
- Mallavalli, S.; Fekih, A. A fault tolerant tracking control for a quadrotor UAV subject to simultaneous actuator faults and exogenous disturbances. Int. J. Control 2020, 93, 655–668. [Google Scholar] [CrossRef]
- Saggai, A.; Zeghlache, S.; Benyettou, L.; Djerioui, A. Fault Tolerant Control against Actuator Faults Based on Interval Type-2 Fuzzy Sliding Mode Controller for a Quadrotor Aircraft. In Proceedings of the 2020 2nd International Workshop on Human-Centric Smart Environments for Health and Well-being (IHSH), Boumerdes, Algeria, 9–10 February 2021; pp. 181–186. [Google Scholar]
- Zeghlache, S.; Djerioui, A.; Benyettou, L.; Benslimane, T.; Mekki, H.; Bouguerra, A. Fault tolerant control for modified quadrotor via adaptive type-2 fuzzy backstepping subject to actuator faults. ISA Trans. 2019, 95, 330–345. [Google Scholar] [CrossRef]
- Naseri, K.; Vu, M.T.; Mobayen, S.; Najafi, A.; Fekih, A. Design of Linear Matrix Inequality-Based Adaptive Barrier Global Sliding Mode Fault Tolerant Control for Uncertain Systems with Faulty Actuators. Mathematics 2022, 10, 2159. [Google Scholar] [CrossRef]
- Nekoukar, V.; Dehkordi, N.M. Robust path tracking of a quadrotor using adaptive fuzzy terminal sliding mode control. Control Eng. Pract. 2021, 110, 104763. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, Y. An adaptive fault-tolerant sliding mode control allocation scheme for multirotor helicopter subject to simultaneous actuator faults. IEEE Trans. Ind. Electron. 2017, 65, 4227–4236. [Google Scholar] [CrossRef] [Green Version]
- Izadi, H.A.; Zhang, Y.; Gordon, B.W. Fault tolerant model predictive control of quad-rotor helicopters with actuator fault estimation. IFAC Proc. Vol. 2011, 44, 6343–6348. [Google Scholar] [CrossRef] [Green Version]
- Li, T.; Zhang, Y.; Gordon, B.W. Nonlinear fault-tolerant control of a quadrotor UAV based on sliding mode control technique. IFAC Proc. Vol. 2012, 45, 1317–1322. [Google Scholar] [CrossRef]
- Wang, F.; Ma, Z.; Gao, H.; Zhou, C.; Hua, C. Disturbance Observer-based Nonsingular Fast Terminal Sliding Mode Fault Tolerant Control of a Quadrotor UAV with External Disturbances and Actuator Faults. Int. J. Control Autom. Syst. 2022, 20, 1122–1130. [Google Scholar] [CrossRef]
- Wang, X.; van Kampen, E.-J.; Chu, Q. Quadrotor fault-tolerant incremental nonsingular terminal sliding mode control. Aerosp. Sci. Technol. 2019, 95, 105514. [Google Scholar] [CrossRef]
- Li, X.; Zhang, H.; Fan, W.; Wang, C.; Ma, P. Finite-time control for quadrotor based on composite barrier Lyapunov function with system state constraints and actuator faults. Aerosp. Sci. Technol. 2021, 119, 107063. [Google Scholar] [CrossRef]
- Wang, J.; Zhao, Z.; Zheng, Y. NFTSM-based Fault Tolerant Control for Quadrotor Unmanned Aerial Vehicle with Finite-Time Convergence. IFAC-PapersOnLine 2018, 51, 441–446. [Google Scholar] [CrossRef]
- Li, T.; Zhang, Y.; Gordon, B.W. Passive and active nonlinear fault-tolerant control of a quadrotor unmanned aerial vehicle based on the sliding mode control technique. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2013, 227, 12–23. [Google Scholar] [CrossRef]
- Aghababa, M.P.; Akbari, M.E. A chattering-free robust adaptive sliding mode controller for synchronization of two different chaotic systems with unknown uncertainties and external disturbances. Appl. Math. Comput. 2012, 218, 5757–5768. [Google Scholar] [CrossRef]
- Boukattaya, M.; Mezghani, N.; Damak, T. Adaptive nonsingular fast terminal sliding-mode control for the tracking problem of uncertain dynamical systems. ISA Trans. 2018, 77, 1–19. [Google Scholar] [CrossRef] [PubMed]
- Labbadi, M.; Cherkaoui, M. Robust adaptive backstepping fast terminal sliding mode controller for uncertain quadrotor UAV. Aerosp. Sci. Technol. 2019, 93, 105306. [Google Scholar] [CrossRef]
- Yu, X.; Zhihong, M. Fast terminal sliding-mode control design for nonlinear dynamical systems. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2002, 49, 261–264. [Google Scholar]
- Nguyen, V.-C.; Vo, A.-T.; Kang, H.-J. A finite-time fault-tolerant control using non-singular fast terminal sliding mode control and third-order sliding mode observer for robotic manipulators. IEEE Access 2021, 9, 31225–31235. [Google Scholar] [CrossRef]
- Obeid, H.; Fridman, L.M.; Laghrouche, S.; Harmouche, M. Barrier function-based adaptive sliding mode control. Automatica 2018, 93, 540–544. [Google Scholar] [CrossRef]
- Obeid, H.; Laghrouche, S.; Fridman, L.; Chitour, Y.; Harmouche, M. Barrier function-based adaptive super-twisting controller. IEEE Trans. Autom. Control 2020, 65, 4928–4933. [Google Scholar] [CrossRef] [Green Version]
- Afshari, M.; Mobayen, S.; Hajmohammadi, R.; Baleanu, D. Global sliding mode control via linear matrix inequality approach for uncertain chaotic systems with input nonlinearities and multiple delays. J. Comput. Nonlinear Dyn. 2018, 13, 031008. [Google Scholar] [CrossRef]
- Yau, H.-T. Design of adaptive sliding mode controller for chaos synchronization with uncertainties. Chaos Solitons Fractals 2004, 22, 341–347. [Google Scholar] [CrossRef]





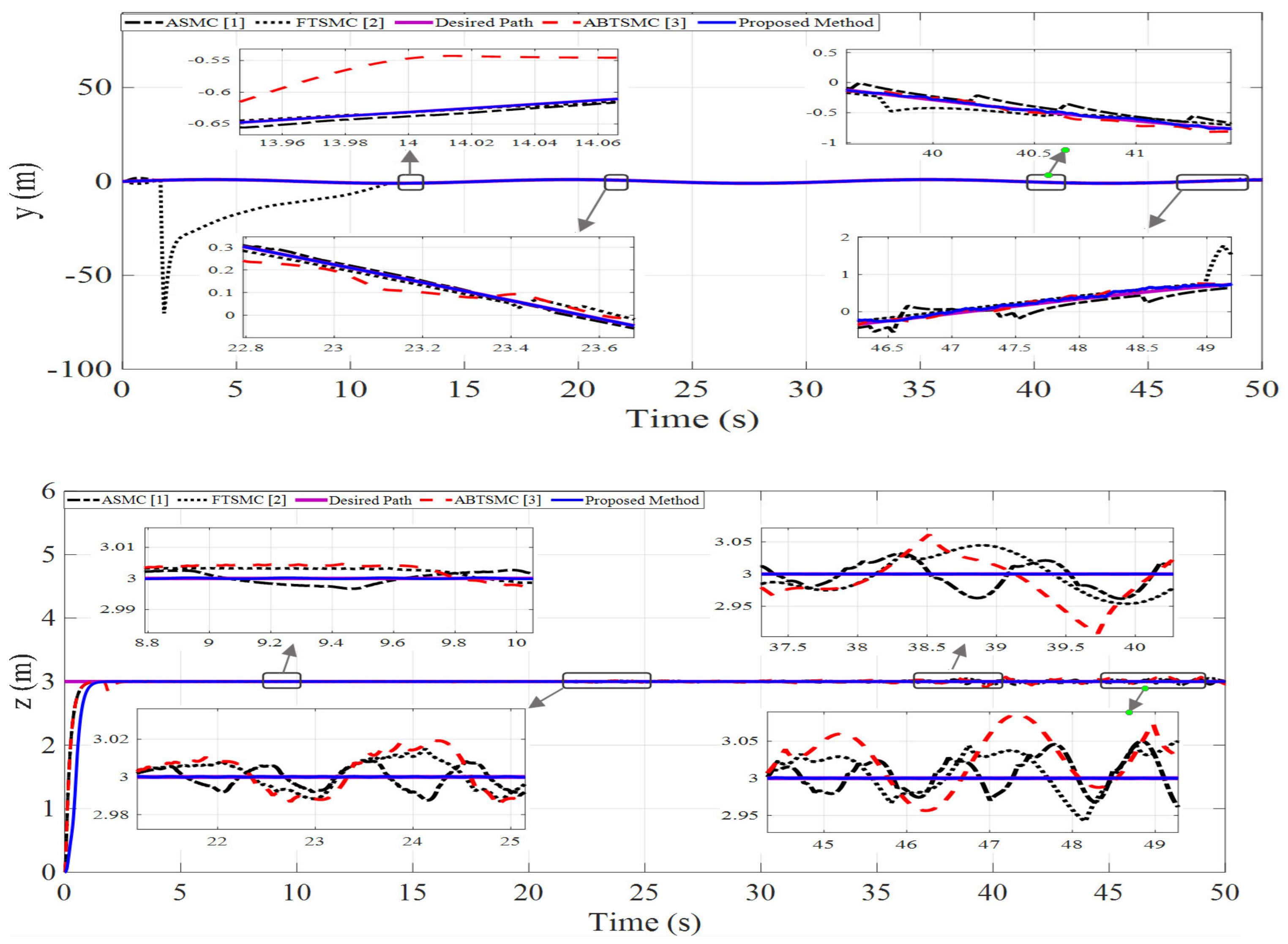
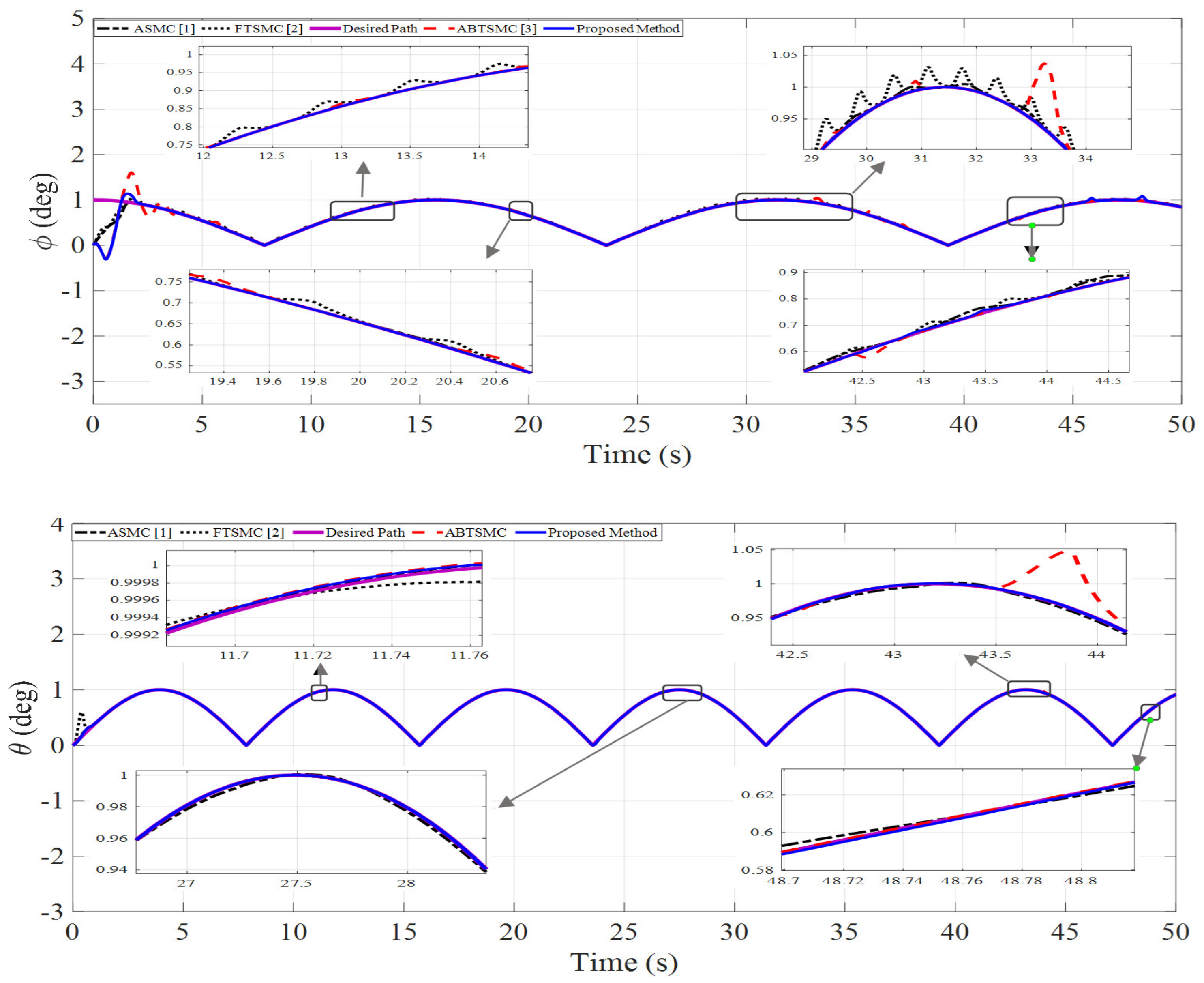
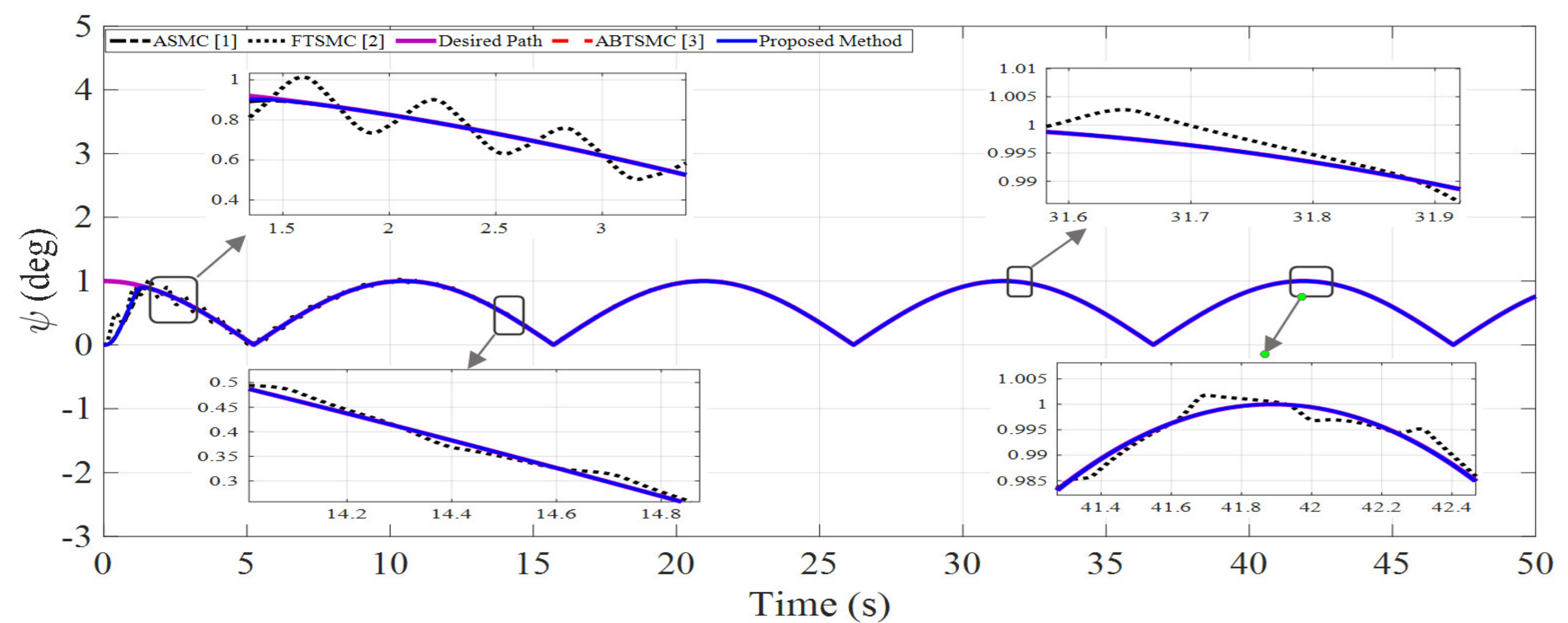
| Variable | Value | Variable | Value |
|---|---|---|---|
| = for () | 5 | = for (,) | 9 |
| 2 | 0 | ||
| 3 | 5 | ||
| 5 | 1 |
| State | Desired Path | Disturbance |
|---|---|---|
| 3 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Najafi, A.; Vu, M.T.; Mobayen, S.; Asad, J.H.; Fekih, A. Adaptive Barrier Fast Terminal Sliding Mode Actuator Fault Tolerant Control Approach for Quadrotor UAVs. Mathematics 2022, 10, 3009. https://doi.org/10.3390/math10163009
Najafi A, Vu MT, Mobayen S, Asad JH, Fekih A. Adaptive Barrier Fast Terminal Sliding Mode Actuator Fault Tolerant Control Approach for Quadrotor UAVs. Mathematics. 2022; 10(16):3009. https://doi.org/10.3390/math10163009
Chicago/Turabian StyleNajafi, Amin, Mai The Vu, Saleh Mobayen, Jihad H. Asad, and Afef Fekih. 2022. "Adaptive Barrier Fast Terminal Sliding Mode Actuator Fault Tolerant Control Approach for Quadrotor UAVs" Mathematics 10, no. 16: 3009. https://doi.org/10.3390/math10163009
APA StyleNajafi, A., Vu, M. T., Mobayen, S., Asad, J. H., & Fekih, A. (2022). Adaptive Barrier Fast Terminal Sliding Mode Actuator Fault Tolerant Control Approach for Quadrotor UAVs. Mathematics, 10(16), 3009. https://doi.org/10.3390/math10163009










