WSA-Supplements and Proper Classes

Abstract

In this paper, we introduce the concept of wsa-supplements and investigate the objects of the class of short exact sequences determined by wsa-supplement submodules, where a submodule U of a module M is called a wsa-supplement in M if there is a submodule V of M with $U+V=M$ and $U\cap V$ is weakly semiartinian. We prove that a module M is weakly semiartinian if and only if every submodule of M is a wsa-supplement in M. We introduce $CC$-rings as a generalization of C-rings and show that a ring is a right $CC$-ring if and only if every singular right module has a crumbling submodule. The class of all short exact sequences determined by wsa-supplement submodules is shown to be a proper class which is both injectively and co-injectively generated. We investigate the homological objects of this proper class along with its relation to $CC$-rings.

1. Introduction

Throughout this study, all rings considered are associative with an identity element and all modules at hand are right and unital. Given such a module M, we use the notations $E\left(M\right)$, $Soc\left(M\right)$, $Z\left(M\right)$, $Rad\left(M\right)$ for the injective hull, socle, singular submodule, and radical of M, respectively. The notation ($N\lneqq M$) $N\le M$ means that N is a (proper) submodule of M. $Mod-R$ denotes the category of all right R-modules over a ring R. For the terminology and notations used in this work we refer the reader to [1,2,3].

For any $M\in Mod-R$, we denote the injectivity domain of M by ${\mathfrak{Jn}}^{-1}\left(M\right)$. It is clear that M is injective if and only if its injectivity domain is as large as it can be, that is, ${\mathfrak{Jn}}^{-1}\left(M\right)=Mod-R$. It is well known that every module is injective relative to any semisimple module. In [4], the authors introduced modules M whose injectivity domain ${\mathfrak{Jn}}^{-1}\left(M\right)$ is minimal possible, namely the class of all semisimple modules and called such modules poor. This definition gives a natural homological opposite to injectivity of modules since only injective modules have the class of all modules as their injectivity domain. It is proved in [5] (Proposition 1) that every ring has a poor module. However, semisimple poor modules need not exist over an arbitrary ring. Recall that a module M is said to crumble (or be a crumbling module) if $Soc(M/N)$ is a direct summand of $M/N$ for every submodule N of M. It follows from [5] (Corollary 2) that a module M crumbles if and only if it is a locally noetherian V-module. It is shown in [5] (Theorem 1) that a ring R has a semisimple poor module if and only if every right crumbling R-module is semisimple. Clearly, a ring R crumbles if and only if it is a right $SSI$-ring, that is, every semisimple right R-module is injective.

Following [6], we denote the sum of all submodules of a module M that crumble by $C\left(M\right)$. By [6] (Propositions 3.1 and 3.4), $C\left(M\right)$ is the largest submodule of M that crumbles and $Soc\left(M\right)\le C\left(M\right)$. A module M is called semiartinian if $Soc(M/N)\ne 0$ for every proper submodule N of M. As a proper generalization of artinian modules, the class of semiartinian modules are extensively studied in the literature. In [6], the authors considered modules of which factor modules have a nonzero crumbling submodule. A module M is called weakly semiartinian if $C(M/N)\ne 0$ for every proper submodule N of M. The sum of all weakly semiartinian submodules of a module M is the largest weakly semiartinian submodule of M which we denote by $wsa\left(M\right)$. Clearly, semiartinian modules and crumbling modules are examples of weakly semiartinian modules. A weakly semiartinian module need not be semiartinian, in general. An example of a weakly semiartinian module which is not semiartinian can be found in [6] (Remark 2). Various properties of weakly semiartinian modules are given in the same work.

It is well known that a module is semisimple if and only if its submodules are direct summands. As a generalization of direct summands, supplement submodules are defined as follows. Let M be a module and $U,V\le M$. V is called a supplement of U in M if it is minimal with respect to $M=U+V$, equivalently if $M=U+V$ and $U\cap V$ is small in V. Here a submodule S of a module M is called small in M, denoted by $S\ll M$, if $M\ne S+L$ for every proper submodule L of M. A module M is called supplemented if every one of its submodules has a supplement in M. Supplement submodules play an important role in ring theory and relative homological algebra. In recent years, types of supplement submodules are extensively studied by many authors. In a series of books and articles [1,2,3,7,8], the authors have obtained detailed information about variations of supplement submodules and related rings.

In [9], the author introduced proper classes to axiomatize conditions under which a class of short exact sequences of modules can be computed as Ext groups corresponding to a certain relative cohomology. The class $\mathcal{S}plit$ of all splitting short exact sequences of right R-modules and the class $\mathcal{A}bs$ of all short exact sequences of right R-modules are trivial examples of proper classes. It follows from [1] (20.7) that the class $\mathcal{S}$upp of all short exact sequences $0⟶M\stackrel{\psi }{⟶}N⟶K⟶0$ such that $Im\psi$ is a supplement in N is a proper class. Examples and properties of proper classes, especially related to supplements can be found in [10,11,12].

Recently defined type of supplement submodules is as follows. A submodule V of a module M is called an sa-supplement of U in M if $M=U+V$ and $U\cap V$ is semiartinian (see [7]). It is shown in [7] that the class $\mathcal{SAS}$ of all short exact sequences $0⟶M\stackrel{\psi }{⟶}N⟶K⟶0$ such that $Im\psi$ is an sa-supplement in N is a proper class. Since semiartinian modules are weakly semiartinian, it is of interest to investigate a new type of supplement submodules by replacing the property of being “semiartinian” by being “weakly semiartinian”. The purpose of this paper is to introduce the concept of wsa-supplement submodules and investigate the objects of the proper class determined by wsa-supplement submodules in relative homological algebra.

The paper is organized as follows. In Section 2, we prove that a module M is weakly semiartinian if and only if every submodule of M is a wsa-supplement in M. In particular, a ring R is weakly semiartinian if and only if every right maximal ideal of R is a wsa-supplement in R.

We introduce right $CC$-rings as a generalization of C-rings and give some characterizations of such rings in Section 3. We show that a ring R is a right $CC$-ring if and only if every singular right R-module has a crumbling submodule. A semilocal right $CC$-ring is a right C-ring. A right noetherian and a right $WV$-ring is a right $CC$-ring.

In Section 4, we show that, over an arbitrary ring, the class of all short exact sequences $0⟶M\stackrel{\psi }{⟶}N⟶K⟶0$ such that $Im\psi$ is a wsa-supplement in N is a proper class. We study the objects of this class, which we call $\mathcal{WSS}$. We show that a module M is $\mathcal{WSS}$-co-injective if and only if it is a wsa-supplement $E\left(M\right)$. Over a right $CC$-ring, a projective module P is $\mathcal{WSS}$-co-injective if and only if $P/wsa\left(P\right)$ is injective. A ring R is weakly semiartinian if and only if every right R-module is $\mathcal{WSS}$-co-injective. Finally, we show that over a crumbling-free ring $\mathcal{WSS}$-coprojective modules are only the projective modules.

2. Weakly Semiartinian Modules

In this section, we give a characterization of weakly semiartinian modules via wsa-supplement submodules. Firstly, let us start by giving the closure properties.

Proposition 1

([6] (Proposition 3.1)). If $f:M⟶N$ is a homomorphism of modules, then $f(C(M)\subseteq C(N)$.

Proposition 2.

The class of weakly semiartinian modules is closed under submodules, factor modules, direct sums, sums and extensions.

Proof. 

By [6] (Propositions 3.1 and 3.4), we get that the class of weakly semiartinian modules is closed under submodules, factor modules, direct sums and sums. Let B be a module and A be a submodule of B with A and $B/A$ weakly semiartinian. Assume that $C(B/X)=0$ for some $X\lneqq B$. By Proposition 1, we have $C(A/A\cap X)\cong C\left(\right(A+X)/X)\le C(B/X)=0$. Since A is weakly semiartinian, $A/A\cap X)=0$ so that $A\le X$. $B/X\cong (B/A)/(X/A)$ is weakly semiartinian which implies that $C(B/X)\ne 0$, a contradiction. Hence, B is weakly semiartinian. □

The sum of all weakly semiartinian submodules of a module M is denoted by $wsa\left(M\right)$. By Proposition 2, $wsa\left(M\right)$ is weakly semiartinian. Therefore M is weakly semiartinian if and only if $wsa\left(M\right)=M$. Using this fact and Proposition 2, we have the following result.

Corollary 1.

For any module M, $wsa(M/wsa(M\left)\right)=0$.

Proof. 

Let $N\le M$ containing $wsa\left(M\right)$ such that $N/wsa\left(M\right)\le wsa(M/wsa(M\left)\right)$. It follows from Proposition 2 that $N/wsa\left(M\right)$ is weakly semiartinian. Since $wsa\left(M\right)$ is weakly semiartinian, applying Proposition 2 once again, we obtain that N is weakly semiartinian. Therefore $N\subseteq wsa\left(M\right)$. This means that $N/wsa\left(M\right)=0$. □

Let M be a module and $U\le M$. We say that U is (has) a weakly semiartinian supplement (wsa-supplement for short) in M if there exists $V\le M$ such that $U+V=M$ and $U\cap V$ is a weakly semiartinian module.

Theorem 1.

An R-module M is weakly semiartinian if and only if every submodule of M is a wsa-supplement in M.

Proof. 

Necessity follows from Proposition 2. For sufficiency, suppose that $C\left(mR\right)=0$ for some $m\in M$. Let U be any submodule of $mR$. By the assumption, there exists a submodule V of M such that $M=U+V$ and $U\cap V$ is weakly semiartinian. Using modular law, we have $mR=U+V\cap mR$. Note that $C(U\cap V)=C(U\cap mR\cap V)\subseteq C\left(mR\right)=0$. It means that U is a direct summand of $mR$ and so $mR$ is semisimple. Therefore $mR=Soc\left(mR\right)=C\left(mR\right)=0$, and hence $m=0$. This completes the proof. □

A module M is said to be crumbling-free if $C\left(M\right)=0$. A ring R is called crumbling-free if $R_R$ is crumbling free. Let R be a ring and A and B be R-modules. Recall that A is B-injective if for any submodule X of B, any homomorphism $f:X\to A$ extends to a homomorphism $g:B\to A$.

Proposition 3.

An R-module M is weakly semiartinian if and only if every crumbling-free R-module is M-injective.

Proof. 

Necessity is clear since $C\left(U\right)\ne 0$ for every submodule U of M. For sufficiency, suppose that N is a submodule of M with $C\left(N\right)=0$. Let $U\le N$. Since N is crumbling-free, U is crumbling-free and so, by the hypothesis, U is M-injective. So we can write $M=U\oplus V$, where V is a submodule of M. By the modular law, we get $N=U\oplus N\cap V$. This means that $N=Soc\left(N\right)=C\left(N\right)=0$. Hence M is weakly semiartinian. □

Proposition 4.

Let M be a module and U be a submodule of M with $M/U$ weakly semiartinian. A submodule V of M is a wsa-supplement of U in M if and only if $M=U+V$ and V is weakly semiartinian.

Proof. 

Let V be a wsa-supplement of U in M. Then $V/(U\cap V)\cong M/U$ is weakly semiartinian. Since $U\cap V$ is also weakly semiartinian, it follows from Proposition 2 that V is weakly semiartinian. The converse is clear by again Proposition 2. □

Since for a maximal submodule U of M we have $M/U$ is simple, therefore weakly semiartinian, the following result is a consequence of Proposition 4.

Corollary 2.

Let M be a module and U be a maximal submodule of M. A submodule V of M is a wsa-supplement of U in M if and only if $M=U+V$ and V is weakly semiartinian.

Recall that a module M is coatomic if every proper submodule of M is contained in a maximal submodule of M.

Corollary 3.

Let M be a coatomic module. Then M is weakly semiartinian if and only if every maximal submodule of M is a wsa-supplement in M.

Proof. 

Necessity follows from Proposition 1. For sufficiency, assume that M is not weakly semiartinian, that is, $wsa\left(M\right)\ne M$. Let N be a maximal submodule of M that contains $wsa\left(M\right)$ and K be a wsa-supplement of N in M. Then K is weakly semiartinian by Corollary 2 and we have $K\le wsa\left(M\right)\le N$ which implies $M=N+K\le N$, contradicting the maximality of N. □

It is well known that a ring R is semisimple artinian if and only if every maximal right ideal of R is a direct summand of R. Now we give an analogous characterization of this fact for right weakly semiartinian rings.

Corollary 4.

A ring R is right weakly semiartinian if and only if every maximal right ideal of R is a wsa-supplement in R.

3. A Generalization of $\mathit{C}$-Rings

In [1] (10.10), a ring R is called a right C-ring if for every right R-module M and for every proper essential submodule N of M, $Soc(M/N)\ne 0$, that is $M/N$ has a simple submodule. The class of right C-rings is studied by many authors in homological algebra. Semiartinian rings and Dedekind domains are examples right C-rings. Since semiartinian rings are weakly semiartinian, motivated by this fact, it is natural to introduce right $CC$-rings as follows: A ring R is called a right $CC$-ring if for every right R-module M and for every proper essential submodule N of M, $C(M/N)\ne 0$, that is $M/N$ has a cyclic crumbling submodule.

Proposition 5.

The following statements are equivalent for a ring R.

1. 

R is a right $CC$-ring;

2. 

Every singular right R-module has a cyclic crumbling submodule;

3. 

For every proper essential right ideal I of R, $C(R/I)\ne 0$.

Proof. 

$(1\Rightarrow 2)$: Let M be a singular right R-module and $0\ne m\in M$. Now consider the isomorphism $f:R/ann\left(m\right)⟶mR$. Since M is singular, $ann\left(m\right)$ is a non-zero proper essential right ideal of R. Then, $R/ann\left(m\right)$ has a cyclic crumbling submodule, that is $C(R/ann(m\left)\right)\ne 0$. It follows from Proposition 1 that $C\left(mR\right)\ne 0$. This completes the proof of $(1\Rightarrow 2)$.

$(2\Rightarrow 3)$ is clear since $R/I$ is a singular right R-module for every proper essential right ideal I of R.

$(3\Rightarrow 1)$: Let M be an R-module and N be a proper essential submodule of M. We shall show that $C(M/N)\ne 0$. Let $0\ne m+N\in M/N$. Since $M/N$ is singular, $ann(m+N)$ is a proper essential right ideal of R. By assumption, $R/ann(m+N)$ has a cyclic crumbling submodule. Applying Proposition 1, we obtain that $C\left(R\right(m+N\left)\right)\ne 0$ and so $C(M/N)\ne 0$. It means that R is a right $CC$-ring. □

As a consequence of Proposition 5, we have the following result.

Corollary 5.

Let R be commutative domain. Then the following statements are equivalent.

1. 

R is a right $CC$-ring;

2. 

Every torsion right R-module has a cyclic crumbling submodule.

A ring R is called a right weakly-V-ring$(WV$-ring for short) if every simple right R-module is $R/I$-injective for any right ideal I of R such that $R/I$ is proper. Clearly, every right V-ring is a right $WV$-ring. Since a right $WV$-ring need not be right noetherian; in general, the authors investigated when a right $WV$-ring is right noetherian in [13] and showed that a right $WV$-ring R is right noetherian if and only if every cyclic right R-module can be written as a direct sum of a projective module and a module which is either CS or right noetherian.

Proposition 6.

A right noetherian and a right $WV$-ring is a right $CC$-ring.

Proof. 

Let R be a right noetherian and a right $WV$-ring. Suppose that N is a proper essential submodule of an R-module M. Let $0\ne m+N\in M/N$. Then there exists a proper essential right ideal I of R such that $R/I\cong R(m+N)$. Clearly, $R(m+N)$ is noetherian. Since R is a right $WV$-ring, $R/I$ is a V-module. It means that $R(m+N)$ crumbles and so $M/N$ has a cyclic crumbling submodule. □

Proposition 7.

Let R be a ring with $R/Soc\left(R_R\right)$ weakly semiartinian. Then R is a right $CC$-ring.

Proof. 

By Proposition 5, it suffices to show that $C(R/I)\ne 0$ for every proper essential right ideal I of R. Since $Soc\left(R_R\right)$ is the intersection of all essential right ideals of R, $Soc\left(R_R\right)\subseteq I$ and so $R/I\cong (R/Soc\left(R_R\right))/(I/Soc\left(R_R\right))$ is a weakly semiartinian R-module by Proposition 2. This means that $C(R/I)\ne 0$. Hence R is a right $CC$-ring. □

A ring R is called semilocal if $R/Rad\left(R\right)$ is semisimple. The class of semilocal rings properly contains the class of semiperfect rings. Note that over a semilocal ring a module with zero radical is semisimple (see [1]).

Proposition 8.

A semilocal and a right $CC$-ring is a right C-ring.

Proof. 

Let I be a proper essential right ideal of R. Since R is a right $CC$-ring, we can write $C(R/I)\ne 0$. Note also by [6] (Lemma 4) that $Rad(C(R/I\left)\right)=0$. By [1] (17.2-3), we obtain that $Soc(R/I)=C(R/I)\ne 0$ since the ring is semilocal. This means that R is a right C-ring. □

Theorem 2.

Let R be a right $CC$-ring. Then an R-module M is semisimple if and only if $Soc\left(M\right)=wsa\left(M\right)$ and every essential submodule of M is a wsa-supplement in M.

Proof. 

Necessity part is clear. For sufficiency, let U be a proper essential submodule of M. Then there is a wsa-supplement V of U in M, that is $U+V=M$ and $U\cap V$ is weakly semiartinian. Since R is a right $CC$-ring, $V/(U\cap V)\cong M/U$ is weakly semiartinian. Then V is weakly semiartinian by Proposition 2 and we have $V\le wsa\left(M\right)=Soc\left(M\right)\le U$. This implies $U=M$, a contradiction. Therefore, M has no proper essential submodules. Hence M is semisimple. □

4. The Objects of the Proper Class $\mathcal{WSS}$

In this section, we consider the class of short exact sequences determined by wsa-supplement submodules. Before doing so, here we give the definition of a proper class which plays a key role in relative homological algebra in terms of examining classes of short exact sequences along with their homological objects (see [9] for an equivalent definition of a proper class).

Definition 1.

Let $\mathcal{P}$ be a class of short exact sequences of right R-modules and R-module homomorphisms. If a short exact sequence $\mathbb{E}:0⟶K\stackrel{f}{⟶}L\stackrel{g}{⟶}M⟶0$ belongs to $\mathcal{P}$, then f is said to be a$\mathcal{P}$-monomorphism and g is said to be a$\mathcal{P}$-epimorphism.

A subfunctor $\mathcal{P}$ of Ext is said to be a proper class if $\mathcal{P}(M,N)$ is a subgroup of $Ext(M,N)$ for every R-modules $M,N$, and one of the following conditions is satisfied.

1.

The composition of two $\mathcal{P}$-monomorphisms is a $\mathcal{P}$-monomorphism whenever this composition is defined;

2.

The composition of two $\mathcal{P}$-epimorphisms is a $\mathcal{P}$-epimorphism whenever this composition is defined.

Let R be a ring and $\mathcal{P}$ be a proper class of right R-modules. An R-module M is said to be $\mathcal{P}$-injective (resp., $\mathcal{P}$-co-injective) if ${Ext}_{\mathcal{P}}(K,M)=0$ (resp., ${Ext}_{\mathcal{P}}(K,M)$ = ${Ext}_R(K,M))$ for all right R-modules K. The smallest proper class for which every module from the class of modules $\mathcal{P}$ is co-injective is called co-injectively generated by $\mathcal{P}$.

A short exact sequence $0⟶A\stackrel{f}{⟶}B⟶C⟶0$ is called WSS if $Imf$ is a wsa-supplement submodule of B. We denote the class of all WSS sequences by $\mathcal{WSS}$. The next result shows that the class $\mathcal{WSS}$ is a proper class over an arbitrary ring.

Proposition 9.

The class $\mathcal{WSS}$ is the proper class co-injectively generated by the class of weakly semiartinian modules.

Proof. 

It follows from Proposition 2 and [14] (Theorem 2). □

Proposition 10.

The class $\mathcal{WSS}$ is injectively generated by the class of crumbling-free modules.

Proof. 

Let $E:0⟶A⟶B⟶C⟶0\in \mathcal{WSS}$, M be a crumbling-free module and $\alpha :A⟶M$ a homomorphism. Then ${\alpha }_{*}E:0⟶M⟶D⟶C⟶0\in \mathcal{WSS}$ since $\mathcal{WSS}$ is a proper class. Then there is a submodule K of D such that $M+K=D$ and $M\cap K$ is weakly semiartinian. By Proposition 1, we have $C(M\cap K)\le C\left(M\right)=0$ so that ${\alpha }_{*}E$ splits. Therefore, M is $\mathcal{WSS}$-injective.

Now let $F:0⟶X⟶Y⟶Z⟶0$ be a short exact sequence such that every crumbling-free module is F-injective. Since $C(X/wsa(X\left)\right)=0$, there is a submodule L of Y with $wsa\left(X\right)\le L$ and $X/wsa\left(X\right)\oplus L/wsa\left(X\right)=Y/wsa\left(X\right)$. Then we have $X+L=Y$ and $X\cap L=wsa\left(X\right)$. Hence $F\in \mathcal{WSS}$. □

We call a module M $\mathcal{WSS}$-co-injective, if every short exact sequence,

$$0⟶M⟶N⟶K⟶0,$$

of right R-modules starting with the module M is in the proper class $\mathcal{WSS}$. It follows that a module M is $\mathcal{WSS}$-co-injective if and only if it is a wsa-supplement in every extension. It is clear that injective modules, semiartinian modules and wsa-supplementing modules are examples of $\mathcal{WSS}$-co-injective modules. Proposition 10 implies that a crumbling-free module is $\mathcal{WSS}$-co-injective if and only if it is injective. Recall that we denote the injective hull of a module M by $E\left(M\right)$.

Theorem 3.

The following statements are equivalent for a module M.

1. 

M is $\mathcal{WSS}$-co-injective;

2. 

M is a wsa-supplement in $E\left(M\right)$.

Proof. 

$(1\Rightarrow 2)$ is clear.

$(2\Rightarrow 1)$: Let M be a wsa-supplement in $E\left(M\right)$ and let N be a module containing M. Since $E\left(M\right)\subseteq E\left(N\right)$, there exists a submodule $U\subseteq E\left(N\right)$ such that $E\left(N\right)=E\left(M\right)\oplus U$. Since M is a wsa-supplement in $E\left(M\right)$, M is a wsa-supplement in $E\left(N\right)$. Hence there exists a submodule V of $E\left(N\right)$ such that $E\left(N\right)=M+V$ and $M\cap V$ is weakly semiartinian. By modular law, we can write $N=N\cap E\left(N\right)=N\cap (M+V)=M+N\cap V$ and $M\cap (N\cap V)=(M\cap N)\cap V=M\cap V$ is weakly semiartinian. It means that M is $\mathcal{WSS}$-co-injective. □

The following result is a consequence of Theorem 3.

Corollary 6.

Let M be a module with $M/wsa\left(M\right)$ injective. Then M is $\mathcal{WSS}$-co-injective.

Proof. 

By the assumption, there exists a submodule K of $E\left(M\right)$ containing $wsa\left(M\right)$ such that $M/wsa\left(M\right)\oplus K/wsa\left(M\right)=E\left(M\right)/wsa\left(M\right)$. Therefore $M+K=E\left(M\right)$ and $M\cap K\subseteq wsa\left(M\right)$. Applying Proposition 2, $M\cap K$ is weakly semiartinian and so M is a wsa-supplement in $E\left(M\right)$. It follows from Theorem 3 that M is $\mathcal{WSS}$-co-injective. □

The next result shows that the class of $\mathcal{WSS}$-co-injective modules is closed under extensions.

Proposition 11.

Let $0⟶M⟶N⟶K⟶0$ be a short exact sequence of modules. If M and K are $\mathcal{WSS}$-co-injective, then so is N.

Proof. 

By [15] (Proposition 1.9 and 1.14). □

Corollary 7.

Every finite direct sum of $\mathcal{WSS}$-co-injective modules is $\mathcal{WSS}$-co-injective.

Proof. 

Let $n\in {\mathbb{Z}}^{+}$ and $M_i(1\le i\le n)$ be any finite collection of $\mathcal{WSS}$-co-injective modules. Let $M=M_1\oplus M_2\oplus \dots \oplus M_n$. Suppose that $n=2$, that is, $M=M_1\oplus M_2$. Then $0⟶M_1⟶M⟶M_2⟶0$ is a short exact sequence. Applying Proposition 11, we have that M is $\mathcal{WSS}$-co-injective. The proof is completed by induction on n. □

We do not know if any direct sum of $\mathcal{WSS}$-co-injective modules is $\mathcal{WSS}$-co-injective. Nevertheless, over right noetherian rings, we show that the class of $\mathcal{WSS}$-co-injective modules is closed under direct sums.

Theorem 4.

Let R be a right noetherian ring and ${\left\{M_i\right\}}_{i\in I}$ be a collection of $\mathcal{WSS}$-co-injective R-modules. Then ${⨁}_{i\in I}{M}_i$ is $\mathcal{WSS}$-co-injective.

Proof. 

Put $M={⨁}_{i\in I}{M}_i$. It is easy to see that $wsa\left(M\right)={⨁}_{i\in I}wsa\left(M_i\right)$. Since R is a right noetherian ring, $E\left(M\right)$ is the direct sum of $E\left(M_i\right)$ for each $i\in I$. Note that $E\left(M\right)/wsa\left(M\right)={⨁}_{i\in I}E\left(M_i\right)/{⨁}_{i\in I}wsa\left(M_i\right)\cong {⨁}_{i\in I}(E\left(M_i\right)/wsa\left(M_i\right))$. Using Theorem 3, we can write $E\left(M_i\right)/wsa\left(M_i\right)=(M_i/wsa\left(M_i\right))\oplus (K_i/wsa\left(M_i\right))$ for some submodule $K_i/wsa\left(M_i\right)$ of $E\left(M_i\right)/wsa\left(M_i\right)$$(i\in I)$. Let $K/wsa\left(M\right)={⨁}_{i\in I}{K}_i/wsa\left(M_i\right)$. Therefore $E\left(M\right)/wsa\left(M\right)=M/wsa\left(M\right)\oplus K/wsa\left(M\right)$. This means that M is a wsa-supplement in $E\left(M\right)$. Applying Theorem 3 once again, we obtain that M is $\mathcal{WSS}$-co-injective. □

In general, a submodule of a $\mathcal{WSS}$-co-injective module need not be $\mathcal{WSS}$-co-injective. For example, the submodule ${\mathbb{Z}}_{\mathbb{Z}}$ of the $\mathcal{WSS}$-co-injective module ${\mathbb{Q}}_{\mathbb{Z}}$ is not $\mathcal{WSS}$-co-injective. We prove that every wsa-supplement submodule of a $\mathcal{WSS}$-co-injective module is $\mathcal{WSS}$-co-injective.

Proposition 12.

Let M be a $\mathcal{WSS}$-co-injective module and V be a wsa-supplement submodule of M. Then V is $\mathcal{WSS}$-co-injective.

Proof. 

Let V be a wsa-supplement in M. Then $\mathbb{E}:0⟶V⟶M⟶M/V⟶0$ is a short exact sequence in $\mathcal{WSS}$, that is, $U+V=M$ and $U\cap V$ is weakly semiartinian for some submodule U of M. Therefore by [15] (Proposition 1.8) V is $\mathcal{WSS}$-co-injective. □

The following fact is direct consequence of Proposition 12.

Corollary 8.

Every direct summand of a $\mathcal{WSS}$-co-injective module is $\mathcal{WSS}$-co-injective.

We call a ring R weakly semiartinian if $R_R$ is weakly semiartinian, or equivalently, if every R-module is weakly semiartinian.

Proposition 13.

The following statements are equivalent for a ring R.

1. 

R is right weakly semiartinian;

2. 

Every $\mathcal{WSS}$-co-injective R-module is weakly semiartinian;

3. 

Every injective R-module is weakly semiartinian.

Proof. 

$(1\Rightarrow 2)$ and $(2\Rightarrow 3)$ are trivial.

$(3\Rightarrow 1)$: $R_R$ is a submodule of $E\left(R_R\right)$ which is weakly semiartinian by assumption. Proposition 2 completes the proof. □

A ring R is called right hereditary if every factor module of an injective module is injective. Now we prove that over right hereditary rings every factor module of a $\mathcal{WSS}$-co-injective module is $\mathcal{WSS}$-co-injective. Firstly, we need the following result.

Proposition 14.

$\mathcal{WSS}$-co-injective modules are closed under quotients if and only if quotients of injective modules are $\mathcal{WSS}$-co-injective.

Proof. 

The necessity part follows from the fact that injective modules are $\mathcal{WSS}$-co-injective. For sufficiency, let M be a $\mathcal{WSS}$-co-injective module and N be a submodule of M. We have the commutative diagram:

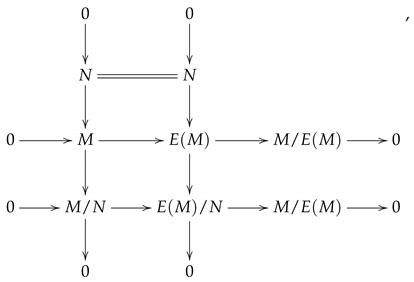with exact rows and columns. Since M is $\mathcal{WSS}$-co-injective it has a wsa-supplement in $E\left(M\right)$. $\mathcal{WSS}$ being a proper class implies that $M/N$ has a wsa-supplement in $E\left(M\right)/N$ which is $\mathcal{WSS}$-co-injective by assumption. By [15] (Proposition 1.8) $M/N$ is $\mathcal{WSS}$-co-injective module. □

Corollary 9.

Let R be a right hereditary ring and M be a $\mathcal{WSS}$-co-injective R-module. Then every factor module of M is $\mathcal{WSS}$-co-injective.

Proposition 15.

Let M be a $\mathcal{WSS}$-co-injective module. Then the following are equivalent:

1. 

$M/wsa\left(M\right)$ is $\mathcal{WSS}$-co-injective;

2. 

$M/wsa\left(M\right)$ is injective;

3. 

$M/N$ is $\mathcal{WSS}$-co-injective for each weakly semiartinian submodule N of M;

4. 

$M/N$ is $\mathcal{WSS}$-co-injective for each wsa-supplement submodule N of M.

Proof. 

$(1\Rightarrow 2)$ follows from Corollary 1.

$(2\Rightarrow 3)$: Let N be a weakly semiartinian submodule of M. We have the short exact sequence $0⟶wsa\left(M\right)/N⟶M/N⟶M/wsa\left(M\right)⟶0$ with $M/wsa\left(M\right)$ injective, hence $\mathcal{WSS}$-co-injective. By Proposition 2, weakly semiartinian modules are closed under quotients and so $wsa\left(M\right)/N$ is $\mathcal{WSS}$-co-injective. By Proposition 11, $M/N$ is also $\mathcal{WSS}$-co-injective.

$(3\Rightarrow 4)$: Let N be a wsa-supplement submodule of M. Then there exists $K\le M$ such that $N+K=M$ and $N\cap K$ is weakly semiartinian. Since $N\cap K\le wsa\left(M\right)$, we have the short exact sequence

$$0⟶wsa\left(M\right)/(N\cap K)⟶M/N\cap K⟶M/wsa\left(M\right)⟶0.$$

By Proposition 2, $wsa\left(M\right)/(N\cap K)$ is $\mathcal{WSS}$-co-injective. $M/wsa\left(M\right)$ is $\mathcal{WSS}$-co-injective by assumption. By Proposition 11, $M/(N\cap K)$ is also $\mathcal{WSS}$-co-injective. Since $M/N$ is isomorphic to a direct summand of $M/(N\cap K)$, $M/N$ is $\mathcal{WSS}$-co-injective module.

$(4\Rightarrow 1)$ follows from the fact that $wsa\left(M\right)$ is a wsa-supplement of M in M. By assumption $M/wsa\left(M\right)$ is $\mathcal{WSS}$-co-injective. □

Corollary 10.

The following statements are equivalent:

1. 

$I/wsa\left(I\right)$ is injective for every injective module I;

2. 

$M/wsa\left(M\right)$ is injective for every $\mathcal{WSS}$-co-injective module M;

3. 

The class of $\mathcal{WSS}$-co-injective modules is closed under wsa-supplement quotients.

Proof. 

The equivalence of 2 and 3 is given in Proposition 15 and $(2\Rightarrow 1)$ is clear.

$(1\Rightarrow 2)$: Let M be a $\mathcal{WSS}$-co-injective module. Then M has a wsa-supplement N in injective hull $E\left(M\right)$ of M. Since $M+N=E\left(M\right)$ and $M\cap N$ is weakly semiartinian, we have $M\cap N\le wsa\left(M\right)$ and hence $E\left(M\right)/wsa\left(M\right)=[M/wsa(M\left)\right]\oplus \left[\right(N+wsa\left(M\right))/wsa(M\left)\right]$. By Proposition 15, $E\left(M\right)/wsa\left(M\right)$ is a $\mathcal{WSS}$-co-injective module and so is $M/wsa\left(M\right)$ as a direct summand of $E\left(M\right)/wsa\left(M\right)$. Corollary 8 completes the proof. □

Corollary 11.

Let R be a right $CC$-ring. Then the class of $\mathcal{WSS}$-co-injective modules is closed under wsa-supplement quotients.

Proof. 

Let R be a right $CC$-ring and I be an injective module. Then every singular module is weakly semiartinian which implies that every crumbling-free module is nonsingular. Since $I/wsa\left(I\right)$ is crumbling-free, it is nonsingular and it follows from [16] (Lemma 2.3) that $wsa\left(I\right)$ is closed I. We have $I\cong wsa\left(I\right)\oplus [I/wsa(I\left)\right]$ and so $I/wsa\left(I\right)$ is injective. The rest of the proof follows from Corollary 10. □

Proposition 16.

The following statements are equivalent for a projective module P.

1. 

P is $\mathcal{WSS}$-co-injective;

2. 

$P/wsa\left(P\right)$ is a homomorphic image of an injective module;

3. 

There exists a weakly semiartinian submodule M of P such that $P/M$ is a homomorphic image of an injective module.

Proof. 

$(1\Rightarrow 2)$: Let $\alpha :P\to E\left(P\right)$ be the inclusion and $\pi :P\to P/wsa\left(P\right)$ the canonical epimorphism. Then we have the diagram

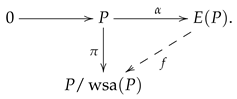
Since P is $\mathcal{WSS}$-co-injective and $P/wsa\left(P\right)$ is crumbling-free, it follows from Proposition 10 that there exists a homomorphism $f:E\left(P\right)\to P/wsa\left(P\right)$ such that $f\alpha =\pi$. Since $\pi$ is an epimorphism, then so is f. Hence $P/wsa\left(P\right)=f\left(E\right(P\left)\right)$.

$(2\Rightarrow 3)$: Since $wsa\left(P\right)$ is weakly semiartinian, taking $M=wsa\left(P\right)$ yields the result by assumption.

$(3\Rightarrow 1)$: Let M be a weakly semiartinian submodule of P such that there is an epimorhism $f:I\to P/M$ with I injective. Consider the diagram

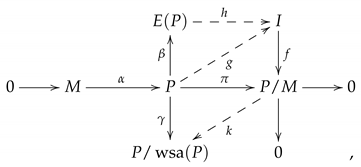where $\alpha :M\to P$ and $\beta :P\to E\left(P\right)$ are inclusions and $\pi :P\to P/M$ and $\gamma :P\to P/wsa\left(P\right)$ are canonical epimorphisms. Since M is weakly semiartinian, there is a homomorphism $k:P/M\to P/wsa\left(P\right)$ such that $k\pi =\gamma$. Since f is an epimorphism and P is projective, there is a homomorphism $g:P\to I$ such that $fg=\pi$. Since $\beta$ is a monomorphism and I is injective, there is a homomorphism $h:E\left(P\right)\to I$ such that $h\beta =g$. We have that the homomorphism $kfh:E\left(P\right)\to P/wsa\left(P\right)$ satisfies $\left(kfh\right)\beta =k\left(f\right(h\beta \left)\right)=k\left(fg\right)=k\pi =\gamma$.

Now let F be a crumbling-free module and $\theta :P\to F$ be a homomorphism. Since $wsa\left(P\right)\le Ker\theta$, by Factor Theorem there is homomorphism $u:P/wsa\left(P\right)\to F$ such that $u\gamma =\theta$. Then, we have the diagram,

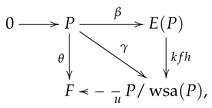with the homomorphism $ukfh:E\left(P\right)\to F$ that satisfies $\left(ukfh\right)\beta =u\left(\right(kfh\left)\beta \right)=u\gamma =\theta$ which implies by Proposition 10 that P is $\mathcal{WSS}$-co-injective. □

Corollary 12.

Every projective module is $\mathcal{WSS}$-co-injective if and only if every crumbling-free module is a homomorphic image of an injective module.

Proof. 

For necessity let M be a crumbling-free module. There is an epimorphism $f:P\to M$ with P projective. Let $E\left(P\right)$ be the injective hull of P and $\alpha :P\to E\left(P\right)$ be the inclusion. Since P is $\mathcal{WSS}$-co-injective, it follows from Proposition 10 that there is a homomorphism $g:E\left(P\right)\to M$ such that $g\alpha =f$. Clearly, f is an epimorphism. Sufficiency follows from Proposition 16. □

Corollary 13.

Over a right $CC$-ring, a projective module P is $\mathcal{WSS}$-co-injective if and only if $P/wsa\left(P\right)$ is injective.

Proof. 

For necessity, let P be a $\mathcal{WSS}$-co-injective module. Then, by Proposition 16, there is an epimorphism $f:I\to P$ for some injective module I. Since $P/wsa\left(P\right)$ is a crumbling-free module over a right $CC$-ring, it is nonsingular. By [16] (Lemma 2.3), $Kerf$ is closed in I, and so $Kerf\oplus [P/wsa(P\left)\right]\cong I$. Hence $P/wsa\left(P\right)$ is injective. Sufficiency follows from the fact that $\mathcal{WSS}$-co-injective modules are closed under extensions. □

Proposition 17.

A ring R is right weakly semiartinian if and only if every right R-module is $\mathcal{WSS}$-co-injective.

Proof. 

Necessity is clear. For sufficiency, it is enough to show that $C\left(M\right)\ne 0$ for every nonzero R-module M. Let N be a crumbling-free module. Then any submodule K of N is also crumbling-free. It follows from Proposition 10 that K is injective, therefore a direct summand of N. This shows that N is semisimple. Then we have $N=SocN\le C\left(N\right)=0$. Hence R is right weakly semiartinian. □

A ring R is called a right $SSI$-ring if all semisimple right R-modules are injective. It is known that a ring R is a right noetherian right V-ring if and only if it is a right $SSI$-ring.

Theorem 5.

The following statements are equivalent for a ring R.

1. 

Every $\mathcal{WSS}$-co-injective R-module is injective;

2. 

Every weakly semiartinian R-module is injective;

3. 

R is semisimple artinian.

Proof. 

$(1\Rightarrow 2)$ and $(3\Rightarrow 1)$ are clear.

$(2\Rightarrow 3)$: Every semisimple module is weakly semiartinian, hence injective by assumption and so R is a right $SSI$-ring. Then every module crumbles by [6] (Theorem 3). Since crumbling modules are weakly semiartinian, R is semisimple artinian by assumption. □

An R-module K is called $\mathcal{WSS}$-coprojective if every short exact sequence,

$$0⟶M⟶N⟶K⟶0,$$

of right R-modules ending with the module K is in the proper class $\mathcal{WSS}$. For an arbitrary ring R, let $C\left(R\right)=C\left(R_R\right)$.

Proposition 18.

Let R be a crumbling-free ring. Then $\mathcal{WSS}$-coprojective R-modules are only projective modules.

Proof. 

Let M be a $\mathcal{WSS}$-coprojective R-module. Since every R-module is a factor module of a free R-module, there exist a free R-module F and an epimorphism $\psi :F⟶M$. Put $U=Ker\left(\psi \right)$. Now we consider the short exact sequence $0⟶U\stackrel{\iota }{⟶}F\stackrel{\psi }{⟶}M⟶0$, where $\iota$ is the canonical injection. By the hypothesis, there exists a submodule V of F such that $F=U+V$ and $U\cap V$ is weakly semiartinian. Since $C\left(R\right)=0$, it follows from [6] (Corollary 8) that $C\left(F\right)=C\left(R\right)F=0$, and so $C(U\cap V)\subseteq C\left(F\right)=0$. It means that the short exact sequence $0⟶U\stackrel{\iota }{⟶}F\stackrel{\psi }{⟶}M⟶0$ splits. Hence M is projective. □

Recall that a module M is flat if every short exact sequence of the form,

$$0⟶M\stackrel{\psi }{⟶}N⟶K⟶0,$$

is pure exact, that is, $Im\psi$ is a pure submodule of N. Clearly, every projective module is flat.

Theorem 6.

Over a commutative C-ring $\mathcal{WSS}$-projective modules are flat.

Proof. 

This follows from [7] (Theorem 3.9) and the fact that $\mathcal{SAS}\subseteq \mathcal{WSS}$. □