Exhaustive Exploitation of Local Seeding Algorithms for Community Detection in a Unified Manner

Abstract

Community detection is an essential task in network analysis and is challenging due to the rapid growth of network scales. Recently, discovering communities from the local perspective of some specified nodes called seeds, rather than requiring the global information of the entire network, has become an alternative approach to addressing this challenge. Some seeding algorithms have been proposed in the literature for finding seeds, but many of them require an excessive amount of effort because of the global information or intensive computation involved. In our study, we formally summarize a unified framework for local seeding by considering only the local information of each node. In particular, both popular local seeding algorithms and new ones are instantiated from this unified framework by adopting different centrality metrics. We categorize these local seeding algorithms into three classes and compare them experimentally on a number of networks. The experiments demonstrate that the degree-based algorithms usually select the fewest seeds, while the denseness-based algorithms, except the one with node mass as the centrality metric, select the most seeds; using the conductance of the egonet as the centrality metric performs best in discovering communities with good quality; the core-based algorithms perform best overall considering all the evaluation metrics; and among the core-based algorithms, the one with the Jaccard index works best. The experimental results also reveal that all the seeding algorithms perform poorly in large networks, which indicates that discovering communities in large networks is still an open problem that urgently needs to be addressed.

1. Introduction

A community is traditionally recognized as a subset of nodes that are densely connected to each other but sparsely connected to the rest of the network, which is also an important mesostructure in many real networks, including protein networks, social networks, citation networks, and information networks. Therefore, the analysis of the community structure in those networks benefits our understanding of the corresponding systems; for example, analyzing communities in citation networks reveals research developments and frontiers in different disciplines. However, in many cases, the communities in those networks are usually implicit and need to be detected according to the network structure. Therefore, community detection has attracted many researchers, and thousands of community detection methods have appeared in the literature [1,2,3,4,5,6,7,8,9,10,11,12,13] since the GN (Girvan–Newman) was proposed in 2002 [14].  We think of GN as the first algorithm for community detection since it initiated the research of community detection in real networks.

Although community detection has been studied extensively, it is still a challenging task due to the complexity of network structures, especially with the rapid increase in network data. In addition, global information may be inaccessible due to privacy or limited permissions. In this scenario, local community detection has been the focus of many studies; the goal is to discover the community containing the seed from the local perspective of that seed (the seed is also called the center or core). Local community detection is also called seed expansion [15,16], and many local community detection algorithms have been proposed in previous publications [17,18,19,20,21,22,23,24,25,26]. Generally, to search for the global community structure, a set of nodes should first be chosen as seeds, and then each seed is expanded to find the community to which the seed belongs. Finally, the communities obtained from all the seeds compose the global community structure of the entire network. Local community detection has great potential in large-scale networks since it is commonly much easier to handle local information in such networks. However, many local community detection algorithms are influenced by the seed [22,27]. That is, if the seed is a good representative of the community to which it belongs, then the community can be detected well; otherwise, it cannot. This means that local community detection is challenged by seeding, which aims to select good seeds.

A good seed is generally in the core of the community or has a high influence on most members of the community. See Figure 1 for an illustration; nodes 4 and 10 are good seeds for the two communities. It is conventional for the core members of a community to be densely connected. Thus, seeding methods always customize a criterion to determine whether a node is in a densely connected area or has high influence and then design a strategy to select seeds according to the criterion. Following this paradigm, dozens of seeding algorithms have been proposed; see Table 1 for the summary of these seeding algorithms (more details are described in “Related work”). The most popular criterion is node centrality, which is used to evaluate the influence or importance of nodes according to the network structure, e.g., degree centrality is used in [16,21,27,28,29,30,31], eigenvector centrality, betweenness centrality, and PageRank centrality are used in [32,33,34], core dominance is used in [28,35], and influence centrality is used in [36]. Other metrics measuring the denseness of the neighborhood of a node can also be used as the node centrality, e.g., the conductance of the egonet is used in [16,28,37], and the node mass is used in [38,39]. There are several selection strategies. Some methods select the nodes with the best centrality values by considering all the nodes in the network, e.g., [16,28,29] select the top K nodes with the highest degree as seeds under the condition that seeds should not be adjacent to each other. Other methods select nodes according to centrality values by considering only the neighborhood, e.g., [30,31] select nodes with degrees no lower than those of all the neighbors as seeds.

Figure 1. A small network with two communities distinguished by color. Nodes 4 and 10 are good seeds for the two communities.

Both the criterion and the selection strategy can be global or local, and therefore, the seeding algorithms can be categorized into two groups, i.e., global algorithms and local algorithms. The global seeding algorithms use the global information of the network to obtain seeds (we assume that as long as one of the criterion and selection strategy requires global information, the corresponding algorithm is global); in contrast, the local algorithms only utilize the local perspective of each node to decide whether it is a seed. Clearly, local seeding algorithms are more efficient and suitable for large-scale networks, but there is no systematic comparison and analysis of them in a unified framework, which is necessary for the development and application of community detection and benefits other studies related to networks, e.g., influence maximization. Therefore, in this paper, a unified framework is summarized from the existing works. Under this unified framework, each node is first evaluated by a local centrality metric, and then nodes with centrality values better than those of the neighbor nodes are chosen as seeds. By adopting different local centrality metrics in the unified framework, the popular local seeding algorithms are included and several new ones are obtained. After that, each seed is expanded by the local community detection algorithm based on a personalized PageRank to obtain communities. Finally, comprehensive experiments are conducted to compare and analyze the local seeding algorithms on real and synthetic networks. On the basis of the experimental results, we summarize some conclusions, which can guide the research on seeding and benefit the application of community detection. The main contributions of this paper are as follows:

(1)

The existing seeding algorithms are summarized and categorized into global and local algorithms according to the criterion and selection strategy.

(2)

A unified local seeding framework is formally summarized, which first measures the local centrality of each node and then selects the nodes with the best centrality in their neighborhoods. From the unified framework, popular local seeding algorithms and new seeding algorithms can be instantiated by adopting different centrality metrics.

(3)

Several new local seeding algorithms are obtained from the unified framework by adopting different local centrality metrics, enriching the research on seeding and other related studies in network science. Moreover, all the obtained local seeding algorithms are categorized into three classes according to the centrality metrics.

(4)

Comprehensive experiments are conducted on a number of networks to provide a comparative analysis of the obtained local seeding algorithms. Based on the experimental results, several suggestive conclusions are obtained: (a) the degree-based algorithms usually select the fewest seeds, while the denseness-based seeding algorithms select the most seeds (except the one that uses node mass centrality); (b) the local seeding algorithm with the conductance of the egonet as the centrality metric performs best in discovering communities of high quality; and (c) in many cases, each algorithm performs differently on different evaluation metrics, but the core-based seeding algorithms perform best overall, and among them, the one with Jaccard index performs best.

The organization of the remaining part of the paper is as follows: Section 2 presents related work about seeding and local community detection algorithms. Section 3 describes the notations and local centrality metrics used in this paper. Section 4 presents the unified framework, the obtained local seeding algorithms and the time complexity analysis of these algorithms. Section 5 presents the local community detection algorithm, the process of obtaining the global community structure by expanding seeds, and the time complexity analysis of this process. The experiments are shown and analyzed in Section 6. Finally, Section 7 concludes our work.

2. Related Work

In this section, we briefly summarize the most related work about seeding methods and local community detection algorithms.

2.1. Seeding

Dozens of algorithms have been proposed to select seeds in the literature. Generally, these seeding algorithms use the following paradigm: (1) customize a criterion to evaluate how good a node is (or a set of nodes are) as a seed (seeds) and (2) design a selection strategy to select seeds according to the criterion. The most popular criterion is node centrality, since a good seed should be important to the connectivity within the community or show strong influence on other members of the community. Some traditional centrality metrics, such as degree, closeness, eigenvectors, betweenness and PageRank, were naturally used as criteria in seeding [16,21,27,28,29,30,31,32,33,34]; moreover, several new centrality metrics, such as the conductance of the egonet [16,28,37], extended degree [40], accumulation degree [22,26,41], core dominance [28,35], core centrality [42], node mass [38,39], and density [43,44,45,46,47,48], were proposed for seeding. It is important to note that the definitions of density centrality vary. Bai et al. defined the density of a node as the number of nodes to which the distance is smaller than a certain threshold, and the distance between a pair of nodes was the reciprocal of the strength of the linkage, which was defined based on the number of routes in specified steps and the node degree [44]. Wang et al. [45] and Jiang et al. [46] defined density in the same way as [44], but the distance between a pair of nodes is the shortest path. Ding et al. applied extended degree as the density to find the center of community in [47]. Deng et al. defined the density as the number of neighbor nodes to which the similarity is larger than a given threshold, and the similarity between two adjacent nodes was evaluated by a composite similarity index based on the shortest path information and the Jaccard index [48]. The core nodes defined in [43] can be also treated as this type of density but using the cosine index over the neighbor sets to evaluate the adjacent nodes’ similarity. In addition, cliques and k-plexes have been used as criteria [15,49], and the nodes in a maximal clique (the size of clique is at least k) or k-plex that do not overlap with other cliques or k-plexes were selected as seeds (see DMC and K-plex in Table 1); the center of each cohesive cluster obtained by graph partitioning using Graclus [50] was also taken as a seed [16] (see Graclus in Table 1). These methods involving the k-plex, k-cliques [51], and cohesive centers are computationally intensive, limiting their application in large-scale networks.

There have been several selection strategies in the literature, which are summarized below:

Selection strategy I: This strategy selects the nodes with the best centrality in its egonet as seeds, i.e., the nodes with a centrality that is no worse than those of all neighbors. Since this strategy only requires comparing the centrality of each node with those of its neighbors, the time complexity of selecting all the seeds by this strategy is $O\left(\right|m\left|\right)$ since for each node, we only need to check the adjacent nodes (m denotes the number of edges in the network, and all the notations used in this paper are denoted in Section 3.1 unless specified otherwise). Examples are given in [16,28,30,31,35].

Selection strategy II: This strategy selects nodes with a centrality larger than a specified value (a parameter) that are not assigned to any community as seeds; this means that the seed selection and seed expansion processes are performed alternately. The time complexity of this strategy is approximately $O\left(\right|n\left|\right)$ if we exclude the cost of seed expansion. This strategy was applied in the community detection algorithm named SCAN (see L-SCAN in Table 1), and the number of similar neighbors was taken as the centrality, which can be treated as the density centrality [43]. Here, the similar neighbors of a node are determined by checking the similarity of each neighbor to that node: if the similarity is larger than a specified value (a parameter), then the neighbor is a similar neighbor; otherwise, it is not.

Selection strategy III: This strategy sorts nodes in descending order of centrality value and then sequentially takes nodes that are not assigned to any community as seeds. The time complexity of this strategy is approximately $O\left(n{log}_{2}n\right)$, which is the cost of the sorting, if we exclude the cost of seed expansion. The seeding algorithms in [21,32,35,39,42] use this strategy; these are listed in Table 1.

Selection strategy IV: This strategy first sorts the nodes in descending order of centrality value and selects the first K nodes as seeds (K is a parameter). The time complexity of this strategy is approximately $O\left(n{log}_{2}n\right)$). This strategy was applied in [16,28,29,34,36]. It is noted that for the seeding algorithm named G-SH (where the degree centrality is used), the seeds are further required to be not adjacent to each other. Thus, the neighbors of each selected seed should be marked as unavailable in the selection process, which has a time complexity of $O\left(K{d}_{max}\right)$ in the worst case. Thus, the time complexity of the strategy in G-SH is approximately $O\left(n{log}_{2}n\right)+K{d}_{max})$, and we name it as selection strategy IV-a.

Selection strategy V: This strategy is for a case in which several centrality metrics are used. It sorts nodes according to each centrality metric and then selects the nodes in the intersection of the first K nodes from each sort as seeds. The time complexity of this strategy is approximately $O\left(n_{c}n{log}_{2}n\right)$, where $n_c$ is the number of centrality metrics. The seeding algorithms in [33] apply this strategy.

Selection strategy VI: This strategy sorts nodes in descending order of centrality value and selects the first two nodes as seeds; then, it sequentially selects the remaining nodes in the sort until the difference in centrality between the last node selected and the current node is more than the difference in centrality between the last two nodes selected. The time complexity of this strategy is approximately $O\left(n{log}_{2}n\right)$. The seeding algorithm G-EXTD applies this selection strategy [40].

Selection strategy VII: This strategy selects nodes with high density that are far away from (or have a weak relation to) nodes with higher density, originating from the idea of an effective traditional clustering algorithm named clustering based on density peaks (CDP) [52]. Thus, the minimum distance to the nearest node with higher density is always used as another indicator and is incorporated with density to determine the seeds (other indices such as fuzzy relations [20] and similarity [48] have also been used to replace distance). As in CDP, the seeds can be selected according to a decision graph, where the density is taken as the x-axis and the minimum distance is taken as the y-axis (we call this selection strategy VII-g1, which needs to be completed manually), or the descending order of the product of the density and minimum distance can be determined and the nodes with much larger products can be considered as seeds (we call this selection strategy VII-g2). From these two basic selection strategies, some adaptive changes have been made to distinguish seeds more accurately. In [44], the density and minimum distance are regularized before using selection strategy VII-g1, and the nodes whose densities are smaller than the average density of a specified number of nearest neighbors (a parameter) are further excluded from the seed set (we call this selection strategy VII-g1-a1, and its time complexity is still $O\left(n{log}_{2}n\right)$) since the adaptive changes do not increase the time complexity). In [48], the nodes are sorted in descending order of density and minimum similarity, and the intersection of the first K nodes from the two sorts are selected as seeds (K is a parameter and different for the two sorts). This method is quite similar to selection strategy V if we take the minimum similarity as another centrality metric, so its time complexity is $O\left(n{log}_{2}n\right)$. We call this selection strategy VII-g1-a2. The selection strategy in [41] can be categorized into this class. Specifically, the accumulation degree is taken as the density, and the nodes are sorted in descending order of density; then, seeds are successively selected from the sort whose minimum fuzzy relation is smaller than a certain threshold, which is obtained manually from the decision graph. We call this selection strategy VII-g1-a3, which runs in $O\left(n{log}_{2}n\right)$. In [45,46], nodes are sorted in the descending order according to the product of density and minimum distance; then, seeds are sequentially chosen from the candidate list obtained from the sort, and in the selection process, nodes in the candidate list that have distances to a chosen seed larger than the cutoff distance (a parameter) will be deleted from the candidate list. The different between [45,46] is that the former only considers the nodes with product value larger than a threshold (a parameter) to compose the candidate list, and the latter takes half of the nodes in the sort-into-candidate list. We call them selection strategy VII-g2-a1 and selection strategy VII-g2-a2, respectively, which run in $O\left(n{log}_{2}n\right)$. In [47], the shortest path distance to nodes with higher density in a 3-step neighborhood is taken as the minimum distance (thus, the minimum distance is at most 3); the nodes with products of density and minimum distance that are $ϵ$-larger than the expected value are selected as seeds, where the expected value is obtained by considering all the nodes ($ϵ$ is a parameter, and we call this selection strategy VII-g2-a3, which runs in $O\left(n\right)$).

Selection strategy VIII: This strategy takes the nodes that have the best centrality in at least one neighborhood as candidate seeds and further applies a biased graph coloring algorithm to select seeds to ensure that the seeds are distributed separately. The time complexity of obtaining candidate seeds is $O\left(m\right)$, and the biased graph coloring algorithm used for enhancing seeding can run in $O\left({log}_{2}n\right)$. This strategy was proposed in [28].

Selection strategy IX: This strategy iteratively selects the node with the highest centrality (specifically, dynamic vote centrality) as a seed, and the centrality of other nodes is updated after a seed is selected. The time complexity is approximated to $O\left(n{log}_{2}n\right)$. This strategy is used in the seeding algorithm named G-VB [53].

Table 1. Summary of seeding algorithms. “L” represents that the criterion or selection strategy is local, and “G” represents that it is global, and “#PRM” represents the number of parameters.

Name	Criterion (L/G, #PRM)	Selection Strategy		Refs
		Strategy (L/G, #PRM)	Time Compleixty
LM-D	Degree centrality (L, 0)	Selection strategy I (L, 0)	$O\left(m\right)$	[30,31]
LM-CE	Centrality defined as conductance of the egonet (L, 0)			[16,28,37]
LM-CORED	Core dominance centrality defined as the sum of similarities to neighbors (L, 0)			[28]
LM-NM-RS	Node mass centrality, relation strength (L, 0)			[38]
L-SCAN	Density centrality defined as the number of neighbors with similarity larger than a given threshold (L, 1)	Selection strategy II (L, 1)	$O\left(n\right)$	[43]
G-D	Degree centrality (L, 0)	Selection strategy III (G, 0)	$O\left(n{log}_{2}n\right)$	[21]
G-E	Eigenvector centrality (G, 0)			[32]
G-C	Core centrality (G, 0)			[42]
G-NM	Node mass centrality (G, 0)			[39]
TOPSIS	Mixed centrality based on degree, betweenness, eigenvector and PageRank centralities (G, 0)	Selection strategy IV (G, 1)	$O\left(n{log}_{2}n\right)$	[34]
G-F	Influence centrality (G, 1)			[36]
G-SH	Degree centrality (L, 0)	Selection strategy IV-a (G, 1)	$O(nlo{g}_{2}n+K{d}_{max})$	[16,28,29]
P4S	Degree, eigenvector, local clustering coefficient and PageRank centralities (G, 0)	Selection strategy V (G, 1)	$O(n_{c}n{log}_{2}n+n_{c}K)$	[33]
G-EXTD	Extended degree centrality (L, 0)	Selection strategy VI (G, 0)	$O\left(n{log}_{2}n\right)$	[40]
G-Density-Bai	Density centrality and minimum distance (L, 1)	Selection strategy VII-g1-a1 (G, 1)	$O\left(n{log}_{2}n\right)$	[44]
G-Density-Deng	—	Selection Strategy VII-g1-a2 (G, 2)		[48]
G-ACCD	Accumulation degree centrality, fuzzy relation (L, 0)	Selection strategy VII-g1-a3 (G, 1)		[41]
G-Density-Wang	Density centrality and minimum distance (L, 1)	Selection strategy VII-g2-a1 (G, 1)		[45]
G-Density-Jiang	—	Selection strategy VII-g2-a2 (G, 0)		[46]
G-Density-Ding	Extended degree and minimum distance (L, 0)	Selection strategy VII-g2-a3 (G, 1)	$O\left(n\right)$	[47]
G-CORED	Core dominance centrality defined as the sum of similarities to neighbors (L, 0)	Selection strategy VII (G, 0)	$O(m+{log}_{2}n)$	[28]
G-VB	Dynamic vote centrality (L, 1)	Selection strategy IX (G, 0)	$O\left(n{log}_{2}n\right)$	[53]
Graclus	Center of each cohesive cluster (G, 1)	Find K cohesive clusters; select the nodes that are the centers of the clusters (L, 1)	$O\left({log}_{2}K(n+m)\right)$	[16]
DMC	Maximal cliques (L, 1)	Select the nodes belonging to a maximal clique whose distance to another clique is less than a threshold (L, 1)	$O\left(k_{max}^2\right)$1	[15]
K-plexes	k-plexes (G, 2)	Select the nodes belonging to distinct k-plexes (L, 1)	$O\left(k\right)$	[49]

¹k_max is size of the largest maximal clique.

Table 1. Summary of seeding algorithms. “L” represents that the criterion or selection strategy is local, and “G” represents that it is global, and “#PRM” represents the number of parameters.

Name	Criterion (L/G, #PRM)	Selection Strategy		Refs
		Strategy (L/G, #PRM)	Time Compleixty
LM-D	Degree centrality (L, 0)	Selection strategy I (L, 0)	$O\left(m\right)$	[30,31]
LM-CE	Centrality defined as conductance of the egonet (L, 0)			[16,28,37]
LM-CORED	Core dominance centrality defined as the sum of similarities to neighbors (L, 0)			[28]
LM-NM-RS	Node mass centrality, relation strength (L, 0)			[38]
L-SCAN	Density centrality defined as the number of neighbors with similarity larger than a given threshold (L, 1)	Selection strategy II (L, 1)	$O\left(n\right)$	[43]
G-D	Degree centrality (L, 0)	Selection strategy III (G, 0)	$O\left(n{log}_{2}n\right)$	[21]
G-E	Eigenvector centrality (G, 0)			[32]
G-C	Core centrality (G, 0)			[42]
G-NM	Node mass centrality (G, 0)			[39]
TOPSIS	Mixed centrality based on degree, betweenness, eigenvector and PageRank centralities (G, 0)	Selection strategy IV (G, 1)	$O\left(n{log}_{2}n\right)$	[34]
G-F	Influence centrality (G, 1)			[36]
G-SH	Degree centrality (L, 0)	Selection strategy IV-a (G, 1)	$O(nlo{g}_{2}n+K{d}_{max})$	[16,28,29]
P4S	Degree, eigenvector, local clustering coefficient and PageRank centralities (G, 0)	Selection strategy V (G, 1)	$O(n_{c}n{log}_{2}n+n_{c}K)$	[33]
G-EXTD	Extended degree centrality (L, 0)	Selection strategy VI (G, 0)	$O\left(n{log}_{2}n\right)$	[40]
G-Density-Bai	Density centrality and minimum distance (L, 1)	Selection strategy VII-g1-a1 (G, 1)	$O\left(n{log}_{2}n\right)$	[44]
G-Density-Deng	—	Selection Strategy VII-g1-a2 (G, 2)		[48]
G-ACCD	Accumulation degree centrality, fuzzy relation (L, 0)	Selection strategy VII-g1-a3 (G, 1)		[41]
G-Density-Wang	Density centrality and minimum distance (L, 1)	Selection strategy VII-g2-a1 (G, 1)		[45]
G-Density-Jiang	—	Selection strategy VII-g2-a2 (G, 0)		[46]
G-Density-Ding	Extended degree and minimum distance (L, 0)	Selection strategy VII-g2-a3 (G, 1)	$O\left(n\right)$	[47]
G-CORED	Core dominance centrality defined as the sum of similarities to neighbors (L, 0)	Selection strategy VII (G, 0)	$O(m+{log}_{2}n)$	[28]
G-VB	Dynamic vote centrality (L, 1)	Selection strategy IX (G, 0)	$O\left(n{log}_{2}n\right)$	[53]
Graclus	Center of each cohesive cluster (G, 1)	Find K cohesive clusters; select the nodes that are the centers of the clusters (L, 1)	$O\left({log}_{2}K(n+m)\right)$	[16]
DMC	Maximal cliques (L, 1)	Select the nodes belonging to a maximal clique whose distance to another clique is less than a threshold (L, 1)	$O\left(k_{max}^2\right)$1	[15]
K-plexes	k-plexes (G, 2)	Select the nodes belonging to distinct k-plexes (L, 1)	$O\left(k\right)$	[49]

¹k_max is size of the largest maximal clique.

According to whether global information is involved in the selection process, the selection strategies described above can be categorized as global or local strategies. Specifically, selection strategies I and II are local, and the remaining strategies are global. Similarly, the criteria can be categorized as global or local criteria; see Table 1, where we explicitly mark the globality and locality of the criterion and selection strategy for each seeding algorithm. Clearly, the local criteria and selection strategies are more suitable for large-scale networks due to efficiency. However, there is no comprehensive comparison and analysis of the existing local seeding algorithms. Thus, we formally unify an efficient local seeding framework based on selection strategy I and provide several local seeding algorithms under this framework; furthermore, we systematically study these local seeding algorithms through comprehensive experiments. It is noted that the other local selection strategy, i.e., selection strategy II, is not considered in our work because it requires a parameter and it is nontrivial to determine the parameter value, which increases the complexity of seeding.

2.2. Local Community Detection

A traditional approach is to take a seed as a singleton community and successively add nodes to the community, with the nodes selected from the shell and giving the maximum gain by a community quality function. Some examples of this approach were proposed in [8,14,15,16,24], and they are mainly different in quality function. In [8], the quality function is R, defined as the ratio of boundary edges to all edges connected to the boundary nodes. The M function, which is the ratio of intracommunity edges to intercommunity edges, was proposed in [14], and local modularity was proposed in [24] to evaluate the quality of the community. Instead of quantifying the gain of community quality when adding one node from the shell, Bagrow selected the node with the smallest “outwardness”, which was defined as the number of neighbor nodes outside the community minus the number of neighbor nodes inside, normalized by the degree [15]. In addition, members may be removed if the removal would lead to an increase in the quality function [14]. To improve the quality of the detected community, Luo et al. divided the expansion process into three stages and proposed three dynamic membership functions for the three stages to add neighbor nodes [20]. LCDNN iteratively added nodes into the community according to two definitions: the nearest node with greater centrality and the fuzzy relation [26]. To discover ambiguous community structures, in [46], link prediction was first used on central nodes to enhance the community structure, and then community expansion was performed by successively adding neighbor nodes whose most similar neighbor with greater SC value was in the community (the SC value is the product of the density and minimum distance). Other expansion methods can be found in [21,32,35,38,39,41,42,54,55]. In addition, an evolutionary algorithm (specifically, PSO) was introduced to perform local community detection in [25], which enriched research on local community detection.

Another approach to expanding the community from seeds is based on random walks. In contrast to the method that optimizes a specified community quality by iteratively adding nodes from the shell, this approach performs a random walk from a seed with probability transformations. Since the random walk is most likely to become trapped in a dense subgraph around the seed, the nodes in the community should have a high probability. A high-quality community is thus obtained from the top-ranked nodes, where the nodes are ranked according to the resulting probability. There are several instances of this approach; see [21,56,57,58]. To simultaneously uncover multiple local communities to which a set of query nodes belong, Bian et al. proposed a memory-based random walk method, which can further avoid the query bias issue by recording the entire visiting history of each walker [27]. In our experiments, we implement the method based on the PageRank-Nibble algorithm as the community finder from a given seed, since it has been demonstrated to be the most effective [21,57] and has been widely used in community detection [16,28,59].

3. Preliminaries

In this section, we present the notations used in this paper, and review some measurements that can be used as local centrality metrics.

3.1. Notations and Problem Statement

An undirected network is denoted as $G=(V,E)$, where V is the set of nodes and E is the set of edges in G. Let $n=\left|V\right|$ and $m=\left|E\right|$ denote the number of nodes and edges respectively, and A denote the adjacent matrix of G, where $A_{(u,v)}=1$ if there is an edge between node u and node v and $A_{(u,v)}=0$ otherwise, while ${\overline{A}}_u$ denotes the mean value of the row corresponding to node u. For a node, $u\in V,N_r\left(u\right)$ denotes the set of neighbors that are most r hops away from u, and $N_r^{+}\left(u\right)=N_r\left(u\right)\cup u$; $u^{\prime }s$r-hops neighborhood is the subgraph only consisting of the nodes in $N_r^{+}\left(u\right)$. For convenience, the subscript is ignored when $r=1$; neighbors refer to a node’s one-hop neighbors when not specified, and egonet is used to indicate the one-hop neighborhood. $d_u$ denotes the degree of node u, and $d_{max}$ is the maximum degree. For a set of nodes U, the volume of U is defined as $vol\left(U\right)={\sum }_{u\in U}{d}_u$.

Given a network $G=(V,E)$, the seeding problem is to find a set of seeds denoted as S, so that the global community structure can be obtained by expanding each seed $s\in S$. Generally, the seeding problem can be solved using global information or local information, resulting in global seeding algorithms and local seeding algorithms. Here the “local” refers to the r-hop neighborhood of a node (r is usually a small integer), and the “global” refers to the entire network and involves the information outside the r-hop neighborhood. Taking node 3 in Figure 1 as an example, when $r=1$, its local information contains nodes in $N^{+}\left(3\right)=\{0,1,3,4,6\}$ and the edges between these nodes. In this paper, we focus on local seeding algorithms.

3.2. Local Centrality Measurements

In the local seeding algorithms, each node’s centrality should be evaluated based on its local information, thus we consider several metrics that can be used to measure local centrality. These local centralities are presented below.

Degree (D). High-degree nodes are usually considered to be “central” nodes since they link to many other nodes. For this reason, degree is often used as a centrality metric [16,21,28,29,30,31].

Extended degree (EXTD). Being adjacent to nodes with many neighbors has a positive effect on one’s influence in the network; therefore, the extended degree, defined as the number of edges linked to the node plus the number of edges linked to each of the node’s neighbors, is used as a centrality metric [40]. For a node u, its extended degree is mathematically formulated as

$$extd\left(u\right)=d_u+\sum _{v\in N\left(u\right)}{d}_v$$

(1)

Accumulated degree (ACCD). Considering that the microenvironment composed of a two-hop (or more) neighborhood can more properly reflect the centrality of a node, the accumulated degree is used as the centrality in [22,26,41] for efficiency. The accumulated degree of a node u is defined as

$$accd\left(u\right)=d_u+\sum _{v\in N\left(u\right)}(d_v+\sum _{w\in N\left(v\right)}{d}_w)$$

(2)

Node mass (NM). The nodes in the core part of a community are generally densely connected to each other. Centrality should have a higher value for nodes with denser neighborhoods. Thus, the node mass, defined as the number of edges in the egonet, is used as the centrality in [38]. The node mass of a node u is mathematically formulated as

$$mass\left(u\right)=|\{(v,w)\in E|v,w\in N_u^{+}\}|$$

(3)

Conductance of the egonet (CE). Conductance, which originally evaluated the ratio of outgoing connections to the total number of connections in a cluster, is also used as a centrality metric [16,28,37]. Specifically, for a node u, its conductance centrality is

$$conductance\left(u\right)=\frac{|\{(v,w)\in E|v\in N^{+}\left(u\right),w\in V-N^{+}\left(u\right)\}|}{vol(N^{+}\left(u\right)}$$

(4)

which evaluates the density level of u’s neighborhood by counting the edges in the egonet and the ones between the egonet and the remaining network. If there are fewer edges leaving the egonet and more edges in it, then the conductance centrality is lower, which means u is egonet is denser. According to the original definition, if the volume of the egonet is larger than that of the remaining network, then the volume of the remaining network is taken as the dominator; however, this does not usually happen when conductance is applied to the egonet and as a local centrality, it is also reasonable to only consider the neighborhood. Note that the opposite value, i.e., zero minus the conductance, is taken in our implementation to incorporate the conductance of the egonet into the seeding framework presented in Section 4.1.

In addition, we apply the definitions of density and the local clustering coefficient to measure a node’s local centrality since for a given node, these two definitions directly quantify the density level of the egonet.

Density of the egonet (DE). Given a node u, the density of its egonet is

$$density\left(u\right)=\frac{|\{(v,w)\in E|v,w\in N^{+}\left(u\right)\}|}{\left(\begin{array}{c}{d}_u+1\\ 2\end{array}\right)}$$

(5)

which evaluates the density of the egonet by comparing the it with a complete graph induced by the same nodes. The closer the egonet is to the complete graph, the higher the density value is.

Local clustering coefficient (LCC). Given a node u, its local clustering coefficient is

$$LCC\left(u\right)=\frac{\left|\right\{(v,w)\in E|v,w\in N(u\left)\right\}|}{\left(\begin{array}{c}{d}_u\\ 2\end{array}\right)}$$

(6)

which evaluates the density of the egonet by counting the number of adjacent neighbors; the more adjacent neighbors there are, the greater the corresponding local clustering coefficient is.

Core dominance (CORED). Based on the intuition that highly similar nodes that are adjacent are expected to belong to the same community and that the core nodes are expected to be adjacent to many members of the community, core dominance is formulated as a centrality metric [35]. The core dominance of a node u is defined as

$$cored\left(u\right)=\sum _{v\in N\left(u\right)}sim(u,v)$$

(7)

where $sim(u,v)$ is the similarity between nodes u and v and can be calculated by the cosine index, Jaccard index or Pearson correlation coefficient, which are defined as follows:

$$si{m}_{Cosine}(u,v)=\frac{\left|N\right(u)\cap N(v\left)\right|}{\sqrt{\left|N\right(u\left)\right|\left|N\right(v\left)\right|}}$$

(8)

$$si{m}_{Jaccard}(u,v)=\frac{\left|N\right(u)\cap N(v\left)\right|}{\left|N\right(u)\cup N(v\left)\right|}$$

(9)

$$si{m}_{Pearson}(u,v)=\frac{{\sum }_k(A_{u,k}-{\overline{A}}_u)(A_{v,k}-{\overline{A}}_v)}{\sqrt{{\sum }_k{(A_{u,k}-{\overline{A}}_u)}^2}\sqrt{{\sum }_k{(A_{v,k}-{\overline{A}}_v)}^2}}$$

(10)

It is noted that in [35], the extended Jaccard similarity (i.e., where the 2-hop neighbors are also considered) was used. However, we experimentally found that the extended similarity works poorly and takes much more running time (seeding with the extended similarity cannot return a result for large-scale networks after more than 12 h). Thus, we only consider the Jaccard standard similarity in this paper. In addition, similarity indices for link prediction can be used, and it was demonstrated that the preference attachment performed best [28], so we also use this similarity index, which is defined as

$$si{m}_{PA}(u,v)=d_u\times d_v$$

(11)

4. Local Seeding in a Unified Framework

In this section, we present a unified framework for local seeding that is efficient and simple, and then we obtain a total of 11 local seeding algorithms (among them, 3 are existing algorithms) from this framework by adopting different centrality metrics to measure the node centralities. In the unified framework, whether a node is chosen as a seed is dependent only on its local information, i.e., the centrality values of it and its neighbors, and the centrality value of each node is measured only by its local information too. Next, we first present the unified framework and the local seeding algorithms obtained from this framework, and then analyze the time complexity of these algorithms.

4.1. The Local Seeding Framework

Given a node u and its r-hop neighborhood, and a predefined local centrality metric (denoted as $local\_centrality$), the local framework that determines whether u is a seed is shown in Algorithm 1. First, we check u’s neighbors: if any of them is chosen as a seed, then u is not chosen anymore (see lines 2–4); otherwise, calculate the $local\_centrality$ of each node $v\in N^{+}\left(u\right)$, using its r-1-hop neighborhood (see line 5); this step is presented in lines 1–6. Then, we check the u local centrality value and those of its neighbors, and if u has the best centrality (i.e., has the largest centrality value), then it is chosen as a seed; otherwise, it is not (see lines 8–12). Note that this framework is obtained from seeding strategy I [30,31], and adjacent nodes will not be simultaneously chosen as seeds to guarantee the seeds being separated from each other.

Algorithm 1 The local seeding framework.

Input:u: the checked node; u’s r-hop neighborhood; local_centrality: the local centrality       metric; $seed\left(v\right)$: whether v is a seed (True) or not (False) for each $v\in N\left(u\right)$

Output:$seed\left(u\right)$

1: for each node $v\in N^{+}\left(u\right)$ do 2:     if v != u and $seed\left(v\right)==True$ then 3:         $seed\left(u\right)=False$; go to line 12 4:     end if 5:     Calculate local_centrality(v) based on v’s r-1-hop neighborhood 6: end for 7: $seed\left(u\right)=True$ 8: for each neighbor $v\in N\left(u\right)$ do 9:     if local_centrality(u) < local_centrality(v) then 10:         $seed\left(u\right)=False$; go to line 12 11:     end if 12: end for

4.2. Local Seeding Algorithms

From the framework presented in Algorithm 1, different local seeding algorithms can be obtained by using different metrics to calculate local_centrality. In this paper, we try all the local centrality metrics presented in Section 3.2 and obtain 11 local seeding algorithms.

See the definitions in Section 3.2: D, EXTD and ACCD (Equations (2) and (3)) are centralities based on degree, and NM, CE, DE and LCC (Equations (3)–(6)) evaluate a node’s local centrality according to the denseness of the neighborhood. CORED (Equations (7)–(11)) measures the similarity of a node to each neighbor and takes the sum of the similarities as that node’s local centrality. Thus, we categorize the 11 local seeding algorithms into three classes according to the centrality metrics: the ones with D, EXTD and ACCD are the degree-based seeding algorithms; the ones with NM, CE, DE and LCC are the denseness-based seeding algorithms; and the ones with COREDC, COREDJ, COREDP and COREDPA are the core-based seeding algorithms. For convenience, we list the abbreviations of these local seeding algorithms in Table 2, and we will use them in the rest of this paper. Moreover, from the definitions of centrality metrics (in Section 3.2) and Algorithm 1, it can be seen that, given a node, all of these local seeding algorithms only require the information in their r-hop neighborhood to check whether it is a seed. Particularly, r is 1 for the local seeding framework, 1 for centrality D, 3 for centrality ACCD and 2 for the other centralities; thus, r is 2 for LM-D, 4 for LM-ACCD and 3 for the others. By iteratively checking each node in the network, these algorithms can find all the seeds.

Table 2. The classes, abbreviations and time complexities of different local seeding algorithms.

Class	Centrality Metric	Abbreviation of the Local Seeding Algorithm	Time Complexity
			Centrality	Seeding
Degree-based	Degree	LM-D	$O\left(1\right)$	$O\left(m\right)$
		Extended degree (Equation (1))	LM-EXTD
		Accumulated degree (Equation (2))	LM-ACCD
Denseness-based	Node mass (Equation (3))	LM-NM	$O\left(d_{max}m\right)$
	Conductance of egonet (Equation (4))	LM-CE	$O\left(d_{max}m\right)$
	Density of egonet (Equation (5))	LM-DE	$O\left(d_{max}m\right)$
	Local clustering coefficient (Equation (6))	LM-LCC	$O\left(d_{max}m\right)$
Core-based	Core dominance with cosine index (Equations (7) and (8))	LM-COREDC	$O\left(d_{max}\left|E\right|\right)$
	Core dominance with Jaccard index (Equations (7) and (9))	LM-COREDJ	$O\left(d_{max}m\right)$
	Core dominance with Pearson correlation coefficient (Equations (7) and (10))	LM-COREDP	$O\left(d_{max}m\right)$
	Core dominance with preference attachment (Equations (7) and (11))	LM-SPA	$O\left(m\right)$

LM-D, LM-CE and LM-COREDPA are three existing local seeding algorithms, while the others are new ones; the centrality metrics COREDC, COREDJ and COREDP are developed in this paper. We also tried the density centrality, i.e., taking the number of similar neighbors as a node’s local centrality, under the three similarity indices shown in Equations (8)–(10). To set a proper value of the parameter, which is required to decide whether two adjacent nodes are similar, we applied the heuristic approach used in [43]. However, there are usually multiple values or no proper value for many networks, leading to bad results. Thus, we do not consider the density centrality in this paper.

4.3. Time Complexity Analysis

Assuming that the centrality measurement for each node has been performed, the local seeding framework decides whether node u is a seed by comparing its centrality value with those of its neighbor nodes with a time complexity of $O\left(d_u\right)$; see lines 4–8 in Algorithm 1. If the centrality value of node u is the best but not the only one in its egonet, we further check whether the neighbor nodes with the best centrality value have already been marked as seeds. This almost does not increase the time complexity if we apply the data structure of a hash table to mark the seeds. To determine all the seeds in the network, each node is sequentially checked by this process, so the total time complexity for this local seeding framework is $O\left(m\right)$. For LM-D, the time complexity is still $O\left(m\right)$ since the degree of each node is usually known when the network is stored in the data structure. For LM-EXTD, the extended degrees of all the nodes can be obtained in $O\left(m\right)$, since the node u extended degree can be obtained in O$\left(d_u\right)$. For LM-ACCD, we can first compute each node’s extended degree in $O\left(m\right)$ and then compute the accumulated degree based on the extended degree, which also runs in $O\left(m\right)$ since it is the same as the calculation of the extended degree; thus, the time complexity is still $O\left(m\right)$. For LM-NM, LM-CE, LM-DE and LM-LCC, all four centrality metrics, i.e., the node mass, the conductance of the egonet, the density of the egonet and the local clustering coefficient, can be calculated by finding the intersection of adjacent nodes’ neighbor sets, which can be done in $O\left(d_{max}\right)$ in the worst case; thus, the time complexity is $O(d_{max}·m)$. LM-COREDC, LM-COREDJ and LM-COREDP need to calculate the similarity between each pair of adjacent nodes, which can be done in $O\left(d_{max}\right)$. Each node’s core dominance can be obtained in $O\left(d_u\right)$, and thus, the total time complexity of the centrality calculation is $O(d_{max}·m)$. For LM-COREDPA, the centrality calculation can be completed in $O\left(m\right)$ since only the node degree is required to compute the core dominance. The time complexities of these local seeding algorithms are summarized in Table 2.

5. Detecting Communities

For a specified seed, an algorithm of local community detection is required to expand this seed to uncover its community. The global community structure of the network is then obtained by expanding all the seeds. In this section, we first describe the used local community detection algorithm and then summarize the process of obtaining all the communities in the network.

Local community exploration. For a specified seed, we apply the technique of approximate personalized PageRank vector to discover its belonging to community, since this technique is very efficient in practice and has been widely used in community detection [16,21,28,56,59]. The approximate personalized PageRank vector related to a seed is a stationary distribution of a random walk starting from that seed, and at each node the random walker moves to neighbors with probability $\alpha$ and jumps back with probability ($1-\alpha$). To compute this vector, we use the method of PageRank Nibble with the time complexity being proportional to the size of the detected community, rather than the size of the network [29]. Nodes corresponding to high element values in the vector are considered to be well connected around the seed, and a sweep over the vector is performed to generate the community to which the seed belongs. The reader is referred to [59] for details due to space limitation.

Global community structure exploration. To obtain the global community structure by expanding seeds, the first step is to select a set of seeds, which is fulfilled by the local seed algorithms presented in Section 3 in this paper. The second step is to perform the local community exploration described above to identify the community that each seed belongs to. Ideally, there is one seed selected per community. Although we have constrained two chosen seeds to be separated from each other in the seeding step, it is also possible that local communities obtained from different seeds correspond to the same one. Thus, the final step is to perform merging operation on the local communities. Particularly, we apply the merging operation in [59]: if the smaller community has at least $\sigma$ percent of members that are also in the larger one, then we merge them.

Time complexity analysis. Discovering a local community in this paper requires computing the approximate personalized PageRank vector and performing a sweep over the vector, whose computational cost is related to the topological structure of the seed’s local view. The time complexity is therefore complicated and hard to be inferred compactly. However, a number of previous publications have demonstrated that the computational cost of this process only depends on the size of the detected community and is approximated to $O\left(vol\left(D_i\right)\right)$ ($D_i$ is the detected community) [21,28,37,56]. Thus, the time complexity of the seed expansion phase is approximated to $O({\sum }_{i=1}^{\left|S\right|}vol\left(D_i\right)$. The merging step can be performed in the time complexity of $O\left({\sum }_{i=1}^{\left|S\right|}\right)i·\left|D_i\right|$.

6. Experiments

In this section, experiments are conducted to evaluate these local seeding algorithms on a number of networks and analyze the experimental results. Before presenting the results, we briefly describe the evaluation metrics and the experimental setting.

6.1. Evaluation Metrics and Experimental Settings

To evaluate the effectiveness of the local seeding algorithms, we consider the number of seeds, the coverage and the quality of the resulting communities. The coverage is the ratio of nodes in the detected communities to all the nodes in the network. Four widely used metrics are used to evaluate the quality of the resulting communities and they are as follows: the F1-score, normalized variation of information (Nvi) [59,60], modularity [61] and conductance. The former two compare the consistency of the detected communities to the ground truth, and the latter two evaluate the cohesiveness in communities and the separateness between communities. For F1-score, we align both the detected and ground-truth communities to each other, resulting in relatively lower values compared with some previous publications. Details are referred to [62,63]. For conductance, we take the average over all the communities. For Nvi and modularity, we apply the overlapping versions since there are overlapping communities in both the detected communities and the ground truth; details can be found in [59,60,61,63]. Higher F1-score, Nvi and modularity indicate a better result, while lower average conductance indicates a better result.

The merging parameter $\theta$ is set to 0.65. The algorithms are all implemented in C++, and all the experiments are performed on a PC with an Intel i7 4.0 GHz and 16 GB RAM.

6.2. Results on Real Networks

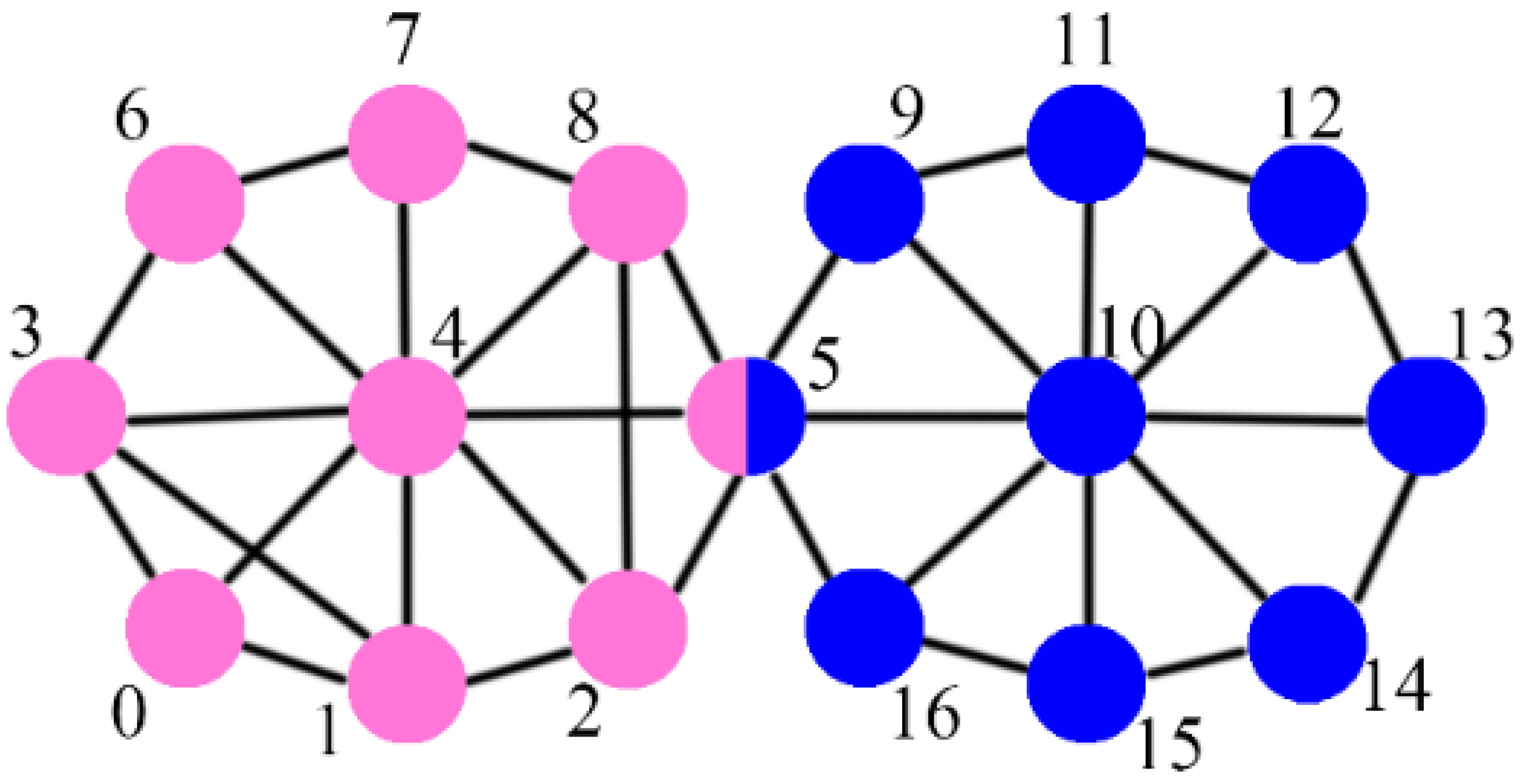
We apply eight widely used real networks with ground-truth communities for this experiment. These networks include (online) social networks, copurchasing networks and collaboration networks. Table 3 shows the information of these networks. The scale of these networks ranges from tens of nodes and edges up to millions of nodes and billions of edges; the number of ground-truth communities spans from several to millions (see the columns “Nodes”, “Edges” and “Coms” for the scale information). The Karate network indicates 78 relationships among 32 members, such as trainees, coaches and administrators, in a karate club. There are two ground-truth communities shown in Figure 2a, and they represent different fractional conflicts. The Dolphin network indicates the communications among 62 dolphins over 7 years, and the ground-truth communities are shown in Figure 3a. The Football network indicates the American college football matches held in 2000. The nodes represent football teams participating in a match, and the edges between two nodes indicate the two corresponding teams that played against each other in the match; the teams from the same conference form one ground-truth community. The Amazon network represents products as nodes, each edge indicates a copurchasing relation, and the ground-truth communities are equivalent to product categories. The DBLP network is a coauthorship network, and the ground-truth communities are created by grouping authors that publish in the same conference or the same journal. The YouTube, LJ and Orkut networks are online social networks, where the nodes represent users and the edges represent the interactions between users; the user-defined groups are considered the ground-truth communities. More detailed information about these networks can be found in the corresponding references, which are listed in the “Ref” in Table 3.

Table 3. The information of real networks. The columns “Nodes”, “Edges” and “Coms“ report the numbers of nodes, edges and ground-truth communities, respectively, and the “Ref” reports the references of these networks.

Networks	Nodes	Edges	Coms	Ref
Karate	34	78	2	[63]
Dolphin	62	159	2	[64]
Football	115	613	12	[14]
Amazon	334,863	925,872	151,039	[21]
DBLP	317,080	1,049,866	13,477	[21]
YouTube	1,134,890	2,987,624	8385	[21]
LJ	3,997,962	34,681,189	287,512	[21]
Orkut	3,072,441	117,185,083	5,043,976	[21]

Figure 2. Visualization of the communities resulting from different local seeding algorithms for the Karate network. The two ground-truth communities are distinguished by squares and triangles. Members of the same detected community are marked with one color, and overlapping members are indicated by circles with several colors corresponding to the communities to which they belong. White nodes do not belong to any community.

Figure 3. Visualization of the communities resulting from different local seeding algorithms for the Dolphin network. The two ground-truth communities are distinguished by squares and triangles. Members of the same detected community are marked with one color, and the overlapping members are indicated by circles with several colors corresponding to the communities to which they belong. White nodes do not belong to any community.

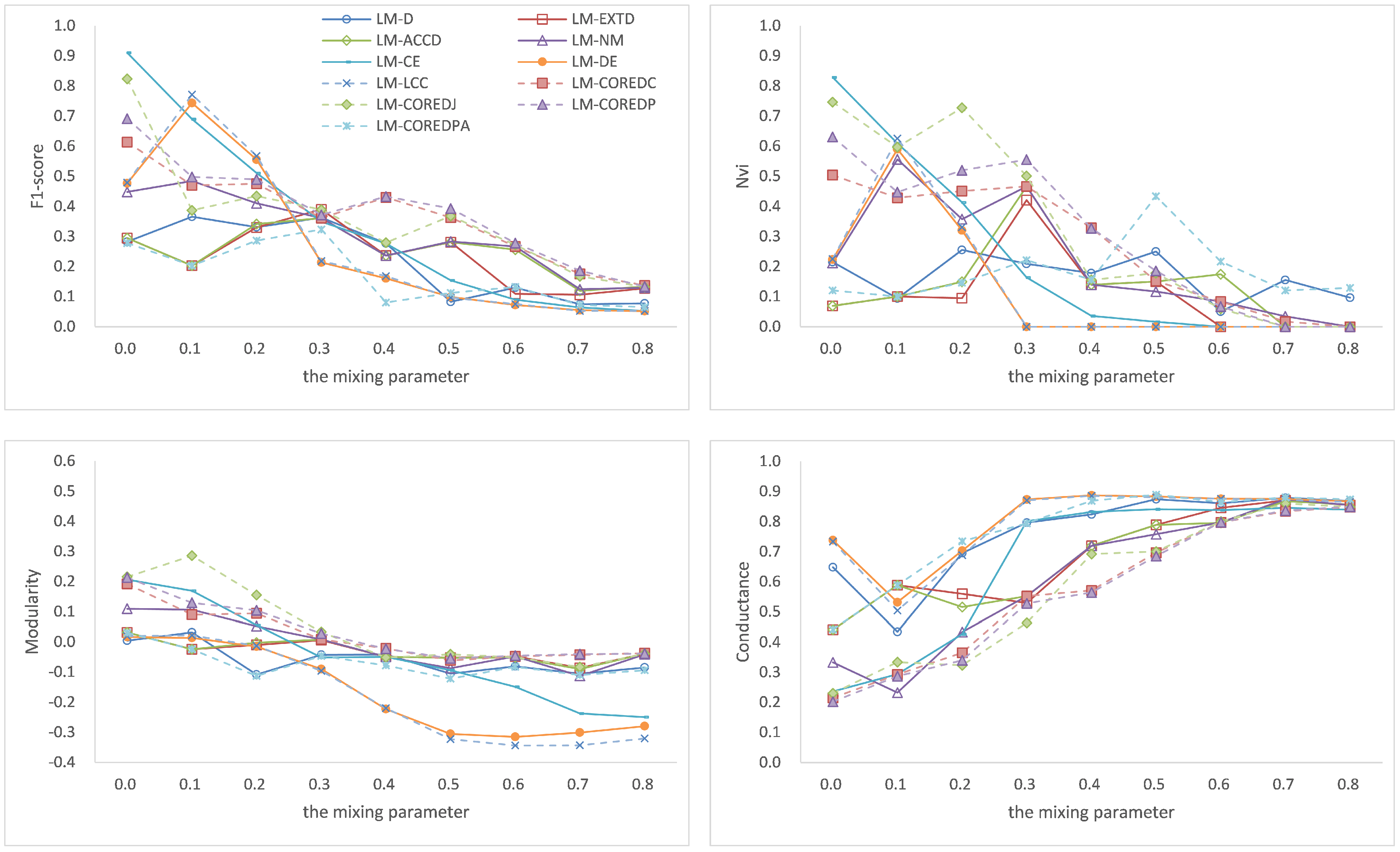
The numbers of seeds and the coverage of the resulting communities by different seeding algorithms are shown in Table 4 and Table 5, respectively. The average F1-score and average Nvi are shown in Table 6, and the modularity and average conductance are shown in Table 7. From Table 4, we can see that the degree-based algorithms clearly select fewer seeds over large networks, especially LM-ACCD and LM-EXTD, while the denseness-based algorithms clearly select more seeds, especially LM-DE and LM-LCC. However, there are two exceptions: LM-NM (a denseness-based algorithm) and LM-COREDPA (a core-based algorithm) select fewer seeds than LM-D (a degree-based algorithm) in most cases. This is because both LM-NM and LM-COREDPA prefer nodes with large degrees, since LM-NM takes the node mass as the centrality metric, which evaluates the denseness of a neighborhood by counting the number of edges between neighbors without normalization by degree, and LM-COREDPA takes the core dominance with preference attachment as the centrality metric, which evaluates the influence of a node by the multiplication of degrees. The coverage of the resulting communities, shown in Table 5, is almost positively correlated with the number of seeds, i.e., the more seeds there are, the higher the coverage is.

Table 4. The number of seeds (with the fraction in parentheses for large-scale networks) chosen by different algorithms.

	Algorithms	Karate	Dolphin	Football	Amazon	DBLP	YouTube	LJ	Orkut
Networks
LM-D		2	4	12	15,461	2735	14,828	8175	162
LM-EXTD		2	2	3	6537	459	1003	729	8
LM-ACCD		2	2	3	6219	281	570	326	1548
LM-NM		2	4	8	13,538	2620	3205	7345	205
LM-CE		4	6	8	34,872	34,039	349,046	562,938	22,744
LM-ED		17	17	9	13,4746	109,412	319,483	1,195,035	470,381
LM-LCC		16	11	9	107,460	107,974	310,884	939,192	326,195
LM-COREDC		2	4	7	16,372	4058	27,369	22,186	625
LM-COREDJ		2	4	6	18,822	8377	37,839	43,548	1427
LM-COREDP		4	5	7	24,192	8662	207,103	105,243	965
LM-COREDPA		2	3	3	8832	799	1701	1197	18

Table 5. The coverage of the resulting communities by different seeding algorithms.

	Algorithms	Karate	Dolphin	Football	Amazon	DBLP	YouTube	LJ	Orkut
Networks
LM-D		0.853	0.919	1.000	0.620	0.107	0.104	0.025	0.001
LM-EXTD		0.853	0.968	0.235	0.403	0.023	0.010	0.004	$7.81\times {10}^{-6}$
LM-ACCD		0.853	0.968	0.235	0.399	0.017	0.006	0.002	0.001
LM-NM		0.853	0.968	0.948	0.586	0.099	0.028	0.033	0.001
LM-CE		0.941	1.000	1.000	0.774	0.564	0.691	0.599	0.094
LM-ED		0.971	1.000	0.991	0.986	0.970	0.875	0.950	0.624
LM-LCC		0.941	1.000	0.991	0.966	0.963	0.826	0.913	0.551
LM-COREDC		0.853	0.968	0.809	0.634	0.147	0.166	0.077	0.004
LM-COREDJ		0.853	0.968	0.704	0.639	0.249	0.206	0.134	0.009
LM-COREDP		0.853	0.903	0.852	0.654	0.174	0.314	0.111	0.005
LM-COREDPA		0.853	0.968	0.235	0.487	0.043	0.018	0.007	$3.03\times {10}^{-5}$

Table 6. The F1-score and Nvi of communities resulting from different local seeding algorithms.

	Algorithms	Karate	Dolphin	Football	Amazon	DBLP	YouTube	LJ	Orkut
Networks
F1-score
LM-D		0.893	0.944	0.762	0.259	0.218	0.012	0.062	0.064
LM-EXTD		0.893	0.963	0.565	0.189	0.250	0.004	0.134	0.066
LM-ACCD		0.893	0.952	0.565	0.176	0.256	0.004	0.141	0.143
LM-NM		0.893	0.963	0.697	0.249	0.242	0.022	0.110	0.098
LM-CE		0.819	0.976	0.637	0.320	0.320	0.134	0.152	0.165
LM-ED		0.795	0.910	0.653	0.272	0.326	0.124	0.168	0.216
LM-LCC		0.761	0.924	0.653	0.292	0.327	0.125	0.167	0.209
LM-COREDC		0.893	0.963	0.704	0.277	0.239	0.028	0.077	0.123
LM-COREDJ		0.893	0.963	0.676	0.295	0.275	0.050	0.087	0.171
LM-COREDP		0.738	0.801	0.601	0.292	0.228	0.058	0.067	0.133
LM-COREDPA		0.893	0.946	0.565	0.210	0.245	0.005	0.130	0.083
Nvi
LM-D		0.535	0.689	0.687	0.221	0.409	0.453	0.522	0.499
LM-EXTD		0.535	0.767	0.823	0.298	0.607	0.500	0.591	0.500
LM-ACCD		0.535	0.729	0.823	0.301	0.625	0.501	0.591	0.505
LM-NM		0.535	0.767	0.535	0.235	0.451	0.477	0.531	0.508
LM-CE		0.526	0.833	0.456	0.211	0.166	0.019	0.048	0.433
LM-ED		0.422	0.701	0.493	0.145	0.105	0.010	0.012	0.087
LM-LCC		0.304	0.765	0.493	0.169	0.107	0.016	0.014	0.116
LM-COREDC		0.535	0.767	0.601	0.227	0.382	0.381	0.431	0.509
LM-COREDJ		0.535	0.767	0.632	0.230	0.296	0.300	0.336	0.521
LM-COREDP		0.465	0.541	0.475	0.224	0.354	0.244	0.383	0.519
LM-COREDPA		0.535	0.692	0.823	0.260	0.539	0.498	0.584	0.500

The best results are highlighted using bold.

Table 7. The modularity and average conductance of communities resulting from different local seeding algorithms.

	Algorithms	Karate	Dolphin	Football	Amazon	DBLP	YouTube	LJ	Orkut
Networks
Modularity
LM-D		0.205	0.172	0.037	0.255	0.403	0.286	0.364	−0.068
LM-EXTD		0.205	0.155	0.262	0.256	0.450	0.223	0.398	−0.034
LM-ACCD		0.205	0.151	0.262	0.232	0.446	0.201	0.339	−0.300
LM-NM		0.205	0.155	0.262	0.316	0.500	0.292	0.424	−0.121
LM-CE		0.189	0.151	0.080	0.280	0.402	0.145	0.084	−0.151
LM-ED		0.160	0.091	0.146	0.116	0.153	0.079	0.019	−0.242
LM-LCC		0.177	0.095	0.146	0.178	0.160	0.125	0.026	−0.253
LM-COREDC		0.205	0.155	0.258	0.296	0.458	0.269	0.323	−0.118
LM-COREDJ		0.205	0.155	0.279	0.327	0.515	0.258	0.304	−0.088
LM-COREDP		0.376	0.150	0.278	0.316	0.506	0.226	0.279	−0.065
LM-COREDPA		0.205	0.146	0.262	0.247	0.395	0.216	0.370	−0.049
Average Conductance
LM-D		0.198	0.123	0.270	0.239	0.195	0.211	0.212	0.925
LM-EXTD		0.198	0.081	0.360	0.193	0.135	0.109	0.119	0.985
LM-ACCD		0.198	0.094	0.360	0.210	0.135	0.105	0.156	0.885
LM-NM		0.198	0.081	0.276	0.207	0.162	0.271	0.217	0.898
LM-CE		0.291	0.071	0.285	0.291	0.370	0.519	0.652	0.786
LM-ED		0.366	0.146	0.314	0.380	0.481	0.637	0.751	0.901
LM-LCC		0.525	0.130	0.314	0.322	0.474	0.552	0.723	0.891
LM-COREDC		0.198	0.081	0.301	0.224	0.185	0.295	0.305	0.822
LM-COREDJ		0.198	0.081	0.304	0.229	0.221	0.344	0.374	0.730
LM-COREDP		0.312	0.198	0.246	0.241	0.201	0.377	0.389	0.762
LM-COREDPA		0.198	0.123	0.360	0.213	0.163	0.120	0.148	0.981

The best results are highlighted using bold.

From Table 6, we can see that all the seeding algorithms lead to relatively high F1-scores and Nvi over small networks, such as Karate, Dolphin and Football and relatively low F1-scores and Nvi over large networks such as Amazon, DBLP, YouTube, LJ and Orkut. In terms of the F1-score, the denseness-based algorithms work best overall, except LM-NM which selects much fewer seeds in many cases. Regarding the degree-based algorithms and core-based algorithm, the latter ones are better overall than the former ones. However, there is an exception: LM-COREDPA performs worse than LM-ACCD, which is the best among the degree-based algorithms, in most cases. LM-COREDJ performs best overall among the core-based algorithms. Moreover, the degree-based algorithms and core-based algorithms can produce much better results over small networks than over large networks. In terms of Nvi, the degree-based algorithms perform best, especially LM-ACCD, which produces the highest Nvi on all the networks except, Dolphin, Football and Orkut (it also produces competitive Nvi values on these three networks). The denseness-based algorithms perform worst overall, except that LM-NM is competitive and LM-CE can produce a good Nvi on some networks, such as Karate, Dolphin and Orkut. Among the core-based algorithms, LM-COREDPA performs best. In summary, over small networks, the degree-based algorithms lead to both a good F1-score and a good Nvi, but over large networks, the result is different: the degree-based algorithms, LM-NM and LM-COREDPA always lead to lower F1-scores but higher Nvi, and among the denseness-based algorithms, LM-DE and LM-LCC always lead to higher F1-scores but lower Nvi, and LM-CE leads to relatively competitive F1-scores and Nvi over all the networks, except YouTube and LJ.

From Table 7, we can see that over the Orkut network, which is relatively dense, all the algorithms lead to very low modularity and very high conductance, which is probably because the relatively high density of the network makes the boundary between communities unclear. In terms of modularity, the core-based algorithms and the degree-based algorithms perform best; among the core-based algorithms, the best algorithm overall is LM-COREDJ, followed by LM-COREDP. The denseness-based algorithms perform worst, except that LM-NM performs quite well (on the networks YouTube and LJ, LM-NM produces the best modularity). In terms of conductance, the degree-based algorithms perform best, among which LM-ACCD is the best. In summary, the core-based algorithms and degree-based algorithms perform best in terms of modularity and conductance, and the denseness-based algorithms perform worst, except LM-NM, which leads to competitive results with those of the core-based and degree-based algorithms.

From the analysis above, we can see that, in terms of F1-score and Nvi, almost all the seeding algorithms lead to much worse results on large networks than on small networks, implying that seeding as well as detecting communities in large networks is complicated and requires more studies. Further, an overall trend in large networks can be inferred from Table 4, Table 5, Table 6 and Table 7: the evaluation metrics Nvi, modularity and conductance generally prefer the obtained community structures that have low coverage (usually corresponding to fewer seeds), while the F1-score metric prefers the ones that have high coverage (usually corresponding to many more seeds). As seen in the last five columns in Table 4, Table 5, Table 6 and Table 7, the degree-based algorithms, LM-NM and LM-COREDPA always yield the lowest coverage, while the corresponding Nvi, modularity and conductance are almost the best (over the Orkut network, the conductance metric does not follow this pattern); the denseness-based algorithms, except LM-NM, always yield the highest coverage, and the corresponding F1-scores are the highest. To explain this, we explore the results from the aspects of network, ground-truth communities, position of seeds, detected communities and evaluation metrics, and find that in the case where the coverage is low, there are fewer seeds selected and those seeds are generally hub nodes, resulting in fewer but large detected communities with relatively good structure (see LM-D and LM-COREDPA for examples); in the case where the coverage is high, a large number of seeds are selected with many improper seeds, resulting in a large number of detected communities but many of them are not good (see LM-DE and LM-LCC for examples). Consequently, the modularity and conductance are generally better in the former case since these two metrics are structural metrics, and the F1-score is generally higher in the latter case, since the large number of detected communities increase the possibility of intersection between the ground truth and the detected communities. The Nvi is generally higher in the former case, which is partially because that several ground-truth communities (probably with overlaps) may be included by a detected community and the conditional entropy of the ground truth with respect to the detected communities is very low according to its definition. However, the comprehensive explanation for the results of F1-score and Nvi needs further study, because many factors, such as the ground-truth communities, detected communities and evaluation metrics themselves, can influence the results, which is quite a complicated issue, and we leave this for future work. The results imply, to some extent, that there is a lack of “perfect” metrics for community evaluation, which is a further challenge to the task of community detection. From the analysis and discussion above, it can be seen that the result of LM-NM is quite different from the ones of the other denseness-based seeding algorithms (i.e., LM-CE, LM-DE and LM-LCC) in many cases. From Equations (3)–(6) it can be seen that NM evaluates a node’s local centrality by counting the internal edges of its neighborhood without normalization, while CE, DE and LCC are all normalized. This causes NM to prefer nodes with high degree compared with CE, DE and LCC, resulting in LM-NM behaving differently.

It is still difficult to infer a clear conclusion, such as which algorithms work better on which networks, since these seeding algorithms perform differently in terms of different evaluation metrics. To obtain a general comparison result, over each network, we rank the algorithms according to each metric and obtain an average rank. For instance, over the Karate network, the LM-D rank is 3 according to the coverage metric since it leads to the third highest coverage; its rank is 1 according to the F1-score, Nvi and conductance metrics; and its rank is 2 according to the modularity metric. Thus, the average rank of LM-D over the Karate network is 1.6. Then, for each network, we list the best and the second best ranked algorithms according to the average rank; see Table 8. We can see that the degree-based algorithms, the core-based algorithms (except LM-COREDP), LM-NM ranks highest over Karate (1.6), followed by LM-CE (2.2); LM-CE ranks highest over Dolphin (1.4), followed by LM-EXTD, LM-NM, LM-COREDC and LM-COREDJ (2.0); LM-D ranks highest over Football (2.4), followed by LM-NM (3.4); LM-COREDJ ranks highest over Amazon (3.8), followed by LM-NM (4.4); LM-EXTD, LM-ACCD and LM-COREDJ rank highest over DBLP (4.8), followed by LM-NM (5.0); LM-NM ranks highest over YouTube (5.0), followed by LM-D (5.2); LM-EXTD ranks highest over LJ (3.8), followed by LM-COREDPA (4.2); and LM-COREDJ ranks highest over Orkut (2.8), followed by LM-COREDP (3.6). Further, we can obtain that the core-based algorithms perform best over four networks (three of them are large networks, and over the three large networks, LM-COREDJ is the best algorithm) and perform second best over three networks (two of them are large networks); the degree-based algorithms perform best over four networks (two of them are large networks), and perform second best over two networks (one of them is a large network); the denseness-based algorithms perform best over three networks (one of them is a large network), and perform second best over five networks (two of them are large networks). Overall, the core-based algorithms perform best, and among them, LM-COREDJ performs best; LM-EXTD performs best among the degree-based algorithms, and LM-NM performs best among the denseness-based algorithms.

Table 8. The best and second best ranked algorithms.

Network	Best Ranked Algorithm		Second Best Ranked Algorithm
	Name	Class	Name	Class
Karate	LM-D (EXTD, ACCD)	degree-based	LM-CE	denseness-based
	LM-NM	denseness-based
	LM-COREDC (J, PA)	core-based
Dolphin	LM-CE	denseness-based	LM-EXTD	degree-based
			LM-NM	denseness-based
			LM-COREDC (J)	core-based
Football	LM-D	degree-based	LM-NM	denseness-based
Amazon	LM-COREDJ	core-based	LN-NM	denseness-based
DBLP	LM-EXTD (ACCD)	degree-based	LN-NM	denseness-based
	LM-COREDJ	core-based
YouTube	LM-NM	denseness-based	LM-D	degree-based
LJ	LM-EXTD	degree-based	LM-COREDPA	core-based
Orkut	LM-COREDJ	core-based	LM-COREDP	core-based

To compare different local seeding algorithms in a fine-grained way, for the two smallest networks, Karate and Dolphin, we visualize the seeds and the communities resulting from different local seeding algorithms, while for the remaining networks, we present the approximations of the ground-truth communities obtained by different local seeding algorithms. Moreover, for the large networks, we only consider the top 5000 ground-truth communities, which are the ones of highest quality (for the YouTube network, only the top 3355 ground-truth communities are provided), since not all the ground-truth communities are structurally good [21].

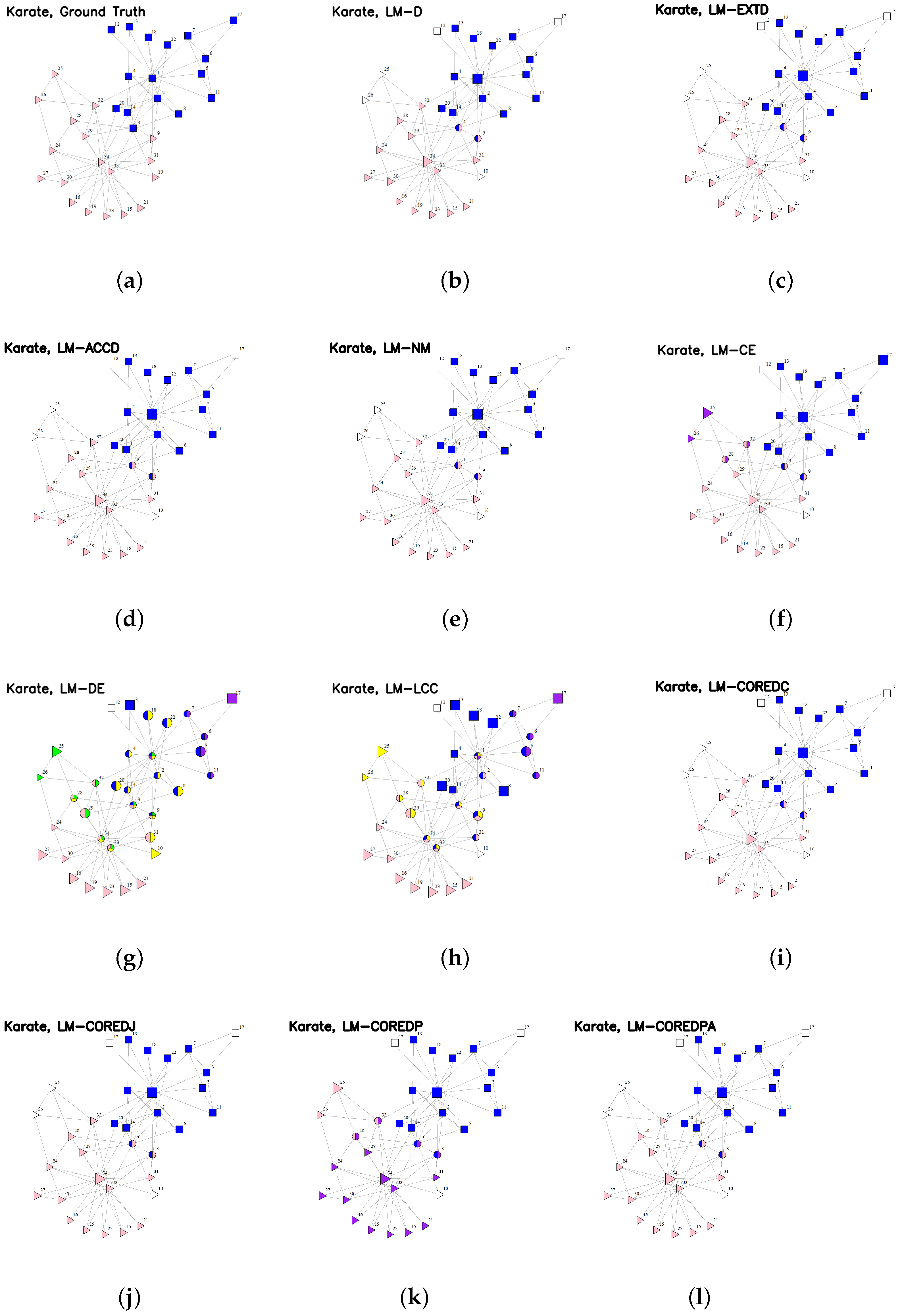
The visualizations of ground-truth communities and detected communities for the Karate and Dolphin networks are shown in Figure 2 and Figure 3, respectively. The ground-truth communities are distinguished by different shapes, i.e., squares and triangles. The members of each detected community are marked with one color, and the overlapping members are indicated by a circle with several colors corresponding to belonging to communities. The nodes not belonging to any community are colored white, and the seeds are enlarged in size. Over the Karate network, the degree-based algorithms and the core-based algorithms (except LM-COREDP) select the same seeds (i.e., nodes 1 and 34) and therefore yield exactly the same results, which are two communities with two overlapping nodes (nodes 3 and 9) and five nodes not belonging to any community (nodes 10, 12, 17, 25 and 26). This result is relatively consistent with the ground truth. From the network structure, we can see that node 12 connects to only one member of the “square” community and is therefore not detected in this community, and node 3 is adjacent to the same number of members in both communities and is therefore taken as an overlapping member. Because of node 3, node 9 is also taken as an overlapping member. Nodes 25 and 26 are relatively far away from the seed, i.e., node 34, so they are not detected in the “triangle” community. LM-CE selects two seeds for each ground-truth community and splits each ground-truth community into two subcommunities. However, for the “square” community, the two corresponding subcommunities merge into one community that is very similar to the ground-truth community. LM-COREDP selects two seeds, i.e., nodes 25 and 30, for the “triangle” community, and splits it into two subcommunities, but these two subcommunities are merged into one that is very similar to the ground-truth community; it selects two seeds, i.e., nodes 4 and 6, for the “square” community, and the communities detected from these two seeds are quite different from the ground-truth community. For LM-ED and LM-LCC, the detected communities are quite different from the ground truth, since many unreasonable seeds are selected.

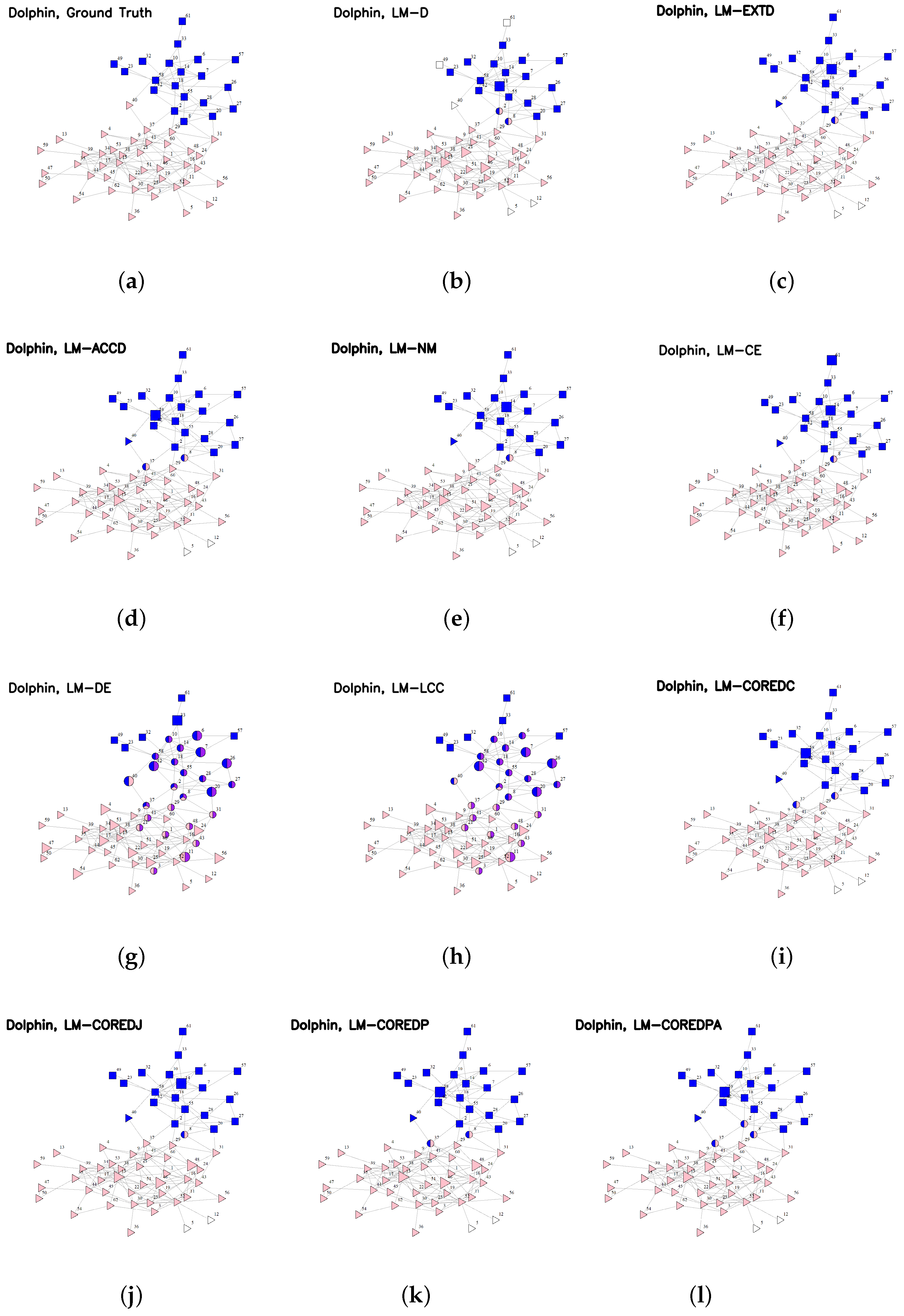
Over the Dolphin network, there are also two ground-truth communities, which can be seen from the visualization in Figure 3. The detected communities that are most similar to the ground truth are yielded by LM-CE, and the only difference is that node 8 is taken as an overlapping member and node 40 is taken as a member of the “square” community. Although LM-CE selects two seeds for the “square” community, this ground-truth community is detected perfectly because the community detected from seed 61 is a subset of the one detected from seed 14. For the “triangle” community, four seeds are chosen by LM-CE, and the ground-truth community is determined by merging the communities expanded from these seeds. LM-EXTD selects nodes 14 and 15 as seeds, and LM-NM, LM-COREDC and LM-COREDJ select the same seeds, which are nodes 14, 15, 46 and 48; but they yield the same communities that very similar to the ones by LM-CE, and the only difference is that nodes 5 and 12 are not detected in the “triangle” community. LM-D selects one seed for the “square” community, and from this seed, the ground-truth community is well detected, except that nodes 49 and 61 are not taken as members, due to their sparse connections to other members. For the “triangle” community, LM-D selects three seeds, and the communities expanded from these seeds are merged into one, where nodes 2, 8, 20, 28, and 55 are taken as overlapping members due to the fuzzy boundary. In addition, nodes 5, 12 and 40 are not taken as members. LM-ACCD selects nodes 15 and 58 as seeds and yields communities that take nodes 8 and 37 as overlap. LM-COREDPA yields communities that are similar to those yielded by LM-CE and LM-D. LM-COREDP selects nodes 14 and 28 as seeds for the “square” community, and this community is well detected by merging the two subcommunities obtained from the seeds, but it selects nodes 34, 46 and 48 as seeds for the “triangle” community, resulting in unreasonable detected communities. For LM-DE and LM-LCC, the detected communities are quite different from the ground truth because too many nodes are chosen as seeds.

Overall, the visualization results for the two smallest networks are consistent with the results shown in Table 5, Table 6 and Table 7. The degree-based algorithms, the core-based algorithms (except LM-COREDP) and LM-NM perform best over Karate, followed by LM-CE; LM-CE performs best over Dolphin, followed by LM-NM, the core-based algorithms (except LM-COREDP) and the degree-based algorithms, which are very similar to each other; and LM-DE and LM-LCC always select too many seeds and cannot discover the ground-truth communities well. In addition, some nodes that have small egonets are chosen as seeds by LM-CE, e.g., nodes 17 and 25 in Karate. These nodes are obviously not the best choices for seeds, which further influences the result of community detection. Other local seeding algorithms have similar disadvantages, especially LM-DE and LM-LCC. A few attempts have been made to filter out those nodes, e.g., Gleich and Seshadhri further excluded the nodes of local minimal conductance whose degrees are lower than a specified value [37], and Whang et al. first removed the nodes with lower degrees by extracting the largest biconnected component of the network and then performed seeding on the largest biconnected component [16]. However, how to eliminate those nodes from the seed set is still a critical issue, which we will study in future work.

The approximations to the (top) ground-truth communities for the remaining networks are presented in Figure 4. The x-axis depicts ground-truth community, and the y-axis is the Jaccard similarity between the ground-truth community and the corresponding detected community. It can be seen that over the Football network, this result is consistent with that corresponding to the F1-score metric, which is reasonable since all 12 ground-truth communities are considered here. Over Amazon, LM-COREDJ and LM-CE yield communities that are most similar to the ground truth, followed by LM-COREDP; over DBLP and YouTube, LM-CE performs best, followed by LM-COREDJ and LM-LCC, respectively; over LJ, LM-CE performs best, followed by LM-DE, LM-LCC and LM-COREDJ; and over Orkut, LM-LCC and LM-DE perform best, followed by LM-CE. The degree-based algorithms, LM-NM and LM-COREDPA always yield the worst results for the large networks, which further indicates to some extent that using only metrics such as Nvi, modularity and conductance to evaluate detected communities is one sided.

Figure 4. Similarity of the detected communities resulting from different local seeding algorithms to the (top) ground-truth communities. The y-axis is the Jaccard similarity between ground-truth community and the corresponding detected community, and the x-axis depicts ground-truth community ranked by similarity.

To evaluate the efficiency, we compare not only the running times consumed by seeding but also those consumed by detecting communities. Here, we do not consider the Karate, Dolphin and Football networks because both seeding and detecting communities over these networks are performed very quickly, and in many cases, the running time is close to zero. To clearly compare the running times of different algorithms, we compute the relative running time for each algorithm over each network. Specifically, for each network, we scale the running time of each algorithm to the range of [0, 1] by dividing by the maximal running time on this network. The relative running times are shown in Figure 5. The most efficient algorithm is LM-D, followed by LM-EXTD and LM-COREDPA. The most time-consuming algorithms are the denseness-based ones overall, among which LM-DE costs the most running time, followed by LM-LCC, LM-CE and LM-NM; the difference among LM-CE, LM-DE and LM-LCC is small, but in the phases of seed expansion and merging, LM-CE takes much less time compared with LM-DE and LM-LCC. This is because LM-DE and LM-LCC select many more seeds than LM-CE, which almost directly determines the running times of seed expansion and merging. Among the core-based algorithms, LM-COREDPA is the most efficient one, and the difference between the other three ones is not large. The running times at the phases of seed expansion and merging for the seeding algorithms are positively related to the number of chosen seeds; for example, because they select the fewest seeds, LM-ACCD, LM-EXTD and LM-COREDPA take the least running time at the phases of seed expansion and merging, followed by LM-D.

Figure 5. The relative running times of seeding, seed expansion and merging by different local seeding algorithms.

6.3. Results on Synthetic Networks

In this experiment, we generate synthetic networks using an LFR generator [65], which can construct networks with realistic properties as well as complete ground-truth communities. Specifically, nine synthetic networks are generated, each containing 2000 nodes, but with an increasing mixing parameter, which indicates the difficulty level of discovering communities. In the first network, the mixing parameter is 0; in the subsequent networks, the mixing parameter sequentially increases by 0.1; and finally, in the last network, the mixing parameter is 0.8, which indicates that the communities are very difficult to discover. The other parameters remain the same over all nine networks and are listed in Table 9.

Table 9. The parameter settings for the synthetic networks.

Parameter	Value
Number of nodes	2000
Average degree	20
Maximum degree	120
Exponent for the degree distribution	2
Exponent for the community size distribution	1
Number of overlapping nodes	200
Number of memberships of the overlapping nodes	3
Community size range	[60, 100]
Mixing parameter	[0, 0.8] with 0.1 interval

The number of seeds selected by different algorithms over different networks is listed in Table 10. The results for synthetic networks are almost consistent with those for real networks. Generally, the denseness-based algorithms (except LM-NM) select the most seeds over each network, especially LM-DE and LM-LCC; the degree-based algorithms, LM-NM and LM-COREDPA select the fewest seeds over each network. Moreover, the number of seeds decreases overall with the increase in the mixing parameter for the denseness-based algorithms (except LM-NM), except that LM-CE selects an increasing number of seeds when the mixing parameter is in the range of [0.5, 0.8]; the number of seeds decreases sharply when the mixing parameter is 0.1 and then changes few for the other algorithms. The coverage resulting from different seeding algorithms is shown in Figure 6. The coverage is positively correlated with the number of seeds; i.e., the more seeds there are, the higher the coverage is. Thus, the coverage shows a downward trend overall along with the increase in the mixing parameter for the denseness-based algorithms (except LM-NM), except that LM-CE has a little increase coverage when the mixing parameter is in the range of [0.5, 0.8]. The coverage decreases sharply when the mixing parameter is 0.1 and then changes little for the other algorithms except LM-D (in contrast, LM-D has an increase, but its coverage is always very low), indicating the challenge for seeding introduced by obscure boundaries among communities.

Table 10. The number of seeds chosen by different algorithms.

	SN0	SN1	SN2	SN3	SN4	SN5	SN6	SN7	SN8
LM-D	4	5	5	8	3	2	4	3	3
LM-EXTD	4	2	5	3	3	1	3	4	4
LM-ACCD	4	2	3	4	3	1	2	4	3
LM-NM	8	1	4	4	3	2	3	3	4
LM-CE	29	19	12	8	7	7	11	23	46
LM-DE	751	705	630	591	618	557	534	510	491
LM-LCC	734	672	576	515	514	401	357	283	296
LM-COERDC	12	2	6	4	5	4	3	2	5
LM-COREDJ	11	1	6	4	3	4	3	5	4
LM-COREDP	23	2	3	1	3	3	3	5	4
LM-COREDPA	16	3	4	3	4	3	4	4	4

Figure 6. The coverage obtained by different local seeding algorithms over different networks.

The F1-score, Nvi, modularity and conductance resulting from different seeding algorithms are shown in Figure 7. First, it can be seen that for all the seeding algorithms, the metric values generally worsen with the increase in the mixing parameter. This is reasonable since the community structure becomes less clear as the mixing parameter increases. Second, several algorithms, such as LM-CE and the core-based algorithms (except LM-COREDPA), perform well when the mixing parameter is 0, especially LM-CE, which performs best in terms of almost all the evaluation metrics. However, when the mixing parameter increases, their performance becomes unstable and is no longer better than that of some other seeding algorithms, e.g., LM-DE and LM-LCC produce higher F1-scores than them when the mixing parameter is 0.1 and 0.2, and LM-COREDJ produces a lower conductance when the mixing parameter is 0.1, but an increasing conductance overall when the community structure becomes increasingly unclear.

Figure 7. The F1-score, Nvi, modularity and conductance of the communities detected by different local seeding algorithms.

7. Conclusions

In this paper, we first summarize the seeding algorithms for community detection in the literature, then obtain a unified framework for local seeding based on the existing local seeding algorithms. Under the unified framework, 11 local seeding algorithms, including 3 existing ones, are instantiated, and are categorized into three classes. Finally, we compare these local seeding algorithms on real networks and synthetic networks, and obtain some suggestive conclusions:

(1)

The degree-based algorithms usually select the fewest seeds, while the denseness-based algorithms (except LM-NM) select the most seeds.

(2)

On the real networks, LM-CE performs best in identifying the communities of high quality, closely followed by LM-COREDJ, and LM-DE and LM-LCC can also discover many communities of high quality, but due to some improper seeds being selected, the denseness-based algorithms (except LN-NM) usually yield poor results in terms of evaluation metrics, such as Nvi, modularity and conductance.

(3)

The algorithms that select a few seeds, including degree-based algorithms, LM-NM and LM-COREDPA, perform well on small real networks but can only discover a few communities in large-scale networks. This is because they prefer to choose nodes with high degree as seeds, and in small networks, the community members are gathered around the high-degree nodes, while in large-scale networks, the community structure is much more complicated, and there are a few high-degree nodes adjacent to a large number of nodes, resulting in detecting a few communities while missing many ground-truth communities. This result indicates, to some extent, that the algorithms that perform well on small networks may not be suitable for large networks, even when the small networks have the same characteristics, such as a power-law distribution of degrees and the small world phenomenon, with the large networks.

(4)

The core-based algorithms seem the most suitable for real networks, considering all the evaluation metrics. Compared with the denseness-based algorithms, they can select fewer improper seeds, resulting in fewer noisy community; compared with the degree-based algorithms, they can select more seeds, thereby discovering more communities. Among the core-based algorithms, LM-COREDJ works best overall.

(5)

The core-based algorithms (especially LM-COREDJ) have the best balance between quality and cost since they perform best overall on real networks and also work well on synthetic network when the mixing parameter is small; they cost more running time than the degree-based algorithms in many cases, but they are more efficient than the denseness-based algorithms.

(6)

For the synthetic networks with mixing parameter 0, i.e., those in which the community structure is very clear, LM-CE performs best; the core-based algorithms (except LM-COREDPA) can also discover the communities well in this case.

Moreover, we find from the experimental results that all the seeding algorithms perform relatively poorly over large networks, which indicates that seeding as well as community detection in large networks is still challenging and requires further study. Several possible lines of future study are as follows:

(1)

Explore approaches to filter out the improper seeds. There are improper seeds in the seed set obtained by many seeding algorithms, which brings noise or redundancy to the subsequent community detection. This can be visually demonstrated by the results in Figure 2 and Figure 3. If those improper seeds are eliminated from the seed set, the phase of community detection can be improved from both cost and quality.

(2)

Explore the formal or mathematical definitions of “seed”. To our best knowledge, there is no standard and formal definition of seed, which probably due to the conceptual definition of community. This makes the problem of seeding more difficult and heavily hinders the exploration of seeding algorithms. Thus, it is critical to mathematically determine what kind of node the seed is. It may be an effective way to further study the problem of seeding (and community detection) from both theoretical and experimental aspects; and regarding the experimental study, the algorithms could be performed on a large number of networks to obtain statistical results.

(3)

Explore new evaluation approaches. We find that each algorithm performs differently on different evaluation metrics, which indicates that there is still a lack of good evaluation metrics for community detection. It is necessary to explore more comprehensive evaluation metrics or methods. An alternative approach is to evaluate algorithms in multiple aspects, but how to combine those multiple results requires more study.

(4)

Explore more applications of seeding. We focus on local seeding for community detection in this paper; however, there must be other interesting problems that involve seeding, e.g., node influence, influence maximization, and information diffusion. What the connections between seeding and those problems are and how seeding is applied to those problems are still unclear and require exploration.