A Novel Multi-Source Domain Adaptation Method with Dempster–Shafer Evidence Theory for Cross-Domain Classification

Abstract

In this era of big data, Multi-source Domain Adaptation (MDA) becomes more and more popular and is employed to make full use of available source data collected from several different, but related domains. Although multiple source domains provide much information, the processing of domain shifts becomes more challenging, especially in learning a common domain-invariant representation for all domains. Moreover, it is counter-intuitive to treat multiple source domains equally as most existing MDA algorithms do. Therefore, the domain-specific distribution for each source–target domain pair is aligned, respectively. Nevertheless, it is hard to combine adaptation outputs from different domain-specific classifiers effectively, because of ambiguity on the category boundary. Subjective Logic (SL) is introduced to measure the uncertainty (credibility) of each domain-specific classifier, so that MDA could be bridged with DST. Due to the advantage of information fusion, Dempster–Shafer evidence Theory (DST) is utilized to reduce the category boundary ambiguity and output reasonable decisions by combining adaptation outputs based on uncertainty. Finally, extensive comparative experiments on three popular benchmark datasets for cross-domain image classification are conducted to evaluate the performance of the proposed method via various aspects.

1. Introduction

Recently, Deep Learning (DL) has made remarkable advances in various fields  [1,2,3,4,5,6,7], especially in classification [8,9,10]. Despite excellent results, the success of deep methods highly relies on: (1) large-scale labeled data for supervised learning and (2) the training and test data meeting the requirement of being Independently Identically Distributed (IID). However, annotation is time-consuming and unaffordable in practice. If a model is trained on a dataset (known as the source domain), but tested on another non-IID dataset (known as the target domain), domain shifts occur and tend to severely degrade the performance of the learned model [11,12]. Therefore, it is necessary to develop models that are trained on the given labeled datasets, but that can generalize well to a non-IID unlabeled dataset.

Domain Adaptation (DA) aims to learn a discriminative model by reducing domain shifts between training and test distributions [13]. DA transfers the given labeled source domain knowledge to tackle the task to the different, but related target domain by learning domain-invariant representation between domains. Most approaches focus on Single-source Domain Adaptation (SDA), where the labeled data from only one single source domain are considered. Many achievements have emerged in this decade [14,15,16,17,18]. For example, DDC [14] adds an adaptation layer to the pre-trained AlexNet model to confuse the feature representation between the single source domain and the target domain. DSAN [16] proposes a novel fine-grained metric function to align the distribution of the single source domain and the target domain. Most of them learn to map the data from both domains into a common feature space to learn domain-invariant representations by minimizing domain distribution discrepancy, so that the source classifier could then be directly applied to target instances.

However, in practice, it is very likely to obtain multiple available source domains, while SDA is not up to employing those source data adequately. Hence, more challenging, Multi-source Domain Adaptation (MDA) is developed to utilize labeled data from multiple source domains with different distributions and has attracted extensive attention these days  [19,20,21]. The most straightforward way is to combine all source domains into one single source domain and, then, directly apply SDA methods to align distributions. Due to the dataset expansion, the methods might improve the performance. However, the improvements might not be sufficient; the more accurate ways are supposed to explore to make full use of source domains.

With the spurt of progress in DL and SDA today, MDA has been gradually developed. However, there are two typical issues with most techniques [22,23,24,25,26,27,28]. (1) Firstly, it is more challenging to learn a common domain-invariant representation for all domains in MDA, because the damages of domain shifts cannot be eliminated even in SDA. Thereby, MDA is processed by aligning the domain-specific distribution for each source–target domain pair. (2) Secondly, multiple source domains are treated as equivalents. However, the benefits of each source domain to the target domain tasks are diverse in reality. The final output should be closer to the adaptation output of the source–target domain pairs with higher credibility. Some studies [29,30] add extra neural network components to measure the credibility (i.e., transferability). In this research study, we employed Subjective Logic (SL) [31] to obtain the uncertainty of every source domain without any addition of the neural network. Regarding source–target domain pairs as witnesses with different credibility (uncertainty), we introduced Dempster–Shafer evidence Theory (DST) to combine all domain-specific adaptation outputs.

As an uncertainty reasoning method, DST can effectively and reliably deal with uncertainty. It relies on Basic Probability Assignment Functions (BPAFs) to measure the initial degree of belief in the occurrence of an event, which is similar to the concept of the “probability” of a random event in probability theory. To generate BPAFs, DST is bridged with MDA and DL by subjective logic.

Our contributions are summarized as follows:

• A novel multi-source domain adaptation method with Dempster–Shafer evidence theory is proposed. We provide an effective cross-domain classification solution without any addition of the neural network.
• There are few studies combining multi-source domain adaptation and Dempster–Shafer evidence theory as of yet. We explored this kind of research early. In our work, DST is employed to fuse all domain-specific adaptation results and output the final credible results.
• The effectiveness of our cross-domain classification method is verified by conducting comprehensive experiments on three well-known benchmarks. The experimental results prove that the proposed method has better performance than other compared approaches.

The rest of this paper is organized as follows. Section 2 reviews the related work. In Section 3, the preliminaries are given. Section 4 describes the proposed method in detail. A series of experiments is reported in Section 5 and discussed in Section 6. Finally, Section 7 summarizes this research study.

2. Related Work

2.1. Single-Source Domain Adaptation

Single-source Domain Adaptation (SDA) is bound up with multi-source domain adaptation. SDA aims to generalize a model learned from a labeled source domain to a related unlabeled target domain with a different data distribution by reducing the domain shift. SDA can be roughly divided into three categories according to different alignment strategies. (1) Discrepancy-based approaches utilize different metric schemas to explicitly measure the distance between the source and target domains and diminish the domain shift. Commonly used discrepancy metrics for domain adaptation include Maximum Mean Discrepancy (MMD) [32,33,34], moment matching [35,36], Kullback–Leibler (KL) divergence [37], correlation alignment [38,39], and mixture distance [40]. (2) Adversarial-based approaches align different data distributions by confusing a well-trained discriminator (domain classifier). Many methods [41,42,43,44,45,46] are based on Generative Adversarial Networks (GANs), which align different data distributions by implicitly learning the metric function (i.e., domain discriminator) between the source and target domains. (3) Reconstruction-based approaches assume that reconstructing the target domain from a latent representation by using the source task model can help learn domain-invariant representations. The reconstruction is usually obtained via an auto-decoder [47,48,49] or a GAN discriminator [50,51,52].

In our work, the first kind of approach was chosen and the most widely used discrepancy MMD was employed to align the distributions.

2.2. Multi-Source Domain Adaptation

In practice, available source data often come from several different, but related domains. Multi-source Domain Adaptation (MDA) is developed to make full use of these data. However, multiple source domain data provide much information, but challenge the processing of domain shifts. (1) Based on the assumption that the target domain distribution can be approximated by mixing the source domain distribution [53,54], some MDA methods focus on the weighted combination of source domains. For example, Sun and Shi [22] designed a method to weight the source domain classifiers based on the Bayesian learning principle. Xu et al. [23] proposed a voting method for multiple classifiers, which is based on the output of domain discriminators. (2) In addition, some methods are devised to map all source domains and the target domain to a unified feature space. For instance, MDAN [24] aligns the distribution of source domains with the target domain through multiple domain discriminators. M${}^3$SDA [25] employs moment matching to align the source–target and source-source domains in a common feature space. HoMM [26] exploits the high-order statistics for domain alignment in a reproducing kernel Hilbert space. (3) Some other methods are based on reconstruction [27,28], which reconstruct multiple source domains into an intermediate single source domain and then directly carry out SDA.

Sadly, the damages of domain shifts cannot be eliminated in SDA. It is more difficult to learn a common domain-invariant representation for all domains in MDA. Following MFSAN [55], the domain-specific distribution and classifier alignment architecture for cross-domain classification has proceeded. However, MFSAN treats every source domain equally. This is counter-intuitive because different source domains help the target task differently. Thus, regarding source–target domain pairs as witnesses with different credibility (uncertainty), DST is employed to combine all domain-specific adaptation results. Specifically, the uncertainty is captured, and BPAFs are generated by using subjective logic.

2.3. Dempster–Shafer Evidence Theory

Dempster–Shafer evidence Theory (DST) was first introduced in the 1960s. Based on the investigation of statistical problems, Arthur P. Dempster introduced the concept of upper and lower probabilities and their combining rules [56]. Then, the form of probability that does not satisfy additivity was defined for the first time [57]. Later, Glenn Shafer reinterpreted the upper and lower probabilities based on the belief function and developed the theory into a general framework for modeling epistemic uncertainty [58]. DST allows beliefs from different sources to be fused with various operators to obtain new beliefs considering all available evidence [59]. Currently, generating the belief function through DL has proven to be successful and efficient [60]. These unique characteristics make DST particularly suitable for information fusion [61,62]. Similar to information fusion, the idea of our MDA method is to combine evidence from multiple sources.

3. Preliminaries

3.1. Unsupervised Multi-Source Domain Adaptation

In this research study, the unsupervised MDA problem is investigated. Let ${\mathcal{D}}_s={\left\{{\mathcal{D}}_{si}\right\}}_{i=1}^N$ denote a collection of N available datasets of source domains, and each labeled source dataset ${\mathcal{D}}_{si}={\left\{({\mathbf{X}}_{si}^{\left(j\right)},y_{si}^{\left(j\right)})\right\}}_{j=1}^{n_{si}}$ with $n_{si}$ samples is sufficient to train a source domain distribution model. Meanwhile, a target dataset ${\mathcal{D}}_t={\left\{{\mathbf{X}}_t^{\left(j\right)}\right\}}_{j=1}^{n_t}$ with $n_t$ samples drawn from the target domain ${\mathcal{D}}_t$ has no labels to support training a reasonable distribution model. With given ${\mathcal{D}}_s\cup {\mathcal{D}}_t$, the general goal of this problem is to train a cross-domain classifier $f_{\theta }\left(\mathbf{x}\right)$, which has a low target risk ${ϵ}_t={\mathbb{E}}_{\mathbf{x}\in {\mathcal{D}}_t}[f_{\theta }\left(\mathbf{x}\right)\ne {\mathbf{y}}_t]$.

The domain-specific distribution and classifier alignment architecture in MFSAN [55] has proceeded to cross-domain classification. Thus, the domain adaptation model involves the source domain task loss ${\mathcal{L}}_s$, the domain adaptation loss ${\mathcal{L}}_d$, and the classifier constraint loss ${\mathcal{L}}_r$. As shown in (1), $\lambda$ and $\gamma$ are trade-off parameters.

$$\mathcal{L}={\mathcal{L}}_s+\lambda {\mathcal{L}}_d+\gamma {\mathcal{L}}_r$$

(1)

3.2. Maximum Mean Discrepancy

Maximum mean discrepancy, inspired by the two-sample test in statistics [63,64], is the most widely used discrepancy to align the distributions in domain adaptation. In general, MMD is interpreted as the maximum value (upper bound) of the expectation difference between two distributions mapped by any function f in a predefined function field $\mathcal{F}$, which is an arbitrary vector in the unit sphere (i.e., $\parallel f\parallel <1$) of the reproducing Hilbert space:

$$MMD[\mathcal{F},p,q]:=\underset{f\in \mathcal{F}}{sup}\left({\mathbf{E}}_p\left[f\left(x\right)\right]-{\mathbf{E}}_q\left[f\left(y\right)\right]\right)$$

(2)

In practice, an estimate of the MMD compares the square distance between the empirical kernel mean embeddings as (3). $\mathcal{H}$ is the Reproducing Kernel Hilbert Space (RKHS) endowed with a characteristic kernel k. k means $k\left({\mathbf{x}}^s,{\mathbf{x}}^t\right)=〈\varphi \left({\mathbf{x}}^s\right),\varphi \left({\mathbf{x}}^t\right)〉$, where $\langle ·,·\rangle$ represents the inner product of vectors and $\varphi (·)$ denotes some feature map to map the original samples to the RKHS $\mathcal{H}$.

$${MMD}^2[\mathcal{F},X_s,X_t]={∥\frac{1}{n_s}\sum _{{\mathbf{x}}_i\in {\mathcal{D}}_s}\varphi \left({\mathbf{x}}_i\right)-\frac{1}{n_t}\sum _{{\mathbf{x}}_j\in {\mathcal{D}}_t}\varphi \left({\mathbf{x}}_j\right)∥}_{\mathcal{H}}^2$$

(3)

3.3. Basic Concepts of DST

The Basic Probability Assignment Function (BPAF) is the fundamental unit of DST, which expresses the initial degree of belief in the proposition. Let $\Theta$ be a frame of discernment, which specifies the proposition range. The function $m:2^{\Theta }\to [0,1]$ becomes the BPAF when it satisfies (4). If $m\left(A\right)>0$, $m\left(A\right)$ is also called the belief mass, and A is named the focal element.

$$\left\{\begin{array}{c}m(\varnothing )=0\hfill \\ \sum _{A\subseteq \Theta }m\left(A\right)=1\hfill \end{array}\right.$$

(4)

Dempster’s rule ⊕ is at the core of DST, as it provides algorithmic rules for combining two pieces of evidence, as shown in (5). Besides, Dempster’s rule is invoked $N-1$ times to combine N sets of evidence.

$$m_1\left(X\right)\oplus m_2\left(X\right)=\left\{\begin{array}{c}0,X=\varnothing \hfill \\ \frac{1}{1-K}\sum _{A_i\cap B_j=X}{m}_1\left(A_i\right)m_2\left(B_j\right),X\ne \varnothing \hfill \end{array}\right.$$

(5)

The definition of conflict factor K, shown in (6), reflects the degree of conflict between $m_1$ and $m_2$, whereby $1/(1-K)$ represents the normalization factor. Obviously, Dempster’s rule tries to fuse shared parts from different sources and ignores conflicting beliefs.

$$K=\sum _{A_i\cap B_j=\varnothing }{m}_1\left(A_i\right)m_2\left(B_j\right)$$

(6)

3.4. Dirichlet Distribution

The Dirichlet distribution is involved in SL, which bridges DL, MDA, and DST. In the context of multi-class classification, SL converts the outputs (from DL and MDA) of the neural networks into the concentration parameter of the Dirichlet distribution and associates it with the belief masses (for DST). Accordingly, DST could combine multi-source evidence after BPAFs are obtained and output the final decision.

If the probability density function of multivariate continuous random variable $\theta =\{{\theta }_1,{\theta }_2,\dots ,{\theta }_k\}$ is (7):

$$p(\theta \mid \alpha )=\frac{\mathsf{\Gamma }\left({\sum }_{i=1}^k{\alpha }_i\right)}{{\prod }_{i=1}^k\mathsf{\Gamma }\left({\alpha }_i\right)}\prod _{i=1}^k{\theta }_i^{{\alpha }_i-1}$$

(7)

where ${\sum }_{i=1}^k{\theta }_i=1,{\theta }_i\ge 0,{\alpha }_i>0,i=1,2,\dots ,k$, and $\mathsf{\Gamma }(·)$ is the Gamma function. Then, the random variable $\theta$ is said to obey the Dirichlet distribution with concentration parameter $\alpha$ and denoted as $\theta \sim Dir\left(\alpha \right)$.

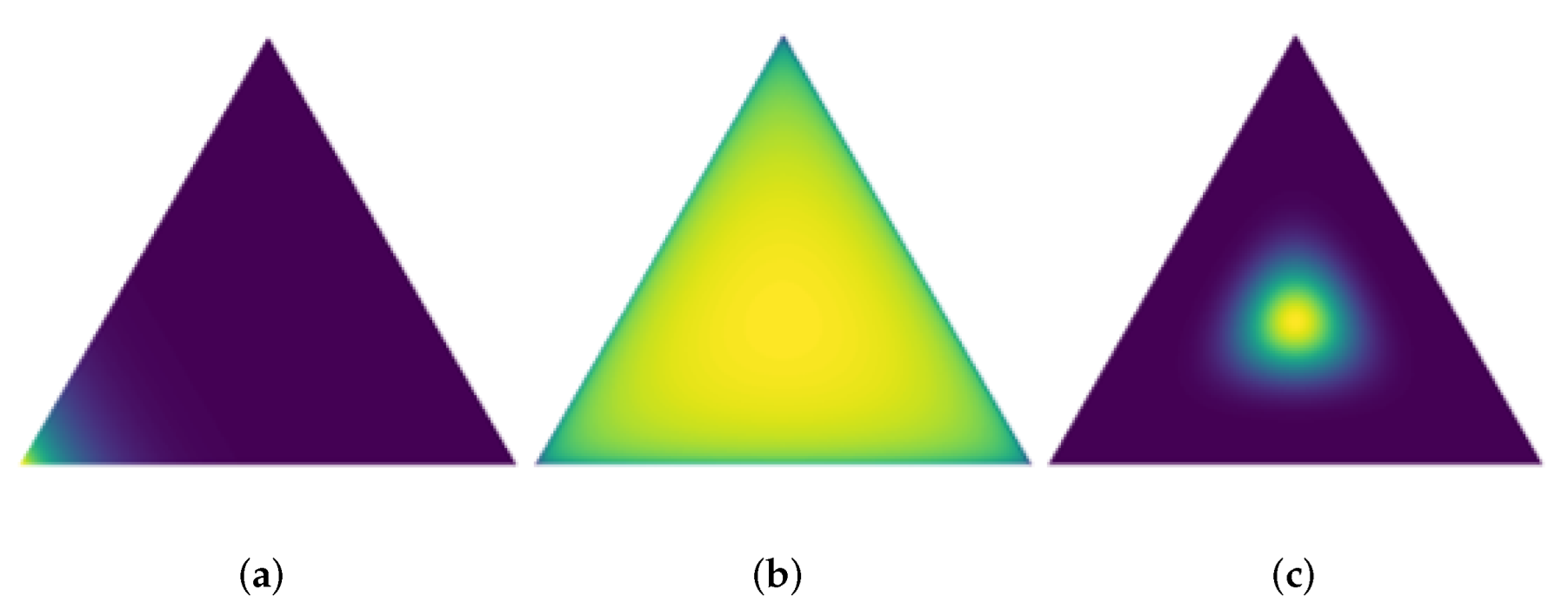
Dirichlet distribution $\theta$ exists on the $(k-1)$-dimensional simplex, as shown in Figure 1.

The most important property of the Dirichlet distribution is that it is the conjugate prior to the multinomial distribution. If $\theta$ follows the Dirichlet distribution, its prior probability distribution is $p\left(\theta \right|\alpha )=Dir(\theta \left|\alpha \right)$ and posterior probability distribution is $p\left(\theta \right|D,\alpha )=Dir(\theta |\alpha +n)$, where D is the given simplex and $n=(n_1,n_2,\dots ,n_k)$ is the observation count of the multinomial distribution. The concentration parameters $\alpha =\{{\alpha }_1,{\alpha }_2,\dots ,{\alpha }_k\}$ of the Dirichlet distribution as a priori distribution are also called the hyperparameters of the posterior distribution. Hence, it is convenient to obtain the posterior distribution from the prior distribution.

4. Research Methodology

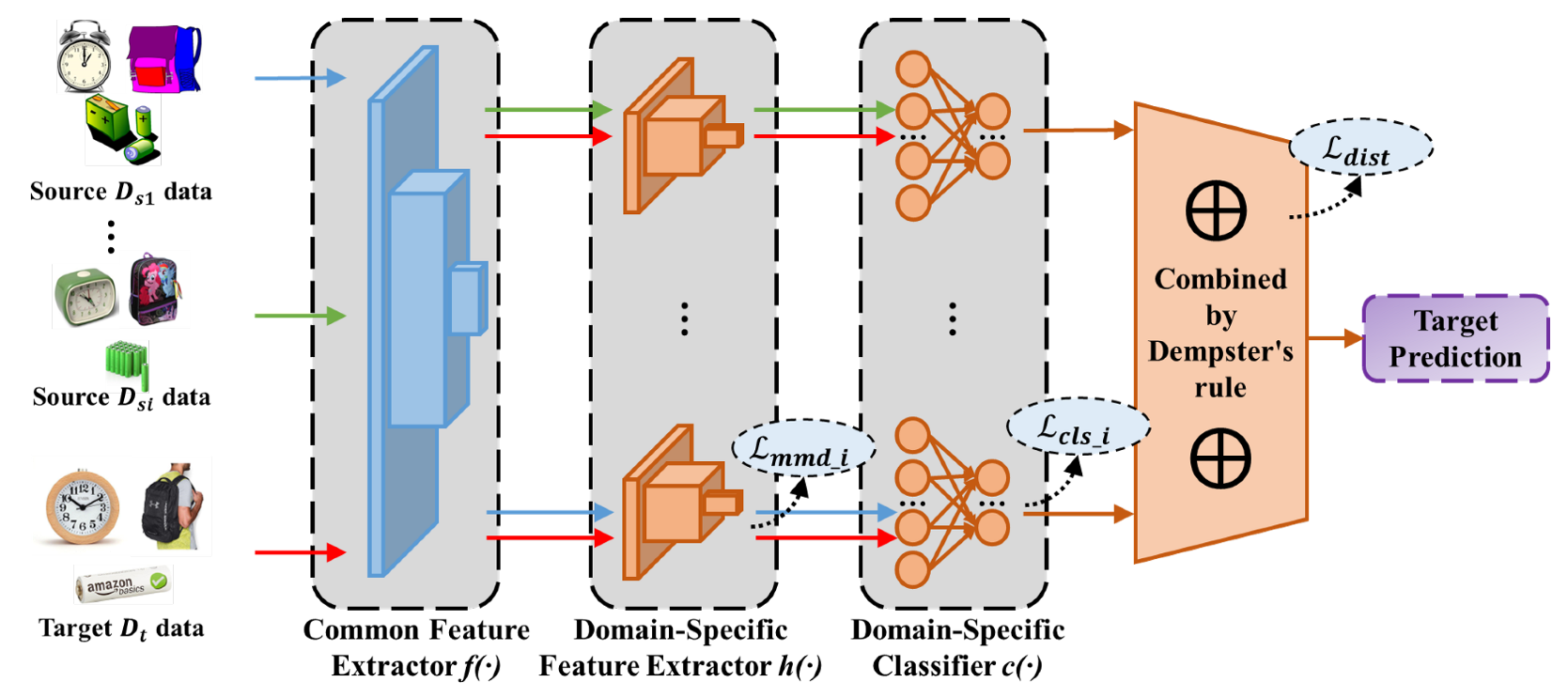
Following the two-stage alignment framework in MFSAN [55], a novel Multi-source domain Adaptation Network with Dempster–Shafer evidence theory (MAN-DS) for cross-domain classification is proposed. MAN-DS aims to train a model based on multi-source domain labeled samples and adapts to classify target instances with different distributions. As shown in Figure 2, the MAN-DS framework consists of four key components, i.e., common feature extractor, domain-specific feature extractor, domain-specific classifier, and Dempster’s combination. Different source domains are extracted into different feature spaces, and then, the distribution alignment of each pair of source and target domains and the output alignment of every source classifier are imposed. Domain-specific adaptation outputs are combined by Dempster’s rule in the end. Besides, the $softmax$ layer of the classifier is replaced with an activation layer (e.g., ReLU).

4.1. Common Feature Extractor

The damages of domain shifts cannot be eliminated in SDA, so it is more difficult to learn a common domain-invariant representation for all domains in MDA. To address this problem, the easiest way is to train multiple networks to map each source–target domain pair into a specific feature space. However, this would take too much time and space. Thus, the feature extractor is divided into two parts. The first part extracts common features, and the second part extracts domain-specific features (see the next section). In the first part, a common convolutional neural subnetwork $f(·)$ is used to automatically map samples in all domains from the original feature space into a common feature space.

4.2. Domain-Specific Feature Extractor

Now, we come to the second part where domain-specific features are extracted by different extractors. For each pair of source and target domains, a specific subnetwork $h_i(·)$ aims to map $f\left({\mathbf{x}}_{si}\right)$ and $f\left({\mathbf{x}}_t\right)$ into the same domain-specific feature space. The objective of domain adaptation is to find a domain-invariant representation between domains. In other words, an $h_i(·)$ is desired, which makes the distribution discrepancy between $h_i\left(f\left({\mathbf{x}}_{si}\right)\right)$ and $h_i\left(f\left({\mathbf{x}}_t\right)\right)$ as small as possible. There are many explicit or implicit methods to achieve this goal. Here, the most widely used MMD is employed to reduce the distribution discrepancy between domains. The MMD loss is reformulated as:

$${\mathcal{L}}_{mmd}=\frac{1}{N}\sum _{i=1}^N{MMD}^2[\mathcal{F},h_i\left(f\left(X_{s}i\right)\right),h_i\left(f\left(X_t\right)\right)]$$

(8)

4.3. Domain-Specific Classifier

Traditionally, a series of $softmax$ classifiers $c_i(·)$ is employed to classify the source domain samples after extracting domain-specific invariant features, respectively. However, the use of the exponent in the $softmax$ function leads to the probability of the predicted category being inflated. It was replaced with an activation function (e.g., RELU) to ensure that the network outputs non-negative values in this research study. The multi-classification problem is a multinomial distribution fitting problem. As the conjugate prior, the Dirichlet distribution is convenient to obtain the posterior distribution from the prior distribution.

Subjective logic [31] defines a theoretical framework for obtaining the probabilities of different classes and the overall uncertainty of the multi-classification problem based on the evidence collected from the data. SL provides an additional mass function, which allows the model to distinguish between a lack of evidence. In our model, SL provides the degree of overall uncertainty of each source, which is important for final decisions to some extent.

For the K-classification problem, the nonnegative-activated output $e=(e_1,e_2,\dots ,e_k)$ of the last fully connected layer of the classifier refers to evidence and is closely related to the concentration parameters $\alpha =({\alpha }_1,{\alpha }_2,\dots ,\alpha +k)$ of the Dirichlet distribution, as shown in the following:

$${\alpha }_k=e_k+1,k=1,2,\dots ,K$$

(9)

With subjective logic, for each pair of the source–target domain, the probability $b_k^{\left(i\right)}$ for the kth category and the overall uncertainty $u^{\left(i\right)}$ are calculated by:

$$\begin{array}{cc}\hfill b_k^{\left(i\right)}& =\frac{e_k^{\left(i\right)}}{S^{\left(i\right)}}=\frac{{\alpha }_k^{\left(i\right)}-1}{S^{\left(i\right)}}\hfill \\ \hfill u^{\left(i\right)}& =\frac{K}{S^{\left(i\right)}}\hfill \end{array}$$

(10)

where $S^{\left(i\right)}={\sum }_{k=1}^K(e_k^{\left(i\right)}+1)={\sum }_{k=1}^K\left({\alpha }_k^{\left(i\right)}\right)$ is the Dirichlet strength. Obviously, $u^{\left(i\right)}+{\sum }_{k=1}^K{b}_k^{\left(i\right)}=1$. Correspondingly, the less total evidence observed, the greater the total uncertainty is. The mean of the corresponding Dirichlet distribution ${\widehat{\mathbf{P}}}_{si}$ for the probability ${\widehat{p}}_i^{\left(k\right)}$ is computed as ${\widehat{p}}_i^{\left(k\right)}=\frac{{\alpha }_i^{\left(i\right)}}{S^{\left(i\right)}}$.

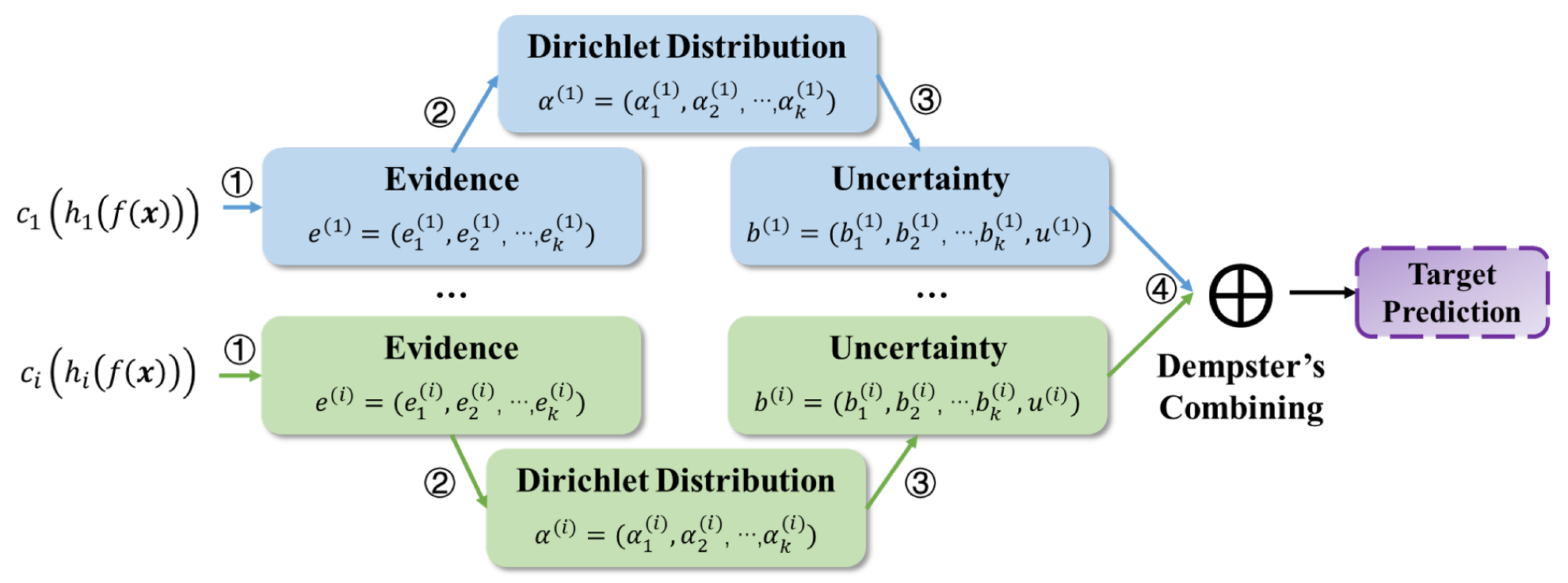
In addition, Figure 3 demonstrates the process of the outputs of multiple domain-specific classifiers in detail. The evidence of each source is obtained using neural networks (Step ①). According to subjective logic [31], the obtained evidence parameterizes the Dirichlet distribution (Step ②) to induce the classification probability and uncertainty (Step ③). The classification probability and overall uncertainty are inferred by combining the belief masses of multiple sources based on Dempster’s rule (Step ④). Dempster’s combining is discussed in Section 4.4.

Source domain task loss ${\mathcal{L}}_{cls}$ is calculated here. To adapt to the Dirichlet distribution [65], the cross-entropy function is formulated as (11).

$$\begin{array}{cc}\hfill {\mathcal{L}}_{ace}\left({\alpha }^{\left(i\right)}\right)& =\int \left[\sum _{k=1}^K-y_{ij}log\left(p_{jk}\right)\right]\frac{1}{B\left({\alpha }_j\right)}\prod _{k=1}^K{p}_{jk}^{{\alpha }_{jk}^{\left(i\right)}-1}d{\mathbf{p}}_j\hfill \\ \hfill & =\sum _{k=1}^K{y}_{jk}\left(\psi \left(S^{\left(i\right)}\right)-\psi \left({\alpha }_{jk}^{\left(i\right)}\right)\right)\hfill \end{array}$$

(11)

where $\psi (·)$ is the digamma function, the parameter ${\alpha }_i$ of the Dirichlet distribution and forming the multinomial opinions $D\left({\mathbf{p}}_i{\mathbf{\alpha }}_i\right)$, where ${\mathbf{p}}_i$ is the category assignment probabilities on a simplex, and $p_{jk}$ is the predicted probability of the $j_{th}$ sample for category k.

The above loss function ensures that more evidence is generated for the correct label of each sample than for other classes, but there is no guarantee that less evidence is generated for the incorrect label. That is, in MAN-DS, the expected evidence of incorrect labels shrinks to 0 [66]. To this end, the following KL divergence term is introduced:

$$\begin{array}{cc}\hfill KL\left[D\left({\mathbf{p}}_j\mid {\tilde{\alpha }}_j\right)\parallel D\left({\mathbf{p}}_j\mid \mathbf{1}\right)\right]& =log\left(\frac{\mathsf{\Gamma }\left({\sum }_{k=1}^K{\tilde{\alpha }}_{jk}\right)}{\mathsf{\Gamma }\left(K\right){\prod }_{k=1}^K\mathsf{\Gamma }\left({\tilde{\alpha }}_{jk}\right)}\right)\hfill \\ \hfill & +\sum _{k=1}^K\left({\tilde{\alpha }}_{jk}-1\right)\left[\psi \left({\tilde{\alpha }}_{jk}\right)-\psi \left(\sum _{r=1}^K{\tilde{\alpha }}_{jr}\right)\right]\hfill \end{array}$$

(12)

Therefore, given parameter ${\mathbf{\alpha }}_j$ of the Dirichlet distribution for each sample j, the loss is:

$$\mathcal{L}\left({\alpha }^{\left(i\right)}\right)=\sum _{j=1}^{n_{si}}\mathcal{L}\left({\alpha }_j\right)=\sum _{j=1}^{n_{si}}\left\{{\mathcal{L}}_{ace}\left({\alpha }_j\right)+\rho KL\left[D\left({\mathbf{p}}_j\mid {\tilde{\alpha }}_{\mathbf{j}}\right)\parallel D\left({\mathbf{p}}_j\mid \mathbf{1}\right)\right]\right\}$$

(13)

where $\rho >0$ is a balance factor. In practice, $\rho$ increases slowly from zero to 1 to avoid paying too much attention to the KL divergence term in the early stage of learning.

That is, the classification loss is formulated as:

$${\mathcal{L}}_{cls}=\sum _i^N\mathcal{L}\left({\alpha }^{\left(i\right)}\right)$$

(14)

4.4. Dempster’s Combination

With subjective logic, there is an FoD $\Theta =\{1,2,\dots ,K\}$ and $K+1$ focal elements $\left\{\right\{1\},\{2\},\dots ,\{K\},\Theta \}$ with belief mass $\{b_1,b_2,\dots ,b_k,u\}$ in every source–target domain pair. To fuse these adaptation outputs from N sources, only call Dempster’s rule (defined in (5)) $N-1$ times as:

$$m_{\oplus }\left(b_k\right)=m_1\left(b_k\right)\oplus m_2\left(b_k\right)\oplus ,\dots ,\oplus m_{N-1}\left(b_k\right)$$

(15)

In addition, the prediction results of multiple classifiers for the same target sample should be consistent. Dempster’s combination could help to avoid ambiguity and large uncertainty on the category boundary, which is demonstrated in Figure 4.

Moreover, the Manhattan distance is used to measure the difference among the classifiers to achieve this goal, as well. Denote $e^{\left(i\right)}=e_1^{\left(i\right)},e_2^{\left(i\right)},\dots ,e_k^{\left(i\right)},e^{\left(i\right)}={\alpha }^{\left(i\right)}-1=b^{\left(i\right)}{S}^{\left(i\right)}$ as the final output of the ith source–target domain pair. The loss-of-label Manhattan distance is formulated as:

$${\mathcal{L}}_{dist}=\frac{1}{N}\sum _i^N|e^{\left(i\right)}-m_{\oplus }\left(e\right)|$$

(16)

4.5. Objective Function and Algorithm

The overall objective function of the proposed model is formulated as (17).

$$\underset{f,h,c}{argmin}({\mathcal{L}}_{cls}+\gamma {\mathcal{L}}_{mmd}+\lambda {\mathcal{L}}_{disc})$$

(17)

In detail, ${\mathcal{L}}_{cls}$ is minimized to accomplish the source domain task; ${\mathcal{L}}_{mmd}$ is minimized to reduce the domain shifts between each source domain and the target domain; ${\mathcal{L}}_{disc}$ is a consistent regular term and minimized to constrain the outputs of domain-specific classifiers. In addition, $\gamma$ and $\lambda$ are trade-off parameters; refer to (1).

The algorithm of [d=Z.]MAN-DSour method is summarized in Algorithm 1, and it can be trained by the standard back-propagation.

Algorithm 1:The algorithm of the proposed method

Input : source domain data ${\left\{{\mathcal{D}}_{si}\right\}}_{i=1}^N$, target domain data ${\mathcal{D}}_t$, the number of training iterations T, and batch size M; Output : model parameters; 1: Initialize the parameters of $f(·)$, $g(·)$, $h_i(·)$, $c_i(·)$; 2: for$t=1,\dots ,T$do 3:    Randomly sample a batch of ${\left\{({\mathbf{x}}_{si}^{\left(j\right)},y_{si}^{\left(j\right)})\right\}}_{j=1}^M$ from ${\mathcal{D}}_{si}$, respectively; 4:    Randomly sample a batch of ${\left\{{\mathbf{x}}_t^{\left(j\right)}\right\}}_{j=1}^M$ from ${\mathcal{D}}_t$; 5:    Extract common features $f\left({\mathbf{x}}_{si}^{\left(j\right)}\right)$ and $f\left({\mathbf{x}}_t^{\left(j\right)}\right)$; 6:    Extract domain-specific features $h_i\left(f\left({\mathbf{x}}_{si}^{\left(j\right)}\right)\right)$ and $h_i\left(f\left({\mathbf{x}}_t^{\left(j\right)}\right)\right)$; 7:    Compute ${\mathcal{L}}_{mmd}$ with $h_i\left(f\left({\mathbf{x}}_{si}^{\left(j\right)}\right)\right)$ and $h_i\left(f\left({\mathbf{x}}_t^{\left(j\right)}\right)\right)$ by (8); 8:    Obtain $c_i\left(h_i\left(f\left({\mathbf{x}}_{si}^{\left(j\right)}\right)\right)\right)$ for classification and compute ${\mathcal{L}}_{cls}$ by (14); 9:    Obtain $c_i\left(h_i\left(f\left({\mathbf{x}}_t^{\left(j\right)}\right)\right)\right)$, and combine them by (5) 10:    Compute ${\mathcal{L}}_{dist}$ by (16); 11:    Update parameters by (17). 12: end for

5. Experiment

The effectiveness of our cross-domain classification method was verified by conducting comprehensive experiments on three well-known benchmarks: ImageCLEF-DA, Office-31, and Office-Home.

5.1. Data Preparation

ImageCLEF-DA [67] is a benchmark dataset for the ImageCLEF 2014 domain adaptation challenge, which is organized by selecting the 12 common categories shared by the following three public datasets, each considered as a domain: Caltech-256(C), ImageNet ILSVRC 2012(I), and Pascal VOC 2012 (P). There are 50 images in each category and 600 images in each domain. All domain combinations were used, and three transfer tasks were built: C, I →P; C,P→I; I,P→ C.

Office-31 [68] is a benchmark for domain adaptation, comprising 4110 images in 31 classes collected from three distinct domains: Amazon (A), which contains images downloaded from amazon.com, Webcam (W), and DSLR (D), which contains images taken by a web camera and digital SLR camera with different photographic settings. The images in each domain are unbalanced. To enable unbiased evaluation, all methods were evaluated on all three transfer tasks: A, W →D; A,W→D; W,D→ A.

Office-Home [69] consists of 15,588 images, larger than Office-31 and ImageCLEF-DA. It consists of images from 4 different domains: Artistic images (A), Clip Art (C), Product images (P), and Real-World images (R). For each domain, the dataset contains images of 65 object categories collected in the office and home settings. All domain combinations were used, and four transfer tasks were built:: A, P, R →C; A, P, C→R; A, R, C→P; P, R, C→ A.

5.2. Compared Method

There is a small amount of MDA work based on a domain-specific distribution and classifier alignment architecture. To verify the effectiveness of our MDSAN model, the Multiple Feature Spaces Adaptation Network (MFSAN) [55] was introduced as the multi-source baseline. In addition, the proposed method was compared with ResNet [70], Deep Domain Confusion (DDC) [14], the Deep Adaptation Network (DAN) [71], Deep CORAL (DCORAL) [72], and Reverse Gradient (RevGrad) [73].

There are several comparative standards for different purposes. (1) Source combine: all source domains are combined into a traditional single-source vs. target setting; (2) Single best: the best single source transfer results among the multiple candidate source domains with SDA methods; (3) Multi-source: the results of MDA methods. The first standard is to verify whether multiple source domains are beneficial for the target task or whether the simple combination of source domains will lead to negative transfer. In addition, the second standard evaluates whether the best SDA method could be further improved by introducing other source domains. The third standard demonstrates the effectiveness of the proposed approach.

Furthermore, ablation experiments were performed to verify the effectiveness of DST for adaptation outputs’ fusion. This variant is denoted as $V_1$, which simply averages the outputs in the end. In addition, variant $V_2$ does not consider ${\mathcal{L}}_{mmd}$, and variant $V_3$ ignores ${\mathcal{L}}_{dist}$.

5.3. Implementation Details

All methods were implemented based on the PyTorch framework and deployed and testified on the same device. For a fair comparison, the same data pre-processing routines and model architecture were utilized in all experiments. The pre-trained ResNet50 [70] was employed as the common feature extractor, where the fine-tuning strategy was used to save time. For all domain-specific feature extractors, the same structure $\left(conv\right(1\times 1)$, $conv(3\times 3)$, $conv(1\times 1))$ was utilized. At the end of the neural network, the channels were reduced to 256, like DDC [14]. According to subjective logic, the $softmax$ layer was replaced with $softplus$ to activate the outputs and avoid negative values. The optimization method was mini-batch stochastic gradient descent with a momentum of $0.9$. The learning rate was gradually decreased by ${\eta }_p=\frac{{\eta }_0}{{(1+\alpha )}^{\beta }}$, where p is the training progress linearly changing from 0 to 1, and ${\eta }_0=0.01,\alpha =10,\beta =0.75$. This would optimize to promote convergence and low error on the source domain. As for the hyperparameters, $\gamma =\rho =100\lambda$ was simply set. They were changed from 0 to 1 by a progressive schedule ${\gamma }_p=\frac{2}{exp(-\theta p)}-1,(\theta =10)$, instead of fixing them throughout the experiments.

5.4. Experimental Results

MAN-DS was compared with the above-mentioned methods on three datasets, and the average results of five repeated experiments are reported in

Table 1. Performance comparison of classification accuracy (%) on Office-31 dataset.

Standards	Method	A,W→D	A,D→W	W,D→A	Average
	ResNet	$99.33$	$96.50$	$61.87$	$85.90$
	DDC	$99.33$	$95.80$	$67.33$	$87.49$
Single Best	DAN	$99.43$	$97.61$	$66.70$	$87.91$
	DCORAL	$99.53$	$98.20$	$65.20$	$87.64$
	RevGrad	$99.27$	$96.67$	$68.53$	$88.16$
	DAN	$99.57$	$97.50$	$67.73$	$88.27$
Source Combine	DCORAL	$99.33$	$98.00$	$67.83$	$88.39$
	RevGrad	$99.73$	$97.67$	$67.77$	$88.39$
	MFSAN	$99.33$	$98.67$	$71.50$	$89.83$
	$V_1$	$99.79$	$98.50$	$67.02$	$88.44$
Multi-Source	$V_2$	$99.73$	$98.74$	$66.02$	$88.16$
	$V_3$	$99.79$	$98.86$	$73.87$	$90.84$
	MAN-DS	100.00	$\mathbf{99}.\mathbf{12}$	$\mathbf{74}.\mathbf{16}$	$\mathbf{91}.\mathbf{09}$

,

Table 2. Performance comparison of classification accuracy (%) on Image-CLEF dataset.

Standards	Method	C,P→I	I,P→C	I,C→P	Average
	ResNet	$74.83$	$91.53$	$83.90$	$83.42$
	DDC	$74.37$	$91.33$	$85.33$	$83.68$
Single Best	DAN	$75.10$	$93.33$	$86.13$	$84.85$
	DCORAL	$76.67$	$93.43$	$88.33$	$86.14$
	RevGrad	$75.07$	$94.00$	$87.07$	$85.38$
	DAN	$77.67$	$93.00$	$91.70$	$87.46$
Source Combine	DCORAL	$77.73$	$93.20$	$91.33$	$87.42$
	RevGrad	$78.00$	$93.03$	$91.87$	$87.63$
	MFSAN	$79.17$	$94.50$	$\mathbf{93}.\mathbf{33}$	$89.00$
	$V_1$	$77.67$	$95.50$	$92.83$	$88.67$
Multi-Source	$V_2$	$77.16$	$93.50$	$91.33$	$87.33$
	$V_3$	$\mathbf{79}.\mathbf{56}$	$94.50$	$91.87$	$88.40$
	MAN-DS	$79.00$	95.67	$93.17$	$\mathbf{89}.\mathbf{28}$

and

Table 3. Performance comparison of classification accuracy (%) on Office-Home dataset.

Standards	Method	C,P,R→A	A,P,R→C	A,C,R→P	A,C,P→R	Average
	ResNet	$65.28$	$48.54$	$77.56$	$74.55$	$66.48$
	DDC	$64.13$	$50.22$	$78.42$	$75.00$	$66.94$
Single Best	DAN	$69.07$	$56.46$	$79.63$	$74.65$	$69.95$
	DCORAL	$66.56$	$55.15$	$81.38$	$76.32$	$69.85$
	RevGrad	$67.58$	$55.88$	$80.32$	$75.86$	$69.91$
	DAN	$69.07$	$59.40$	$78.41$	$82.50$	$72.35$
Source Combine	DCORAL	$68.24$	$57.62$	$79.67$	$83.24$	$72.19$
	RevGrad	$67.88$	$57.22$	$79.52$	$82.74$	$71.84$
	MFSAN	$72.86$	$62.34$	$80.32$	$81.86$	$74.35$
	$V_1$	$74.32$	$62.12$	$82.31$	$83.13$	$75.47$
Multi-Source	$V_2$	$72.86$	$62.34$	$80.32$	$81.86$	$74.35$
	$V_3$	$74.12$	$63.56$	$82.52$	$82.74$	$75.74$
	MAN-DS	74.50	$\mathbf{64}.\mathbf{44}$	$\mathbf{82}.\mathbf{56}$	$\mathbf{83}.\mathbf{29}$	$\mathbf{76}.\mathbf{20}$

, respectively. The maximum accuracy in a transfer task is marked in bold.

6. Discussion

6.1. Result Observations

From these experimental results, insightful observations are given:

• The results of Source combine were better than Single best, which shows that the knowledge of the multi-source domain is useful to the target task. That is, the multi-source domains have transferability. Combining sources into a single source is helpful in most domain adaptation methods. The performance improvement might be attributed to the data enrichment.
• MAN-DS outperformed all compared methods on most transfer tasks in all three datasets, especially in the Office-Home dataset. The results indicate that it is beneficial to learn the domain-invariant representation and align the distribution in each pair of the source and target domain with considering domain-specific category boundaries. Besides, DST alleviates the ambiguity and uncertainty of the prediction and promotes classification accuracy successfully.
• Comparing MAN-DS with the variant $V_1$, the only difference is that the proposed method employs DST to fuse the adaptation outputs, while $V_1$ averages them simply. Although DST was applied in ${\mathcal{L}}_{dist}$ to align domain-specific boundaries, the proposed method still has an improvement over $V_1$. Thus, DST is excellent to tackle the ambiguity and uncertainty of the prediction.
• Comparing MAN-DS with the variant $V_2$, the only difference is that $V_2$ does not consider ${\mathcal{L}}_{mmd}$. The experimental results show that MMD helps domain adaptation very little. Meanwhile, the proposed ${\mathcal{L}}_{dist}$ and Dempster’s combination rule could also help to align the distribution to some extent.
• Comparing MAN-DS with the variant $V_3$, the only difference is that $V_3$ ignores ${\mathcal{L}}_{dist}$. There is little difference in the experimental results, which indicates that DST is powerful to handle the prediction conflicts on the category boundaries.

6.2. Ablation Experiment

Ablation experiments were implemented by conducting $V_1$, $V_2$, and $V_3$, as shown in Table 1, Table 2 and Table 3. The encouraging results show that every component of MAN-DS is positive to improve performance.

To further verify the effectiveness of the DST fusion strategy, supplementary experiments were carried out where $S_i$ is the isth domain-specific classifier, as reported in

Table 4. Classification accuracy (%) with and without DST fusion strategy on Office-Home dataset.

Method	C,P,R→A	A,P,R→C	A,C,R→P	A,C,P→R
$S_1$	$72.56$	$59.48$	$80.33$	$80.59$
$S_2$	$65.58$	$61.54$	$75.54$	$75.78$
$S_3$	$71.39$	$60.56$	$79.87$	$82.36$
DST	74.50	$\mathbf{64}.\mathbf{44}$	$\mathbf{82}.\mathbf{56}$	$\mathbf{83}.\mathbf{29}$

. The maximum accuracy in a transfer task is marked in bold.

6.3. Feature Visualization

Feature visualization is demonstrated in Figure 5. The category boundaries of the domain-specific classifier on the task D,W→A learned by MAN-DS and MFSAN are visualized by using t-SNE embeddings. It is clear that MAN-DS is more effective in dealing with prediction conflicts, in which DST is effective.

6.4. Parameter Sensitivity

Parameter sensitivity was tested by sampling the trade-off parameter (where $\gamma =\rho =100\lambda$ for simplicity) values in $\{0.01,0.02,0.05,0.1,0.2,0.5,1,2\}$. To study the parameters’ sensitivity, the experiments were implemented on task D,W→A and A,C→R, and the results are shown in Figure 6. As observed, the accuracy increases with the increase of $\gamma$ and reaches a peak at $\gamma =1$, then decreases. The proposed method MAN-DS can keep a relatively stable result in the range of $(0.1,2)$ of $\gamma$, which is higher than the baseline. Generally, MAN-DS is not sensitive to changes in the parameters in a certain range. Hence, setting $\gamma$ to $(0.1,2)$ is recommended to achieve better performance. In the reported experiment, the parameters $\{\gamma ,\rho ,\lambda \}$ were set to $\{1,1,0.01\}$, respectively.

6.5. Computational Complexity

The FLoating point OPerations (FLOPs) were used to measure the operation times of forward propagation in neural network; the smaller the FLOPs, the faster the computation speed is. In addition, the smaller the number of PARAMeters (PARAMs) in the neural network, the smaller the size of the model is.

Table 5. FLOPs and PARAMs.

Method	FLOPs	PARAMs
MAN-DS	$4.23$ G	$25.88$ M
MFSAN	$4.23$ G	$25.88$ M
ResNet50	$4.12$ G	$25.56$ M

shows the FLOPs and PARAMs of MAN-DS, MFSAN, and ResNet50. Compared with ResNet50, the small increase of computational complexity mainly comes from the component of domain-specific feature extractors and classifiers. Compared with the baseline MFSAN, MAN-DS improves the accuracy without increasing the computational complexity.

Moreover, Dempster’s combination does not increase the computational complexity of the algorithm. For the K-classification task, MAN-DS always obtains $K+1$ instead of $2^K$ focal elements, which is $\{1,2,\dots ,K,\Theta \}$. That is, the computational complexity caused by Dempster’s combination is not $O\left(2^n\right)$, but $O\left(n\right)$.

7. Conclusions

The core of MDA is making full use of available source data collected from several different, but related domains. However, it becomes difficult and challenging due to the multiple domain shifts. Following the domain-specific alignment architecture, this study proposed a novel multi-source domain adaptation network combing Dempster–Shafer evidence theory for cross-domain image classification to reduce multiple domain shifts and enhance transfer accuracy. In addition, SL and the Dirichlet distribution were employed to bridge MDA with DST.

To evaluate the effectiveness of the proposed method, three popular benchmark datasets were used and ten transfer tasks were devised to train and validate MAN-DS. Extensive experiments demonstrated that MAN-DS outperforms its competitors in cross-domain image classification. The insightful conclusions are as follows:

• MAN-DS achieved good accuracy in all ten transfer tasks of three datasets. On the Office-Home dataset, MAN-DS even improved the average adaptation accuracy to $76.20\%$, which is about 2% higher than the best baseline.
• Feature visualization shows that MAN-DS could alleviate boundary conflicts to some extent, due to effective DST.
• MAN-DS is not sensitive to changes in parameters in a certain range $\gamma \in (0.1,2)$, generally.
• MAN-DS improved accuracy without increasing computational complexity. Compared with the baseline MFSAN, the FLOPs and PARAMs of MAN-DS were 4.23 G and 25.88 M, which are close to the 4.12 G and 25.56 M of ResNet. Especially, MAN-DS reduced the computational overhead of the outputs’ combination from $O\left(2^n\right)$ to $O\left(n\right)$.
• Ablation experiments indicated that every component of MAN-DS is positive to improve performance.
• The encouraging results show that SL could effectively bridge MDA with DST.
• This research study empirically demonstrates DST could reduce the category boundary ambiguity, so as to mitigate the negative impact of multiple domain shifts.

In this research study, the original and unimproved Dempster’s rule was used. In the future, the combination rules will be optimized based on the improved information entropy method to take more evidence information into account. Besides, more effective MDA and DST bridging methods will be investigated.