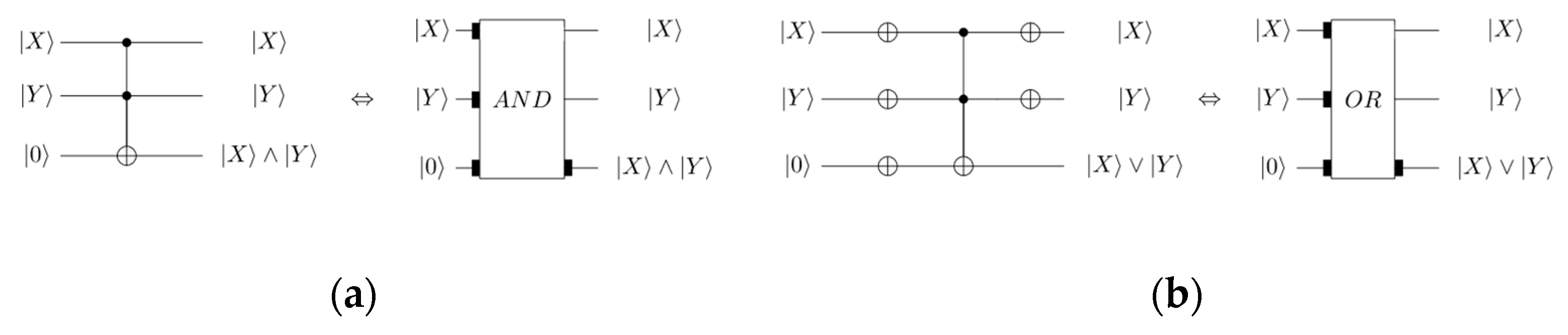1. Introduction
Image processing involves certain operations that help improve aesthetics and enhance comprehensibility of what the image conveys. This is widely used in environment, agriculture, military, industry, and medical sciences to extract valuable information. Due to the rapid development of information technology, data handled in image processing have undergone exponential growth. Usage of classical image processing has declined and therefore quantum image processing has emerged as a feasible way to solve the problems. The coherent superposition characteristics of the quantum state and other unique quantum mechanical principles are used for generating data processing capability in quantum image processing, which can accelerate the process significantly compared to classical algorithms.
In the last two decades or so, a large number of productive techniques have emerged for quantum image processing, which serves two purposes. The first is to construct models for representation of the digital image mainly including qubit lattice [
1], entangled image [
2], flexible representation of the quantum image (FRQI) [
3], quantum log-polar image [
4], a novel enhanced quantum representation of digital images (NEQR) [
5], and Quantum Boolean image processing [
6], a simple quantum representation of infrared images (SQR) [
7] and some extensions from FRQI or NEQR [
8,
9,
10,
11,
12,
13,
14,
15,
16]. The other is applications based on the above which vary with types of representation, such as geometric transform [
17,
18,
19], image scaling [
20,
21,
22,
23], image scrambling [
24,
25], image segmentation [
26,
27,
28,
29], image edge extraction [
30,
31,
32,
33,
34,
35], image matching [
36,
37,
38], image watermarking [
39,
40], and so on.
Although many issues are studied by researchers, as mentioned above, quantum image processing is still an emerging field and, compared with classical image processing, it is still in its infancy. To the best of our knowledge, image component labeling has not yet been extended to the quantum imaging processing domain. Image component labeling is the most fundamental preprocessing required for image understanding, pattern recognition, and computer vision. By use of the labeling operation, a unique label is assigned to each connected region so that higher-level operations can process different regions separately. In some applications, image component labeling is still an active area of research in classical image processing, which has been proved to be one of the most time-consuming tasks in pattern recognition [
41]. The parallel processing characteristic is the great advantage of quantum computation, which is one feasible way to accelerate image component labeling.
This paper proposes a fast quantum image component labeling algorithm based on a modified NEQR representation model for binary images, a quantum counterpart of classical local-operator techniques [
42]. The quantum image component labeling algorithm consists of three main steps. Firstly, a binary image is represented by the quantum version using the modified NEQR model. Secondly, all pixels of the image are simultaneously worked upon by the quantum parallel-shrink operator several times until each black pixel changes to white, and the connectivity relations are reserved during the processing. Finally, the quantum label-propagate operator is executed on each pixel to restore the pixels with changed colors and each pixel assigns different numbers to different connected areas at the same time. The process is in reverse order to the image generated by the quantum parallel-shrink operations.
The rest of the paper is organized as follows.
Section 2 briefly introduces classical local-operator techniques, giving a detailed example specifying how to operate the binary image to obtain the labels for the connected area. The purposed quantum version of the local-operator technique, as well as circuit design, is described in
Section 3.
Section 4 analyzes the circuit complexity. Simulation results based on the classical computer’s Python software are given in
Section 5. Finally, the conclusions are drawn in
Section 6.
2. Local-Operator Technique
A connected region or component in a binary image is a maximal connected set of black pixels. The image component labeling algorithm assigns a unique label to each connected region in the image. Thus, in the labeled image, any two black pixels have the same label if and only if they lie in the same connected region. Local-operator techniques involve two types of local operations used for image region labeling: Parallel-shrink and Label-propagate. The two operators use local information from the neighborhood of a pixel to determine its new value.
2.1. Basic Definitions
The following basic definitions constitute some of the concepts required for Local-operator techniques [
42]. Assume black pixels have value 1 and white pixels have value 0. Let
denote the source binary image on the point set
with
being the value at pixel
. Two pixels are said to be
neighbors if they share one edge, one vertex, or both. The pixels are chosen to be squares, and then a pixel may have either 4 or 8 neighbors in terms of edges or both edges and vertices. Two pixels
and
are called 4-neighbors if
and 8-neighbors if
. Let
be the
connectivity relation defined on an image as follows: for all pairs of pixels,
if and only if
p and
q are both black and are connected by a path in
. The
internal distance between two black pixels is defined as the length of a shortest 4- or 8-neighbor path connecting them within the component. The
internal diameter of a connected component is defined as the maximum of lengths of all internal distances among all pairs of pixels within the component. Local-operator techniques use a part of 8-neighbor components of a given
binary image. The parallel-shrink operator uses neighborhood
shown in
Figure 1 which is the set of points
, and the label-propagate operator uses neighborhood
(
Figure 1), which is the set of points
.
2.2. The Parallel-Shrink Operator
The parallel-shrink operator
was first designed by Levialdi [
43] and it used the Heaviside operator
defined on
neighborhoods, such that, if
, then:
where
is the Heaviside operator defined by
for
and
if
. Since
is a binary image, it is easy to express
using the logic operations
and
as follows:
The parallel-shrink operator shrinks the components toward the top left corner of the bounding rectangles of connected components. The two important properties of the shrinking procedure are as follows:
A component with an internal diameter will shrink to a single black pixel after shrinking steps, and then disappear in the next shrinking step. After each shrinking operation, a different image is obtained and the result of applying the shrinking operation times to the original image is called partial result . Thus, we have a sequence of images , representing the initial binary image.
2.3. The Label-Propagate Operator
The label-propagate operators are applied in the reverse order to the images generated by the parallel-shrink operations. Suppose at a certain time of the label-propagate operator, black pixels of are labeled with the correct labels and the labels can be used to label the black pixels of . The label-propagate operator then continues to label the black pixels until the image returns to the initial image .
Let
be a global variable that saves the maximum label in the image, the initial number is 0, and
is the label of pixel
in
. The parallel-shrink operator
is defined on
neighborhoods, such that, if
, then:
where
,
is a bit-wise logic or operation.
Note that, first, we must ensure that labels of the four neighbors for whom the value is not zero on
remain the same after Equation (3) is executed, then:
Second, we should backfill the value 1 of pixels based on partial result during propagating.
2.4. A Simple Example of the Local-Operator Technique
In this subsection, we give a simple example to explain how the label-propagate operator functions. The binary image consists of two connected regions or components as shown in
Figure 2a, and the maximum internal diameter of two connected regions is 3. The detailed process is described below.
Phase 1 Preparation: When every pixel has its
and
neighbors, the original image is extended by a 1-pixel outer border that pads the border of the image with white. The white pixels (0 value) are ignored in the board so that we can focus better on changes in the black regions (1 value), as shown in
Figure 2b.
Phase 2 Parallel shrinking: In Phase 2, the parallel-shrink operator, (1) or (2), is performed on every pixel simultaneously. Since the maximum value of the
internal diameter of the two connected regions is 3, the operator would be applied three times, and then all pixels of the image will change to 0 and that completes Phase 2.
Figure 2c–e depict the performance process. In
Figure 2c–e, we only show the pixels that were changed using the red dotted box.
Phase 3 Label propagating: As mentioned before, label propagating is a reverse-order process, so Equations (3) and (4) are applied for the same number of times as Phase 2. The process order is indicated in
Figure 2f–h using the left arrow, and the purple dotted boxes are used for marking the label change. In
Figure 2h,
,
, and
are labeled with different numbers based on (3) at the same time. We use the row–column criterion to label the pixels. In
Figure 2f, serial numbers of the pixels that have been labeled are represented in the upper left corner box,
,
,
,
need new labels based on Equation (3), and
needs a change of the labeled number based on Equation (4) to keep consistent with
’s
neighbors. In
Figure 2f, the last two pixels,
and
, are labeled, which means that label propagating is finished, and two different label numbers are obtained.
The example shows that the local-operator technique is a parallel method that is performed simultaneously on every pixel, so it only takes time and is a type of fast image component labeling method.
3. Quantum Version of the Local-Operator Technique
In this section, a series of specific quantum circuits are designed to realize the local-operator technique.
3.1. Modified NEQR Model Representation of a Binary Image
The NEQR is a deterministic image retrieval model that facilitates the operations on an image, so we modified the model to represent the quantum image as required [
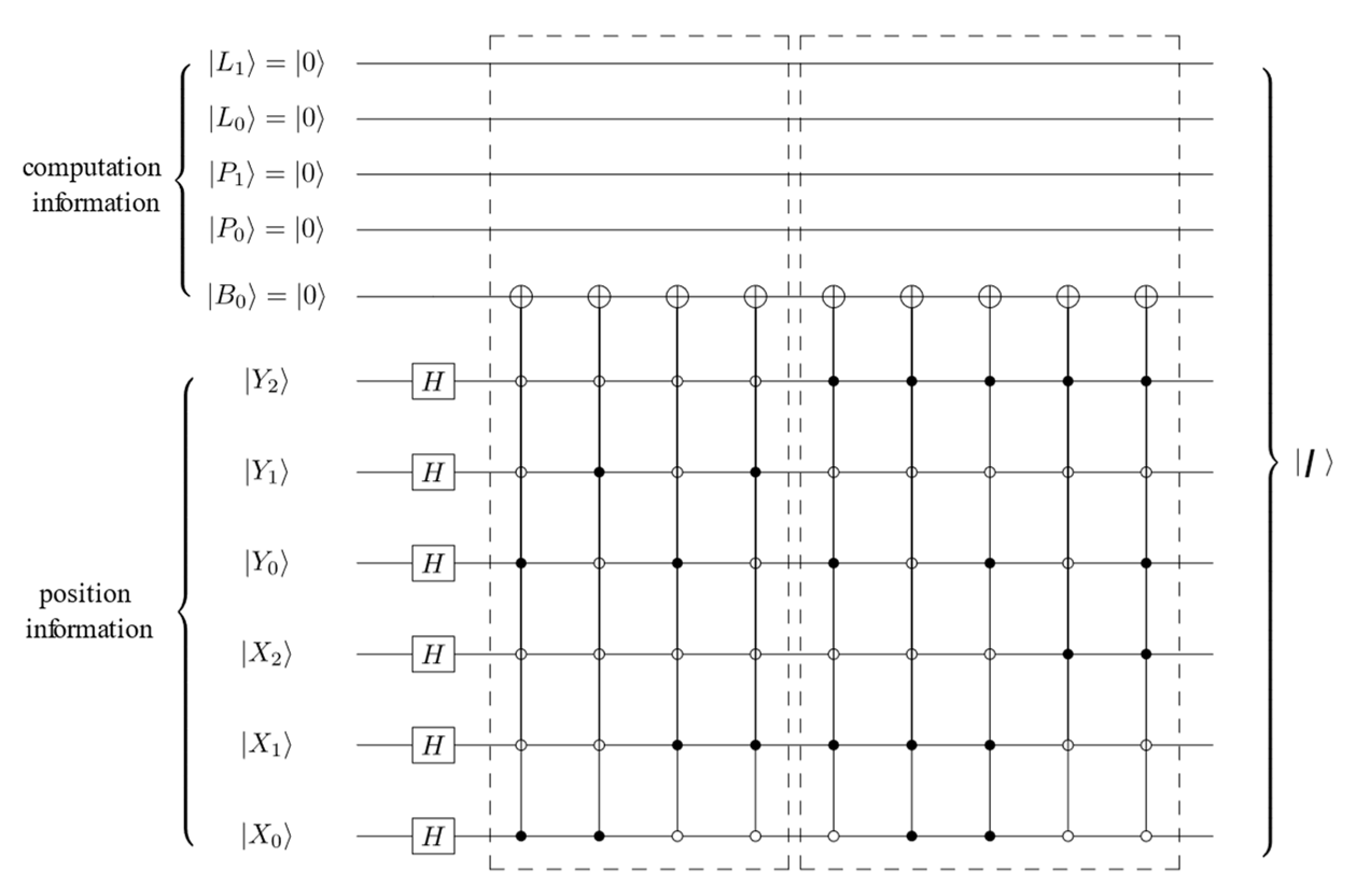
5]. In the modified model, one qubit sequence is employed for storing the position information on the Cartesian coordinate system and another sequence represents the information required, including color, number of partial results, and label number. Two entangled qubit sequences are in superposition states.
The binary image with size
can be represented by modified NEQR as the following equation:
where
address qubits represent the position information,
is row number,
is column number,
work qubits represent the computation information,
is color,
is number of partial results,
is label number, and
,
,
,
,
.
A quantum circuit equivalent to Equation (5) can be used to prepare the initial image state.
Figure 3 is an example that presents the quantum circuit of
Figure 2b, the address qubits are entangled using six Hadamard gates, and the information circuit of two connected regions are in dotted boxes.
3.2. Basic Quantum Functional Circuits
To realize the complex quantum circuit, a series of quantum functional operation modules are prepared for local-operator, including address shift operation module, logic operation module, assignment operation module, compare operation, full addition module, and full subtraction module.
3.2.1. Address Shift Operation Circuits
It is an important operation for a large number of quantum algorithms to obtain the neighborhood information [
34,
35]. Shift transformation is a geometric operation that can be used to shift the whole image and it skillfully helps us to obtain the information of every pixel’s adjacent information simultaneously. For example, make a one-unit shift right for an image, the pixel
will be transformed to
and the value
can be visited. Shift − and + are defined in Equations (7) and (8). When it is applied on
, the image moves left and right, and when it is applied on
, the image moves up and down.
Based on the above analysis, Equations (7) and (8) are equivalent to Equations (9) and (10), respectively.
where
and
.
For a two-dimensional digital image,
Figure 4 is an example for
, and
is similar to
. We call the shift transformation circuit an address shift operation circuit just like the address-of operator in classical programming.
3.2.2. Logic Operation Circuit
In reversible computing, the TOFFOLI gate is universal gate, and it can be used for simulating classical irreversible standard gates with ancilla qubits.
Figure 5 is the circuit of the necessary logic operations for computation of Equations (2) and (3) for convenience, and the inputs and results are connected by black blocks. The following figures are used for the same notation.
3.2.3. Control Assignment Operation Circuit
Assignment operation is the most basic statement in classical programming. To achieve the function, we design the control assignment operation circuit (
Figure 6). The circuit consists of two parts, the first part is shown in a dotted block that is to clear the original data of the quantum wires
by using a group of swap gates, the original data are saved in the ancilla qubits. The second part assigns the value of
to
using a group of CNOT gates. The whole circuits are controlled by using a CNOT gate, such that, if the control wire is 1, then assignment operation is executed. As described, the designed circuit is a reversible circuit, and, by using ancilla qubits, both
and
are stored during the operation.
3.2.4. Compare Operation Circuit
The compare operation circuit can be used to compare two n-qubits sequences
and
illustrated in
Figure 7 [
32], where
,
,
,
. The output two-qubit
can be used to represent the result of comparison: if
, then
; if
, then
; if
, then
.
3.2.5. Full Addition Circuit
Full adder is an adder with carry, a common arithmetic unit in various algorithms. In this paper, 1-bit full addition circuit is composed of quantum CNOT and CCNOT gate, and n-bit full addition circuit is a cascade of 1-bit full addition circuit as shown in
Figure 8 [
44].
is the
th carry qubit,
is the
th augend number,
is the
th addend number,
is the
th carry qubit, and
is the sum of
. The relationships among
,
,
,
and
are given by
3.2.6. Full Subtraction Circuit
The full subtractor circuit is similar to full addition circuit, the n-bit full subtraction circuit is a cascade of the 1-bit full subtraction circuit, as shown in
Figure 9 [
44].
is the
th borrow qubit,
is the
th minuend number,
is the
th subtrahend number,
is the
th borrow qubit, and
is the
th qubit of difference
. The relationships among
,
,
,
, and
are given by
3.3. Implementing Quantum Image Component Labeling
The entire workflow of the proposed procedure can be accomplished in four steps. First, the classical color digital image is converted into binary format and a 1-pixel outer border as described in
Section 2.4 is added. Next, the quantum image
is prepared as the input image using a modified NEQR model. The quantum circuit is similar to
Figure 3. Then, the quantum counterpart of parallel shrinking is executed repeatedly until color value of all pixels is zero in the image. Finally, the quantum counterpart of label propagating is executed repeatedly for labeling regions or components in the image, and the number of executions is the same as in Step 3. Similar to its classical counterpart, the most important steps of quantum image component labeling are quantum parallel shrinking and quantum label propagating.
3.3.1. Quantum Parallel Shrinking
Quantum parallel shrinking is to repeat the following three steps until all pixels in the image are zero where pixel zero is the background color.
In the first step, neighborhood
is obtained through address shift operation circuits, the designed circuit is shown in
Figure 10, and the color information is saved in the ancilla qubits. Note that the state of
should return to the initial value after using the address shift operation circuit four times, for later use.
The second step, the Levialdi operator, is implemented through Logic operation circuits, and the designed circuit is shown in
Figure 11. The number of ancilla qubits used is the same as the number of Logic operators.
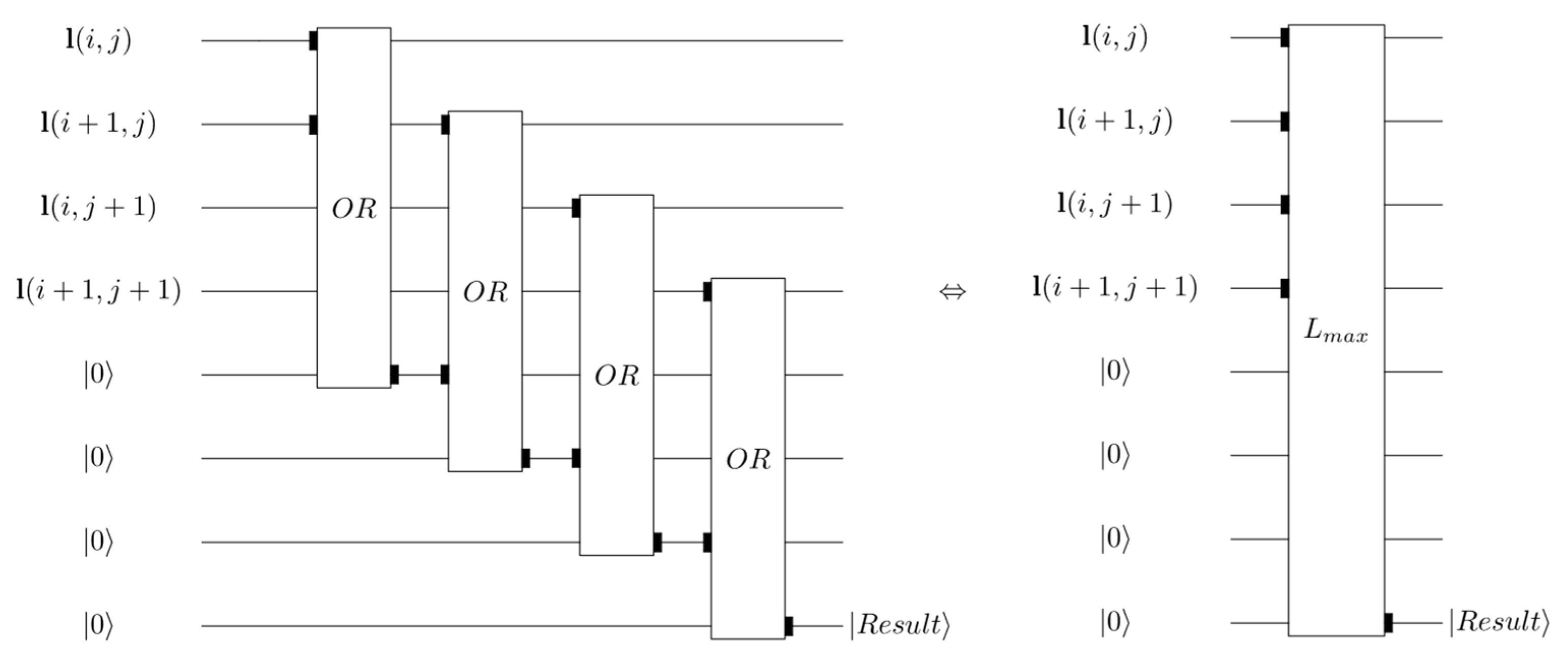
The third step, the number of
partial results, is stored in
through the full addition circuit, and the designed circuit is shown in Part 3 of
Figure 12. If
and
, then
. Fourthly, the value of pixels
is updated through CNOT gate (Part 4 of
Figure 12). Finally, the number of loops
through the full addition circuit is shown in Part 5 of
Figure 12. The circuit of Equation (2) is shown in
Figure 12.
3.3.2. Quantum Label Propagating
Quantum label propagating is to repeat the following four steps until the manipulated image becomes the original image.
The first step, neighborhood
, is obtained through address shift operation circuits, the designed circuit is shown in
Figure 13, and label numbers
are saved in the ancilla qubits.
The second step, the computation of
, is implemented through Logic operation circuits, and the designed circuit is shown in
Figure 14.
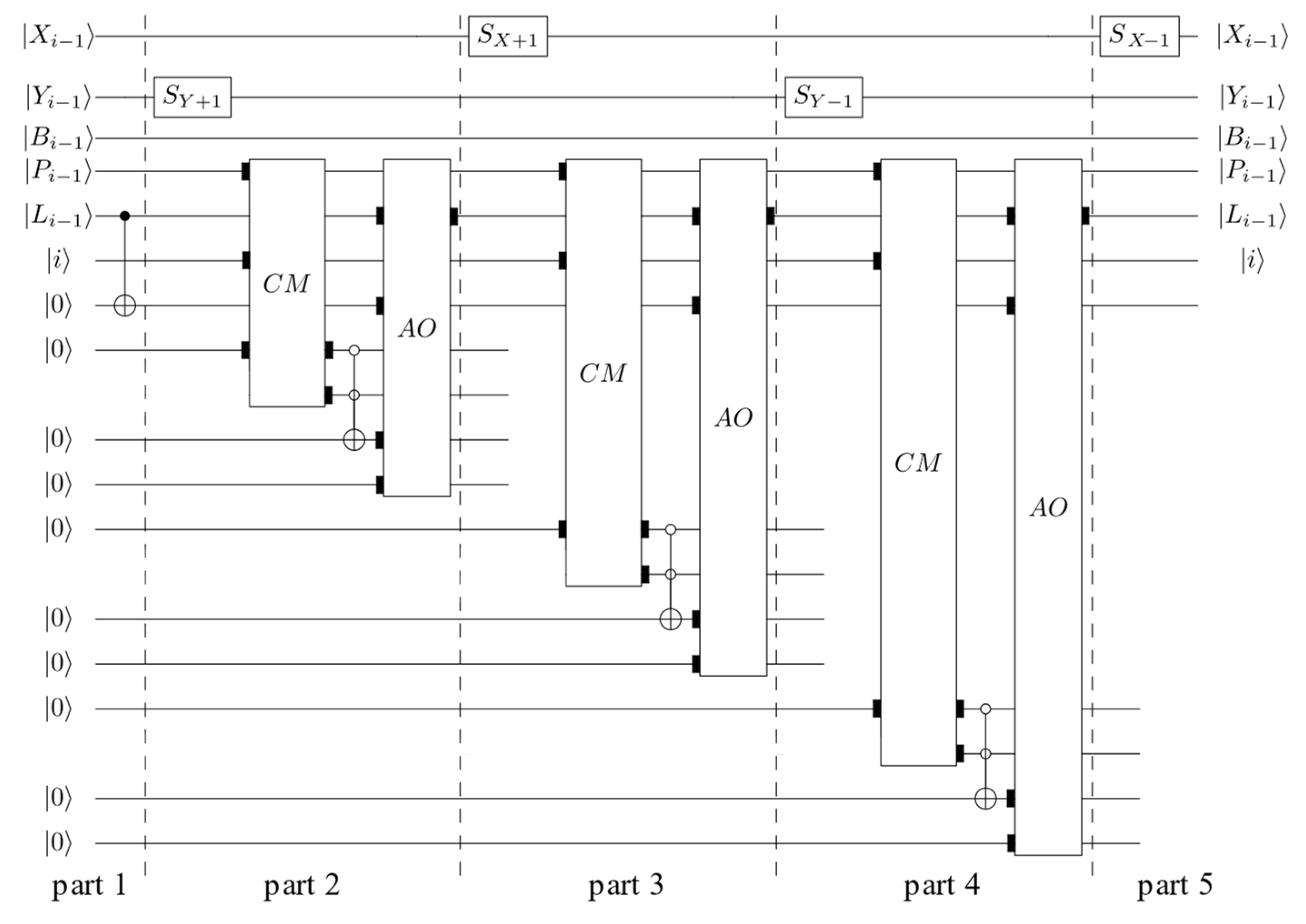
In the third step, the global variable i − 1 and Equation (3) are implemented through the designed circuit shown in
Figure 15. The condition of Equation (3) is realized in part 1,
, and
as input to comparer CM1, and
means that the color of the pixel changes from 1 to 0, so
is equivalent to
. Comparer CM2 is used to determine if
. If
and
, part 2 is executed, the global variable
, then assign
to
using control assignment operator AO. If
and
, part 3 is executed, and the control assignment operator AO is used to implement
.
In the fourth step, Equation (4) is implemented through the designed circuit shown in
Figure 16.
is stored in ancilla qubits using CNOT gate in part 1. In part 2,
is obtained using address shift operator
, the condition of
is realized using comparer CM, and then equation
is implemented using control assignment operator AO. Part 3 and part 4 use the same circuits as part 2 to achieve the same assignment function. In part 5, the initial state is restored.
4. Quantum Circuit Complexity Analysis
Section 2 introduced the classical local-operator technique, label propagating, and parallel shrinking executed the same number of times, depending on the Manhattan diameter of the largest component, so its time complexity is just
. Thanks to Levialdi’s pioneering work, the classical local-operator technique is much faster than scan type algorithms
[
41].
In this section, we focus on the quantum circuit complexity. The time complexity depends on the number of elementary gates used. The elementary gates include the NOT gate, Hadamard gate, CNOT gate, and 2 × 2 unitary operator. The time complexity of elementary gates is 1. The spatial complexity mainly refers to the ancilla qubits employed in the circuits.
4.1. Time Complexity
From [
45], one Toffoli gate can be further approximately simulated by six CNOT gates and [
46] points out that an n-controlled NOT (n-CNOT) gate is equivalent to
Toffoli gates and 1 CNOT gate. One SWAP gate is equivalent to three CNOT gates.
Section 3.2 introduced six basic quantum functional circuits, and label propagating and parallel shrinking circuits are composed of the functional circuits. One address shift operation circuit costs the time complexity of
. Logic operation
is one Toffoli gate, and the time complexity is
. Logic operation
needs five NOT gates and one Toffoli gate, and the time complexity is
. Control Assignment Operation needs
SWAP gates and
Toffoli gates, and the time complexity is
. Compare Operation needs 4 Toffoli gates and no more than 4n n-CNOT gates, and the time complexity is
. The 1-bit full addition circuit needs two Toffoli gates and two CNOT gates, and the n-bit full addition circuit needs
1-bit full addition circuit, so the n-bit full addition circuit’s time complexity is
. The 1-bit full subtractor circuit needs two NOT gates, four CNOT gates, and two Toffoli gates, the n-bit full subtractor circuit needs
1-bit full subtractor circuits, and the time complexity of the n-bit full subtractor circuit is
.
Considering a binary image, , the time complexity is analyzed as follows:
4.1.1. Quantum Parallel Shrinking
From
Figure 10 and
Figure 11, the quantum parallel shrinking circuit is composed of four address shift operation circuits, three Logic operation
, two Logic operation
, and four CNOT, so the time complexity is
.
4.1.2. Quantum Label Propagating
From
Figure 13,
Figure 14 and
Figure 15, the quantum label propagating circuit is composed of four address shift operations, four Logic operation
, one n-bit full subtractors, two compare operation, one n-bit full addition circuit, and two assignment operations, so the time complexity is:
According to the above analysis, time complexity of the proposed quantum image component labeling algorithm is , which is only the second-order polynomial function of image size.
4.2. Spatial Complexity
Table 1 shows that the number of ancilla qubits in basic quantum functional circuits is a linear function of image size. Therefore, ancilla qubits of the proposed quantum image component labeling algorithm is also a linear function of image size. That is, the spatial complexity of the quantum circuits designed in this paper is
.
Although quantum complexity is discussed, lots of quantum algorithms still cannot be applied to the quantum computer or a quantum simulator. Quantum computers and quantum simulations are in their infancy, quantum computing will be limited to about 10 qubits in quantum computer, and a quantum simulator can only operate at most 30 qubits. LaRose [
47] has given a detailed explanation of quantum software platforms. Therefore, in the next section, we give the use of matrix calculation to complete the algorithm simulation, which is also a common practice at present.
5. Simulation on Classical Computer
This section describes simulations of the quantum image component labeling algorithm on a classical computer, while quantum computers are currently not at hand. The simulations were run on a classical computer with Inter (R) Core (TM) i7-7500U @2.70 GHz 8.0 GB RAM and 64-bit operating system. The simulations are based on linear algebra with complex vectors as quantum states and unitary matrices as unitary transforms with calculations performed using Python 3.9.
In order to compare with classical algorithms, YACCLAB [
48] (Yet Another Connected Components Labeling Benchmark) is used, which is an open-source C++ benchmarking framework for component labeling. YACCLAB allows researchers to test classical component labeling algorithms under the same environment and with the same collection of datasets, which provides a rich and varied dataset that includes both synthetic and real images and lots of well-written programs for classical algorithms.
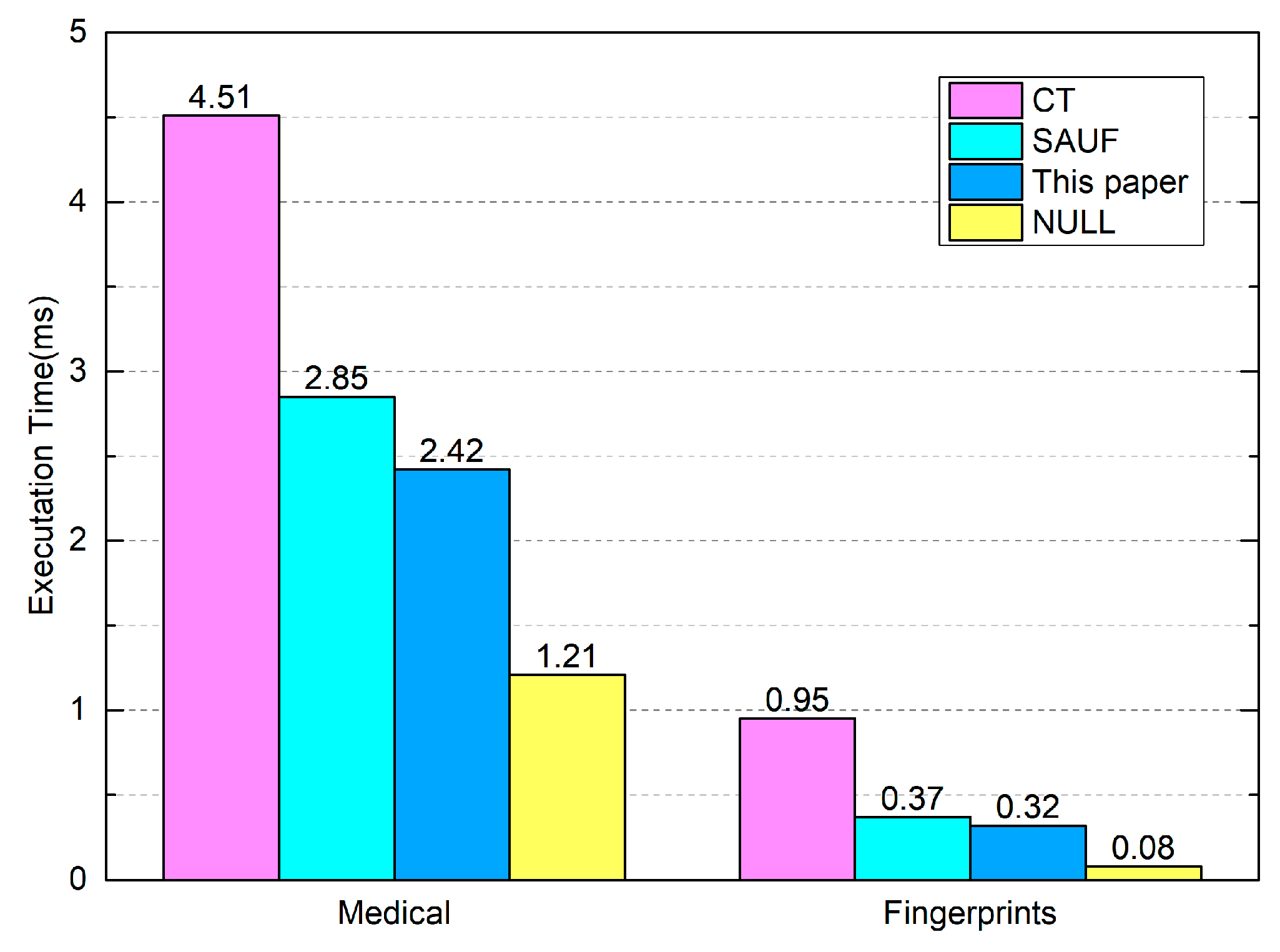
In the experiments, the library Boost.python is used for Python calling C++, and the quantum image component labeling algorithm is compared with CT [
49] (Contour Tracing approach), SAUF [
50] (Scan plus Array-based Union-Find algorithm), and NULL, which are three classical component labeling types in YACCLAB. The NULL is a fake algorithm that performs the basic assignment operation defining a lower bound limit of the execution time. The experimental results (
Figure 17) show that the proposed algorithm is better than the two classical algorithms, and the execution time is the average time for labeling on the image dataset.
To visually present the result of the proposed algorithm, the two images in traffic scenarios are used for testing. The first image is a traffic sign (
Figure 18), the size of the image is 256 × 265, the second image (
Figure 19) is the license plate held by the author, the size is 654 × 220. In the experiment, we used different colors to distinguish different components. The traffic sign and the license plate have execution time of 0.21 ms and 0.26 ms, respectively. Two tests in the experiment verify the correctness of the quantum image component labeling algorithm in this paper.
6. Conclusions
In recent years, with the sharp increase in image data processing, the problem of real-time processing has become a limitation in classical image processing. An image component labeling algorithm is an important pre-processing operation in many image processing algorithms. However, in quantum image processing, component labeling algorithm has not been reported in extant literature. In this paper, we develop a quantum version of the image component labeling algorithm which makes full use of quantum parallelism. Firstly, the modified NEQR model is used to represent the information of binary image. Secondly, basic function circuits are prepared. Thirdly, the quantum circuits of parallel shrinking and label propagating are designed by using the basic function circuits. The purposed circuits can process information of all the pixels simultaneously, which can improve the efficiency of image preprocessing.
Quantum image processing applications have developed only in recent years. The results obtained in this paper could be used in more quantum image processing algorithms. In the future, we will be working to develop new quantum image analysis algorithms based on the quantum component labeling algorithm, especially in the fields of transportation, logistics, and robot navigation.
Author Contributions
Conceptualization, Y.L. and D.H; methodology, K.L.; software, D.H.; validation, Y.X.; writing—original draft preparation, Y.L.; writing—review and editing, D.H.; supervision, K.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors are thankful to the editor and the reviewers for their valuable comments and suggestions that helped to improve the quality of the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Venegas-Andraca, S.E.; Bose, S. Storing, Processing, and Retrieving an Image Using Quantum Mechanics. Quantum Inf. Comput. 2003, 5105, 137–147. [Google Scholar]
- Venegas-Andraca, S.E.; Ball, J. Processing images in entangled quantum systems. Quantum Inf. Processing 2010, 9, 1–11. [Google Scholar] [CrossRef]
- Le, P.Q.; Dong, F.; Hirota, K. A flexible representation of quantum images for polynomial preparation, image compression, and processing operations. Quantum Inf. Processing 2011, 10, 63–84. [Google Scholar] [CrossRef]
- Zhang, Y.; Lu, K.; Gao, Y.; Xu, K. A novel quantum representation for log-polar images. Quantum Inf. Processing 2013, 12, 3103–3126. [Google Scholar] [CrossRef]
- Zhang, Y.; Lu, K.; Gao, Y.; Wang, M. NEQR: A novel enhanced quantum representation of digital images. Quantum Inf. Processing 2013, 12, 2833–2860. [Google Scholar] [CrossRef]
- Mastriani, M. Quantum Boolean image denoising. Quantum Inf. Processing 2015, 14, 1647–1673. [Google Scholar] [CrossRef] [Green Version]
- Yuan, S.; Mao, X.; Xue, Y.; Chen, L.; Xiong, Q.; Compare, A. SQR: A simple quantum representation of infrared images. Quantum Inf. Processing 2014, 13, 1353–1379. [Google Scholar] [CrossRef]
- Sun, B.; Iliyasu, A.; Yan, F.; Dong, F.; Hirota, K.J. An RGB multi-channel representation for images on quantum computers. J. Adv. Comput. Intell. Intell. Inform. 2013, 17, 404–415. [Google Scholar] [CrossRef]
- Li, H.-S.; Zhu, Q.; Zhou, R.-G.; Song, L.; Yang, X.-J. Multi-dimensional color image storage and retrieval for a normal arbitrary quantum superposition state. Quantum Inf. Processing 2014, 13, 991–1011. [Google Scholar] [CrossRef]
- Sang, J.; Wang, S.; Li, Q. A novel quantum representation of color digital images. Quantum Inf. Processing 2017, 16, 42. [Google Scholar] [CrossRef]
- Abdolmaleky, M.; Naseri, M.; Batle, J.; Farouk, A.; Gong, L.-H. Red-Green-Blue multi-channel quantum representation of digital images. Optik 2017, 128, 121–132. [Google Scholar] [CrossRef]
- Xu, G.; Xu, X.; Wang, X.; Wang, X. Order-encoded quantum image model and parallel histogram specification. Quantum Inf. Processing 2019, 18, 346. [Google Scholar] [CrossRef]
- Khan, R.A. An improved flexible representation of quantum images. Quantum Inf. Processing 2019, 18, 201. [Google Scholar] [CrossRef]
- Wang, L.; Ran, Q.; Ma, J.; Yu, S.; Tan, L. QRCI: A new quantum representation model of color digital images. Opt. Commun. 2019, 438, 147–158. [Google Scholar] [CrossRef]
- Chen, G.-L.; Song, X.-H.; Venegas-Andraca, S.E.; El-Latif, A.; Ahmed, A. QIRHSI: Novel quantum image representation based on HSI color space model. Quantum Inf. Processing 2022, 21, 5. [Google Scholar] [CrossRef]
- Zhu, H.-H.; Chen, X.-B.; Yang, Y.-X. Image preparations of multi-mode quantum image representation and their application on quantum image reproduction. Optik 2022, 251, 168321. [Google Scholar] [CrossRef]
- Le, P.Q.; Iliyasu, A.M.; Dong, F.; Hirota, K. Strategies for designing geometric transformations on quantum images. Theor. Comput. Sci. 2011, 412, 1406–1418. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Jiang, N.; Wang, L. Quantum image translation. Quantum Inf. Processing 2015, 14, 1589–1604. [Google Scholar] [CrossRef]
- Le, P.Q.; Iliyasu, A.M.; Dong, F.; Hirota, K. Fast Geometric Transformations on Quantum Images. Int. J. Appl. Math. 2010, 40, 3. [Google Scholar]
- Jiang, N.; Wang, J.; Mu, Y. Quantum image scaling up based on nearest-neighbor interpolation with integer scaling ratio. Quantum Inf. Processing 2015, 14, 4001–4026. [Google Scholar] [CrossRef]
- Sang, J.; Wang, S.; Niu, X. Quantum realization of the nearest-neighbor interpolation method for FRQI and NEQR. Quantum Inf. Processing 2016, 15, 37–64. [Google Scholar] [CrossRef]
- Li, P.; Liu, X. Bilinear interpolation method for quantum images based on quantum Fourier transform. Int. J. Quantum Inf. 2018, 16, 1850031. [Google Scholar] [CrossRef]
- Zhou, R.-G.; Cheng, Y.; Liu, D. Quantum image scaling based on bilinear interpolation with arbitrary scaling ratio. Quantum Inf. Processing 2019, 18, 267. [Google Scholar] [CrossRef]
- Jiang, N.; Wang, L. Analysis and improvement of the quantum Arnold image scrambling. Quantum Inf. Processing 2014, 13, 1545–1551. [Google Scholar] [CrossRef]
- Zhou, R.-G.; Sun, Y.-J.; Fan, P. Quantum image Gray-code and bit-plane scrambling. Quantum Inf. Processing 2015, 14, 1717–1734. [Google Scholar] [CrossRef]
- Caraiman, S.; Manta, V.I. Histogram-based segmentation of quantum images. Theor. Comput. Sci. 2014, 529, 46–60. [Google Scholar] [CrossRef]
- Caraiman, S.; Manta, V.I. Image segmentation on a quantum computer. Quantum Inf. Processing 2015, 14, 1693–1715. [Google Scholar] [CrossRef]
- Wang, X.; Yang, C.; Xie, G.-S.; Liu, Z. Image thresholding segmentation on quantum state space. Entropy 2018, 20, 728. [Google Scholar] [CrossRef] [Green Version]
- Li, P.; Shi, T.; Zhao, Y.; Lu, A. Design of threshold segmentation method for quantum image. Int. J. Theor. Phys. 2020, 59, 514–538. [Google Scholar] [CrossRef]
- Zhang, Y.; Lu, K.; Gao, Y. QSobel: A novel quantum image edge extraction algorithm. Sci. China Inf. Sci. 2015, 58, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Fan, P.; Zhou, R.-G.; Hu, W.W.; Jing, N. Quantum image edge extraction based on Laplacian operator and zero-cross method. Quantum Inf. Processing 2019, 18, 27. [Google Scholar] [CrossRef]
- Fan, P.; Zhou, R.-G.; Hu, W.; Jing, N. Quantum image edge extraction based on classical Sobel operator for NEQR. Quantum Inf. Processing 2019, 18, 24. [Google Scholar] [CrossRef]
- Zhou, R.-G.; Yu, H.; Cheng, Y.; Li, F.-X. Quantum image edge extraction based on improved Prewitt operator. Quantum Inf. Processing 2019, 18, 261. [Google Scholar] [CrossRef]
- Li, P.; Shi, T.; Lu, A.; Wang, B. Quantum implementation of classical Marr–Hildreth edge detection. Quantum Inf. Processing 2020, 19, 64. [Google Scholar] [CrossRef]
- Chetia, R.; Boruah, S.; Sahu, P. Quantum image edge detection using improved Sobel mask based on NEQR. Quantum Inf. Processing 2021, 20, 21. [Google Scholar] [CrossRef]
- Jiang, N.; Dang, Y.; Wang, J. Quantum image matching. Quantum Inf. Processing 2016, 15, 3543–3572. [Google Scholar] [CrossRef] [Green Version]
- Dang, Y.; Jiang, N.; Hu, H.; Zhang, W. Analysis and improvement of the quantum image matching. Quantum Inf. Processing 2017, 16, 269. [Google Scholar] [CrossRef]
- Luo, G.; Zhou, R.-G.; Liu, X.; Hu, W.; Luo, J. Fuzzy matching based on gray-scale difference for quantum images. Int. J. Theor. Phys. 2018, 57, 2447–2460. [Google Scholar] [CrossRef]
- Heidari, S.; Naseri, M. A novel LSB based quantum watermarking. Int. J. Theor. Phys. 2016, 55, 4205–4218. [Google Scholar] [CrossRef]
- Hu, W.; Zhou, R.-G.; Luo, J.; Liu, B. LSBs-based quantum color images watermarking algorithm in edge region. Quantum Inf. Processing 2019, 18, 16. [Google Scholar] [CrossRef]
- He, L.; Ren, X.; Gao, Q.; Zhao, X.; Yao, B.; Chao, Y. The connected-component labeling problem: A review of state-of-the-art algorithms. Pattern Recognit. 2017, 70, 25–43. [Google Scholar] [CrossRef]
- Alnuweiri, H.M.; Prasanna, V.K. Parallel architectures and algorithms for image component labeling. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 1014–1034. [Google Scholar] [CrossRef]
- Levialdi, S. On shrinking binary picture patterns. Commun. ACM 1972, 15, 7–10. [Google Scholar] [CrossRef]
- Cheng, K.-W.; Tseng, C.-C. Quantum full adder and subtractor. Electron. Lett. 2002, 38, 1343–1344. [Google Scholar] [CrossRef]
- Barenco, A.; Bennett, C.H.; Cleve, R.; DiVincenzo, D.P.; Margolus, N.; Shor, P.; Sleator, T.; Smolin, J.A.; Weinfurter, H. Elementary gates for quantum computation. Phys. Rev. A 1995, 52, 3457. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nielsen, M.A.; Chuang, I. Quantum Computation and Quantum Information, 10th ed.; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- LaRose, R. Overview and comparison of gate level quantum software platforms. Quantum 2019, 3, 130. [Google Scholar] [CrossRef] [Green Version]
- Bolelli, F.; Cancilla, M.; Baraldi, L.; Grana, C.J. Toward reliable experiments on the performance of connected components labeling algorithms. J. Real Time Image Processing 2020, 17, 229–244. [Google Scholar] [CrossRef] [Green Version]
- Chang, F.; Chen, C.-J.; Lu, C.-J. A linear-time component-labeling algorithm using contour tracing technique. Comput. Vis. Image Underst. 2004, 93, 206–220. [Google Scholar] [CrossRef] [Green Version]
- Wu, K.; Otoo, E.; Suzuki, K. Optimizing two-pass connected-component labeling algorithms. Pattern Anal. Appl. 2009, 12, 117–135. [Google Scholar] [CrossRef]
Figure 2.
The simple example of local-operator techniques. (a) original image. (b) adding border. (c) partial result 1. (d) partial result 2. (e) partial result 3. (f) propagate 3. (g) propagate 2. (h) propagate 1.
Figure 2.
The simple example of local-operator techniques. (a) original image. (b) adding border. (c) partial result 1. (d) partial result 2. (e) partial result 3. (f) propagate 3. (g) propagate 2. (h) propagate 1.
Figure 3.
The quantum circuit of
Figure 2b.
Figure 3.
The quantum circuit of
Figure 2b.
Figure 4.
Address shift operation circuit. (a) Shift + operator circuit. (b) Shift − operator circuit.
Figure 4.
Address shift operation circuit. (a) Shift + operator circuit. (b) Shift − operator circuit.
Figure 5.
Logic operation circuit. (a) Logic operation (AND). (b) Logic operation (OR).
Figure 5.
Logic operation circuit. (a) Logic operation (AND). (b) Logic operation (OR).
Figure 6.
Assignment operation circuit.
Figure 6.
Assignment operation circuit.
Figure 7.
Compare operation circuit.
Figure 7.
Compare operation circuit.
Figure 8.
Full addition circuit. (a) 1-bit full addition circuit. (b) n-bit full addition circuit.
Figure 8.
Full addition circuit. (a) 1-bit full addition circuit. (b) n-bit full addition circuit.
Figure 9.
Full subtractor circuit. (a) 1-bit full subtractor circuit. (b) n-bit full subtractor circuit.
Figure 9.
Full subtractor circuit. (a) 1-bit full subtractor circuit. (b) n-bit full subtractor circuit.
Figure 10.
Obtaining of information of .
Figure 10.
Obtaining of information of .
Figure 11.
Execution of the Levialdi operator.
Figure 11.
Execution of the Levialdi operator.
Figure 12.
The circuit of Equation (2).
Figure 12.
The circuit of Equation (2).
Figure 13.
Obtaining of information of .
Figure 13.
Obtaining of information of .
Figure 14.
The computation of .
Figure 14.
The computation of .
Figure 15.
The quantum circuit of Equation (3).
Figure 15.
The quantum circuit of Equation (3).
Figure 16.
The quantum circuit of Equation (4).
Figure 16.
The quantum circuit of Equation (4).
Figure 17.
Experimental comparison of CF, SAUF, and NULL.
Figure 17.
Experimental comparison of CF, SAUF, and NULL.
Figure 18.
The example of traffic signs. (a) original image. (b) binary image. (c) component labeling.
Figure 18.
The example of traffic signs. (a) original image. (b) binary image. (c) component labeling.
Figure 19.
The example of license plates, “陕” in figure means Shanxi Province. (a) original image. (b) binary image. (c) component labeling.
Figure 19.
The example of license plates, “陕” in figure means Shanxi Province. (a) original image. (b) binary image. (c) component labeling.
Table 1.
Number of ancilla qubits used by the basic quantum functional circuits.
Table 1.
Number of ancilla qubits used by the basic quantum functional circuits.
| No. | Function | Ancilla Qubits |
|---|
| 1 | Address Shift Operation Circuit | 0 |
| 2 | Logic Operation Circuit | 1 |
| 3 | Control Assignment Operation Circuit | n + 1 |
| 4 | Compare Operation Circuit | 2n |
| 5 | Full Addition Circuit | 2n + 1 |
| 6 | Full Subtraction Circuit | 2n + 1 |
| Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).