DCA for Sparse Quadratic Kernel-Free Least Squares Semi-Supervised Support Vector Machine

Abstract

With the development of science and technology, more and more data have been produced. For many of these datasets, only some of the data have labels. In order to make full use of the information in these data, it is necessary to classify them. In this paper, we propose a strong sparse quadratic kernel-free least squares semi-supervised support vector machine ($SSQLS{S}^{3}VM$), in which we add a ${\ell }_0$norm regularization term to make it sparse. An NP-hard problem arises since the proposed model contains the ${\ell }_0$ norm and another nonconvex term. One important method for solving the nonconvex problem is the DC (difference of convex function) programming. Therefore, we first approximate the ${\ell }_0$ norm by a polyhedral DC function. Moreover, due to the existence of the nonsmooth terms, we use the sGS-ADMM to solve the subproblem. Finally, empirical numerical experiments show the efficiency of the proposed algorithm.

1. Introduction

In today’s information society, more and more data is emerging, and in order to make reasonable and full use of the information contained in the data, it is common to classify or categorize the data, which usually involves a high cost (money or time). Machine learning is based on sample data. Supervised learning is a learning method that predicts a function or classifier from a labeled training dataset, and one of the most famous methods is the support vector machine (SVM), which has been widely used for data classification [1,2,3,4]. Nevertheless, in the real world, there are a large number of data that are unlabeled or only partially labeled, and it is difficult to obtain labels. Usually, a lot of work is needed to tag the data, which means that it is often unacceptable to invest a lot of resources in the work at a high (monetary or time) cost. For example, computer-aided diagnosis (CAD) with a breast cancer system is usually characterized by a special professional method to mark a large number of collected data. However, we know that it is very difficult to collect the pathological records of patients with labels. Generally, it takes at least five years to mark the patient record as alive or not alive. A major problem is the need for experts to spend a lot of time labeling. Supervised learning cannot be used in these contexts, and it is difficult to obtain a learner with good prediction results and strong generalization ability by using only a small amount of labeled data in supervised learning. In order to overcome this difficulty, researchers have proposed the semi-supervised learning method, which has attracted more and more attention [5,6]. When only a small portion of data has labels, exploiting potential information contained in them can help improve the learning performance [7,8].

Therefore, some researchers have introduced the idea of semi-supervised learning into SVM, for which a semi-supervised support vector machine ($S^{3}VM$) is proposed, similar to the SVM, that maximizes the margin between labeled and unlabeled data points. The $S^{3}VM$ was originally proposed by Vapnik and Sterin [9] in 1977. It considered that the hyperplane needs to pass through the low-density area of data. In 1999, Bennett and Demiriz [10] proposed the first optimization formula of $S^{3}VM$ and proved that $S^{3}VM$ can be re-expressed as a mixed integer programming problem. They then used the method of solving integer programming to solve it accurately. Traditionally, since the categories of unlabeled data need to be predicted, $S^{3}VM$ is usually formulated as a nonconvex nonsmooth optimization problem, and this raises some analytical and computational difficulties. In order to solve $S^{3}VM$ with better results, scholars have proposed many semi-supervised methods to improve $S^{3}VM$, and many effective algorithms have been proposed. For more details of $S^{3}VM$ methods, the reader is referred to [11,12,13,14,15,16,17,18] and references therein.

In addition, for linearly indivisible datasets, most traditional methods use kernel functions to map each data point from the original space to a higher dimensional space, and then find a hyperplane in the high dimensional space so that it can separate all mapped data points. However, selection of the appropriate kernel function for a given dataset becomes a new problem. To avoid this situation, Dagher [19] first proposed a kernel-free quadratic support vector machine (QSVM), which tries to find a quadratic decision function that can nonlinearly separate the data at the largest margin. Based on the above model, Yan et al. [20] proposed a kernel-free quadratic $S^{3}VM$, called SSQSSVM. They reformulated SSQSSVM as a mixed-integer programming problem, which they proved to be equivalent to a nonconvex optimization problem with absolute-value constraints. Then, using convex relaxation techniques, it can be transformed into a semidefinite programming optimization problem, which a CVX package can be used to solve. In 2018, Zhan [21] proposed a sparse quadratic kernel-free least squares semi-supervised support vector machine ($SQLS{S}^{3}VM$) with a ${\ell }_1$ norm regularization term for the binary classification problem and used the proximal alternating direction method of multipliers (P-ADMM) to solve it. Tian et al. [22] applied this to online credit scoring, and also added fuzzy weights to further improve the accuracy and robustness of the classification. Gao et al. [23] proposed a new quadratic kernel-free least square twin support vector machine (QLSTSVM) for binary classification problems. They adopted the alternating direction method of multipliers to solve it and achieved good numerical results.

We know that to accurately characterize the sparsity, it is suggested to impose the ${\ell }_0$ norm, which is the most natural and suitable concept for modeling the sparsity. There are two main ways to deal with the ${\ell }_0$ norm: one is to approximate it with a convex function [24] or nonconvex function [25], and the other is to deal with it directly [26]. The ${\ell }_1$ norm is the best convex approximation of the ${\ell }_0$ norm, and it can encourage sparsity in only some cases with restrictive assumptions [27]. It has also been shown to be, in certain cases, inconsistent and biased [28]. With the in-depth study of the properties of ${\ell }_0$ norm, previous application works have shown that the ${\ell }_0$ norm has better properties and better sparse performance and robustness than the ${\ell }_1$ norm approach [29,30,31,32].

In this paper, we propose a new strong sparse quadratic kernel-free least squares semi-supervised support sector machine model with ${\ell }_0$ norm regularization term that has stronger interpretability, which finds a separating hyperplane surface far away from both the labeled and unlabeled points with the least number of features.The main contributions of the paper are summarized as follows:

(I)

We propose a new strong sparse quadratic kernel-free least squares semi-supervised support vector machine model called the strong sparse quadratic kernel-free least squares semi-supervised support vector machine ($SSQLS{S}^{3}VM$). In order to make it have better sparse performance and robustness, we add an ${\ell }_0$ norm regularization term directly to the objective rather than its approximation.

(II)

We treat the problem by nonconvex methods based on the difference of the convex function (DC) program and DCA (DC algorithm), which is one of the most important methods for nonconvex problems [33,34,35]. Therefore, we used a nonconvex function (which can be expressed as the form of difference of two convex functions) to approximate the ${\ell }_0$ norm, and the third term can be expressed in the form of a subtractive convex function.

(III)

We conducted experiments on all proposed models and algorithms on several benchmark datasets to investigate their efficiency in classification.

The rest of this paper is organized as follows: DC programming and $SSQLS{S}^{3}VM$ are briefly presented in Section 2, while Section 3 is devoted to the development of DCA with sGS-ADMM for solving the $SSQLS{S}^{3}VM$. In Section 4, the computational experiments are reported. Finally, we conclude the paper with future work in Section 5.

2. Preliminaries

In this section, we will recall some elementary concepts of the quadratic kernel-free semi-supervised support vector machine and the outline of DC programming and DCA.

2.1. Sparse Quadratic Kernel-Free Least Squares Semi-Supervised Support Vector Machine

Given a training set that consists of m labeled points $\{(x_i,y_i)\in R^n\times \{+1,-1\},i=1,\dots ,s\}$ and p unlabeled points $x_i\in R^n,i=s+1,\dots ,n$, our goal is to find a quadratic surface $f\left(x\right)=x^{T}Qx+b^{T}x+c=0$ that can directly separate the data into two classes with the largest margin, where Q is a symmetric matrix.

According to [20], the formula of the $S^{3}VM$ problem can be written as follows

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \underset{w,b,c,{\xi }_i,{\eta }_i,{\gamma }_i}{min}& \sum _{i=1}^n\left|\right|Qx+{b\left|\right|}^2+C_1\sum _{i=1}^s{\xi }_i+C_2\sum _{i=s+1}^{n}min({\eta }_i,{\gamma }_i)\hfill \\ \hfill s.t.& y_i(x^{T}Qx+b^{T}x+c)\ge 1-{\xi }_i,{\xi }_i\ge 0,i=1,2,\dots ,s,\hfill \\ & (x^{T}Qx+b^{T}x+c)\ge 1-{\eta }_i,{\eta }_i\ge 0,i=s+1,s+2,\dots ,n,\hfill \\ & -(x^{T}Qx+b^{T}x+c)\ge 1-{\gamma }_i,{\gamma }_i\ge 0,i=s+1,s+2,\dots ,n.\hfill \end{array}\end{array}$$

(1)

Take the upper triangular element of matrix Q, denoted as vector a, that is

$$a={[a_{11},a_{12},\cdots ,a_{1m},a_{22},a_{23},\cdots ,a_{2m},\cdots ,a_{mm}]}^T\in {\mathbf{R}}^{\frac{m^2+m}{2}}.$$

If the data $x_i=\{x_{i1},\dots ,x_{im}\}\in R^m$, then $h_{x_i}$ is a vector formed as follows

$$h_{x_i}={[\frac{1}{2}{x}_{i1}^2,x_{i1}{x}_{i2},\cdots ,x_{i1}{x}_{im},\frac{1}{2}{x}_{i2}^2,\cdots ,x_{i2}{x}_{im},\cdots ,\frac{1}{2}{x}_{im}^2]}^T\in {\mathbf{R}}^{\frac{m^2+m}{2}}.$$

Then, we can construct a $m\times \frac{m^2+m}{2}$-dimensional matrix $H_{x_i}$. In each jth column of $H_{x_i}$, find the positions of all the components of Q that have the form $a_{jk}$ or $a_{kj}$ (where k can be any value), set those positions in the jth column of $H_{x_i}$ to $x_{ik}$, and set the other positions to zero.

Denoting $g_{x_i}=\left[\begin{array}{c}{h}_{x_i}\\ x_i\\ 1\end{array}\right]$,$w=\left[\begin{array}{c}a\\ b\\ c\end{array}\right]$,$G=\frac{1}{l}\left[\begin{array}{ccc}{\sum }_{i=1}^l{H}_{x_i}^T{H}_{x_i}& {\sum }_{i=1}^n{H}_{x_i}^T& 0\\ {\sum }_{i=1}^l{H}_{x_i}& nE& 0\\ 0& 0& 0\end{array}\right]$

We have

$$y_i(\frac{1}{2}{x}_i^{T}Q{x}_i+b^T{x}_i+c)=y_i(h_{x_i}^{T}a+b^T{x}_i+c)=y_i\left(g_{x_i}^{T}w\right),$$

$$\frac{1}{2}{x}_i^{T}Q{x}_i+b^T{x}_i+c=h_{x_i}^{T}a+b^T{x}_i+c=\left(g_{x_i}^{T}w\right),$$

and

$$\frac{1}{2n}\sum _{i=1}^n\left|\right|Q{x}_i+{b\left|\right|}_2^2=\frac{1}{2n}\sum _{i=1}^n\left|\right|H_{x_i}a+b{\left|\right|}_2^2=\frac{1}{2}{w}^{T}Gw$$

Therefore, $Q{S}^{3}VM$ can be rewritten as

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \underset{w,{\xi }_i,{\eta }_i,{\gamma }_i}{min}& \frac{1}{2}{w}^{T}Gw+C_1\sum _{i=1}^s{\xi }_i+C_2\sum _{i=s+1}^{n}min({\eta }_i,{\gamma }_i)\hfill \\ \hfill s.t.& y_i\left(g_{x_i}^{T}w\right)\ge 1-{\xi }_i,{\xi }_i\ge 0,i=1,2,\dots ,s,\hfill \\ & \left(g_{x_i}^{T}w\right)\ge 1-{\eta }_i,{\eta }_i\ge 0,i=s+1,s+2,\dots ,n,\hfill \\ & -\left(g_{x_i}^{T}w\right)\ge 1-{\gamma }_i,{\gamma }_i\ge 0,i=s+1,s+2,\dots ,n.\hfill \end{array}\end{array}$$

(2)

To obtain sparse solutions, we add the ${\ell }_0$ norm regularization term to the objective function. Hence, the strong sparse quadratic kernel-free least squares semi-supervised support vector machine ($SSQLS{S}^{3}VM$) can be written as

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \underset{w,{\xi }_i,{\eta }_i,{\gamma }_i}{min}& {\lambda \parallel w\parallel }_0+\frac{1}{2}{w}^{T}Gw+C_1\sum _{i=1}^s{\xi }_i+C_2\sum _{i=s+1}^{n}min({\eta }_i,{\gamma }_i)\hfill \\ \hfill s.t.& y_i\left(g_{x_i}^{T}w\right)\ge 1-{\xi }_i,{\xi }_i\ge 0,i=1,2,\dots ,s,\hfill \\ & \left(g_{x_i}^{T}w\right)\ge 1-{\eta }_i,{\eta }_i\ge 0,i=s+1,s+2,\dots ,n,\hfill \\ & -\left(g_{x_i}^{T}w\right)\ge 1-{\gamma }_i,{\gamma }_i\ge 0,i=s+1,s+2,\dots ,n,\hfill \end{array}\end{array}$$

(3)

where ${\parallel ·\parallel }_0$ is defined as the number of its nonzero components.

2.2. Outline of DCA

DC programming and DCA solve the problem of minimizing function f, which is the difference between two convex functions on the subspace $X\subset R^n$ and the dual space Y of X. In general, the DC program is an optimization problem in the following forms

$$\begin{array}{cc}\hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\alpha =\inf \{f\left(x\right)=g\left(x\right)-h\left(x\right),x\in R^n\}\hfill & \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\left(P_{dc}\right),\end{array}$$

where $g,h$ are lower semi-continuous proper convex functions on $R^n$.

For a convex function $g\left(x\right)$, its conjugate function is defined as

$$g^{*}\left(y\right)=sup\{\langle x,y\rangle -g\left(x\right)|x\in X\}.$$

For $ϵ>0$ and $x^0\in domg$, the symbol ${\partial }_{ϵ}g\left(x^0\right)$ denotes $ϵ-$subdifferential of g at $x^0,$ that is,

$${\partial }_{ϵ}g\left(x^0\right)=\{y\in Y:g\left(x\right)\ge g\left(x^0\right)+\langle x-x^0,y\rangle -ϵ\forall x\in X\},$$

while $\partial g\left(x^0\right)$ stands for the usual (or exact) subdifferential of g at $x^0$.

According to the subdifferential calculus of a lower semi-continuous proper convex function [36], we can get

$$y_0\in \partial f\left(x_0\right)\iff x_0\in \partial f^{*}\left(y_0\right)\iff \langle x_0,y_0\rangle =f\left(x_0\right)+f^{*}\left(y_0\right).$$

On the basis of the definition of conjugate functions, we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \alpha & =\inf \left\{f\right(x)=g(x)-h(x),x\in X\}\hfill \\ & =\inf \{g\left(x\right)-sup\{\langle x,y\rangle -h^{*}\left(y\right):y\in Y\}:x\in X\}\hfill \\ & =\inf \left\{\beta \right(y):y\in Y\}\hfill \\ \hfill \end{array}\end{array}$$

with

$$\beta \left(y\right)=\inf \{g\left(x\right)-(\langle x,y\rangle -h^{*}\left(y\right)):x\in X\}.$$

Then, the following program is called the dual program of $\left(P_{dc}\right)$,

$$\begin{array}{cc}\hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\alpha =\inf \{h^{*}\left(y\right)-g^{*}\left(y\right):y\in Y\}.\hfill & \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\left(D_{dc}\right)\end{array}$$

We observe perfect symmetry between primal and dual programs $\left(P_{dc}\right)$ and $\left(D_{dc}\right)$: the dual program to $\left(D_{dc}\right)$ is exactly $\left(P_{dc}\right)$.

Definition 1

([37]). A point $x^{*}$ is said to be a critical point of $g-h$ if

$$\begin{array}{c}\hfill \partial g\left(x^{*}\right)\cap \partial h\left(x^{*}\right)\ne \varnothing .\end{array}$$

(4)

Theorem 1

([38]). Let P and D denote the solution sets of problems $\left(P_{dc}\right)$ and $\left(D_{dc}\right)$. Then,

$\left(i\right)$$x\in P$ if and only if ${\partial }_{ϵ}h\left(x\right)\subset {\partial }_{ϵ}g\left(x\right)$.

$\left(ii\right)$ Dually,$y\in D$ if and only if ${\partial }_{ϵ}{g}^{*}\left(y\right)\subset {\partial }_{ϵ}{h}^{*}\left(y\right)$.

$\left(iii\right)$$\cup \{\partial h\left(x\right):x\in P\}\subset D\subset dom{h}^{*}$.

$\left(iv\right)$$\cup \{\partial g^{*}\left(y\right):y\in D\}\subset P\subset domg$.

Theorem 2

([38]). Let

$$P_l=\{x^{*}\in X:\partial h\left(x^{*}\right)\subset \partial g\left(x^{*}\right\},$$

$$D_l=\{y^{*}\in Y:\partial g^{*}\left(y^{*}\right)\subset \partial h^{*}\left(y^{*}\right\}.$$

Then,

$\left(i\right)$$x^{*}$ is a local minimizer of $g-h$, then $x^{*}\in P_l$.

$\left(ii\right)$ Let $x^{*}$ be a critical point of $g-h$ and $y^{*}\in \partial g\left(x^{*}\right)\cap \partial h\left(x^{*}\right)$. Let U be a neighborhood of $x^{*}$ such that $U\cap domg\subset dom\partial h.$ If for any $x\in U\cap domg$ there is $y\in \partial h$ such that $h^{*}\left(y\right)-g^{*}\left(y\right)\ge h^{*}\left(y^{*}\right)-g^{*}\left(y^{*}\right)$, then $x^{*}$ is a local minimizer of $g-h$. More precisely,

$$\begin{array}{c}\hfill g\left(x\right)-h\left(x\right)\ge g\left(x^{*}\right)-h\left(x^{*}\right),\forall x\in U\cap domg.\end{array}$$

(5)

The necessary local optimality condition for (primal) DC program $P_{dc}$ is

$$\begin{array}{c}\hfill \partial g\left(x^{*}\right)\cap \partial h\left(x^{*}\right)\ne \varnothing .\end{array}$$

(6)

According to [38], for each fixed $x^{*}\in X$, we solve the following optimization problem

$$\begin{array}{cc}\hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\inf \{h^{*}\left(y\right)-g^{*}\left(y\right):y\in \partial h\left(x^{*}\right)\}.\hfill & \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\left(S\left(x^{*}\right)\right)\end{array}$$

This is equal to

$$\inf \left\{\langle x^{*},y\rangle \right)-g^{*}\left(y\right):y\in \partial h\left(x^{*}\right)\}.$$

In the same way, for each $y^{*}\in Y$, we define the problem

$$\begin{array}{cc}\hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\inf \{g\left(x\right)-h\left(x\right):x\in \partial g^{*}\left(y^{*}\right)\}.\hfill & \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\left(T\left(y^{*}\right)\right)\end{array}$$

Similarly, it can be rewritten as

$$\inf \left\{\langle x,y^{*}\rangle \right)-h\left(x\right):x\in \partial g^{*}\left(y^{*}\right)\}.$$

Let $\mathcal{S}\left(x^{*}\right),\mathcal{T}\left(y^{*}\right)$ denote the solution sets of problems $\left(S\left(x^{*}\right)\right)$ and $\left(T\left(y^{*}\right)\right)$, respectively. Based on the above, we give the DCA.

Given an initial point $x^0\in domg$, we calculate the following two sequences $\left\{x^k\right\}$ and $\left\{y^k\right\}$, which are defined by

$$y^k\in \mathcal{S}\left(x^k\right);x^{k+1}\in \mathcal{T}\left(y^k\right).$$

Namely, at the k-th iteration, we calculate

$$\begin{array}{c}\hfill \begin{array}{cc}& x^k\in \partial g^{*}\left(y^{k-1}\right)\to y^k\in \partial h\left(x^k\right)\hfill \\ & =argmin\{h^{*}\left(y\right)-[g^{*}\left(y^{k-1}\right)+\langle x^k,y-y^{k-1}\rangle ]:y\in Y\}\hfill \end{array}\end{array}$$

(7)

$$\begin{array}{c}\hfill \begin{array}{cc}& y^k\in \partial h\left(x^k\right)\to x^{k+1}\in \partial g^{*}\left(y^k\right)\hfill \\ & =argmin\{g\left(x\right)-[h\left(x^k\right)+\langle y^k,x-x^k\rangle ]:x\in X\}\hfill \end{array}\end{array}$$

(8)

According to [36], sequences $\left\{x^k\right\},\left\{y^k\right\}$ in DCA are well defined if and only if

$$dom\partial g\subset dom\partial handdom\partial h^{*}\subset dom\partial g^{*}.$$

The convergence properties of DCA and its theoretical basic can be found in [37,39].

3. ${\mathit{SSQLSS}}^{\mathbf{3}}\mathit{VM}$ by DCA

The $SSQLS{S}^{3}VM$ can be rewritten as follows

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \underset{w,\xi ,\eta ,\gamma }{min}& {\lambda \parallel w\parallel }_0+\frac{1}{2}{w}^{T}Gw+C_1\langle e,\xi \rangle +C_2\langle e,min\{\eta ,\gamma \}\rangle \hfill \\ \hfill s.t.& D\left(Aw\right)+\xi \ge e,\hfill \\ & Bw+\eta \ge e,\hfill \\ & -Bw+\gamma \ge e,\hfill \\ & \xi ,\eta ,\gamma \ge 0,\hfill \end{array}\end{array}$$

(9)

where A is a matrix of the label data, D is a diagonal matrix whose diagonal elements are the label, and B is the unlabeled data, while $\xi ,\eta ,\gamma$ are the relaxation variables.

We can see that the constraint set is a polyhedral convex set, denoted by K. Therefore, (9) can be rewritten as follows

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \underset{w,\xi ,\eta ,\gamma }{min}& F(w,\xi ,\eta ,\gamma )={\lambda \parallel w\parallel }_0+\frac{1}{2}{w}^{T}Gw+C_1\langle e,\xi \rangle +C_2\langle e,min\{\eta ,\gamma \}\rangle \hfill \\ \hfill s.t.& (w,\xi ,\eta ,\gamma )\in K.\hfill \end{array}\end{array}$$

(10)

A ${\ell }_0$ norm DC polyhedron approximation is given in [40], and its practical effect is verified in [41]. Now, we will add this approximation to the problem (10).

For $x\in \mathbb{R}$, we define the function $\theta$ as follows

$$\theta \left(x\right):=min\{1,{\lambda }_1\left|x\right|\}=1+{\lambda }_1\left|x\right|-max\{1,{\lambda }_1\left|x\right|\},$$

where ${\lambda }_1$ is a known parameter. Hence, ${\parallel w\parallel }_0$ can be approximately expressed by ${\parallel w\parallel }_0\simeq {\displaystyle \sum _{i=1}^{\frac{m^2+3m+2}{2}}}\theta \left(w_i\right).$ We redefine ${\lambda }_1={\lambda }_1\lambda .$ Therefore, we can conclude that $\theta$ is a DC function with the following DC decomposition: $\theta \left(x\right)=g\left(x\right)-h\left(x\right)$, where

$$g\left(x\right)=\lambda +{\lambda }_1\left|x\right|,h\left(x\right)=max\{\lambda ,{\lambda }_1\left|x\right|\}.$$

According to the above description, the problem of (10) can be represented as

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \underset{w,\xi ,\eta ,\gamma }{min}& F(w,\xi ,\eta ,\gamma )=\sum _{i=1}^{\frac{m^2+3m+2}{2}}\theta \left(w_i\right)+\frac{1}{2}{w}^{T}Gw+C_1\langle e,\xi \rangle +C_2\langle e,min\{\eta ,\gamma \}\rangle \hfill \\ \hfill s.t.& (w,\xi ,\eta ,\gamma )\in K.\hfill \end{array}\end{array}$$

(11)

We note that $F(w,\xi ,\eta ,\gamma )$ is a DC function

$$F(w,\xi ,\eta ,\gamma )=G(w,\xi ,\eta ,\gamma )-H(w,\xi ,\eta ,\gamma ),$$

where

$$\begin{array}{c}\hfill \begin{array}{c}\hfill G(w,\xi ,\eta ,\gamma )=\frac{1}{2}{w}^{T}Gw+C_1\langle e,\xi \rangle +\sum _{i=1}^{\frac{m^2+3m+2}{2}}g\left(w_i\right),\end{array}\end{array}$$

(12)

and

$$\begin{array}{c}\hfill \begin{array}{c}\hfill H(w,\xi ,\eta ,\gamma )=-C_2\langle e,min\{\eta ,\gamma \}\rangle +\sum _{i=1}^{\frac{m^2+3m+2}{2}}h\left(w_i\right).\end{array}\end{array}$$

(13)

Obviously, G and H are convex functions. Therefore, the approximation problem of (10) has the following form

$$\begin{array}{c}\hfill \begin{array}{c}\hfill min\left\{G\right(w,\xi ,\eta ,\gamma )-H(w,\xi ,\eta ,\gamma ):(w,\xi ,\eta ,\gamma )\in K\}.\end{array}\end{array}$$

(14)

We can apply the DCA to the problem (14) and obtain the Algorithm 1 as follows.

Algorithm 1: Algorithm DCA.

$\mathbf{Step}\mathbf{0}$ Given the initial value $(w^0,{\xi }^0,{\eta }^0,{\gamma }^0),$ set $k\Leftarrow 0$; $\mathbf{Step}\mathbf{1}$ Compute $({\overline{w}}^k,{\overline{\xi }}^k,{\overline{\eta }}^k,{\overline{\gamma }}^k)\in \partial H(w^k,{\xi }^k,{\eta }^k,{\gamma }^k))$ $\mathbf{Step}\mathbf{2}$ Solve the convex program; $\begin{array}{cc}(w^{k+1},{\xi }^{k+1},{\eta }^{k+1},{\gamma }^{k+1})=& argmin\{\frac{1}{2}{w}^{T}Gw+C_1\langle e,\xi \rangle +{\lambda }_1{\parallel w\parallel }_1\\ & -\langle ({\overline{w}}^k,{\overline{\xi }}^k,{\overline{\eta }}^k,{\overline{\gamma }}^k)(w,\xi ,\eta ,\gamma )\rangle \}\hfill \end{array}$ $s.t.(w,\xi ,\eta ,\gamma )\in K$; $\mathbf{Step}\mathbf{3}$ If $\parallel x^{k+1}-x^k\parallel \le ϵ,$ then stop; otherwise $k\Leftarrow k+1,$ go to $\mathbf{Step}\mathbf{1}$.

We know that the computation of a subgradient of H is easy, so we can take   $({\overline{w}}^k,{\overline{\xi }}^k,{\overline{\eta }}^k,{\overline{\gamma }}^k)\in \partial H(w^k,{\xi }^k,{\eta }^k,{\gamma }^k))$ as follows:

First, we compute ${\overline{\eta }}^k$ by

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\overline{\eta }}^k=0if{\eta }^k\ge {\gamma }^k,{\overline{\eta }}^k=-C_{2}if{\eta }^k<{\gamma }^k.\end{array}\end{array}$$

(15)

Then, ${\overline{\gamma }}^k$ can be obtained by

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\overline{\gamma }}^k=0if{\gamma }^k\ge {\eta }^k,{\overline{\gamma }}^k=-C_{2}if{\gamma }^k<{\eta }^k.\end{array}\end{array}$$

(16)

$${\overline{w}}_i^k=\left\{\begin{array}{ccc}0\hfill & & if-\frac{1}{{\lambda }_1}\le w_i^k\le \frac{1}{{\lambda }_1},\hfill \\ \lambda \hfill & & if{w}_i^k>\frac{1}{{\lambda }_1},\hfill \\ -\lambda \hfill & & if{w}_i^k<-\frac{1}{{\lambda }_1}.\hfill \end{array}\right.$$

(17)

Furthermore, we solve the subproblem in Step  2, that is,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill min& \frac{1}{2}{w}^{T}Gw+C_1\langle e,\xi \rangle +{\lambda }_1{\parallel w\parallel }_1-\langle ({\overline{w}}^k,{\overline{\xi }}^k,{\overline{\eta }}^k,{\overline{\gamma }}^k),(w,\xi ,\eta ,\gamma )\rangle \hfill \\ \hfill s.t.& D\left(Aw\right)+\xi \ge e,\hfill \\ & Bw+\eta \ge e,\hfill \\ & -Bw+\gamma \ge e,\hfill \\ & \xi ,\eta ,\gamma \ge 0.\hfill \end{array}\end{array}$$

(18)

We introduce relaxation variables $r_1,r_2,r_3,z$ into (18) as follows

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill min& \frac{1}{2}{w}^{T}Gw+C_1\langle e,\xi \rangle +{\lambda }_1{\parallel z\parallel }_1-\langle ({\overline{w}}^k,{\overline{\xi }}^k,{\overline{\eta }}^k,{\overline{\gamma }}^k),(w,\xi ,\eta ,\gamma )\rangle \hfill \\ \hfill s.t.& D\left(Aw\right)+\xi -r_1=e,\hfill \\ & Bw+\eta -r_2=e,\hfill \\ & -Bw+\gamma -r_3=e,\hfill \\ & w-z=0,\hfill \\ & \xi ,\eta ,\gamma \ge 0,r_1,r_2,r_3\ge 0.\hfill \end{array}\end{array}$$

(19)

The above optimization problem (19) can be written equivalently as the following convex programming

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill min& \frac{1}{2}{w}^{T}Gw+C_1\langle e,\xi \rangle +{\lambda }_1{\parallel z\parallel }_1-\langle ({\overline{w}}^k,{\overline{\xi }}^k,{\overline{\eta }}^k,{\overline{\gamma }}^k),(w,\xi ,\eta ,\gamma )\rangle +{\delta }_{+}\left(\xi \right)\hfill \\ & +{\delta }_{+}\left(\eta \right)+{\delta }_{+}\left(\gamma \right)+{\delta }_{+}\left(r_1\right)+{\delta }_{+}\left(r_2\right)+{\delta }_{+}\left(r_3\right)\hfill \\ \hfill s.t.& D\left(Aw\right)+\xi -r_1=e,\hfill \\ & Bw+\eta -r_2=e,\hfill \\ & -Bw+\gamma -r_3=e,\hfill \\ & w-z=0,\hfill \end{array}\end{array}$$

(20)

where

$${\delta }_{+}\left(u\right)=\left\{\begin{array}{cc}0,\hfill & \hfill ifu\in R_{+}^n\\ \infty ,\hfill & \hfill otherwise.\end{array}\right.$$

(21)

In (20), there are three blocks, and only the first problem of block w is smooth. The problems of the second block $\{\xi ,\eta ,\gamma \}$ and third block $\{r_1,r_2,r_3,z\}$ are nonsmooth terms, so we applied sGS-ADMM to the above problem.

Let $\sigma >0$ be given. The augmented Lagrange function for (20) is defined by

$$\begin{array}{c}\hfill \begin{array}{cc}& L_{\sigma }(w,\xi ,\eta ,\gamma ,r_1,r_2,r_3,z;s_1,s_2,s_3,s_4)\hfill \\ & =\frac{1}{2}{w}^{T}Gw+C_1\langle e,\xi \rangle +{\lambda }_1{\parallel z\parallel }_1-\langle ({\overline{w}}^k,{\overline{\xi }}^k,{\overline{\eta }}^k,{\overline{\gamma }}^k),(w,\xi ,\eta ,\gamma )\rangle +{\delta }_{+}\left(\xi \right)+{\delta }_{+}\left(\eta \right)+{\delta }_{+}\left(\gamma \right)\hfill \\ & +{\delta }_{+}\left(r_1\right)+{\delta }_{+}\left(r_2\right)+{\delta }_{+}\left(r_3\right)+\langle D\left(Aw\right)+\xi -r_1-e,s_1\rangle +\langle Bw+\eta -r_2-e,s_2\rangle \hfill \\ & +\langle -Bw+\gamma -r_3-e,s_3\rangle +\langle w-z,s_4\rangle +\frac{\sigma }{2}{\parallel D\left(Aw\right)+\xi -r_1-e\parallel }^2\hfill \\ & +\frac{\sigma }{2}\parallel Bw+\eta -r_2{-e\parallel }^2+\frac{\sigma }{2}\parallel -Bw+\gamma -r_3{-e\parallel }^2+\frac{\sigma }{2}{\parallel w-z\parallel }^2.\hfill \end{array}\end{array}$$

(22)

We provide the framework of sGS-ADMM for solving (20) and its more details are shown in Algorithm 2 below.

Algorithm 2 Algorithm sGS-ADMM.

Let$\sigma >0$ and $\tau \in (0,\infty )$ be the given parameters, Choose $(w^0,{\xi }^0,{\eta }^0,{\gamma }^0,r_1^0,r_2^0,r_3^0,z^0),$

and $s_1^0,s_2^0,s_3^0,s_4^0,$ set $l\Leftarrow 0$. Perform the $l+1$th iteration as follows:

$\mathbf{Step}\mathbf{1}$ Compute $w^{l+\frac{1}{2}}=argmin{L}_{\sigma }(w,{\xi }^l,{\eta }^l,{\gamma }^l,r_1^l,r_2^l,r_3^l,z^l;s_1^l,s_2^l,s_3^l,s_4^l)$;

$\mathbf{Step}\mathbf{2}$ Compute ${\xi }^{l+1}=argmin{L}_{\sigma }(w^{l+\frac{1}{2}},\xi ,{\eta }^l,{\gamma }^l,r_1^l,r_2^l,r_3^l,z^l;s_1^l,s_2^l,s_3^l,s_4^l)$,

${\eta }^{l+1}=argmin{L}_{\sigma }(w^{l+\frac{1}{2}},{\xi }^{l+1},\eta ,{\gamma }^l,r_1^l,r_2^l,r_3^l,z^l;s_1^l,s_2^l,s_3^l,s_4^l)$,

${\gamma }^{l+1}=argmin{L}_{\sigma }(w^{l+\frac{1}{2}},{\xi }^{l+1},{\eta }^{l+1},\gamma ,r_1^l,r_2^l,r_3^l,z^l;s_1^l,s_2^l,s_3^l,s_4^l)$;

$\mathbf{Step}\mathbf{3}$ Compute $w^{l+1}=argmin{L}_{\sigma }(w,{\xi }^{l+1},{\eta }^{l+1},{\gamma }^{l+1},r_1^{l+1},r_2^{l+1},r_3^{l+1},z^{l+1};s_1^l,s_2^l,s_3^l,s_4^l)$

$\mathbf{Step}\mathbf{4}$ Compute $r_1^{l+1}=argmin{L}_{\sigma }(w^{l+\frac{1}{2}},{\xi }^{l+1},{\eta }^{l+1},{\gamma }^{l+1},r_1,r_2^l,r_3^l,z^l;s_1^l,s_2^l,s_3^l,s_4^l)$,

$r_2^{l+1}=argmin{L}_{\sigma }(w^{l+\frac{1}{2}},{\xi }^{l+1},{\eta }^{l+1},{\gamma }^{l+1},r_1^{l+1},r_2,r_3^l,z^l;s_1^l,s_2^l,s_3^l,s_4^l)$,

$r_3^{l+1}=argmin{L}_{\sigma }(w^{l+\frac{1}{2}},{\xi }^{l+1},{\eta }^{l+1},{\gamma }^{l+1},r_1^{l+1},r_2^{l+1},r_3,z^l;s_1^l,s_2^l,s_3^l,s_4^l)$,

$z^{l+1}=argmin{L}_{\sigma }(w^{l+\frac{1}{2}},{\xi }^{l+1},{\eta }^{l+1},{\gamma }^{l+1},r_1^{l+1},r_2^{l+1},r_3^{l+1},z;s_1^l,s_2^l,s_3^l,s_4^l)$;

$\mathbf{Step}\mathbf{5}$ Compute $s_1^{l+1}=s_1^l+\tau \sigma (D\left(A{w}^{l+1}\right)+{\xi }^{l+1}-r_1^{l+1}-e)$,

$s_2^{l+1}=s_2^l+\tau \sigma (B{w}^{l+1}+{\eta }^{l+1}-r_2^{l+1}-e)$,

$s_3^{l+1}=s_3^l+\tau \sigma (-B{w}^{l+1}+{\gamma }^{l+1}-r_3^{l+1}-e)$,

$z^{l+1}=z^l+\tau \sigma (w^{l+1}-z^{l+1})$.

It is obvious that every subproblem is convex and easy to compute. Therefore, we will compute the subproblems in the algorithm sGS-ADMM one by one.

Firstly, we compute the first block about w.

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill w^{l+\frac{1}{2}}& =argmin{L}_{\sigma }(w,{\xi }^l,{\eta }^l,{\gamma }^l,r_1^l,r_2^l,r_3^l,z^l;s_1^l,s_2^l,s_3^l,s_4^l)\hfill \\ & =\frac{1}{2}{w}^{T}Gw-\langle w,{\overline{w}}^k-A^{*}{D}^{*}{s}_1^l-B^{*}{s}_2^l+B^{*}{s}_3^l-s_4^l\rangle +\frac{\sigma }{2}{\parallel D\left(Aw\right)+{\xi }^l-r_1^l-e\parallel }^2\hfill \\ & +\frac{\sigma }{2}\parallel Bw+{\eta }^l-r_2^l{-e\parallel }^2+\frac{\sigma }{2}\parallel -Bw+{\gamma }^l-r_3^l{-e\parallel }^2+\frac{\sigma }{2}{\parallel w-z^l\parallel }^2.\hfill \end{array}\end{array}$$

(23)

The problem (23) is a convex and smooth optimization problem. Based on the optimality condition of the convex programming, we can obtain the following result

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill w^{l+\frac{1}{2}}& ={[G+\sigma (A^{*}{D}^{*}DA+2B^{*}B+I)]}^{-1}[{\overline{w}}^k-A^{*}{D}^{*}{s}_1^l-B^{*}{s}_2^l+B^{*}{s}_3^l-s_4^l\hfill \\ & -\sigma A^{*}{D}^{*}({\xi }^l-r_1^l-e)-\sigma B^{*}({\eta }^l-r_2^l-e)+\sigma B^{*}({\gamma }^l-r_3^l-e)+\sigma z^l].\hfill \end{array}\end{array}$$

(24)

Then, we compute the subproblem in Step 2 and use the last result $w^{l+\frac{1}{2}}$ to solve the second block, which contains the same structure of the variables $\xi ,\eta$, and $\gamma$

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\xi }^{l+1}& =argmin{L}_{\sigma }(w^{l+\frac{1}{2}},\xi ,{\eta }^l,{\gamma }^l,r_1^l,r_2^l,r_3^l,z^l;s_1^l,s_2^l,s_3^l,s_4^l)\hfill \\ & =C_1\langle e,\xi \rangle +{\delta }_{+}\left(\xi \right)+\langle D\left(A{w}^{l+\frac{1}{2}}\right)+\xi -r_1^l-e,s_1^l\rangle +\frac{\sigma }{2}{\parallel D\left(A{w}^{l+\frac{1}{2}}\right)+\xi -r_1^l-e\parallel }^2\hfill \\ & ={\delta }_{+}\left(\xi \right)+\frac{\sigma }{2}{\parallel \xi +DA{w}^{l+\frac{1}{2}}-r_1^l-e+\frac{C_{1}e+s_1^l}{\sigma }\parallel }^2\hfill \\ & ={\mathsf{\Pi }}_{+}(r_1^l+e-DA{w}^{l+\frac{1}{2}}-\frac{C_{1}e+s_1^l}{\sigma }).\hfill \end{array}\end{array}$$

(25)

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\eta }^{l+1}& =argmin{L}_{\sigma }(w^{l+\frac{1}{2}},{\xi }^{l+1},\eta ,{\gamma }^l,r_1^l,r_2^l,r_3^l,z^l;s_1^l,s_2^l,s_3^l,s_4^l)\hfill \\ & =-\langle {\overline{\eta }}^k,\eta \rangle +{\delta }_{+}\left(\eta \right)+\langle B{w}^{l+\frac{1}{2}}+\eta -r_2^l-e,s_2^l\rangle +\frac{\sigma }{2}{\parallel B{w}^{l+\frac{1}{2}}+\eta -r_2^l-e\parallel }^2\hfill \\ & ={\delta }_{+}\left(\eta \right)+\frac{\sigma }{2}{\parallel \eta +B{w}^{l+\frac{1}{2}}-r_2^l-e+\frac{s_2^l-{\overline{\eta }}^k}{\sigma }\parallel }^2\hfill \\ & ={\mathsf{\Pi }}_{+}(r_2^l+e-B{w}^{l+\frac{1}{2}}-\frac{s_2^l-{\overline{\eta }}^k}{\sigma }).\hfill \end{array}\end{array}$$

(26)

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\gamma }^{l+1}& =argmin{L}_{\sigma }(w^{l+\frac{1}{2}},{\xi }^{l+1},{\eta }^{l+1},\gamma ,r_1^l,r_2^l,r_3^l,z^l;s_1^l,s_2^l,s_3^l,s_4^l)\hfill \\ & =-\langle {\overline{\gamma }}^k,\gamma \rangle +{\delta }_{+}\left(\gamma \right)+\langle -B{w}^{l+\frac{1}{2}}+\gamma -r_3^l-e,s_3^l\rangle +\frac{\sigma }{2}{\parallel -B{w}^{l+\frac{1}{2}}+\gamma -r_3^l-e\parallel }^2\hfill \\ & ={\delta }_{+}\left(\gamma \right)+\frac{\sigma }{2}{\parallel \gamma -B{w}^{l+\frac{1}{2}}-r_3^l-e+\frac{s_3^l-{\overline{\gamma }}^k}{\sigma }\parallel }^2\hfill \\ & ={\mathsf{\Pi }}_{+}(B{w}^{l+\frac{1}{2}}+r_3^l+e-\frac{s_3^l-{\overline{\gamma }}^k}{\sigma }).\hfill \end{array}\end{array}$$

(27)

Next, we update w again.

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill w^{l+1}& =argmin{L}_{\sigma }(w,{\xi }^{l+1},{\eta }^{l+1},{\gamma }^{l+1},r_1^{l+1},r_2^{l+1},r_3^{l+1},z^{l+1};s_1^l,s_2^l,s_3^l,s_4^l)\hfill \\ & =\frac{1}{2}{w}^{T}Gw-\langle w,{\overline{w}}^k-A^{*}{D}^{*}{s}_1^l-B^{*}{s}_2^l+B^{*}{s}_3^l-s_4^l\rangle +\frac{\sigma }{2}{\parallel D\left(Aw\right)+{\xi }^{l+1}-r_1^{l+1}-e\parallel }^2\hfill \\ & +\frac{\sigma }{2}\parallel Bw+{\eta }^{l+1}-r_2^{l+1}{-e\parallel }^2+\frac{\sigma }{2}\parallel -Bw+{\gamma }^{l+1}-r_3^{l+1}{-e\parallel }^2+\frac{\sigma }{2}{\parallel w-z^{l+1}\parallel }^2,\hfill \end{array}\end{array}$$

(28)

Thus,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill w^{l+1}& ={[G+\sigma (A^{*}{D}^{*}DA+2B^{*}B+I)]}^{-1}[{\overline{w}}^k-A^{*}{D}^{*}{s}_1^l-B^{*}{s}_2^l+B^{*}{s}_3^l-s_4^l\hfill \\ & -\sigma A^{*}{D}^{*}({\xi }^{l+1}-r_1^{l+1}-e)-\sigma B^{*}({\eta }^{l+1}-r_2^{l+1}-e)\hfill \\ & +\sigma B^{*}({\gamma }^{l+1}-r_3^{l+1}-e)+\sigma z^{l+1}].\hfill \end{array}\end{array}$$

(29)

Finally, we compute the update of the relaxation variables $r_1,r_2,r_3,z$.

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill r_1^{l+1}& =argmin{L}_{\sigma }(w^{l+\frac{1}{2}},{\xi }^{l+1},{\eta }^{l+1},{\gamma }^{l+1},r_1,r_2^l,r_3^l,z^l;s_1^l,s_2^l,s_3^l,s_4^l)\hfill \\ & ={\delta }_{+}\left(r_1\right)+\langle DA{w}^{l+\frac{1}{2}}+{\xi }^{l+1}-r_1-e,s_1^l\rangle +\frac{\sigma }{2}{\parallel DA{w}^{l+\frac{1}{2}}+{\xi }^{l+1}-r_1^l-e\parallel }^2\hfill \\ & ={\delta }_{+}\left(r_1\right)+\frac{\sigma }{2}{\parallel DA{w}^{l+\frac{1}{2}}+{\xi }^{l+1}-r_1-e+\frac{s_1^l}{\sigma }\parallel }^2\hfill \\ & ={\mathsf{\Pi }}_{+}(DA{w}^{l+\frac{1}{2}}+{\xi }^{l+1}+\frac{s_1^l}{\sigma }-e).\hfill \end{array}\end{array}$$

(30)

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill r_2^{l+1}& =argmin{L}_{\sigma }(w^{l+\frac{1}{2}},{\xi }^{l+1},{\eta }^{l+1},{\gamma }^{l+1},r_1^{l+1},r_2,r_3^l,z^l;s_1^l,s_2^l,s_3^l,s_4^l)\hfill \\ & ={\delta }_{+}\left(r_2\right)+\langle B{w}^{l+\frac{1}{2}}+{\eta }^{l+1}-r_2-e,s_2^l\rangle ++\frac{\sigma }{2}{\parallel B{w}^{l+\frac{1}{2}}+{\eta }^{l+1}-r_2-e\parallel }^2\hfill \\ & ={\delta }_{+}\left(r_2\right)+\frac{\sigma }{2}{\parallel B{w}^{l+\frac{1}{2}}+{\eta }^{l+1}-r_2-e+\frac{s_2^l}{\sigma }\parallel }^2\hfill \\ & ={\mathsf{\Pi }}_{+}(B{w}^{l+\frac{1}{2}}+{\eta }^{l+1}+\frac{s_2^l}{\sigma }-e).\hfill \end{array}\end{array}$$

(31)

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill r_3^{l+1}& =argmin{L}_{\sigma }(w^{l+\frac{1}{2}},{\xi }^{l+1},{\eta }^{l+1},{\gamma }^{l+1},r_1^{l+1},r_2^{l+1},r_3,z^l;s_1^l,s_2^l,s_3^l,s_4^l)\hfill \\ & ={\delta }_{+}\left(r_3\right)+\langle -B{w}^{l+\frac{1}{2}}+{\gamma }^{l+1}-r_3-e,s_3^l\rangle +\frac{\sigma }{2}{\parallel -B{w}^{l+\frac{1}{2}}+{\gamma }^{l+1}-r_3-e\parallel }^2\hfill \\ & ={\delta }_{+}\left(r_3\right)+\frac{\sigma }{2}{\parallel -B{w}^{l+\frac{1}{2}}+{\gamma }^{l+1}-r_3-e+\frac{s_3^l}{\sigma }\parallel }^2\hfill \\ & ={\mathsf{\Pi }}_{+}(-B{w}^{l+\frac{1}{2}}+{\gamma }^{l+1}+\frac{s_3^l}{\sigma }-e).\hfill \end{array}\end{array}$$

(32)

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill z^{l+1}& =argmin{L}_{\sigma }(w^{l+\frac{1}{2}},{\xi }^{l+1},{\eta }^{l+1},{\gamma }^{l+1},r_1^{l+1},r_2^{l+1},r_3^{l+1},z;s_1^l,s_2^l,s_3^l,s_4^l)\hfill \\ & ={\lambda }_1{\parallel z\parallel }_1+\langle w^{l+\frac{1}{2}}-z,s_4^l\rangle +\frac{\sigma }{2}{\parallel w^{l+\frac{1}{2}}-z\parallel }^2\hfill \\ & ={\lambda }_1{\parallel z\parallel }_1+\frac{\sigma }{2}{\parallel w^{l+\frac{1}{2}}-z+\frac{s_4^l}{\sigma }\parallel }^2\hfill \\ & =Pro{x}_{{\lambda }_1{\parallel ·\parallel }_1}(w^{l+\frac{1}{2}}+\frac{s_4^l}{\sigma }).\hfill \end{array}\end{array}$$

(33)

Lemma 1.

Let

$$P=\left[\begin{array}{c}DA\\ B\\ -B\\ I\end{array}\right],Q=\left[\begin{array}{ccc}I& & \\ & I& \\ & & I\end{array}\right],R=\left[\begin{array}{cccc}-I& & & \\ & -I& & \\ & & -I& \\ & & & -I\end{array}\right].$$

Then, $P^{T}P$, $Q^{T}Q$ and $R^{T}R$ are positive definite.

Theorem 3

([42]). Suppose that $(w^l,{\xi }^l,{\eta }^l,{\gamma }^l)$ is generated by the sGS-ADMM. Then, it converges to a solution of (18).

The proof of Theorem 3 is similar to that in [42], and we omit it here. Before we give the convergence of the DCA algorithm, we first provide a useful lemma.

Lemma 2

([38]). Let r be a proper lower semi-continuous convex function and $\left\{x^k\right\}$ be a sequence such that

$\left(i\right)$$x^k\to x;$

$\left(ii\right)$ There exists a bounded sequence $\left\{y^k\right\}$ with $y^k\in \partial r\left(x^k\right);$

$\left(iii\right)$$\partial r\left(x^{*}\right)$ is nonempty.

Then, $\underset{k\to \infty }{lim}r\left(x^k\right)=r\left(x^{*}\right)$

On the basis of the above lemma, we can obtain the following convergence theorem.

Theorem 4

(Convergence of DCA). Suppose the sequence $\left\{(w^k,{\xi }^k,{\eta }^k,{\gamma }^k)\right\}$ is generated by DCA. Then,

$\left(i\right)$ The sequence $\left\{F(w^k,{\xi }^k,{\eta }^k,{\gamma }^k)\right\}$ is monotonously decreasing.

$\left(ii\right)$ Suppose be a accumulation point $(w^{*},{\xi }^{*},{\eta }^{*},{\gamma }^{*})$ of the sequence $\left\{(w^k,{\xi }^k,{\eta }^k,{\gamma }^k)\right\}$; then, the point $(w^{*},{\xi }^{*},{\eta }^{*},{\gamma }^{*})$ is a critical point of the F.

$\left(iii\right)$ If

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill w^{*}\notin \{\frac{1}{{\lambda }_1},-\frac{1}{{\lambda }_1}\},& \forall i=1,\dots ,\frac{m^2+3m+2}{2},\hfill \\ \hfill {\eta }^{*}\ne {\gamma }^{*},& \forall i=s+1,\dots ,n,\hfill \end{array}\end{array}$$

(34)

then $(w^{*},{\xi }^{*},{\eta }^{*},{\gamma }^{*})$ is a local minimizer of F.

Proof. 

Let $a^k=(w^k,{\xi }^k,{\eta }^k,{\gamma }^k),b^k=({\overline{w}}^k,{\overline{\xi }}^k,{\overline{\eta }}^k,{\overline{\gamma }}^k).$

$\left(i\right)$ Since $b^k\in \partial H\left(a^k\right)$, it follows that $H\left(a^{k+1}\right)\ge H\left(a^k\right)+\langle a^{k+1}-a^k,b^k\rangle$. We have

$$\begin{array}{c}\hfill \begin{array}{c}\hfill (G-H)\left(a^{k+1}\right)\le G\left(a^{k+1}\right)-\langle a^{k+1}-a^k,b^k\rangle -H\left(a^k\right)\end{array}\end{array}$$

(35)

Likewise, $a^{k+1}\in \partial G^{*}\left(b^k\right)$ implies $G\left(a^k\right)\ge G\left(a^{k+1}\right)+\langle a^k-a^{k+1},b^k\rangle .$

Therefore,

$$\begin{array}{c}\hfill \begin{array}{c}\hfill G\left(a^{k+1}\right)-\langle a^{k+1}-a^k,b^k\rangle -H\left(a^k\right)\le (G-H)\left(a^k\right).\end{array}\end{array}$$

(36)

Finally, combining (35) and (36), we get

$$\begin{array}{c}\hfill \begin{array}{c}\hfill (G-H)\left(a^{k+1}\right)\le (H^{*}-G^{*})\left(b^k\right)\le (G-H)\left(a^k\right).\end{array}\end{array}$$

(37)

$\left(ii\right)$ We know that H is a polyhedral convex function. Then,

$$\begin{array}{c}\hfill \begin{array}{c}\hfill -\langle C_{2}e,min\{\eta ,\gamma \}\rangle =max\{-C_2\langle (u,e-u),(\eta ,\gamma )\rangle :u\in {\{0,1\}}^{n-s}\},\end{array}\end{array}$$

(38)

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \sum _{i=1}^{\frac{m^2+3m+2}{2}}max\{1,\lambda |w_i\left|\right\}={max\{\langle \mu ,\lambda w\rangle +\langle e-|\mu |,e\rangle :\mu \in \{-1,0,1\}}^{\frac{m^2+3m+2}{2}}\}.\end{array}\end{array}$$

(39)

Combine (38) and (39), and we have

$$\begin{array}{c}\hfill \begin{array}{c}\hfill H=max\{-\langle (-\frac{\mu }{\lambda },0,C_{2}u,C_2(e-u)),(w,\xi ,\eta ,\gamma )\rangle +\frac{1}{\lambda }\langle \left|\mu \right|-e,e\rangle :\\ \hfill u\in {\{0,1\}}^{n-s},\mu \in {\{-1,0,1\}}^{\frac{m^2+3m+2}{2}}\}.\end{array}\end{array}$$

(40)

For simplicity, we redefine

$$\begin{array}{c}\hfill \begin{array}{c}\hfill H=max\{\langle {\alpha }^i,a\rangle -b^i:i\in I\},\end{array}\end{array}$$

(41)

where $a=(w,\xi ,\eta ,\gamma ),I=\{1,\dots ,2^{n-s}\times 3^{\frac{m^2+3m+2}{2}}\}$.

It is clear that $\partial H$ is finite. In this case, the sequence $b^k$ is discrete (i.e., it has only finitely many different elements, at most $2^{n-l}\times 3^{\frac{m^2+3m+2}{2}}$).

Let

$$\begin{array}{ccccccccccccccccccccccccccccccccccccc}& & & & & & & & & & & & & & & & minG\left(a\right)-[\langle {\alpha }^i,a\rangle -a^i]& & & & & & & & & & & & & & & & & & & & \left(P_i\right).\end{array}$$

Solving the subproblem in Step 2 at every iteration is equivalent to solving $\left(P_i\right)$. Thus, the algorithm will be terminated after at most $2^{n-l}\times 3^{\frac{m^2+3m+2}{2}}$ steps.

Suppose $a^{*}$ is an accumulation point of the sequence $\left\{a^k\right\}$. For the sake of simplicity, we denote

$$\underset{k\to \infty }{lim}{a}^k=a^{*}.$$

According to the proof of Theorem 3, we know that every $\left\{a^k\right\}$ generated by the sGS-ADMM is bounded, so we can obtain that $\left\{a^k\right\}$ is bounded. Thus, with the generation of $\left\{b^k\right\}$, $\left\{b^k\right\}$ is bounded.

We can suppose (extracting subsequences if necessary) that the sequence $\left\{b^k\right\}$ converges to a point $b^{*}\in \partial H\left(a^{*}\right)$, and according to $\left(i\right)$, it follows that

$$\underset{k\to \infty }{lim}\{G\left(a^k\right)+G^{*}\left(b^k\right)-\langle a^k,b^k\rangle \}=0$$

Thus,

$$\underset{k\to \infty }{lim}\{G\left(a^k\right)+G^{*}\left(b^k\right)\}=\underset{k\to \infty }{lim}\langle a^k,b^k\rangle =\langle a^{*},b^{*}\rangle .$$

Set $\theta (a,b)=G\left(a\right)+G^{*}\left(b\right)$. It is clear that $\theta$ is a proper lower semi-continuous convex function. By Lemma 2, we have

$$\theta (a^{*},b^{*})\le \underset{k\to \infty }{lim\; inf}\theta (a^k,b^k)=\underset{k\to \infty }{lim}\theta (a^k,b^k)=\langle a^{*},b^{*}\rangle ,$$

that is, $\theta (a^{*},b^{*})=G\left(a^{*}\right)+G^{*}\left(b^{*}\right)=\langle a^{*},b^{*}\rangle .$ In other words, $b^{*}\in \partial G\left(a^{*}\right).$

Thus, $a^{*}$ is a critical point of the F.

$\left(iii\right)$ The formula (13), the second component of F, is a polyhedral convex function. According to the condition (41), H is differentiable at $a^{*}$. We define $J\left(a^{*}\right)=\{i\in I:F\left(a^{*}\right)=G\left(a^{*}\right)-[\langle {\alpha }^i,a^{*}\rangle -b^i]\}$. There also exists at least one $j\in J(a^{*}$ such that F is convex. Then, there is a neighborhood $\mathcal{U}(a^{*},0)$ such that $0\in \partial F\left(a^{*}\right)$. Therefore, $a^{*}$ is a local minimizer of F. □

4. Numerical Experiments

In this section, we evaluate the proposed method. All codes are written in MATLAB, and all computations are performed on a Lenovo IdeaPad with Windows 10 Inter(R) Core(TM)i5-6200U CPU @2.30 GHz 2.40 GHz and 4 GB memory.

In particular, we apply this method to a simple example. In this dataset, there are 100 data points in each class, 10 of which are labeled. Circles represent positive classes, triangles represent negative classes, solid ones represent data with labels, and hollow ones represent data without labels. The distributions of the datasets are shown in Figure 1. From Figure 2, we can conclude the good performance of our algorithm.

We draw the separating surfaces derived by solving $SSQLS{S}^{3}VM$ for the simulated datasets in Figure 2. From Figure 2, we can conclude that our method performs well, and only three negative classes appear on the curved surface.

In this subsection, we perform several numerical experiments on real datasets. We use 10 public datasets (Iris, Skin, Seeds, Pima, Glass, Heart, Hepatitis, Iono, Sonar and BCI) obtained from the UCI Machine Learning Repository and Benchmark datasets. In the details column of the datasets from

Table 1. Details of datasets.

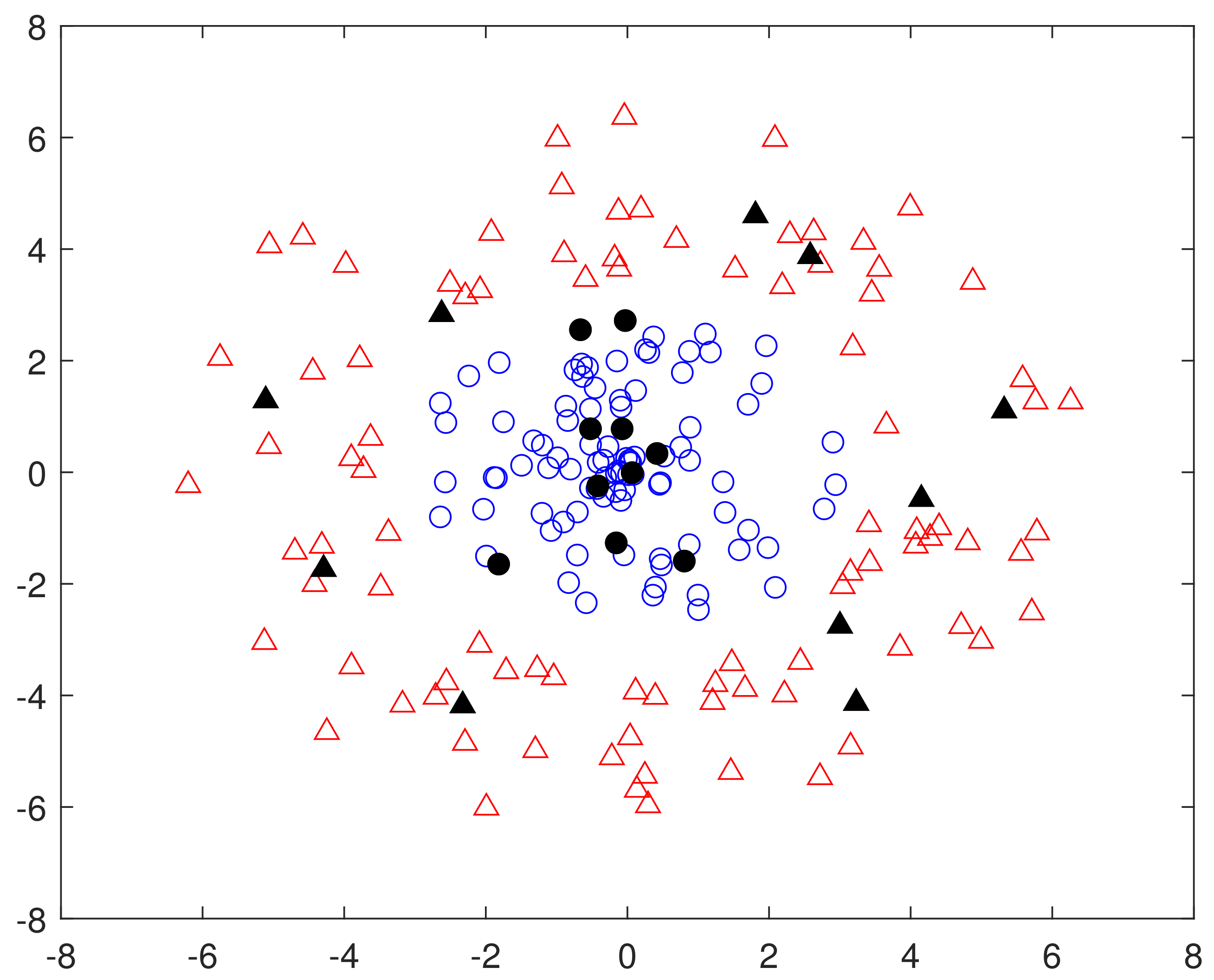
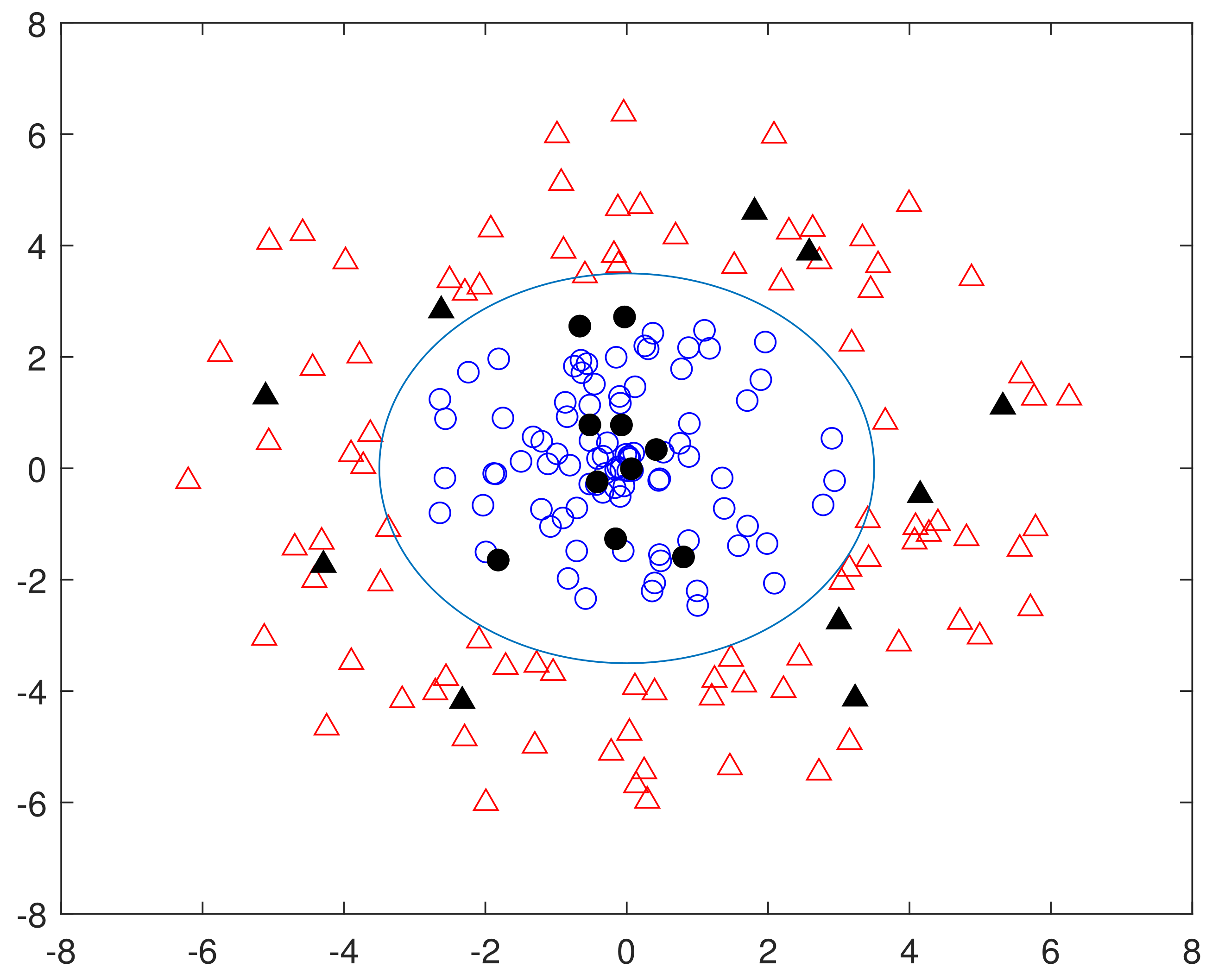
Data Sets	Feature	Total Numbers	Labeled Number
Iris	4	100	10
Skin	4	245,057	24,505
Seeds	7	140	14
Pima	8	768	40
Glass	10	146	15
Heart	12	270	27
Hepatitis	19	80	8
Iono	34	351	20
Sonar	60	208	20
BCI	117	400	40

, the Iris and Seeds datasets contain multiple classes, and we select only two classes for numerical experiments. For each dataset, we perform 100 trials, each time randomly selecting the labeled data points, while the rest are considered as unlabeled.

To illustrate the effectiveness of our proposed model $SSQLS{S}^{3}VM$, as well as the method, several alternative state-of-the-art methods are selected for comparison, such as SSQSSVM, CTSVM, Cut$S^3$VM, SVMlin, and LapSVM. First, the misclassification rate of several methods are shown in

Table 2. Misclassification rates (%) for datasets.

Data Sets	P-ADMM	SSQSSVM	CTSVM	CutS${}^3$VM	SVMlin	DCA
2circles	2.50	4.50	5.00	20.00	36.50	2.30
Hyperbola	1.50	10.00	11.67	13.43	45.50	1.20
Iris	0.00	4.53	5.00	8.50	0.00	0.00
Skin	8.60	-	-	-	-	5.30
Seeds	5.00	7.86	6.43	8.33	7.14	5.20
Pima	29.81	-	31.64	31.24	60.87	27.70
Glass	0.00	2.05	2.05	10.81	3.64	0.60
Heart	28.52	30.00	31.11	37.73	33.33	24.40
Hepatitis	23.75	33.75	31.25	43.21	50.00	21.40
Iono	11.40	-	9.97	21.65	31.13	11.20
Sonar	23.56	-	25.96	36.54	46.7	23.78
BCI	42.00	-	35.25	53.10	64.17	41.60

Remark: - indicates that the computer is out of memory.

. The best results are shown in bold in the table. We observe that the misclassification rates of the $SSQLS{S}^3$VM achieves the best accuracy rates, that is, the smallest misclassification rates on most of the data sets. In addition, due to the large size of the Skin dataset, SSQSSVM, CTSVM, Cut$S^3$VM, and SVMlin can lead to computational memory overflow, which is a common phenomenon for solving the relaxations of the $S^3$VM model; we present those results as -. We can also obtain low misclassification rates, which indicates that our proposed method can solve large-scale datasets and also shows the efficiency of our proposed method. The misclassification rates on the Seeds, Glass, and Sonar datasets are only a little higher than the P-ADMM method. Better results are achieved on the remaining other datasets, such the Heart dataset. We achieve 24.40% vs. 28.52%, 30.00%, 31.11%, 37.73%, and 33.33%, respectively, which are improved by 4.12%, 5.60%, 6.71%, 13.33%, and 8.93%, which shows that our proposed method is effective.

The average CPU time of the 100 experiments is reported in

Table 3. CPU time(s) for data sets.

Datasets	P-ADMM	SSQSSVM	CTSVM	CutS${}^3$VM	SVMlin	DCA
2circles	2.41	137.46	5.27	7.05	0.15	3.47
Hyperbola	2.36	137.60	5.16	6.45	0.15	4.34
Iris	1.38	19.40	2.97	2.28	0.10	3.24
Skin	2907.80	-	-	-	-	3457.42
Seeds	2.31	92.59	4.13	3.00	0.12	3.45
Pima	11.89	-	51.55	26.90	2.08	15.67
Glass	3.02	209.49	2.29	0.97	0.11	5.34
Heart	5.19	1902.90	8.22	2.57	0.29	8.96
Hepatitis	3.59	548.57	1.01	1.14	0.11	6.73
Iono	36.33	-	11.12	6.35	0.50	50.24
Sonar	12.30	-	5.48	1.15	0.54	16.58
BCI	405.89	-	12.91	9.50	4.25	526.73

Remark: - presents that the computer is out of memory.

. The best results are shown in bold in the table. We can observe that SVMlin and P-ADMM are much faster than our method. Since our method is a nesting of two algorithms, the inner layer is sGS-ADMM, and the outer layer is DCA, it takes a longer time than the methods such as P-ADMM and SVMlin.

Overall, although our method is not the fastest, it has the best misclassification rate on most of the datasets, which shows the effectiveness of our model and algorithm.

5. Conclusions and Discussion

In this paper, we deal with a strong sparse quadratic kernel-free least squares semi-supervised support vector machine model by adding an ${\ell }_0$ norm regularization term to the objective function. We use the DC program (difference of convex function) and DCA (DC algorithm) to solve it. Firstly, we approximate the ${\ell }_0$ norm by a polyhedral DC function. Secondly, when solving the subproblem, we used sGS-ADMM due to the existence of the nonsmooth term. Empirical numerical experiments show the efficiency of the proposed algorithm.

Since the ${\ell }_0$ norm is highly nonconvex and computationally NP-hard, we use the convex difference method to overcome this problem. The next step is to directly use the ${\ell }_0$ norm regularity or the ${\ell }_0$ norm constraint to solve the $SSQLS{S}^{3}VM$. In addition, the optimality condition of the model is not established here. These will be addressed in our future work.