Abstract
The paper deals with modelling and analytical solving of a strong nonlinear oscillator with position-dependent mass. The oscillator contains a nonlinear restoring force, a quadratic damping force and a constant force which excites vibration. The model of the oscillator is a non-homogenous nonlinear second order differential equation with a position-dependent parameter. In the paper, the closed-form exact solution for periodic motion of the oscillator is derived. The solution has the form of the cosine Ateb function with amplitude and frequency which depend on the coefficient of mass variation, damping parameter, coefficient of nonlinear stiffness and excitation value. The proposed solution is tested successfully via its application for oscillators with quadratic nonlinearity. Based on the exact closed-form solution, the approximate procedure for solving an oscillator with slow-time variable stiffness and additional weak nonlinearity is developed. The proposed method is named the ‘approximate time variable Ateb function solving method’ and is applicable to many nonlinear problems in physical and applied sciences where parameters are time variable. The method represents the extended and adopted version of the time variable amplitude and phase method, which is rearranged for Ateb functions. The newly developed method is utilized for vibration analysis of grafted skin on the human body. It is found that the grafted skin vibration properties, i.e., amplitude, frequency and phase, vary in time and depend on the dimension, density and nonlinear viscoelastic properties of the skin and also on the force which acts on it. The results obtained analytically are compared with numerically and experimentally obtained ones and show good agreement.
Keywords:
position-dependent mass; strong nonlinear oscillator; time variable stiffness; analytic solving procedure; Ateb function; vibration of grafted skin MSC:
34C15
1. Introduction
The problem of mass variable bodies has been known for a long time [1]. Even in 1884 it was known that mass variation of the body may be a time or position function [2]. In the last hundred years oscillators with time variable mass have been widely studied especially regarding rocket dynamics [3]. On the other hand, oscillators with position-dependent mass remain not sufficiently investigated. Two types of research directions for the oscillators with position-dependent mass have developed: the ‘quantum-mechanical type’ and the so called ‘classical-mechanical type’.
If oscillators represent models of problems in quantum mechanics [4,5,6,7], molecular physics [8] and solid-state physics [9], which include semiconductors [10,11,12], quantum dots and nanocrystals [13], microstructures [14], micro-electro-mechanical systems [15], etc., quantum-mechanical type procedures are applied. Oscillators which have been widely used to weak signal detection and mechanical fault diagnosis [16,17] are considered in the same way.
Classical-mechanical type procedures are mainly utilized for mass-spring oscillators, which are vital parts of devices applied in seismic vibration reduction and vibration elimination in high buildings using the damping property tuned via displacement—dependent mass [18,19,20,21]. In research, various types of mass variation functions are considered: from infinitely increasing [22,23,24,25], bounded mass variation functions [26], to decreasing mass function which tends to zero [27,28]. It is obvious that due to position-dependent mass, the mathematical model of the system is a weakly perturbed differential equation [29,30]. To solve dynamic equations of motion, the gradient method, the single-component method and the field method are applied [31].
However, Ortiz [32] stated that in the Newtonian dynamic approach to oscillators, the position-dependent mass function causes a force which is quadratic in the velocity. Due to this fact, the model of the oscillator is a strong nonlinear differential equation with a position-dependent parameter. To solve the equation, new mathematical procedures need to be developed. Nowadays, a significant number of efficient analytic and numeric procedures for solving strong nonlinear equations with constant parameters are being developed. Thus, in the papers [33,34,35,36,37], using the advanced intelligent computational approach and the feed-forward artificial neural networks model, numerical solutions of singular nonlinear differential equations are presented which seems to represent an improvement to the classical RK45 method. To find the approximate solutions of strong nonlinear oscillators, different methods [38,39,40,41,42], such as the variational iteration method, energy balance method, parameterized perturbation method, homothopy method, etc., have been utilized. The aforementioned analytic methods are not suitable to be applied for strong nonlinear differential equations with variable parameters. The extension and modification of the methods is required.
The aim of this paper is to analyze the vibration of a strong nonlinear oscillator (of any integer or non-integer order) with position-dependent mass and slow-time variable stiffness. The considered excitation force is constant. The model of the oscillator is a non-homogenous second order strong nonlinear differential equation with quadratic damping. In the paper, a new analytical procedure for solving the equation is developed. The method is based on the already known principle for homogenous strong nonlinear equations [43]. Vibrations are studied for certain mass variation. The influence of parameters and order of mass variation are discussed. The method is applied for solving the problem of a medical problem, i.e., vibration in skin grafts where mass variation and stiffness of the grafted skin vary in slow time.
The paper is divided into 6 sections. After the Introduction, in Section 2, a one-degree-of-freedom oscillator with position variable mass and time variable stiffness is modeled. The mathematical form of the oscillator is a strong nonlinear non-homogenous second order differential equation with time and position variable parameters. In Section 3, the exact closed-form analytic solution for the forced and nonlinear oscillator with mass which is the linear function of position is introduced. The periodic solution of the equation is obtained in the form of the Ateb function and considered for the first time. Using the aforementioned solution, in Section 4, the approximate procedure for solving the equation with the additional slow time variable parameter is developed. The method represents the extended and adopted version of the Krylov–Bogolubov time-variable amplitude and phase method for the Ateb function. In Section 5, the oscillatory motion of the grafted skin is modeled. The aforementioned procedure is applied for analysis of the vibration properties of the system. The calculated values are compared with experimentally obtained ones and show good agreement. The paper ends with Conclusions.
2. Model of the Oscillator
The considered oscillator is a one-degree-of-freedom mass-spring-damper system. The displacement function is x. The mass is assumed as a position-dependent function m(x). The elastic force in the oscillator is strong nonlinear with the order of nonlinearity α. The stiffness coefficient is assumed to be the function of the slow time τ. In the system, damping occurs. The damping force depends on the velocity and constant coefficient b. The system is excited with a constant force F. Then, in general, the kinetic energy T, potential energy V, dissipative function ϕ and the generalized force are, respectively,
where is the slow time, ε << 1 is the small parameter, α is the order of nonlinearity (integer or non-integer) and is a nonlinear function. Based on the Lagrange formulation
the differential equation of motion is
Relation (3) is a non-homogenous second order strong nonlinear differential equation with time variable stiffness and position variable mass. Comparing (3) with the mathematical model of the oscillator with constant mass, it is evident that a term with quadratic velocity appears, which is the result of the position-dependent mass (it is already mentioned in [32]).
The aim of the paper is to solve Equation (3).
3. Closed-Form Exact Analytic Solution
For the case when mass variation is a linear position function, Equation (3) modifies into
where a is a positive constant. Analyzing Equation (4), it is concluded that it represents the perturbed version of the equation
where k = k(0) = const. Namely, Equation (5) is the special case of (4) for ε = 0 and τ = 0. Thus, it is obvious that (5) is the generating equation of the trial Equation (4).
Equation (5) describes the oscillatory motion and the solution is assumed in the form of a periodical Ateb function [43]
where A, θ and are unknown constants and ca is the cosine Ateb function with period
and complete beta function B [44]. Using (6) and the time derivatives of the Ateb function
Equation (5) transforms into
where is the sine Ateb function. Applying the relation between Ateb functions (see [44])
and separating the terms with the same order of ca in (9), two nonlinear algebraic equations are obtained
Solving relations (11) and (12) it is
where
Finally, the closed-form solution of (5) is according to (6)
Using (14) and the period of Ateb function the period of vibration follows as
Then, the frequency of vibration Ω is
It is obvious that the period T and the frequency Ω of vibration depend on the amplitude of vibration, as is already known for nonlinear oscillatory systems.
Special Case
For the special case when α = 1, Equation (5) transforms into
and solution (6) into
Namely, for α = 1 the ca Ateb function modifies into a trigonometric cosine function [43].
Analyzing (19) it is seen that in spite of the fact that Equation (18) is strong nonlinear, the frequency and period of vibration are independent on the amplitude, i.e.,
To prove the correctness of the analytical solutions (15) and (20), they are compared with the numeric solution of (5) and (18), respectively. The numeric solutions are obtained by applying of the Runge–Kutta procedure. In Figure 1, the analytic and numeric solutions for a = 5 kg/m, b = 0.5 kg/m, F = 4 N, initial conditions , and α = 3, k = 0.5 N/mm4 (Figure 1a) and α = 1, k = 0.5 N/mm2 (Figure 1b) are plotted. It is found that the analytic solutions are on the top of the numerical ones.
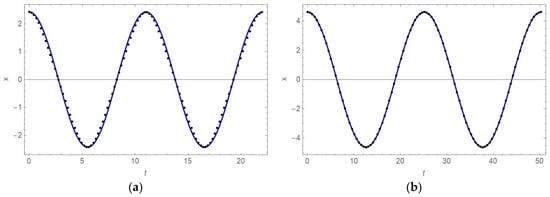
Figure 1.
x-t diagrams obtained analytically (dotted line) and numerically (full line) for: (a) for α = 3 and (b) for α = 1.
Using (7), (13), (14) and (16), the amplitude of vibration, frequency and period of Ateb function and the period and frequency of vibration are for α = 3: A = 2.4265 mm, ω = 0.95175 s−1, 2Π = 10.4882, T = 11.020 s and Ω = 0.57017 s−1. According to (20), amplitude, frequency and period of vibration for α = 1 are ω = 0.25 s−1, . Comparing Figure 1a,b, the influence of the order of nonlinearity α is evident. For a higher order of nonlinearity, the amplitude of vibration and the period of vibration are smaller, while the frequency of vibration is higher than for low values of α.
Remark 1.
In the following text the calculated amplitude and frequency of vibration in generating solution (6) are utilized as initial vibration values A0 and ω0.
4. Approximate Solution Procedure
In the previous section the closed-form solution of Equation (5) is derived. However, it is known that there is no exact analytical result for the original Equation (4). In this section, based on the closed-form solution (15) of the generating Equation (5) the approximate solving procedure for an oscillator with a slow time variable parameter and additional weak nonlinear terms (4) is developed. The procedure is named ‘approximate time variable Ateb function solving method’.
Comparing Equations (4) and (5), it is obtained that, for ε is a small parameter, Equation (4) represents the perturbed version of the generating Equation (5). Using this fact, it is assumed that the solution of (4) has to be the perturbed version of the solution (15) of Equation (5). Then, the solution of (4) has the form of solution (15) with time variable parameters.
Let us assume the trial solution of (4) and its time derivative in the form of the generating solution (15) and its first time derivative, with time variable amplitude, frequency and phase.
Comparing the time derivative of (21) with the assumed (22), the constraint follows as
where
and
For (22) the time derivative is
Introducing (21), (22) and (26) into (4), the transformed expression is
where , , . The relations (23) and (27) represent the transformed version of Equation (4) in new variables A(t) and Using (14), the time derivative of the amplitude and frequency product is
where . Substituting (28) into (27) and after some modification of (23) and (27) it is
Unfortunately, finding the exact closed-form solution of (29) and (30) is impossible. This is at the point where the averaging over the period T of the Ateb functions in Equations (29) and (30) is introduced
where . The obtained Equations (31) and (32) are the averaged ones, and the task is to solve them.
Special Case
For the case when f = 0, Equations (31) and (32) simplify into
where , . Integrating (33) and (34) for initial conditions A(0) = A0, ω(0) = ω0, θ(0)= θ0 and using expression (25), the amplitude and phase angle are
Correlation between the vibration amplitude and stiffness property is indirect: the increase of the stiffness causes decrease of the amplitude of vibration. Using the expressions (25), (35) and (36), Equation (24) is rewritten into
Analyzing relation (37) it is obvious that stiffness variation causes frequency variation, which depends on the mass parameter a, damping coefficient b and order of nonlinearity α.
5. Example: Mathematical Description of Treatment in Grafted Skin
Skin grafting is the standard surgical procedure for the case of loss of skin (traumatic or due to malignity) [45]. In spite of the fact that the procedure has been known for a long time, little is known about the recovery of skin grafts in time, especially with regards sensation over free non-neurotized muscle flaps [46]. Namely, the human skin is a dynamic self-renewing barrier that is subjected to large-scale extrinsic mechanical forces [47]. The process of self-renewing is a time function. The grafted skin needs a long healing time, and in the meantime, there is the possibility of wound infection, hypertrophic scarring and hyperpigmentation. To overcome these problems and to shorten the skin renewing time, investigation and introduction of new treatments are necessary. In the papers [48,49,50] it is shown that vibration stimulation may be of use for healing of wounds and to speed up the process. Thus, for example, whole body low-intensity vibration is anabolic for bone by stimulating the release of growth factors and modulating stem cell proliferation and differentiation [51]. In addition, it is reported that vibration is a pain reducer and is a welcome tool in the plastic surgery clinic [48,52]. Using the idea of vibration application, we investigated how vibration treatments may affect better and more rapid skin renewing.
5.1. Modeling of the Grafted Skin on the Human Body
In Figure 2, the grafted skin on the leg and its physical model are shown. The grafted skin is settled in a certain position on the body and has to be joined with the already existing skin of the human. This process needs time, which depends on variations of the skin properties and on forces which act on the grafted skin. The force which acts along the leg during human motion causes the effect of grafted skin deformation, i.e., its compression and elongation. Motion of the grafted skin becomes oscillatory.
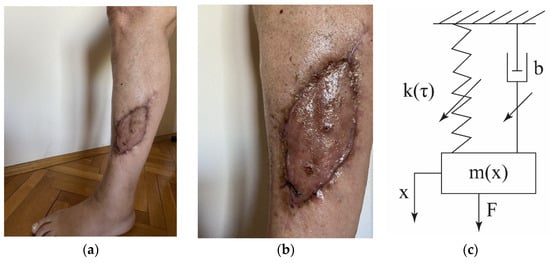
Figure 2.
(a) Position of the graft skin, (b) shape of the grafted skin, (c) physical model.
In this paper we modeled the motion of the grafted skin as an oscillator with periodic motion which is excited with the constant force. The physical model is the mass-spring-dashpot system shown in Figure 2c. The system has one degree-of-freedom and the generalized coordinate is in x direction. As it is known that the mass, stiffness and damping property of the grafted skin vary, we assumed that the corresponding parameters in the model have to be changed. As the skin is not homogenous and the shape of the grafted skin does not have a strict geometrical form, for calculation reasons mass variation is assumed to be the linear function of position x, i.e.,
where a = const. includes the depth, wideness and density properties.
m(x) = ax
Results of investigation in [53,54,55] show that human skin deformation is the result of a nonlinear displacement function, i.e., the skin mechanics is strong nonlinear. Based on the results obtained in [56] the fitting function for the elastic force Fe is strong nonlinear with the order of nonlinearity α which depends on the skin surface—mass ratio, i.e.,
where is the stiffness coefficient.
5.2. Stiffness Coefficient as a Slow Time Variable Function
A key step in characterization of the skin behavior is based on the mechanical properties of skin [57]. Coefficients of stiffness, extensibility and strength are experimentally measured. It is obtained that the results strongly depend on the measuring direction and also on the position, shape and dimension of the considered skin [58]. The stiffness coefficient measured on human skin varies from a small value (8 kPa) in the soft layer of the skin to a high value (100 kPa) in the surface skin layer [52]. Due to a change in the structure and depth of the skin, the stiffness coefficient varies during the long time period of skin healing from an initial to a boundary value. The stiffness variation is slow, and it is appropriate to be modeled as the slow time τ function
where and p are constant values, τ = εt is slow time and ε << 1 is a small parameter. According to (40), it is found that the stiffness function increases in time. Namely, the stiffness coefficient increases from its initial value up to k() = k0. The difference between the initial and final stiffness coefficient value corresponds to the value of the small parameter p.
In Figure 3, for κ = the κ-p-τ diagram is plotted. Varying the dimensionless parameter p from 0 to 0.06 and the slow time from 0 to 1, the stiffness relation κ increases with τ. The stiffness variation is more significant for the higher value of parameter p. The value of epsilon in (40) is valid in the interval from zero to 0.1.
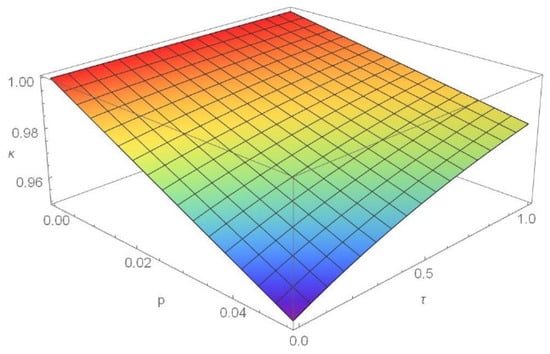
Figure 3.
Stiffness coefficient κ as function of slow time τ and parameter p.
5.3. Initial Amplitude and Frequency of Vibration for Various Skin Grafts
Using the mass function (38), elastic nonlinear force (39) and the modeling procedure given in Section 2, the motion of the oscillator in Figure 2c is described with the differential equation
with initial amplitude (13) and initial frequency (14)
which depend on the added mass parameter a, damping coefficient b, order and coefficient of nonlinearity, α and k, respectively, and on the excitation force F. In the following text the influence of these parameters on the vibration is analyzed.
In Figure 4 the influence of the excitation force F and the added mass a on the amplitude (a) and frequency (b) of vibration are plotted. For k = 1.5 N/mm4, α = 3 and a/b = 0–20, the A0-F-a and ω0-F-a are shown in Figure 4a,b, respectively, where the amplitude A0 varies in the interval (0–1.5) mm, F = (0–2) N and = (0–3) s−1. It is obtained that the amplitude of vibration has the tendency of increasing with an increase of the intensity of force F and also with an increase of mass parameter a. For the constant excitation force, the amplitude of vibration is higher if the added mass is higher. For certain added mass, the amplitude of vibration is increased by increasing the force F (Figure 4a). The quantity of the added mass has significant influence on the frequency of vibration, too. For a constant value of F, the frequency of vibration is higher if the added mass parameter a is smaller, i.e., the frequency is low for a high value of added mass. The frequency of vibration has the tendency to increase with an increase of the excitation force F and decrease with an increase of the added mass. For certain forces, the frequency of vibration is higher for a smaller amount of added mass (Figure 4b).
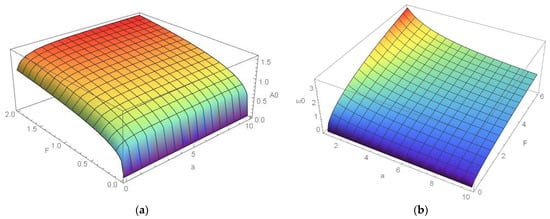
Figure 4.
(a) A0-F-a and (b) ω0-F-a diagrams for constant α, k, b.
In Figure 5, the influence of mass variation parameter and rigidity coefficient on the amplitude (a) and frequency (b) of vibration is considered. Namely, the A0-k-a (Figure 5a) and ω0-k-a (Figure 5b) diagrams are plotted for constant α = 3, F = 1N and a/b = 0–20. The amplitude varies in the interval A0 = (0–3) mm, the frequency = (0–4) s−1 and k = (0–2) N/mm4. It is shown that the amplitude of vibration decreases with k: if the added mass is larger, the amplitude of vibration is higher and decreases slower than for small added mass. However, it is seen that the amplitude of vibration is almost constant in the interval a = (1–10) kg/mm for k = (1–2) N/mm4. In addition, the frequency of vibration is almost constant for a = (5–10) kg/mm and k = (0.5–2) N/mm4. For small added mass the influence of k on the frequency is more significant than for a large mass quantity.
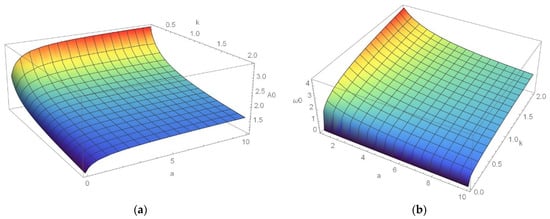
Figure 5.
(a) A0-k-a and (b) ω0-k-a diagrams for constant α, F, b.
In Figure 6, amplitude (a) and frequency (b) plots for various values of damping coefficient and order of nonlinearity are plotted. Namely, in the amplitude interval A0 = (0–3) mm, frequency = 0–4 mm and nonlinearity order α = 1–5, the A0-α-b and ω0-α-b diagrams for k = 1.5 N/mm4, F = 1.5 N and a/b = 10 are shown in Figure 6a,b, respectively. The amplitude of vibration decreases with increasing of the order of nonlinearity and damping coefficient (Figure 6a). Independently, on parameter b, the amplitude of vibration is higher for a smaller value of α than for a higher one. For extremely high α the influence of b is negligible (Figure 6a). In contrast, the frequency of vibration is higher for higher values of α than for α = 1 (Figure 6b). For a higher order of nonlinearity, the influence of the damping coefficient on vibration properties is negligible. Analyzing the diagram in Figure 6a and Equation (43) with the damping coefficient b equal to zero (the skin is assumed as an elastic material), it is found that . The amplitude of vibration depends only on the force F, initial stiffness and the characteristics of the system but is independent of the mass which is added.
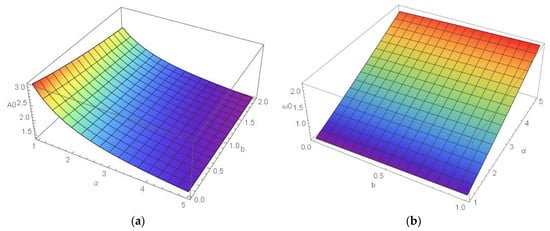
Figure 6.
(a) A0-α-b and (b) ω0-α -b diagrams for constant a, k, F.
5.4. Amplitude and Frequency Variation for Time Variable Stiffness Parameter
If the stiffness is varying with slow time (40), the averaged amplitude (35) and frequency (37) ratios follow as
where κ = . In Figure 7a, amplitude as a function of stiffness coefficient κ and nonlinearity order α is presented. In Figure 7b the frequency ratio due to stiffness and order of nonlinearity is plotted. It is found that the amplitude ratio is almost constant for the case for κ =1. For a high order of nonlinearity α, the effect of stiffness ratio on the amplitude variation is not significant. In contrast, for α = 1 the stiffness ratio causes amplitude variation: the amplitude ratio decreases with κ (Figure 7a). The frequency ratio increases with κ for all values of order of nonlinearity. The frequency ratio has higher values for higher stiffness. It seems that for stiffness change from the initial to final value the frequency of vibration moves from a low to high value (see Figure 7b).
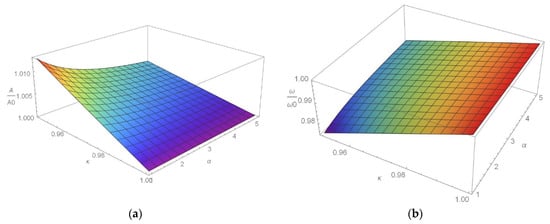
Figure 7.
(a) A/A0-α-κ and (b) ω/ω0-α-κ diagrams.
Remark 2.
For the special case when α = 1, the amplitude—time and frequency—time functions (42) and (43), respectively, simplify into
In general, the averaged analytic solution of (41) for α = 1 is
Let us solve Equation (41) numerically for a = 5 kg/mm, k = 5.5 N/mm2, b = 0.5 kg/mm, p = 0.01, ε = 0.01, α = 1 and initial conditions . In Figure 8, the solutions obtained for constant stiffness (Figure 8a) and for the time variable stiffness parameter (40) (Figure 8b) are compared.
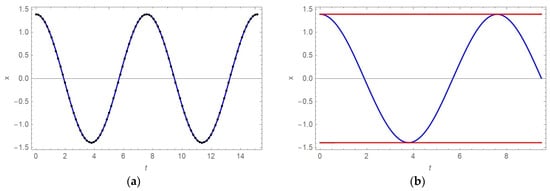
Figure 8.
(a) x-t diagrams obtained numerically (full line) and analytically (dotted line) for k = 5.5 = const. and (b) x-t diagram obtained numerically (blue line) and A-t diagram obtained analytically (red line) for k(τ) according to (40).
In Figure 8b, the analytically obtained averaged amplitude function (44) is also shown. It is concluded that the analytically obtained amplitude is the envelope of the x-t function which is obtained numerically. In addition, Figure 8 shows that due to an increase of the stiffness coefficient, the amplitude and the period of vibration decrease over time. Thus, using (40) and (44), these values are calculated: the amplitude varies from A0 = 1.3926 mm to 1.3891 mm, the stiffness coefficient increases from 5.5 N/mm2 to 5.556 N/mm2, and the period of vibration decreases from 7.5778 s to 7.5398 s.
6. Conclusions
The following is concluded:
- (1)
- The classical study of an oscillator with position-dependent mass is based on investigation of the strong nonlinear oscillator. Namely, position-dependent mass transforms the mathematical model of the oscillator into a nonlinear one by introducing the new nonlinear term which is the product of the acceleration and mass function. In addition, position-dependent mass variation gives a quadratic damping term in the differential equation of oscillation (as was previously mentioned in [32]).
- (2)
- In the paper, the new closed-form analytic solution for the strong nonlinear differential equation of an oscillator with linear position-dependent mass function is introduced. The solution has the form of a cosine Ateb function. The correctness of the solution was proved by comparing it with the numerical one.
- (3)
- An approximate analytic procedure for solving a strong nonlinear equation with variable mass, which is linear position dependent, and a slow time-variable stiffness coefficient is developed. The procedure is based on perturbation of the exact solution of the model with constant coefficients. The trial solution of the equation is the small perturbed version of the generating solution of the nonlinear equation with constant parameters. An analytically obtained solution of the position-dependent mass strong nonlinear oscillator with a slow-time variable stiffness coefficient is compared with a numerically obtained solution. It is found that there is high agreement in the results and the difference is negligible.
- (4)
- The vibration method is suggested for application in the treatment of skin grafts. For the trial force and known added mass, the amplitude of vibration should be measured. From the parameter relations given in the paper the corresponding values which describe the specific properties of the skin may be calculated. Varying the excitation force, the vibration characteristics (amplitude and frequency) would be changed until the required stiffness of the grafted skin is reached.
Future investigation will be oriented toward application of the suggested modelling and solving methodology for solving nonlinear problems in applied science, medicine and techniques.
Author Contributions
Conceptualization, L.C. and M.J.; methodology, L.C.; validation, I.N., N.H. and M.J.; investigation, L.C.; resources, M.J.; writing—original draft preparation, L.C. and I.N.; writing—review and editing, L.C.; visualization, I.N.; supervision, N.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Informed Consent Statement
Informed consent was obtained from all subjects involved in this study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Meshcherski, I.V. Rabotji po Mehanike tel Peremennoj Massji; Mir: Moscow, Russia, 1952. [Google Scholar]
- Oppalzer, A. Ueber der Ursache, welche den unterschied zwischen der theoretischen berechneten Secularacceleration in der Laenge des Mondes und der tatsachliches bedingen kann. Astron. Nachr. 1884, 108, 67–72. [Google Scholar] [CrossRef]
- Cveticanin, L. Dynamics of Bodies with Time—Variable Mass; Sprinter: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Costa Filho, R.N.; Almeida, M.P.; Farias, G.A.; Andrade, J.S. Displacement operator for quantum systems with position-dependent mass. arXiv 2011, arXiv:1110.1582. [Google Scholar] [CrossRef]
- Mazharimousavi, S.H. Revisiting the displacement operator for quantum systems with position-dependent mass. Phys. Rev. A 2012, 85, 034102, Erratum in Phys. Rev. A 2014, 89, 049904(E). [Google Scholar] [CrossRef]
- Vubangsi, M.; Tchoffo, M.; Fai, L.C. Position-dependent effective mass system in a variable potential: Displacement operator method. Phys. Scr. 2014, 89, 7. [Google Scholar] [CrossRef]
- El-Nabulsi, R.A. Nonlocal uncertainty and its implications in quantum mechanics at ultramicroscopic scales. Quant. Stud. Math. Found. 2019, 6, 123–133. [Google Scholar] [CrossRef]
- El-Nabulsi, R.A. On a new fractional uncertainty relation and its implications in quantum mechanics and molecular physics. Proc. R. Soc. A 2020, 476, 20190729. [Google Scholar] [CrossRef]
- Ruby, V.C.; Senthilvelan, M. On the construction of coherent states of position dependent mass Schrödinger equation endowed with effective potential. J. Math. Phys. 2010, 51, 052106. [Google Scholar] [CrossRef]
- El-Nabulsi, R.A. A new approach to the Schrodinger equation with position-dependent mass and its implications in quantum dots and semiconductors. J. Phys. Chem. Solids 2020, 140, 109384. [Google Scholar] [CrossRef]
- El-Nabulsi, R.A. A generalized self-consistent approach to study position-dependent mass in semiconductors organic heterostructures and crystalline impure materials. Phys. E Low-Dimens. Syst. Nanostruct. 2020, 124, 114295. [Google Scholar] [CrossRef]
- El-Nabulsi, R.A. Time-fractional Schrödinger equation from path integral and its implications in quantum dots and semiconductors. Eur. Phys. J. Plus 2018, 133, 394–406. [Google Scholar] [CrossRef]
- El-Nabulsi, R.A. Path integral method for quantum dissipative systems with dynamical friction: Applications to quantum dots/zero-dimensional nanocrystals. Superlattices Microstruct. 2020, 144, 106581. [Google Scholar] [CrossRef]
- El-Nabulsi, R.A. Dynamics of position-dependent mass particle in crystal lattices microstructures. Phys. E Low-Dimens. Syst. Nanostruct. 2020, 127, 114525. [Google Scholar] [CrossRef]
- Shuo, Z.; Lu, L.; Chunhua, W. Stationary response of a kind of nonlinear stochastic systems with variable mass and fractional derivative damping. Fractal Fract. 2022, 6, 342. [Google Scholar]
- Qiao, Z.; Elhattab, A.; Shu, X.; He, C. A second-order stochastic resonance method enhanced by fractional-order derivative for mechanical fault detection. Nonlinear Dyn. 2021, 106, 707–723. [Google Scholar] [CrossRef]
- He, Y.; Fu, Y.; Qiao, Z.; Kang, Y. Chaotic resonance in a fractional-order oscillator system with application to mechanical fault diagnosis. Chaos Solitons Fractals 2021, 142, 110536. [Google Scholar] [CrossRef]
- Zhang, M.D.R.; Sun, H.; Song, Y. A method for analyzing the dynamic response of a structural system with variable mass, damping and stiffness. Shock Vib. 2001, 7, 85–94. [Google Scholar] [CrossRef][Green Version]
- Shakib, A.; Ghorbani-Tanha, A.K. An innovative adaptive tuned vibration absorber with variable mass moment of inertia for mitigation of transient response of systems. Struct. Control Health Monit. 2020, 27, 5. [Google Scholar] [CrossRef]
- Chakraborty, S.; Ghosh, A.D.; Ray-Chaudhuri, S. A novel tuned mass-conical spring system for passive vibration control of a variable mass structure. J. Vib. Control 2021, 28, 1565–1579. [Google Scholar] [CrossRef]
- Lee, B.H.; Chen, C.C.; Chen, T.W.; Shiao, S.Y.; Jiang, C.R.; Yeh, F.Y. Enhancement of structural seismic performance of low-rise buildings using displacement-dependent tuned mass damper. Structures 2022, 37, 1119–1128. [Google Scholar] [CrossRef]
- Lakshmanan, M.; Chandrasekar, V.K. Generating finite dimensional integrable nonlinear dynamical systems. Eur. Phys. J. Spec. Top. 2013, 222, 665–688. [Google Scholar] [CrossRef][Green Version]
- Musielak, Z.E. Standard and non-standard Lagrangians for dissipative dynamical systems with variable coefficients. J. Phys. A Math. Theor. 2008, 41, 055205. [Google Scholar] [CrossRef]
- Yañez-Navarro, G.; Guo-Hua, S.; Dytrych, T.; Launey, K.D.; Shi-Hai, D.; Draayer, J.P. Quantum information entropies for position-dependent mass Schrödinger problem. Ann. Phys. 2014, 348, 153–160. [Google Scholar] [CrossRef]
- Guo-Hua, S.; Popov, D.; Camacho-Nieto, O.; Shi-Hai, D. Shannon information entropies for position-dependent mass Schrödinger problem with a hyperbolic well. Chin. Phys. B 2015, 24, 100303. [Google Scholar] [CrossRef]
- Rath, B.; Mallick, P.; Mohapatra, P.; Asad, I.; Shanak, H.; Jarrar, R. Position-dependent finite symmetric mass harmonic like oscillator: Classical and quantum mechanical study. Open Phys. 2021, 19, 266–276. [Google Scholar] [CrossRef]
- Chargui, Y.; Dhahbi, A.; Trabelsi, A. A novel approach for constructing kinetic energy operators with position dependent mass. Results Phys. 2019, 13, 102329. [Google Scholar] [CrossRef]
- Negro, J.; Nieto, L.M. On position-dependent mass harmonic oscillators. J. Phys. Conf. Ser. 2008, 128, 012053. [Google Scholar]
- Chandrasekar, V.K.; Senthilvelan, M.; Lakshmanan, M. Unusual Liénard-type nonlinear oscillator. Phys. Rev. E 2005, 72, 066203–066211. [Google Scholar] [CrossRef] [PubMed]
- Tiwari, A.K.; Pandey, S.N.; Santhilvelan, M.; Lakshmanan, M. Classification of Lie point symmetries for quadratic Liénard type equation ẍ + f(x)ẋ2 + g(x) = 0. J. Math. Phys. 2013, 54, 053506. [Google Scholar] [CrossRef]
- Chen, X.; Luo, S. Integration method for the dynamics equation of relative motion of variable mass nonlinear nonholonomic system. Appl. Math. Mech. 1998, 19, 479–488. [Google Scholar]
- Ortiz, O.R. Position-Dependent Mass Systems: Classical and Quantum Pictures; Birkhauser: Basel, Switzerland, 2020. [Google Scholar]
- Khan, J.A.; Raja, M.A.Z.; Qureshi, I.M. Novel approach for a Van der Pol oscillator in the continuous time domain. Chin. Phys. Lett. 2011, 28, 110205. [Google Scholar] [CrossRef]
- Khan, J.A.; Raha, M.A.Z.; Syam, M.I.; Tanoli, S.A.K.; Awan, S.E. Design and application of nature inspired computing approach for nonlinear stiff oscillatory problems. Neural Comput. Appl. 2015, 26, 1763–1780. [Google Scholar] [CrossRef]
- Sabir, Z.; Nisar, K.; Raja, M.A.Z.; Ibrahim, A.A.B.A.; Rodrigues, J.J.P.C.; Al-Basyouni, K.S.; Mahmoud, S.R.; Rawaat, D.B. Heuristic computational design of Morlet wave for solving the higher order singular nonlinear differential equations. Alex. Eng. J. 2021, 60, 5935–5947. [Google Scholar] [CrossRef]
- Nisar, K.; Sabir, Z.; Raja, M.A.Z.; Ibrahim, A.A.A.A.; Erdogan, F.; Haque, M.R.; Rodrigues, J.J.P.C.; Rawaat, D.B. Design of Morlet wavelet neural network for solving a class of singular pantograph nonlinear differential models. IEEE Access 2021, 9, 77845–77862. [Google Scholar] [CrossRef]
- Junswang, P.; Sabir, Z.; Raja, M.A.Z.; Soheil, S.; Botmart, T.; Weera, W. An advanced stochastic numerical approach for host-vector-predator nonlinear model. Comput. Mater. Contin. 2022, 72, 5823–5843. [Google Scholar] [CrossRef]
- Bayindir, C.; Ozaydin, F. Self-localized soliton solutions of the nonlineaer quantum harmonic oscillator. J. Appl. Eng. Math. 2022, 12, 412–425. [Google Scholar]
- Guo, H.; Yang, T.; Chen, Y.; Chen, L.Q. Singularity analysis on vibration reduction of a nonlinear energy sink system. Mech. Syst. Signal Process. 2022, 173, 109074. [Google Scholar] [CrossRef]
- Beléndez, A.; Hernández, A.; Beléndez, T.; Arribas, E.; Álvarez, M.L. Closed-form solutions for the quadratic mixed-parity nonlinear oscillator. Indian J. Phys. 2021, 95, 1213–1224. [Google Scholar] [CrossRef]
- Big-Alabo, A.; Ekpruke, E.O.; Ossia, C.V. Quasi-static quintication method for periodic solution of strong nonlinear oscillators. Sci. Afr. 2021, 11, e00704. [Google Scholar] [CrossRef]
- Lashkarboluki, A.; Hosseini, H.; Ganji, D.D. Investigating the solutions of two classical nonlinear oscillators by the AG method. Int. J. Appl. Comput. Math. 2021, 7, 110. [Google Scholar] [CrossRef]
- Cveticanin, L. Strong Nonlinear Oscillators, Analytical Solutions, 2nd ed.; Mathematical Engineering; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Cveticanin, L. Strongly Nonlinear Oscillators—Analytical Solutions; Undergraduate Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Kohlhauser, M.; Luze, H.; Nischwitz, S.P.; Kamolz, L.P. Historical evolution of skin grafting—A journey through time. Medicina 2021, 57, 348. [Google Scholar] [CrossRef]
- Tremp, M.; Waldkirchen, N.J.; Wang, W.; Oranges, C.M.; di Summa, P.G.; Zhang, Y.; Wang, W.; Schaefer, D.J.; Kalbermatten, D.F. Sensory assessment of meshed skin grafts over free gracilis muscle flaps without nerve coatation for lower extremity reconstruction. Arch. Plast. Surg. 2021, 48, 224–230. [Google Scholar]
- Biggs, L.C.; Kim, C.S.; Miroshnikova, Y.A.; Wickstom, S.A. Mechanical forces in the skin: Roles in tissue architecture, stability, and function. J. Investig. Dermatol. 2020, 140, 284–290. [Google Scholar] [CrossRef] [PubMed]
- Eichhorn, M.G.; Karadsheh, M.J.; Krebiehl, J.R.; Ford, D.M.; Ford, R.D. Vibration for pain reduction in a plastic surgery clinic. Plast. Surg. Nurs. 2016, 36, 63–68. [Google Scholar] [CrossRef] [PubMed]
- Pilch, W.; Czerwinska-Ledwig, O.; Chutryiewicz-Rostek, J.; Nastabek, M.; Krezalek, P.; Jedrychowska, D.; Totko-Borkusewicz, N.; Uher, I.; Kasko, D.; Tota, A.; et al. The impact of vibration therapy interventions on skin condition and skin temperature changes in young womaen with lifodystrophy: A pilot study. Evid.-Based Complement. Altern. Med. 2019, 8436325, 9. [Google Scholar]
- Sari, Y.; Saryono, S.; Sutrisna, E.; Hartono, H. A comparative study of the effects of vibration and electrical stimulation therapies on the acceleration of wound healing in diabetic ulcers. J. Ners 2017, 12, 253–260. [Google Scholar] [CrossRef]
- Weinheimer-Haus, E.M.; Judex, S.; Ennis, W.J.; Koh, T.J. Low-intensity vibration improves angiogenesis and wound healing in diabetic mice. PLoS ONE 2014, 9, e91355. [Google Scholar] [CrossRef]
- Liang, X.; Boppart, S.A. Biomechanical properties of In Vivo human skin from dynamic optical coherence elastography. IEEE Trans Biomed. Eng. 2010, 57, 953–959. [Google Scholar] [CrossRef]
- Limbert, G. Mathematical and computational modelling of skin biophysics: A review. Proc. R. Soc. A 2017, 473, 20170257. [Google Scholar] [CrossRef]
- Romero, C.; Otaduy, M.A.; Casas, D.; Perez, J. Modeling and estimation of nonlinear skin mechanics for animated avatars. Eurographics 2020, 39, 77–88. [Google Scholar] [CrossRef]
- Joodaki, H.; Panzer, M.B. Skin mechanical properties and modeling: A review. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2018, 232, 323–343. [Google Scholar] [CrossRef]
- Wei, J.C.J.; Edwards, G.A.; Martin, D.J.; Huang, H.; Crichton, M.L.; Kendall, M.A.F. Allometric scaling of skin thickness, elasticity, viscoelasticiety to mass for micro-medical device translation: From mice, rats, rabbits, pigs to humans. Sci. Rep. 2017, 4, 15885. [Google Scholar] [CrossRef] [PubMed]
- Graham, H.K.; McConnell, J.C.; Lambert, G.; Sherratt, M.J. How stiff is skin? Exp. Dermatol. 2019, 28, 4–9. [Google Scholar] [CrossRef] [PubMed]
- Kalra, A.; Lowe, A.; Al-Jumaily, A.M. Mechanical behavior of skin: A review. J. Mater. Sci. Eng. 2016, 5, 1000254. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).