On Robust Stability and Stabilization of Networked Evolutionary Games with Time Delays
Abstract
:1. Introduction
- Using STP of matrices and dimension augmenting technique, an auxiliary system is constructed to formulate the dynamics of NEGs with time delays and disturbances. The auxiliary system is a linear-like system. It reduces the difficulty of analyzing NEG dynamics with time-varying delays.
- Based on the auxiliary system, an explicit criterion is derived for robust stability. It is presented as a matrix and is easily verified by mathematical software such as Matlab.
- In order to stabilize NEG to the target equilibrium, the robust stability problem is transformed into the robust stabilization problem. Based on the auxiliary system, the necessary and sufficient condition is derived for set stabilization. Moreover, an algorithm is developed to design the set stabilization controller.
2. Preliminaries
- (1)
- is the set of all real matrices
- (2)
- ,
- (3)
- (4)
- () denotes the i-th column (row) of matrix A
- (5)
- (6)
- (7)
- is a logical matrix, which is abbreviated as
- (8)
- represents the set of -dimensional logical matrices
- (9)
- ∘ denotes the Hadamard product of matrices
- (1)
- Define . Then, .
- (2)
- Define and . Then, and
3. Formulation and Robust Stability Analysis of NEGs with Time Delays
3.1. Model Description
- (1)
- The set of players ;
- (2)
- Each player has a strategy set . The strategies of all players constitute a profile, and the set of a profile is denoted by ;
- (3)
- Each player has a payoff function, .
- (1)
- is a network graph with node set and edge set ;
- (2)
- is a fundamental game set, where is an edge-related fundamental game played by players i and j;
- (3)
- is an SUR set, where is the SUR of player ;
- (4)
- is the time-varying delay that occurs when players receive information from others;
- (5)
- is a disturbance set.
3.2. Algebraic Formulation
3.3. Robust Stability Analysis
4. Stabilization Analysis of NEGs with Time Delays and Disturbances
4.1. Model Description
4.2. Stabilization Analysis
| Algorithm 1: Find the largest control-invariant subset . |
| Step 1: Assume and . Set and Step 2: Let , . Step 3: If , set , stop. Step 4: Compute and set . Step 5: If , let , stop; otherwise, let , return to Step 3 and repeat the calculation. |
- (1)
- is stabilized at the robust-Nash equilibrium under control.
- (2)
- System (19) is set stabilized at .
- (3)
- There exists a positive integer such that
| Algorithm 2: Design control matrix such that and . |
| Step 1: Let . Assume . Step 2: For , if , set Step 3: Calculate . Set . Step 4: If , there is no . Stop the calculation. Step 5: If , set ; otherwise, set and go back to Step 2. Step 6: Set . is designed as where Stop. |
5. Example
5.1. Model Description
- (1)
- The network graph is shown in Figure 1.
- (2)
- (3)
- Imitating the strategy of the neighbor who has the optimal payoff is the SUR of each player, namely,
- (4)
- .
- (5)
- The external disturbance system iswhere , , , .
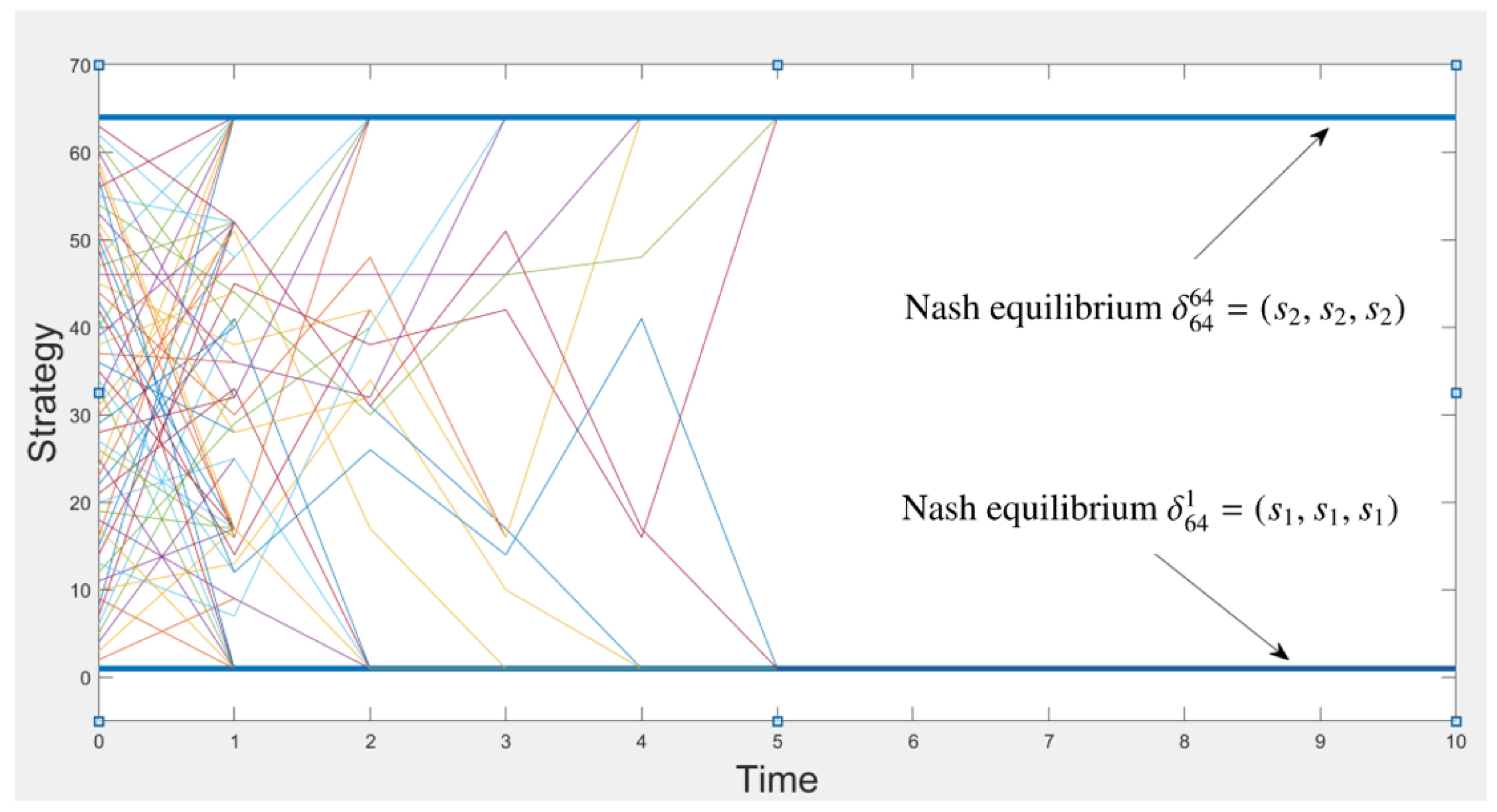
5.2. Robust Stability Analysis
5.3. Robust Stabilization Analysis
6. Problems
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Neumann, J.V.; Morgenstern, O. Theory of Game and Economic Behavior; Princeton University Press: Princeton, NJ, USA, 1944. [Google Scholar]
- Lieberman, E.; Hauert, C.; Nowak, M.A. Evolutionary dynamics on graphs. Nature 2005, 433, 312–316. [Google Scholar] [CrossRef]
- Boccaletti, S.; Latora, V.; Moreno, Y.; Chavez, M.; Hwang, D.U. Complex networks structure and dynamics. Phys. Rev. E 2006, 424, 175–308. [Google Scholar] [CrossRef]
- Hauert, C.; Doebeli, M. Spatial structure often inhibits the evolution of cooperation in the snowdrift game. Nature 2004, 428, 643–646. [Google Scholar] [CrossRef] [PubMed]
- Cheng, D.; He, F.; Qi, H.; Xu, T. Modeling, analysis and control of networked evolutionary games. IEEE Trans. Autom. Control 2015, 61, 2402–2415. [Google Scholar] [CrossRef]
- Sugden, R. The Economics of Rights, Cooperation and Welfre; Blackwwell: Oxford, UK, 1986. [Google Scholar]
- Ohtsuki, H.; Hauert, C.; Liberman, E.; Nowak, M. A simple rule for the evolution of cooperation on graphs and social networks. Nature 2006, 441, 502–505. [Google Scholar] [CrossRef] [PubMed]
- Mojica, E.; Macana, C.A.; Quijano, N. Dynamic population games for optimal dispatch on hierarchical microgrid control. IEEE Trans. Syst. Man Cybern.-Syst. 2017, 44, 306–317. [Google Scholar] [CrossRef]
- Sun, S.; Yang, H.; Yang, G.; Pi, J. Evolutionary games and dynamics in public goods supply with repetitive actions. Mathematics 2021, 9, 1726. [Google Scholar] [CrossRef]
- Yang, P.; Guo, F.; Zhang, H. Multi-player evolutionary game of network attack and defense based on system dynamics. Mathematics 2021, 9, 3014. [Google Scholar] [CrossRef]
- Nash, J. Non-cooperative games. Ann. Math. 1951, 54, 286–295. [Google Scholar] [CrossRef]
- Jimenez, M.; Poznyak, A. ϵ-equilibrium in LQ differential games with bounded uncertain disturbances: Robustness of standard strategies and new strategies with adaptation. Int. J. Control 2006, 79, 786–797. [Google Scholar] [CrossRef]
- Jimenez, M.; Basin, M.; Rodriguez, V.; Rodriguez, P. Open-loop Nash equilibrium in polynomial differential games via state-dependent Riccati equation. Automatica 2015, 53, 155–163. [Google Scholar] [CrossRef]
- Yuan, Y.; Wang, Z.; Guo, L. Event-triggered strategy design for discrete-time nonlinear quadratic games with disturbance compensations: The noncooperative case. IEEE Trans. Syst. Man Cybern.-Syst. 2017, 48, 1885–1896. [Google Scholar] [CrossRef]
- Yang, Y.; Fan, J.; Zhu, D. Research on construction supply chain quality management based on stochastic evolutionary game. J. Eng. Manag. 2020, 34, 19–24. [Google Scholar]
- Qin, S.; Shi, J. Effect of memory on the prisoner’s dilemma game in a square lattice. Phys. Rev. E 2008, 78, 041129. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stewart, A.; Plotkin, J. Small groups and long memories promote cooperation. Sci. Rep. 2016, 6, 26889. [Google Scholar] [CrossRef]
- Cheng, D.; Qi, H.; Li, Z. Analysis and Control of Boolean Networks: A Semi-Tensor Product Approach; Springer: London, UK, 2011. [Google Scholar]
- Cheng, D.; Qi, H.; Zhao, Y. An Introduction to Semi-Tensor Product of Matrices and Its Applications; World Scientific: Singapore, 2012. [Google Scholar]
- Li, Y.; Li, H.; Ding, X. Set stability of switched delayed logical networks with application to finite-field consensus. Automatica 2020, 113, 108768. [Google Scholar] [CrossRef]
- Cheng, D.; Qi, H.; Liu, Z. From STP to game-based control. Sci. China-Inf. Sci. 2018, 61, 9–27. [Google Scholar] [CrossRef] [Green Version]
- Zheng, Y.; Li, H.; Feng, J. State feedback set stabilization of logical control networks with state-dependent delay. Sci. China-Inf. Sci. 2021, 64, 169203. [Google Scholar] [CrossRef]
- Zhong, J.; Lu, J.; Huang, C.; Li, L.; Cao, J. Finding graph minimum stable set and core via semi-tensor product approach. Neurocomputing 2016, 174, 588–596. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, Z.; Liu, Z. Modeling and reachability of probabilistic finite automata based on semi-tensor product of matrices. Sci. China-Inf. Sci. 2018, 61, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Li, R.; Yang, M.; Chu, T. State feedback stabilization for Boolean control networks. IEEE Trans. Autom. Control 2013, 58, 1853–1857. [Google Scholar] [CrossRef]
- Wang, S.; Feng, J.; Yu, Y.; Zhao, J. Further results on dynamic-algebraic Boolean control networks. Sci. China-Inf. Sci. 2019, 61, 012208. [Google Scholar] [CrossRef] [Green Version]
- Yu, Y.; Meng, M.; Feng, J. Observability of Boolean networks via matrix equations. Automatica 2020, 111, 108621. [Google Scholar] [CrossRef]
- Cheng, D. On finite potential games. Automatica 2014, 50, 1793–1801. [Google Scholar] [CrossRef]
- Cheng, D.; Liu, T.; Zhang, K. On decomposed subspaces of finite games. IEEE Trans. Autom. Control 2016, 61, 3651–3656. [Google Scholar] [CrossRef]

| 1111 | 1112 | 1121 | 1122 | 1211 | 1212 | 1221 | 1222 | 2111 | 2112 | 2121 | 2122 | 2211 | 2212 | 2221 | 2222 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 2 | 1 | 1 | 1 | 0 | 1 | 2 | 0 | 0 | 3 | 3 | 0 | 4 | 2 | |
| 0 | 1 | 2 | 1 | 0 | 0 | 2 | 0 | 1 | 2 | 1 | 0 | 0 | 1 | 2 | 4 |
| 1111 | 1112 | 1121 | 1122 | 1211 | 1212 | 1221 | 1222 | 2111 | 2112 | 2121 | 2122 | 2211 | 2212 | 2221 | 2222 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 2 | 0 | 2 | 0 | 1 | 0 | 4 | 1 | 4 | 1 | 2 | 0 | 1 | 4 | |
| 1 | 0 | 1 | 4 | 1 | 1 | 2 | 3 | 0 | 0 | 1 | 0 | 1 | 3 | 1 | 2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
An, Q.; Guo, H.; Zheng, Y. On Robust Stability and Stabilization of Networked Evolutionary Games with Time Delays. Mathematics 2022, 10, 2695. https://doi.org/10.3390/math10152695
An Q, Guo H, Zheng Y. On Robust Stability and Stabilization of Networked Evolutionary Games with Time Delays. Mathematics. 2022; 10(15):2695. https://doi.org/10.3390/math10152695
Chicago/Turabian StyleAn, Qiguang, Hongfeng Guo, and Yating Zheng. 2022. "On Robust Stability and Stabilization of Networked Evolutionary Games with Time Delays" Mathematics 10, no. 15: 2695. https://doi.org/10.3390/math10152695
APA StyleAn, Q., Guo, H., & Zheng, Y. (2022). On Robust Stability and Stabilization of Networked Evolutionary Games with Time Delays. Mathematics, 10(15), 2695. https://doi.org/10.3390/math10152695






