Application of Compound Poisson Process in Pricing Catastrophe Bonds: A Systematic Literature Review
Abstract
1. Introduction
- (a)
- This study discusses a technical problem in CPP application in pricing CAT bonds;
- (b)
- This study analyzes the conceptual and nonconceptual structures of the literature;
- (c)
- This study discusses the gaps in previous studies.
- (a)
- Financial and catastrophic factors involved;
- (b)
- The method used to measure risks of financial and catastrophe;
- (c)
- The method used to estimate CAT bond price.
2. Materials and Methods
2.1. Literature Collection
- (a)
- The type of literature is the final journal article;
- (b)
- The title, abstract, or keyword of the literature contains the words (“catastrophe bond” OR “CAT bond” OR “catastrophic bond”) AND (“price” OR “pricing”). We specifically do not use keywords related to CPP. It is conducted so that the collected literature becomes more general and more numerous;
- (c)
- The literature is written in English;
- (d)
- The literature is published in peer-reviewed international journals;
- (e)
- The literature aims to design a way for pricing CAT bonds using CPP.
2.2. Methods of Literature Selection
- (a)
- Removing duplicates and the unavailable literature from each database;
- (b)
- Reading the abstract of articles;
- (c)
- The reading of articles one-by-one in its entirety.
2.3. A Brief Explanation of Bibliometric Analysis
3. Results
3.1. Literature Selection
- (a)
- The first stage is removing duplicates and the unavailable literature from each database. After each piece of literature is checked, all the literature is available, and the number of duplicate literature found is 18. We deleted these 18 pieces of literature, leaving 81 pieces of literature selected for the next stage.
- (b)
- The second stage is the advanced literature selection stage through reading the abstract. In the abstract section, we look at the purpose of the literature. The literature that aims to design ways to price CAT bonds is chosen. After each literature abstract is read, 49 pieces of literature are obtained and then selected for the next stage.
- (c)
- The third stage is the final literature selection stage by reading it one-by-one in its entirety. The selected article is an article on CAT bond pricing that applies CPP. The result is a total of the 30 articles obtained. These articles are reviewed later.
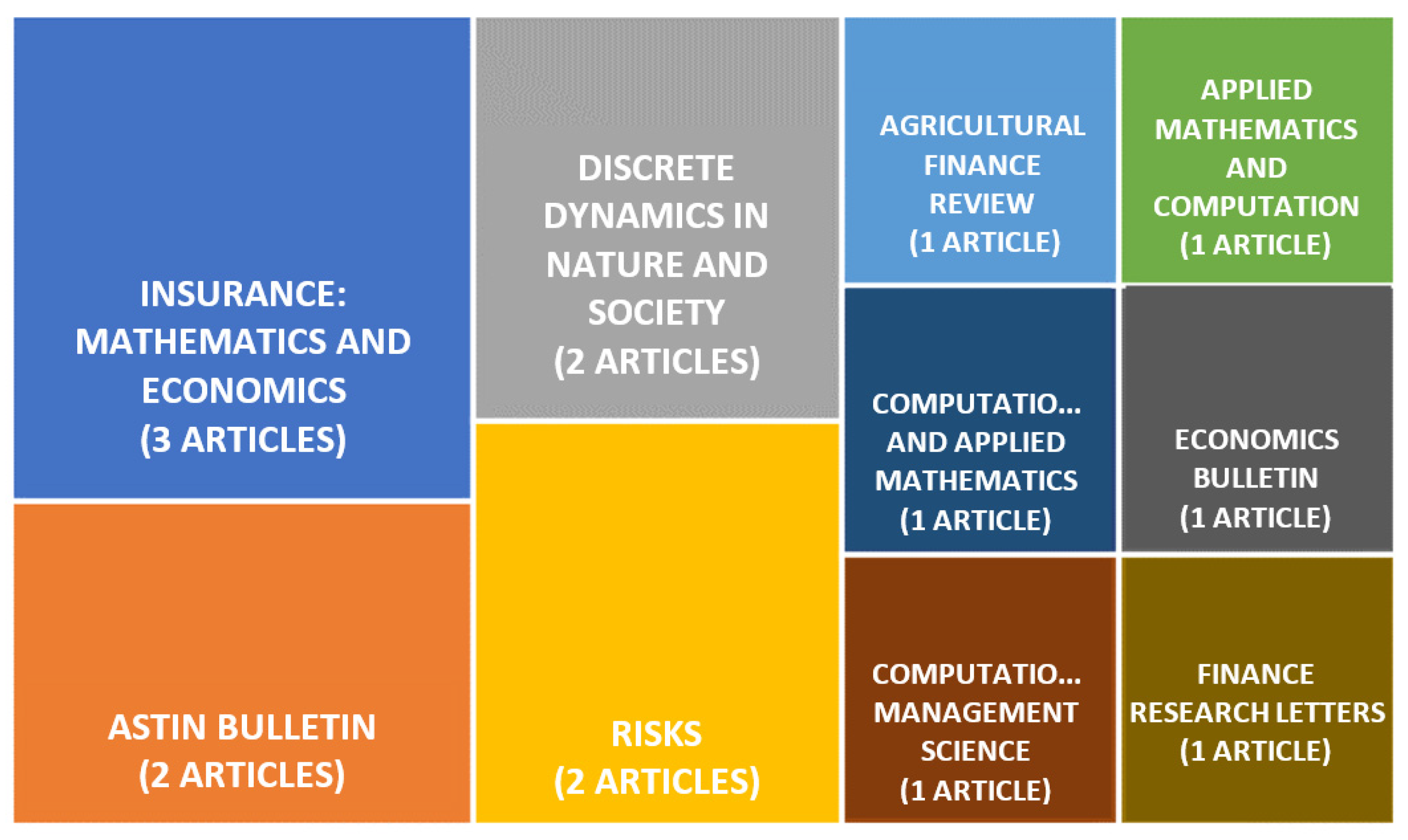
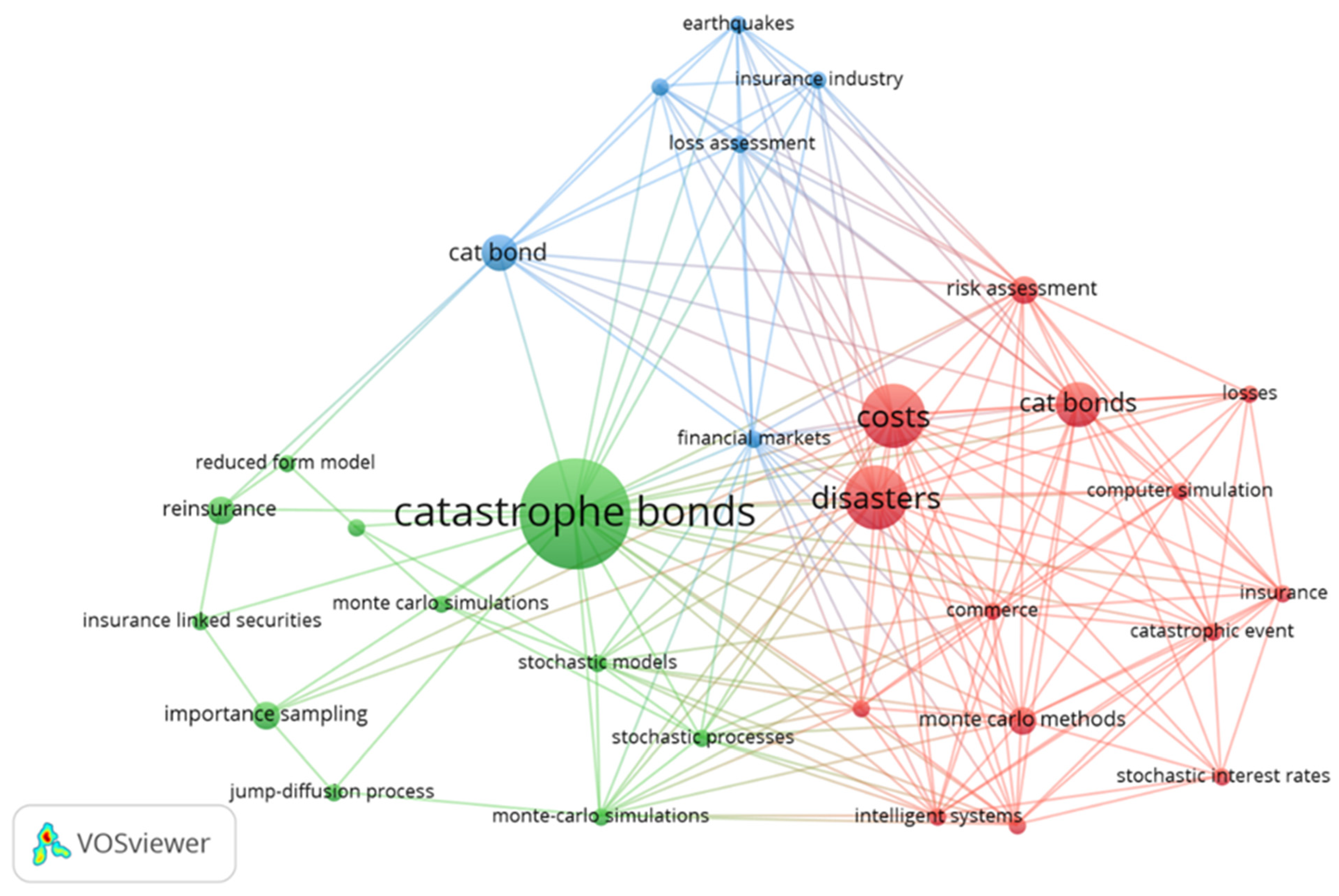
3.2. Bibliometric Analysis
3.3. SLR Results
3.3.1. The Application of CPP in the Pricing of CAT Bonds
- (a)
- Losses for each catastrophe are assumed to be independent and identically distributed. In other words, the losses of one catastrophe with those of another do not affect each other, and the losses of each catastrophe follow the same probability distribution.
- (b)
- The number of catastrophe events is independent of catastrophe losses. In other words, the number of catastrophe events does not affect the losses experienced.
- (a)
- The number of deaths for each catastrophe is assumed to be independent and identically distributed. It means that the number of deaths of one catastrophe with those of another does not affect each other, and the number of deaths for each catastrophe follows an equal probability distribution.
- (b)
- The number of catastrophe events is independent of the number of catastrophe deaths. It means that the number of catastrophic events does not affect the number of deaths and vice versa.
- (c)
- Catastrophic losses are independent of the number of catastrophe deaths. It means that catastrophe losses do not affect the number of deaths and vice versa.
3.3.2. Analysis of Financial Factors Involved in Pricing CAT Bonds
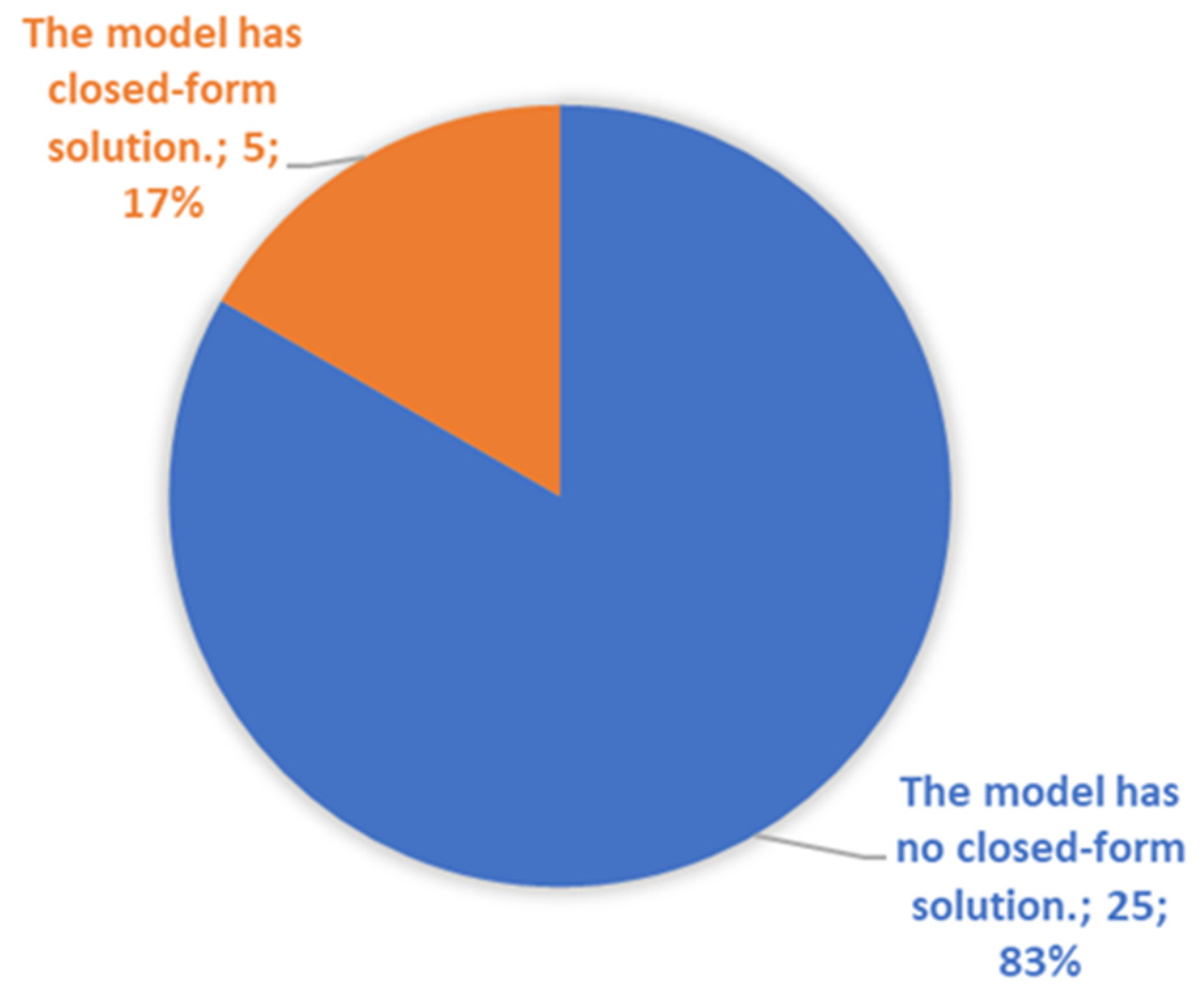
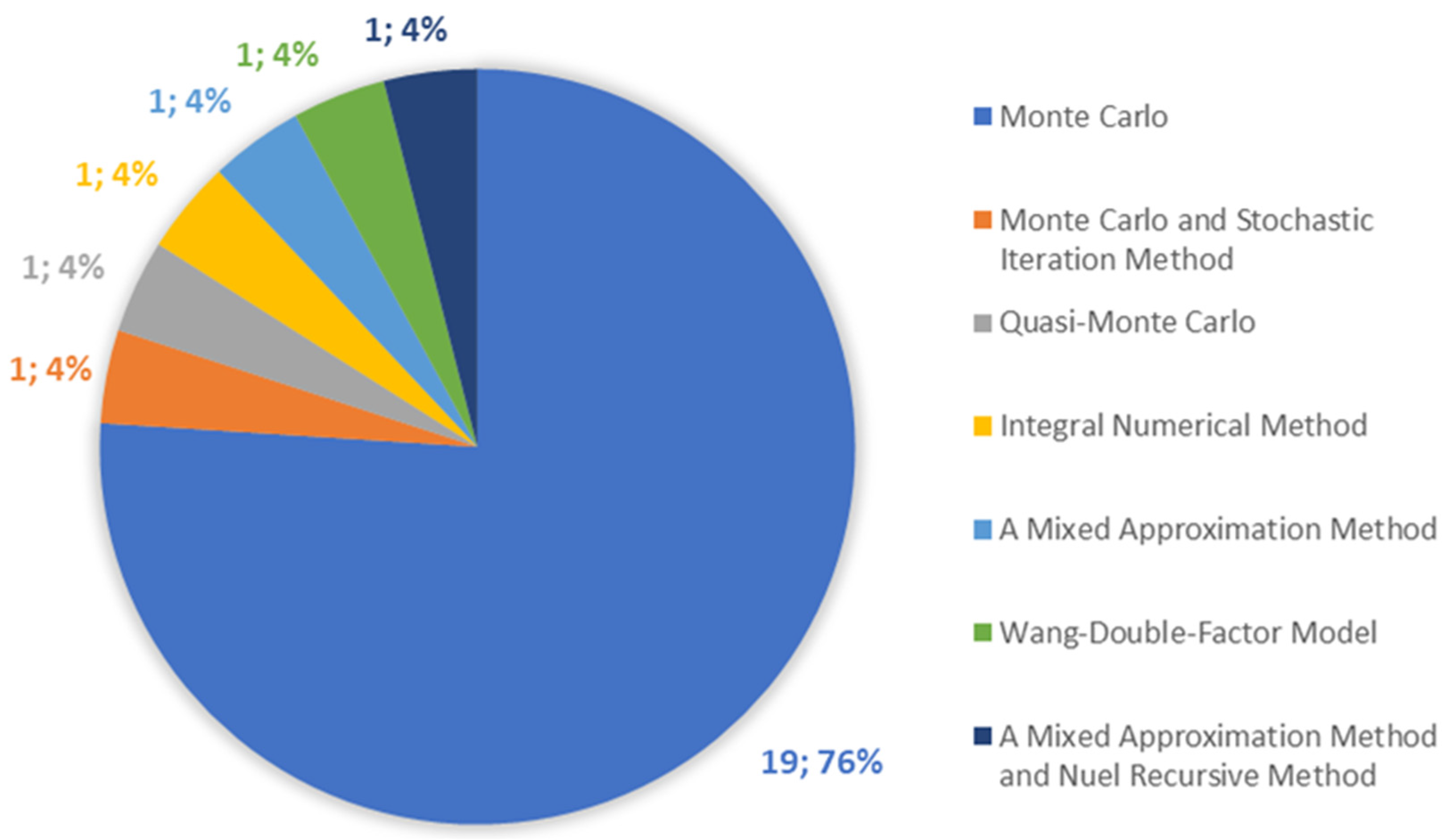
3.3.3. The Analysis of the CAT Bond Price Estimation Methods
4. Discussions
4.1. The Facts of Bibliometric Analysis and SLR Results
4.2. Gap Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Taalas, P.; Manaenkova, E.; Zhang, W. The ocean, our climate and weather. J. World Meteorol. Organ. 2021, 70, 1–114. [Google Scholar]
- Coronese, M.; Lamperti, F.; Keller, K.; Chiaromonte, F.; Roventini, A. Evidence for sharp increase in the economic damages of extreme natural disasters. Proc. Natl. Acad. Sci. USA 2019, 116, 21450–21455. [Google Scholar] [CrossRef] [PubMed]
- Chao, W.; Zou, H. Multiple-event catastrophe bond pricing based on CIR-Copula-POT model. Discret. Dyn. Nat. Soc. 2018, 2018, 5068480. [Google Scholar] [CrossRef]
- Cummins, J.D. CAT bonds and other risk-linked securities: State of the market and recent developments. Risk Manag. Insur. Rev. 2008, 11, 23–47. [Google Scholar] [CrossRef]
- Lee, J.P.; Yu, M.T. Valuation of catastrophe reinsurance with catastrophe bonds. Insur. Math. Econ. 2007, 41, 264–278. [Google Scholar] [CrossRef]
- Froot, K.A. The market for catastrophe risk: A clinical examination. J Financ. Econ. 2001, 60, 529–571. [Google Scholar] [CrossRef]
- Liu, J.; Xiao, J.; Yan, L.; Wen, F. Valuing catastrophe bonds involving credit risks. Math. Probl. Eng. 2014, 2014, 563086. [Google Scholar] [CrossRef]
- Härdle, W.K.; Cabrera, B.L. Calibrating CAT bonds for Mexican earthquakes. J Risk Insur. 2010, 77, 625–650. [Google Scholar] [CrossRef]
- Deng, G.; Liu, S.; Li, L.; Deng, C. Research on the pricing of global drought catastrophe bonds. Math. Probl. Eng. 2020, 2020, 3898191. [Google Scholar] [CrossRef]
- Cox, S.H.; Pedersen, H.W. Catastrophe risk bonds. N. Am. Actuar. J. 2000, 4, 56–82. [Google Scholar] [CrossRef]
- Ross, S.M. Stochastic Processes, 2nd ed.; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 1996; pp. 59–78. [Google Scholar]
- Canabarro, E.; Finkemeier, M.; Anderson, R.R.; Bendimerad, F. Analyzing insurance-linked securities. J. Risk Financ. 2000, 1, 49–75. [Google Scholar] [CrossRef]
- Linnerooth-Bayer, J.; Amendola, A. Global change, natural disasters and loss-sharing: Issues of efficiency and equity. Geneva Pap. Risk Insur.-Issues Pract. 2000, 25, 203–219. [Google Scholar] [CrossRef]
- Skees, J.R.; Barnett, B.J.; Murphy, A.G. Creating insurance markets for natural disaster risk in lower income countries: The potential role for securitization. Agric. Financ. Rev. 2008, 68, 151–167. [Google Scholar] [CrossRef]
- Achmad, A.L.H.; Chaerani, D.; Perdana, T. Robust optimization and agent-based modeling in disaster management: A brief review and opportunities. Alexandria Eng. J. 2020, preprint. [Google Scholar]
- Firdaniza, F.; Ruchjana, B.N.; Chaerani, D.; Radianti, J. Information Diffusion Model in Twitter: A Systematic Literature Review. Information 2022, 13, 13. [Google Scholar] [CrossRef]
- Ellegaard, O.; Wallin, J.A. The bibliometric analysis of scholarly production: How great is the impact? Scientometrics 2015, 105, 1809–1831. [Google Scholar] [CrossRef]
- Aria, M.; Cuccurullo, C. Comprehensive Science Mapping Analysis. Available online: https://cran.r-project.org/web/packages/bibliometrix/bibliometrix.pdf (accessed on 15 May 2022).
- Lee, J.P.; Yu, M.T. Pricing default-risky CAT bonds with moral hazard and basis risk. J. Risk Insur. 2002, 69, 25–44. [Google Scholar] [CrossRef]
- Nowak, P.; Romaniuk, M. Pricing and simulations of catastrophe bonds. Insur. Math. Econ. 2013, 52, 18–28. [Google Scholar] [CrossRef]
- Vaugirard, V.E. Pricing Catastrophe Bonds by An Arbitrage Approach. Q. Rev. Econ. Financ. 2003, 43, 119–132. [Google Scholar] [CrossRef]
- Egami, M.; Young, V.R. Indifference prices of structured catastrophe (CAT) bonds. Insur. Math. Econ. 2008, 42, 771–778. [Google Scholar] [CrossRef]
- Jarrow, R.A. A simple robust model for CAT bond valuation. Financ. Res. Lett. 2010, 7, 72–79. [Google Scholar] [CrossRef]
- Ma, Z.G.; Ma, C.Q. Pricing catastrophe risk bonds: A mixed approximation method. Insur. Math. Econ. 2013, 52, 243–254. [Google Scholar] [CrossRef]
- Schmidt, T. Catastrophe insurance modeled by shot-noise processes. Risks 2014, 2, 3–24. [Google Scholar] [CrossRef]
- Nowak, P.; Romaniuk, M. Catastrophe bond pricing for the two-factor Vasicek interest rate model with automatized fuzzy decision making. Soft Comput. 2017, 21, 2575–2597. [Google Scholar] [CrossRef][Green Version]
- Lai, V.S.; Parcollet, M.; Lamond, B.F. The valuation of catastrophe bonds with exposure to currency exchange risk. Int. Rev. Financ. Anal. 2014, 33, 243–252. [Google Scholar] [CrossRef]
- Nowak, P.; Romaniuk, M. Valuing catastrophe bonds involving correlation and CIR interest rate model. Comput. Appl. Math. 2018, 37, 365–394. [Google Scholar] [CrossRef]
- Romaniuk, M. Pricing the risk-transfer financial instruments via Monte Carlo methods. Syst. Anal. Model. Simul. 2003, 43, 1043–1064. [Google Scholar] [CrossRef][Green Version]
- Haslip, G.; Kaishev, V. Pricing of reinsurance contracts in the presence of catastrophe bonds. ASTIN Bull. 2010, 40, 307–329. [Google Scholar] [CrossRef]
- Chen, J.; Liu, G.; Yang, L.; Shao, Q.; Wang, H. Pricing and simulation for extreme flood catastrophe bonds. Water Resour. Manag. 2013, 27, 3713–3725. [Google Scholar] [CrossRef]
- Georgiopoulos, N. Pricing catastrophe bonds with multistage stochastic programming. Comput. Manag. Sci. 2017, 14, 297–312. [Google Scholar] [CrossRef]
- Zhang, X.; Tsai, C.C.L. The optimal write-down coefficients in a percentage for a catastrophe bond. N. Am. Actuar. J. 2018, 22, 1–21. [Google Scholar] [CrossRef]
- Godin, F.; Lai, V.L.; Trottier, D.A. A general class of distortion operators for pricing contingent claims with applications to CAT bonds. Scand. Actuar. J. 2019, 2019, 558–584. [Google Scholar] [CrossRef]
- Vaugirard, V. A canonical first passage time model to pricing nature-linked bonds. Econ. Bull. 2004, 7, 1–7. [Google Scholar]
- Tang, Q.; Yuan, Z. Cat bond pricing under a product probability measure with POT risk characterization. ASTIN Bull. J. IAA 2019, 49, 457–490. [Google Scholar] [CrossRef]
- Albrecher, H.; Hartinger, J.; Tichy, R. QMC techniques for CAT bond pricing. Monte Carlo Methods Appl. 2004, 10, 197–211. [Google Scholar] [CrossRef][Green Version]
- Burnecki, K.; Guiricich, M.N. Stable weak approximation at work in index-linked catastrophe bond pricing. Risks 2017, 5, 64. [Google Scholar] [CrossRef]
- Guiricich, M.N.; Burnecki, K. Modeling of left-truncated heavy-tailed data with application to catastrophe bond pricing. Phys. A Stat. Mech. Appl. 2019, 525, 498–513. [Google Scholar] [CrossRef]
- Sun, L.; Turvey, C.G.; Jarrow, R.A. Designing catastrophic bonds for catastrophic risks in agriculture: Macro hedging long and short rains in Kenya. Agric. Financ. Rev. 2015, 75, 47–62. [Google Scholar] [CrossRef]
- Shao, J.; Papaioannou, A.D.; Pentelous, A.A. Pricing and simulating catastrophe risk bonds in a Markov-dependent environment. Appl. Math. Comput. 2017, 309, 68–84. [Google Scholar] [CrossRef]
- Ma, Z.; Ma, C.; Xiao, S. Pricing zero-coupon catastrophe bonds using EVT with doubly stochastic Poisson arrivals. Discret. Dyn. Nat. Soc. 2017, 2017, 3279647. [Google Scholar] [CrossRef]
- Hofer, L.; Zanini, M.A.; Gardoni, P. Risk-based catastrophe bond design for a spatially distributed portfolio. Struct. Saf. 2020, 83, 101908. [Google Scholar] [CrossRef]
- Hofer, L.; Gardoni, P.; Zanini, M.A. Risk-based CAT bond pricing considering parameter uncertainties. Sustain. Resilient Infrastruct. 2021, 6, 315–329. [Google Scholar] [CrossRef]
- Beer, S.; Braun, A. Market-consistent valuation of natural catastrophe risk. J. Bank. Financ. 2022, 134, 106350. [Google Scholar] [CrossRef]
- Ibrahim, R.A.; Sukono; Napitupulu, H. Multiple-trigger catastrophe bond pricing model and its simulation using numerical methods. Mathematics 2022, 10, 1363. [Google Scholar] [CrossRef]
- Duan, J.C.; Moreau, A.F.; Sealey, C.W. Deposit insurance and bank interest rate risk: Pricing and regulatory implication. J. Bank. Financ. 1995, 19, 1091–1108. [Google Scholar] [CrossRef]



| Literature Database | The Number of Literature |
|---|---|
| Scopus | 81 |
| Science Direct | 18 |
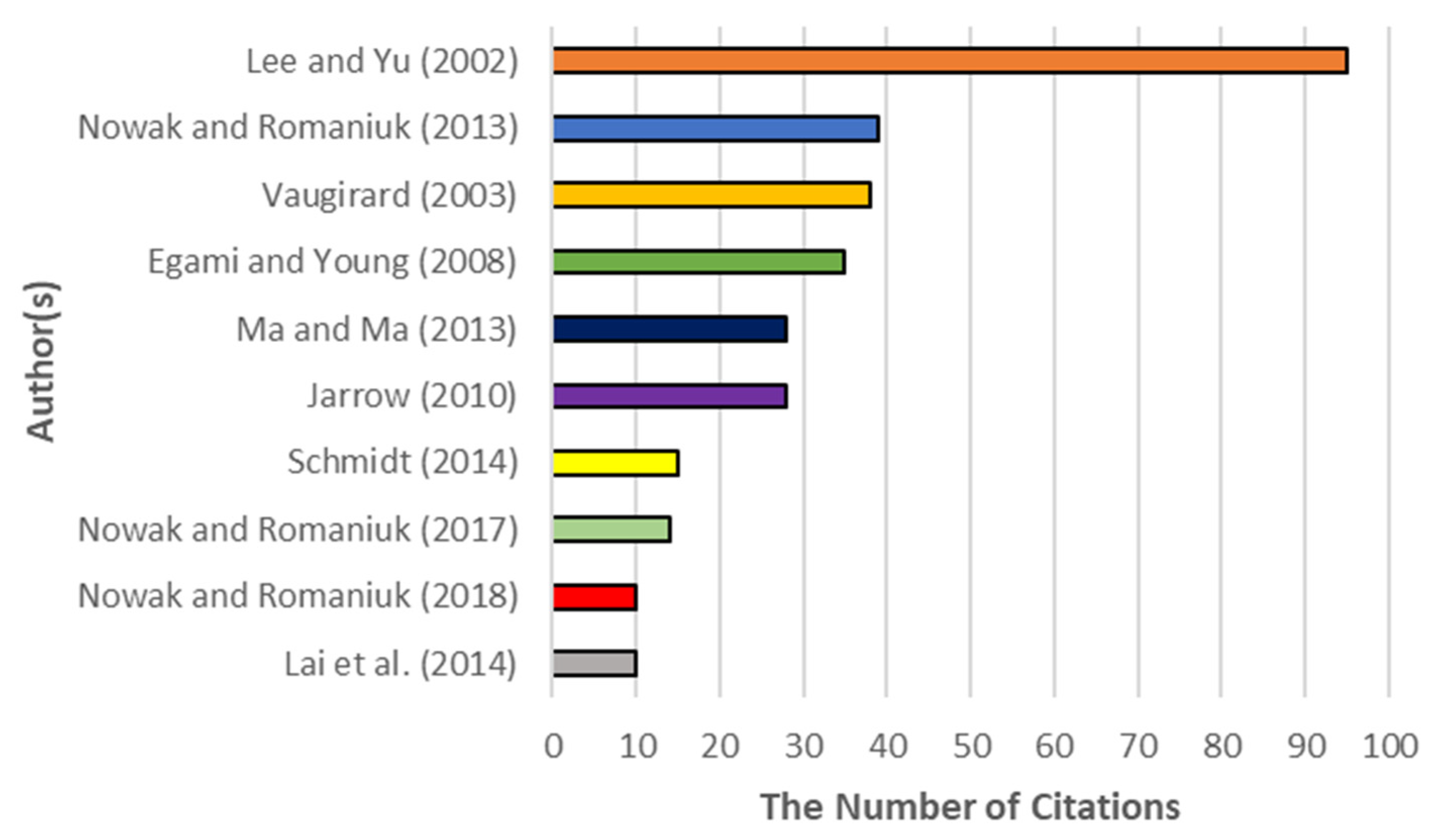
| Author(s) | Title | Keywords | Indexed Database | The Number of Citations |
|---|---|---|---|---|
| Lee and Yu [19] | Pricing Default-Risky CAT Bonds with Moral Hazard and Basis Risk | - | Scopus | 95 |
| Nowak and Romaniuk [20] | Pricing and Simulations of Catastrophe Bonds | Catastrophe Bonds, Monte Carlo Simulations, Risk, Stochastic Processes | Scopus and Science Direct | 39 |
| Vaugirard [21] | Pricing Catastrophe Bonds by an Arbitrage Approach | Catastrophe Bonds, Incomplete Market, Jump-diffusion Process, Monte Carlo Simulations, Path-dependent Digital Options | Scopus | 38 |
| Egami and Young [22] | Indifference Prices of Structured Catastrophe (CAT) Bonds | Catastrophe (CAT) Bond, Exponential Utility, Indifference Price, Jump-diffusion, Reinsurance Strategy, Structured Derivative Security | Scopus and Science Direct | 35 |
| Jarrow [23] | A Simple Robust Model for CAT Bond Valuation | CAT Bond, Catastrophe Events, Reduced Form Model, Reinsurance | Scopus and Science Direct | 28 |
| Ma and Ma [24] | Pricing Catastrophe Risk Bonds: A Mixed Approximation Method | Catastrophe Risk Bonds, Compound Nonhomogeneous Poisson Process, Mixed Approximation Method, PCS Loss, Stochastic Interest Rates | Scopus | 28 |
| Schmidt [25] | Catastrophe Insurance Modeled by Shot Noise Processes | CAT Bonds, Catastrophe Derivatives, Marked Point Process, Minimum Distance Estimation, Self-Exciting Processes, Shot Noise Processes, Tail Dependence | Scopus | 15 |
| Nowak and Romaniuk [26] | Catastrophe Bond Pricing for The Two-Factor Vasicek Interest Rate Model with Automatized Fuzzy Decision Making | Automated Decision Making, Catastrophe Bonds, Fuzzy Numbers, Monte Carlo Simulations, Stochastics Processes, Vasicek Model | Scopus | 14 |
| Lai et al. [27] | The Valuation of Catastrophe Bonds with Exposure to Currency Exchange Risk | 3D Brownian Motion, Brownian Bridge, CAT Bond Valuation, Catastrophic and Currency Exchange Risk, Importance Sampling, Jump-Diffusion Process | Scopus and Science Direct | 10 |
| Nowak and Romaniuk [28] | Valuing Catastrophe Bonds Involving Correlation and CIR Interest Rate Model | Asset Pricing, Catastrophe Bonds, CIR Model, Monte Carlo Simulations, Stochastic Models | Scopus | 10 |
| CPP Type | Frequency of Article | The Articles |
|---|---|---|
| Homogeneous | 17 | [3,9,19,20,21,22,25,27,28,29,30,31,32,33,34,35,36] |
| Nonhomogeneous | 13 | [23,24,26,37,38,39,40,41,42,43,44,45,46] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sukono; Juahir, H.; Ibrahim, R.A.; Saputra, M.P.A.; Hidayat, Y.; Prihanto, I.G. Application of Compound Poisson Process in Pricing Catastrophe Bonds: A Systematic Literature Review. Mathematics 2022, 10, 2668. https://doi.org/10.3390/math10152668
Sukono, Juahir H, Ibrahim RA, Saputra MPA, Hidayat Y, Prihanto IG. Application of Compound Poisson Process in Pricing Catastrophe Bonds: A Systematic Literature Review. Mathematics. 2022; 10(15):2668. https://doi.org/10.3390/math10152668
Chicago/Turabian StyleSukono, Hafizan Juahir, Riza Andrian Ibrahim, Moch Panji Agung Saputra, Yuyun Hidayat, and Igif Gimin Prihanto. 2022. "Application of Compound Poisson Process in Pricing Catastrophe Bonds: A Systematic Literature Review" Mathematics 10, no. 15: 2668. https://doi.org/10.3390/math10152668
APA StyleSukono, Juahir, H., Ibrahim, R. A., Saputra, M. P. A., Hidayat, Y., & Prihanto, I. G. (2022). Application of Compound Poisson Process in Pricing Catastrophe Bonds: A Systematic Literature Review. Mathematics, 10(15), 2668. https://doi.org/10.3390/math10152668