Weighted Log-Rank Test for Clinical Trials with Delayed Treatment Effect Based on a Novel Hazard Function Family

Abstract

In clinical trials with delayed treatment effect, the standard log-rank method in testing the difference between survival functions may have problems, including low power and poor robustness, so the method of weighted log-rank test (WLRT) is developed to improve the test performance. In this paper, a hyperbolic-cosine-shaped ($CH$) hazard function family model is proposed to simulate delayed treatment effect scenarios. Then, based on Fleming and Harrington’s method, this paper derives the corresponding weight function and its regular corrections, which are powerful in test, theoretically. Alternative methods of parameters selection based on potential information are also developed. Further, the simulation study is conducted to compare the power performance between $CH$ WLRT, classical WLRT, modest weighted log-rank test and WLRT with logistic-type weight function under different hazard scenarios and simulation settings. The results indicate that the $CH$ statistics are powerful and robust in testing the late difference, so the $CH$ test is useful and meaningful in practice.

1. Introduction

Recently, with the rapid development of medicine, clinical trials, as important processes in the evaluation of new drugs, have received more attention, and the related biostatistics methods need to be improved. In many clinical trials collecting time-to-event data as the endpoint and conducting data analysis under the framework of survival analysis, one of the most significant problem is how to compare two survival curves, or using a mathematical expression, how to test whether there exists a difference between survival functions from different groups.

The log-rank test [1] and Cox regression [2] are two of the most classical and widely used statistical methods in comparing survival functions. The log-rank test as a non-parametric method is usually used in randomized controlled trials (RCT) which matches covariates between groups through randomization before starting the trial, while Cox regression is often used in population studies to quantify the effects of covariates [3]. Both of these methods are actually based on the proportional hazard assumption, which assumes that the hazard ratio of two groups are constant through time, and the standard log-rank test has the highest power in that case [1]. Most traditional clinical trials satisfy proportional hazard approximately, so subsequent statistical inferences are usually based on the assumption.

However, the advances in immuno-oncology have presented many cases violating the proportional hazard assumption, and that is called the non-proportional hazard (NPH) scenario. The mechanism of immunotherapy, such as the PD-1/PD-L1 inhibitor, is motivating the human body’s immune system to take anti-tumor reactions [4]. Its treatment effects are indirect and need a transition period to reveal and stabilize compared with the traditional treatment methods, such as chemotherapy [5], so the situation of the delayed treatment effect is such that the difference between the treatment and control group is not revealed at once but, after a certain period, it often takes place in related studies. Some examples are nivolumab versus docetaxel in treating advance non-squamous non-small-cell lung cancer [6], pembrolizumab versus docetaxel for treating the same disease [7] and eribulin mesylate versus capecitabine in treating locally advanced or metastatic breast cancer [8]. Besides the immuno-oncology study, the delayed treatment effect is also observed in RCT studies on other diseases, such as nephrosis [9], cardiovascular disease [10], bone marrow transplantation [11] and even infectious disease [12]. The delayed treatment effect is the most common NPH scenario in practice [13] and deserves special methods in order to be dealt with.

Delayed treatment effect scenarios represented by immunotherapy have brought challenges to traditional test methods. Plenty of numeric simulation results have shown that the standard log-rank test has problems, including low power and poor robustness in the existing NPH scenario [13,14,15], while the result of Cox regression is difficult to interpret when the proportional hazard assumption is violated. Therefore, classical test methods need to be improved when there is a potential delayed treatment effect.

There are two main alternative test methods under RCT designs, including the weighted log-rank test (WLRT) [16] and methods based on weighted difference in survival curves, such as restricted mean survival time (RMST) [17,18]. The latter one has not received wide recognition in the field of medicine and clinical trials [19]. The WLRT is an improved method of the standard log-rank test, which is the most common test method in clinical trials and has gained more attention, so this paper is mainly about the WLRT.

The basic idea of WLRT is adding weights to different observations, according to the scenarios of the hazard ratio, and a related theoretical framework was proposed by Fleming and Harrington [20]. Using notations from martingale theory, the general form of WLRT statistics $W_K$ is as follows:

$$W_K=\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}{\int }_0^{\infty }W(t)\frac{{\overline{Y}}_1(t){\overline{Y}}_2(t)}{{\overline{Y}}_1(t)+{\overline{Y}}_2(t)}\left\{\frac{d{\overline{N}}_1(t)}{{\overline{Y}}_1(t)}-\frac{d{\overline{N}}_2(t)}{{\overline{Y}}_2(t)}\right\},$$

(1)

where $n_i$ denotes the sample size of the ith group, ${\overline{Y}}_i(t)$ denotes the number of individuals at risk in the ith group at time t, ${\overline{N}}_i(t)$ denotes the number of individuals taking events in the ith group by time t, and $W(t)$ denotes the weight function. Fleming and Harrington proved that $W_K$ follows normal distribution asymptotically in a large sample [16], so

$$Z_K=W_K/\sqrt{{\hat{\sigma }}_{W_K}}\sim N(0,1),$$

(2)

where

$${\hat{\sigma }}_{W_K}^2=\int \left(\frac{K^2}{{\overline{Y}}_1(t)}+\frac{K^2}{{\overline{Y}}_2(t)}\right)\left(1-\frac{\Delta {\overline{N}}_1(t)+\Delta {\overline{N}}_2(t)-1}{{\overline{Y}}_1(t)+{\overline{Y}}_2(t)-1}\right)\frac{d({\overline{N}}_1(t)+{\overline{N}}_2(t))}{{\overline{Y}}_1(t)+{\overline{Y}}_2(t)},$$

(3)

and

$$K={\left(\frac{n_1{n}_2}{n_1+n_2}\right)}^{1/2}W(t)\frac{{\overline{Y}}_1{\overline{Y}}_2}{n_1{n}_2}\frac{n_1+n_2}{{\overline{Y}}_1+{\overline{Y}}_2}.$$

(4)

By selecting different weight functions $W(t)$, different WLRT statistics can be acquired. A classical weight function called the $G^{\rho ,\gamma }$ family proposed by Fleming and Harrington [20] is

$$W(t)={(S(t))}^{\rho }{(1-S(t))}^{\gamma },$$

(5)

where $S(t)$ is the survival function at time t (usually use Kaplan–Meier estimation [21] to approximate), and $\rho$ and $\gamma$ are two parameters that can be selected. When $\rho =0,\gamma >0$, more weight is put on the late observations, thus the corresponding WLRT can have better performance in testing the delayed treatment effect. $G^{0,1}$ and $G^{0,2}$ are two common $G^{\rho ,\gamma }$ tests.

Besides the $G^{\rho ,\gamma }$ family, other forms of weight function have also been developed in the literature. Magirr et al. proposed the modestly weighted log-rank (mWLRT) test which has the following weight function:

$$W_{mWLRT}(t)=\frac{1}{max\{\widehat{S}(t),\widehat{S}(t^{*})\}},$$

(6)

where $\hat{S}(t^{*})$ is the estimation of survival function at some certain time $t^{*}$, and the time $t^{*}$ can be calculated using their method and is associated with the expected occurrence time of treatment effect [22]. Magirr et al. proved that their method is non-inferior to the standard log-rank test under almost all scenarios. Unlike other WLRT, Yu et al. considered the weight function based on the time instead of the estimation of survival functions, and a logistic-like weight function (denoted as $wLRT$) proposed by them is as follows:

$$W_{wLRT}=\frac{e^{a(t-\tau )}}{1+e^{a(t-\tau )}},$$

(7)

where $\tau$ is associated with the median time of transition period and a is associated with the length of transition period [23]. Moreover, Breslow et al. [24], Xu et al. [25], Zucker and Lakatos [26], Yang and Prentice [27] and others also developed various WLRT methods to deal with NPH scenarios.

However, all of these WLRT are not uniformly most powerful under various delayed treatment effect scenarios. The simulation results from these studies and other review studies [14,28] show that a proper selection of the weight function and corresponding parameters is vital to the performance of the test. If the selection does not meet the real situation well, the power of the test may be very low, and the robustness will be affected a lot. Some methods, such as the $wLRT$ proposed by Yu et al., rely on prior information a lot, so they may be not very powerful when such information is lacking. Furthermore, these weight functions may be hard to interpret from the medical perspective and not associated with the expression of survival curves intuitively. Moreover, although there have been many studies on improved WLRT, the references to be compared in these studies are the classical $G^{\rho ,\gamma }$ test, and there are rare parallel comparisons between these novel methods.

It should be mentioned that versatile combination tests based on WLRT have been proposed recently. Such tests, such as the “Max-Combo” test, take the maximum or linear combination of some WLRT [14,20], so they are more robust than the single WLRT in general situations and do not require too much prior information [13,26,29,30]. However, the construction of these combination tests does rely on the selection of single WLRT, and their performances are greatly influenced by the properties of single WLRT. Additionally, though combination tests have good robustness, their power in specific scenarios will not exceed the most powerful WLRT or their component test statistics. In that case, our study still focuses on the single WLRT under the specific situation that the delayed treatment effect appears.

This paper aims to establish a parametric model of hazard functions family to fit the delayed treatment effect scenarios and solve its corresponding most theoretically powerful WLRT under the Fleming and Harrington framework. Additionally, this paper compares the novel WLRT with the classical $G^{\rho ,\gamma }$ test and other latest WLRT in the simulation study, and two application examples are analyzed to evaluate their practical performance. The rest of this paper is organized as follows: In Section 2, we define the novel $CH$ hazard function family to fit the delayed treatment effect scenario and discuss its associated properties. In Section 3, the corresponding $CH$ weight function is derived to construct the powerful WLRT, and methods of parameter selection are also demonstrated. We conduct numerical simulation study to evaluate the performance of different WLRT under various settings and report the results in Section 4. In Section 5, we demonstrate two examples with real world data. In Section 6, we discuss some inspirations from our study and give some suggestions on testing the delayed treatment effect in practice. We summarize the content of this paper and give the conclusion in Section 7.

2. $\mathit{CH}$ Hazard Function Family

2.1. Definition

In order to establish the model of hazard function to fit the scenario of the delayed treatment effect and obtain its related weight function, the features of delayed treatment effect in clinical trials should be considered first, and they can be summarized as follows:

• In the early stage of trial, the control group which applies traditional treatment has revealed certain treatment effects, while the effect of the treatment group remains invalid or not obvious due to the mechanism of drugs. In that case, the hazard ratio at this time can be considered equivalent to 1 or belonging to a neighborhood containing 1.
• As the trial goes on, the effect of the treatment group begins to be revealed, so the hazard ratio decreases gradually and is less than 1 in the end.
• In the late stage of the trial, the effect of the treatment group is fully revealed and tends to be stable. The scenario in this stage can be considered approximate to the proportional hazard [31], so the hazard ratio asymptotically converges to a constant less than 1.

Based on such features and inspired by properties of the hyperbolic cosine ($cosh$) function $f(x)=\frac{1}{2}(e^{-x}+e^x)$, we propose a hazard function family called the $CH$ family, which has the following form:

$${\lambda }_{\theta }(t;\rho ,\gamma )=\gamma ·(\frac{\rho }{e^{t+\theta }}+e^{t+\theta }),t\ge 0,\rho \ge 0,\gamma >0,$$

(8)

where t is the time, $\{\rho ,\gamma \}$ is defined as the shape parameters, which determines the shape of the hazard function and corresponding survival function, and $\theta$ is defined as the group parameter which distinguishes different groups. In fact, it should be mentioned that this model can be simplified to two parameters by reparameterization. However, we write the function family in this form for two main reasons: (1) each parameter can have relatively intuitive meaning in this form, which will be illustrated soon; and (2) the most powerful weight function of $CH$ family can be easily derived in this form. As the name implies, the differences between the clinical trials are determined by shape parameters, while the difference between groups in one clinical trial is determined by the group parameter. In other words, only group parameters define the specific $CH\{\rho ,\gamma \}$ family and we assume that groups from one trial share the same shape parameters. Therefore, the role of $\theta$ is reflected in fitting the survival curve, and it is inessential for testing the difference between groups from a family. Knowing the relationship between hazard function $\lambda (t)$ and survival function $S(t)=exp(-{\int }_0^t\lambda (s)ds)$, the statistical inference on survival functions can be conducted with hazard functions as the medium, and the corresponding $CH$ survival function family has the following form:

$$S_{\theta }(t;\rho ,\gamma )=exp(-{\int }_0^t\lambda (s,\theta ;\rho ,\gamma )ds)=exp{(\rho ·e^{-t-\theta }-e^{t+\theta }+e^{\theta }-\rho ·e^{-\theta })}^{\gamma }$$

(9)

The clinical trial with hazard functions in the $CH$ family can almost fit three features of the delayed treatment effect discussed above, and the details of the proof are shown in the Appendix A. Therefore, the $CH$ function family can simulate different scenarios of the delayed treatment effect and help conduct further inference.

2.2. Properties

We consider the properties of the $CH$ function family and discuss how it can fit delayed treatment effect scenarios first. Because two hazard functions of groups in a clinical trial share the same shape parameters, we denote them as $\{{\rho }_0,{\gamma }_0\}$, and we assume that the group parameters of the control and treatment group are ${\theta }_C$ and ${\theta }_T$, respectively. Without loss of generality, we assume that ${\theta }_C>{\theta }_T$. Thus, the hazard functions of two groups are

$${\lambda }_{{\theta }_C}(t)={\gamma }_0·({\rho }_0{e}^{-(t+{\theta }_C)}+e^{t+{\theta }_C}),$$

(10)

$${\lambda }_{{\theta }_T}(t)={\gamma }_0·({\rho }_0{e}^{-(t+{\theta }_T)}+e^{t+{\theta }_T}).$$

(11)

The role of group parameter $\theta$ is discussed under the scene of fitting survival functions. It should be noted that all graphs of the $CH$ family hazard function are the same when the shape parameters are fixed as $\{{\rho }_0,{\gamma }_0\}$, and can be obtained by shifting the graph of $\lambda (t;\rho ,\gamma )=\gamma ·(\rho e^{-t}+e^t)$ by $\theta$ horizontally. A larger difference between two group parameters ${\theta }_C-{\theta }_T$ will lead to a larger difference in performance between the two groups. As $t\to +\infty$, the hazard ratio $r(t)$ converges to the constant $e^{{\theta }_C-{\theta }_T}$. Meanwhile, the sum of group parameters ${\theta }_C+{\theta }_T$ is associated with the time when two survival curves separate, and we recommend controlling the range of $\theta$ in an interval near 0 to have a better fitting effect based on plenty of numerical experiments.

Various combinations of group parameters lead to different initial survival scenarios and hazard ratios in the long term. To illustrate the effect of various parameters selection on the relative relation of survival functions and hazard ratio between groups, we present some graphs. Fixing $\rho =2$, $\gamma =0.1$, the survival curves and the hazard ratio with different alternatives of $\theta$ are shown in Figure 1. For obviousness, we choose some extreme value of parameters, so the graphs may be not as typical as the delayed treatment effect scenario. When the value of ${\theta }_C-{\theta }_T$ is relatively small, the survival function may cross in the beginning and this situation actually corresponds to the scenario that the experimental drug is ineffective, while the other is effective at that time. If the superiority is slight, this scenario can be considered a special delayed treatment effect case rather than a cross hazard.

When $\rho =0$, $\lambda (t;\gamma )=\gamma ·e^t$, the $CH$ function family degenerates to the classical exponential function and the survival time follows an exponential distribution. In the beginning of trials, the first term of the $CH$ family function outweighs the second term but the difference between the different functions is relatively small. However, the situation becomes opposite as the time increases. In fact, parameter $\rho$ is the relative weight between two terms of the $CH$ function family, and its influence on the value of the function is from the horizontal dimension. The relatively smaller the $\rho$, the closer the time-to-event data follows the exponential distribution, while the relatively larger the $\rho$, the later the second term $e^{t+\theta }$ takes effect on the value of the function. Thus, by altering $\rho$, the time for the two survival curves to separate, which is also the initial time of the relative treatment effect, will be different. Fixing $\gamma =0.1$, ${\theta }_C=-0.4$ and ${\theta }_T=0.4$, the survival curves and hazard ratio with different alternatives of $\rho$ are illustrated in Figure 2. Therefore, to increase $\rho$, the expected relative treatment effect of the experiment drug will be postponed, but its long-term effects will remain the same.

As for the parameter $\gamma$, its influence on the value of the function is from the vertical dimension. Since the value of $\rho$ is often determined by the specific scenario of the delayed treatment effect and the value of the hazard function will remain at a high level when $\rho$ is large, the role of $\gamma$ is to balance the range of hazard functions. Fixing $\rho =1$, ${\theta }_C=-0.4$ and ${\theta }_T=0.4$, the survival curves and hazard ratio with different alternatives of $\gamma$ are illustrated in Figure 3. Therefore, increasing $\gamma$, the time when the relative treatment effect occurs will not change, but the expected survival rate at that time will decrease, which means that the trial will reach its designed end earlier.

With proper parameters setting, a pair of $CH$ hazard functions can fit the delayed treatment effect scenario intuitively as expected, and the specific pattern can be constructed by adjusting parameters.

3. $\mathit{CH}$ Weight Function and CH Test

3.1. CH Class Weight Function

Since the $CH$ function family can simulate the delayed treatment effect scenario, we can solve its corresponding weight function, which is most theoretically powerful, and construct the WLRT for the delayed treatment effect thusly. Using the method that solves the most powerful weight function with the hazard function family known proposed by Fleming and Harrington [20], the corresponding weight function and test statistics of $CH$ hazard function family can be derived with the following expressions:

$$W_{CH}(t)=\frac{8\rho }{4\rho +{(\sqrt{m^2+4\rho }+m)}^2}-1,$$

(12)

where

$$m=\frac{1}{\gamma }log\hat{S}(t)+\rho -1,$$

(13)

and $\hat{S}(t)$ is the pooled estimation of survival function at time t.

However, the result through direct derivation may not meet the regulation conditions of WLRT sometimes, so its asymptotic normality in large sample may have problems. We give two alternative correction forms of the $CH$ weight function. The first one is to take the non-negative part of (12) and we have the $C{H}_{+}$ weight function as follows:

$$W_{C{H}_{+}}(t)=max\{0,\frac{8\rho }{4\rho +{(\sqrt{m^2+4\rho }+m)}^2}-1\}.$$

(14)

However, this correction is rough and gives extreme weights to early observations, which may be difficult to interpret. Therefore, we propose the second correction $C{H}_C$ which is a smooth version of (12), and the weight function has the expression of

$$W_{C{H}_C}(t)=\frac{8{\rho }^2}{4{\rho }^2+{(\sqrt{m^2+4\rho }+m)}^2}-1.$$

(15)

The m in the (14) and (15) is the same as m in the (12). The WLRT with the $C{H}_{+}$ and $C{H}_C$ weight function follows normal distribution asymptotically, and the detailed derivation of these weight functions and the proof of their large sample properties are shown in Appendix B. For simplicity, the $CH$ weight function refers to $C{H}_{+}$ and $C{H}_C$ in the following part of this paper, and we can derive their $CH$ test statistics and construct corresponding $CH$ tests. Though the expressions of the $CH$ weight functions are more complex than $G^{\rho ,\gamma }$ to some degree, it will not increase the computational burden a lot when using statistical software. As for the two-sided hypothesis test that

$$H_0:\forall t,S_C(t)=S_T(t)vs{H}_1:\exists t,S_C(t)\ne S_T(t),$$

(16)

the null hypothesis will be rejected when

$$\frac{|W_{CH}|}{\sqrt{{\widehat{{\sigma }^2}}_{CH}}}>z_{1-\alpha /2},$$

(17)

where $\widehat{{\sigma }^2}$ can be obtained from (3) and (4), $W_{CH}$ is the WLRT statistics in (1) with $CH$ weight function $W_{C{H}_{\_}}(t)$ and $z_{1-\alpha /2}$ is the $1-\alpha /2$ quantile of normal distribution. The one-sided test can be constructed similarly.

Though the expressions of the two $CH$ weight functions have slight differences from the original version, they share its properties generally. Since the $CH$ function family can simulate the delayed treatment effect scenario well, the two $CH$ weight functions derived from the original version should have high power in testing the delayed treatment effect, especially for the trial data fitting the $CH$ function family.

3.2. Selection of Parameters

There are two undefined parameters $\{\rho ,\gamma \}$ in the $CH$ weight functions, so how to select proper parameters in practice is very important. According to the process of derivation, we learn that when the shape parameters of the $CH$ statistics $\{\rho ,\gamma \}$ are the same as the actual parameters of the real data, the test will have the highest power. However, the statistical decision must be taken before conducting the clinical trial, so it is impossible to select the best parameters when the data are inaccessible. In that case, we propose two methods of parameter selection for the $CH$ test.

3.2.1. Prior Information Method

Because the effects of shape parameters $\{\rho ,\gamma \}$ are relatively obvious and each combination can map to a specific delayed treatment effect scenario, some prior information about hazard functions or treatment effects can help us select better parameters. In fact, in practice, some information about the specific delayed treatment effect scenario is often accessible [23,27], and this information may come from pilot trials, clinical trials of previous phase, parallel studies, the literature, an estimation based on professional experience or knowledge, etc.

Under the scenario of the delayed treatment effect, some significant indices of interest in the clinic include the constant hazard ratio in the late stage of trials, the time when two survival functions or hazard functions separate, the survival rate when the treatment take delayed effects, etc. Using the expression of $CH$ weight functions, we can derive parameters with such available prior information. In derivation, to control the range of $\theta$, we can let ${\theta }_C=-{\theta }_T={\theta }_0>0$. Because the derivatives of the $CH$ function family increase as t goes up and the difference between the two functions keeps increasing, we can consider the time $t_0$, letting ${\lambda }_{{\theta }_C}(t_0)={\lambda }_{{\theta }_T}(t_0)$ as the time when the hazard functions of two groups begin to be different and we have

$$exp{(\rho ·e^{-t_0-{\theta }_0}-e^{t_0+{\theta }_0}+e^{{\theta }_0}-\rho ·e^{-{\theta }_0})}^{\gamma }=exp{(\rho ·e^{-t_0+{\theta }_0}-e^{t_0-{\theta }_0}+e^{-{\theta }_0}-\rho ·e^{{\theta }_0})}^{\gamma }.$$

(18)

Meanwhile, having let ${\theta }_C=-{\theta }_T$, we can use ${\lambda }_0(t)$ to approximate ${\lambda }_{{\theta }_C}(t)$ and ${\lambda }_{{\theta }_T}(t)$ or $S_0(t)$ to approximate $S_{{\theta }_C}(t)$ and $S_{{\theta }_T}(t)$. Thus, if the approximate total survival rate at time $t_0$ is $P_0$, we can let

$$P_0=S_0(t_0)={[exp(\rho e^{-t_0}-e^{t_0}+1-\rho )]}^{\gamma }.$$

(19)

In that case, if we have information about the time $t_0$ when the hazards of two groups differ and the total survival rate $P_0$ at time $t_0$, by solving (18) and (19), we have

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill & \hat{\rho }=e^{2t_0}\hfill \\ \hfill & \hat{\gamma }=\frac{log{P}_0}{1-e^{2t_0}}.\hfill \end{array}\right.\end{array}$$

Thus, $\hat{\rho }$ and $\hat{\gamma }$ can be used to in $CH$ statistics to test the expected scenario with the prior information. The above derivation is only an example for illustration. If other types of prior information can be acquired, such as information about survival functions, similar derivation of parameters can be conducted.

It should be noted that sometimes when the time scale of trial data is small, e.g., using day as the unit, the value of time data will be large and the shape parameter $\gamma$ cannot control the range of the hazard function as a result. Therefore, estimating parameters through information associated with absolute time directly may cause numerical inflation, and the result may have large errors and be unreliable. In that case, we recommend conducting unit conversion or numerical transformation to decrease the magnitude of time data before analysis. When using weeks or months as the time unit or scaling the data so that $t_0=1$, the method will have better performance. The expected median survival time should be not longer than 15 after the numerical transformation.

3.2.2. Default Selection Method

Just as $G^{0,1}$ is often the default selection from $G^{\rho ,\gamma }$ family statistics in testing the delayed treatment effect, there is little or no prior information about hazard functions or survival curves when making the statistical decision sometimes, so we give a pair of shape parameters as the default selection. Through plenty of numerical simulation experiments, we recommend $\rho =2,\gamma =0.1$ as the default selection because of its high power and robustness.

By altering $\theta$, the $CH\{2,0.1\}$ survival function family can represent an “average” scenario of the delayed treatment effect. If we consider that the trial enters the late period when the survival rate is below 0.2, the $CH\{2,0.1\}$ survival functions will separate around the $1/3$ start time of the late period. The hazard ratio will be similar to the proportional hazard scenario if the treatment effect occurs too early, while the treatment effect may be not so clinically significant if it occurs too late. Figure 4 shows the survival curves of the $CH\{2,0.1\}$ family with different settings of $\theta$ ($0.4$, $0.2$, 0, $-0.2$ and $-0.4$ for $\theta$ from left to right).

Though the default selection method is not so sensitive to the scale of data as the prior information method, we still recommend conducting similar data transformation to improve its performance.

4. Simulation Study

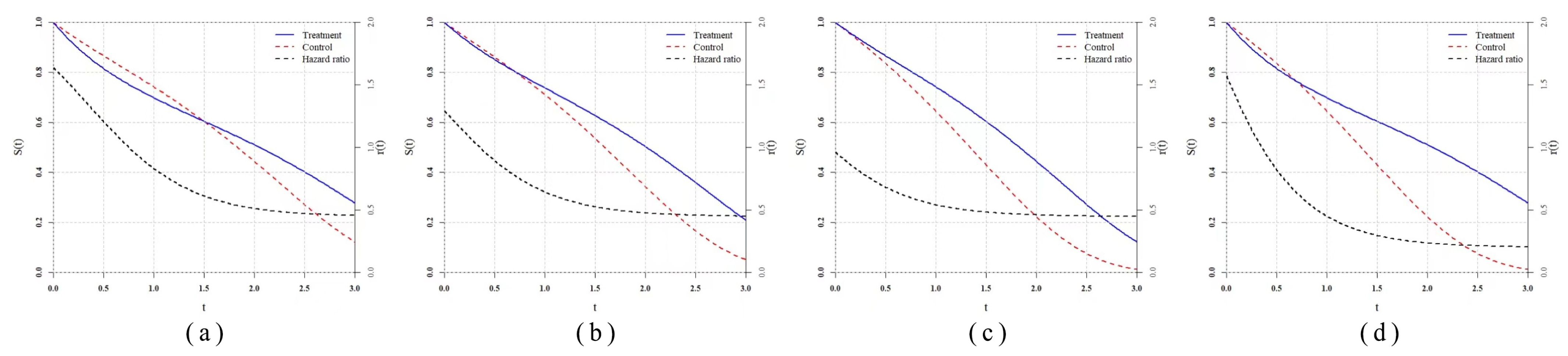
In order to evaluate the performance of $CH$ weight functions in practice and compare them with other WLRT dealing with the delayed treatment effect, we conduct comprehensive simulation studies. The simulation is set up as an RCT with two arms, treatment and control separately. The hypothesis test is set as two-sided, and the significant level $\alpha$ is $0.05$. The type I error rate under null hypothesis and the empirical power under alternative hypothesis of various test will be calculated and compared to evaluate their performance under different scenarios. The survival functions of the treatment and control group are denoted as $S_T$ and $S_C$, and hazard functions are denoted as ${\lambda }_T$ and ${\lambda }_C$, respectively. Like other parallel studies, most scenarios in this paper are simulated by generating time-to-event data following piece-wise exponential distribution, so different settings are distinguished by hazard functions.

Two test statistics $C{H}_{+}\{\rho ,\gamma \}$ and $C{H}_C\{\rho ,\gamma \}$ are proposed in this paper, and each statistic has two methods to select the parameter pair, so the $C{H}_{+}\{\rho ,\gamma \}$ using the prior information method and default selection method, and $C{H}_C\{\rho ,\gamma \}$ using these two methods are denoted as $C{H}_{+}^P$, $C{H}_{+}^D$, $C{H}_C^P$ and $C{H}_C^D$, respectively. In the $G^{\rho ,\gamma }$ family, we choose $G^{0,1}$ and $G^{0,2}$, which put weights on the late observations and $G^{0,0}$, which is the standard log-rank test as comparisons. In other types of WLRT, we choose the modestly weighted log-rank test ($mWLRT$) proposed by Magirr et al. [22] and a novel WLRT ($wLRT$) proposed by Yu et al. [23] to make comparisons. Both these two weight functions were introduced briefly in Section 1. We choose these two WLRT for two main reasons: (1) Both them are relatively recent methods and have shown good performance in their simulation studies according to the literature. (2) There are also undetermined parameters that may depend on prior information before trials in these two WLRT, which ensures comparability with the $CH$ WLRT.

A total of four statistics have parameters depending on prior information: $C{H}_{+}^P$, $C{H}_C^P$, $mWLRT$ and $wLRT$. Similar to the example shown in Section 3.2.1, as for $CH$ statistics based on the prior information method ($C{H}_{+}^P$ and $C{H}_C^P$), we use the time $t_0$ when the two survival curves separate and $P_0$, which is the total survival rate at $t_0$, to help determine the parameters. We assume we have certain information about $t_0$ in each scenario and the average hazard function of two groups before $t_0$ (${\lambda }_0$) can be obtained by the pilot study or previous studies to calculate the expected $P_0$. The $mWLRT$ also depends on the separation time of two curves, so it shares the same $t_0$ with $C{H}_{+}^P$ and $C{H}_C^P$ in our simulation. The method of $wLRT$ has two parameters: a is the length of the transition period that the drug takes to be effective, and $\tau$ is the center of the transition period. All of this information will be specified in their applicable range later. In order to control the range of parameters, all time-related data will be scaled so that $t_0=1$ in dealing with $CH$ statistics.

4.1. Type I Error Rate

First, we set ${\lambda }_T(t)={\lambda }_C(t)$ to evaluate the type I error rate of these statistics. The total sample size (denoted as n) is 50, 100 and 200, respectively, with a $1:1$ ratio to the two groups, and the number of repetitions is set as 10,000 to see whether the type I error rate can be controlled well. In this series of simulations, $t_0=5$, $a=5$, $\tau =7.5$, and $P_0$ is estimated by the hazard function before $t_0$. Three scenarios under a null hypothesis (NH) are shown in

Table 1. Hazard functions of scenarios under null hypothesis.

Scenarios	$0\le \mathit{t}<5$	$5\le \mathit{t}<10$	$10\le \mathit{t}$
$N{H}_1$	0.1	0.1	0.1
$N{H}_2$	0.04	0.08	0.12
$N{H}_3$	0.1	0.08	0.05

, and hazard functions of two groups are the same in each scenarios.

The simulation result is shown in

Table 2. Type I error rates.

Scenarios	n	${\mathit{CH}}_{+}^{\mathit{P}}$	${\mathit{CH}}_{+}^{\mathit{D}}$	${\mathit{CH}}_{\mathit{C}}^{\mathit{P}}$	${\mathit{CH}}_{\mathit{C}}^{\mathit{D}}$	$\mathit{wLRT}$	$\mathit{mWLRT}$	${\mathit{G}}^{0,1}$	${\mathit{G}}^{0,2}$	${\mathit{G}}^{0,0}$
$N{H}_1$	50	0.064	0.064	0.062	0.062	0.067	0.065	0.072	0.081	0.058
	100	0.054	0.054	0.051	0.051	0.055	0.051	0.057	0.062	0.049
	200	0.050	0.049	0.052	0.052	0.055	0.052	0.049	0.050	0.051
$N{H}_2$	50	0.059	0.058	0.059	0.059	0.057	0.059	0.066	0.079	0.057
	100	0.054	0.053	0.052	0.052	0.053	0.051	0.057	0.063	0.051
	200	0.050	0.049	0.052	0.052	0.055	0.052	0.049	0.050	0.051
$N{H}_3$	50	0.061	0.061	0.059	0.059	0.062	0.062	0.068	0.079	0.058
	100	0.055	0.053	0.055	0.055	0.055	0.053	0.058	0.063	0.054
	200	0.050	0.049	0.052	0.052	0.055	0.052	0.049	0.050	0.051

. The result shows that all these statistics arise with a type I error rate inflation to a different degree when $n=50$. As the sample size increases to 100, only $G^{0,2}$ shows a slight type I error rate inflation ($\alpha >0.06$), while all statistics can generally control the type I error rate when $n=200$. Therefore, the recommended total sample size should be more than 100 to ensure the reliability of the test in practice. Four $CH$ family statistic of interests in this study can control the type I error rate relatively well and show non-inferiority to other WLRT.

4.2. Simple Settings

Then, we consider the simulation of the delayed treatment effect with simple settings and compare powers of various statistics in the test. “Simple” means we generate the time-to-event data based on the designated hazard functions directly using the Monte Carlo method, and there will be no censoring in that case. In this series of simulations, $t_0=0.5$, $a=0.5$, $\tau =0.75$, and $P_0$ is estimated by the hazard function of control group before $t_0$.

Table 3. Hazard functions of scenarios in simple settings.

Scenario	Group	$0\le \mathit{t}<0.5$	$0.5\le \mathit{t}<1$	$1\le \mathit{t}$
$D{T}_1$	Control	2	4	4
	Treatment	2	0.4	0.4
$D{T}_2$	Control	1	2	4
	Treatment	1	1.4	1.8
$D{T}_3$	Control	$C{H}_{\theta =0.1}\{3,0.05$}
	Treatment	$C{H}_{\theta =-0.1}\{3,0.05$}
$D{T}_4$	Control	$C{H}_{\theta =0.11}\{4,0.02$}
	Treatment	$C{H}_{\theta =-0.11}\{4,0.02$}
$P{H}_1$	Control	1.4	1.4	1.4
	Treatment	1.0	1.0	1.0
$P{H}_2$	Control	1.2	1.5	1.8
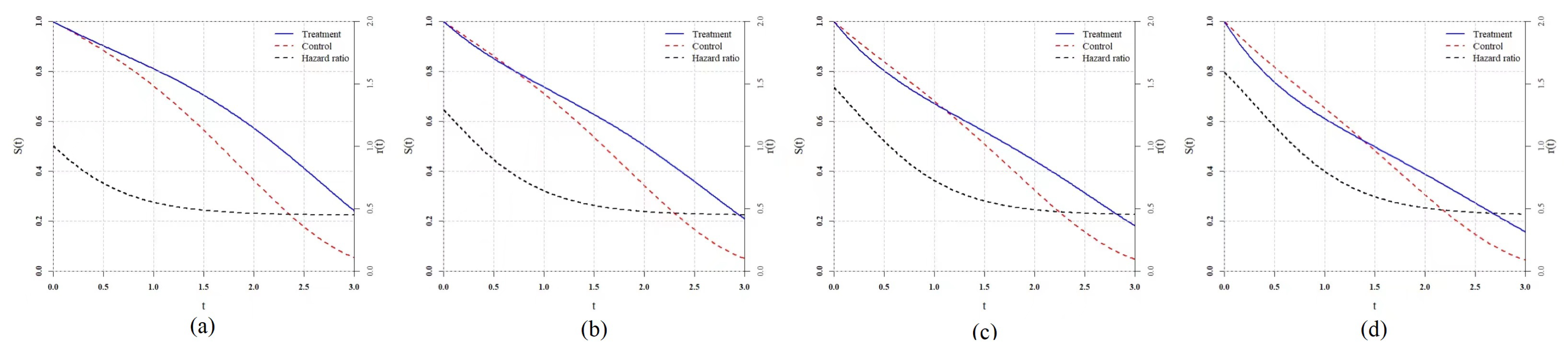
	Treatment	0.8	1.0	1.2

shows the hazard functions of each scenario. As for the delayed treatment effect scenario (denoted by DT), we copy the classical scenario which was studied by Fleming [32], Lee [33] et al. in $D{T}_1$ and set the $D{T}_2$ in which the treatment takes a longer time to be effective. We set two scenarios $D{T}_3$ and $D{T}_4$ with the $CH$ family hazard function, so $CH$ family test statistics should be the most powerful, theoretically, in that case. Thus, in these two scenarios, we use the exact $\{\rho ,\gamma \}$ for $C{H}_{+}^P$ and $C{H}_C^P$ rather than the estimated. Moreover, we add $P{H}_1$ and $P{H}_2$, which are two proportional hazard scenarios to evaluate their robustness. In $P{H}_1$ and $P{H}_2$, we assume the prior information is known exactly and set $t_0=0$, $a=0$, and $\tau =0$. The total sample size is fixed as 200 and the group ratio remains at $1:1$, while the repetition number is 5000.

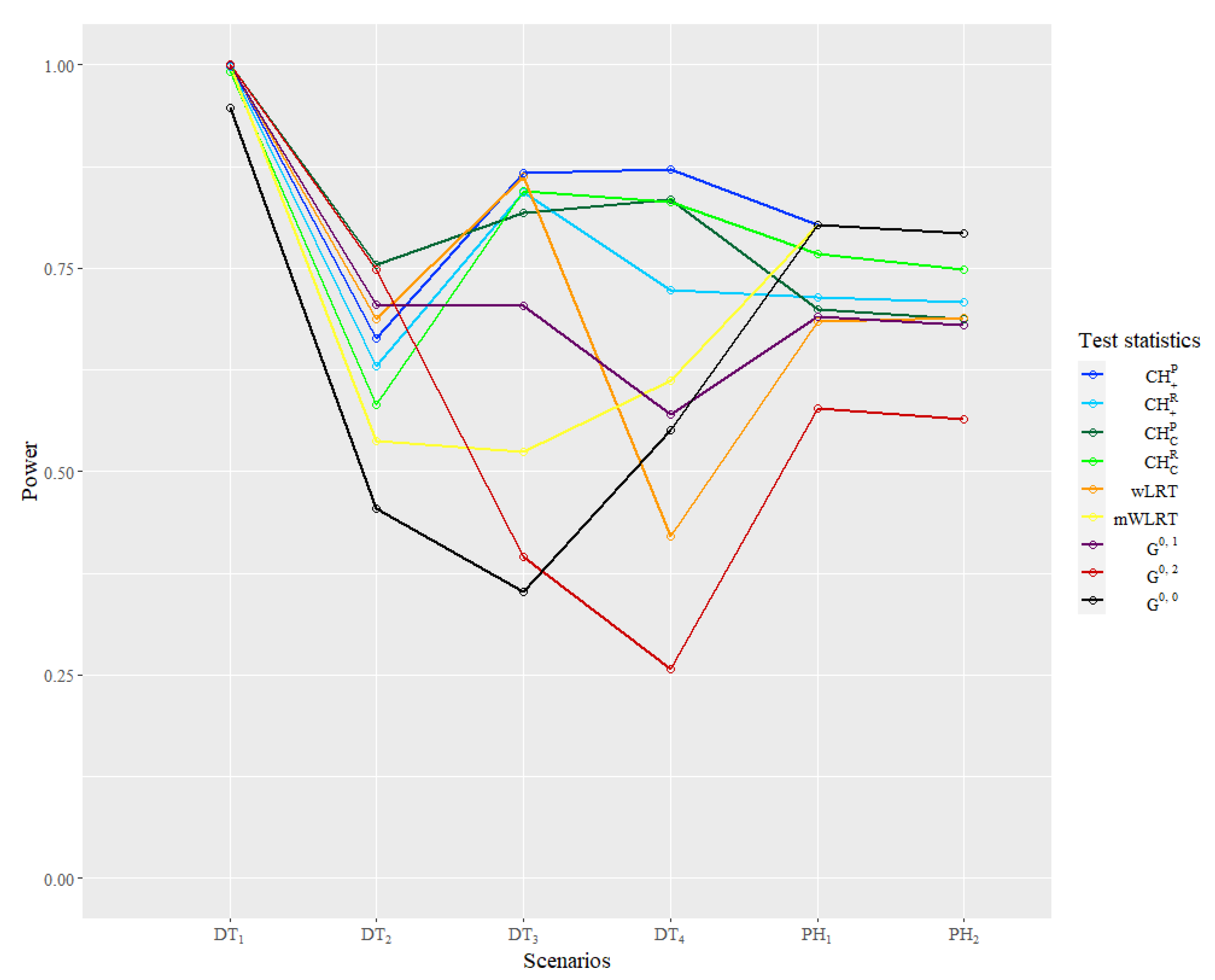
The power result of the simulation is reported in

Table 4. Empirical power in simple settings.

Scenarios	${\mathit{CH}}_{+}^{\mathit{P}}$	${\mathit{CH}}_{+}^{\mathit{D}}$	${\mathit{CH}}_{\mathit{C}}^{\mathit{P}}$	${\mathit{CH}}_{\mathit{C}}^{\mathit{D}}$	$\mathit{wLRT}$	$\mathit{mWLRT}$	${\mathit{G}}^{0,1}$	${\mathit{G}}^{0,2}$	${\mathit{G}}^{0,0}$
$D{T}_1$	1.000	0.997	1.000	0.991	1.000	1.000	1.000	1.0000	0.947
$D{T}_2$	0.663	0.629	0.755	0.582	0.687	0.537	0.705	0.748	0.455
$D{T}_3$	0.868	0.844	0.819	0.845	0.863	0.524	0.704	0.395	0.353
$D{T}_4$	0.872	0.723	0.835	0.831	0.420	0.612	0.570	0.257	0.551
$P{H}_1$	0.803	0.714	0.699	0.768	0.685	0.803	0.691	0.578	0.803
$P{H}_2$	0.792	0.709	0.687	0.749	0.689	0.792	0.679	0.564	0.792

and Figure 5. In the classical scenario $D{T}_1$, powers of all statistics are close to 1 because of the larger sample size compared to the literature, so this result is seldom reflected, except the good large sample properties of all statistics. In the $D{T}_2$, $C{H}_C^P$ is the most powerful one and $G^{\rho ,\gamma }$ WLRT has relatively good performance, while powers of other WLRT are relatively low. In $D{T}_3$ and $D{T}_4$ generated from the $CH$ function family, four $CH$ test statistics are almost the most powerful as expected. In $D{T}_3$, the $G^{\rho ,\gamma }$ WLRT shows great disadvantages compared with other statistics. The performance of $wLRT$ is still good in $D{T}_3$ but very poor in $D{T}_4$. In $D{T}_4$, $CH$ statistics outperform other WLRT overwhelmingly. The powers of $wLRT$ and $G^{0,2}$ are lower than 0.5, which is very likely to cause a type II error in practice. As for the same type of $CH$ statistics, the statistic using the prior information method are more powerful than using the default selection method, while the latter one can still let the power remain at a relatively high level.

As for the $P{H}_1$ and $P{H}_2$, the standard log-rank test $G^{0,0}$ is the most powerful one as expected. The statistics based on prior information actually degenerate to $G^{0,0}$, so they share the same power. Powers of $CH$ statistics using the default selection method are much higher than $G^{0,1}$ and $G^{0,2}$, which also have default parameters. In particular, the power of $C{H}_C^D$ is very close to the power of $G^{0,0}$.

4.3. Clinical Trial Settings

In simple settings, we only consider the ideal situation in which time-to-event data follow the designate distribution completely and the settings of hazard function are relatively simple. However, the data in clinical trials have certain differences from the ideal situation:

• The order of magnitude of hazard function will be smaller, while the order of magnitude of time will be larger. The duration will be longer.
• Subjects will not be enrolled in the trial simultaneously but during a enrollment period lasting for several months one by one.
• Due to the factors including cost and efficiency, the trial will be ended after a certain time, or a planned proportion of subjects will show endpoint events rather than all endpoints observed. In that case, there will be type III censoring in practice.

The existence of censoring may be the most influential factor for power of test statistics, and the features of real trials discussed above should be simulated to evaluate their practical performance. In this part, we do not consider the censoring caused by accidents such as a drop-out or adverse event. In this series of simulations, $t_0=3$, $a=4$, $\tau =5$ and $P_0$ are estimated by the hazard function of the control group before $t_0$ in each scenario.

Taking the study of Ray et al. [13] as a reference, we set the time unit as month, and the patient enrollment follows a Poisson process with a parameter equal to 25. The total enrollment period lasts for 12 months, which means about 300 subjects will be enrolled in the trial. The end of the trial is set as $70\%$ of the total, which is that about 210 subjects are observed to occur endpoint events. The group ratio is still $1:1$ and the number of repetition is 5000.

To ensure the comparability, we take the simulation study settings in the study of Ray et al. [13] as references and copy four delayed treatment effect scenarios denoted as $C-D{T}_1$, $C-D{T}_2$, $C-D{T}_3$ and $C-D{T}_4$. $C-D{T}_1$ and $C-D{T}_2$ are two typical delayed treatment effect scenarios, while $C-D{T}_3$ and $C-D{T}_4$ are more complex with converging tails. To enrich the scenarios and evaluate the performance of statistics when prior information is lacking or unreliable, we set $C-D{T}_5$ and $C-D{T}_6$ where the delayed treatment effects do not take at $t_0=3$, so the distributions of analysis data are different from the distributions expected by prior information. Furthermore, we add two proportional hazard scenarios $C-P{H}_1$ and $C-P{H}_2$ to make the comparison, and statistics based on prior information keep the same parameter selection as above rather than the real. The specific hazard function settings are shown in the

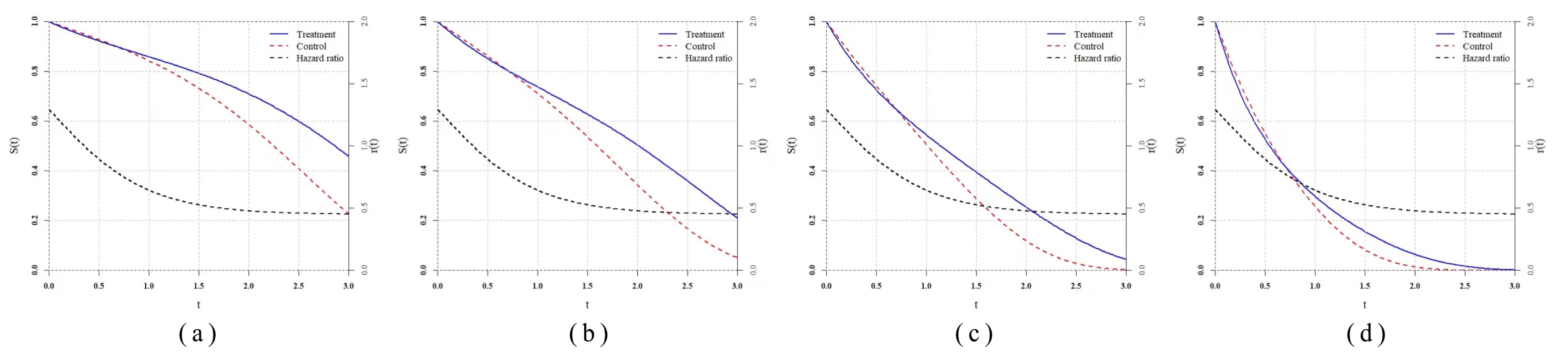
Table 5. Hazard functions of scenarios in clinical trial settings.

Scenario	Group	$0\le \mathit{t}<3$	$3\le \mathit{t}<7$	$7\le \mathit{t}$
$C-D{T}_1$	Control	0.104	0.161	0.161
	Treatment	0.103	0.077	0.077
$C-D{T}_2$	Control	0.226	0.222	0.222
	Treatment	0.210	0.079	0.079
$C-D{T}_3$	Control	0.104	0.161	0.140
	Treatment	0.103	0.077	0.168
$C-D{T}_4$	Control	0.104	0.161	0.161
	Treatment	0.103	0.077	0.137
$C-D{T}_5$	Control	0.072	0.072	0.223
	Treatment	0.072	0.072	0.112
$C-D{T}_6$	Control	0.097	0.097	0.097
	Treatment	0.103	0.065	0.049
$C-P{H}_1$	Control	0.121	0.121	0.121
	Treatment	0.083	0.083	0.083
$C-P{H}_2$	Control	0.080	0.105	0.140
	Treatment	0.056	0.074	0.098

.

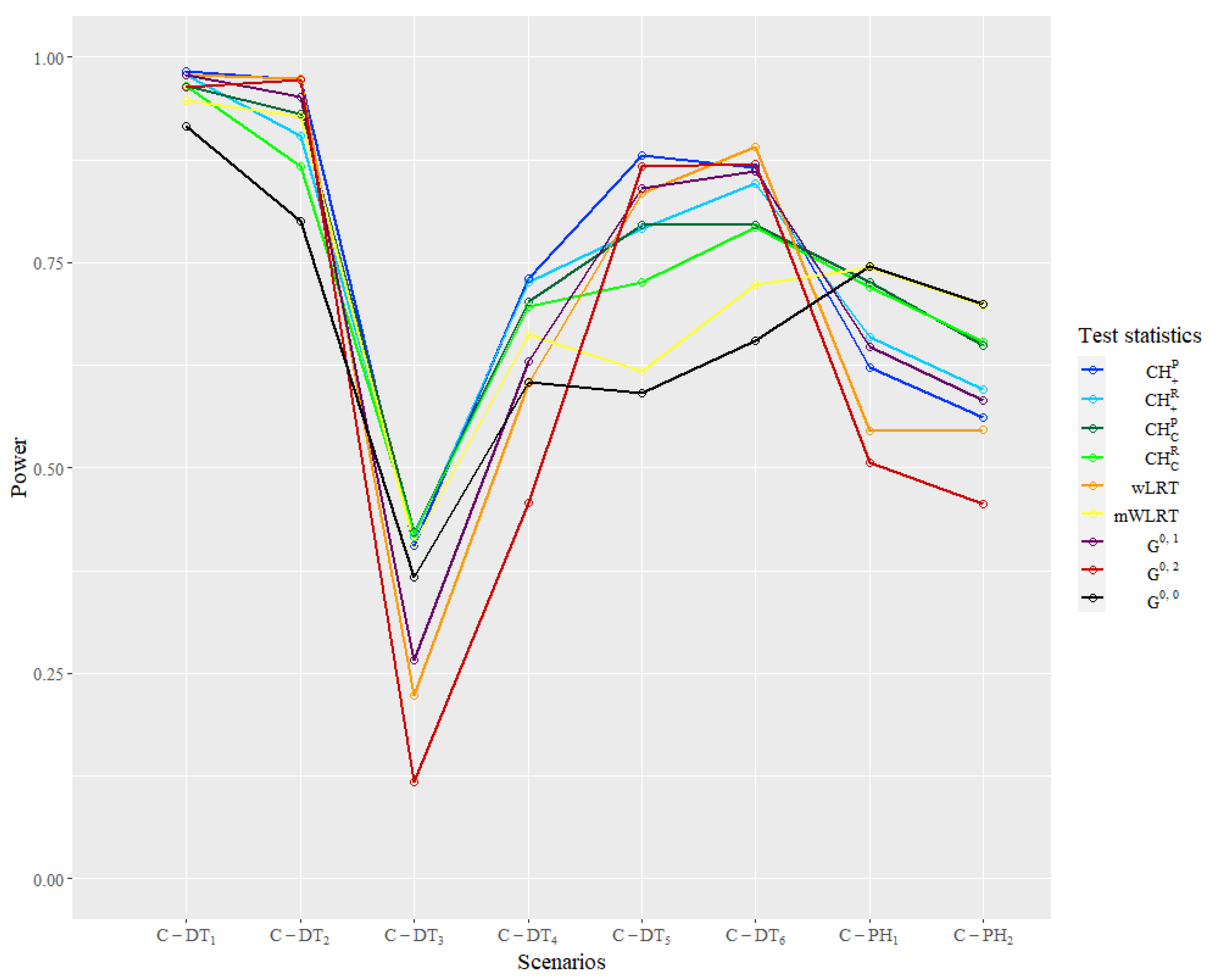
The empirical power result of the simulation in the clinical trial settings is reported in

Table 6. Empirical power in clinical trial settings.

Scenarios	${\mathit{CH}}_{+}^{\mathit{P}}$	${\mathit{CH}}_{+}^{\mathit{D}}$	${\mathit{CH}}_{\mathit{C}}^{\mathit{P}}$	${\mathit{CH}}_{\mathit{C}}^{\mathit{D}}$	$\mathit{wLRT}$	$\mathit{mWLRT}$	${\mathit{G}}^{0,1}$	${\mathit{G}}^{0,2}$	${\mathit{G}}^{0,0}$
$C-D{T}_1$	0.983	0.979	0.965	0.965	0.978	0.947	0.978	0.963	0.916
$C-D{T}_2$	0.972	0.904	0.931	0.867	0.974	0.928	0.951	0.972	0.801
$C-D{T}_3$	0.405	0.416	0.421	0.420	0.223	0.409	0.265	0.118	0.368
$C-D{T}_4$	0.7300	0.726	0.702	0.696	0.602	0.662	0.630	0.457	0.604
$C-D{T}_5$	0.880	0.792	0.796	0.726	0.835	0.618	0.841	0.8672	0.590
$C-D{T}_6$	0.865	0.846	0.796	0.793	0.890	0.724	0.861	0.871	0.655
$C-P{H}_1$	0.623	0.659	0.726	0.721	0.545	0.744	0.647	0.507	0.746
$C-P{H}_2$	0.561	0.595	0.650	0.654	0.547	0.698	0.582	0.456	0.700

and Figure 6. In the classic scenarios of $C-D{T}_1$ and $C-D{T}_2$, $G^{0,0}$ has the lowest power, while other statistics maintain good performance. $C{H}_{+}^P$, $wLRT$, $G^{0,1}$ and $G^{0,2}$ have relative higher powers over 0.9, and $mWLRT$ and $C{H}_C^P$ are in the second tier. In $C-D{T}_3$ and $C-D{T}_4$ with a converging tail, the $CH$ family statistics manifest an obvious advantage over others. In $C-D{T}_3$, only $CH$ and $mWLRT$ statistics have power over 0.4, while other statistics perform very poorly. In $C-D{T}_4$, the power of $CH$ statistics is over 0.1 above the power of the $G^{\rho ,\gamma }$ family. The power of $wLRT$ and $G^{0,2}$ are the lowest in these two scenarios and have great contrasts with the first two scenarios, which shows relatively poor robustness of these two statistics. In $C-D{T}_5$ and $C-D{T}_6$, where the delayed treatment effect occurs later, powers of $C{H}_{+}^P$, $wLRT$, $G^{0,1}$ and $G^{0,2}$ are the highest and over 0.8, while powers of the other three $CH$ statistics are in the second tier but higher than $mWLRT$ and $G^{0,0}$ obviously. In $C-P{H}_1$ and $C-P{H}_2$ that belong to the proportional hazard scenarios, $G^{0,0}$ is the most powerful one as expected. Similar to the simple settings, the power of $mWLRT$ is very close to the $G^{0,0}$, and the $CH$ family statistics also have robust performance. The powers of $C{H}_C^P$ and $C{H}_C^D$ are very close to the highest one with differences less than 0.05. The performance of $wLRT$ is relatively poor in the proportional hazard ratio when the prior information is unreliable and is only higher than $G^{0,2}$.

5. Application in Real Studies

To evaluate and compare the performance of $CH$ test statistics in practical application, we conduct an analysis on some simple real world studies that fit the scenario of the delayed treatment effect. Similar to the simulation study, four $CH$ statistics, $wLRT$, $mWLRT$ and three $G^{\rho ,\gamma }$ statistics are used to test the difference in each example.

5.1. Head-and-Neck-Cancer Study

The Northern Oncology Group (NCOG) studied the effects of a different treatment strategy on head-and-neck-cancer patients, and their survival time was collected [34]. Patients who took radiation therapy alone were allocated randomly to Group 1, or Group 2 if they took radiation plus chemotherapy. The Kaplan–Meier curves of these time-to-event data are shown in Figure 7.

It is obvious that two curves are almost the same at the beginning, but Group 2 shows better survival performance later. This example is a typical delayed treatment effect scenario, and we set $t_0=5$, $P_0=0.75$, $a=2$, $\tau =5$ based on the KM plot for statistics depending on prior information.

Table 7. p-values of the tests for the head-and-neck cancer data.

	${\mathit{CH}}_{+}^{\mathit{P}}$	${\mathit{CH}}_{+}^{\mathit{R}}$	${\mathit{CH}}_{\mathit{C}}^{\mathit{P}}$	${\mathit{CH}}_{\mathit{C}}^{\mathit{R}}$	$\mathit{wLRT}$	$\mathit{mWLRT}$	${\mathit{G}}^{0,1}$	${\mathit{G}}^{0,2}$	${\mathit{G}}^{0,0}$
p-value	0.018	0.021	0.019	0.022	0.017	0.020	0.014	0.012	0.022

gives the p-values of various tests.

The result shows that the p-values of all statistics, including four $CH$ statistics, are less than 0.05. Thus, the null hypothesis is rejected and we can draw the conclusion that radiation plus chemotherapy has a better treatment effect on head-and-neck cancer. Even the standard log-rank test $G^{0,0}$ can reject the null hypothesis; the reason may be that the difference is too large between two groups and the performance of Group 2 is always better than Group 1 actually.

5.2. Kidney Infection Study

Nahman et al. conducted a study to assess the time to first exit-site infection in patients with renal insufficiency, and 43 patients utilized a surgically placed catheter (Group 1), while 76 patients utilized a percutaneous placement of their catheter (Group 2) [35]. The Kaplan–Meier curves of the time-to-event data are shown in Figure 8.

We can intuitively find that two curves are close in the beginning of the study, while Group 1 has slight better survival performance. From the 5th to 9th month, two curves cross and separate finally, and Group 2 overwhelming has a survival advantage after. In that case, this study can be considered an example of the delayed treatment effect generally.

The setting of prior information is as following: $t_0=7$, $P_0=0.85$, $a=4$, $\tau =7$.

Table 8. p-values of the tests for the kidney infection data.

	${\mathit{CH}}_{+}^{\mathit{P}}$	${\mathit{CH}}_{+}^{\mathit{R}}$	${\mathit{CH}}_{\mathit{C}}^{\mathit{P}}$	${\mathit{CH}}_{\mathit{C}}^{\mathit{R}}$	$\mathit{wLRT}$	$\mathit{mWLRT}$	${\mathit{G}}^{0,1}$	${\mathit{G}}^{0,2}$	${\mathit{G}}^{0,0}$
p-value	0.008	0.005	0.019	0.005	0.002	0.067	0.005	0.009	0.112

gives the p-values of various tests.

The p-values of $mWLRT$ and $G^{0,0}$ are greater than 0.05, while the other statistics have a p-value less than 0.05 and reject the null hypothesis. Since the difference between the two groups is obvious, $mWLRT$ and $G^{0,0}$ have relatively poor performance and will cause a type II error in this example.

These two examples show that the $CH$ statistics can test the delayed treatment effect correctly while some tests may not, so the $CH$ statistics is useful in certain application scenarios.

6. Discussion

How to deal with the delayed treatment effect and conduct a corresponding hypothesis test is a very significant topic in the clinical trial research. There has been rich work about WLRT, but their comparisons and adaptive scenarios remain to be figured out. We propose a novel parametric family of hazard function to fit the delayed treatment effect and derive the corresponding weight function based on the method develop by Fleming and Harrington. The flexibility of the $CH$ family parameters in fitting the delayed treatment effect and the good performance of $CH$ statistics show that setting up a useful and adaptive hazard function family first and then solving a corresponding weight function may be a feasible way to develop practical WLRT. Theoretically, the most powerful test can always be found through this idea, but how to improve the compatibility of the function family model and whether the result from Fleming and Harrington’s method has an analytical expression and meets the regularity conditions are problems that seem to be contradictory sometimes and need to be solved. Compared with methods defining the weight function directly, deriving the weight function based on a specific hazard function family can connect the statistical inference to the actual survival scenarios closely and thus have better clinical interpretations. This study offers an example, but the application of such ideas should not be limited. It should be mentioned that all WLRT, including $CH$ statistics, can be used for constructing combination tests according to the related large sample properties proposed by Fleming and Harrington [20], so a similar Max–Combo test (for example, $max\{C{H}_C^R,G^{0,0}\}$) can also be constructed to improve the robustness.

No test statistic can remain the most powerful uniformly under all scenarios through the result of simulation, so the relatively high power under certain common scenarios and the property of robustness are very important. From this study, the performance of $mWLRT$ is poor and only better than the standard log-rank test. Its high power under proportional hazard scenarios reflects that it is a rather conservative weight compared to other WLRT. The performance of $wLRT$ is a little extreme in the simulation: very high power in some settings and very low power in others. This phenomenon may be associated with its relatively extreme weight compared to others and the high dependence on the prior information. Apparently, such features will influence its practicability when little information is known before the trial. Generally, the $CH$ test is the recommended single WLRT of this paper. Its similar power to the standard log-rank test under proportional hazard and relative high power dealing with the delayed treatment effect ensures its robustness in testing various scenarios. Moreover, different forms of $g(t)$ in (A1) can be considered to derive test statistics that are more powerful and generalized. Both $C{H}_{+}$ and $C{H}_C$ have their advantages and disadvantages in different settings, but $C{H}_C$ has a smoother and simpler expression, which also inspires us to find better correction forms. The power of test using the prior information method is generally higher than the default selection method, but the latter one still remains at a high level. Even when there is little or no information about the pattern of the treatment effect, the $CH$ test can ensure a relative high power and increase the efficiency. In practice, the decision on the selection of test methods should be based on the properties of such test statistics and conditions of known information, and data simulation is recommended to be conducted in advance if the conditions permit.

7. Conclusions

The $CH$ hazard function has a certain significance for the modeling of delayed treatment effect with its better performance and clear parameter selection, and $CH$ tests have good robustness in application. It not only has high power in different delayed treatment effect scenarios, but is also very powerful in proportional hazards scenarios, regardless of whether the prior information is known or not. Because of these good features and stable robustness, $CH$ tests are helpful and meaningful in clinical trials when there is delayed treatment effect scenario.