Signature-Based Analysis of the Weighted-r-within-Consecutive-k-out-of-n: F Systems

Abstract

In the present paper, we deliver a reliability study of the weighted-r-consecutive-k-out-of-n: F reliability systems consisting of independent and identically distributed components. The signature vector of the structures is arithmetically determined by the aid of an appropriate Monte-Carlo simulation scheme. Several conclusions for the corresponding reliability polynomials are also drawn. An extensive numerical investigation is carried out to evaluate the performance of the weighted-r-consecutive-k-out-of-n: F reliability systems. Some stochastic signature-based comparisons among several members of the underlying family of reliability structures are also discussed.

1. Introduction

In the field of Statistical Reliability Modeling, the consecutive-type systems offer a competitive alternative with several applications in different fields, such as Telecommunication Networks, Computer Science or Industrial Management. Generally speaking, a consecutive-type reliability system consists of n linearly (or circularly) ordered components. These components are arranged in such a way that the failure criterion of the resulting scheme is activated when a pre-determined condition (or even more than one) is fulfilled.

Several consecutive-type systems are already known in the literature. One of the prevailing members of this family is the linear consecutive-k-out-of-n: F structure consisting of n linearly ordered components. The particular structure fails if and only if at least k consecutive components break down (see, e.g., [1,2,3]). Moreover, several generalizations of the aforementioned scheme have been introduced in the literature. For example, the m-consecutive-k-out-of-n: F structure consisting of n components offers a modification of the ordinary m-out-of-n: F and the consecutive-k-out-of-n: F systems; the specific reliability structure stops its operation if and only if there are at least m non-overlapping runs of k consecutive failed units (see, e.g., [4]).

Further modifications of the traditional consecutive-k-out-of-n: F structure have been studied in the literature. For instance, ref. [5] considered the combined m-consecutive-k-out-of-n: F & consecutive k_c-out-of-n: F model, which stops its operation if and only if at least k_c consecutive components stop working or at least m non-overlapping runs of k consecutive components stop their operation (k_c < mk). It is noticeable that several reliability schemes with two common failure criteria have been introduced for covering real-life applications (see, e.g., refs. [6,7] or the recent advances provided by [8,9]). In addition, the well-known r-within-consecutive k-out-of-n: F system was established by [10] and stops its operation if and only if there exist k consecutive units which include among them at least r failed components (see also [4,11,12,13]). For a detailed survey on the consecutive-type structures, one may refer to [14,15] or the well-documented monographs by [16,17]. A review work referring to reliability statistical methods in different areas of Mechanical or Industry Engineering and Physical Sciences can be found in [18].

In a traditional setup of reliability applications, the components of a structure are supposed to be identical concerning their contribution to the operation of the system. Therefore, the weight of each unit is assumed to be equal. However, there exist several real-life applications, where some components contribute more (or less) than others. On such occasions, the failure of the underlying structure depends not only on which particular units have already failed but also on their individual contributions (weights). Refs. [19,20] extended the k-out-of-n: F (consecutive-k-out-of-n: F) structures by defining a non-negative integer valued coefficient to each component. In their framework, the system stops its operation if and only if the total sum of coefficients of failed components (failed consecutive components) is at least k. Several generalizations of the weighted schemes proposed by [19,20] have been introduced in the literature. For example, the so-called weighted-r-within-consecutive-k-out-of-n: F structure fails if and only if the total weight of failed components among k consecutive components is at least r (see, e.g., [21,22]). It is evident that weighted consecutive systems have attracted a lot of reseacrh attention recently. For instance, ref. [23] studied the joint reliability importance of such structures. Ref. [24] investigated the performance of the so-called linear weighted (n,f,k) and <n,f,k> systems, while the case of assigning random weights to a system’s components is considered by [25]. Further recent advances on the topic of weighted reliability systems are provided by [26,27,28].

Throughout the lines of the present manuscript, a signature-based investigation of the weighted-r-within-consecutive-k-out-of-n: F systems is carried out. An algorithmic approach to delivering the signature coordinates of the underlying structure is described in some detail (See Section 2). Section 3 provides a closed formula for determining the reliability function of the weighted-r-consecutive-k-out-of-n: F structure. A detailed numerical experimentation sheds light on the performance of the weighted-r-consecutive-k-out-of-n: F structure. In Section 4, signature-based stochastic comparisons among several consecutive-type systems are illustrated.

2. The Signature of the Weighted-r-within-Consecutive-k-out-of-n: F System

In the following lines, we provide a step-by-step algorithmic process to determine the signature vector of the weighted-r-within-consecutive-k-out-of-n: F systems consisting of n independent and identically distributed units (i.i.d. hereafter). It is necessary to mention that, having at hand the signature of the underlying structure, we could readily deduce insightful remarks about its ability to work properly. It is evident that the signature vector of the weighted-r-within-consecutive-k-out-of-n: F system will help the practitioner to detect when the failure probability of the whole structure becomes low enough in order to take some action.

In order to make the text more readable, a list of notations seems to be necessary. The main symbols that are used in the sequel are given below.

$r,k,n:$ design parameters of the weighted-r-within-consecutive-k-out-of-n: F system

$w_i:$ weight of the $i$-th component, $i=1,2,\dots ,n$

$L_i:$ lifetime of the $i$-th component, $i=1,2,\dots ,n$

$L_{i:n}:$ ordered lifetime of the $i$-th failed component, $i=1,2,\dots ,n$

$s_i\left(w_i,r,k,n\right):$ the $i$-th coordinate of the signature vector of the weighted-r-within-consecutive-k-out-of-n: F system

$p:$ reliability of each component

$R\left(p\right):$ reliability of the whole structure.

We first assume that L corresponds to the lifetime of a weighted-r-within-consecutive-k-out-of-n: F system with n i.i.d. and by $L_1,L_2,\dots ,L_n$, the lifetimes of its units. The probability vector $\left(s_1\left(w_i,r,k,n\right), s_2\left(w_i,r,k,n\right),\dots ,s_n\left(w_i,r,k,n\right)\right)$ corresponds to the signature of the the weighted-r-within-consecutive-k-out-of-n: F structure, where

$$s_i\left(w_i,r,k,n\right)=P\left(L=L_{i:n}\right),i=1,2,\dots ,n$$

(1)

while $L_{1:n}\le L_{2:n}\le \cdots \le L_{n:n}$ are the corresponding order statistics which correspond to the lifetimes of its components. To be more clear, the ith coordinate defined in (1) provides the value of the portion $A_i/n!$. Note that $A_i$ corresponds to the amount of the specific orderings of the $L_i^{\prime }s.i=1,2,\dots ,n$, whose realization means that, when the i-th component fails, the whole system stops its operation (see, e.g., [26,27]). The positive weights, which are assigned to the components of the system, are denoted by $w_i,i=1,2,\dots ,n$. Under the assumption that the components are i.i.d., the coordinates of the signature rely only on the system structure. In other words, the signatures are not connected to the shared distribution of $L_i^{\prime }s$. Therefore, the signature is a nonparametric measure of the performance of a reliability structure.

We next describe the stepwise procedure for delivering the signature vector of the weighted-r-within-consecutive-k-out-of-n: F system, which is comprised of n i.i.d. units.

Step I. 

Define the vector $y=\left(y_1,y_2,\dots ,y_n\right)$, where its coordinates $y_i$ are assumed to be initially equal to zero for every value of i.

Step II. 

Generate a sample of size n from a continuous distribution, which represents the components’ random lifetimes of the resulting weighted-r-within-consecutive-k-out-of-n: F system.

Step III. 

Specify the design parameters r, k and $w_i,i=1,2,\dots ,n$, where $1\le k\le n,r>0,w_i>0$.

Step IV. 

Determine the random quantity C as the chronologically ordered lifetime, which leads to the failure of the weighted-r-within-consecutive-k-out-of-n: F structure. C ranges from 1 to n in respect of which the unit makes the whole system stop operating.

Step V. 

Compute the C-value for the specific sample of the order n generated at Step II. Whenever C equals i, the corresponding coordinate of $y$ becomes larger unitarily—namely, $y_i$ increases to $y_i+1$.

After realizing steps II–V δ times, we can determine the probability that the resulting structure fails upon the failure of a specific unit. In other words, the probability that the weighted-r-within-consecutive-k-out-of-n: F system stops its operation at the chronologically i-th ordered unit failure is equal to $y_i$ divided by δ—namely, $s_i\left(w_i,r,k,n\right)=y_i/\delta ,i=1,2,\dots ,n$. The numerical experimentation has been carried out by the aid of appropriate Monte-Carlo techniques. It is widely known that Monte-Carlo methods are quite capable for handling several computational problems, such as the calculation of multiple integrals or the extraction of mutual capacitances for a system of conductors (see, e.g., [29,30,31]). Note that the MATLAB package has been used. The corresponding codes are available upon request.

To numerically confirm the accuracy of the algorithmic approach described above, we first implement the proposed process for the special cases $r=2,k=2,w_1=w_2=\dots =w_n=1$ and $r=2,k=3,w_1=w_2=\dots =w_n=1$. In other words, we next provide numerical results for the weighted-2-within-consecutive-2-out-of-n: F structure and the weighted-2-within-consecutive-3-out-of-n: F system consisting of n i.i.d. units with equal weights. For these special cases, the signature vector of the resulting structures has already been determined by the aid of a generating function approach provided by [13]. Therefore, we next recalculate the signature of the weighted-2-within-consecutive-2-out-of-n: F structure and the weighted-2-within-consecutive-3-out-of-n: F structure by the aid of the proposed simulation algorithm. Our target is to verify the accuracy of the simulation results in comparison with the corresponding ones provided by [13]. For each result displayed in the following tables, 40,000 iterations have been accomplished in order to reach the required level of accuracy.

Table 1 and Table 2 illustrate the signature vectors of the weighted-2-within-consecutive-2-out-of-n: F structure and the weighted-2-within-consecutive-3-out-of-n: F structures with equal weights for n = 3, 4, …, 10. Each cell of these tables gives us not only the accurate value but also the simulated one. Specifically, the upper entry of each cell has been computed basd on the new algorithmic procedure, whilst the lower entry expresses the accurate value of the corresponding vector.

Table 1. Accurate and simulation-based signatures of the weighted-2-within-consecutive-2-out-of-n: F system for specific designs.

n	k	i = 1	i = 2	i = 3	i = 4	i = 5	i = 6	i = 7	i = 8	i = 9	i = 10
3	2	0	0.66778	0.33222
		0	0.667	0.333
4	2	0	0.50100	0.49900	0
		0	0.500	0.500	0
5	2	0	0.40377	0.49662	0.09960	0
		0	0.400	0.500	0.100	0
6	2	0	0.33353	0.46627	0.20020	0	0
		0	0.333	0.467	0.200	0	0
7	2	0	0.28747	0.42673	0.25755	0.02825	0	0
		0	0.286	0.428	0.257	0.029	0	0
8	2	0	0.25025	0.39108	0.28532	0.07335	0	0	0
		0	0.250	0.393	0.286	0.071	0	0	0
9	2	0	0.21852	0.36567	0.29763	0.11013	0.00805	0	0	0
		0	0.22222	0.36111	0.29762	0.11111	0.00794	0	0	0
10	2	0	0.20108	0.33220	0.29810	0.14447	0.02415	0	0	0	0
		0	0.200	0.333	0.300	0.143	0.024	0	0	0	0

Each cell displays the simulation-based value (upper case) and the accurate one (lower case).

Table 2. Accurate and simulation-based signatures of the weighted-2-within-consecutive-3-out-of-n: F system for specific designs.

n	k	i = 1	i = 2	i = 3	i = 4	i = 5	i = 6	i = 7	i = 8	i = 9	i = 10
3	3	0	1	0
		0	1	0
4	3	0	0.83430	0.16570	0
		0	0.833	0.167	0
5	3	0	0.69740	0.30260	0	0
		0	0.700	0.300	0	0
6	3	0	0.60025	0.39975	0	0	0
		0	0.600	0.400	0	0	0
7	3	0	0.51738	0.45290	0.02973	0	0	0
		0	0.524	0.448	0.028	0	0	0
8	3	0	0.46723	0.45893	0.07385	0	0	0	0
		0	0.464	0.464	0.071	0	0	0	0
9	3	0	0.41723	0.46155	0.12122	0	0	0	0	0
		0	0.417	0.464	0.119	0	0	0	0	0
10	3	0	0.37705	0.45660	0.16150	0.00485	0	0	0	0	0
		0	0.378	0.456	0.162	0.004	0	0	0	0	0

Each cell displays the simulation-based value (upper case) and the accurate signature (lower case).

According to Table 1, one may easily observe that the differences between the simulation-based results and the exact results are slight in all the cases presented. For example, under the weighted-2-within-consecutive-2-out-of-9: F structure, the exact non-zero entries are positioned at entries 2-6 of the corresponding signature vector. These values are equal to 22.222%, 36.111%, 29.762%, 11.111% and 0.794%, respectively. On the other hand, the simulation-based signature entries being produced by the aid of the proposed process are 21.852%, 36.567%, 29.763%, 11.013% and 0.805%, correspondingly.

According to Table 2, the simulation-based results do not differ significantly from the exact results (in all cases illustrated). For example, under the weighted-2-within-consecutive-3-out-of-6: F structure, the exact non-zero entries are positioned at the 2nd and 3rd entry of the signature vector. These entries are equal to 60.0% and 40.0% respectively. On the other hand, the simulation-based signature entries being produced by the aid of the proposed process are 60.025% and 39.975%, correspondingly.

In the sequel, the proposed approach is implemented to compute the signatures of weighted-r-within-consecutive-k-out-of-n: F structures for different scenarios and unequal weights. Specifically, it is of some interest to investigate the performance of the underlying system for several choices of design parameters and components’ weights. More precisely, Table 3, Table 4, Table 5 and Table 6, provide the signature vectors of the weighted-r-within-consecutive-k-out-of-n: F structures of order n = 7, 8, 9, 10 under different design scenarios.

Table 3. The signature of the weighted-r-within-consecutive-k-out-of-7: F systems.

n	k	r	wi	i = 1	i = 2	i = 3	i = 4	i = 5	i = 6	i = 7
7	4	3	1,2,1,2,1,2,1	0	0.57230	0.31225	0.08697	0.02848	0	0
			1,1,1,2,2,2,2	0	0.56850	0.32010	0.11140	0	0	0
			1,2,2,2,2,2,1	0	0.71027	0.28973	0	0	0	0
		4	1,2,1,2,1,2,1	0	0.09420	0.36168	0.37495	0.16917	0	0
			1,1,1,2,2,2,2	0	0.28523	0.45282	0.20355	0.05840	0	0
			1,2,2,2,2,2,1	0	0.42685	0.37355	0.17070	0.02890	0	0
		5	1,2,1,2,1,2,1	0	0	0.17290	0.28582	0.20708	0.18925	0.14495
			1,1,1,2,2,2,2	0	0	0.22837	0.37215	0.30323	0.09625	0
			1,2,2,2,2,2,1	0	0	0.37045	0.45945	0.17010	0	0
	5	3	1,2,1,2,1,2,1	0	0.61950	0.32330	0.05720	0	0	0
			1,1,1,2,2,2,2	0	0.71660	0.25462	0.02877	0	0	0
			1,2,2,2,2,2,1	0	0.86187	0.13813	0	0	0	0
		4	1,2,1,2,1,2,1	0	0.14427	0.64425	0.14238	0.0691	0	0
			1,1,1,2,2,2,2	0	0.28628	0.54243	0.14237	0.02892	0	0
			1,2,2,2,2,2,1	0	0.47425	0.38203	0.14372	0	0	0
		5	1,2,1,2,1,2,1	0	0	0.25712	0.45522	0.29023	0	0
			1,1,1,2,2,2,2	0	0	0.49855	0.35432	0.14622	0	0
			1,2,2,2,2,2,1	0	0	0.62555	0.34430	0.03012	0	0
	6	3	1,2,1,2,1,2,1	0	0.71047	0.23337	0.05615	0	0	0
			1,1,1,2,2,2,2	0	0.80858	0.19143	0	0	0	0
			1,2,2,2,2,2,1	0	0.95145	0.04855	0	0	0	0
		4	1,2,1,2,1,2,1	0	0.14145	0.65880	0.17150	0.02825	0	0
			1,1,1,2,2,2,2	0	0.28400	0.62740	0.08860	0	0	0
			1,2,2,2,2,2,1	0	0.47287	0.38380	0.14333	0	0	0
		5	1,2,1,2,1,2,1	0	0	0.37330	0.42512	0.20158	0	0
			1,1,1,2,2,2,2	0	0	0.54473	0.42720	0.02807	0	0
			1,2,2,2,2,2,1	0	0	0.85780	0.14220	0	0	0

For example, under the design $n=7,r=5,k=4,w_1=w_3=w_5=w_7=1,w_2=w_4=w_6=2$, the non-zero entries are positioned at places 3–7 of the signature vector and are equal to 0.17290, 0.28582, 0.20708, 0.18925 and 0.14495, respectively. In simple words, the weighted-5-within-consecutive-4-out-of-7: F structure consisting of i.i.d. components fails upon its i-th ordered component’s failure (I = 3, 4, 5, 6, 7), with a probability equal to 17.29%, 28.582%, 20.708%, 18.925% and 14.495%, respectively. As is readily observed from Table 3, as the weights increase, the performance of the resulting system worsens.

Table 4. The signature of the weighted-r-within-consecutive-k-out-of-8: F systems.

n	k	r	wi	i = 1	i = 2	i = 3	i = 4	i = 5	i = 6	i = 7	i = 8
8	4	3	1,2,1,2,1,2,1,2	0	0.53400	0.37833	0.07380	0.01387	0	0	0
			1,1,1,1,2,2,2,2	0	0.42365	0.39393	0.18243	0	0	0	0
			1,2,2,2,2,2,2,1	0	0.64480	0.35520	0	0	0	0	0
		4	1,2,1,2,1,2,1,2	0	0.11048	0.31998	0.37035	0.19920	0	0	0
			1,1,1,1,2,2,2,2	0	0.21077	0.35570	0.29092	0.14260	0	0	0
			1,2,2,2,2,2,2,1	0	0.42755	0.35763	0.17085	0.04398	0	0	0
		5	1,2,1,2,1,2,1,2	0	0	0.14213	0.27455	0.28273	0.19615	0.10445	0
			1,1,1,1,2,2,2,2	0	0	0.14413	0.27185	0.29568	0.21513	0.07322	0
			1,2,2,2,2,2,2,1	0	0	0.28578	0.42923	0.28500	0	0	0
	5	3	1,2,1,2,1,2,1,2	0	0.60375	0.34225	0.05400	0	0	0	0
			1,1,1,1,2,2,2,2	0	0.56927	0.35647	0.07425	0	0	0	0
			1,2,2,2,2,2,2,1	0	0.78122	0.21877	0	0	0	0	0
		4	1,2,1,2,1,2,1,2	0	0.17833	0.46437	0.28408	0,07322	0	0	0
			1,1,1,1,2,2,2,2	0	0.21295	0.4662	0.23505	0.0858	0	0	0
			1,2,2,2,2,2,2,1	0	0.501	0.35435	0.12932	0.01533	0	0	0
		5	1,2,1,2,1,2,1,2	0	0	0.25012	0.42102	0.25675	0,0721	0	0
			1,1,1,1,2,2,2,2	0	0	0.24825	0.42137	0.25733	0.07305	0	0
			1,2,2,2,2,2,2,1	0	0	0.50195	0.41573	0.08232	0	0	0
	6	3	1,2,1,2,1,2,1,2	0	0.71535	0.24913	0.03553	0	0	0	0
			1,1,1,1,2,2,2,2	0	0.67463	0.30755	0.01783	0	0	0	0
			1,2,2,2,2,2,2,1	0	0.89412	0.10587	0	0	0	0	0
		4	1,2,1,2,1,2,1,2	0	0.17895	0.57308	0.2196	0.02838	0	0	0
			1,1,1,1,2,2,2,2	0	0.21352	0.5736	0.18295	0.02993	0	0	0
			1,2,2,2,2,2,2,1	0	0.5383	0.35673	0.10497	0	0	0	0
		5	1,2,1,2,1,2,1,2	0	0	0.36023	0.41652	0.18812	0.03513	0	0
			1,1,1,1,2,2,2,2	0	0	0.36092	0.4803	0.14037	0	0	0
			1,2,2,2,2,2,2,1	0	0	0.7153	0.27117	0.01353	0	0	0
	7	3	1,2,1,2,1,2,1,2	0	0.74775	0.25225	0	0	0	0	0
			1,1,1,1,2,2,2,2	0	0.75065	0.24935	0	0	0	0	0
			1,2,2,2,2,2,2,1	0	0.96572	0.03427	0	0	0	0	0
		4	1,2,1,2,1,2,1,2	0	0.21545	0.66355	0.121	0	0	0	0
			1,1,1,1,2,2,2,2	0	0.21455	0.66038	0.12507	0	0	0	0
			1,2,2,2,2,2,2,1	0	0.53233	0.36023	0.10745	0	0	0	0
		5	1,2,1,2,1,2,1,2	0	0	0.44758	0.49528	0.05715	0	0	0
			1,1,1,1,2,2,2,2	0	0	0.446	0.49517	0.05883	0	0	0
			1,2,2,2,2,2,2,1	0	0	0.89425	0.10575	0	0	0	0

For example, under the design $n=8,r=3,k=7,w_1=w_2=w_3=w_4=1,w_5=w_6=w_7=w_8=2$, the non-zero entries are positioned at the 2nd and 3rd places of the signature vector and are equal to 0.75065 and 0.24935, respectively. In simple words, the weighted-3-within-consecutive-7-out-of-8: F structure consisting of i.i.d. components fails upon its i-th ordered component’s failure (I = 2, 3), with a probability equal to 75.065% and 24.395%, respectively. As is readily observed from Table 4, a large number of weights over 1 leads to a worse design.

Table 5. The signature of the weighted-r-within-consecutive-k-out-of-9: F systems.

n	k	r	wi	i = 1	i = 2	i = 3	i = 4	i = 5	i = 6	i = 7	i = 8	i = 9
9	4	3	1,2,1,2,1,2,1,2,1	0	0.4714	0.38418	0.10502	0.0315	0.0079	0	0	0
			1,1,1,1,2,2,2,2,2	0	0.41887	0.3815	0.19962	0	0	0	0	0
			1,2,2,2,2,2,2,2,1	0	0.5862	0.40168	0.01213	0	0	0	0	0
		4	1,2,1,2,1,2,1,2,1	0	0.08687	0.2597	0.34075	0.26655	0.04612	0	0	0
			1,1,1,1,2,2,2,2,2	0	0.25405	0.34437	0.26967	0.1319	0	0	0	0
			1,2,2,2,2,2,2,2,1	0	0.41668	0.35607	0.17922	0.04802	0	0	0	0
		5	1,2,1,2,1,2,1,2,1	0	0.10627	0.219	0.25025	0.19998	0.14203	0.08248	0	0
			1,1,1,1,2,2,2,2,2	0	0	0.13225	0.2492	0.28835	0.22548	0.10472	0	0
			1,2,2,2,2,2,2,2,1	0	0	0.22595	0.38445	0.34123	0.04838	0	0	0
	5	3	1,2,1,2,1,2,1,2,1	0	0.5254	0.3684	0.0989	0.0073	0	0	0	0
			1,1,1,1,2,2,2,2,2	0	0.55915	0.32348	0.11737	0	0	0	0	0
			1,2,2,2,2,2,2,2,1	0	0.72142	0.27858	0	0	0	0	0	0
		4	1,2,1,2,1,2,1,2,1	0	0.14085	0.39625	0.32913	0.12577	0	0	0	0
			1,1,1,1,2,2,2,2,2	0	0.27658	0.4393	0.20458	0.07955	0	0	0	0
			1,2,2,2,2,2,2,2,1	0	0.50125	0.3457	0.12943	0.02363	0	0	0	0
		5	1,2,1,2,1,2,1,2,1	0	0	0.17335	0.35105	0.30967	0.15388	0.01205	0	0
			1,1,1,1,2,2,2,2,2	0	0	0.23805	0.35718	0.2786	0.10343	0.02275	0	0
			1,2,2,2,2,2,2,2,1	0	0	0.40445	0.43475	0.1608	0	0	0	0
	6	3	1,2,1,2,1,2,1,2,1	0	0.63997	0.27823	0.0743	0.0075	0	0	0	0
			1,1,1,1,2,2,2,2,2	0	0.6681	0.283	0.0489	0	0	0	0	0
			1,2,2,2,2,2,2,2,1	0	0.83217	0.16783	0	0	0	0	0	0
		4	1,2,1,2,1,2,1,2,1	0	0.14028	0.49067	0.2909	0.0705	0.00765	0	0	0
			1,1,1,1,2,2,2,2,2	0	0.27713	0.50775	0.16708	0.04805	0	0	0	0
			1,2,2,2,2,2,2,2,1	0	0.5534	0.33827	0.10045	0.00788	0	0	0	0
		5	1,2,1,2,1,2,1,2,1	0	0	0.2769	0.36657	0.24695	0.09832	0.01125	0	0
			1,1,1,1,2,2,2,2,2	0	0	0.35745	0.42592	0.18548	0.03115	0	0	0
			1,2,2,2,2,2,2,2,1	0	0	0.59745	0.35433	0.04822	0	0	0	0
	7	3	1,2,1,2,1,2,1,2,1	0	0.66895	0.29523	0.03583	0	0	0	0	0
			1,1,1,1,2,2,2,2,2	0	0.7502	0.23822	0.01158	0	0	0	0	0
			1,2,2,2,2,2,2,2,1	0	0.9177	0.0823	0	0	0	0	0	0
		4	1,2,1,2,1,2,1,2,1	0	0.16337	0.59345	0.2192	0.02397	0	0	0	0
			1,1,1,1,2,2,2,2,2	0	0.2792	0.57685	0.1272	0.01675	0	0	0	0
			1,2,2,2,2,2,2,2,1	0	0.5855	0.33095	0.08355	0	0	0	0	0
		5	1,2,1,2,1,2,1,2,1	0	0	0.33187	0.47747	0.18245	0.0082	0	0	0
			1,1,1,1,2,2,2,2,2	0	0	0.4626	0.4405	0.08843	0.00847	0	0	0
			1,2,2,2,2,2,2,2,1	0	0	0.77555	0.21657	0.00788	0	0	0	0
	8	3	1,2,1,2,1,2,1,2,1	0	0.72528	0.23835	0.03637	0	0	0	0	0
			1,1,1,1,2,2,2,2,2	0	0.80548	0.19453	0	0	0	0	0	0
			1,2,2,2,2,2,2,2,1	0	0.9713	0.0287	0	0	0	0	0	0
		4	1,2,1,2,1,2,1,2,1	0	0.16748	0.66978	0.14008	0.02268	0	0	0	0
			1,1,1,1,2,2,2,2,2	0	0.27882	0.64035	0.08082	0	0	0	0	0
			1,2,2,2,2,2,2,2,1	0	0.58268	0.3335	0.08382	0	0	0	0	0
		5	1,2,1,2,1,2,1,2,1	0	0	0.40463	0.45863	0.12837	0.00838	0	0	0
			1,1,1,1,2,2,2,2,2	0	0	0.5466	0.42095	0.03245	0	0	0	0
			1,2,2,2,2,2,2,2,1	0	0	0.91548	0.08453	0	0	0	0	0

For example, under the design $n=9,r=5,k=7,w_1=w_9=1,w_2=w_3=w_4=w_5=w_6=w_7=w_8=2,$ the non-zero entries are positioned at the 3rd, 4th and 5th places of the signature vector and are equal to 0.77555, 0.21657 and 0.00788, respectively. In simple words, the weighted-5-within-consecutive-7-out-of-9: F structure consisting of i.i.d. components fails upon its i-th ordered component’s failure (i = 3, 4, 5), with a probability equal to 77.555%, 21.657% and 0.788%, respectively. Under the specific design, the failure of the resulting scheme seems to occur quickly with a large probability.

Table 6. The signature of the weighted-r-within-consecutive-k-out-of-10: F systems.

n	k	r	wi	i = 1	i = 2	i = 3	i = 4	i = 5	i = 6	i = 7	i = 8	i = 9	i = 10
10	4	3	1,2,1,2,1,2,1,2,1,2	0	0.44203	0.41375	0.11585	0.02467	0.0037	0	0	0	0
			1,1,1,1,1,2,2,2,2,2	0	0.33215	0.37557	0.25988	0.0324	0	0	0	0	0
			1,2,2,2,2,2,2,2,2,1	0	0.52785	0.43895	0.0332	0	0	0	0	0	0
		4	1,2,1,2,1,2,1,2,1,2	0	0.0881	0.2476	0.32238	0.26127	0.07568	0.00498	0	0	0
			1,1,1,1,1,2,2,2,2,2	0	0.19903	0.28975	0.27298	0.1856	0.05265	0	0	0	0
			1,2,2,2,2,2,2,2,2,1	0	0.40053	0.3668	0.18498	0.0477	0	0	0	0	0
		5	1,2,1,2,1,2,1,2,1,2	0	0	0.09287	0.20017	0.25975	0.2208	0.1363	0.06775	0.02235	0
			1,1,1,1,1,2,2,2,2,2	0	0.09227	0.19037	0.24195	0.23242	0.1671	0.07587	0	0	0
			1,2,2,2,2,2,2,2,2,1	0	0	0.1826	0.34168	0.35652	0.11432	0.00487	0	0	0
	5	3	1,2,1,2,1,2,1,2,1,2	0	0.51067	0.38965	0.09517	0.0045	0	0	0	0	0
			1,1,1,1,1,2,2,2,2,2	0	0.4453	0.39045	0.16425	0	0	0	0	0	0
			1,2,2,2,2,2,2,2,2,1	0	0.66385	0.33615	0	0	0	0	0	0	0
		4	1,2,1,2,1,2,1,2,1,2	0	0.15593	0.36018	0.32117	0.15047	0.01225	0	0	0	0
			1,1,1,1,1,2,2,2,2,2	0	0.2237	0.3591	0.27585	0.14135	0	0	0	0	0
			1,2,2,2,2,2,2,2,2,1	0	0.49078	0.34495	0.1363	0.02797	0	0	0	0	0
		5	1,2,1,2,1,2,1,2,1,2	0	0	0.16937	0.32877	0.30245	0.16578	0.03363	0	0	0
			1,1,1,1,1,2,2,2,2,2	0	0	0.16687	0.28613	0.28447	0.19168	0.07085	0	0	0
			1,2,2,2,2,2,2,2,2,1	0	0	0.3339	0.43012	0.23597	0	0	0	0	0
	6	3	1,2,1,2,1,2,1,2,1,2	0	0.62013	0.31233	0.06267	0.00487	0	0	0	0	0
			1,1,1,1,1,2,2,2,2,2	0	0.55217	0.36428	0.08355	0	0	0	0	0	0
			1,2,2,2,2,2,2,2,2,1	0	0.77623	0.22378	0	0	0	0	0	0	0
		4	1,2,1,2,1,2,1,2,1,2	0	0.15627	0.44222	0.31055	0.08678	0.00417	0	0	0	0
			1,1,1,1,1,2,2,2,2,2	0	0.22418	0.44505	0.23615	0.09463	0	0	0	0	0
			1,2,2,2,2,2,2,2,2,1	0	0.55615	0.3285	0.10095	0.0144	0	0	0	0	0
		5	1,2,1,2,1,2,1,2,1,2	0	0	0.25152	0.3629	0.2596	0.11167	0.0143	0	0	0
			1,1,1,1,1,2,2,2,2,2	0	0	0.25188	0.38925	0.25385	0.09577	0.00925	0	0	0
			1,2,2,2,2,2,2,2,2,1	0	0	0.50103	0.40395	0.09502	0	0	0	0	0
	7	3	1,2,1,2,1,2,1,2,1,2	0	0.6656	0.3003	0.0341	0	0	0	0	0	0
			1,1,1,1,1,2,2,2,2,2	0	0.64505	0.3229	0.03205	0	0	0	0	0	0
			1,2,2,2,2,2,2,2,2,1	0	0.86387	0.13612	0	0	0	0	0	0	0
		4	1,2,1,2,1,2,1,2,1,2	0	0.20147	0.52873	0.23023	0.03957	0	0	0	0	0
			1,1,1,1,1,2,2,2,2,2	0	0.22268	0.52987	0.19945	0.048	0	0	0	0	0
			1,2,2,2,2,2,2,2,2,1	0	0.60393	0.31398	0.07698	0.00513	0	0	0	0	0
		5	1,2,1,2,1,2,1,2,1,2	0	0	0.33127	0.4449	0.18902	0.0348	0.0348	0	0	0
			1,1,1,1,1,2,2,2,2,2	0	0	0.33435	0.45038	0.17633	0.03895	0	0	0	0
			1,2,2,2,2,2,2,2,2,1	0	0	0.66695	0.30338	0.02967	0	0	0	0	0
	8	3	1,2,1,2,1,2,1,2,1,2	0	0.7321	0.2432	0.0247	0	0	0	0	0	0
			1,1,1,1,1,2,2,2,2,2	0	0.71167	0.2795	0.00882	0	0	0	0	0	0
			1,2,2,2,2,2,2,2,2,1	0	0.9346	0.0654	0	0	0	0	0	0	0
		4	1,2,1,2,1,2,1,2,1,2	0	0.20112	0.60693	0.17222	0.01972	0	0	0	0	0
			1,1,1,1,1,2,2,2,2,2	0	0.22095	0.60665	0.15825	0.01415	0	0	0	0	0
			1,2,2,2,2,2,2,2,2,1	0	0.62	0.31355	0.06645	0	0	0	0	0	0
		5	1,2,1,2,1,2,1,2,1,2	0	0	0.40725	0.43665	0.13962	0.01648	0	0	0	0
			1,1,1,1,1,2,2,2,2,2	0	0	0.40718	0.47513	0.1055	0.0122	0	0	0	0
			1,2,2,2,2,2,2,2,2,1	0	0	0.81342	0,18157	0.005	0	0	0	0	0
	9	3	1,2,1,2,1,2,1,2,1,2	0	0.75662	0.24338	0	0	0	0	0	0	0
			1,1,1,1,1,2,2,2,2,2	0	0.75818	0.24183	0	0	0	0	0	0	0
			1,2,2,2,2,2,2,2,2,1	0	0.9773	0.0227	0	0	0	0	0	0	0
		4	1,2,1,2,1,2,1,2,1,2	0	0.2208	0.66055	0.11865	0	0	0	0	0	0
			1,1,1,1,1,2,2,2,2,2	0	0.22332	0.6617	0.11497	0	0	0	0	0	0
			1,2,2,2,2,2,2,2,2,1	0	0.61687	0.3165	0,06663	0	0	0	0	0	0
		5	1,2,1,2,1,2,1,2,1,2	0	0	0.47085	0.4762	0.05295	0	0	0	0	0
			1,1,1,1,1,2,2,2,2,2	0	0	0.46847	0.4815	0.05003	0	0	0	0	0
			1,2,2,2,2,2,2,2,2,1	0	0	0.93598	0.06402	0	0	0	0	0	0

For example, under the design $n=10,r=4,k=8,w_1=w_3=w_5=w_7=w_9=1,w_2=w_4=w_6=w_8=2)$, the non-zero entries are positioned at the 2nd, 3rd, 4th and 5th places of the signature vector and are equal to 0.20112, 0.60693, 0.17222 and 0.01972, respectively. In simple words, the weighted-4-within-consecutive-8-out-of-10: F consisting of i.i.d. components fails upon its i-th ordered component’s failure (i = 2, 3, 4 and 5), with a probability equal to 20.112%, 60.693%, 17.222% and 1.972%, respectively.

Based on the numerical results illustrated in Table 3, Table 4, Table 5 and Table 6, we next investigate the impact of the design parameters on the attitude of the corresponding weighted-r-within-consecutive-k-out-of-n: F system. Specifically, it seems that the practitioner should take into consideration the following practical remarks:

• the larger the parameter n, the larger the life expectancy of the resulting weighted-r-within-consecutive-k-out-of-n: F system (when the design parameters $r,k,w_i$ are pre-determined)
• the larger the parameter r, the larger the life expectancy of the resulting weighted-r-within-consecutive-k-out-of-n: F system (when the design parameters $n,k,w_i$ are pre-determined)
• the larger the parameter k, the smaller the life expectancy of the resulting weighted-r-within-consecutive-k-out-of-n: F system (when the design parameters $r,n,w_i$ are pre-determined)
• the larger the weights, the smaller the life expectancy of the resulting weighted-r-within-consecutive-k-out-of-n: F structure (for given $r,k,n$).

3. Performance Aspects of the Weighted-r-within-Consecutive-k-out-of-n: F System

Generally speaking, the signature vector of coherent systems is very useful for carrying out a reliabiltiy study. This is evident since several reliability characteristics of a structure can be evaluated based on the signature (e.g., the reliability polynomial of a structure or the stochastic orderings among structures (see [32,33]).

We next study the weighted-r-within-consecutive-k-out-of-n: F system under the assumption that it is comprised of i.i.d. units with a shared reliability p. It is known that the reliability polynomial of the particular structure is determined by the aid of the following formula (see, e.g., [33])

$$R\left(p\right)={\displaystyle \sum }_{j=1}^n\left({\displaystyle \sum }_{i=n-j+1}^n{s}_i\left(w_i,r,k,n\right)\right)\left(\begin{array}{c}n\\ j\end{array}\right)p^j{(1-p)}^{n-j}.$$

(2)

The proposed procedure described in Section 2 can now be implemented for delivering exact expressions for the reliability polynomial of the class of weighted-r-within-consecutive-k-out-of-n: F structures. Table 7 provides the respective polynomials of weighted-r-within-consecutive-k-out-of-n: F structures consisting of n = 7 units under different schemes. Note that for all the designs considered in Table 7, the corresponding signature vector has already been determined previously.

Table 7. Reliability polynomials of weighted-r-within-consecutive-k-out-of-n: F structures of order n = 7.

(k,r)	wi	Reliability Polynomial
(4,3)	(1,2,1,2,1,2,1)	$0.9968p^3+0.05355p^4+2.84025p^5-2.82835p^6-0.06225p^7$
	(1,1,1,2,2,2,2)	$3.899p^4-2.6166p^5+0.5425p^6-0.824p^7$
	(1,2,2,2,2,2,1)	$6.04653p^5-5.10566p^6+0.05733p^7$
(4,4)	(1,2,1,2,1,2,1)	$5.92095p^3-4.6396p^4-2.5851p^5+2.4052p^6-0.10145p^7$
	(1,1,1,2,2,2,2)	$2.044p^3+0.99225p^4-0.23058p^5-3.69159p^6+1.88592p^7$
	(1,2,2,2,2,2,1)	$1.0115p^3+2.94p^4-2.85285p^5-0.1603p^6+0.06165p^7$
(4,5)	(1,2,1,2,1,2,1)	$1.01465p+0.9303p^2-0.92645p^3+3.0583p^4-7.13895p^5+5.0694p^6-1.00725p^7$
	(1,1,1,2,2,2,2)	$2.02125p^2+3.87555p^3-8.707654p^4+3.65715p^5+0.2002p^6-0.0465p^7$
	(1,2,2,2,2,2,1)	$5.9535p^3-1.77975p^4-9.38175p^5+7.28875p^6-1.08075p^7$
(5,3)	(1,2,1,2,1,2,1)	$2.002p^4+1.9845p^5-2.975p^6-0.0115p^7$
	(1,1,1,2,2,2,2)	$1.00695p^4+2.93034p^5-1.8816p^6-1.0557p^7$
	(1,2,2,2,2,2,1)	$2.90073p^5+1.19854p^6-3.09927p^7$
(5,4)	(1,2,1,2,1,2,1)	$2.4185p^3-2.2722p^4+10.27593p^5-16.40926p^6+6.98703p^7$
	(1,1,1,2,2,2,2)	$1.0122p^3+1.94635p^4+3.075873p^5-9.03959p^6+4.00517p^7$
	(1,2,2,2,2,2,1)	$5.0302p^4-4.04985p^5+0.0091p^6+0.010551p^7$
(5,5)	(1,2,1,2,1,2,1)	$10.15805p^3-14.54145p^4+3.73002p^5+2.5501p^6-0.89415p^7$
	(1,1,1,2,2,2,2)	$5.1177p^4-4.84176p^5+1.32405p^6-0.6009p^7$
	(1,2,2,2,2,2,1)	$1.0542p^3+8.8879p^4-11.98953p^5+0.09835p^6+2.94905p^7$
(6,3)	(1,2,1,2,1,2,1)	$1.96525p^4+0.18417p^5+0.73584p^6-1.885272p^7$
	(1,1,1,2,2,2,2)	$4.02003p^5-1.03999p^6-1.98003p^7$
	(1,2,2,2,2,2,1)	$1.01955p^5+4.9609p^6-4.98045p^7$
(6,4)	(1,2,1,2,1,2,1)	$0.98875p^3+3.03625p^4+2.9883p^5-12.04035p^6+6.02705p^7$
	(1,1,1,2,2,2,2)	$3.101p^4+5.733p^5-13.76899p^6+5.9349p^7$
	(1,2,2,2,2,2,1)	$5.01655p^4-3.97992p^5-0.08981p^6+0.05318p^7$
(6,5)	(1,2,1,2,1,2,1)	$7.0553p^3-6.2867p^4-2.4717p^5+2.5823p^6+0.1208p^7$
	(1,1,1,2,2,2,2)	$0.98245p^3+12.00465p^4-20.90865p^5+8.87355p^6+0.048p^7$
	(1,2,2,2,2,2,1)	$4.977p^4+6.069p^5-20.069p^6+10.023p^7$

We next investigate the impact of the design parameters on the performance of the weighted-r-within-consecutive-k-out-of-n: F systems. For this reason, we illustrate the reliability polynomials versus the common components’ reliability p. Figure 1 and Figure 2 offer some evidence about the influence of the design parameters k, r on the reliability of the resulting structure.

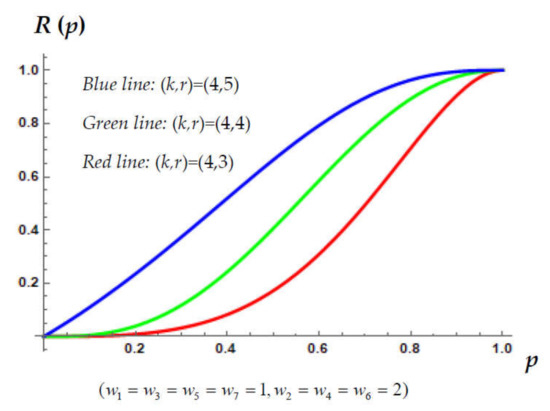
Figure 1. The reliability polynomials weighted-r-within-consecutive-4-out-of-n: F systems of order 7.

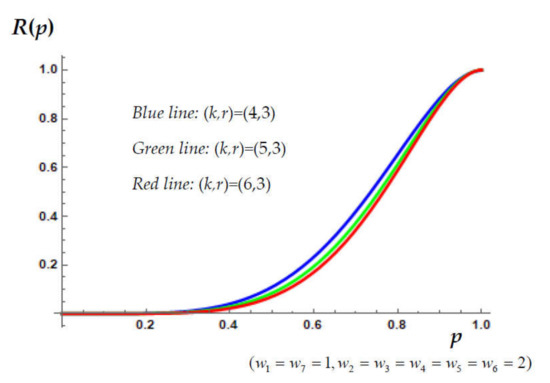
Figure 2. The reliability polynomials weighted-3-within-consecutive-k-out-of-n: F systems of order 7.

The horizontal axis of both figures represents the common reliability p of each component of the underlying structure. On the other hand, the vertical axis represents the reliability of the resulting system. For both figures, three different reliability schemes have been considered.

At Figure 1, three systems of order $n=7$ with common weights $w_i,i=1,2,\dots ,7$ are displayed. More precisely, the blue line corresponds to the weighted-5-within-consecutive-4-out-of-7: F system, the green line corresponds to the weighted-4-within-consecutive-4-out-of-7: F system and the red line corresponds to the weighted-3-within-consecutive-4-out-of-7: F structure. It is readily observed that all the structures displayed in Figure 1 share common values for design parameters $k,n,w_i$. Based on Figure 1, as parameter r increases, the resulting system strengthens its reliability. Among the cases illustrated therein, the worst design seems to be the one with r = 3 (while the remaining parameters do not differ).

In Figure 2 three systems of order $n=7$ with common weights $w_i,i=1,2,\dots ,7$ are displayed. More precisely, the blue line corresponds to the weighted-3-within-consecutive-4-out-of-7: F system, the green line corresponds to the weighted-3-within-consecutive-5-out-of-7: F system and the red line corresponds to the weighted-3-within-consecutive-6-out-of-7: F structure. It is readily observed that all the structures displayed in Figure 1 share common values for design parameters $r,n,w_i$. Based on Figure 2, we readily deduce that, as parameter k increases, the resulting system weakens its reliability. Among the cases illustrated therein, the worst design seems to be the one with k = 6 (while the remaining parameters do not differ). It is easily observed that larger values of k do not seem to be optimal choices.

4. Signature-Based Orderings between Members of the Class of the Weighted-r-within-Consecutive-k-out-of-n: F Systems

In the following lines, the signatures are used to establish stochastic orderings between members of the class of the weighted-r-within-consecutive-k-out-of-n: F systems. We shall consider only the so-called usual stochastic order. By denoting $L_1,L_2$, the lifetimes of two structures, we assume that $L_1,L_2$ follow (different) continuous distributions. If the next condition is satisfied

$$P\left(L_1>g\right)\le P\left(L_2>g\right),g\in \left(-\infty ,+\infty \right),$$

then $L_2$ is said to be stochastically larger than $L_1$ in the usual stochastic order, namely, $L_1{\le }_{st}{L}_2.$

Alternatively, $L_1{\le }_{st}{L}_2$ if and only if $L_2$ is more likely than $L_1$ to take on values beyond g. In [34], a sufficient proposition is stated by the aid of the establishing stochastic orderings among structures’ lifetimes. In other words, if $s_{1j}\left(w_j,r,k,n\right)$, $s_{2j}\left(w_j,r,k,n\right),j=1,2,\dots ,n$ correspond to the signature coordinates of two members from the class of the weighted-r-within-consecutive-k-out-of-n: F systems., they proved that if

$${{\displaystyle \sum }}_{j=1}^n{s}_{1j}\left(w_j,r,k,n\right)\le {{\displaystyle \sum }}_{j=1}^n{s}_{2j}\left(w_j,r,k,n\right)$$

(3)

for all $j=1,2,\dots ,n$, $L_1{\le }_{st}{L}_2$. Note that the above condition has also been studied by [35], and some extensions to coherent structures with (possibly) dependent units have been made. We next consider six different weighted systems of order n = 7 with $w_1=w_3=w_5=w_7=1$ $w_1=w_3=w_5=w_7=1,w_2=w_4=w_6=2$. Our target is to stochastically compare their lifetimes by the aid of (3). We next consider the following systems

• weighted-3-within-consecutive-4-out-of-7: F system (S₁)
• weighted-4-within-consecutive-4-out-of-7: F system (S₂)
• weighted-5-within-consecutive-4-out-of-7: F system (S₃)
• weighted-3-within-consecutive-5-out-of-7: F system (S₄)
• weighted-4-within-consecutive-5-out-of-7: F system (S₅)
• weighted-5-within-consecutive-5-out-of-7: F system (S₆).

Table 8 provides some relative stochastic orderings among systems S₁–S₆.

Table 8. Stochastic orderings among consecutive-type structures of order n = 7.

	S1	S2	S3	S4	S5	S6
S1	${=}_{st}$	${\le }_{st}$	${\le }_{st}$	${\ge }_{st}$	${\le }_{st}$	${\le }_{st}$
S2		${=}_{st}$	${\le }_{st}$	${\ge }_{st}$	${\ge }_{st}$	${\le }_{st}$
S3			${=}_{st}$	${\ge }_{st}$	${\ge }_{st}$	${\ge }_{st}$
S4				${=}_{st}$	${\le }_{st}$	${\le }_{st}$
S5					${=}_{st}$	${\le }_{st}$
S6						${=}_{st}$

By the aid of inequality (3) we can deliver stochastic orderings between the consecutive-type structures in Table 8. As is readily obtained, among the reliability structures considered, the weighted-5-within-consecutive-4-out-of-7: F system seems to perform stochastically better than the remaining competitors.

5. Discussion

In the present paper, the weighted-r-within-consecutive-k-out-of-n: F structure with i.i.d. units is considered. An algorithmic approach for delivering the coordinates of the signature vector of the weighted-r-within-consecutive-k-out-of-n: F system is discussed. The main contribution of the present manuscript is that it offers a pioneering way to determine the signature of the weighted-r-within-consecutive-k-out-of-n: F system. The signature vector of the particular structure has never been studied before. This fact turns the main result of the paper into an important tool for delivering a reliabiltiy study of the underlying system. Several numerical results are presented, and the performance of the aforementioned family under specific scenarios is evaluated. Furtherore, some signature-based results concerning the behavior of the weighted-r-within-consecutive-k-out-of-n: F systems are deduced. The impact of the design parameters on the performance of the resulting structures is studied in some detail. Among others, some practical guidelines for designing the weighted-r-within-consecutive-k-out-of-n: F structure are also illustrated. The practitioners should take into account that the reliabiltiy of the resulting scheme strengthens for large values of design parameter r and for small values of design parameter k. Moreover, the practitioner is encouraged to consult the signatures of the underlying system and evaluate the risk for the occurrence of its total failure. Since the idea of repairable reliability structures has attracted a lot of research attention lately (see [36,37,38]), potential future work could include the investigation of repairable weighted-r-within-consecutive-k-out-of-n: F systems. Moreover, the relaxation of the i.i.d. assumption seems to strengthen the applicability of the proposed reliability structures.