Thermal-Economic Optimization of Plate–Fin Heat Exchanger Using Improved Gaussian Quantum-Behaved Particle Swarm Algorithm
Abstract
:1. Introduction
2. Materials and Methods
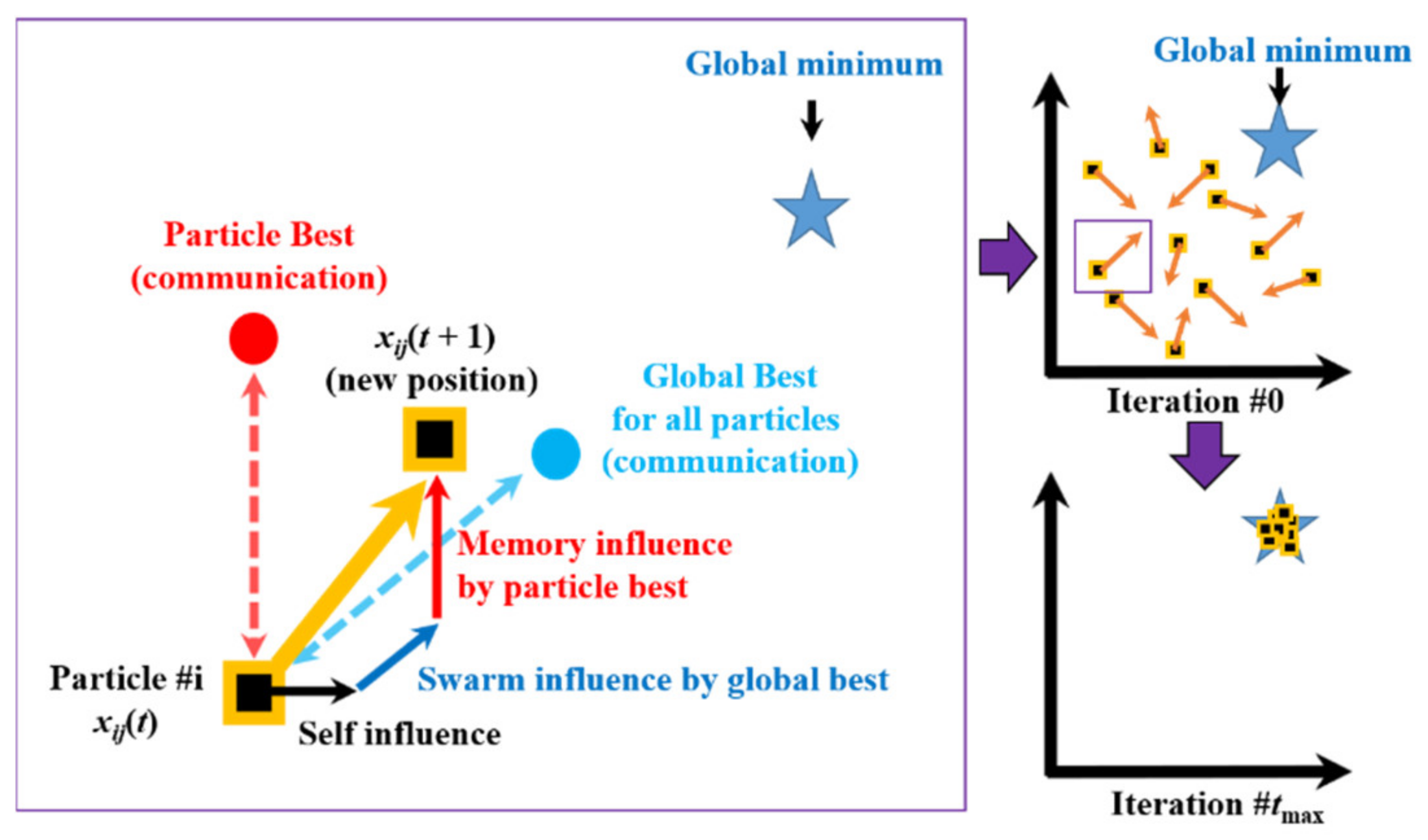
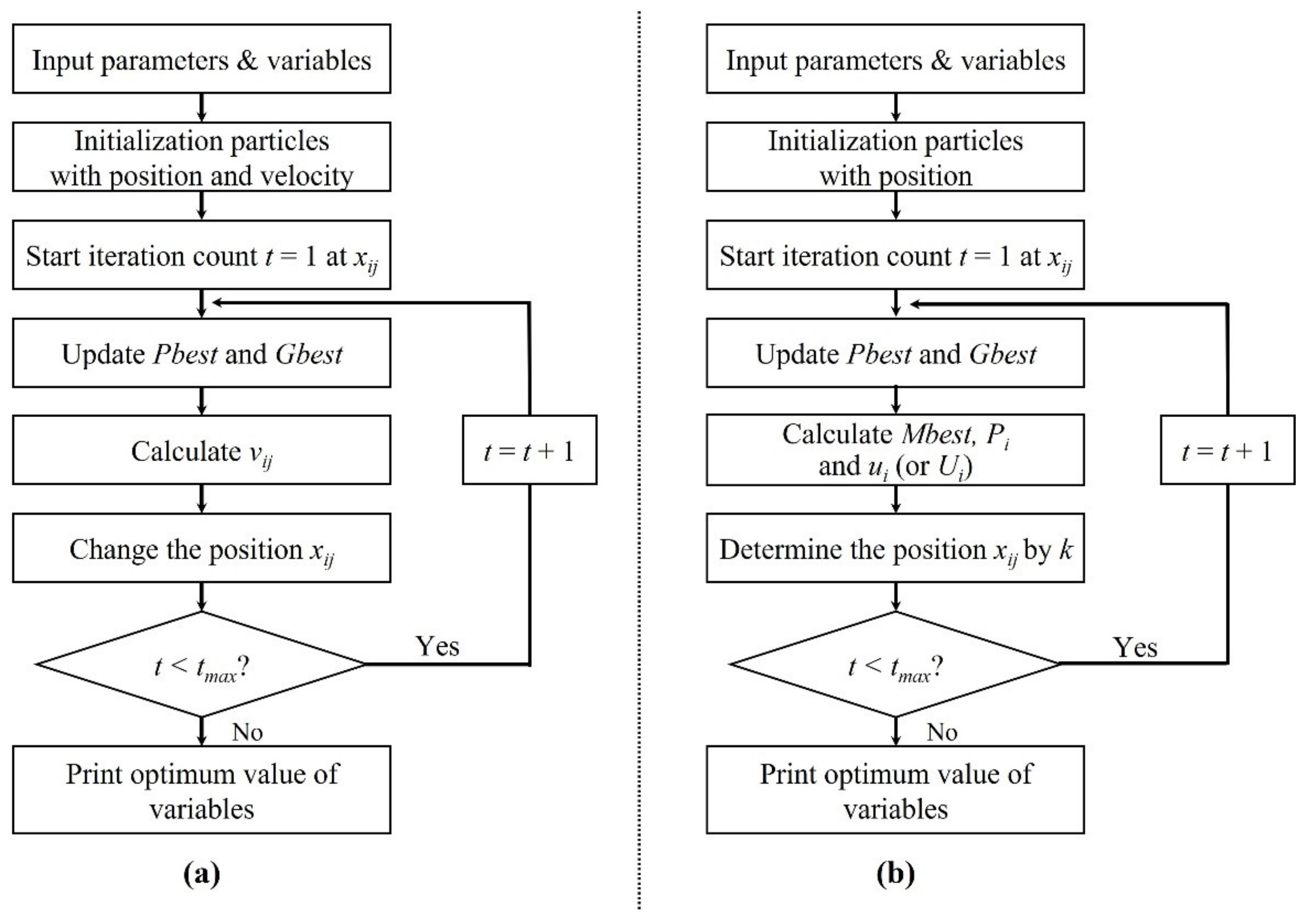
2.1. Particle Swarm Optimization
2.2. Gaussian Quantum-Behaved Particle Swarm Optimization
- Approach 1: use Ui = abs[N(0,1)] instead of ui
- Approach 2: use G = abs[N(0,1)] and g = abs[N(0,1)] instead of c1 and c2 at Pi;
- Approach 3: use both Approach 1 and Approach 2.
- 4.
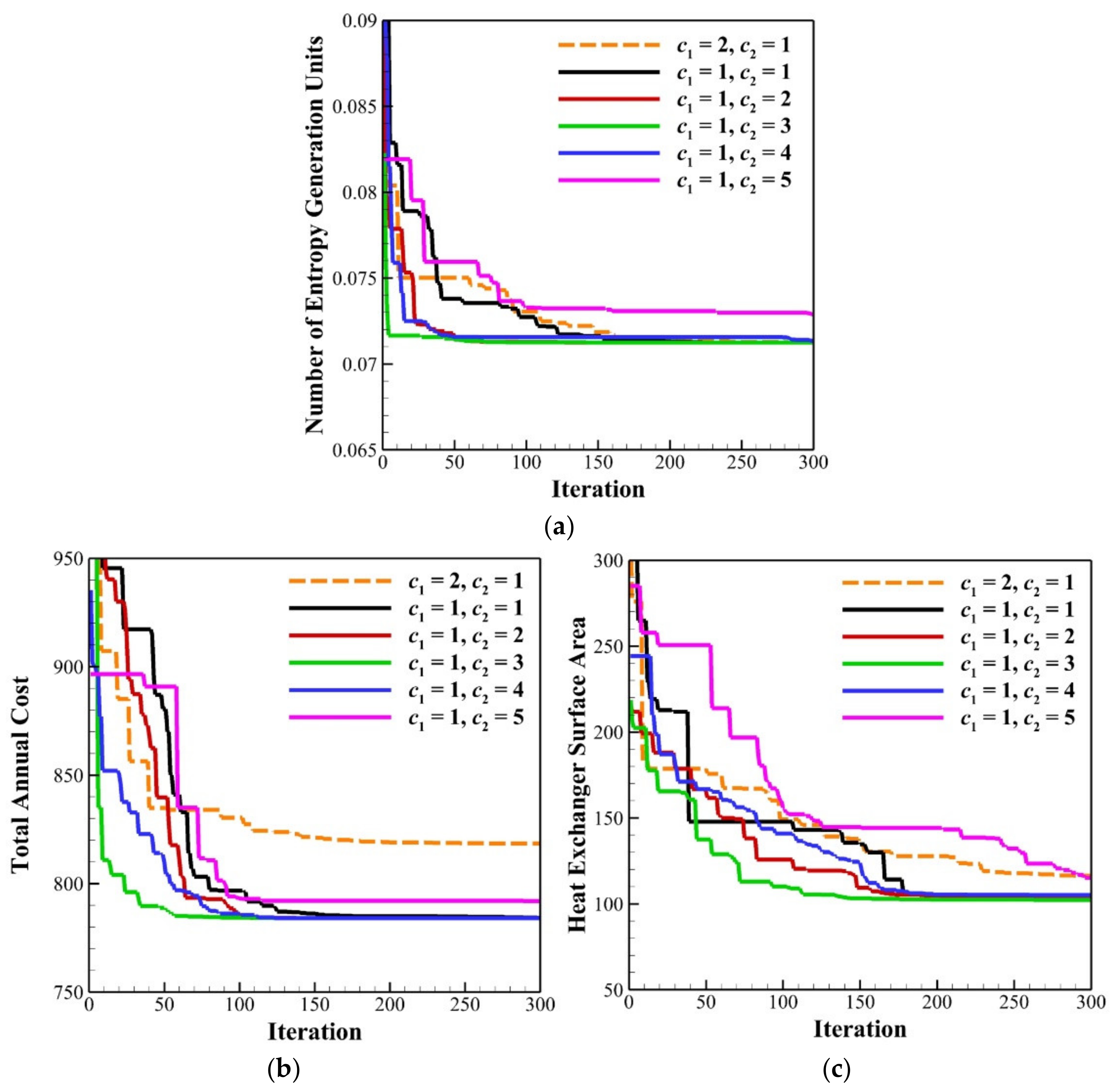
- Newly improved approach: use Equation (7) with Ui = abs[N(0,1)] and modified local attractor Pias defined in Equation (9), the improved GQPSO approach employs random number generation based on Gaussian distribution when calculating its local attractor Pi; c1 and c2 are the weighting constants, similar to those of the basic PSO. In addition, G, g, and Ui are different Gaussian distributed random numbers used for the original GQPSO algorithm (Approaches 1, 2 and 3). Moreover, c2 is weighted to Gbest to balance with Pbest in the improved GQPSO, and c2 is assumed to be increased by a multiple of c1 (for example, c1 = 1 and c2 = 3).
2.3. Constraints Handling
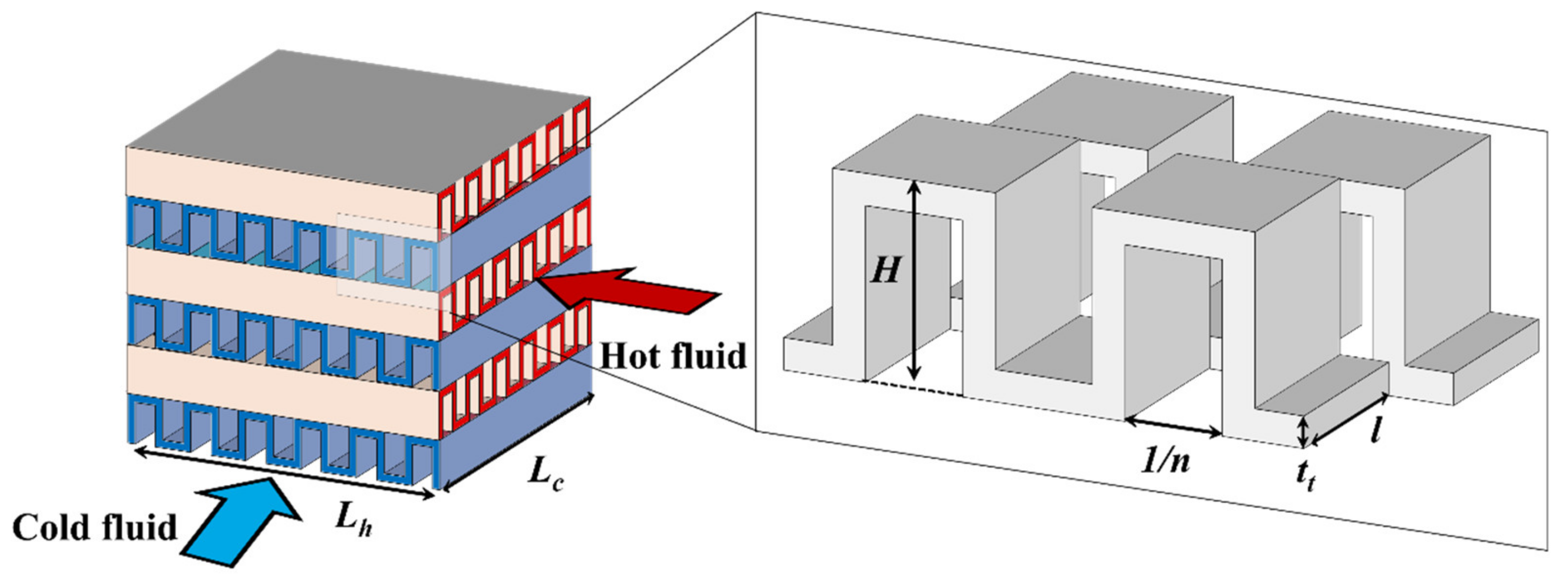
3. Crossflow Plate–Fin Heat Exchanger
- Nc = Nh + 1, where Nc and Nh are the number of fin layers for cold and hot fluids, respectively.
- Heat exchange and heat distribution are considered uniform.
- The heat exchanger works under a steady-state.
- Longitudinal thermal resistance or heat transfer of the walls is negligible.
- The fouling or aging effect is neglected for the heat exchanger.
- The fluid physical property does not change with temperature.
- The geometry of offset-strip-fins is identical for both gases.
- Hot and cold gases are considered the ideal gases.
4. Results and Discussion
4.1. Validation of PFHE Design Model
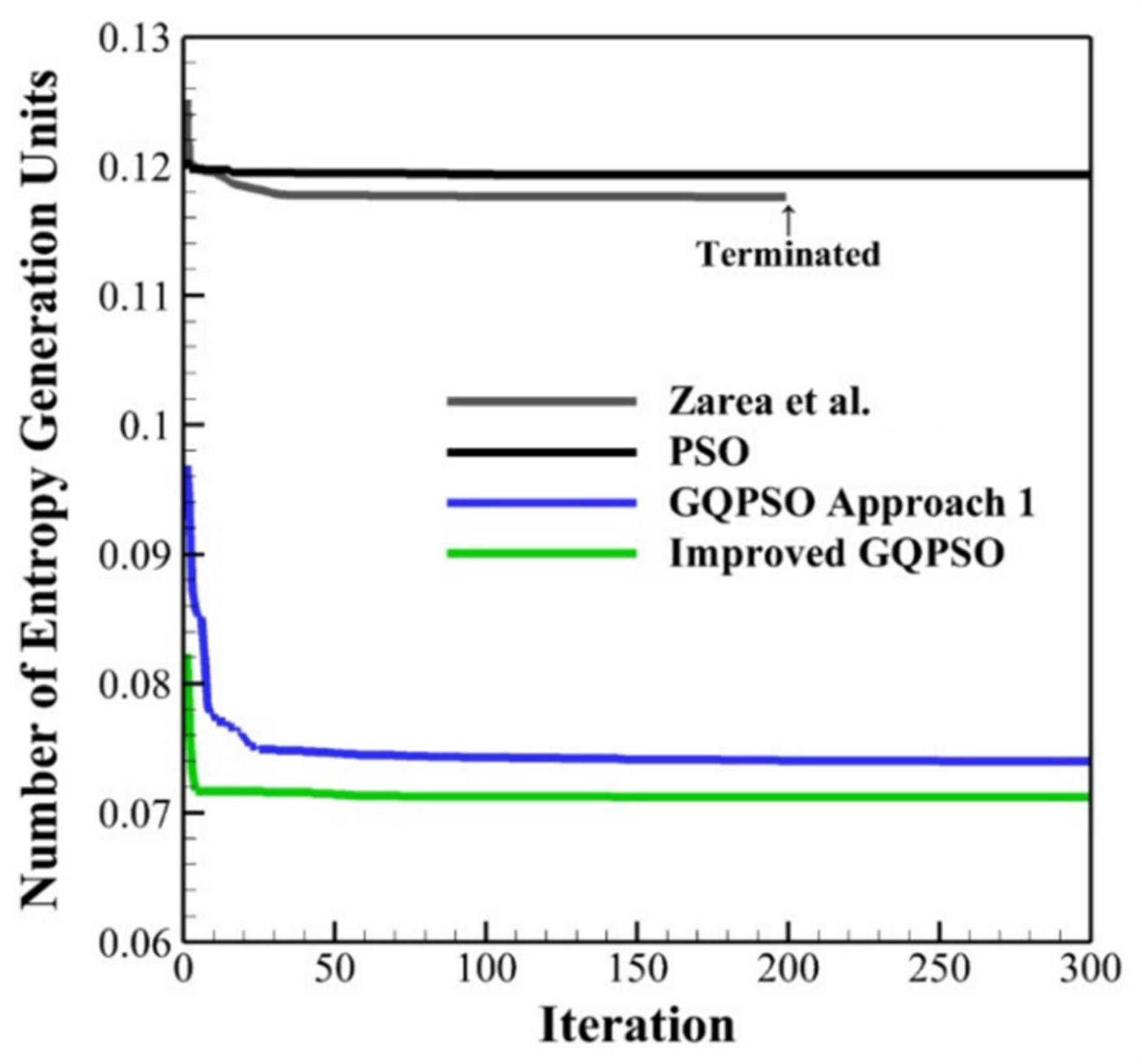
4.2. Thermal-Economic Optimization of PFHE Using Improved GQPSO
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AMTOA | adaptive multitracker optimization algorithm |
| Gbest | global best |
| GQPSO | Gaussian Quantum-Behaved Particle Swarm Optimization |
| ICA | imperialist competitive algorithm |
| LB | lower bound |
| Mbest | mean particle best |
| NEGUs | number of entropy generation units |
| NTU | number of transfer units |
| Pbest | particle best |
| PFHE | crossflow plate–fin heat exchanger |
| PSO | Particle Swarm Optimization |
| QPSO | Quantum-behaved Particle Swarm Optimization |
| TAC | total annual cost, $/yr |
| UB | upper bound |
| Nomenclature | |
| A | heat exchanger surface area, m2 |
| Acf | annual coefficient factor |
| Aff | free flow area, m2 |
| CA | cost per unit surface area, $/m2 |
| Ccp | capital cost, $ |
| Cop | operating cost, $ |
| Cp | heat capacity, J/K |
| Cp,r | heat capacity ratio |
| c1 | particle cognition coefficient |
| c2 | social collaboration coefficient |
| d | hydraulic diameter, m |
| e | exponent of nonlinear increase with area |
| f | fanning factor |
| f(x) | objective function |
| G | random number by Gaussian distribution |
| g | random number by Gaussian distribution |
| g(x) | constraint function |
| H | height of the fin, m |
| h | heat transfer coefficient, W/m2 K |
| J | mass flux velocity, kg/m2 s |
| j | Colburn factor |
| k | random number |
| L | heat exchanger length, m |
| l | lance length of the fin, m |
| mass flux, kg/s | |
| N | normal distribution function |
| Nc | number of fin layers at the cold fluid |
| Nh | number of fin layers at the hot fluid |
| Np | number of particles |
| Nv | number of variables |
| n | fin frequency, fin/m |
| Pc | pressure at the cold side, Pa |
| Ph | pressure at the hot side, Pa |
| Pi | local attractor, m |
| pg | global best position, m |
| pi | particle best position, m |
| Pr | Prandtl number |
| Q | heat power, W |
| q | constant |
| R | ideal gas constant, J/kgK |
| Re | Reynolds number |
| r | interest rate |
| rand | random function |
| r1 | random number |
| r2 | random number |
| entropy generation rate, W/mK | |
| s | fin spacing, m |
| T | temperature, K |
| t | iteration |
| tmax | maximum iteration |
| tt | thickness of the heat exchanger, m |
| Ui | random number by Gaussian distribution |
| ui | random number |
| Vj | variable |
| vij | particle velocity, m |
| w | inertia weight |
| xij | particle position, m |
| y | depreciation time, yr |
| Subscripts | |
| avg | average for different runs |
| best | best fitness function for different runs |
| c | cold side |
| h | hot side |
| i | ith particle |
| in | inlet |
| j | variable |
| max | maximum |
| min | minimum |
| out | outlet |
| stdev | standard deviation |
| Greek Symbols | |
| α | dimensionless aspect ratio for offset-strip-fin geometry |
| β | contraction-expansion coefficient |
| γ | dimensionless ratio for offset-strip-fin geometry |
| ΔPc | pressure drop at the cold side, Pa |
| ΔPh | pressure drop at the hot side, Pa |
| δ | dimensionless ratio for offset-strip-fin geometry |
| ε | effectiveness, % |
| ζ | electricity price, $/Wh |
| η | efficiency |
| µ | viscosity, Ns/m2 |
| ρ | density, kg/m3 |
| τ | operation hours, hr |
| ψ | wave function |
| Ω | feasible calculation region |
References
- Taborek, J.; Hewitt, G.; Afgan, N. Heat Exchangers—Theory and Practice; Hemisphere Publishing: Washington, DC, USA, 1983; Volume 1. [Google Scholar]
- Yousefi, M.; Darus, A.N.; Mohammadi, H. An imperialist competitive algorithm for optimal design of plate-fin heat exchangers. Int. J. Heat Mass Transf. 2012, 55, 3178–3185. [Google Scholar] [CrossRef]
- Wang, Z.; Li, Y. Irreversibility analysis for optimization design of plate fin heat exchangers using a multi-objective cuckoo search algorithm. Energy Convers. Manag. 2015, 101, 126–135. [Google Scholar] [CrossRef]
- Khosravi, R.; Khosravi, A.; Nahavandi, S.; Hajabdollahi, H. Effectiveness of evolutionary algorithms for optimization of heat exchangers. Energy Convers. Manag. 2015, 89, 281–288. [Google Scholar] [CrossRef]
- Naruei, I.; Keynia, F. Wild horse optimizer: A new meta-heuristic algorithm for solving engineering optimization problems. Eng. Comput. 2021. [Google Scholar] [CrossRef]
- Turgut, M.S.; Turgut, O.E. Global best-guided oppositional algorithm for solving multidimensional optimization problems. Eng. Comput. 2019, 36, 43. [Google Scholar] [CrossRef]
- Mohanty, D.K. Application of firefly algorithm for design optimization of a shell and tube heat exchanger from economic point of view. Int. J. Therm. Sci. 2016, 102, 228–238. [Google Scholar] [CrossRef]
- Shaukat, N.; Ahmad, A.; Mohsin, B.; Khan, R.; Khan, S.U.-D.; Khan, S.U.-D. Multiobjective core reloading pattern optimization of PARR-1 using modified genetic algorithm coupled with Monte Carlo methods. Sci. Technol. Nucl. Install. 2021, 2021, 1802492. [Google Scholar] [CrossRef]
- Cao, Y.; Zhang, H.; Li, W.; Zhou, M.; Zhang, Y.; Chaovalitwongse, W.A. Comprehensive learning particle swarm optimization algorithm with local search for multimodal functions. IEEE Trans. Evol. Comput. 2019, 23, 718–731. [Google Scholar] [CrossRef]
- Zhang, S.; Wu, X.; Shi, S.; Sun, X.; Christensen, R.; Yoder, G. A coupled heat transfer and tritium mass transport model for a double-wall heat exchanger design for FHRs. Ann. Nucl. Energy 2018, 122, 328–339. [Google Scholar] [CrossRef]
- Patel, V.K.; Savsani, V.J.; Tawhid, M.A. Thermal System Optimization; Springer: Cham, Switzerland, 2019; Volume 1. [Google Scholar]
- Lee, K.H. Inverse estimation of various surface emissivity distributions using repulsive particle swarm optimization. Int. J. Heat Mass Transf. 2019, 134, 1323–1332. [Google Scholar] [CrossRef]
- Zhang, B.; Qi, H.; Sun, S.-C.; Ruan, L.-M.; Tan, H.-P. Solving inverse problems of radiative heat transfer and phase change in semitransparent medium by using Improved Quantum Particle Swarm Optimization. Int. J. Heat Mass Transf. 2015, 85, 300–310. [Google Scholar] [CrossRef]
- Sun, J.; Feng, B.; Xu, W. Particle swam optimization with particles having quantum behavior. In Proceedings of the 2004 Congress on Evolutionary Computation, Portland, OR, USA, 19–23 June 2004; pp. 325–331. [Google Scholar]
- Turgut, O.E. Hybrid chaotic quantum behaved particle swarm optimization algorithm for thermal design of plate fin heat exchangers. Appl. Math. Model. 2016, 40, 50–69. [Google Scholar] [CrossRef]
- Mariani, V.C.; Duck, A.R.K.; Guerra, F.A.; dos Santos Coelho, L.; Rao, R.V. A chaotic quantum-behaved particle swarm approach applied to optimization of heat exchangers. Appl. Therm. Eng. 2012, 42, 119–128. [Google Scholar] [CrossRef]
- Cai, Y.; Sun, J.; Wang, J.; Ding, Y.; Tian, N.; Liao, X.; Xu, W. Optimizing the codon usage of synthetic gene with QPSO algorithm. J. Theor. Biol. 2008, 254, 123–127. [Google Scholar] [CrossRef]
- Dos Santos Coelho, L. Gaussian quantum-behaved particle swarm optimization approaches for constrained engineering design problems. Expert. Syst. Appl. 2010, 37, 1676–1683. [Google Scholar] [CrossRef]
- Zarea, H.; Kashkooli, F.M.; Soltani, M.; Rezaeian, M. A novel single and multi-objective optimization approach based on bees algorithm hybrid with particle swarm optimization (BAHPSO): Application to thermal-economic design of plate fin heat exchangers. Int. J. Therm. Sci. 2018, 129, 552–564. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Too, J.; Abdullah, A.R.; Mohd Saad, N. A new co-evolution binary particle swarm optimization with multiple inertia weight strategy for feature selection. Informatics 2019, 6, 21. [Google Scholar] [CrossRef] [Green Version]
- Shi, Y.; Eberhart, R. A modified particle swarm optimizer. In Proceedings of the 1998 IEEE International Conference on Evolutionary Computation Proceedings, IEEE World Congress on Computational Intelligence (Cat. No.98TH8360), Anchorage, AK, USA, 4–9 May 1998; pp. 69–73. [Google Scholar]
- Gupta, A.K.; Kumar, P.; Sahoo, R.K.; Sahu, A.K.; Sarangi, S.K. Performance measurement of plate fin heat exchanger by exploration: ANN, ANFIS, GA, and SA. J. Comput. Des. Eng. 2016, 4, 60–68. [Google Scholar] [CrossRef] [Green Version]
- Incropera, F.P.; Dewitt, D.P.; Bergman, T.L.; Lavine, A.S.; Middleman, S. Fundamentals of Heat and Mass Transfer, 7th ed.; John Wiley & Sons Incorporated: Hoboken, NJ, USA, 2007; Volume 1. [Google Scholar]
- Bejan, A. The concept of irreversibility in heat exchanger design: Counterflow heat exchangers for gas-to-gas applications. J. Heat Transf. 1977, 99, 374–380. [Google Scholar] [CrossRef]
- Patel, V.K. An efficient optimization and comparative analysis of ammonia and methanol heat pipe for satellite application. Energy Convers. Manag. 2018, 165, 382–395. [Google Scholar] [CrossRef]
- Patel, V.K.; Rao, R.V. Design optimization of shell-and-tube heat exchanger using particle swarm optimization technique. Appl. Therm. Eng. 2010, 30, 1417–1425. [Google Scholar] [CrossRef]
- Rao, R.V.; Patel, V.K. Thermodynamic optimization of cross flow plate-fin heat exchanger using a particle swarm optimization algorithm. Int. J. Therm. Sci. 2010, 49, 1712–1721. [Google Scholar] [CrossRef]

| Parameters | Hot Side | Cold Side |
|---|---|---|
| (kg/s) | 1.66 | 2 |
| Inlet Temperature, T (K) | 1173 | 473 |
| Density, ρ (kg/m3) | 0.6296 | 0.9638 |
| Specific Heat, Cp (J/kgK) | 1122 | 1073 |
| Viscosity, μ (Ns/m2) | 4.01 × 10−5 | 3.36 × 10−5 |
| Prandtl Number, Pr | 0.731 | 0.694 |
| Parameters | Value |
|---|---|
| Cost per Unit Area, CA ($/m2) | 90 |
| Electricity Price, ζ ($/MWh) | 20 |
| Operation Hours, τ (hr) | 5000 |
| Exponent of Nonlinear Increase with Area, e | 0.6 |
| Depreciation Time, y (yr) | 10 |
| Compressor Efficiency, η (%) | 60 |
| Interest Rate, r | 0.1 |
| Parameters | Lower Bound (LB) | Upper Bound (UB) |
|---|---|---|
| Hot Flow Length, Lh (m) | 0.1 | 1 |
| Cold Flow Length, Lc (m) | 0.1 | 1 |
| Fin Height, H (mm) | 2 | 10 |
| Fin Thickness, tt (mm) | 0.1 | 0.2 |
| Fin Frequency, n (fin/m) | 100 | 1000 |
| Lance Length, l (mm) | 1 | 10 |
| Number of Fin Layers at the Hot Fluid, Nh | 1 | 200 |
| Parameters | Zarea et al. [19] | Present Study | Relative Difference (%) |
|---|---|---|---|
| γ | 0.346 | 0.346 | - |
| α | 0.016 | 0.016 | - |
| δ | 0.052 | 0.052 | - |
| ΔPh (Pa) | 920 | 918 | 0.22 |
| ε (%) | 87.0 | 86.8 | 0.23 |
| NEGUs | 0.1176 | 0.1155 | 1.82 |
| Parameters | 100/100 | 300/100 | 100/300 | 300/300 |
|---|---|---|---|---|
| Best Fitness Value (NEGUsbest) | 0.0717 | 0.0712 | 0.0712 | 0.0712 |
| Average Fitness Value (NEGUsavg) | 0.0719 | 0.0713 | 0.0712 | 0.0712 |
| Standard Deviation of Fitness Values (NEGUsstdev, %) | 1.069 | 0.0112 | 0.01 | 4.3 × 10−4 |
| Best Calculation Time (s) | 0.77 | 2.37 | 1.84 | 7.40 |
| Average Calculation Time (s) | 0.85 | 2.66 | 1.97 | 8.03 |
| Total Calculation Time (s) | 24.7 | 78.0 | 58.4 | 241.5 |
| Parameters | Zarea et al. [19] | Basic PSO | GQPSO (Approach 1) | Improved GQPSO |
|---|---|---|---|---|
| Best Fitness Value (NEGUsbest) | 0.1176 | 0.1194 | 0.0730 | 0.0712 |
| Average Fitness Value (NEGUsavg) | - | 0.1207 | 0.0737 | 0.0712 |
| Standard Deviation of Fitness Values (NEGUsstdev, %) | - | 1.95 | 1.52 | 0.0005 |
| Best Calculation Time (s) | - | 1.60 | 1.75 | 1.61 |
| Average Calculation Time (s) | - | 1.63 | 2.03 | 1.88 |
| Total Calculation Time (s) | - | 48.2 | 60.3 | 55.0 |
| Maximum Number of Penalty Particles | - | 98 | 94 | 84 |
| Minimum Number of Penalty Particles | - | 44 | 0 | 0 |
| Average Number of Penalty Particles | - | 73 | 37 | 32 |
| Parameters for NEGUs | Zarea et al. [19] | Basic PSO | GQPSO (Approach 1) | Improved GQPSO |
| Hot Flow Length, Lh (m) | 1 | 1 | 0.9994 | 1 |
| Cold Flow Length, Lc (m) | 0.999 | 1 | 0.7778 | 1 |
| Fin Height, H (mm) | 7.03 | 10 | 6.80 | 6.76 |
| Fin Thickness, tt (mm) | 0.129 | 0.2 | 0.1004 | 0.1079 |
| Fin Frequency, n (fin/m) | 397.3 | 304.5 | 998.8 | 1000 |
| Lance Length, l (mm) | 7.98 | 10 | 1.19 | 1 |
| Number of Fin Layers at the Hot Fluid, Nh | 66 | 200 | 108 | 83 |
| Effectiveness, ε (%) | 87.0 | 86.0 | 94.9 | 95.2 |
| Best Fitness Value, NEGUsbest | 0.1176 | 0.1194 | 0.0730 | 0.0712 |
| Parameters for TAC | Zarea et al. [19] | Basic PSO | GQPSO (Approach 1) | Improved GQPSO |
| Hot Flow Length, Lh (m) | 0.8954 | 0.3266 | 0.3108 | 0.3076 |
| Cold Flow Length, Lc (m) | 0.9988 | 0.4112 | 0.3928 | 0.3884 |
| Fin Height, H (mm) | 0.9977 | 10 | 10 | 10 |
| Fin Thickness, tt (mm) | 0.1929 | 0.2 | 0.2 | 0.2 |
| Fin Frequency, n (fin/m) | 216 | 470 | 445 | 440 |
| Lance Length, l (mm) | 0.9635 | 10 | 10 | 10 |
| Number of Fin Layers at the Hot Fluid, Nh | 71 | 200 | 200 | 200 |
| Effectiveness, ε (%) | 82.1 | 83.4 | 82.1 | 81.8 |
| Best Fitness Value, TACbest ($/yr) | 939 | 868 | 798 | 784 |
| Parameters for A | Zarea et al. [19] | Basic PSO | GQPSO (Approach 1) | Improved GQPSO |
| Hot Flow Length, Lh (m) | 0.2099 | 0.1851 | 0.3378 | 0.1703 |
| Cold Flow Length, Lc (m) | 0.2211 | 0.1851 | 0.3641 | 0.1733 |
| Fin Height, H (mm) | 6.7 | 6.8 | 5.3 | 6.6 |
| Fin Thickness, tt (mm) | 0.107 | 0.1 | 0.116 | 0.108 |
| Fin Frequency, n (fin/m) | 1000 | 990.7 | 878.7 | 1000 |
| Lance Length, l (mm) | 2.24 | 1 | 7.49 | 1 |
| Number of Fin Layers at the Hot Fluid, Nh | 81 | 110 | 56 | 123 |
| Effectiveness, ε (%) | 81.8 | 82.3 | 82.0 | 81.8 |
| Best Fitness Value, Abest (m2) | 107.2 | 110.4 | 140.4 | 101.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moon, J.H.; Lee, K.H.; Kim, H.; Han, D.I. Thermal-Economic Optimization of Plate–Fin Heat Exchanger Using Improved Gaussian Quantum-Behaved Particle Swarm Algorithm. Mathematics 2022, 10, 2527. https://doi.org/10.3390/math10142527
Moon JH, Lee KH, Kim H, Han DI. Thermal-Economic Optimization of Plate–Fin Heat Exchanger Using Improved Gaussian Quantum-Behaved Particle Swarm Algorithm. Mathematics. 2022; 10(14):2527. https://doi.org/10.3390/math10142527
Chicago/Turabian StyleMoon, Joo Hyun, Kyun Ho Lee, Haedong Kim, and Dong In Han. 2022. "Thermal-Economic Optimization of Plate–Fin Heat Exchanger Using Improved Gaussian Quantum-Behaved Particle Swarm Algorithm" Mathematics 10, no. 14: 2527. https://doi.org/10.3390/math10142527
APA StyleMoon, J. H., Lee, K. H., Kim, H., & Han, D. I. (2022). Thermal-Economic Optimization of Plate–Fin Heat Exchanger Using Improved Gaussian Quantum-Behaved Particle Swarm Algorithm. Mathematics, 10(14), 2527. https://doi.org/10.3390/math10142527







