Abstract
This study extends the newsvendor model to address customer balking and its penalty under service-level constraints. The model designed in this study determines the optimal order quantity to derive the maximum expected profit when a customer is reluctant to buy a product and the available inventory falls below a certain threshold. In addition, the service level is introduced into the procedure to determine the optimal order quantity, thus facilitating the process. Under these circumstances, we also propose a corresponding distribution-free model to determine tight lower bounds on expected profits under the worst-case scenario. To quantitatively evaluate our model’s performance, we compared profits based on the presence or absence of demand distribution, and demonstrated the effect of varying balking penalty costs and probabilities. Introducing a practical service level that can be used as a trade-off tool to help determine reasonable estimates and profitable decisions is beneficial when determining order quantity by comparing goodwill and holding costs.
MSC:
90B05
1. Introduction
The advent of the Fourth Industrial Revolution has ushered in the evolution of IoT, human–machine interaction, value-added services and businesses, and data-based communication, resulting in industry-wide digitization, optimization, and production customization [1]. Consequently, goods are manufactured with increased flexibility, efficiency, and interchangeability. However, it is crucial to plan for unpredictable changes in demand and the shrinking life cycle of various industries, as consumer preferences are becoming increasingly fickle [2]. Consequently, the newsvendor problem has become frequently utilized to address the challenge posed by unpredictability of demand in a single-period model [3]. However, it is not always the case that the collected demand data follow a probability distribution, or that there is sufficient information available, making it a challenge to infer a population. Scarf [4] devised a “distribution-free” strategy that addresses these challenges by simply considering the average and standard deviation of demand, enabling us to make the best of worst-case scenarios. This model was simplified by Gallego and Moon [5], who applied it to various scenarios, such as multiproduct and random yield cases. The newsvendor model has since been extended across various fields and industries [6], and remains one of the most intensively explored models [7].
Consequently, the newsvendor model is now used to reflect a variety of circumstances and societal phenomena. For example, doughnut sales exemplify the phenomenon of balking, where consumers hesitate to make a purchase when the stock level of fresh products falls below a certain threshold [8]. Typically, issues are raised regarding perishable products, which are defined as products whose physical quality or value deteriorates with time. Typical perishable products include fresh foods such as vegetables, fruits, and dairy products that bear an expiration date [9]. Because these products are easily discarded as a result of poor operational management, it is crucial and challenging to establish when and how much inventory to reorder [10,11]. More recently, this has become particularly noticeable in the fashion and high-tech industries, where products become obsolete or deprecate after a relatively short period of time [12,13]. Owing to the expansive market structure, new products are rapidly introduced as a result of continually advancing technology and diverse customer demands. Balking also occurs when the amount of clothing products with slightly varying designs on shelves falls below a threshold point [14]. In the case of high-tech products, customer balking occurs after a given sales period following the launch of a new product, or the release of a comparable product with superior technology (i.e., for products with a shorter product life cycle and diminished value as a result of rapid technological advancement). The rapid evolution of markets significantly limits product lifetime [15,16]. To address this issue, decision makers must manage inventory levels based on demand data, and decrease the costs associated with overstocking, shortages, and balking. Moon and Choi [17] approached this problem by identifying the probability that a consumer would not buy goods () due to balking when the inventory level is below a threshold . Liao et al. [18] introduced a penalty for lost sales when consumer balking exceeds inventory levels. In addition, Yu and Zhai [19] noted that it is crucial to penalize sales losses due to lost sales costs and balking. By implementing such a penalty, goodwill costs become segmented, which can serve as a tool for making trade-offs [14].
Conversely, it is crucial to accurately estimate lost sales costs, which include intangible values such as lost goodwill within the market as a result of failure to meet the service level required by the customer, as well as market share loss. However, because it is difficult to measure sales loss in practice, the concept of a quantity-oriented -service level (or fill-rate), which is widely used in industry, has frequently become employed. In this paper, we present a method to determine the optimal order quantity under the service-level constraint, which accounts for the impact of lost sales, as well as the balking penalty. The potential contributions of this study are as follows.
- (1)
- In the newsvendor problem of customer balking behavior, a penalty is given to calculate the goodwill cost, and the procedure for determining the optimal order quantity is constituted by introducing the -service level.
- (2)
- In the case where demand distribution is known, the influence of balking is incorporated into the model, and techniques to determine and optimize order quantity are employed while accounting for sales loss through the service-level constraint.
- (3)
- In the absence of demand distribution information, an approach for obtaining the optimal order quantity is applied, and its robustness demonstrated quantitatively.
The remainder of this paper is organized as follows. Section 2 provides a literature review, and Section 3 presents the base model for the concomitant problem of interest with a known demand distribution, as well as its extension into the distribution-free model. Section 4 quantitatively evaluates the distribution-free approach, and presents several sensitivity analyses to gain managerial insights. Finally, conclusions and future research opportunities are discussed in Section 5.
2. Literature Review
In this section, we examine prior literature pertaining to the newsvendor model with customer balking, a phenomenon where purchasing behavior is negatively affected by inventory shortages, causing customers to avoid the product. Pasternack [8] was the first to study a fundamental newsvendor model for customer balking. Moon and Choi [17] established a distribution-free approach for a basic balking model, and expanded the fixed ordering cost situation. Liao et al. [18] augmented the model by including lost sales costs due to stock shortages. Based on the fact that consumer balking occurs when the supply of perishable items falls below a threshold level, Jung and Lee [20] improved the model by implementing a random yield scenario. Jung and Lee [21] subsequently proposed a model where each customer’s purchase likelihood decreases proportionally to several threshold levels as the stock level decreases for a single-period selling product. Later, Lee and Jung [22] also examined the impact of consumer resistance on demand by considering both worst- and best-case scenarios in their study. Yu and Zhai [19] addressed the costs of sales loss and balking in the newsvendor model, and defined the balking penalty using values below the threshold level. Lan et al. [14] modified the model to incorporate the random yield scenario, which covers the sales loss and balking penalty costs. Furthermore, a nonlinear holding cost function demonstrated the varying influence of balking on stock levels, and the model was extended to include characteristics such as a penalty for lost sales and partial backlog [23]. Zhang et al. [24] provided insight into information asymmetry, information sharing, and credit transaction contracts in the second-stage supply chain under customer balking. Nagare et al. [25] used expert judgment to mathematically aggregate demand forecast adjustments, thereby considering the updated forecast. Thus, constraints for order size and maintenance of a predefined service level α were set for practical use.
We compared our model with those developed in prior studies, as summarized in Table 1.

Table 1.
Literature related to this study.
3. Model and Analysis
In this section, we consider a mathematical model for the single-period stochastic inventory problem with balking penalty and service-level constraints, and present its distribution-free counterpart. First, the following notations in Table 2 are used throughout this study.

Table 2.
Notation.
Considering customer balking under service level constraints, we present the following expected profit function for a single-period newsvendor model with a balking penalty based on the formulation from [17].
The first term represents the expected revenue when the inventory level does not fall below the threshold after demand is realized; thus, there is no balking or lost sales. The second term indicates the expected revenue when the demand level is between and ; i.e., the inventory level falls below the threshold after demand is met but lost sales do not occur. Because inventory drops below the threshold level, balking may occur, and customers purchase products with probability . Notably, is the amount of realized demand. In this case, we should impose the balking penalty of . The third term is the expected profit when demand exceeds stock and all products are sold out. As there is a probability of balking on demand that has passed the threshold (although there has been sufficient demand), the balking penalty cost becomes . The last term represents total purchase cost. Explanations of all terms in the expected profit function are shown in Figure 1.
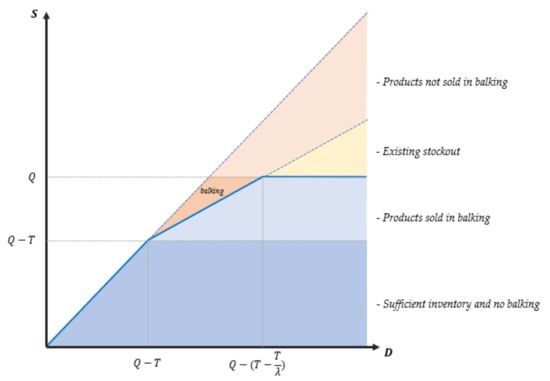
Figure 1.
Classification by terms in depending on the level of demand and inventory.
As previously noted, we employed the -service level (fill rate) constraint to handle lost sales. Several studies have indicated that lost sales can be equivalently addressed by the service level constraint [26], which is a performance measure based on inventory quantity [27].
The expected lost sales based on Equation (1) is
and the balking penalty with probability (1 − λ) of excess demand must be considered. Thus, the quantity of lost sales should be
The -service level is a function of order quantity , expressed as follows:
Assuming that the ideal -service level is , the optimal order quantity is determined based on the constraint , i.e.,
In the aforementioned equation, if the demand distribution ) is known, the optimal order quantity required to maintain the desired service level specified by the decision maker is
Using the previously defined notations, the expected profit function can be simplified. With the definition of = max we have
Thus, by substituting the aforementioned expression, all terms in the expected profit function can be simplified as follows:
and
These terms can be summed to obtain
Remark 1.
Given thatand, Equation (2) is equivalent to the expected profit function of the original newsvendor model.
Remark 2.
Given that, Equation (2) is equivalent to the expected profit function presented in [11].
Notably, maximizing the expected profit function is identical to minimizing the expected cost function :
Equation (3) can be shown to be strictly convex by calculating its derivative with respect to ; consequently, the optimal order quantity can be determined based on the first-order optimality.
Lemma 1.
The expected costis strictly convex in.
Proof.
Given.
taking the first- and second-order derivatives of Equation (3) with respect to yields the following:
Assuming that , the equation is greater than 0 and hence, is strictly convex with respect to . □
Based on the result from Lemma 1, taking the first-order derivative of Equation (3) yields the optimal order quantity that satisfies the equation (i.e., ).
Next, we determine the optimal order quantity under the -service level constraint in Equation (3), which accounts for lost sales. Here, the -service level constraint can be rewritten as
and the function is defined as follows:
Note that Equation (5) is convex, as demonstrated in Lemma 2.
Lemma 2.
is convex in.
Proof.
The first-order derivative of with respect to is expressed as
and the second-order derivative of becomes
Referring to the assumption that , we get . Thus, is strictly convex and provides the realizable solution set that satisfies the -service level constraint. □
From Lemma 2, the feasible solution set is convex; hence, the mathematical programming model is a convex optimization model. We now discuss the procedure for determining the optimal order quantity . Assuming that satisfies Equation (4), if (i.e., , then . If this condition is not satisfied, the optimal order quantity must be the boundary point in . In other words, should satisfy the -service level constraint with equality (i.e., ). Algorithm 1 summarizes the aforementioned discussion.
| Algorithm 1. Determining the optimal order quantity when the demand distribution is available. | |
| Step 1. | Find satisfying Equation (4)—i.e., or . then and stop. Otherwise, proceed to Step 2. |
| Step 2. | Find that satisfies Equation (5) with equality—i.e., , or Then and stop. |
Next, we discuss a distribution-free approach. The goal is to maximize Equation (2) given that information on the demand distribution is unknown, and only and are available. The corresponding expected profit function is then maximized under the worst-case scenario. Based on the lemmas in [5,17,28], the following can be obtained:
Lemma 3.
Proof.
Let be constant (that is, ). When is a function of that is independent of ,
By the Cauchy Schwarz and Jensen’s inequalities,
holds, and hence,
Under the aforementioned condition,
is equivalent to the following:
□
Lemma 4.
Proof.
can be proved equivalently to Lemma 3. □
Lemma 5.
For every, a distributionexists where theinequality inLemma 3istight, whereis the set of worst-casedemanddistributions.
Proof.
For every , consider the demand random variable that yields the tight bounds in Equation (6). In this case, is a constant and is expressed as follows:
where
with indicates that is the appropriate random variable when is nonzero. Thus, with and , becomes
Hence,
□
With Lemmas 3–5, the upper bound of , , can be derived as follows:
Given that is the worst-case cost function in the absence of demand distribution, it is straightforward to show that is also strictly convex by checking the second-order derivative with respect to . The first-order derivative of Equation (7) is
and the second-order derivative of Equation (7) is as follows:
Knowing that , the aforementioned equation produces a positive value, making convex in Equation (7). Thus, the optimal order quantity can be determined (without constraints) from the first-order derivative of Equation (7).
Next, the distribution-free version of the -service level constraint becomes where
From the second-order derivative, it is known that is convex at . Moreover, the realizable group of solutions is also convex. Thus, as the distribution-free model remains identical to the case with a known demand distribution, the goal is to find that minimizes over the set Denoting this value as results in . Algorithm 2 summarizes the argument in the same manner as Algorithm 1.
| Algorithm 2. Determining the optimal order quantity only when the average and standard deviation are available. | |
| Step 1. | Find satisfying Equation (8)—i.e., or If then and stop. Otherwise, proceed to Step 2. |
| Step 2. | Find that satisfies Equation (9) along with equality—i.e., , or |
4. Numerical Experiment
This section compares results from the models described in Section 3. For numerical experiments, models with the following parameters were examined: the selling price per unit () was USD 60, cost per unit () was USD 25, salvage value per unit () was USD 15, and penalty cost for balking per unit () was USD 10. When the chance of sales per unit when balking occurs () is 0.8, the balking level parameter () is 200, and the target -service level () is 0.85. For product demand, we assumed a uniform distribution with U(540,1060). For the distribution-free case, the same mean and variance were utilized to derive the optimal distribution-free order quantity.
Table 3 shows that the ratio of expected profits in the presence or absence of demand distribution data is extremely close to 1, which can be checked visually in Figure 2. This indicates that the expected profit using the distribution-free approach approximates the expected profit when the distribution information is available. Thus, these results demonstrate a potentially robust approach that ensures effective results.

Table 3.
Order quantity, expected profit and cost depending on demand distribution availability.
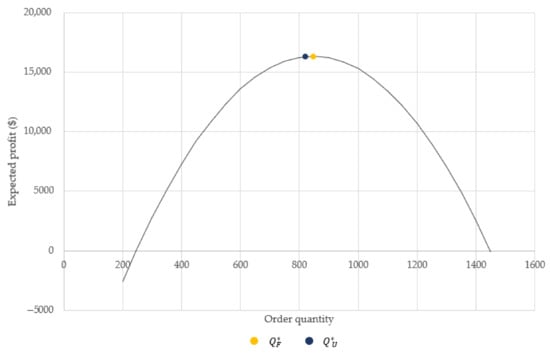
Figure 2.
Expected profits.
Next, we evaluate the effect of the balking penalty cost on the performance of the distribution-free approach by varying the balking penalty cost by 10–40% of the sales price. Figure 3a shows the changes in the expected profit ratio and optimal order quantity when the demand distribution is known and unknown, according to the increase in the balking penalty cost. The average ratio of expected profits when the demand distribution is known and unknown is less than 0.18%, which implies that profit degradation due to the distribution-free approach is not significant. Figure 3b demonstrates the impact of sale probability during balking. It is apparent that the performance of the distribution-free approach degrades when the sales probability under balking is less than 60%. However, our results indicate that the distribution-free approach is robust when the sales probability under balking exceeds 60%.
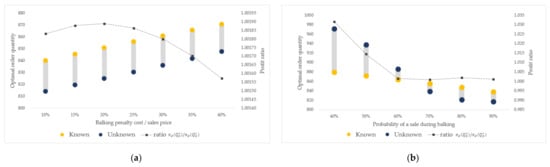
Figure 3.
Optimal order quantity based on degree of change in two factors. (a) Effect of balking penalty cost and (b) effect of probability of a sale within customer balking behavior.
5. Conclusions
In this study, we examined the service-level-constrained distribution-free newsvendor problem with a balking penalty. Incorporating the balking penalty enables the estimation of the impact of lost sales due to customer balking, which was further facilitated with the concept of the -service level. The fractionalization of costs aids decision makers in determining optimal order quantities, despite the fact that balking penalty costs should be estimated. The distribution-free approach was demonstrated to be robust by using quantitative results produced by the discussed models. However, estimating the balking penalty cost is still challenging, necessitating a quantity-based approach, such as the widely-used service level. Although the balking penalty cost may also be calculable by understanding the relationship between the holding cost and balking effect, further research is required to ascertain this. Future studies could also examine optimal order quantities depending on changes in service level, as well as other models, such as models with fixed ordering cost and random yield. Furthermore, quantification of the balking penalty and its practical applications could also be considered. Finally, conducting research on the opposite case of customer balking behavior could potentially yield useful results, as extreme situations, such as pandemics and wars, lead to a breakdown in the supply system. This results in an explosive increase in the demand for products such as smartphones, electric vehicles, and high-end luxury goods while their supply is scarce.
Author Contributions
Conceptualization, Y.L. and T.C.; methodology, Y.L.; software, Y.L.; validation, T.C.; formal analysis, Y.L.; investigation, Y.L.; writing—original draft preparation, Y.L.; writing—review and editing, T.C.; visualization, Y.L.; supervision, T.C.; project administration, T.C.; funding acquisition, T.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by Korea Institute for Advancement of Technology (KIAT) grant funded by the Korea Government (MOTIE) (P0008691 and P0020649, The Competency Development Program for Industry Specialist). And The APC was funded by P0008691.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lu, Y. Industry 4.0: A survey on technologies, applications and open research issues. J. Ind. Inf. Integr. 2017, 6, 1–10. [Google Scholar] [CrossRef]
- Oh, W. Recognizing the Necessity for Developing Customer-Oriented New Products for the 4th Industrial Revolution. J. Inf. Technol. Appl. Manag. 2020, 27, 97–109. [Google Scholar]
- Arrow, K.J.; Harris, T.; Marshak, J. Optimal inventory policy. Econometrica 1951, 19, 250–272. [Google Scholar] [CrossRef]
- Scarf, H.; Arrow, K.J.; Karlin, S. A min-max solution of an inventory problem. In Studies in the Mathematical Theory of Inventory and Production; Stanford University Press: Stanford, CA, USA, 1958; pp. 201–209. [Google Scholar]
- Gallego, G.; Moon, I. The distribution free newsboy problem: Review and extensions. J. Oper. Res. Soc. 1993, 44, 825–834. [Google Scholar] [CrossRef]
- Khouja, M. The single-period (news-vendor) problem: Literature review and suggestions for future research. Omega 1999, 27, 537–553. [Google Scholar] [CrossRef]
- Qin, Y.; Wang, R.; Vakharia, A.J.; Chen, Y.; Seref, M. The newsvendor problem: Review and directions for future research. Eur. J. Oper. Res. 2011, 213, 361–374. [Google Scholar] [CrossRef]
- Pasternack, B.A. The newsboy problem with balking. In Proceedings of the ORSA/TIMS Conference, Philadelphia, PA, USA, 28–31 October 1990. [Google Scholar]
- Mirabelli, G.; Solina, V. Optimization Strategies for the Integrated Management of Perishable Supply Chains: A Literature Review. J. Ind. Eng. Manag. 2022, 15, 58–91. [Google Scholar] [CrossRef]
- Palak, G.; Eksioglu, S.D.; Geunes, J. Heuristic algorithms for inventory replenishment with perishable products and multiple transportation modes. IISE Trans. 2018, 50, 345–465. [Google Scholar] [CrossRef]
- Rohmer, S.U.K.; Claassen, G.D.H.; Laporte, G. A two-echelon inventory routing problem for perishable products. Comput. Oper. Res. 2019, 107, 156–172. [Google Scholar] [CrossRef]
- Coelho, L.C.; Laporte, G. Optimal joint replenishment, delivery and inventory management policies for perishable products. Comput. Oper. Res. 2014, 47, 42–52. [Google Scholar] [CrossRef]
- Jadidi, O.; Jaber, M.Y.; Zolfaghari, S. Joint pricing and inventory problem with price dependent stochastic demand and price discounts. Comput. Ind. Eng. 2017, 114, 45–53. [Google Scholar] [CrossRef]
- Lan, C.; Ji, H.; Li, J. A Distribution-Free Newsvendor Model with Balking Penalty and Random Yield. J. Ind. Eng. Manag. 2015, 8, 1051–1068. [Google Scholar] [CrossRef]
- Singh, O.; Anand, A.; Kapur, P.K.; Aggrawal, D. Consumer behaviour-based innovation diffusion modelling using stochastic differential equation incorporating change in adoption rate. Int. J. Technol. Mark. 2012, 7, 346–360. [Google Scholar] [CrossRef]
- Panwar, S.; Kapur, P.K.; Singh, O. Technology diffusion model with change in adoption rate and repeat purchases: A case of consumer balking. Int. J. Syst. Assur. Eng. Manag. 2021, 12, 29–36. [Google Scholar] [CrossRef]
- Moon, I.; Choi, S. The distribution free newsboy problem with balking. J. Oper. Res. Soc. 1995, 46, 537–542. [Google Scholar] [CrossRef]
- Liao, Y.; Banerjee, A.; Yan, C. A distribution-free newsvendor model with balking and lost sales penalty. Int. J. Prod. Econ. 2011, 133, 224–227. [Google Scholar] [CrossRef]
- Yu, H.; Zhai, J. The distribution-free newsvendor problem with balking and penalties for balking and stockout. J. Syst. Sci. Syst. Eng. 2014, 23, 153–175. [Google Scholar] [CrossRef]
- Jung, U.; Lee, S.W. Robust Newsvendor model with random yield and customer balking. J. Korean Soc. Qual. Manag. 2012, 40, 441–452. [Google Scholar] [CrossRef][Green Version]
- Jung, U.; Lee, S.W. Robust Newsvendor Model with Customer Balking by the Bi-levels of Inventory Threshold. J. Soc. Korea Ind. Syst. Eng. 2013, 36, 36–43. [Google Scholar] [CrossRef]
- Lee, S.W.; Jung, U. Customer balking behavior in the newsvendor model: Its impact on performance measures and decision under uncertain balking parameters. Int. J. Prod. Econ. 2014, 154, 274–283. [Google Scholar] [CrossRef]
- Pal, B.; Sana, S.S.; Chaudhuri, K. A distribution-free newsvendor problem with nonlinear holding cost. Int. J. Syst. Sci. 2015, 46, 1269–1277. [Google Scholar] [CrossRef]
- Zhang, B.; Wu, D.D.; Liang, L. Trade credit model with customer balking and asymmetric market information. Transp. Res. Part E Logist. Transp. Rev. 2018, 110, 31–46. [Google Scholar] [CrossRef]
- Nagare, M.; Dutta, P.; Cheikhrouhou, N. Extended distribution-free newsvendor models with demand updates using experts’ judgment. Int. Trans. Oper. Res. 2021, 28, 3536–3576. [Google Scholar] [CrossRef]
- Geunes, J.; Panos, M.; Pardalos, H.; Romejin, E. Supply Chain Management: Models, Applications, and Research Directions, 1st ed.; Kluwer Academic Publishers: Dordrecht, The Netherland, 2002; pp. 19–32. [Google Scholar]
- Cachon, G.; Terwiesch, C. Matching Supply with Demand: An Introduction to Operations Management, 3rd ed.; McGraw-Hill Irwin: New York, NY, USA, 2011; p. 451. [Google Scholar]
- Gallego, G. A minmax distribution free procedure for the (Q, R) inventory model. Oper. Res. Lett. 1992, 11, 55–60. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).