Validation of a New Telenursing Questionnaire: Testing the Test
Abstract
1. Introduction
2. Materials and Methods
- Perceived usefulness
- Prospective acceptance
- Appropriateness for nursing tasks
3. Results
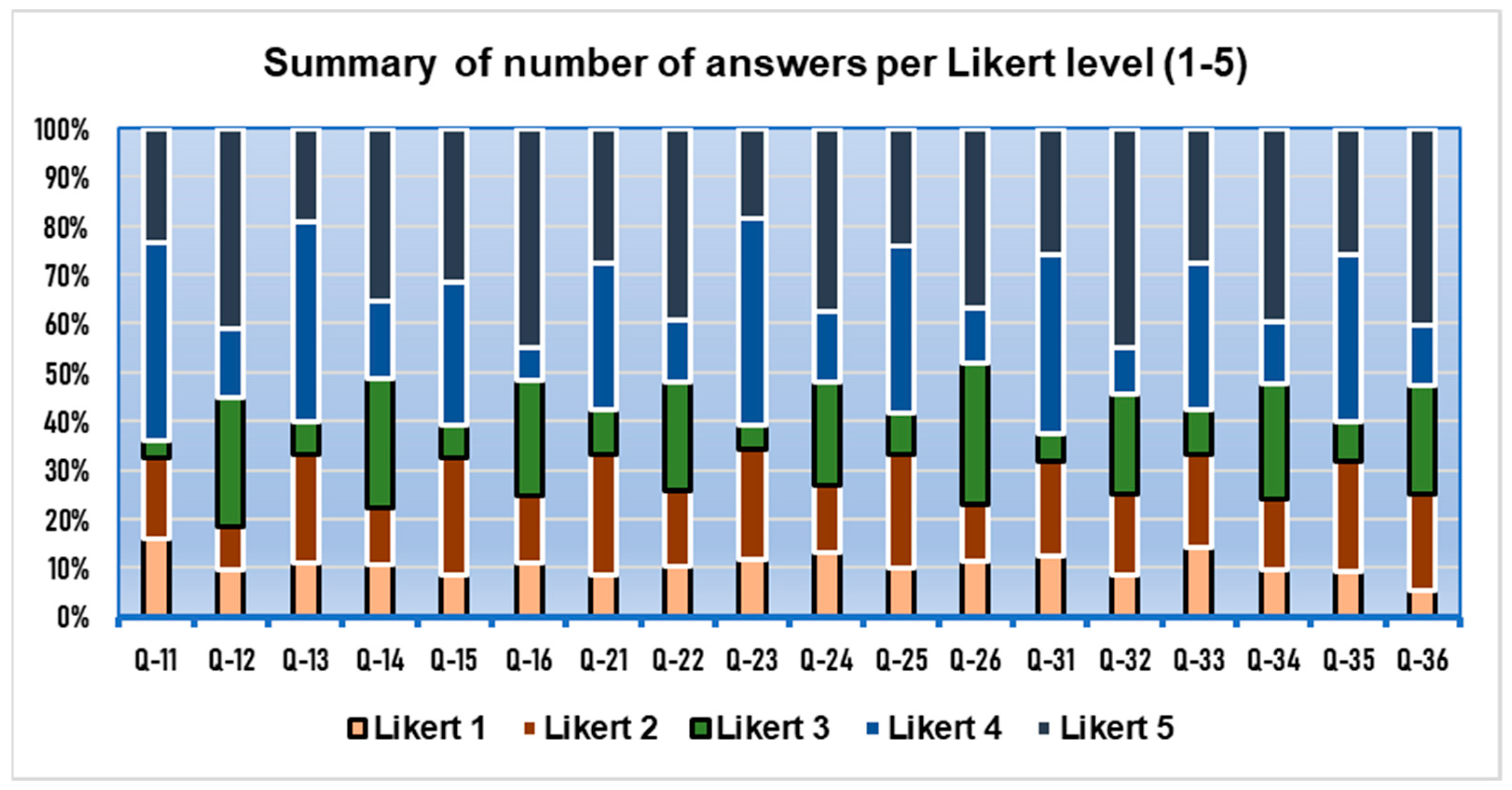
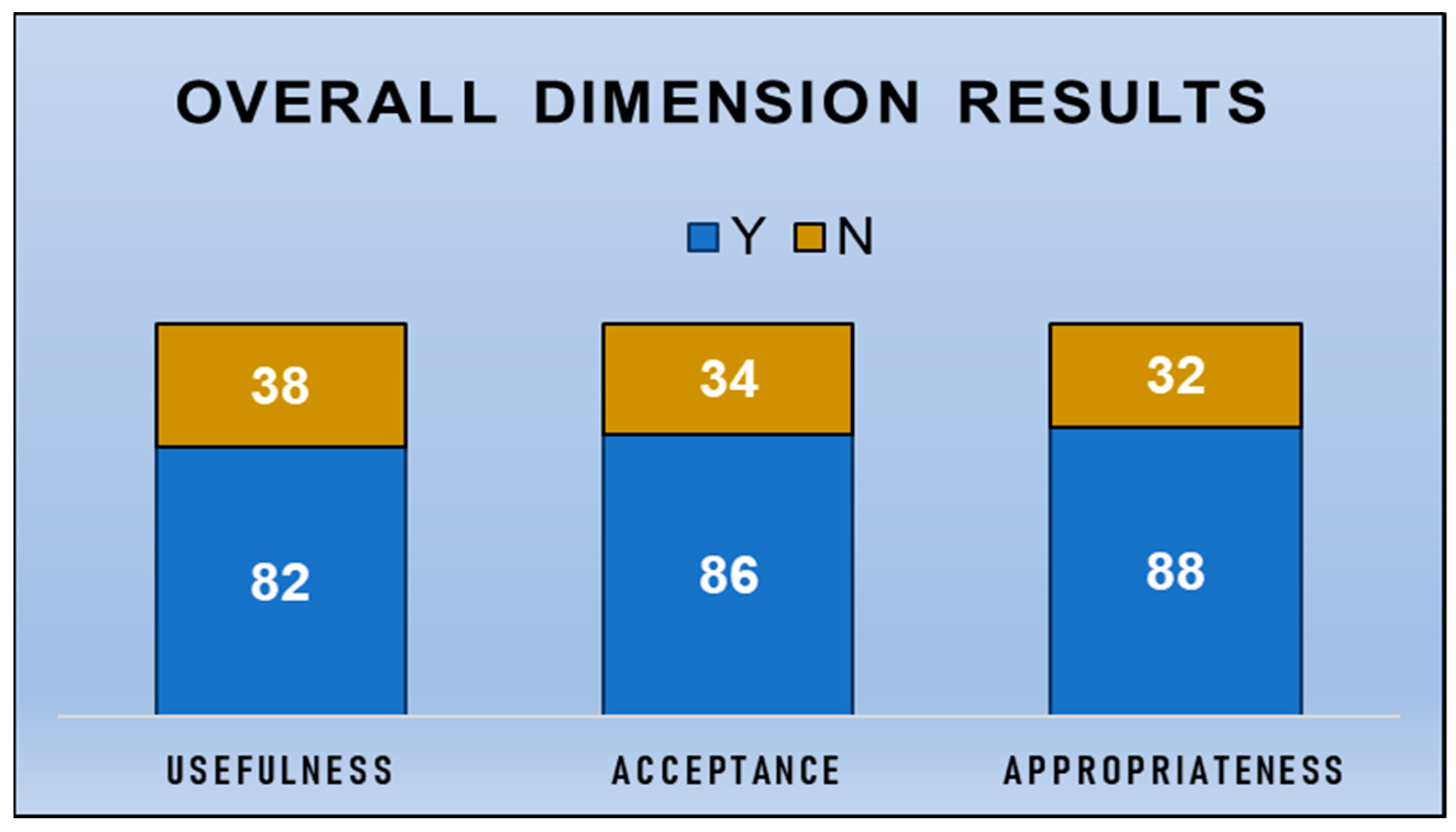
3.1. Descriptive Statistic Results
3.2. CTT Statistics Results
3.3. IRT-Rasch Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, J.; Lim, M.K.; Wang, C.; Tseng, M.L. The Evolution of the Internet of Things (IoT) over the Past 20 Years. Comput. Ind. Eng. 2021, 155, 107174. [Google Scholar] [CrossRef]
- Mieronkoski, R.; Azimi, I.; Rahmani, A.M.; Aantaa, R.; Terävä, V.; Liljeberg, P.; Salanterä, S. The Internet of Things for Basic Nursing Care—A Scoping Review. Int. J. Nurs. Stud. 2017, 69, 78–90. [Google Scholar] [CrossRef] [PubMed]
- Buchan, J.; Catton, H.; Shaffer, F. Sustain and Retain in 2022 and Beyond. Int. Counc. Nurses 2022, 71, 1–71. [Google Scholar]
- Quinn, P. A Grounded Theory Study of How Nurses Integrate Pregnancy and Full-Time Employment: Becoming Someone Different. Nurs. Res. 2016, 65, 170–178. [Google Scholar] [CrossRef]
- Alex, M.R. Occupational Hazards for Pregnant Nurses. Am. J. Nurs. 2011, 111, 28–37. [Google Scholar] [CrossRef][Green Version]
- Gan, I. A Scoping Review of the Nursing Workforce’s Changing Demography: Supporting Baby-Boomer Nurses. J. Nurs. Manag. 2020, 28, 1473–1480. [Google Scholar] [CrossRef]
- Hübner, U.; Flemming, D.; Heitmann, K.U.; Oemig, F.; Thun, S.; Dickerson, A.; Veenstra, M. The Need for Standardised Documents in Continuity of Care: Results of Standardising the ENursing Summary. Stud. Health Technol. Inform. 2010, 160, 1169–1173. [Google Scholar]
- Kumar, S.; Snooks, H. Telenursing; Kumar, S., Snooks, H., Eds.; Springer: London, UK, 2011; ISBN 978-0-85729-528-6. [Google Scholar]
- Holmström, I. Decision Aid Software Programs in Telenursing: Not Used as Intended? Experiences of Swedish Telenurses. Nurs. Health Sci. 2007, 9, 23–28. [Google Scholar] [CrossRef]
- Haghi Kashani, M.; Madanipour, M.; Nikravan, M.; Asghari, P.; Mahdipour, E. A Systematic Review of IoT in Healthcare: Applications, Techniques, and Trends. J. Netw. Comput. Appl. 2021, 192, 103164. [Google Scholar] [CrossRef]
- Hung, T.N.K.; Le, N.Q.K.; Le, N.H.; Van Tuan, L.; Nguyen, T.P.; Thi, C.; Kang, J.-H. An AI-Based Prediction Model for Frug-Drug Interactions in Osteoporosis and Paget’s Diseases from SMILES. Mol. Inform. 2022, 41, 2100264. [Google Scholar] [CrossRef]
- Kindle, R.D.; Badawi, O.; Celi, L.A.; Shawn, S. Intensive Care Unit Telemedicine in the Era of Big Data, Artificial Intelligence, and Computer Clinical Decision Support Systems. Crit. Care Clin. 2019, 25, 483–495. [Google Scholar] [CrossRef] [PubMed]
- Paolilli, D.; Mertens, K.; Wickersham, C.; Rodriguez, E. Telecommuting for Nurses: Developing a Model for the Outpatient Oncology Nurse. Oncol. Nurs. Forum 2007, 34, 540. [Google Scholar]
- Clancy, T.R. Artificial Intelligence and Nursing: The Future Is Now. J. Nurs. Administation 2020, 50, 125–127. [Google Scholar] [CrossRef] [PubMed]
- Erlingsdottir, G.; Ersson, A.; Borell, J.; Rydenfält, C. Driving for Successful Change Processes in Healthcare by Putting Staff at the Wheel. J. Health Organ. Manag. 2018, 32, 69–84. [Google Scholar] [CrossRef]
- Snooks, H.A.; Williams, A.M.; Griffiths, L.J.; Peconi, J.; Rance, J.; Snelgrove, S.; Sarangi, S.; Wainwright, P.; Cheung, W.Y. Real Nursing? The Development of Telenursing. J. Adv. Nurs. 2008, 61, 631–640. [Google Scholar] [CrossRef]
- Parmanto, B.; Lewis, A.N., Jr.; Graham, K.M.; Bertolet, M.H. Development of the Telehealth Usability Questionnaire (TUQ). Int. J. Telerehabilitation 2016, 8, 3–10. [Google Scholar] [CrossRef]
- Kitchenham, B.; Pfleeger, S.L. Principles of Survey Research Part 3: Constructing a Survey Instrument. ACM SIGSOFT Softw. Eng. Notes 2002, 27, 20. [Google Scholar] [CrossRef]
- Lewis, J.R. The System Usability Scale: Past, Present, and Future. Int. J. Hum. Comput. Interact. 2018, 34, 577–590. [Google Scholar] [CrossRef]
- Davis, F.D. User Acceptance of Information Technology: System Characteristics, User Perceptions and Behavioral Impacts. Int. J. Man. Mach. Stud. 1993, 38, 475–487. [Google Scholar] [CrossRef]
- Venkatesh, V.; Bala, H. Technology Acceptance Model 3 and a Research Agenda on Interventions. Decis. Sci. 2008, 39, 273–315. [Google Scholar] [CrossRef]
- Mattisson, M.; Johnson, C.; Börjeson, S.; Årestedt, K.; Lindberg, M. Development and Content Validation of the Telenursing Interaction and Satisfaction Questionnaire (TISQ). Health Expect. 2019, 22, 1213–1222. [Google Scholar] [CrossRef] [PubMed]
- Solnyshkina, M.I.; Zamaletdinov, R.R.; Gorodetskaya, L.A.; Gabitov, A.I. Evaluating Text Complexity and Flesch-Kincaid Grade Level. J. Soc. Stud. Educ. Res. 2017, 8, 238–248. [Google Scholar] [CrossRef]
- Bakken, S.; Grullon-Figueroa, L.; Izquierdo, R.; Lee, N.J.; Morin, P.; Palmas, W.; Teresi, J.; Weinstock, R.S.; Shea, S.; Starren, J. Development, Validation, and Use of English and Spanish Versions of the Telemedicine Satisfaction and Usefulness Questionnaire. J. Am. Med. Inform. Assoc. 2006, 13, 660–667. [Google Scholar] [CrossRef]
- Fan, X.; Yin, P. Examinee Characteristics and Score Reliability: An Empirical Investigation. Educ. Psychol. Meas. 2003, 63, 357–368. [Google Scholar] [CrossRef]
- Krosnick, J.A.; Presser, S. Question and Questionnaire Design. In Handbook of Survey Research; Marsden, P.V., Wright, J.D., Eds.; Emerald Group Publishing Limited: Bingley, UK, 2010; pp. 263–313. ISBN 978-1-84855-224-1. [Google Scholar]
- Flake, J.K.; Fried, E.I. Measurement Schmeasurement: Questionable Measurement Practices and How to Avoid Them. Adv. Methods Pract. Psychol. Sci. 2020, 3, 456–465. [Google Scholar] [CrossRef]
- Hopper, J. How Many Questions in a 10-Minute Survey? Versta Research Methodology 2017. Available online: https://verstaresearch.com/blog/how-many-questions-in-a-10-minute-survey/ (accessed on 23 May 2022).
- Amaresan, S. How Long Should a Survey Be? 2021. Available online: https://blog.hubspot.com/service/ideal-survey-length (accessed on 23 May 2022).
- Taylor, E. How Many Questions Should I Ask in My Survey? 2018. Available online: https://www.driveresearch.com/market-research-company-blog/how-many-questions-should-i-ask-in-my-survey/ (accessed on 23 May 2022).
- Hair, J.F.; Black, W.C.; Babin, B.J.; Anderson, R.E. Multivariate Data Analysis: Pearson New International Edition; Pearson Education Limited: London, UK, 2013; ISBN 978-1292021904. [Google Scholar]
- Kampen, J.; Swyngedouw, M. The Ordinal Controversy Revisited. Qual. Quant. 2000, 34, 87–102. [Google Scholar] [CrossRef]
- Rasch, G. Probabilistic Models for Some Intelligence and Attainment Tests; Danish Institute for Educational Research: Copenhagen, Denmark, 1960; ISBN 0-226-70554-4. [Google Scholar]
- Andrich, D. A Rating Formulation for Ordered Response Categories. Psychometrika 1978, 43, 561–573. [Google Scholar] [CrossRef]
- Hohensinn, C. Pcirt: An r Package for Polytomous and Continuous Rasch Models. J. Stat. Softw. 2018, 84, 1–14. [Google Scholar] [CrossRef]
- Nicklin, C.; Vitta, J.P. Assessing Rasch Measurement Estimation Methods across R Packages with Yes/No Vocabulary Test Data. Lang. Test. 2022, 02655322211066822. [Google Scholar] [CrossRef]
- Sawatzky, R.; Ratner, P.A.; Kopec, J.A.; Zumbo, B.D. Latent Variable Mixture Models: A Promising Approach for the Validation of Patient Reported Outcomes. Qual. Life Res. 2012, 21, 637–650. [Google Scholar] [CrossRef] [PubMed]
- Streiner, D.L. Starting at the Beginning: An Introduction to Coefficient Alpha and Internal Consistency. J. Pers. Assess. 2003, 80, 99–103. [Google Scholar] [CrossRef] [PubMed]
- Embretson, S.E.; Hershberger, S.L. The New Rules of Measurement: What Every Psychologist and Educator Should Know; Embretson, S.E., Hershberger, S.L., Eds.; Lawrence Erlbaum Associates Publishers: Mahwah, NJ, USA, 1999; ISBN 0-8058-2860-5 (Hardcover). [Google Scholar]
- Baker, F.B.; Kim, S.-H. Item Response Theory. Parameter Estimation Techniques, 2nd ed.; Baker, F.B., Kim, S.-H., Eds.; Marcel Dekker Inc.: New York, NY, USA, 2004; ISBN 9780824758257. [Google Scholar]
- TenVergert, E.; Gillespie, M.; Kingma, J. Testing the Assumptions and Interpreting the Results of the Rasch Model Using Log-Linear Procedures in SPSS. Behav. Res. Methods Instrum. Comput. 1993, 25, 350–359. [Google Scholar] [CrossRef]
- Bond, T.G.; Yan, Z.; Heene, M. Applying the Rasch Model: Fundamental Measurement in the Human Sciences, 4th ed.; Routledge: New York, NY, USA, 2020; ISBN 978-0-367-14142-4. [Google Scholar]
- Linacre, J.M. What Do Infit and Outfit, Mean-Square and Standardized Mean? Rasch Meas. Trans. 2002, 16, 878. [Google Scholar]
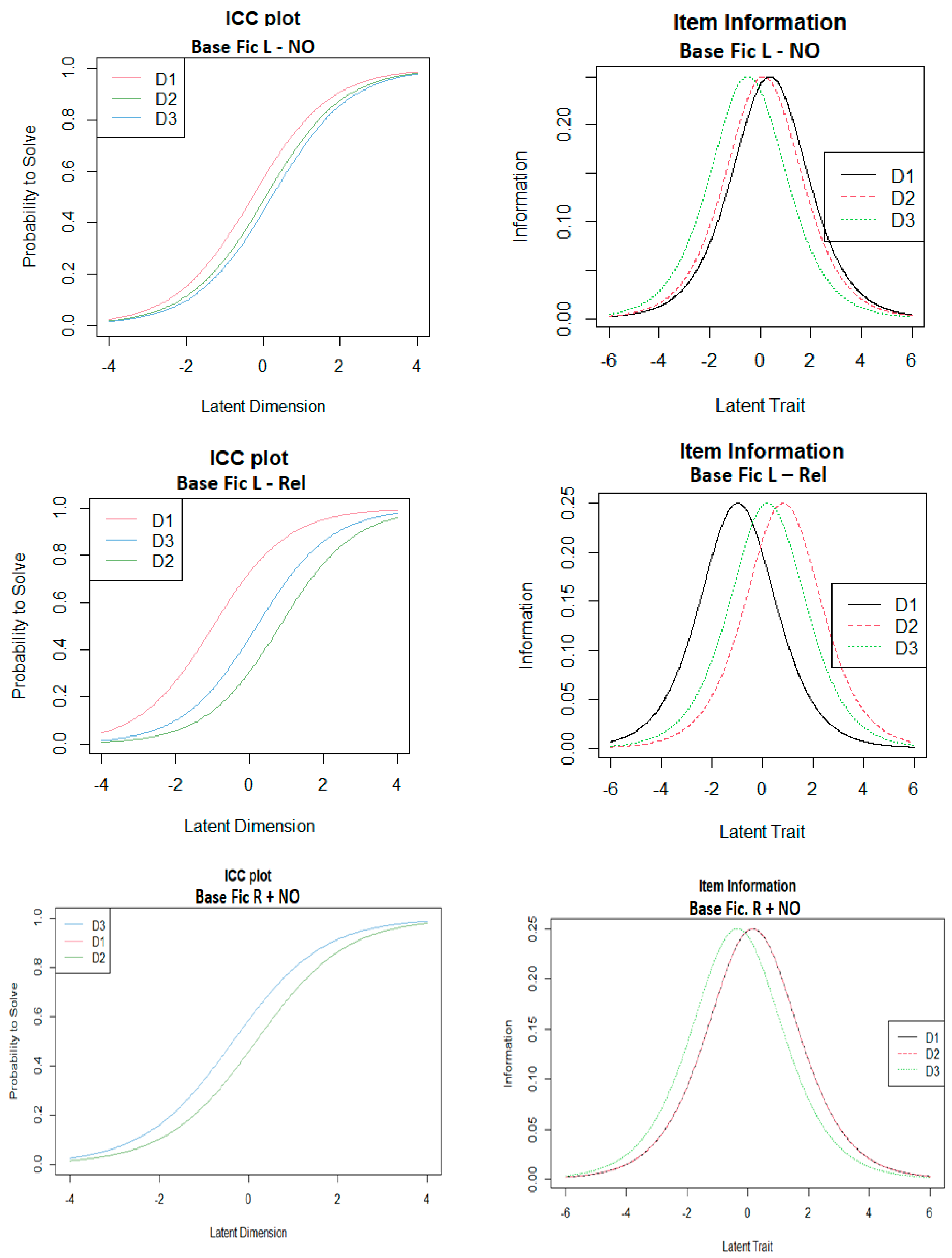

| Database Code | Symmetry | Pairwise Difference |
|---|---|---|
| Fic R + NO | Positive | Poor |
| Fic R + Rel | Positive | Good |
| Fic Syim NO | Central | Poor |
| Fic Sym Rel | Central | Good |
| Fic L—NO | Negative | Poor |
| Fic L—Rel | Negative | Good |
| Polytomous | |||
|---|---|---|---|
| Usefulness | Acceptance | Appropriateness | |
| −18 | 4 | 17 | |
| −8 | −14 | −10 | |
| 5 | 2 | 15 | |
| −3 | −19 | −11 | |
| 21 | 12 | 20 | |
| −13 | −16 | −6 | |
| Dichotomous | 1 | 7 | 9 |
| Database | Fic R + NO | Fic R + Rel | Fic Sym NO | Fic Sym Rel | Fic L—NO | Fic L—Rel | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Data (Ӯ) | Categorial | Ordinal | Categorial | Ordinal | Categorial | Ordinal | Categorial | Ordinal | Categorial | Ordinal | Categorial | Ordinal |
| Mean | 0.55 | 0.47 | 0.67 | 0.62 | 0.74 | 0.73 | ||||||
| Standard error | 0.05 | 0.05 | 0.04 | 0.04 | 0.04 | 0.04 | ||||||
| Median of medians | 2.8 | 2.0 | 3.0 | 3.0 | 4.0 | 4.0 | ||||||
| Standard deviation | 0.50 | 0.50 | 0.47 | 0.49 | 0.44 | 0.44 | ||||||
| Variance | 0.25 | 0.25 | 0.22 | 0.24 | 0.20 | 0.20 | ||||||
| Kurtosis | −1.99 | −2.02 | −1.51 | −1.78 | −0.83 | −0.86 | ||||||
| Skewness | −0.20 | 0.12 | −0.72 | −0.50 | −1.09 | −1.07 | ||||||
| Mean of sums | 66.00 | 56.33 | 85.00 | 74.33 | 88.33 | 88.00 | ||||||
| Subject count | 120 | 120 | 120 | 120 | 120 | 120 | ||||||
| Positive responses (%) | 55.0 | 46.9 | 66.7 | 61.9 | 73.6 | 73.3 | ||||||
| Database | Fic R + NO | Fic R + Rel | Fic Sym NO | Fic Sym Rel | Fic L—NO | Fic L—Rel | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Domains | Us | Acc | App | Us | Acc | App | Us | Acc | App | Us | Acc | App | Us | Acc | App | Us | Acc | App |
| Cronbach α | 0.84 | 0.86 | 0.84 | 0.94 | 0.95 | 0.94 | 0.83 | 0.80 | 0.82 | 0.94 | 0.95 | 0.94 | 0.82 | 0.83 | 0.84 | 0.94 | 0.95 | 0.95 |
| Cronbach α | 0.94 | 0.98 | 0.93 | 0.98 | 0.94 | 0.98 | ||||||||||||
| 95% CI | 0.93–0.96 | 0.91–0.98 | 0.91–0.95 | 0.97–0.98 | 0.92–0.95 | 0.97–0.98 | ||||||||||||
| (Covariances) | ||||||||||||||||||
| Database | Fic R + NO | Fic R + Rel | Fic Sym NO | Fic Sym Rel | Fic L—NO | Fic L—Rel |
|---|---|---|---|---|---|---|
| KMO | 0.93 | 0.95 | 0.94 | 0.93 | 0.93 | 0.94 |
| Bartlett | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Database | Fic R + NO | Fic R + Rel | Fic Sym NO | Fic Sym Rel | Fic L—NO | Fic L—Rel | Averages | |
|---|---|---|---|---|---|---|---|---|
| Dichotomous | EAP Real | 0.74 | 0.75 | 0.67 | 0.72 | 0.64 | 0.66 | 0.70 |
| D1-Infit-t | 0.35 | −0.98 | 0.45 | 0.21 | 0.47 | −1.10 | −0.10 | |
| D2-Infit-t | 0.35 | 0.23 | −0.43 | −0.66 | −1.61 | 2.03 | −0.01 | |
| D3-Infit-t | −1.04 | 0.34 | 0.05 | 0.52 | 0.91 | −0.57 | 0.04 | |
| D1-Outfit-t | 0.33 | −1.01 | 0.44 | 0.20 | 0.45 | 1.24 | −0.14 | |
| D2-Outfit-t | 0.33 | 0.23 | −0.44 | −0.67 | −1.61 | 1.98 | −0.03 | |
| D3-Outfit-t | −1.14 | 0.32 | 0.05 | 0.53 | 0.89 | −0.60 | 0.01 | |
| Beta-D1 (0.95 CI) | −0.17 | −0.37 | −0.11 | 0.14 | 0.28 | 0.99 | 0.13 | |
| Beta-D2 (0.95 CI) | −0.17 | −0.12 | 0.11 | −0.07 | −0.06 | −0.81 | −0.19 | |
| Beta-D3 (0.95 CI) | 0.34 | 0.48 | 0.00 | −0.07 | −0.22 | −0.19 | 0.06 | |
| D1-Dffclt | 0.03 | −0.03 | −0.47 | −0.13 | −0.71 | −0.10 | −0.24 | |
| D1-Dscrmn | 37.058 | 17.332 | 4.559 | 13.038 | 12.757 | 37.206 | 20.325 | |
| D1-P (x = 1|z = 0) | 0.265 | 0.748 | 0.894 | 0.852 | 1.000 | 0.974 | 0.789 | |
| D2-Dffclt | 0.028 | -0.076 | −0.517 | −0.118 | −0.683 | −0.051 | −0.236 | |
| D2-Dscrmn | 37.058 | 17.332 | 4.559 | 13.038 | 12.757 | 37.206 | 20.325 | |
| D2-P (x = 1|z = 0) | 0.265 | 0.789 | 0.913 | 0.823 | 1.000 | 0.870 | 0.777 | |
| D3-Dffclt | 0.014 | −0.063 | −0.492 | −0.118 | −0.670 | −0.066 | −0.233 | |
| D3-Dscrmn | 37.058 | 17.332 | 4.559 | 13.038 | 12.757 | 37.206 | 20.325 | |
| D3-P (x = 1|z = 0) | 0.38 | 0.8683 | 0.90 | 0.82 | 0.9998 | 0.922 | 0.816 | |
| Polytomous | EAP reliab. | 0.93 | 0.97 | 0.92 | 0.97 | 0.92 | 0.96 | 0.94 |
| WLE reliab. | 0.92 | 0.96 | 0.91 | 0.97 | 0.92 | 0.96 | 0.94 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marco-Franco, J.E.; Reis-Santos, M.; Barrachina-Martínez, I.; González-de-Julián, S.; Camaño-Puig, R. Validation of a New Telenursing Questionnaire: Testing the Test. Mathematics 2022, 10, 2463. https://doi.org/10.3390/math10142463
Marco-Franco JE, Reis-Santos M, Barrachina-Martínez I, González-de-Julián S, Camaño-Puig R. Validation of a New Telenursing Questionnaire: Testing the Test. Mathematics. 2022; 10(14):2463. https://doi.org/10.3390/math10142463
Chicago/Turabian StyleMarco-Franco, Julio Emilio, Margarida Reis-Santos, Isabel Barrachina-Martínez, Silvia González-de-Julián, and Ramón Camaño-Puig. 2022. "Validation of a New Telenursing Questionnaire: Testing the Test" Mathematics 10, no. 14: 2463. https://doi.org/10.3390/math10142463
APA StyleMarco-Franco, J. E., Reis-Santos, M., Barrachina-Martínez, I., González-de-Julián, S., & Camaño-Puig, R. (2022). Validation of a New Telenursing Questionnaire: Testing the Test. Mathematics, 10(14), 2463. https://doi.org/10.3390/math10142463







