Abstract
In this work, we seek to design a model that contributes to the study and resolution of a multi-objective rescheduling problem in dynamic permutation flow shop contexts. In this type of problem, where the objectives can be valued in heterogeneous units, the difficulty of achieving an optimal solution leads to finding a set of non-dominated efficient solutions (also called Pareto front). On the other hand, we will also consider the potential appearance of disruptions in planned scheduling (such as machine breakdowns or arrival of new priority jobs) that require a rapid re-planning of the aforementioned scheduling. In this paper, a hybrid dynamic non-dominated sorting genetic II metaheuristic (HDNSGA-II) is proposed to find the optimal Pareto front. The algorithm is applied to a benchmark already tested in previous studies, defined by three conflicting objective functions (makespan, total weighted tardiness, and stability) and three different types of disruption (machine breakdowns, incorporation of new jobs, and modifications in process times). According to the statistical comparison performed, the HDNSGA-II algorithm performs better in the designed environment, especially in larger problems.
MSC:
90-08; 90C29
1. Introduction
1.1. Flow Shop Problems
The problem of scheduling a set of jobs assigned to different machines in specific production environments has been studied profusely since the 1950s, highlighting its non-deterministic polynomial-time hardness (NP-hardness), as exposed by [1].
In flow shop production systems of “n” jobs to be processed in “m” machines, the usual goal is to seek the optimal scheduling of the “n” jobs. Each job integrates “m” possible operations to be performed on each of the machines. Because each machine must process jobs at specific periods of time, to complete a job on an available machine j, processing must have previously completed on the j-1 machine.
In the factorial permutation flow shop problems (PFSPs), the scheduling of jobs to be processed is the same on all machines. It is usually considered that there are no established orders of precedence among job operations (completed without interruption) and that machines can only perform one operation at a time.
Single-objective flow shop optimization consists of sequencing n jobs on m machines minimizing or maximizing a single determined criterion. There are multiple objective functions applied to flow shop optimization. The most common is the maximum task completion time (makespan). As for the techniques proposed in the literature to solve this problem, they range from exact to approximate methods, based on metaheuristics or using simple heuristics depending on the selected objective.
There are several methods based on mathematical models of integer linear programming (MILP) applied to the problem of minimizing the makespan. As remarkable studies, [2] describes a MILP model of the PFSP problem to minimize the makespan with an exponential growth in the number of restrictions. They propose a technique based on row generation to solve the linear relaxation of the problem in polynomial time. On the other hand, [3] exhibits different formulations for the flow shop problem with permutation, with and without unlimited buffers and with the aim of minimizing the delay of jobs. When solved with exact methods such as branch and bound, the global optimal solution can be found. However, the factorial complexity of the sequencing problems makes it possible to solve them in reasonable time only in small problems, producing memory and execution time troubles with instances starting from 20 jobs to 10 machines ([4]).
Due to the high computational requirements of the aforementioned methods in the face of factorial complexity problems, multiple heuristics have been proposed in the literature (see for example [5,6,7,8]). Ref. [9] carries out an exhaustive comparison of 22 heuristics applied to the problem of minimizing the total flow time in flow shop problems with permutation.
According to [10], on average, the NEH heuristic [7] calculates a makespan close to 3% of the optimum, for a total of jobs varying in the range 5–500 and a number of machines between 5 and 25. Both the NEH and Rajendran and Ziegler heuristics are important because they are widely used in the literature in the process of initializing solutions for later improvement through a metaheuristic. An example of a solution initialization procedure that uses both heuristics is that proposed by [11], used by the RIPG algorithm defined in [12].
Multi-objective optimization problems seek to identify efficient solutions (not dominated) for multiple conflicting objectives (such as cost, quality, or time) by determining the so-called Pareto front, a set of solutions from which the decision maker will choose the one that best meet the specific requirements of the problem.
In this type of problem, it is necessary to choose efficiency metrics that allow comparing the solutions of the Pareto front obtained with the different algorithms used in their resolution. From the analysis of the literature, the following efficiency indicators have been chosen:
- Hypervolume metric, according to the calculation proposed by [13].
- Unary Epsilon Indicator [14,15,16].
- Convergence metric, suggested by [17].
- Rate of non-dominated solutions [18].
The methods applied in multi-objective optimization can be categorized in scalar-based and metaheuristic-based techniques [19]. Regarding the scalar techniques, there are different strategies that convert the starting problem into a single-objective type in order to establish the objective weights which allow to obtain the Pareto front, such as CWA (conventional weighted aggregation), DWA (dynamic weighted aggregation), RWA (randomly weighted aggregation), and BWA (bang-bang weighted aggregation).
Regarding metaheuristic techniques, we highlight those based on: genetic algorithms [20,21,22,23,24,25,26], particle swarms [27], tabu search [28], simulated annealing [11,29], ant colonies [30,31], decomposition-based kernel techniques [32], greedy algorithms [12], fuzzy-based techniques [33], hybrid algorithms [34], student learning-based approaches [35], or techniques based on local search [36]. Most articles on these methods study two-objective problems that are graphically representable in a simple way and whose results are easier to analyze.
Recent studies indicate the need to first understand the limitations of current algorithms when working with a greater number of objective functions and later to design new techniques that work properly when the number of these functions increases [37,38].
The investigation is structured as follows. The rescheduling systems described in the literature are illustrated first. Then, after defining the integer linear programming model that describes the problem, a rescheduling system is proposed to solve it according to a predictive-reactive strategy. Subsequently, the novel HDNSGA-II metaheuristic is described and validated on Dubois-Lacoste instances in a static and bi-objective environment. Next, after calibrating the model parameters, the HDNSGA-II and RIPG metaheuristics are applied to a benchmark previously designed in this context. Finally, the comparative results obtained by both algorithms are shown and discussed and the main conclusions of the work are presented.
1.2. Rescheduling Systems
Static scheduling problems determine the processing sequence of an initial set of previously established jobs on the available machines of a system whose conditions are known in advance and unchanged over time. In real production environments, disruptions can arise, such as changes in the priority of carrying out jobs, breakdowns, or maintenance operations on machines. These disruptions lead to dynamic scheduling systems, which require the rescheduling of jobs. The literature shows three main strategic approaches for this rescheduling [39,40]: predictive-reactive, proactive (or robust), and dynamic. One of the most used is the predictive-reactive strategy, which will be chosen in this paper. Additionally, the three main decision policies to reschedule jobs in the predictive-reactive approach [41] are: event-driven, periodic, and hybrid (periodic being the one chosen in this paper). There are also three main methods to update an infeasible schedule when interruptions arise in the system (disabling the initial schedule): right-shift rescheduling [42,43], partial regeneration [42], and complete regeneration [44,45]. The complete regeneration method is the one used in this study.
Usual performance indicators for rescheduling systems can be efficiency metrics (e.g., makespan, mean flow time, or total weighted tardiness) or robustness metrics (such as solution robustness metrics, as known as stability metrics as described in [46]) (e.g., system mean stability [41,47,48]).
The literature on rescheduling in dynamic flow shop environments with permutation and multiple objective functions is still scarce. The algorithms for finding non-dominated solutions in PFSP environments, with a proactive-reactive strategy proposed by [49,50], do not use weighting of the objective functions. Ref. [49] utilises the MOSA (multi-objective simulated annealing algorithm) while [50] proposes metaheuristics based on hyper-volume known as IBEA (indicator-based evolutionary algorithm). Ref. [51] proposes the application of a state-of-the-art greedy algorithm for scheduling problems, called RIPG (restarted iterated Pareto greedy) to solve a three-objective permutation flow shop rescheduling problem.
The literature on rescheduling in environments other than the flow shop with permutation is not abundant either. Ref. [52] adjusts the NSGA-II—non-dominated sorting genetic algorithm [21]—for a stochastic FJSP (flexible job shop problem). Ref. [53] builds a multi-objective genetic algorithm to minimize the schedule’s total tardiness and stability in an environment with parallel machines and variations in job delivery dates. Ref. [54] developed a hybrid MPGA-CP (multiple populations genetic algorithm with constraint programming) to solve a three-objective flexible job shop problem under uncertainties. In reviews on rescheduling methods by [55,56], the predictive-reactive strategy is recognised as the most frequent.
2. Problem Statement
The aim followed in this paper is minimizing three objective functions: makespan, weighted total tardiness, and stability. The selection of these objective functions seeks to improve the productivity in the production environment (by minimizing the makespan), the customer service (by minimizing the total weighted tardiness), and the schedule stability in the rescheduling process when sudden disruptions arise. The mathematical formulation of the problem studied in this paper is described below and can be found in detail in [51].
As it is a predictive-reactive rescheduling process, the mathematical formulation can be expressed as a MILP (mixed integer linear problem) and be performed each time we need to reschedule. At each rescheduling point, events (disruptions such as new jobs, machine breakdowns, or processing time variations) are considered in the mathematical formulation as new inputs, affecting the generation of the next schedule as those events represent changes in the scheduling environment.
The problem formulation considers three input sets that define the environment to deal with: J represents the set of jobs (from 1…n) to be scheduled in the permutation flow shop problem, M identifies the processing machines (from 1…m) in the environment, and O defines the operations specified at each machine for each job.
Inputs used by the model are listed below:
- Factors related to the readiness of jobs and machines:
- ○
- rli is the time when job Ji is available for being processed after arriving to the shop floor (known as release time).
- ○
- rtj is the time when machine Mj is ready to process an incoming job (known as ready time).
- Jobs-related specification factors:
- ○
- pij indicates the processing time needed by the job Ji to be processed on the machine Mj.
- ○
- di represents the due date for job Ji, as requested by the client.
- ○
- wi indicates a weight for the job Ji, representing its urgency.
- Predictive-reactive-related factors:
- ○
- RT is the current rescheduling instant time.
- ○
- represents the starting time of job Ji on machine Mj in the predictive baseline schedule calculated initially.
- Disruption events-related factors:
- ○
- represents the starting time of a breakdown disruption for machine Mj.
- ○
- represents the end time of a breakdown disruption for machine Mj.
Variables optimized and calculated by the model are described below:
- xij are binary variables indicating the position of each Job Ji in the schedule:
- Si,j represents the starting time of job Ji on machine Mj in the calculated new optimal schedule.
- Ci indicates the completion time of job Ji, and it depends on the competition time on each machine Mj (Ci,j).
- yi,j,1, yi,j,2, and yi,j,3 are binary variables that represents three possible situations of machine breakdowns:
- ○
- is 1 (job already processed situation) in case operation of job Ji on machine Mj finishes before we have a breakdown in the machine; otherwise takes 0 value.
- ○
- is 1 (conflict situation) in case operation is not finished when the breakdown occurs; otherwise takes 0 value.
- ○
- is 1 (job starting time displacement situation) in case operation needs to be done after a machine breakdown; otherwise takes 0 value.
As objectives to optimize, we need to minimize the following to get the Pareto frontier (PF): makespan (Cmax), total weighted tardiness (TWT), and stability (STB).
Makespan (first objective function) indicates the maximum completion time for all jobs. It is a common objective to be minimized in permutation flow shop problems and it is calculated as the completion time of the last scheduled job in the sequence:
Completion time for each job depends on the processing in the last machine M in a permutation flow shop problem:
The three defined machine breakdowns situations are considered in this mathematical formulation to adjust the competition time of jobs in the machines:
Job already processed situation:
Conflict situation (in this case, job needs to re-start after machine is ready):
Job starting time displacement situation (in this case, job waits to start):
The next equation ensures that only one out of the three previous situations occurs for a job, when a machine breakdown event arises in the production environment:
Starting times for jobs Ji on each machine Mj, need to be calculated depending on the completion times:
To linearise the Max function and completely model the starting times, we include the equations below:
A job cannot start in a machine if a previous job has not finished on the same machine:
and if its previous operation has not yet finished:
Starting time in the first machine of the production environment needs to respect the jobs release times:
Moreover, the formulation needs to respect the machine readiness specifications:
The second objective considered in this problem is the total weighted tardiness (TWT) that depends on the differences between the due dates of the jobs and their completion time in the permutation flow shop system, weighted by its urgency, that is:
The next equations are included to linearise the Max function:
Stability (STB) is the third objective optimized in our problem statement. It represents the differences in starting times of unprocessed scheduled jobs in the baseline schedule of the predictive-reactive paradigm versus their new starting times as calculated by the optimization. STB is calculated following the next equation:
As the absolute value function is non-linear and non-differentiable, we add the next equations to model STB in a suitable shape for the MILP formulation. We initially replace the absolute function by a variable, DeltaStartTime:
Then, we add binary variables to define two different situations (d1 and d2):
In case d1 takes value 1, it means that the DeltaStartTime variable will take: ; otherwise .
Finally, we add equations to ensure that the jobs can only be located at just one position in the schedule and that there cannot be more than one job in the same position:
3. Proposed Solution
The architecture of the proposed rescheduling system and the HDNSGA-II proposed algorithm are subsequently described.
HDNSGA-II is a population algorithm based on the NSGA-II technique, developed by [21], which incorporates various improvement mechanisms. In particular, it adds a probabilistic model for estimating distributions to restart the population when stagnation occurs, a local tabu search process, and an initialization of the population based on a GRASP procedure and prior knowledge. In addition to the improvements introduced in the NSGA-II, the algorithm is applied to a context where the NSGA-II has never been applied, that is, in the multi-objective framework for task rescheduling. Additionally, the HDNSGA-II algorithm is compared with the RIPG algorithm [51].
3.1. Rescheduling Architecture
In this paper, the rescheduling strategy used builds on the predictive-reactive approach. Thus, in the first place a baseline schedule is established that is later updated according to the disruptions that appear in the system. It is essential to indicate the appropriate period for the rescheduling cycles, depending on the dimensions of the problem. In the paper, this period is obtained dividing the maximum jobs’ completion time (Cmax) by the total number of rescheduling points to be executed in the system (five rescheduling points were considered as being an adequate number to evaluate the capacity of adaptation of the architecture without having to excessively increase the number of executions in the system) [51].
3.2. Hybrid Dynamic NSGA-II Algorithm
The HDNSGA-II algorithm proposed in this study is based on the NSGA-II multi-object evolutionary algorithm, developed by [21], considered one of the best multi-object techniques in the scientific literature. The HDNSGA-II algorithm adapts the NSGA-II technique to dynamic rescheduling environments, hybridizing it with estimation of distribution algorithms (EDAs) and implementing a memetic approach to improve each individual in the population based on a local search using a Tabu technique.
The built-in probabilistic learning model is based on the probability of dependence of each job on their predecessors and successors and on the probability of sorting and placing each job in the sequence corresponding to the best individuals. The model allows to generate good quality artificial chromosomes (new individuals) when there is a stagnation of the algorithm, avoiding convergence towards local optimal solutions.
There are previous studies that use memetics and EDAs. Thus, [57] proposes a genetic memetic algorithm for a bi-objective flow shop problem with permutation called NNMA that integrates NEH heuristic (as a local search improvement procedure) with NSGA-II metaheuristic. On the other hand, [58] develops a hybrid genetic algorithm for a mono-objective flow shop problem with permutation. In addition to classic crossover and mutation operators, artificial chromosomes are generated through estimation of distributions algorithms (EDAs) modelling, learning, and sampling. This hybridization seeks to develop the solution population both evolutionarily and artificially. The proposed algorithm is called ACGA (artificial chromosomes with genetic algorithm), applying genetic evolution until the process reaches a stable situation. At that point, the distribution estimation algorithm (EDA) is alternated with the genetic algorithm, during a certain number of pre-set iterations. The EDA strategy is based on the combination of univariate and bivariate modelling. The univariate probabilistic model represents the importance of job order in the sequence, and the bivariate model represents the block structure in the sequence, that is, the probability that one job precedes or succeeds another. Figure 1 shows an outline of the proposed HDNSGA-II algorithm, consisting of the following steps:
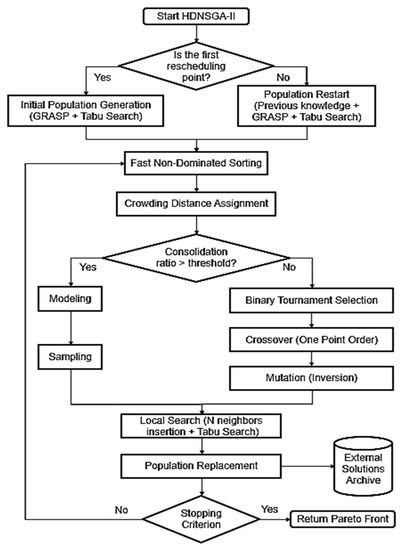
Figure 1.
Flow diagram of the HDNSGA-II technique.
Step 1. The population of solutions is initialized. Initialization incorporates knowledge of previous reschedules when building individuals taking advantage of previously performed optimizations in order to start from a good set of initial solutions. If the system is in the first rescheduling period, lacking knowledge about previous searches, initialization is performed using a GRASP (greedy randomized adaptive search procedure) algorithm along with a tabu local search procedure.
This idea of GRASP initialization is used to obtain good candidate solutions at the start of a genetic algorithm [59]. During this initialization, two solutions are generated by applying the NEH heuristic with the aim of minimizing makespan and the NEH-EDD technique in order to minimize total weighted tardiness [60]. In the NEH-EDD procedure, the jobs are initially scheduled according to their delivery date (applying the EDD rule) and later, the final sequence is obtained by applying NEH. The remaining N-2 individuals, N being the size of the initial population, are generated randomly to subsequently apply a process to improve the quality of each individual, using a GRASP algorithm together with a local tabu search.
The GRASP algorithm [59,61] is an iterative search process in two phases, where each iteration carries out a constructive process and a local search procedure. In the construction phase, a greedy randomized function is used to construct initial solutions, generating feasible solutions at each iteration. Subsequently, this solution is exposed to a local search procedure to improve its quality. Finally, the best solution found in all iterations is returned. In the construction phase, a greedy randomized adaptive procedure is applied, based on a restricted list of candidates, called RCL (restricted candidate list), where elements are iteratively incorporated into a structure, initially empty, until a solution of the problem is obtained. The choice of the next element to include is based on heuristic information on how convenient it is to include the element in the solution. A single execution of the GRASP algorithm is carried out for each solution to be generated in order to quickly obtain an initial set of solutions.
In GRASP construction phase, the evaluation of incremental costs is carried out by calculating the distances after incorporating new candidate elements (jobs) in the solution through the CDA (crowding distance assignment) operator of the NSGA-II. After the incremental evaluation, the best solutions will be those with the highest CDA value, within the set of partial non-dominated solutions, in order to achieve greater diversification in the search process. The Tabu search used in the construction of the solution initial population follows a scheme based on the neighbourhood exchange operator by permutation of two randomly selected jobs.
When the dynamic system is at rescheduling points after the initial one, an alternative “population reinitialization method” is used. In these situations, a prior knowledge mechanism is incorporated into the proposed HDNSGA-II method. In this case, N/4 individuals, N being the population size, are selected from the Pareto front obtained in the previous rescheduling point by the HDNSGA-II metaheuristic. For each of the chosen solutions, jobs already processed in the system are eliminated and jobs previously scheduled are assigned in the same order specified by the selected non-dominated solution. Subsequently, new jobs arriving at the system are scheduled according to NEH and NEH-EDD heuristics. Thus, for each of the N/4 solutions found, two solutions are generated and consequently N/2 individuals from the initial population are covered. The remaining N/2 solutions in the population are generated as in the first rescheduling period, that is, by random initialization together with a GRASP and Tabu search-based improvement procedure. The reason for this random initialization in half population is to allow the algorithm the possibility of obtaining many changes on the new Pareto front.
Step 2. The elements of the population are sorted using the NSGA-II fast non-dominated sorting method.
Step 3. According to the crowding distance assignment (CDA) method of the NSGA-II, a distance value assigned to each individual in the population is calculated. The MCDA (modified crowding distance assignment) method applied in the RIPG is not used in this case as selection mechanism. The MCDA method was proposed to avoid population stagnation, avoiding the selection of the same solution in consecutive iterations, when there is no improvement [62]. In the case of HDNSGA-II, this stagnation is controlled by applying EDAs, which reinitialize the solution population when a certain threshold of the consolidation ratio is exceeded (Step 4).
Step 4. The descendant population generation method is selected using the traditional evolutionary genetic approach or through the generation of artificial chromosomes, depending on the EDA implemented. To select one or the other method, the mechanism proposed by [63] is used, considering the consolidation ratio as an online mechanism for stopping and detecting stagnation of solutions in multi-objective problems. This ratio is a convergence metric based on the concept of dominance and the total set of non-dominated solutions found during the entire execution of the algorithm. It is defined as the relative number of non-dominated solutions that still hold on the approximate Pareto front calculated in the current iteration. In the algorithm improvement phases, the consolidation ratio has a low value, reaching high values as the Pareto front converges. In HDNSGA-II, when the population consolidation ratio reaches a certain threshold, the population is reinitialized by generating artificial chromosomes using an EDA. In this way, the knowledge obtained in previous searches is used to generate as individuals of the new population those with the greatest potential from a probabilistic point of view.
Step 5. If the consolidation ratio has been exceeded, the implemented EDA is used to generate artificial chromosomes until the maximum size of the population is reached. The EDA algorithm consists of two phases: a first phase of modelling and learning and later a solution sampling phase. In the modelling phase, two learning models are used analogously to the proposal presented by [58]: a univariate and a bivariate modelling. The univariate model represents the existing correlations in the order of the different jobs in the sequence. On the other hand, the bivariate model represents the structure of job blocks in the sequence, allowing to evaluate the probability that one job precedes or succeeds another, characterizing the job transition relationships. Finally, in the sampling phase, the solution population in the current generation is reinitialized. For this reason, the two statistics calculated in the modelling phase are used, creating a probabilistic model which evaluates the probability that a job i is located in position i.
Step 6. If the consolidation threshold limit is not reached, the population of descendants is generated by selecting pairs of individuals from the population, by means of a selection process through a binary tournament and applying genetic operators. The one point order (OP) is used as crossing operator. This method has been selected as it provides good results in scheduling problems [64]. On the other hand, inversion is used as mutation operator [65].
Step 7. After crossing and mutating individuals (Step 6) or having generated the population using the EDA (Step 5), a local search is performed on the descendants of the population, specializing and improving the new generation. Therefore, an iterated memetic search is incorporated based on a hybrid algorithm through the local search process mentioned in the RIPG algorithm [51] together with an improvement of the solutions through a tabu search. Hence, in a similar way to RIPG, the selected job is reinserted in nneigh positions close to a random position in the sequence, obtaining a set of solutions of which only the non-dominated solutions are considered. From the obtained solutions, the solution with the greatest distance (using the CDA method) is selected through the local RIPG search to subsequently improve it by means of a local Tabu search procedure, following the same scheme used in Step 1 of this algorithm.
Step 8. Finally, the total set of non-dominated solutions is returned, storing them in an external file that is updated in each iteration of the genetic.
4. Results
For the algorithm, the benchmark proposed by [51] is used. Instances can be accessed at http://dx.doi.org/10.17632/4p4jcwdwpt.2 (accessed on 20 May 2022) (Mendeley Website).
4.1. Parameter Calibration
The hardware used in the experimentation was a computer with an Intel Xeon X5675 Quad-Core 3.07 GHz processor and 16 GB of RAM. The operating system used was Windows 7 Enterprise Edition, 64-bit architecture. The software was developed on the .NET platform with the C# programming language and using Microsoft Visual Studio 2010 Development Framework.
To fairly compare all algorithms, the same stopping criterion was used. This criterion is defined from different approaches in the literature [64,66,67,68,69,70]. Most of them use a maximum execution time as stopping criterion, estimated in relation to the size of the problem, which is defined by the number of jobs and machines that the system has available. In this paper, the time limit was calculated with the following equation:
where t is the total time expressed in milliseconds, n indicates the number of jobs considered in the problem instance, and m is the number of machines defined. The above equation is used to calculate the execution time because both the number of jobs and the number of machines played a role in the complexity of the problem to be solved. In addition, it allows to use more calculation time in problems with greater complexity.
Likewise, an automatic configuration methodology of the parameters defining the algorithms is proposed, based on an extension of the iterated F-Race method, implemented in the irace tool [71]. For this, hypervolume is defined as the metric to evaluate the configurations, as it is the most used criterion. To select the training instances, a complexity analysis is performed based on the results provided by the scientific literature on the Taillard instances [36,72].
A total of six problems have been selected (ta02, ta031, ta047, ta061, ta080, and ta024) as representative instances. Two of them of low complexity, in terms of resolution difficulty, another two of medium complexity, and another two of high complexity. The criterion selected to assess the complexity of an instance was based on a trade-off between the number of non-dominated solutions found in the scientific literature in terms of bi-objective static problems (makespan and total weighted tardiness) and the relative error found in single-objective problems considering the makespan criterion. The instances employed in the calibration phase were not subsequently used for algorithm evaluation in order to avoid overfitting.
After analyzing the Irace results, the HDNSGA-II algorithm has greater variability in the face of changes in the parameters. Table 1 shows the results of the automatic configuration using the HDNSGA-II algorithms.

Table 1.
Automatic HDNSGA-II configuration via Irace.
4.2. Comparison of HDNSGA-II and RIPG Metaheuristics in Dynamic Multi-Objective Environments
In order to verify the performance of the proposed HDNSGA-II metaheuristic, it is executed together with the RIPG [51] metaheuristic on the 50 benchmark problems, specifically developed in this work for a flow shop rescheduling environment.
The main differences between HDNSGA-II and RIPG are focused on its architecture: HDNSGA-II is a population-based algorithm, whereas RIPG is a constructive algorithm. HDNSGA-II integrates a learning method based on EDAs to learn from past searches (previous knowledge), while RIPG restarts the working set to avoid stagnation effect. Finally, HDNSGA-II integrates an advanced Tabu local search to improve the solutions.
Each algorithm is executed 10 times independently for each of the experiments, in order to be able to perform a statistical analysis of confidence. Wilcoxon statistical test is used to evaluate the comparison between the HDNSGA-II and RIPG at an α = 0.05 level of significance.
Next, a comparison of the metaheuristics is represented for each of the performance metrics used and based on the types of problems analyzed. Figure 2 shows the evolution of the median of the hypervolume during 10 independent executions of the algorithms. It can be seen how RIPG performs better, reaching a higher hypervolume value than HDNSGA-II in small-sized instances (20 jobs). With 50, 100, and 200 jobs, HDNSGA-II exceeds RIPG, clearly accentuating this difference the larger the size of the problem to be solved.
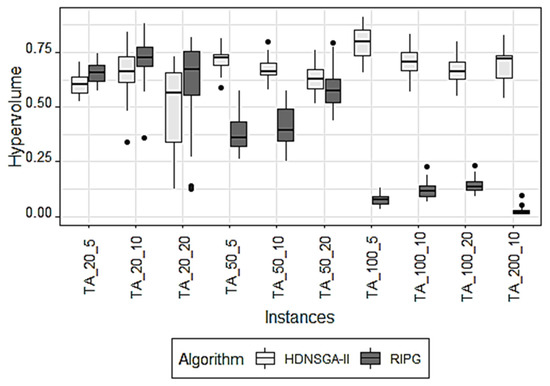
Figure 2.
Comparison of the hypervolume evolution with HDNSGA-II and RIPG in each type of instance.
The unary multiplicative epsilon indicator behaves in a similar way to hypervolume, as shown in Figure 3. In this case, the lower the value, the better the algorithm.
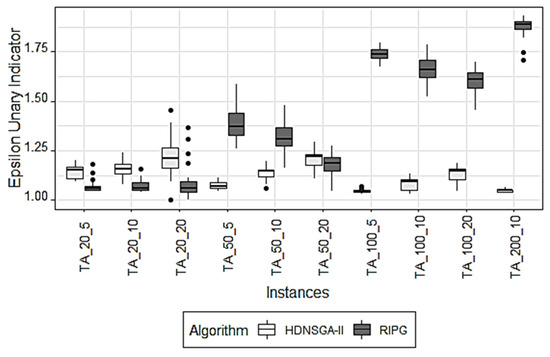
Figure 3.
Comparison of the Epsilon unary indicator evolution with HDNSGA-II and RIPG in each type of instance.
Regarding the ratio of non-dominated solutions (see Figure 4), RIPG exceeds HDNSGA-II in instances of 20 jobs. In the rest of the problems, HDNSGA-II clearly improves, reaching a ratio of non-dominated solutions of 1 against the RIPG, which is around 0.25 in most of the problems. Finally, with respect to the D1R metric, the situation is analogous to the rest of the metrics. RIPG is better for scenarios with 20 jobs, and HDNSGA-II far exceeds RIPG the larger the problem size, as shown in Figure 5.
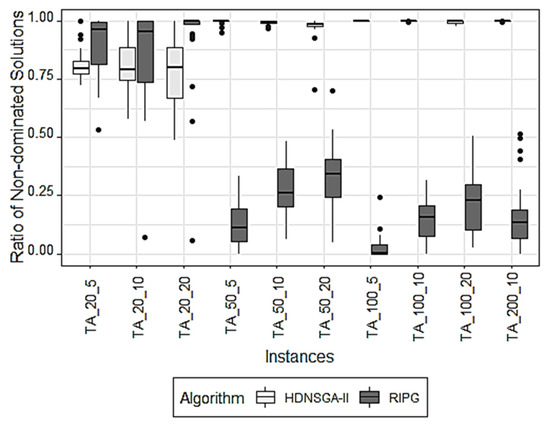
Figure 4.
Comparison of the non-dominated solutions ratio evolution with HDNSGA-II and RIPG in each type of instance.
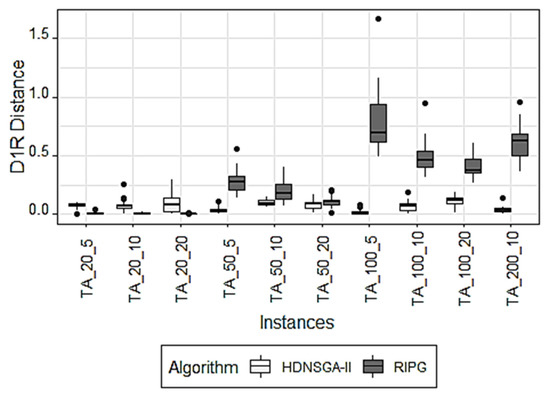
Figure 5.
Comparison of the D1R distance evolution with HDNSGA-II and RIPG in each type of instance.
As a result of the performed analysis, HDNSGA-II performs worse than RIPG technique for small instances (20 jobs). However, when the number of jobs and machines increases, HDNSGA-II performs better than the non-population RIPG technique. One of the reasons for this worsening of RIPG as the size of the problem increases is the growth of the number of non-dominated solutions in the constructive/destructive process of the algorithm, increasing the computational strength of the technique. To statistically demonstrate this conclusion, the results of the Wilcoxon statistical test are shown below, depending on the dimensions of the problem. Thus, Table 2 describes the comparative results between HDNSGA-II and RIPG algorithms in problems with 20 and 50 jobs. This table shows HDNSGA-II outperforms RIPG (W+) if it has a worse performance (W−) or if there are no significant differences between them (W=). The best results of RIPG can be seen in problems with 20 jobs, improving in all metrics to the HDNSGA-II. Better results are obtained in 90.67% of the instances for hypervolume, 80% for the epsilon unary indicator, 92% for D1R, and 57.33 for the ratio of non-dominated solutions. For issues with 50 jobs, HDNSGA-II outperforms RIPG on all performance metrics evaluated. Table 3 presents the results of the Wilcoxon test for the largest problems (100 and 200 jobs). It is observed how HDNSGA-II surpasses RIPG in all cases. Therefore, it can be concluded that HDNSGA-II performs better in dynamic multi-objective environments than RIPG, except in smaller problems (20 jobs).

Table 2.
Wilcoxon test results on metaheuristics for problems with 20 and 50 jobs.

Table 3.
Wilcoxon test results on metaheuristics for problems with 100 and 200 jobs.
Below is the evolution of Pareto fronts in some instances selected for the HDNSGA-II and RIPG algorithms at different rescheduling points (nevertheless, all Pareto fronts obtained with RIPG and HDNSGA-II can be found on http://dx.doi.org/10.17632/4p4jcwdwpt.2 (accessed on 20 May 2022)—Mendeley Website). Different symbols and grey levels in the charts represent different rescheduling points.
Figure 6 depicts the Pareto fronts obtained by HDNSGA-II at each rescheduling point in a problem with 20 jobs and 10 machines.

Figure 6.
Dynamic Pareto evolution for HDNSGA-II in TA_20_10_3.
Figure 7 shows the Pareto fronts obtained by RIPG, observing its better performance against the HDNSGA-II by allowing to distribute in a more uniform way the non-dominated solutions and covering better alongside the three axes (makespan, total weighted tardiness, and stability), as it is clearly shown in rescheduling points 4 and 5.
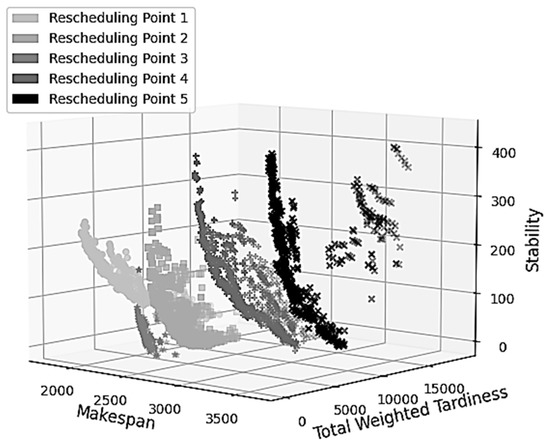
Figure 7.
Dynamic Pareto evolution for RIPG in TA_20_10_3.
Figure 8 illustrates the dynamic evolution of the Pareto front obtained by HDNSGA-II in a problem with 100 jobs and 20 machines.
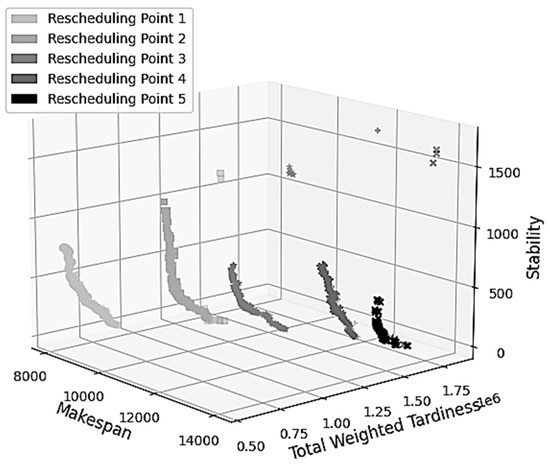
Figure 8.
Dynamic Pareto evolution for HDNSGA-II in TA_100_20_6.
In RIPG (see Figure 9), the solution space is not explored as uniformly as in HDNSGA-II.

Figure 9.
Dynamic Pareto evolution for RIPG in TA_100_20_6.
Finally, with the aim of being able to make a fair comparison, it should be noted that the execution times used to run every instance are the same for each of the metaheuristics. Figure 10 illustrates a graphical summary of the execution times of each instance according to the size of the problem.
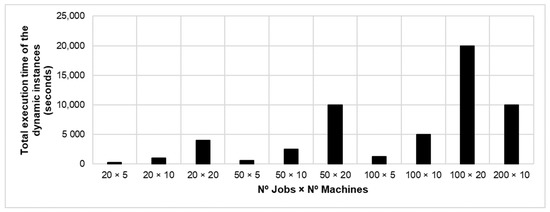
Figure 10.
Total execution times on every rescheduling instance for each metaheuristic.
5. Conclusions and Future Lines of Research
Several relevant contributions are made in this study. First, a benchmark has been generated to model dynamic rescheduling problems incorporating potential disruptions in the production environment. Likewise, a periodic rescheduling architecture has been designed and implemented, based on a predictive-reactive strategy. On the other hand, a population metaheuristic (HDNSGA-II) has been developed and compared with another non-population metaheuristic (RIPG) in dynamic rescheduling systems. Finally, it should be noted that the proposed HDNSGA-II algorithm incorporates the knowledge gained in previous rescheduling points in the population reinitialization process.
The HDNSGA-II algorithm proposed in this study notably improves the RIPG—commonly used in the state of the art of bi-objective flow shop optimization problems—except for small problems (20 jobs)—in all the performance metrics evaluated. On the other hand, it should be noted that the RIPG technique is more robust than the HDNSGA-II population technique since any parameterization of the algorithm achieves similar results in median value. Finally, the number of evaluations of the objective functions is greater in the RIPG algorithm than in the HDNSGA-II. This is due to the greedy phase of solution construction, where the set of non-dominated solutions has to be maintained. For this reason, the number of iterations executed by RIPG is less than in HDNSGA-II when scaling the number of objective functions.
As future lines of research, the impact of using probabilistic models (EDAs) in the HDNSGA-II algorithm and the consideration of previous rescheduling points in the population reinitialization process in future rescheduling periods could be analyzed. Likewise, the study of local search in the HDNSGA-II genetic algorithm could be deepened. The results of the automatic parameterization given by Irace in the algorithm do not ensure the efficiency of the local search in the genetic, since the optimal parameterization of HDNSGA-II only takes into account a single neighboring position in which to reinsert the selected job in the local search phase (parameter named nneigh). The interaction between the two steps applied in the local search—GRASP process and improvement of the solution through a Tabu search—could also be analyzed.
On the other hand, the influence of the baseline used in the evaluation of the objective stability function could also be analyzed. Likewise, the dynamic system could be evaluated according to the number of rescheduling points chosen. In the study, all the experiments were analyzed using five rescheduling points, but the variations could be evaluated with a number of rescheduling points between 0 and 1000, as is done in [73]. Finally, the proposed metaheuristics could be adapted to dynamic environments in problems called many-objective optimization, where the number of objective functions is greater than three.
Author Contributions
Conceptualization, P.V. and A.G.; Data curation, J.P.; Formal analysis, P.V.; Investigation, P.V., A.G., J.P. and I.F.; Methodology, P.V., A.G. and J.P.; Software, P.V.; Supervision, J.P. and I.F.; Validation, P.V., A.G. and I.F.; Writing—original draft, P.V. and A.G.; Writing—review & editing, J.P. and I.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Instances and Solutions Dataset referred in this paper can be accessed at http://dx.doi.org/10.17632/4p4jcwdwpt.2 (accessed on 20 May 2022) (Mendeley Website).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Garey, M.R.; Johnson, D.S.; Sethi, R. The Complexity of Flowshop and Jobshop Scheduling. Math. Oper. Res. 1976, 1, 117–129. [Google Scholar] [CrossRef]
- Frieze, A.; Yadegar, J. A new integer programming formulation for the permutation flowshop problem. Eur. J. Oper. Res. 1989, 40, 90–98. [Google Scholar] [CrossRef]
- Birgin, E.G.; Ronconi, D.P. Heuristic methods for the single machine scheduling problem with different ready times and a common due date. Eng. Optim. 2012, 44, 1197–1208. [Google Scholar] [CrossRef]
- Šeda, M. Mathematical models of flow shop and job shop scheduling problems. World Acad. Sci. Eng. Technol. 2007, 1, 122–127. [Google Scholar]
- Palmer, D.S. Sequencing Jobs Through a Multi-Stage Process in the Minimum Total Time—A Quick Method of Obtaining a Near Optimum. J. Oper. Res. Soc. 1965, 16, 101–107. [Google Scholar] [CrossRef]
- Gupta, J.N.D. A Functional Heuristic Algorithm for the Flowshop Scheduling Problem. J. Oper. Res. Soc. 1971, 22, 39–47. [Google Scholar] [CrossRef]
- Nawaz, M.; Enscore, E.E.; Ham, I. A heuristic algorithm for the m-machine, n-job flow-shop sequencing problem. Omega 1983, 11, 91–95. [Google Scholar] [CrossRef]
- Rajendran, C.; Ziegler, H. An efficient heuristic for scheduling in a flowshop to minimize total weighted flowtime of jobs. Eur. J. Oper. Res. 1997, 103, 129–138. [Google Scholar] [CrossRef]
- Pan, Q.-K.; Ruiz, R. A comprehensive review and evaluation of permutation flowshop heuristics to minimize flowtime. Comput. Oper. Res. 2013, 40, 117–128. [Google Scholar] [CrossRef]
- Modrak, V.; Semanco, P.; Kulpa, W. Performance Measurement of Selected Heuristic Algorithms for Solving Scheduling Problems. In Proceedings of the 2013 IEEE 11th International Symposium on Applied Machine Intelligence and Informatics (SAMI), Herlany, Slovakia, 31 January–2 February 2013; pp. 205–209. [Google Scholar]
- Varadharajan, T.; Rajendran, C. A multi-objective simulated-annealing algorithm for scheduling in flowshops to minimize the makespan and total flowtime of jobs. Eur. J. Oper. Res. 2005, 167, 772–795. [Google Scholar] [CrossRef]
- Ciavotta, M.; Minella, G.; Ruiz, R. Multi-objective sequence dependent setup times permutation flowshop: A new algorithm and a comprehensive study. Eur. J. Oper. Res. 2013, 227, 301–313. [Google Scholar] [CrossRef]
- Zitzler, E.; Thiele, L. Multiobjective evolutionary algorithms: A comparative case study and the strength Pareto approach. IEEE Trans. Evol. Comput. 1999, 3, 257–271. [Google Scholar] [CrossRef]
- Knowles, J.; Thiele, E.; Zitzler, E. A Tutorial on the Performance Assessment of Stochastic Multiobjective Optimizers; No. Tech. Rep. 214; Computer Engineering and Networks Laboratory (TIK), ETH Zurich: Zurich, Switzerland, 2006. [Google Scholar]
- Zitzler, E.; Thiele, L.; Laumanns, M.; Fonseca, C.; da Fonseca, V. Performance assessment of multiobjective optimizers: An analysis and review. IEEE Trans. Evol. Comput. 2003, 7, 117–132. [Google Scholar] [CrossRef]
- Zitzler, E.; Brockhoff, D.; Thiele, L. The Hypervolume Indicator Revisited: On the Design of Pareto-compliant Indicators Via Weighted Integration. In Evolutionary Multi-Criterion Optimization, Lecture Notes in Computer Science; Obayashi, S., Deb, K., Poloni, C., Hiroyasu, T., Murata, T., Eds.; Springer: Berlin, Germany, 2007; pp. 862–876. [Google Scholar]
- Czyzżak, P.; Jaszkiewicz, A. Pareto simulated annealing—a metaheuristic technique for multiple-objective combinatorial optimization. J. Multi-Criteria Decis. Anal. 1998, 7, 34–47. [Google Scholar] [CrossRef]
- Ishibuchi, H.; Yoshida, T.; Murata, T. Balance between genetic search and local search in memetic algorithms for multiobjective permutation flowshop scheduling. IEEE Trans. Evol. Comput. 2003, 7, 204–223. [Google Scholar] [CrossRef]
- Minella, G.; Ruiz, R.; Ciavotta, M. A Review and Evaluation of Multiobjective Algorithms for the Flowshop Scheduling Problem. Inf. J. Comput. 2008, 20, 451–471. [Google Scholar] [CrossRef]
- Amirian, H.; Sahraeian, R. Multi-objective differential evolution for the flow shop scheduling problem with a modified learning effect. Int. J. Eng.Trans. C Asp. 2014, 27, 1395. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Ishibuchi, H.; Murata, T. Multi-Objective Genetic Local Search Algorithm. In Proceedings of the IEEE International Conference on Evolutionary Computation, Nagoya, Japan, 20–22 May 1996; pp. 119–124. [Google Scholar]
- Karimi, N.; Davoudpour, H. A high performing metaheuristic for multi-objective flowshop scheduling problem. Comput. Oper. Res. 2014, 52, 149–156. [Google Scholar] [CrossRef]
- Li, B.-B.; Wang, L. A Hybrid Quantum-Inspired Genetic Algorithm for Multiobjective Flow Shop Scheduling. IEEE Trans. Syst. Man, Cybern. Part B Cybernetics 2007, 37, 576–591. [Google Scholar] [CrossRef]
- Pasupathy, T.; Rajendran, C.; Suresh, R. A multi-objective genetic algorithm for scheduling in flow shops to minimize the makespan and total flow time of jobs. Int. J. Adv. Manuf. Technol. 2006, 27, 804–815. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Abouhawwash, M.; Chakrabortty, R.; Ryan, M. A Simple and Effective Approach for Tackling the Permutation Flow Shop Scheduling Problem. Mathematics 2021, 9, 270. [Google Scholar] [CrossRef]
- Sha, D.Y.; Lin, H.H. A particle swarm optimization for multi-objective flowshop scheduling. Int. J. Adv. Manuf. Technol. 2009, 45, 749–758. [Google Scholar] [CrossRef]
- Allouche, M.A. Manager’s Preferences Modeling within Multi-Criteria Flowshop Scheduling Problem: A Metaheuristic Approach. Int. J. Bus. Res. Manag. 2010, 1, 33–45. [Google Scholar]
- Lin, S.-W.; Ying, K.-C. Minimizing makespan and total flowtime in permutation flowshops by a bi-objective multi-start simulated-annealing algorithm. Comput. Oper. Res. 2013, 40, 1625–1647. [Google Scholar] [CrossRef]
- Gravel, M.; Price, W.L.; Gagné, C. Scheduling continuous casting of aluminum using a multiple objective ant colony optimization metaheuristic. Eur. J. Oper. Res. 2002, 143, 218–229. [Google Scholar] [CrossRef]
- Rabanimotlagh, A. An efficient ant colony optimization algorithm for multiobjective flow shop scheduling problem. Int. J. Ind. Manuf. Eng. 2011, 5, 598–604. [Google Scholar]
- Zangari, M.; Constantino, A.A.; Ceberio, J. A decomposition-based kernel of Mallows models algorithm for bi- and tri-objective permutation flowshop scheduling problem. Appl. Soft Comput. 2018, 71, 526–537. [Google Scholar] [CrossRef]
- Yuan, F.; Xu, X.; Yin, M. A novel fuzzy model for multi-objective permutation flow shop scheduling problem with fuzzy processing time. Adv. Mech. Eng. 2019, 11, 1687814019843699. [Google Scholar] [CrossRef]
- Ojstersek, R.; Brezocnik, M.; Buchmeister, B. Multi-objective optimization of production scheduling with evolutionary computation: A review. Int. J. Ind. Eng. Comput. 2020, 11, 359–376. [Google Scholar] [CrossRef]
- Sasmito, A.; Pratiwi, A.B. Chaotic Student Psychology based Optimization Algorithm for Bi-Objective Permutation Flowshop Scheduling Problem. Int. J. Intell. Eng. Syst. 2021, 14, 109–118. [Google Scholar] [CrossRef]
- Dubois-Lacoste, J.; López-Ibáñez, M.; Stützle, T. A hybrid TP+PLS algorithm for bi-objective flow-shop scheduling problems. Comput. Oper. Res. 2011, 38, 1219–1236. [Google Scholar] [CrossRef]
- Deb, K.; Jain, H. An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point-Based Nondominated Sorting Approach, Part I: Solving Problems With Box Constraints. IEEE Trans. Evol. Comput. 2014, 18, 577–601. [Google Scholar] [CrossRef]
- Yuan, Y.; Xu, H.; Wang, B. An Improved NSGA-III Procedure for Evolutionary Many-Objective Optimization. In Proceedings of the 2014 Annual Conference on Genetic and Evolutionary Computation, GECCO’14, Vancouver, BC, Canada, 12–16 July 2014; ACM: New York, NY, USA; pp. 661–668. [Google Scholar]
- Kuster, J.; Jannach, D.; Friedrich, G. Applying Local Rescheduling in response to schedule disruptions. Ann. Oper. Res. 2008, 180, 265–282. [Google Scholar] [CrossRef]
- Zakaria, Z.; Petrovic, S. Genetic algorithms for match-up rescheduling of the flexible manufacturing systems. Comput. Ind. Eng. 2012, 62, 670–686. [Google Scholar] [CrossRef]
- Pfeiffer, A.; Kádár, B.; Monostori, L. Stability-oriented evaluation of rescheduling strategies, by using simulation. Comput. Ind. 2007, 58, 630–643. [Google Scholar] [CrossRef]
- Abumaizar, R.J.; Svestka, J. Rescheduling job shops under random disruptions. Int. J. Prod. Res. 1997, 35, 2065–2082. [Google Scholar] [CrossRef]
- Smith, S.F. Reactive Scheduling Systems. In Intelligent Scheduling Systems, Operations Research/Computer Science Interfaces Series; Brown, D.E., Scherer, W.T., Eds.; Springer: Boston, MA, USA, 1995; pp. 155–192. [Google Scholar]
- Church, L.K.; Uzsoy, R. Analysis of periodic and event-driven rescheduling policies in dynamic shops. Int. J. Comput. Integr. Manuf. 1992, 5, 153–163. [Google Scholar] [CrossRef]
- Vieira, G.E.; Herrmann, J.W.; Lin, E. Analytical models to predict the performance of a single-machine system under periodic and event-driven rescheduling strategies. Int. J. Prod. Res. 2000, 38, 1899–1915. [Google Scholar] [CrossRef]
- Herroelen, W.; Leus, R. Project scheduling under uncertainty: Survey and research potentials. Eur. J. Oper. Res. 2005, 165, 289–306. [Google Scholar] [CrossRef]
- Matsveichuk, N.M.; Sotskov, Y.N.; Werner, F. Partial job order for solving the two-machine flow-shop minimum-length problem with uncertain processing times. Optimization 2011, 60, 1493–1517. [Google Scholar] [CrossRef]
- Matsveichuk, N.M.; Sotskov, Y.N.; Egorova, N.G.; Lai, T.C. Schedule execution for two-machine flow-shop with interval processing times. Math. Comput. Model. 2009, 49, 991–1011. [Google Scholar] [CrossRef]
- Ben Itayef, A.; Loukil, T.; Teghem, J. Rescheduling a Permutation Flowshop Problems Under the Arrival a New Set of Jobs. In Proceedings of the 2009 International Conference on Computers & Industrial Engineering, Troyes, France, 6–9 July 2009; pp. 188–192. [Google Scholar]
- Liefooghe, A.; Basseur, M.; Humeau, J.; Jourdan, L.; Talbi, E.-G. On optimizing a bi-objective flowshop scheduling problem in an uncertain environment. Comput. Math. Appl. 2012, 64, 3747–3762. [Google Scholar] [CrossRef]
- Valledor, P.; Gomez, A.; Priore, P.; Puente, J. Modelling and Solving Rescheduling Problems in Dynamic Permutation Flow Shop Environments. Complexity 2020, 2020, 2862186. [Google Scholar] [CrossRef]
- Xiong, J.; Xing, L.-N.; Chen, Y.-W. Robust scheduling for multi-objective flexible job-shop problems with random machine breakdowns. Int. J. Prod. Econ. 2013, 141, 112–126. [Google Scholar] [CrossRef]
- Lima, H. Genetic algorithm approach to multiobjective rescheduling on parallel machines. IFAC Proc. Vol. 2005, 38, 139–144. [Google Scholar] [CrossRef]
- Zhang, S.; Tang, F.; Li, X.; Liu, J.; Zhang, B. A hybrid multi-objective approach for real-time flexible production scheduling and rescheduling under dynamic environment in Industry 4.0 context. Comput. Oper. Res. 2021, 132, 105267. [Google Scholar] [CrossRef]
- Vieira, G.E.; Herrmann, J.W.; Lin, E. Rescheduling Manufacturing Systems: A Framework of Strategies, Policies, and Methods. J. Sched. 2003, 6, 39–62. [Google Scholar] [CrossRef]
- Ouelhadj, D.; Petrovic, S. A survey of dynamic scheduling in manufacturing systems. J. Sched. 2009, 12, 417–431. [Google Scholar] [CrossRef]
- Chiang, T.-C.; Cheng, H.-C.; Fu, L.-C. NNMA: An effective memetic algorithm for solving multiobjective permutation flow shop scheduling problems. Expert Syst. Appl. 2011, 38, 5986–5999. [Google Scholar] [CrossRef]
- Chen, Y.-M.; Chen, M.-C.; Chang, P.-C.; Chen, S.-H. Extended artificial chromosomes genetic algorithm for permutation flowshop scheduling problems. Comput. Ind. Eng. 2012, 62, 536–545. [Google Scholar] [CrossRef]
- Marinakis, Y.; Migdalas, A.; Pardalos, P.M. Expanding Neighborhood GRASP for the Traveling Salesman Problem. Comput. Optim. Appl. 2005, 32, 231–257. [Google Scholar] [CrossRef]
- Holthaus, O.; Rajendran, C. A fast ant-colony algorithm for single-machine scheduling to minimize the sum of weighted tardiness of jobs. J. Oper. Res. Soc. 2005, 56, 947–953. [Google Scholar] [CrossRef]
- Resende, M.; Ribeiro, C. Greedy randomized adaptive search procedures. In Handbook of metaheuristics. International Series in Operations Research and Management Science; Glover, F., Kochenberger, G., Eds.; Springer: New York, NY, USA, 2003; Volume 57, pp. 219–249. [Google Scholar]
- Minella, G.G. Optimización Multi-Objetivo Para La Programación De La Producción. Ph.D. Thesis, Universitat Politècnica de València, Valencia, Spain, 2014. [Google Scholar]
- Goel, T.; Stander, N. A Study on the Convergence of Multiobjective Evolutionary Algorithms. In Proceedings of the Presented at the 13th Multidisciplinary Analysis and Optimization Conference, Fort Worth, TX, USA, 13–15 September 2010; pp. 1–18. [Google Scholar]
- Vallada, E.; Ruiz, R. Genetic algorithms with path relinking for the minimum tardiness permutation flowshop problem. Omega 2010, 38, 57–67. [Google Scholar] [CrossRef]
- Mirabi, M.; Ghomi, S.M.T.F.; Jolai, F. A novel hybrid genetic algorithm to solve the make-to-order sequence-dependent flow-shop scheduling problem. J. Ind. Eng. Int. 2014, 10, 57. [Google Scholar] [CrossRef][Green Version]
- Abdelhadi, A.; Mouss, L.H. An efficient hybrid approach based on multi agent system and emergence method for the integration of systematic preventive maintenance policies in hybrid flow-shop scheduling to minimize makespan. J. Mech. Eng. Res. 2013, 5, 112–122. [Google Scholar] [CrossRef]
- Costa, A.; Cappadonna, F.A.; Fichera, S. A Hybrid Metaheuristic Approach for Minimizing the Total Flow Time in A Flow Shop Sequence Dependent Group Scheduling Problem. Algorithms 2014, 7, 376–396. [Google Scholar] [CrossRef]
- Hatami, S.; Ruiz, R.; Romano, C.A. Two Simple Constructive algorithms for the Distributed Assembly Permutation Flowshop Scheduling Problem. In Managing Complexity, Lecture Notes in Management and Industrial Engineering; Hernández, C., López-Paredes, A., Pérez-Ríos, J.M., Eds.; Springer International Publishing: Cham, Switzerland, 2014; pp. 139–145. [Google Scholar]
- Ruiz, R.; Stützle, T. A simple and effective iterated greedy algorithm for the permutation flowshop scheduling problem. Eur. J. Oper. Res. 2007, 177, 2033–2049. [Google Scholar] [CrossRef]
- de Souza, D.L.; Sergio, F.; Gedraite, R.A. A Comparative Study Using Bio-Inspired Optimization Methods Applied to Controllers Tuning. In Frontiers in Advanced Control System; INTECH: London, UK, 2012; pp. 143–162. [Google Scholar]
- López-Ibáñez, M.; Dubois-Lacoste, J.; Cáceres, L.P.; Birattari, M.; Stützle, T. The irace package: Iterated racing for automatic algorithm configuration. Oper. Res. Perspect. 2016, 3, 43–58. [Google Scholar] [CrossRef]
- Taillard, E.D. Éric Taillard’s Page. 2014. Available online: http://mistic.heig-vd.ch/taillard/problemes.dir/ordonnancement.dir/ordonnancement.html (accessed on 20 May 2022).
- Sabuncuoglu, I.; Karabuk, S. Rescheduling frequency in an FMS with uncertain processing times and unreliable machines. J. Manuf. Syst. 1999, 18, 268–283. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).