Bifurcation Theory, Lie Group-Invariant Solutions of Subalgebras and Conservation Laws of a Generalized (2+1)-Dimensional BK Equation Type II in Plasma Physics and Fluid Mechanics
Abstract
:1. Introduction
2. Lie Symmetry Analysis
2.1. Lie Point Symmetries
2.2. Optimal System of One-Dimensional Subalgebras
Optimal Classification
- Case 1.
- 1.1. ,
- 1.1.1. ,
- 1.1.1.1. ,
- 1.1.2. .
- 1.1.2.1. .
- 1.2. ,
- 1.2.1. ,
- 1.2.1.1. ,
- 1.2.1.2. .
- 1.2.2. ,
- 1.2.2.1. ,
- Case 2. .
- 2.1. ,
- 2.1.1. .
- 2.1.2. .
- 2.2. .
- 2.2.1. ,
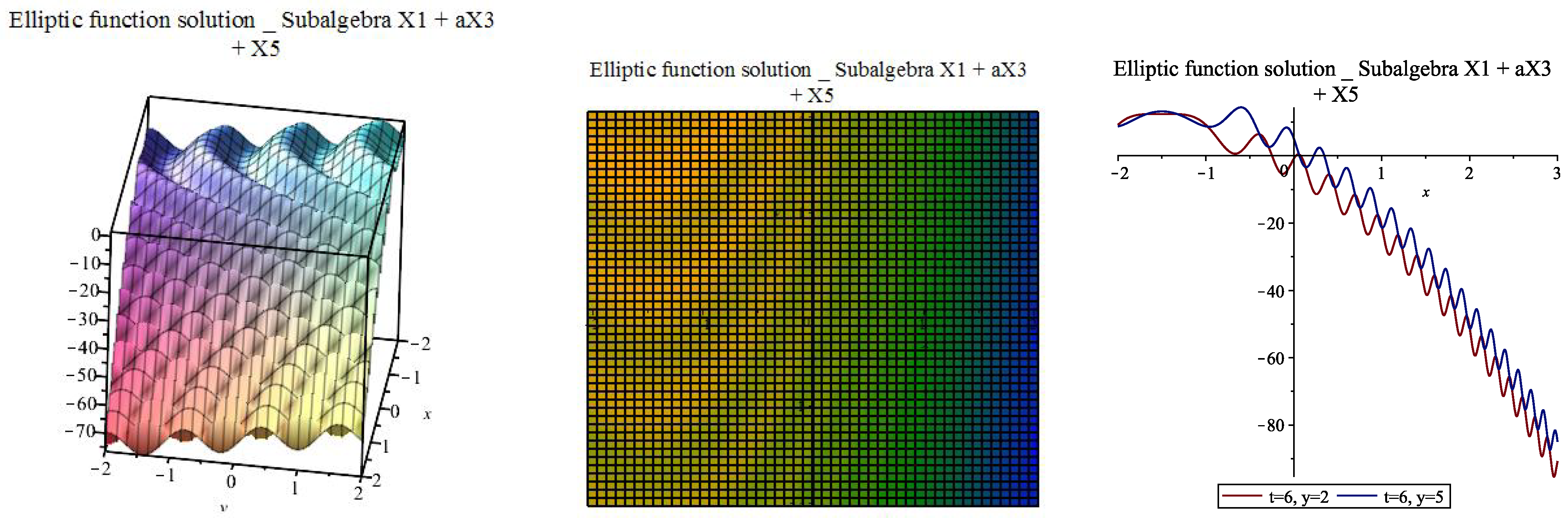
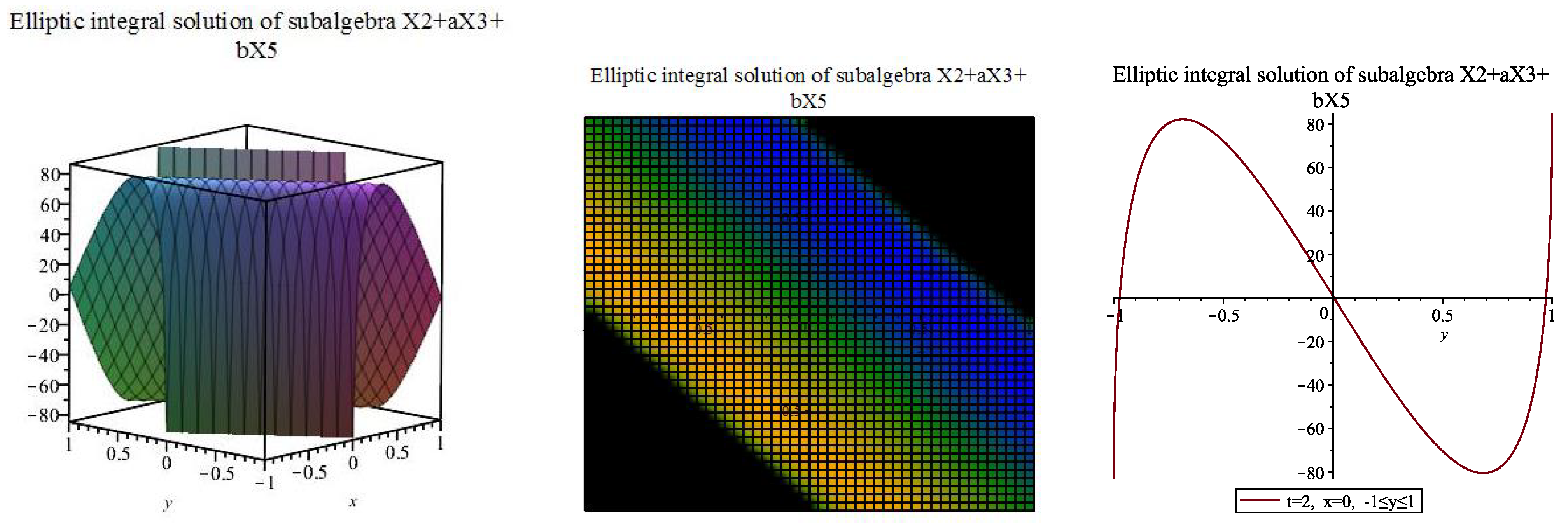
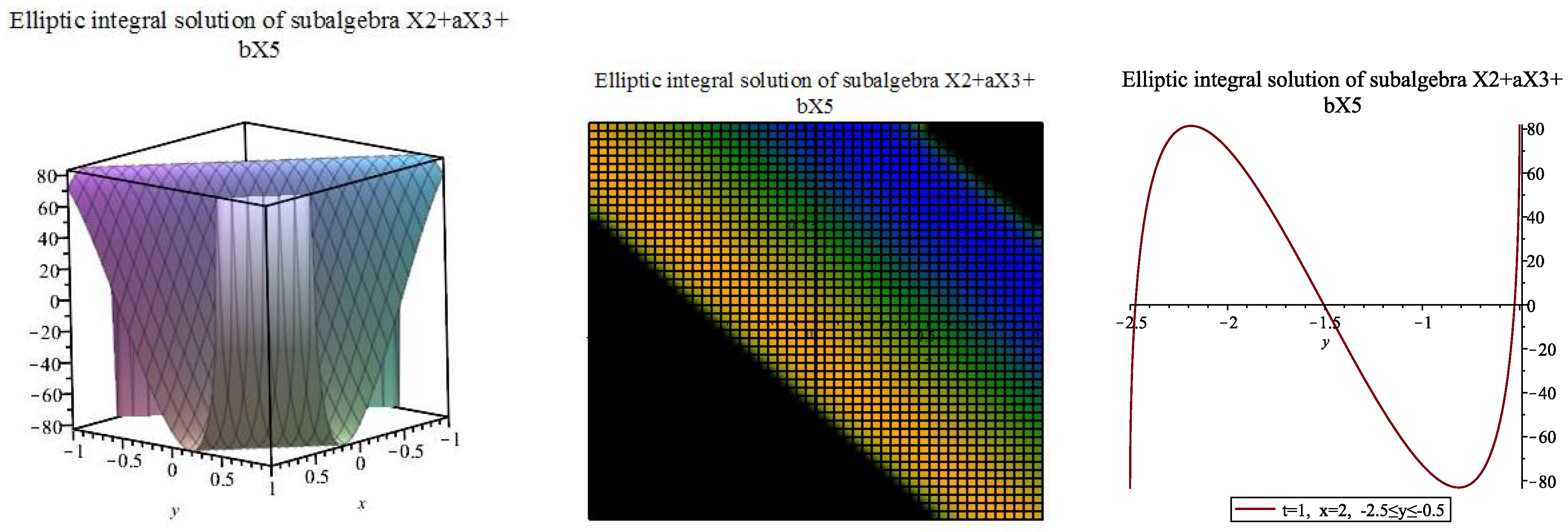
2.3. Group-Invariants and Some Exact Solutions
2.3.1. Optimal Subalgebra
2.3.2. Optimal Subalgebra
2.3.3. Optimal Subalgebra
2.3.4. Optimal Subalgebra
2.3.5. Optimal Subalgebra
2.3.6. Optimal Subalgebra
2.3.7. Optimal Subalgebra
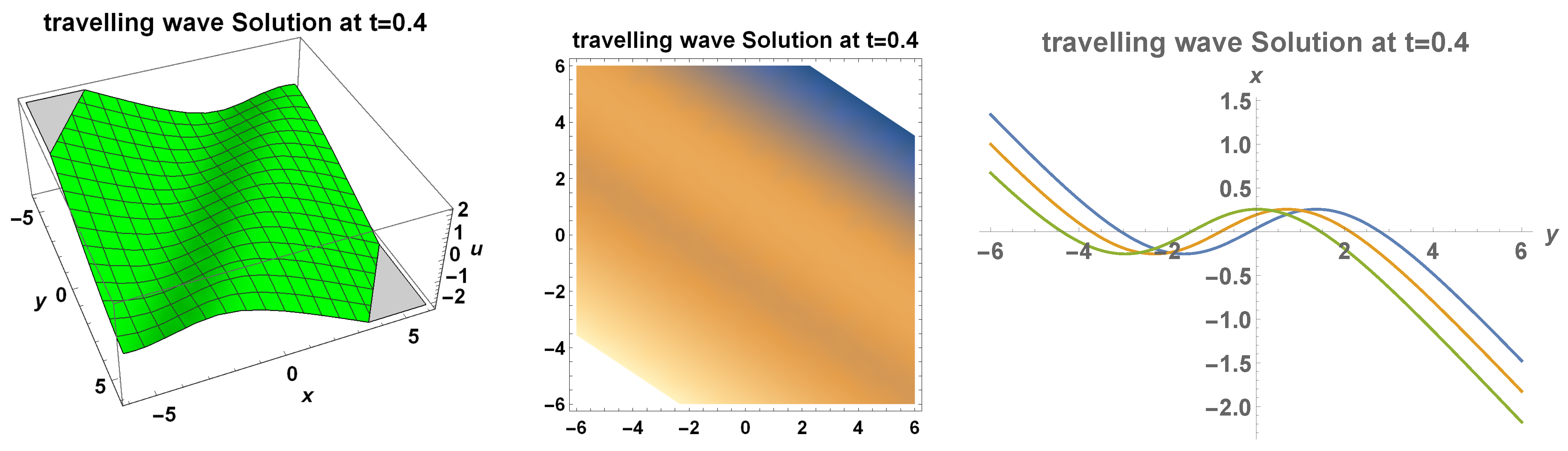
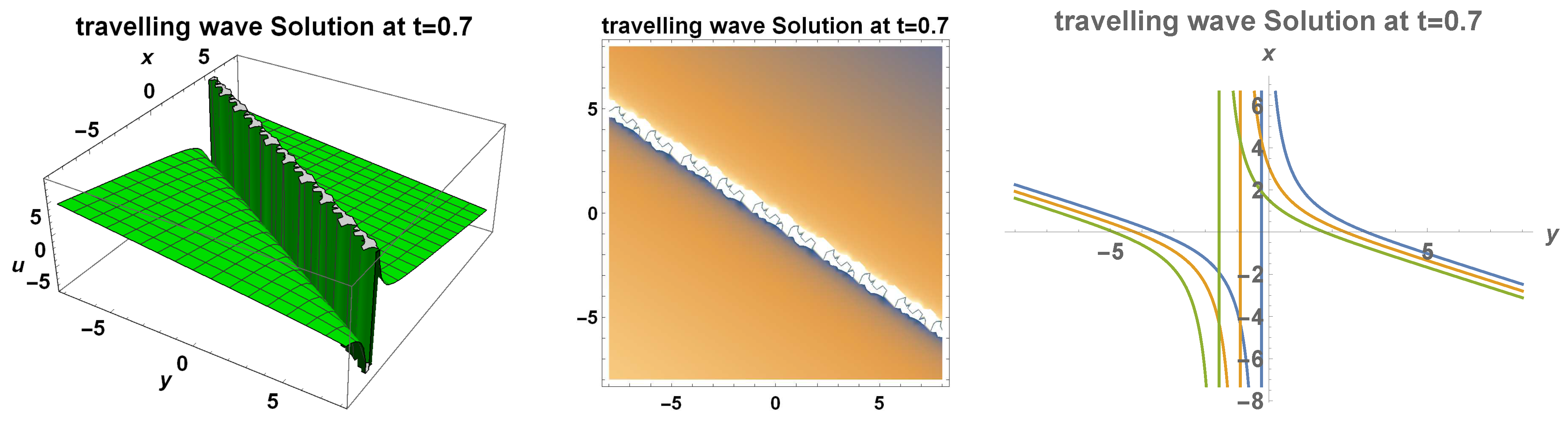
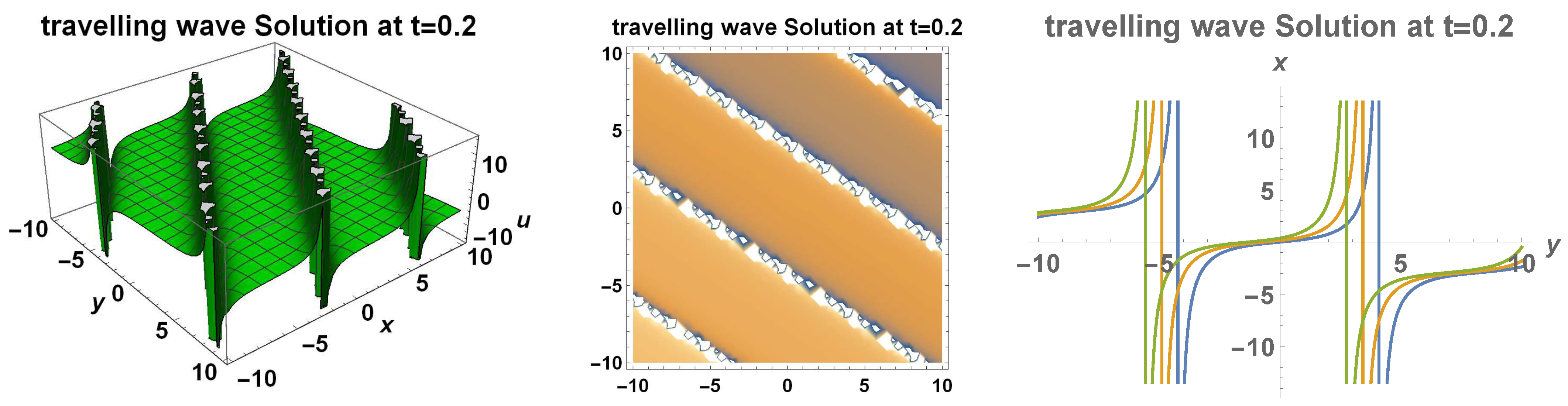
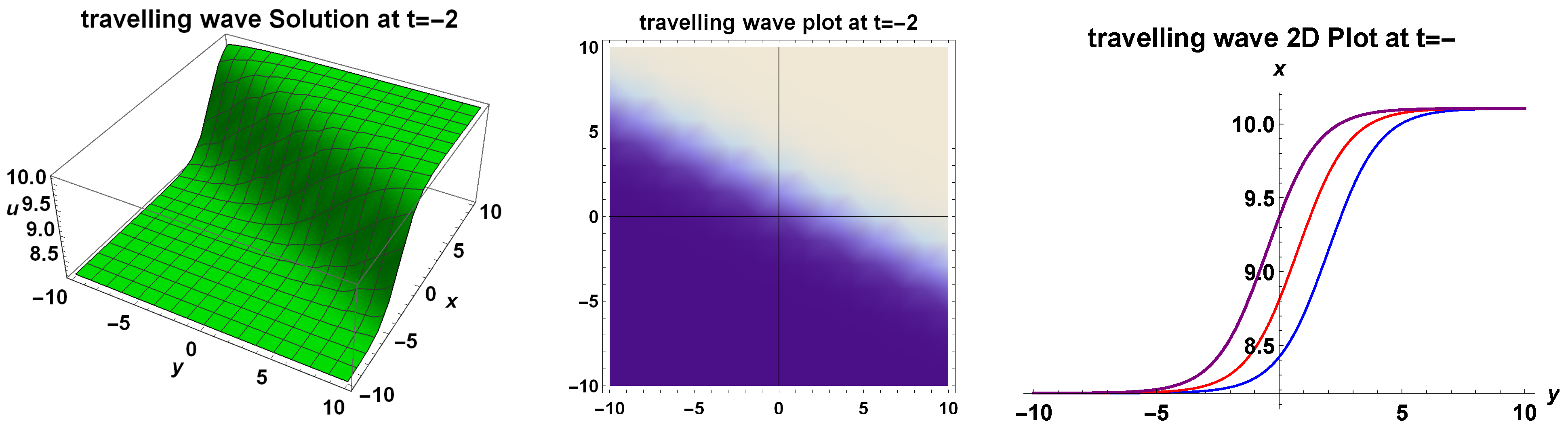
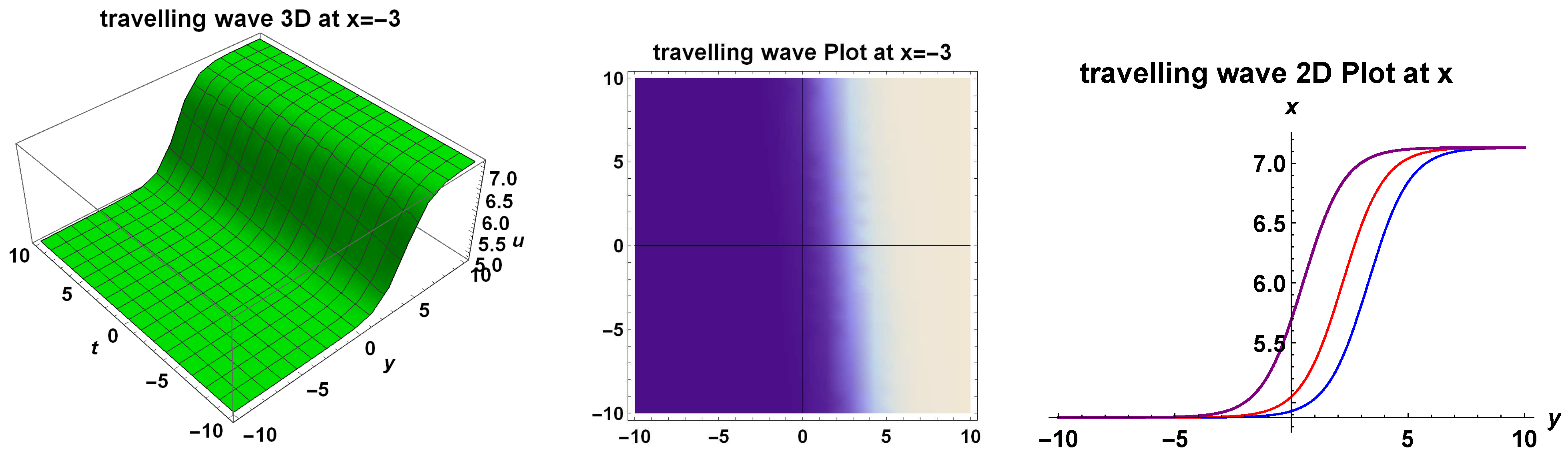
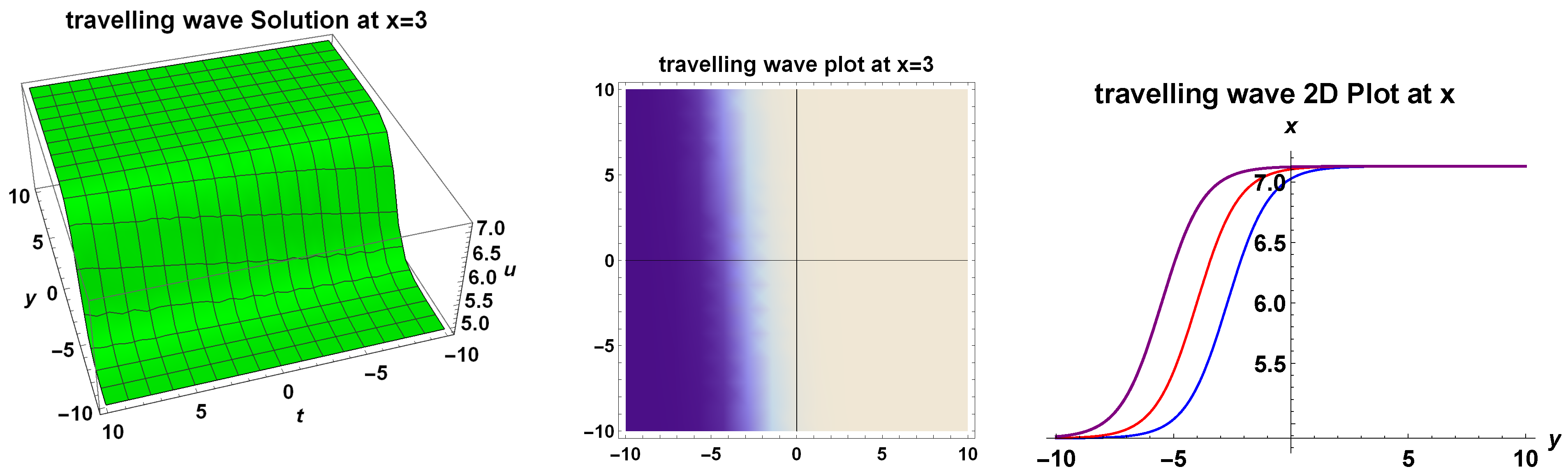
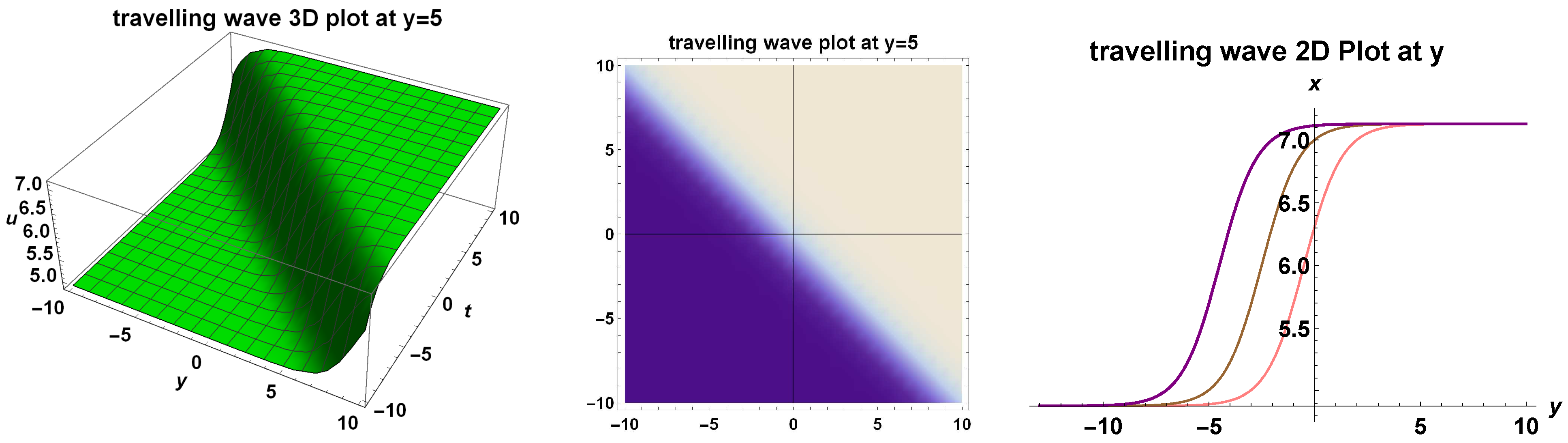
3. Travelling Wave Solutions
3.1. Bifurcation and Explicit Solutions
Bounded Travelling Wave Solutions to the Generalized (2+1)-Dimensional Bogoyavlensky–Konopelchenko Equation
- (1)
- The generalized (2+1)-dimensional Bogoyavlensky–Konopelchenko equation has a family of analytic bounded kink travelling wave solutions:where and are two arbitrary constants;
- (2)
- The generalized (2+1)-dimensional Bogoyavlensky–Konopelchenko equation possesses at least two families of bounded periodic travelling wave solutions which are determined implicitly by (109) andwhere and is an arbitrary constant.
4. Dynamical Wave Behaviour and Analysis of Solutions
5. Conservation Laws
5.1. Conserved Vectors via Homotopy Formula
5.2. Conserved Vectors via Noether Theorem
6. Particular Notes on the Conservation Laws
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations and Abbreviations
Abbreviations
Abbreviations
| ODEs | Ordinary Differential equations |
| LODEs | Linear Ordinary Differential equations |
| NODEs | Nonlinear Ordinary Differential equations |
| PDEs | Partial differential equations |
| NLDEs | Nonlinear differential equations |
| NLPDEs | Nonlinear partial differential equations |
| LIPDEs | Linear partial differential equations |
| KdV | Kortweg-de Vries |
| KP | Kadomtsev–Petviashvili |
| KP-MEW | Kadomtsev–Petviashvili-Modified Equal Width equation |
| KP-BBM | Kadomtsov-Petviashivilli-Benjamin-Bona-Mahony |
| (2+1)-D genBKe | (2+1)-dimensional generalized Bogoyavlensky–Konopelchenko equation |
| 2D | Two-dimensional |
| 3D | Three-dimensional |
References
- Adeyemo, O.D.; Motsepa, T.; Khalique, C.M. A study of the generalized nonlinear advection-diffusion equation arising in engineering sciences. Alex. Eng. J. 2022, 61, 185–194. [Google Scholar] [CrossRef]
- Khalique, C.M.; Adeyemo, O.D. A study of (3+1)-dimensional generalized Korteweg–de Vries–Zakharov–Kuznetsov equation via Lie symmetry approach. Results Phys. 2020, 18, 103197. [Google Scholar] [CrossRef]
- Shafiq, A.; Khalique, C.M. Lie group analysis of upper convected Maxwell fluid flow along stretching surface. Alex. Eng. J. 2020, 59, 2533–2541. [Google Scholar] [CrossRef]
- Gao, X.Y.; Guo, Y.J.; Shan, W.R. Cosmic dusty plasmas via a (3+1)-dimensional generalized variable-coefficient Kadomtsev-Petviashvili-Burgers-type equation: Auto-Bäcklund transformations, solitons and similarity reductions plus observational/experimental supports. Waves Random Complex Media 2021, 1–21. [Google Scholar] [CrossRef]
- Khalique, C.M.; Adeyemo, O.D. Langrangian formulation and solitary wave solutions of a generalized Zakharov-Kuznetsov equation with dual power-law nonlinearity in physical sciences and engineering. J. Ocean Eng. Sci. 2021. [Google Scholar] [CrossRef]
- Khalique, C.M.; Adeyemo, O.D. Closed-form solutions and conserved vectors of a generalized (3+1)-dimensional breaking soliton equation of engineering and nonlinear science. Mathematics 2020, 8, 1692. [Google Scholar] [CrossRef]
- Adeyemo, O.D. Applications of cnoidal and snoidal wave solutions via an optimal system of subalgebras for a generalized extended (2+1)-D quantum Zakharov-Kuznetsov equation with power-law nonlinearity in oceanography and ocean engineering. J. Ocean Eng. Sci. 2022, in press. [Google Scholar] [CrossRef]
- Adeyemo, O.D.; Khalique, C.M. Dynamics of soliton waves of group-invariant solutions through optimal system of an extended KP-like equation in higher dimensions with applications in medical sciences and mathematical physics. J. Geom. Phys. 2022, 177, 104502. [Google Scholar] [CrossRef]
- Adeyemo, O.D.; Khalique, C.M. Dynamical soliton wave structures of one-dimensional Lie subalgebras via group-invariant solutions of a higher-dimensional soliton equation in ocean physics and mechatronics engineering. Commun. Appl. Math. Comput. 2022, in press. [Google Scholar]
- Jiong, S. Auxiliary equation method for solving nonlinear partial differential equations. Phys. Lett. A 2003, 309, 387–396. [Google Scholar]
- Wazwaz, A.M. The tanh and sine-cosine method for compact and noncompact solutions of nonlinear Klein Gordon equation. Appl. Math. Comput. 2005, 167, 1179–1195. [Google Scholar] [CrossRef]
- He, J.H.; Wu, X.H. Exp-function method for nonlinear wave equations. Chaos Soliton Fract. 2006, 30, 70. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Clarkson, P.A. Solitons, Nonlinear Evolution Equations and Inverse Scattering; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- Adomian, G. Solving Frontier Problems of Physics: The Decomposition Method; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1994. [Google Scholar]
- Agrawal, G.P. Nonlinear Fiber Optics; Academic Press: New York, NY, USA, 1995. [Google Scholar]
- Shukla, P.K.; Mamun, A.A. Introduction to Dusty Plasma Physics; Institute of Physics Publishing: Bristol, UK, 2002. [Google Scholar]
- Kochanov, M.B.; Kudryashov, N.A.; Sinel’shchikov, D.I. Non-linear waves on shallow water under an ice cover, higher order expansions. J. Appl. Math. Mech. 2013, 77, 25–32. [Google Scholar] [CrossRef]
- Korteweg, D.J.; Vries, G.D. On the change of form of long waves advancing in a rectangular canal, and on a new type of long stationary waves. Lond. Edinb. Dubl. Phil. Mag. 1895, 39, 422–443. [Google Scholar] [CrossRef]
- El-Tantawy, S.A.; Moslem, W.M. Nonlinear structures of the Korteweg-de Vries and modified Korteweg-de Vries equations in non-Maxwellian electron-positron-ion plasma: Solitons collision and rogue waves. Phys. Plasmas 2014, 21, 052112. [Google Scholar] [CrossRef]
- Gardner, C.S.; Greene, J.M.; Kruskal, M.D.; Miura, R.M. Method for solving the Korteweg-de Vries equation. Phys. Rev. Lett. 1967, 19, 1095–1097. [Google Scholar] [CrossRef]
- Yu, J.; Lou, S.Y. Deformation and (3+1)-dimensional integrable model. Sci. China Ser. A 2000, 43, 655–660. [Google Scholar] [CrossRef]
- Lou, S.Y. Searching for higher dimensional integrable models from lower ones via Painlevé analysis. Phys. Lett. 1998, 80, 5027–5031. [Google Scholar] [CrossRef]
- El-Wakii, S.A.; Abdou, M.A.; Elhanbaly, A. New solitons and periodic wave solutions for nonlinear evolution equations. Phys. Lett. A 2006, 353, 40–47. [Google Scholar] [CrossRef]
- Gu, C.H. Soliton Theory and Its Application; Zhejiang Science and Technology Press: Hangzhou, China, 1990. [Google Scholar]
- Zhou, Y.; Wang, M.; Wang, Y. Periodic wave solutions to a coupled KdV equations with variable coefficients. Phys. Lett. A 2003, 308, 31–36. [Google Scholar] [CrossRef]
- Kudryashov, N.A.; Loguinova, N.B. Extended simplest equation method for nonlinear differential equations. Appl. Math. Comput. 2008, 205, 396–402. [Google Scholar] [CrossRef]
- Ovsiannikov, L.V. Group Analysis of Differential Equations; Academic Press: New York, NY, USA, 1982. [Google Scholar]
- Bluman, G.W.; Kumei, S. Symmetries and Differential Equations; Springer: New York, NY, USA, 1989. [Google Scholar]
- Olver, P.J. Applications of Lie Groups to Differential Equations, Graduate Texts in Mathematics, 2nd ed.; Springer: Berlin, Germany, 1993; Volume 107. [Google Scholar]
- Ibragimov, N.H. CRC Handbook of Lie Group Analysis of Differential Equations; CRC Press: Boca Raton, FL, USA, 1994; Volume 1. [Google Scholar]
- Ibragimov, N.H. Elementary Lie Group Analysis and Ordinary Differential Equations; John Wiley & Sons: Chichester, NY, USA, 1999. [Google Scholar]
- Wang, M.; Li, X.; Zhang, J. The (G′/G)- expansion method and travelling wave solutions for linear evolution equations in mathematical physics. Phys. Lett. A 2005, 24, 1257–1268. [Google Scholar]
- Matveev, V.B.; Salle, M.A. Darboux Transformations and Solitons; Springer: New York, NY, USA, 1991. [Google Scholar]
- Chen, Y.; Yan, Z. New exact solutions of (2+1)–dimensional Gardner equation via the new sine-Gordon equation expansion method. Chaos Solitons Fract. 2005, 26, 399–406. [Google Scholar] [CrossRef]
- Kudryashov, N.A. Simplest equation method to look for exact solutions of nonlinear differential equations. Chaos Solitons Fract. 2005, 24, 1217–1231. [Google Scholar] [CrossRef] [Green Version]
- Hossain, A.K.M.K.S.; Akbar, M.A. Traveling wave solutions of nonlinear evolution equations via modified simple equation method. Int. J. Appl. Math. Theor. Phys. 2017, 3, 20–25. [Google Scholar] [CrossRef] [Green Version]
- Seadawy, A.R. Fractional solitary wave solutions of the nonlinear higher-order extended KdV equation in a stratified shear flow: Part I. Comput. Math. Appl. 2015, 70, 345–352. [Google Scholar] [CrossRef]
- Hirota, R. The Direct Method in Soliton Theory; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Zhang, L.; Khalique, C.M. Classification and bifurcation of a class of second-order ODEs and its application to nonlinear PDEs. Discret. Contin. Dyn. Syst. Ser. S 2018, 11, 777–790. [Google Scholar] [CrossRef]
- Jiang, B.; Liu, Y.; Zhang, J. Bifurcations and some new travelling wave solutions for the CH-γ equation. App. Math. Comput. 2014, 228, 220–233. [Google Scholar] [CrossRef]
- Saha, A. Bifurcation of travelling wave solutions for the generalized KP-MEW eequations. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 3539–3551. [Google Scholar] [CrossRef]
- Ganguly, A.; Das, A. Explicit solutions and stability analysis of the (2+1)-dimensional KP-BBM equation with dispersion effect. Commun. Nonlinear Sci. Numer. Simul. 2015, 25, 102–117. [Google Scholar] [CrossRef]
- Das, A.; Ganguly, A. Existence and stability of dispersive solutions to the Kadomtsev–Petviashvili equation in the presence of dispersion effect. Commun. Nonlinear Sci. Numer. Simul. 2017, 48, 326–339. [Google Scholar] [CrossRef]
- Xin, X.; Liu, X.; Zhang, L. Explicit solutions of the Bogoyavlensky-Konoplechenko equation. Appl. Math. Comput. 2010, 215, 3669–3673. [Google Scholar] [CrossRef]
- Ray, S.S. On conservation laws by Lie symmetry analysis for (2+1)-dimensional Bogoyavlensky–Konopelchenko equation in wave propagation. Comput. Math. Appl. 2017, 74, 1158–1165. [Google Scholar] [CrossRef]
- Triki, H.; Jovanoski, Z.; Biswa, A. Shock wave solutions to the Bogoyavlensky–Konopelchenko equation. Indian J. Phys. 2014, 88, 71–74. [Google Scholar] [CrossRef]
- Konopelchenko, B.G. Solitons in Multidimensions-Inverse Spectral Transfrom Method; World Scientific: River Edge, NJ, USA, 1993. [Google Scholar]
- Prabhakar, M.V.; Bhate, H. Exact solutions of the Bogoyavlensky-Konoplechenco equation. Lett. Math. Phys. 2003, 64, 1–6. [Google Scholar] [CrossRef]
- Bogoyavlenski, O.I. Overturning solitons in new two-dimensional integrable equations. Math. USSR-Izv. 1990, 34, 245–259. [Google Scholar] [CrossRef]
- Chen, S.T.; Ma, W.X. Exact solutions to a generalized Bogoyavlensky–Konopelchenko equation via maple symbolic computations. Complexity 2019, 2019, 8787460. [Google Scholar] [CrossRef]
- Li, Q.; Chaolu, T.; Wang, Y. Lump-type solutions and lump solutions for the (2+1)-dimensional generalized Bogoyavlensky–Konopelchenko equation. Comp. Math. Appl. 2019, 77, 2077–2085. [Google Scholar] [CrossRef]
- Chen, S.T.; Ma, W.X. Lump solution to a generalized Bogoyavlensky–Konopelchenko equation. Front. Math. China 2018, 13, 525–534. [Google Scholar] [CrossRef]
- Pouyanmehr, R.; Hosseini, K.; Ansari, R. Different wave structures to the (2+1)-dimensional generalized Bogoyavlensky–Konopelchenko equation. Int. J. Appl. Comput. Math. 2019, 5, 1–12. [Google Scholar] [CrossRef]
- Liu, F.Y.; Gao, Y.T.; Yu, X.; Li, L.Q.; Ding, C.C. Lie group analysis and analytic solutions for a (2+1)-dimensional generalized Bogoyavlensky–Konopelchenko equation in fluid mechanics and plasma physics. Eur. Phys. J. Plus 2021, 136, 1–14. [Google Scholar] [CrossRef]
- Bluman, G.W.; Cole, J.D. Similarity Methods for Differential Equations; Springer: New York, NY, USA, 1974. [Google Scholar]
- Olver, P.J. Application of Lie Groups to Differential Equations; Springer: New York, NY, USA, 1993. [Google Scholar]
- Grigoriev, Y.N.; Kovalev, V.F.; Meleshko, S.V.; Ibragimov, N.H. Symmetries of Integro-Differential Equations: With Applications in Mechanics and Plasma Physics; Springer: New York, NY, USA, 2010. [Google Scholar]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products, 7th ed.; Academic Press: New York, NY, USA, 2007. [Google Scholar]
- Akhiezer, N.I. Elements of The Theory of Elliptic Functions; American Mathematical Society: Providence, RI, USA, 1990. [Google Scholar]
- Kudryashov, N.A. Analytical Theory of Nonlinear Differential Equations; Igevsk Institute of Computer Investigations: Moskow, Russia, 2004. [Google Scholar]
- Kudryashov, N.A. First integrals and general solution of the Fokas-Lenells equation. Optik 2019, 195, 163135. [Google Scholar] [CrossRef]
- Billingham, J.; King, A.C. Wave Motion; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Chow, S.N.; Hale, J.K. Method of Bifurcation Theory; Springer: New York, NY, USA, 1981. [Google Scholar]
- Guckenheimer, J.; Holmes, P. Dynamical Systems and Bifurcations of Vector Fields; Springer: New York, NY, USA, 1983. [Google Scholar]
- Zhang, L.; Khalique, C.M. Traveling wave solutions and infinite-dimensional linear spaces of multiwave solutions to Jimbo-Miwa equation. Abstr. Appl. Anal. 2014, 2014, 963852. [Google Scholar] [CrossRef]
- Drazin, P.G.; Johnson, R.S. Solitons: An Introduction; Cambridge University Press: Cambridge, UK, 1989. [Google Scholar]
- Anco, S.C.; Bluman, G.W. Direct construction method for conservation laws of partial differential equations. Part I: Examples of conservation law classifications. Eur. J. Appl. Math. 2002, 13, 545–566. [Google Scholar] [CrossRef] [Green Version]
- Noether, E. Invariante variationsprobleme. Nachrichten Ges. Wiss. Göttingen Math.-Phys. Kl. 1918, 2, 235–257. [Google Scholar]
- Anco, S.C. Generalization of Noethers Theorem in modern Form to Nonvariational Partial Differential Equations. In Recent Progress and Modern Challenges in Applied Mathematics, Modeling and Computational Science; Melnik, R., Makarov, R., Beglair, J., Eds.; Fields Institute Communications; Springer: New York, NY, USA, 2017; Volume 79. [Google Scholar]
- Sarlet, W. Comment on ‘conservation laws of higher order nonlinear PDEs and the variational conservation laws in the class with mixed derivatives’. J. Phys. A Math. Theor. 2010, 43, 458001. [Google Scholar] [CrossRef]


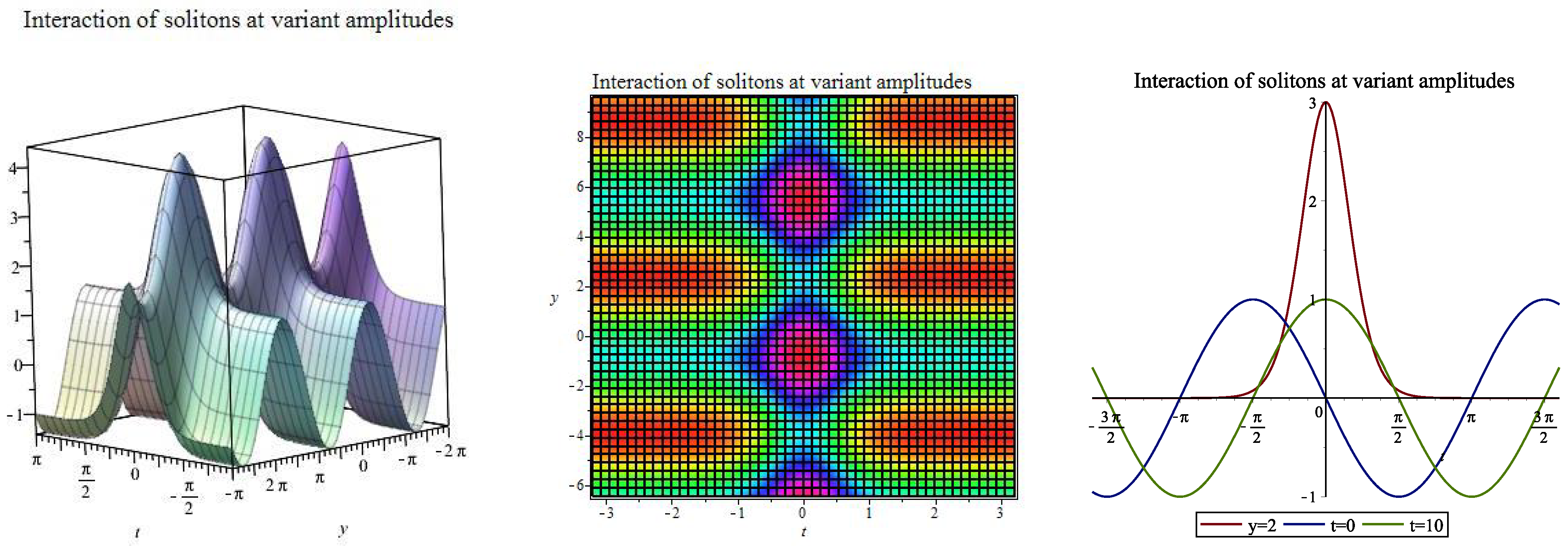
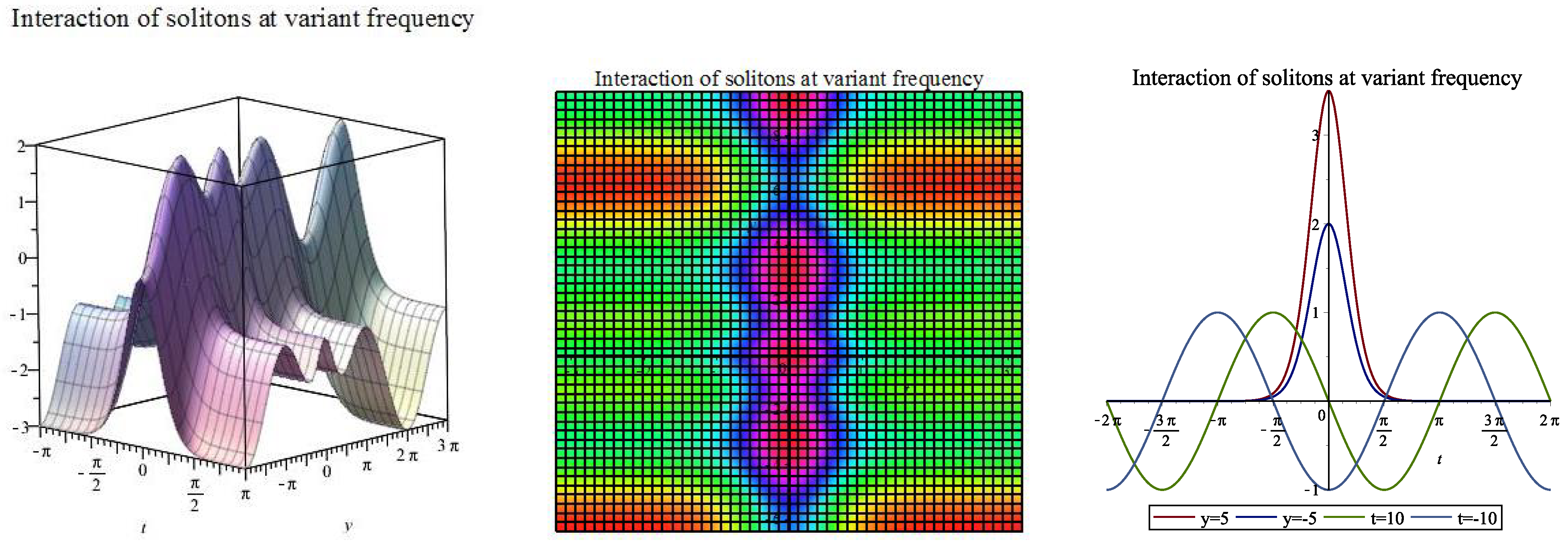
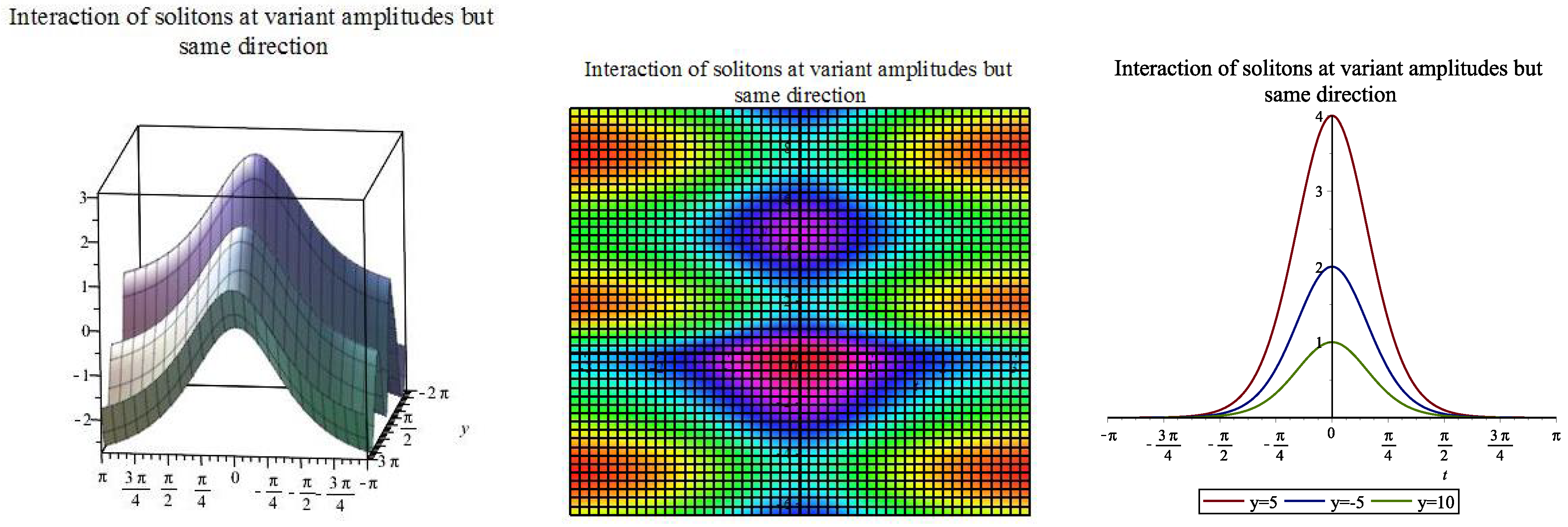
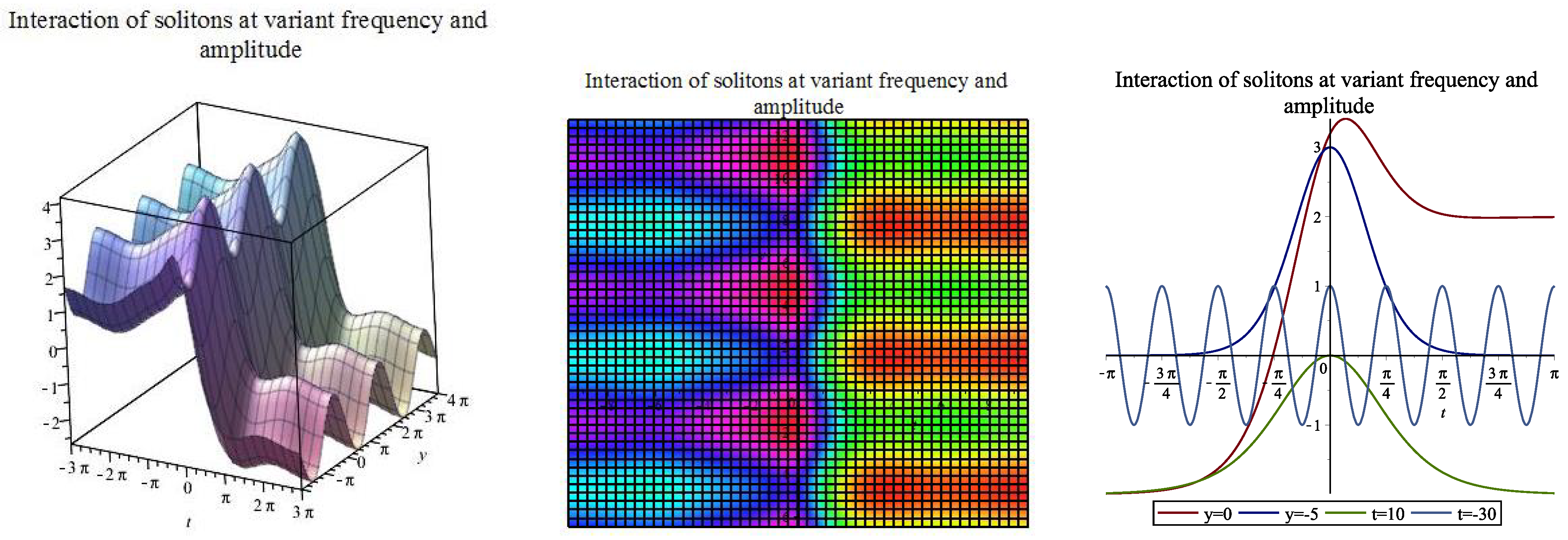
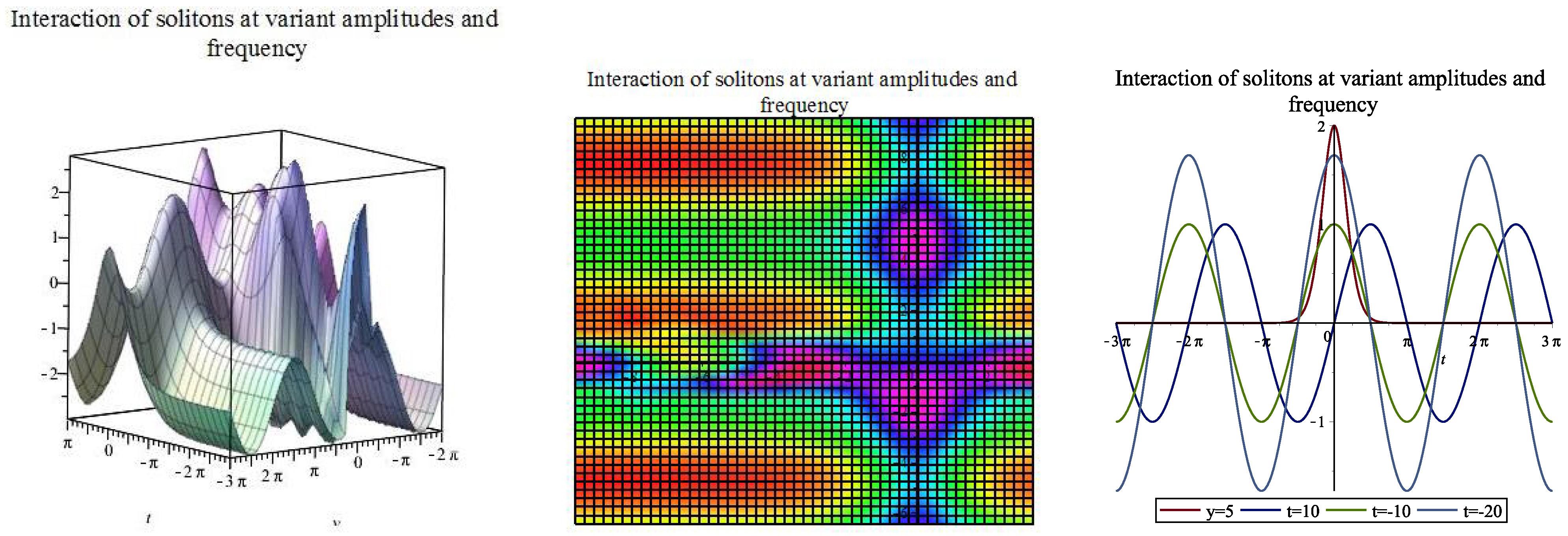
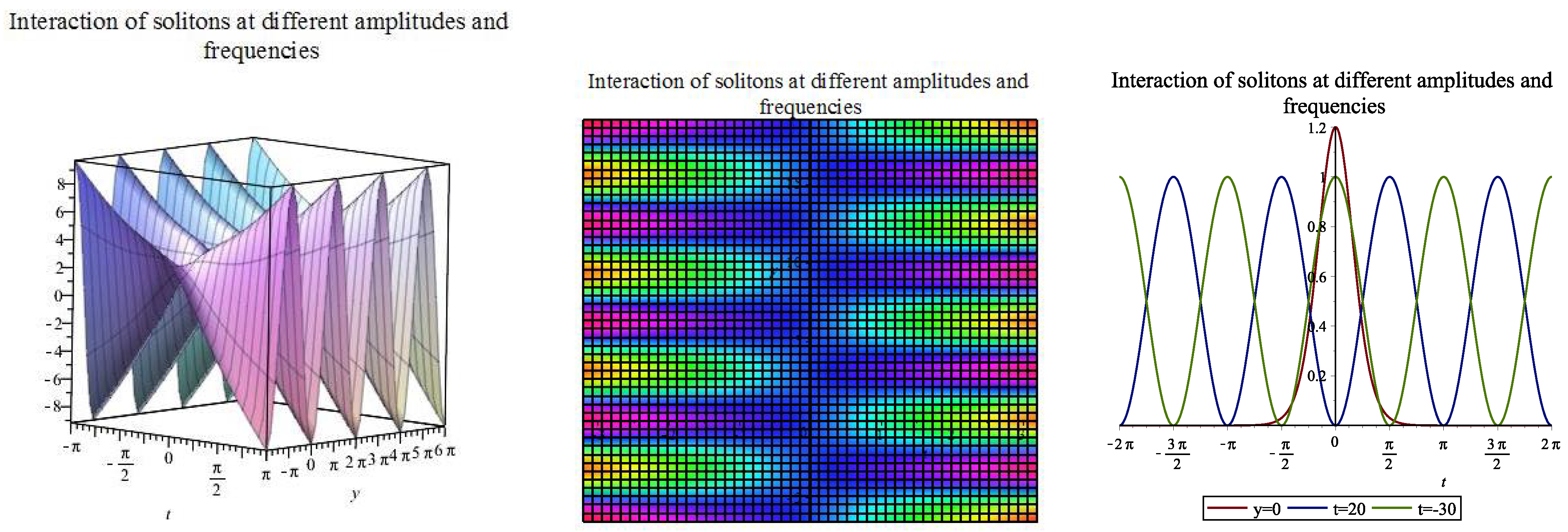
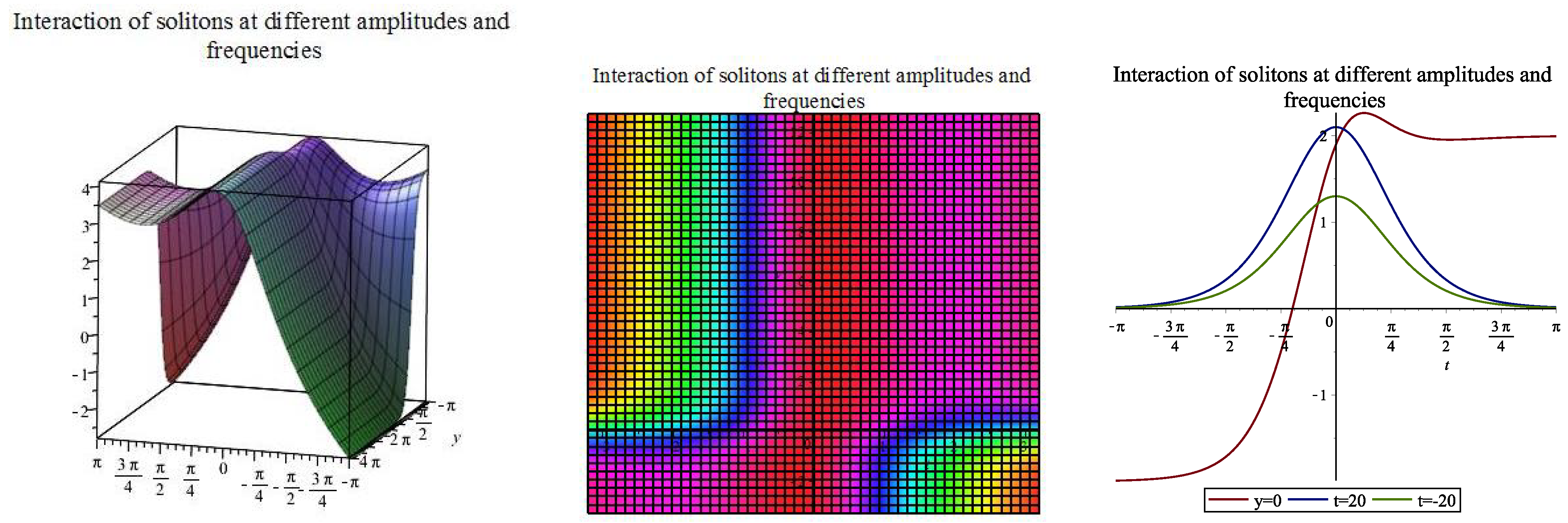

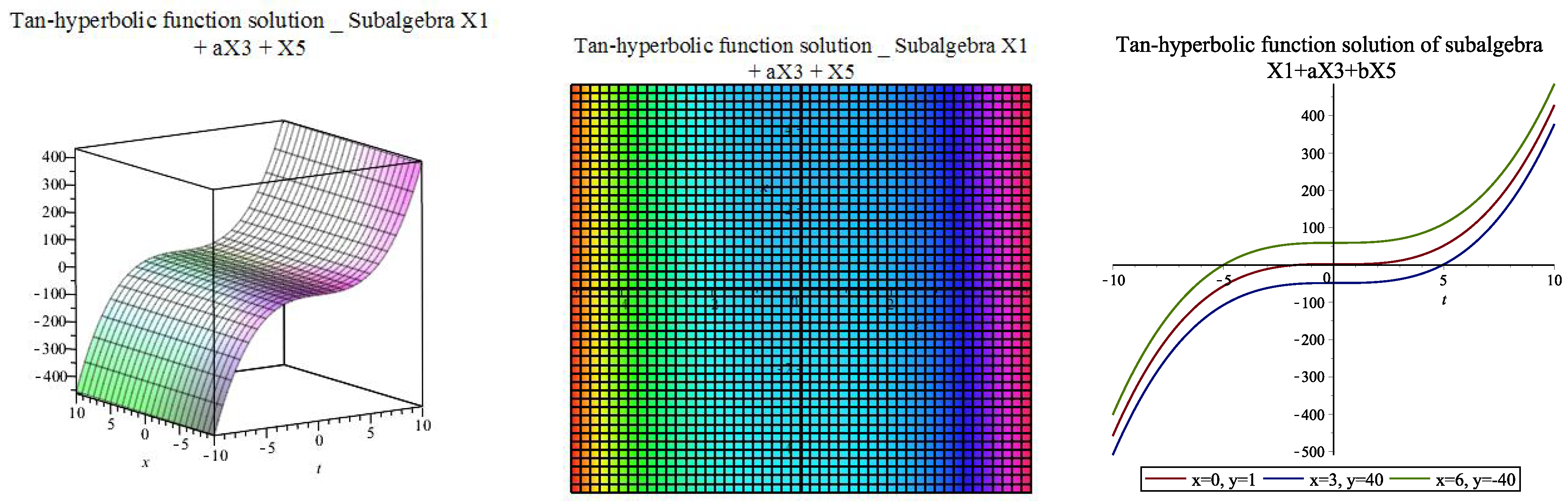
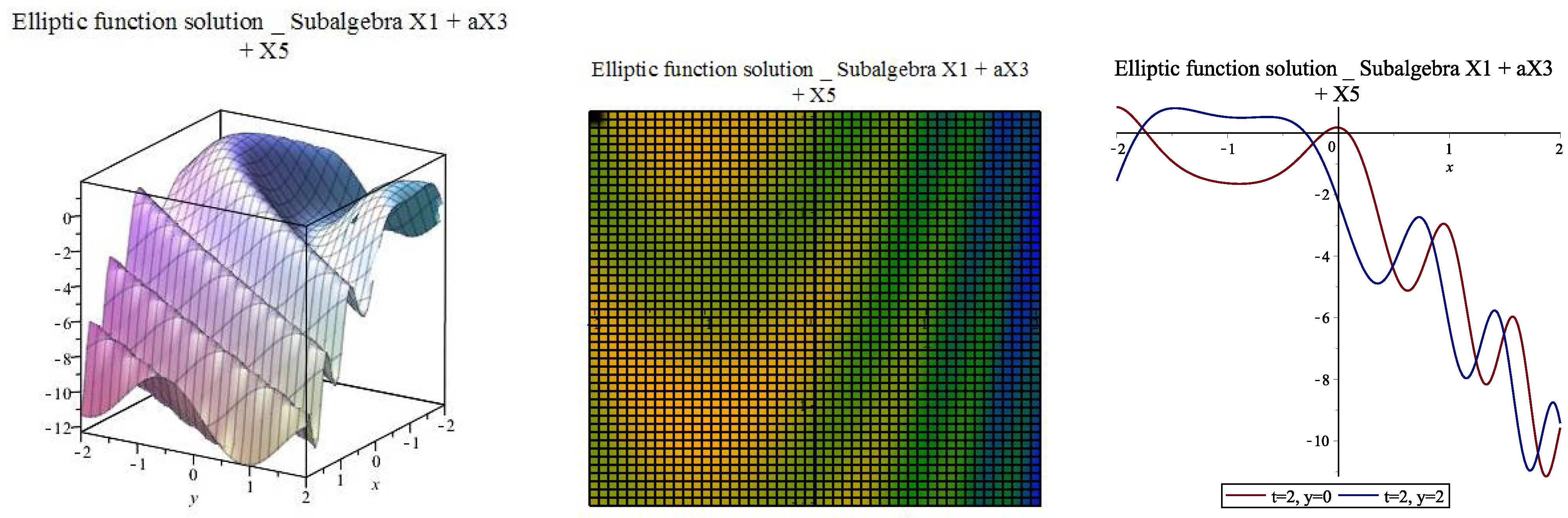
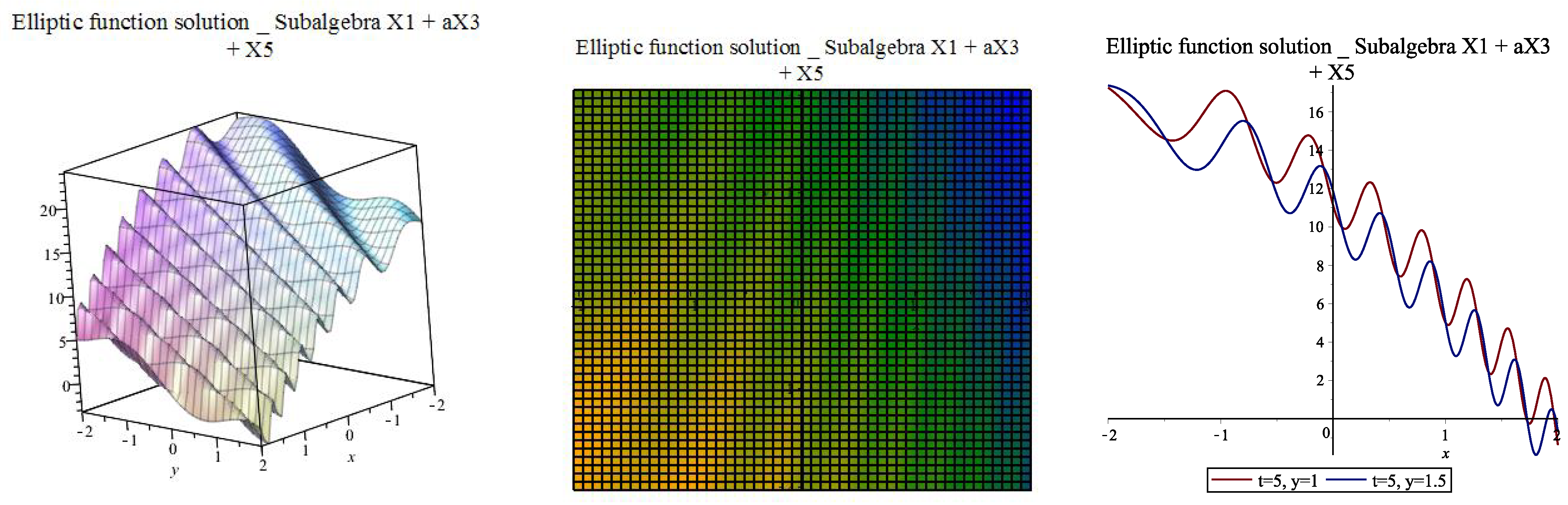
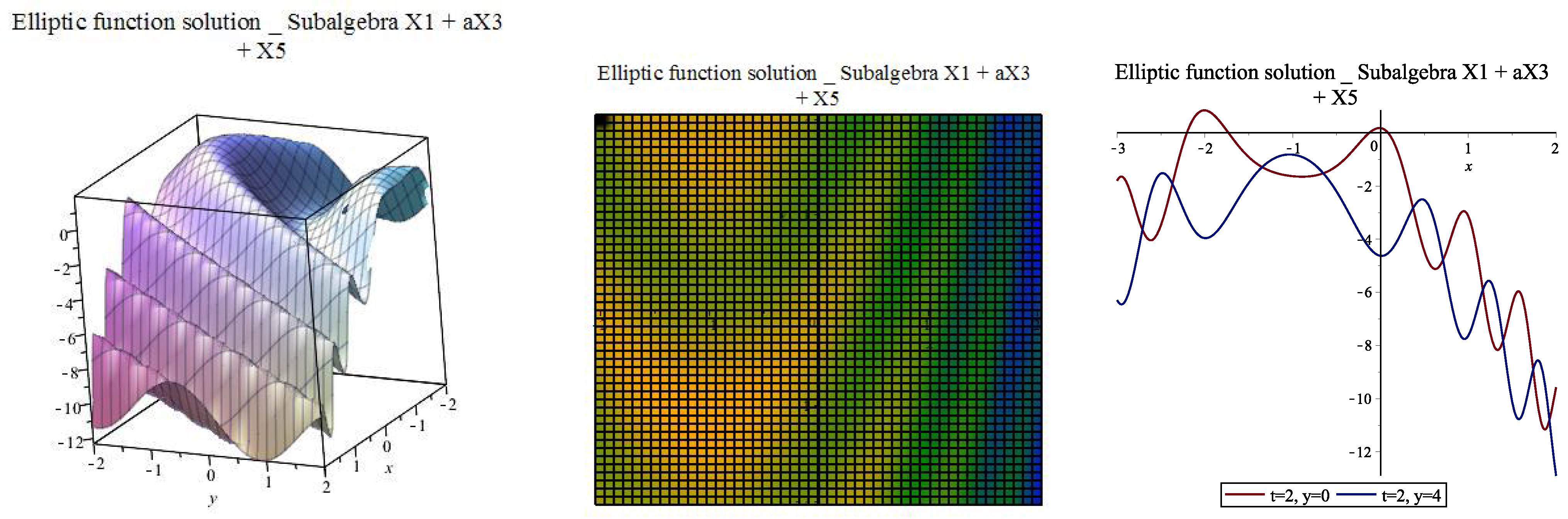
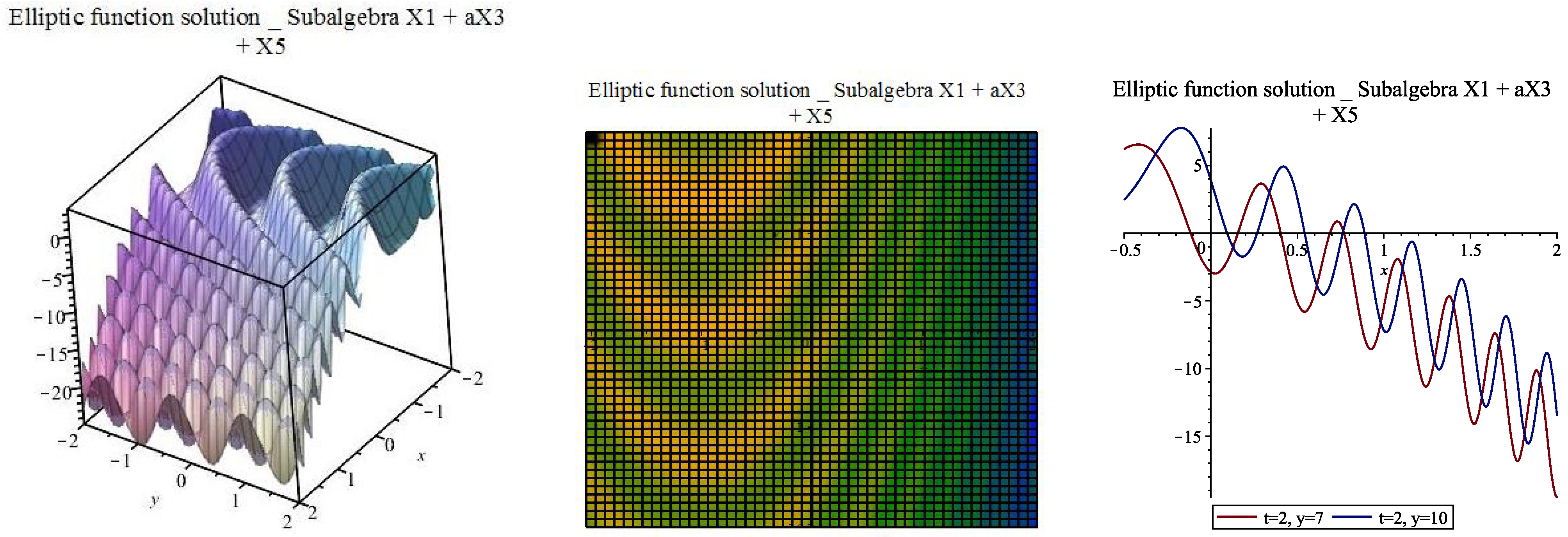



| [, ] | |||||
| 0 | 0 | 0 | 0 | ||
| 0 | 0 | 0 | 0 | ||
| 0 | 0 | 0 | 0 | ||
| 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adeyemo, O.D.; Zhang, L.; Khalique, C.M. Bifurcation Theory, Lie Group-Invariant Solutions of Subalgebras and Conservation Laws of a Generalized (2+1)-Dimensional BK Equation Type II in Plasma Physics and Fluid Mechanics. Mathematics 2022, 10, 2391. https://doi.org/10.3390/math10142391
Adeyemo OD, Zhang L, Khalique CM. Bifurcation Theory, Lie Group-Invariant Solutions of Subalgebras and Conservation Laws of a Generalized (2+1)-Dimensional BK Equation Type II in Plasma Physics and Fluid Mechanics. Mathematics. 2022; 10(14):2391. https://doi.org/10.3390/math10142391
Chicago/Turabian StyleAdeyemo, Oke Davies, Lijun Zhang, and Chaudry Masood Khalique. 2022. "Bifurcation Theory, Lie Group-Invariant Solutions of Subalgebras and Conservation Laws of a Generalized (2+1)-Dimensional BK Equation Type II in Plasma Physics and Fluid Mechanics" Mathematics 10, no. 14: 2391. https://doi.org/10.3390/math10142391
APA StyleAdeyemo, O. D., Zhang, L., & Khalique, C. M. (2022). Bifurcation Theory, Lie Group-Invariant Solutions of Subalgebras and Conservation Laws of a Generalized (2+1)-Dimensional BK Equation Type II in Plasma Physics and Fluid Mechanics. Mathematics, 10(14), 2391. https://doi.org/10.3390/math10142391








