Functional Data Analysis for the Detection of Outliers and Study of the Effects of the COVID-19 Pandemic on Air Quality: A Case Study in Gijón, Spain
Abstract
:1. Introduction
2. Materials and Methods
2.1. Case Study —Air Quality in Gijon, Spain
- Sulfur oxides (): they are a group of molecules formed of sulfur and oxygen atoms. The vast majority are released into the atmosphere as the result of some human activities, including the burning of oil and coal, and their respective industrial processes. When these fuels are burned, the sulfur in them reacts with the oxygen in the atmosphere, resulting in sulfur oxides. If they are inhaled regularly, it can lead to bronchitis and/or asthma. Moreover, these components can combine with water droplets in the atmosphere, originating acid rain with harmful effects on plants and animals. The most dangerous compound in this group is sulfur dioxide (), which is usually a product of the combustion of coal and petroleum;
- Nitrogen oxides (): similarly to the previous pollutant, they are a group of molecules formed of oxygen and nitrogen atoms that form when fuel is burned at high temperatures, usually in internal combustion engines, power plants, or industrial boilers. Regarding their environmental impact, nitrogen oxides are of great importance in the formation of photochemical smog. This is due to their bonding capabilities with other atmospheric pollutants (such as the non-methane volatile organic compounds), which affect the formation of ozone at ground level. Moreover, they are poisonous and can react with water in the atmosphere to produce acid rain;
- Particulate matter (): very small particles of solid and/or liquid compounds suspended in the atmosphere. Some dark and large enough particles, including dust, dirt, soot, or smoke, can be seen with the naked eye. These particles comprise a great variety of sizes and shapes and can be made up of hundreds of different chemicals. Their sources are fires, fields, constructions sites, unpaved roads, and smokestacks. They can be inhaled, causing serious health problems (asthma, bronchitis, high blood pressure, and heart attack) and even getting into the blood stream. refers to particles with aerodynamic diameters equal to or less than 10 m.
- Ground level ozone (): ozone forms naturally in the upper atmosphere, where it is beneficial for life on Earth, as it protects from ultraviolet rays. At ground level, it forms through chemical reactions between and volatile organic compounds (VOCs) emitted from cars, power plants, refineries, chemical plants, etc. This reaction usually takes place in hot summer days within urban settings, and it results in harmful air for animals and plants.
2.2. Analysis Methods
2.2.1. Classical Analysis
2.2.2. Statistical Process Control
2.2.3. Functional Data Analysis
2.2.4. Functional Depth
- Fraiman–Muniz depth (Integrated depth): consider as the cumulative empirical distribution function [57] for the curve values in a time ruled by the following expression [58]:where is the indicator function. Consequently, the Fraiman–Muniz depth of a curve in a set of curves is defined by:where is the depth of the point obtained by:
- Modified Band Depth: this functional depth is a second iteration of the graph-based band depth developed by Lopez-Pintado et al. [59]. Considering j as a fixed value within , is defined aswhere the set in the interval for a function x is in the collection of real functions , which is in the band defined by the observations . If is the Lebesgue measure on , outputs the amount of time that x is inside the band. Subsequently,andFor the finite dimensional case, the value of is specified as the fraction of coordinates of in the interval defined by j different points from the next sample:
2.2.5. Outlier Detection
- Obtaining the robust Mahalanobis distance from a sample of size :where J denominates the group of h points which minimizes the determinant of the corresponding covariance matrix, and . The robustness of the method is controlled by the sub-sample of size h. For a p-dimensional distribution, the maximum finite sample breakdown point is , where denotes the integer part of [34];
- Approximate the tail of this distance distribution with Equation (21) according to Hardin et al. [65],where c and m define the degrees of freedom of the F-distribution and the scaling factor, respectively. The value of these two parameters is calculated by a simulation program provided by Hardin et al. [65]. Then a value for the cutoff, C, is chosen as the quantile of . Dai et al. [34] set , which is used in the classical box plot for detecting outliers under a normal distribution [34], and the results of the Monte Carlo simulation studies with four different contamination models show that it is more accurate to use the quantile of the than the empirical quantile of the data or the quantile of the distribution;
- Consider as outliers all those curves for which their distance satisfies Equation (22),
3. Results
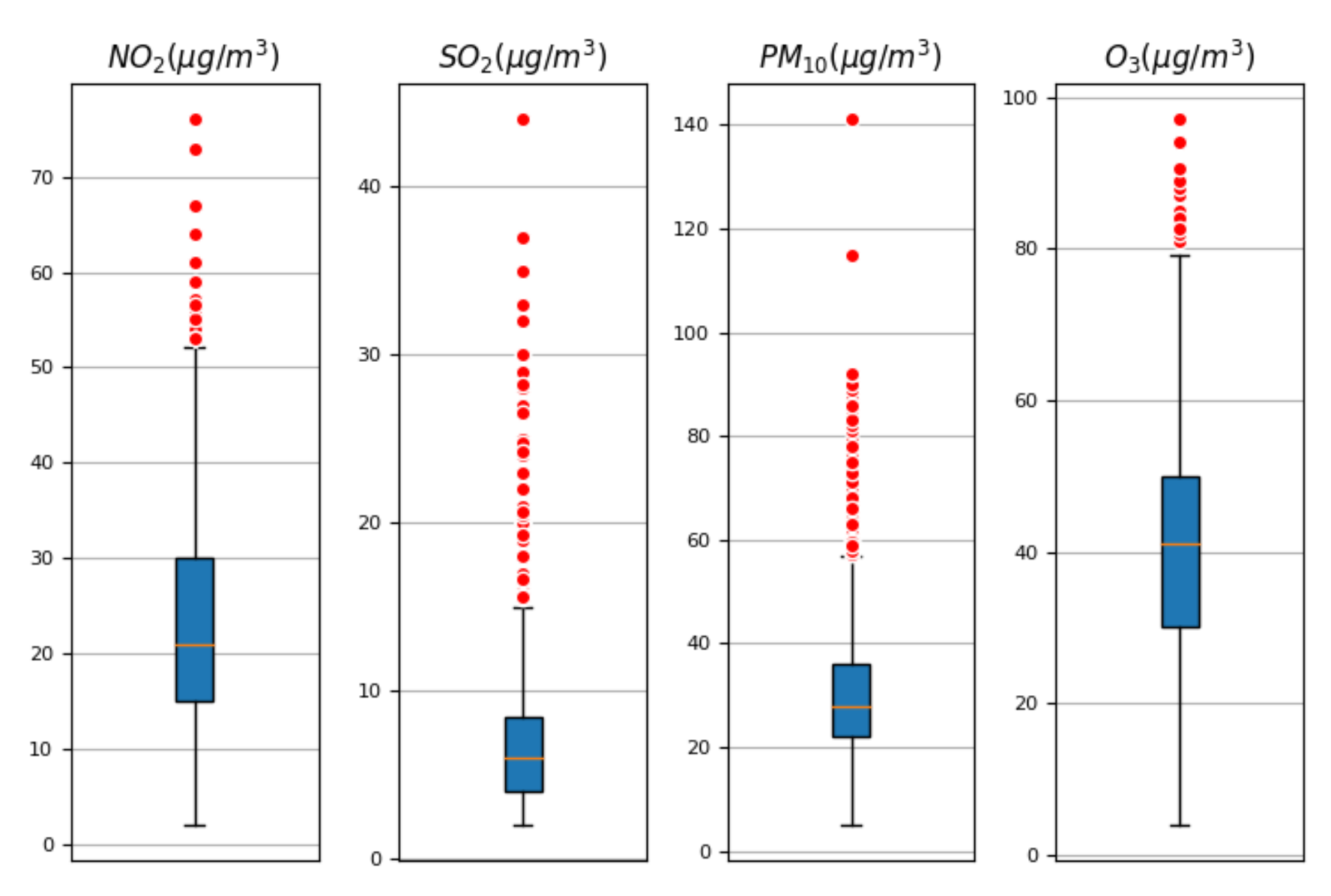
3.1. Results of the Classical Analysis
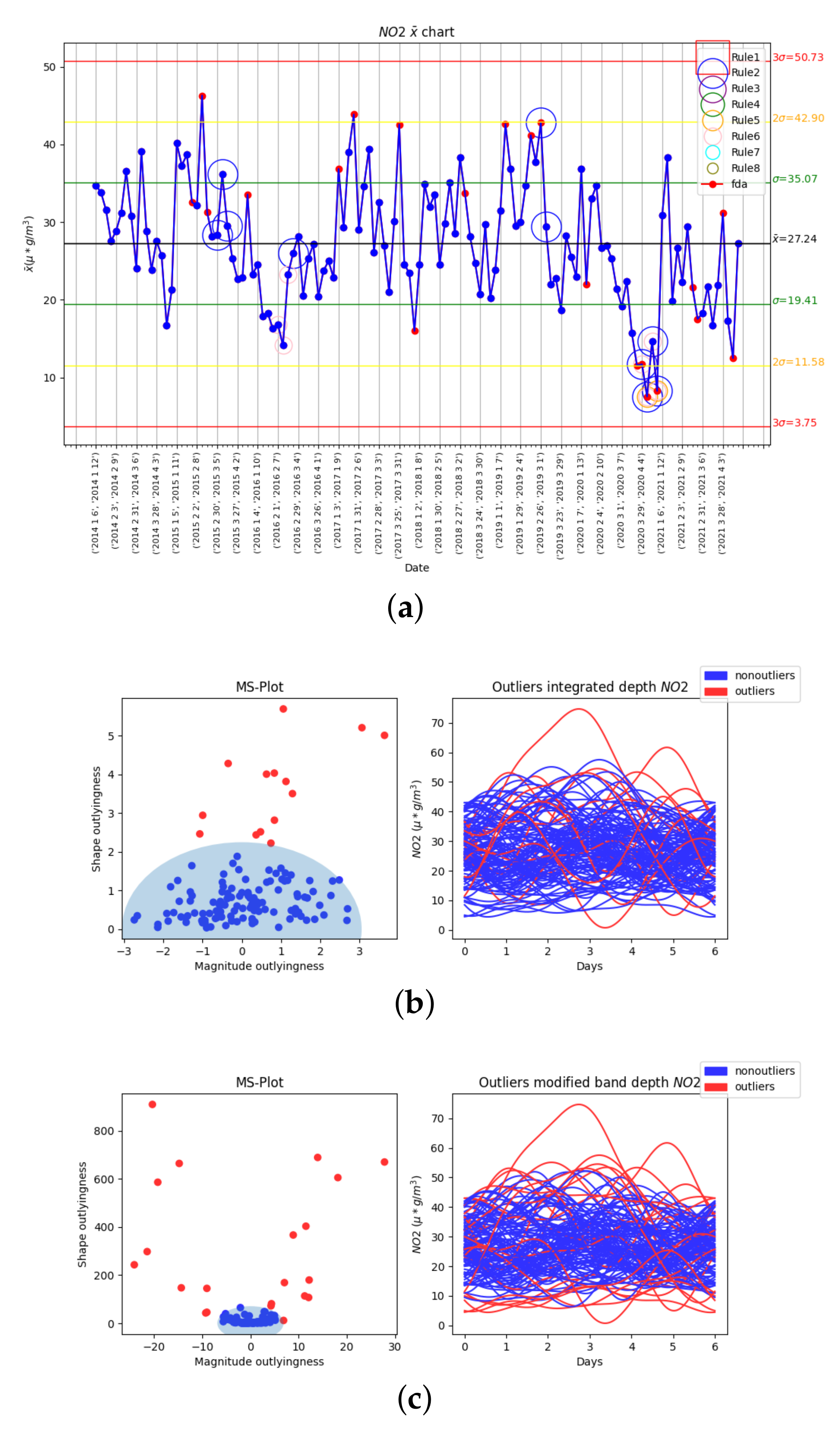
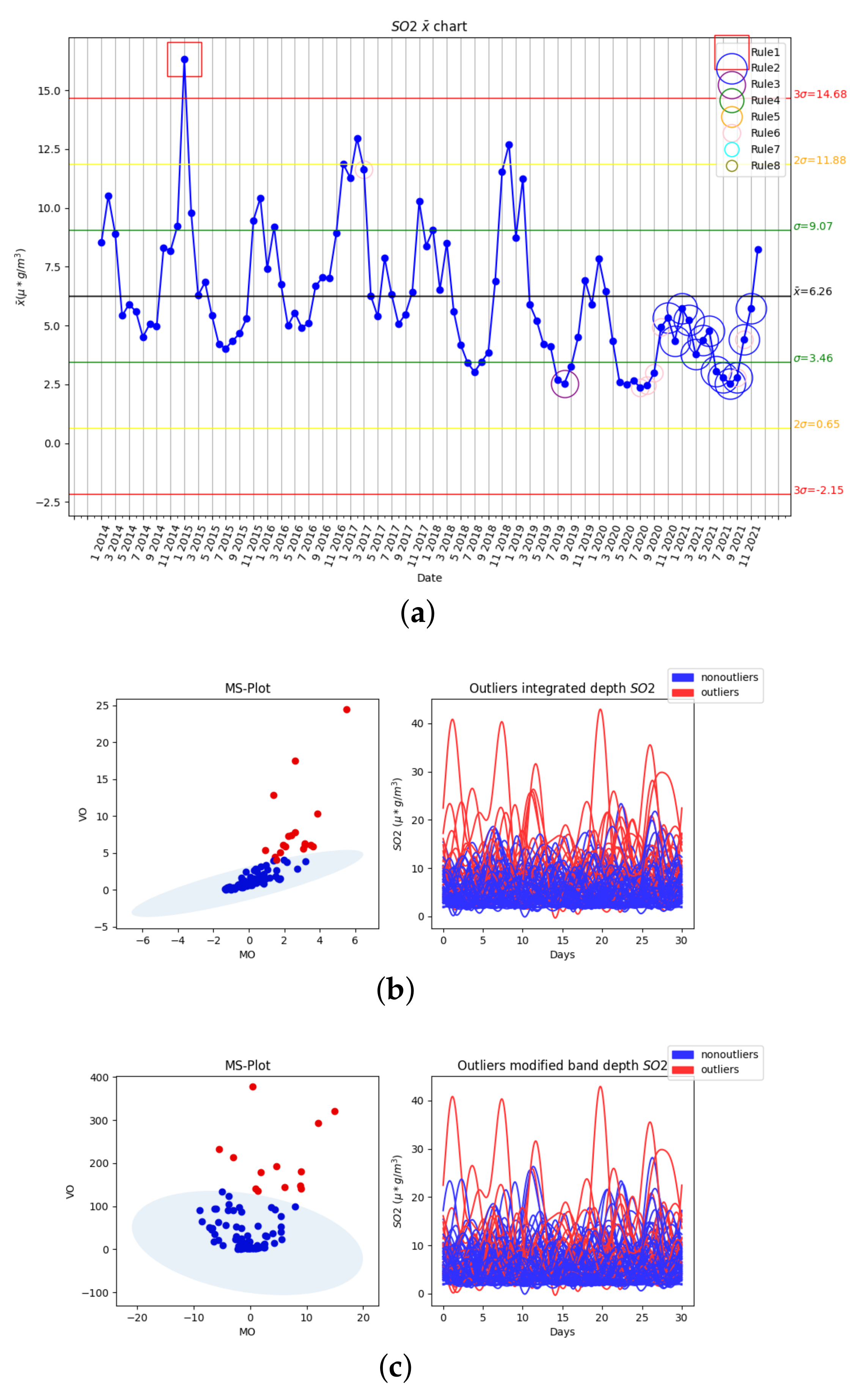
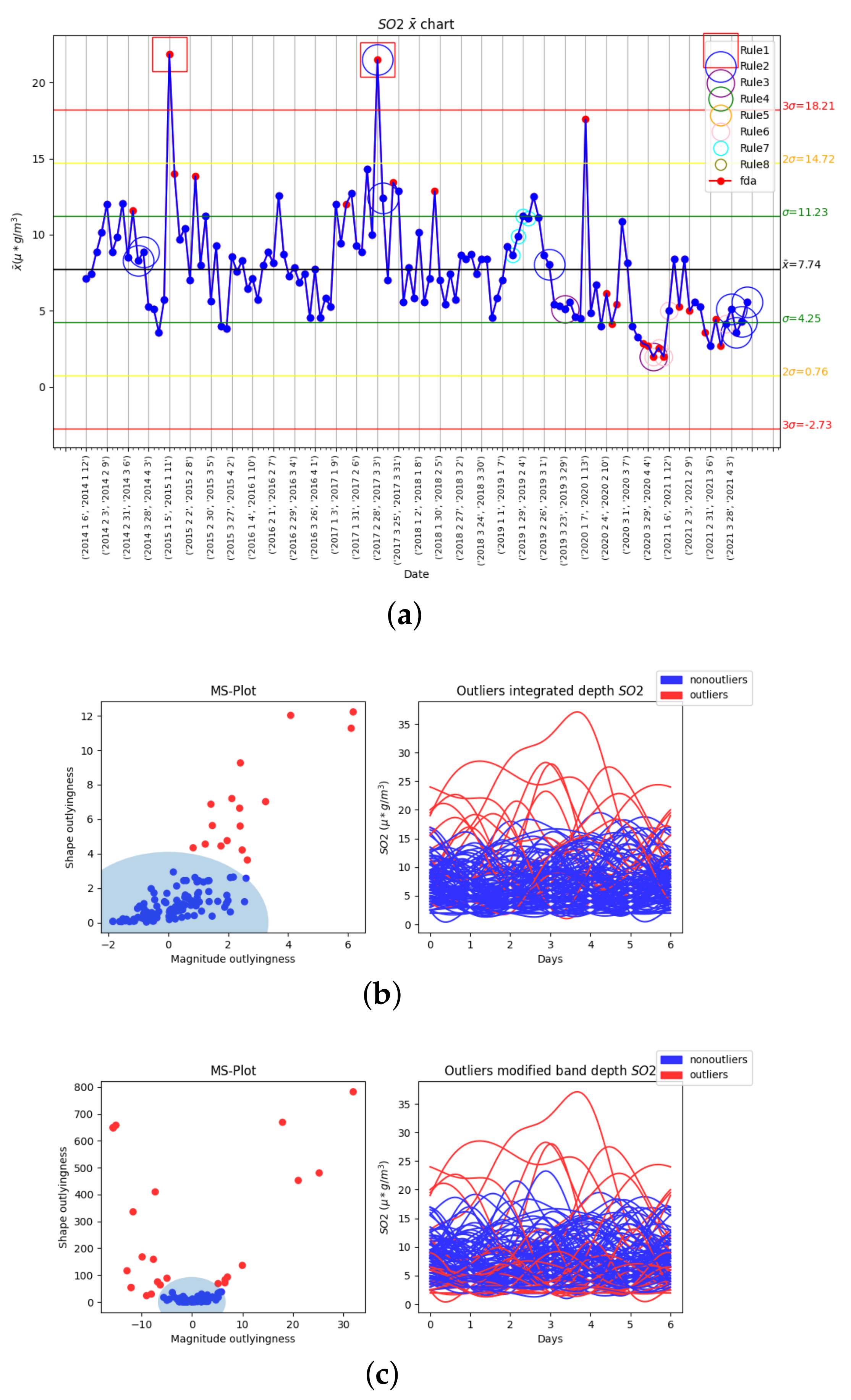
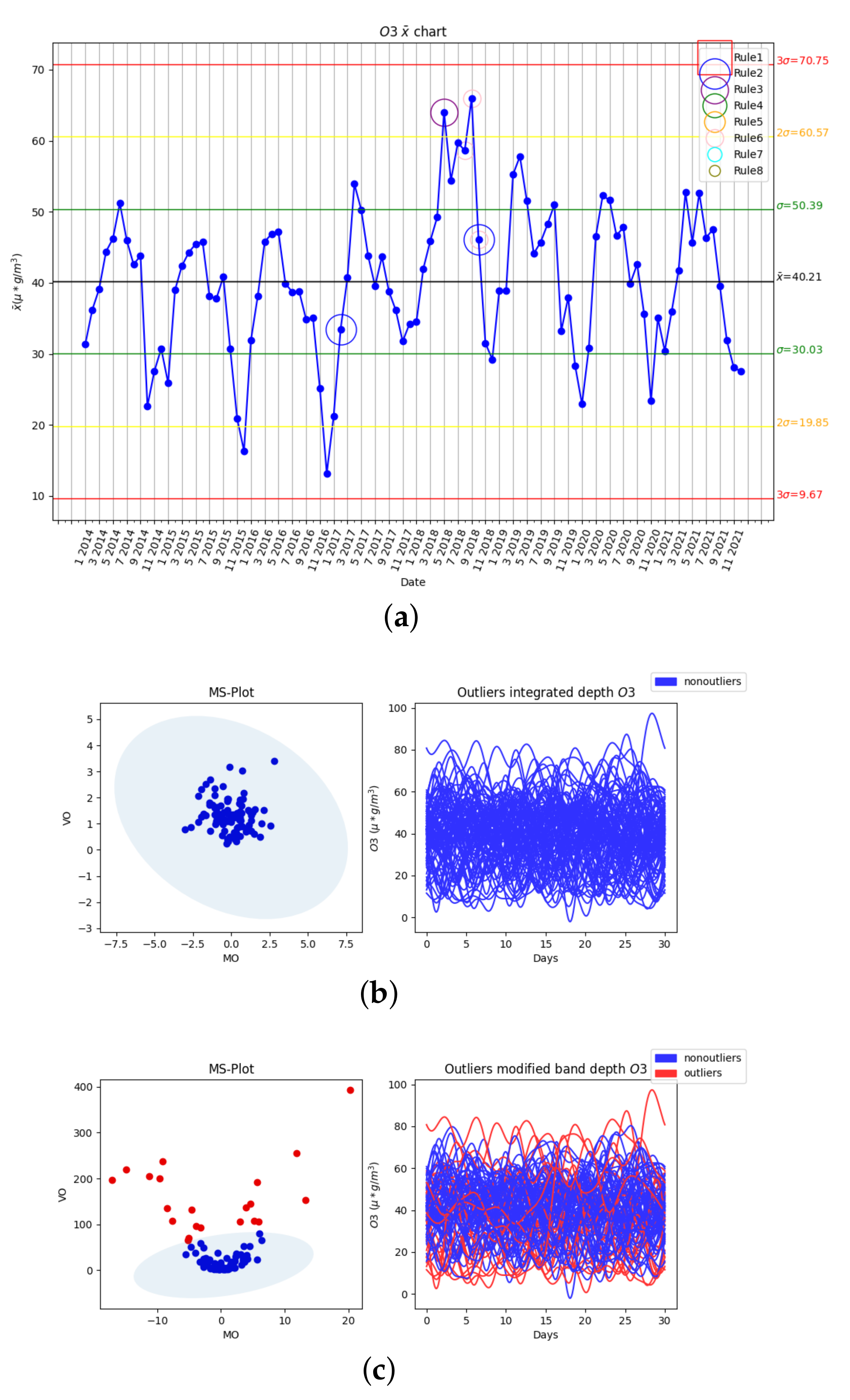
3.2. Results of Statistical Process Control and Functional Data Analysis
3.2.1. First Variable: NO2
3.2.2. Second Variable: SO2
3.2.3. Third Variable: PM10
3.2.4. Fourth Variable: O3
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| FDA | Functional data analysis |
| SPC | Statistical process control |
References
- Schwartz, J.; Ballester, F.; Saez, M.; Pérez-Hoyos, S.; Bellido, J.; Cambra, K.; Arribas, F.; Cañada, A.; Pérez-Boillos, M.J.; Sunyer, J. The concentration-response relation between air pollution and daily deaths. Environ. Health Perspect. 2001, 109, 1001–1006. [Google Scholar] [CrossRef] [PubMed]
- García-Nieto, P.J. Parametric study of selective removal of atmospheric aerosol by coagulation, condensation and gravitational settling. Int. J. Environ. Health Res. 2001, 11, 149–160. [Google Scholar] [CrossRef] [PubMed]
- Karaca, F.; Alagha, O.; Ertürk, F. Statistical characterization of atmospheric PM10 and PM 2.5 concentrations at a non-impacted suburban site of Istanbul, Turkey. Chemosphere 2005, 59, 1183–1190. [Google Scholar] [CrossRef] [PubMed]
- García-Nieto, P.J. Study of the evolution of aerosol emissions from coal-fired power plants due to coagulation, condensation, and gravititational settling and health impact. J. Environ. Manag. 2006, 79, 372–382. [Google Scholar] [CrossRef] [PubMed]
- López-Cima, M.F.; García-Pérez, J.; Pérez-Gómez, B.; Aragonés, N.; López-Abente, G.; Tardón, A.; Pollán, M. Lung cancer risk and pollution in an industrial region of Northern Spain: A hospital-based case-control study. Int. J. Health Geogr. 2011, 10, 10. [Google Scholar] [CrossRef] [PubMed]
- Gao, H.; Chen, J.; Wang, B.; Tan, S.C.; Lee, C.M.; Yao, X.; Yan, H.; Shi, J. A study of air pollution of city clusters. Atmos. Environ. 2011, 45, 3069–3077. [Google Scholar] [CrossRef]
- Megido, L.; Suárez-Peña, B.; Negral, L.; Castrillón, L.; Fernández-Nava, Y. Suburban air quality: Human health hazard assessment of potentially toxic elements in PM10. Chemosphere 2017, 177, 284–291. [Google Scholar] [CrossRef]
- Ahmed, M.; Xiao, Z.; Shen, Y. Estimation of Ground PM2.5 Concentrations in Pakistan Using Convolutional Neural Network and Multi-Pollutant Satellite Images. Remote Sens. 2022, 14, 1735. [Google Scholar] [CrossRef]
- Choi, H.J.; Roh, Y.M.; Lim, Y.W.; Lee, Y.J.; Kim, K.Y. Land-Use Regression Modeling to Estimate NO2 and VOC Concentrations in Pohang City, South Korea. Atmosphere 2022, 13, 577. [Google Scholar] [CrossRef]
- Qi, N.; Tan, X.; Wu, T.; Tang, Q.; Ning, F.; Jiang, D.; Xu, T.; Wu, H. Temporal and Spatial Distribution Analysis of Atmospheric Pollutants in Chengdu—Chongqing Twin-City Economic Circle. Int. J. Environ. Res. Public Health 2022, 19, 4333. [Google Scholar] [CrossRef]
- WHO. Review of Evidence on Health Aspects of Air Pollution—REVIHAAP Project: Technical Report; World Health Organization: Copenhagen, Denmark, 2013. [Google Scholar]
- Royal College of Physicians. Report of a Working Party February 2016; Technical Report; Royal College of Physicians: London, UK, 2016. [Google Scholar]
- Kumar, P.; Druckman, A.; Gallagher, J.; Gatersleben, B.; Allison, S.; Eisenman, T.S.; Hoang, U.; Hama, S.; Tiwari, A.; Sharma, A.; et al. The nexus between air pollution, green infrastructure and human health. Environ. Int. 2019, 133, 105181. [Google Scholar] [CrossRef]
- Real Decreto 102/2011, de 28 de Enero, Relativo a la Mejora de la Calidad del Aire. 2011. Available online: https://www.boe.es/buscar/act.php?id=BOE-A-2011-1645 (accessed on 15 April 2022).
- Parlaiment, E.; The Council of the European Union. Directive 2008/50/EC of the European Parliament and of the Council. 2008. Available online: https://eur-lex.europa.eu/legal-content/en/ALL/?uri=CELEX%3A32008L0050 (accessed on 15 April 2022).
- Lutgens, F.; Tarbuck, E. The Atmosphere: An Introduction to Meteorology; Prentice Hall: New York, NY, USA, 2001. [Google Scholar]
- Cooper, C.; Alley, F. Air Pollution Control; Waveland Press: New York, NY, USA, 2002. [Google Scholar]
- Betancourt-Odio, M.A.; Martínez-De-ibarreta, C.; Budría-Rodríguez, S.; Wirth, E. Local analysis of air quality changes in the community of madrid before and during the COVID-19 induced lockdown. Atmosphere 2021, 12, 659. [Google Scholar] [CrossRef]
- Briz-Redón, Á.; Belenguer-Sapiña, C.; Serrano-Aroca, Á. Changes in air pollution during COVID-19 lockdown in Spain: A multi-city study. J. Environ. Sci. 2021, 101, 16–26. [Google Scholar] [CrossRef] [PubMed]
- Slezakova, K.; Pereira, M.C. 2020 COVID-19 lockdown and the impacts on air quality with emphasis on urban, suburban and rural zones. Sci. Rep. 2021, 11, 21336. [Google Scholar] [CrossRef] [PubMed]
- Tobías, A.; Carnerero, C.; Reche, C.; Massagué, J.; Via, M.; Minguillón, M.C.; Alastuey, A.; Querol, X. Changes in air quality during the lockdown in Barcelona (Spain) one month into the SARS-CoV-2 epidemic. Sci. Total Environ. 2020, 726, 138540. [Google Scholar] [CrossRef] [PubMed]
- Venter, Z.S.; Aunan, K.; Chowdhury, S.; Lelieveld, J. COVID-19 lockdowns cause global air pollution declines. Proc. Natl. Acad. Sci. USA 2020, 117, 18984–18990. [Google Scholar] [CrossRef]
- Jeanjean, A.P.; Gallagher, J.; Monks, P.S.; Leigh, R.J. Ranking current and prospective NO2 pollution mitigation strategies: An environmental and economic modelling investigation in Oxford Street, London. Environ. Pollut. 2017, 225, 587–597. [Google Scholar] [CrossRef] [Green Version]
- Febrero, M.; Galeano, P.; Gonz, W. Outlier detection in functional data by depth measures, with application to identify abnormal NO x levels. Environmetrics 2008, 19, 331–345. [Google Scholar] [CrossRef]
- Matías, J.M.; Ordóñez, C.; Taboada, J.; Rivas, T. Functional support vector machines and generalized linear models for glacier geomorphology analysis. Int. J. Comput. Math. 2009, 86, 275–285. [Google Scholar] [CrossRef]
- Torres, J.M.; Nieto, P.J.; Alejano, L.; Reyes, A.N. Detection of outliers in gas emissions from urban areas using functional data analysis. J. Hazard. Mater. 2011, 186, 144–149. [Google Scholar] [CrossRef]
- Martínez, J.; Saavedra, Á.; García-Nieto, P.J.; Piñeiro, J.I.; Iglesias, C.; Taboada, J.; Sancho, J.; Pastor, J. Air quality parameters outliers detection using functional data analysis in the Langreo urban area (Northern Spain). Appl. Math. Comput. 2014, 241, 1–10. [Google Scholar] [CrossRef]
- Sancho, J.; Iglesias, C.; Piñeiro, J.; Martínez, J.; Pastor, J.J.; Araújo, M.; Taboada, J. Study of Water Quality in a Spanish River Based on Statistical Process Control and Functional Data Analysis. Math. Geosci. 2016, 48, 163–186. [Google Scholar] [CrossRef]
- Ordòñez, C.; Martìnez, J.; Saavedra, À.; Mourelle, A. Intercomparison Exercise for Gases Emitted by a Cement Industry in Spain: A Functional Data Approach. J. Air Waste Manag. Assoc. 2011, 61, 135–141. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sancho, J.; Pastor, J.J.; Martínez, J.; García, M.A. Evaluation of harmonic variability in electrical power systems through statistical control of quality and functional data analysis. Procedia Eng. 2013, 63, 295–302. [Google Scholar] [CrossRef] [Green Version]
- Wu, D.; Huang, S.; Xin, J. Dynamic compensation for an infrared thermometer sensor using least-squares support vector regression (LSSVR) based functional link artificial neural networks (FLANN). Meas. Sci. Technol. 2008, 19, 105202. [Google Scholar] [CrossRef]
- Ordoñez, C.; Martínez, J.; de Cos Juez, J.F.; Lasheras, F.S. Comparison of GPS observations made in a forestry setting using functional data analysis. Int. J. Comput. Math. 2012, 89, 402–408. [Google Scholar] [CrossRef]
- Dombeck, D.A.; Graziano, M.S.; Tank, D.W. Functional clustering of neurons in motor cortex determined by cellular resolution imaging in awake behaving mice. J. Neurosci. 2009, 29, 13751–13760. [Google Scholar] [CrossRef]
- Dai, W.; Genton, M.G. Multivariate Functional Data Visualization and Outlier Detection. J. Comput. Graph. Stat. 2018, 27, 923–934. [Google Scholar] [CrossRef] [Green Version]
- Grubbs, F.E. Procedures for Detecting Outlying Observations in Samples. Technometrics 1969, 11, 1–21. [Google Scholar] [CrossRef]
- Jäntschi, L. A test detecting the outliers for continuous distributions based on the cumulative distribution function of the data being tested. Symmetry 2019, 11, 835. [Google Scholar] [CrossRef] [Green Version]
- Lara, R.; Negral, L.; Querol, X.; Alastuey, A.; Canals, A. Estudio de Contribución de Fuentes a PM10 en Gijón INFORME A2-4B; Technical Report; Ministerio para la Transición Ecológica y el Reto Demográfico: Madrid, Spain, 2021. [Google Scholar]
- González-Marco, D.; Sierra, J.P.; Fernández de Ybarra, O.; Sánchez-Arcilla, A. Implications of long waves in harbor management: The Gijón port case study. Ocean. Coast. Manag. 2008, 51, 180–201. [Google Scholar] [CrossRef]
- Sánchez Lasheras, F.; García Nieto, P.J.; García Gonzalo, E.; Bonavera, L.; de Cos Juez, F.J. Evolution and forecasting of PM10 concentration at the Port of Gijon (Spain). Sci. Rep. 2020, 10, 11716. [Google Scholar] [CrossRef] [PubMed]
- García Nieto, P.J.; Álvarez Antón, J.C. Nonlinear air quality modeling using multivariate adaptive regression splines in Gijón urban area (Northern Spain) at local scale. Appl. Math. Comput. 2014, 235, 50–65. [Google Scholar] [CrossRef]
- Hu, W.; Zhao, T.; Bai, Y.; Shen, L.; Sun, X.; Gu, Y. Contribution of Regional PM2.5 Transport to Air Pollution Enhanced by Sub-Basin Topography: A Modeling Case over Central China. Atmosphere 2020, 11, 1258. [Google Scholar] [CrossRef]
- Cetin, E.; Odabasi, M.; Seyfioglu, R. Ambient volatile organic compound (VOC) concentrations around a petrochemical complex and a petroleum refinery. Sci. Total Environ. 2003, 312, 103–112. [Google Scholar] [CrossRef]
- Van Rossum, G.; Drake, F.L. Python 3 Reference Manual; CreateSpace: Scotts Valley, CA, USA, 2009. [Google Scholar]
- Ramos-Carreño, C.; Suárez, A.; Torrecilla, J.L.; Carbajo Berrocal, M.; Marcos Manchón, P.; Pérez Manso, P.; Hernando Bernabé, A.; García Fernández, D.; Hong, Y.; Rodríguez-Ponga Eyriès, P.M.; et al. GAA-UAM/scikit-fda: Version 0.7.1; Grupo de Aprendizaje Automatico—Universidad Autonoma de Madrid: Madrid, Spain, 2022. [Google Scholar] [CrossRef]
- D’Agostino, R.B. An omnibus test of normality for moderate and large sample size. Biometrika 1971, 58, 341–348. [Google Scholar] [CrossRef]
- D’Agostino, R.B.; Pearson, E.S. Tests for departure from normality. Biometrika 1973, 60, 613–622. [Google Scholar]
- Chen, Y.K. Economic design of X control charts for non-normal data using variable sampling policy. Int. J. Prod. Econ. 2004, 92, 61–74. [Google Scholar] [CrossRef]
- Freeman, J.; Modarres, R. Inverse Box-Cox: The power-normal distribution. Stat. Probab. Lett. 2006, 76, 764–772. [Google Scholar] [CrossRef]
- Box, G.E.P.; Cox, D.R. An analysis of transformations. J. R. Stat. Soc. Ser. B 1964, 26, 211–252. [Google Scholar] [CrossRef]
- Shewhart, W.A. Economic Control of Quality of Manufactured Product; Van Nostrand Company, Inc.: New York, NY, USA, 1931; p. 501. [Google Scholar]
- Grant, E.L.; Leavenworth, R.S. Statistical Quality Control, 5th ed.; McGraw-Hill: New York City, NY, USA, 1980; p. 684. [Google Scholar]
- Champ, C.W.; Woodall, W.H. Exact results for shewhart control charts with supplementary runs rules. Technometrics 1987, 29, 393–399. [Google Scholar] [CrossRef]
- Zhang, S.; Wu, Z. Designs of control charts with supplementary runs rules. Comput. Ind. Eng. 2005, 49, 76–97. [Google Scholar] [CrossRef]
- Electric, W. Statistical Quality Control Handbook; Western Electric Corporation: Indianapolis, Indiana, 1956. [Google Scholar]
- Nelson, L.S. The Shewhart Control Chart—Tests for Special Causes. J. Qual. Technol. 1984, 16, 237–239. [Google Scholar] [CrossRef]
- Ramsay, J.O.; Silverman, B. Functional Data Analysis, 1st ed.; Springer International Publishing: New York, NY, USA, 2002; p. 317. [Google Scholar]
- Fraiman, R.; Muniz, G. Trimmed means for functional data. Test 2001, 10, 419–440. [Google Scholar] [CrossRef]
- Díaz Muñiz, C.; García Nieto, P.J.; Alonso Fernández, J.R.; Martínez Torres, J.; Taboada, J. Detection of outliers in water quality monitoring samples using functional data analysis in San Esteban estuary (Northern Spain). Sci. Total Environ. 2012, 439, 54–61. [Google Scholar] [CrossRef]
- Lopez-Pintado, S.; Romo, J. On the concept of depth for functional data. J. Am. Stat. Assoc. 2009, 104, 718–734. [Google Scholar] [CrossRef] [Green Version]
- Ojo, O.; Lillo, R.E.; Anta, A.F. Outlier Detection for Functional Data with R Package fdaoutlier. arXiv 2021, arXiv:2105.05213. [Google Scholar]
- Möttönen, J.; Oja, H. Multivariate spatial sign and rank methods. J. Nonparametric Stat. 1995, 5, 201–213. [Google Scholar] [CrossRef]
- Claeskens, G.; Hubert, M.; Slaets, L.; Vakili, K. Multivariate Functional Halfspace Depth. J. Am. Stat. Assoc. 2014, 109, 411–423. [Google Scholar] [CrossRef]
- López-Pintado, S.; Sun, Y.; Lin, J.K.; Genton, M.G. Simplicial band depth for multivariate functional data. Adv. Data Anal. Classif. 2014, 8, 321–338. [Google Scholar] [CrossRef]
- Rousseeuw, P.J. Multivariate estimation with high breakdown point. Math. Stat. Appl. 1985, B, 283–297. [Google Scholar]
- Hardin, J.; Rocke, D.M. The Distribution of Robust Distances. J. Comput. Graph. Stat. 2005, 14, 928–946. [Google Scholar] [CrossRef] [Green Version]
- Dai, W.; Genton, M.G. Directional outlyingness for multivariate functional data. Comput. Stat. Data Anal. 2019, 131, 50–65. [Google Scholar] [CrossRef] [Green Version]




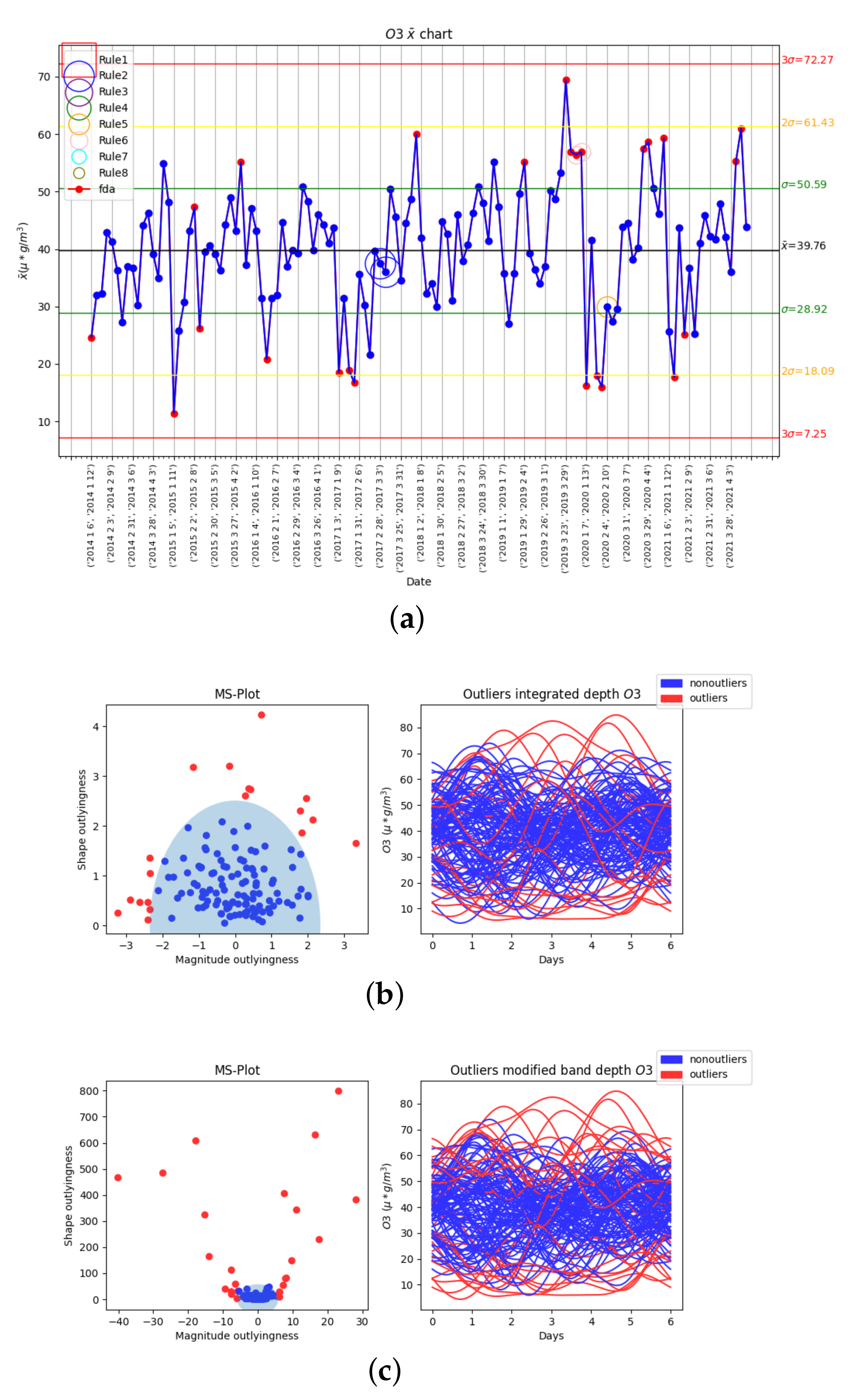
| Date | Magnitude Outlyingness | Shape Outlyingness |
|---|---|---|
| 26 January 2015 → 1 February 2015 | 13.94 | 689.94 |
| 9 February 2015 → 15 February 2015 | 27.84 | 670.24 |
| 16 February 2015 → 22 February 2015 | 4.35 | 81.42 |
| 10 April 2015 → 16 April 2015 | 11.52 | 403.41 |
| 12 February 2019 → 18 February 2019 | 12.19 | 179.78 |
| 26 February 2019 → 1 March 2019 | 11.27 | 113.62 |
| 14 January 2020 → 20 January 2020 | −14.35 | 676.87 |
| 22 March 2020 → 28 March 2020 | −14.39 | 146.50 |
| 29 March 2020 → 4 April 2020 | −9.05 | 45.80 |
| 5 April 2020 → 11 April 2020 | −24.11 | 243.15 |
| 19 April 2020 → 25 April 2020 | −22.03 | 293.41 |
| 17 February 2021 → 23 February 2021 | −20.34 | 909.81 |
| 24 February 2021 → 30 February 2021 | −9.04 | 145.01 |
| 28 March 2021 → 3 April 2021 | 4.29 | 72.27 |
| 11 April 2021 → 17 April 2021 | −19.23 | 586.20 |
| Date | Magnitude Outlyingness | Shape Outlyingness |
|---|---|---|
| 7 March 2014 → 13 March 2014 | 5.626255 | 63.812306 |
| 5 January 2015 → 11 January 2015 | 31.910835 | 782.922973 |
| 12 January 2015 → 18 January 2015 | 6.574228 | 82.721158 |
| 9 February 2015 → 15 February 2015 | 9.991058 | 136.293751 |
| 17 January 2017 → 23 January 2017 | 6.462673 | 72.093495 |
| 28 February 2017 → 3 March 2017 | 25.187203 | 480.681219 |
| 18 March 2017 → 24 March 2017 | 17.930567 | 669.504009 |
| 23 January 2018 → 29 January 2018 | 7.053569 | 92.688184 |
| 7 January 2020 → 13 January 2020 | 21.048451 | 452.726218 |
| 4 February 2020 → 10 February 2020 | −7.972081 | 419.256577 |
| 11 February 2020 → 17 February 2020 | −9.399330 | 166.035485 |
| 18 February 2020 → 24 February 2020 | −15.593749 | 649.645403 |
| 22 March 2020 → 28 March 2020 | −6.807899 | 74.728096 |
| 29 March 2020 → 4 April 2020 | −11.164611 | 338.940421 |
| 5 April 2020 → 11 April 2020 | −11.988441 | 54.003313 |
| 12 April 2020 → 18 April 2020 | −12.839921 | 115.184531 |
| 19 April 2020 → 25 April 2020 | −11.988441 | 54.003313 |
| 20 January 2021 → 26 January 2021 | −7.605015 | 158.613293 |
| 3 February 2021 → 9 February 2021 | −14.618797 | 669.824183 |
| 24 February 2021 → 30 February 2021 | −8.993194 | 22.934123 |
| 7 March 2021 → 13 March 2021 | −15.645523 | 645.544555 |
| 14 March 2021 → 20 March 2021 | −7.828102 | 27.494763 |
| Average: | 0.11 | 54.55 |
| Date | Magnitude Outlyingness | Shape Outlyingness |
|---|---|---|
| 13 January 2014 → 19 January 2014 | 4.89 | 94.36 |
| 7 March 2014 → 13 March 2014 | 19.53 | 282.79 |
| 14 March 2014 → 20 March 2014 | 8.95 | 125.27 |
| 19 January 2015 → 25 January 2015 | −7.74 | 30.78 |
| 26 January 2015 → 1 February 2015 | −5.79 | 44.07 |
| 2 February 2015 → 8 February 2015 | −14.26 | 324.18 |
| 23 February 2015 → 29 February 2015 | −19.06 | 580.55 |
| 20 February 2015 → 5 March 2015 | −13.96 | 303.93 |
| 20 March 2015 → 26 March 2015 | −19.61 | 593.69 |
| 10 April 2015 → 16 April 2015 | 8.27 | 84.65 |
| 15 February 2016 → 21 February 2016 | −8.82 | 142.91 |
| 5 March 2016 → 11 April 2016 | −13.21 | 80.98 |
| 19 March 2016 → 25 March 2016 | −6.31 | 177.74 |
| 26 March 2016 → 1 April 2016 | −8.24 | 40.49 |
| 2 April 2016 → 8 April 2016 | −6.64 | 57.83 |
| 16 April 2016 → 22 April 2016 | −24.70 | 597.71 |
| 10 January 2017 → 16 January 2017 | −7.49 | 87.34 |
| 19 February 2019 → 25 Feb 2019 | 8.30 | 23.86 |
| 25 February 2020 → 31 February 2020 | 10.91 | 149.45 |
| 5 April 2020 → 11 April 2020 | −10.46 | 355.77 |
| 17 February 2021 → 23 February 2021 | 4.58 | 93.48 |
| 28 March 2021 → 3 April 2021 | 57.11 | 277.13 |
| 18 April 2021 → 24 April 2021 | 9.43 | 140.62 |
| Average: | −0.02 | 42.04 |
| Date | Magnitude Outlyingness | Shape Outlyingness |
|---|---|---|
| 6 January 2014 → 12 January 2014 | −6.39 | 57.99 |
| 5 January 2015 → 11 January 2015 | −40.13 | 466.26 |
| 2 February 2015 → 8 February 2015 | 7.63 | 405.32 |
| 9 February 2015 → 15 February 2015 | −5.68 | 30.89 |
| 3 April 2015 → 9 April 2015 | 6.39 | 28.17 |
| 18 January 2016 → 24 January 2016 | −13.93 | 164.05 |
| 3 January 2017 → 9 January 2017 | −17.78 | 607.46 |
| 17 January 2017 → 23 January 2017 | −7.52 | 18.98 |
| 24 January 2017 → 30 January 2017 | −7.58 | 28.62 |
| 15 April 2017 → 21 April 2017 | 23.21 | 798.25 |
| 29 January 2019 → 4 February 2019 | 9.77 | 147.90 |
| 23 March 2019 → 29 March 2019 | 28.24 | 381.43 |
| 30 March 2019 → 5 April 2019 | 6.28 | 26.29 |
| 6 April 2019 → 12 April 2019 | 16.52 | 630.17 |
| 13 April 2019 → 19 April 2019 | 8.21 | 81.09 |
| 7 January 2020 → 13 January 2020 | −15.18 | 323.62 |
| 21 January 2020 → 27 January 2020 | −9.32 | 39.16 |
| 28 January 2020 → 3 February 2020 | −27.23 | 484.60 |
| 22 March 2020 → 28 March 2020 | 7.35 | 53.58 |
| 29 March 2020 → 4 April 2020 | 17.65 | 228.64 |
| 19 April 2020 → 25 April 2020 | 6.27 | 8.71 |
| 13 January 2021 → 19 January 2021 | −5.94 | 2.77 |
| 27 January 2021 → 2 February 2021 | −7.57 | 111.92 |
| 4 April 2021 → 10 April 2021 | 7.99 | 79.31 |
| 11 April 2021 → 17 April 2021 | 10.98 | 344.05 |
| Average | 0.0047 | 48.53 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rigueira, X.; Araújo, M.; Martínez, J.; García-Nieto, P.J.; Ocarranza, I. Functional Data Analysis for the Detection of Outliers and Study of the Effects of the COVID-19 Pandemic on Air Quality: A Case Study in Gijón, Spain. Mathematics 2022, 10, 2374. https://doi.org/10.3390/math10142374
Rigueira X, Araújo M, Martínez J, García-Nieto PJ, Ocarranza I. Functional Data Analysis for the Detection of Outliers and Study of the Effects of the COVID-19 Pandemic on Air Quality: A Case Study in Gijón, Spain. Mathematics. 2022; 10(14):2374. https://doi.org/10.3390/math10142374
Chicago/Turabian StyleRigueira, Xurxo, María Araújo, Javier Martínez, Paulino José García-Nieto, and Iago Ocarranza. 2022. "Functional Data Analysis for the Detection of Outliers and Study of the Effects of the COVID-19 Pandemic on Air Quality: A Case Study in Gijón, Spain" Mathematics 10, no. 14: 2374. https://doi.org/10.3390/math10142374
APA StyleRigueira, X., Araújo, M., Martínez, J., García-Nieto, P. J., & Ocarranza, I. (2022). Functional Data Analysis for the Detection of Outliers and Study of the Effects of the COVID-19 Pandemic on Air Quality: A Case Study in Gijón, Spain. Mathematics, 10(14), 2374. https://doi.org/10.3390/math10142374








