Evolution over Two Decades of CAS-Active Senior Secondary Mathematics Curriculum and Assessment

Abstract

The Victorian Curriculum and Assessment Authority (VCAA) introduced the use of Computer Algebra System (CAS) technology (calculator and software) into the senior secondary mathematics curriculum and examination assessment in three phases, starting with a research-based pilot from 2000, followed by parallel implementation of CAS and non-CAS subjects from 2006 and culminating in transition to CAS-assumed subjects in 2010. This paper reports reflections on these developments over two decades from the perspectives of a researcher and the state mathematics manager (the authors) in consultation with four implementing teachers (the consultants). The authors critically examined the strategic design decisions that were made for the initiative over time. Then, with contributions from the four consultants, technical design issues relating to assessment and to teaching and the changes over a decade were investigated. A range of modifications have been made over the two decades, driven by changes in device capability and progressively increasing teaching expertise. The place of CAS in senior mathematics is now widely accepted, partly because an examination component not allowing any technology has been implemented. Examination questions have become more general, which may have added difficulty, but more questions involve setting up a real situation mathematically.

1. Introduction

In Victoria, Australia, under the auspices of the Victorian Curriculum and Assessment Authority (VCAA), the Victorian Certificate of Education (VCE) senior secondary mathematics curriculum, and the related external assessment, incorporated the use of computer algebra (CAS) for the last two decades. This paper presents the reflections of four leading teachers, the system mathematics manager, and a researcher, all of whom have been involved in this development from the initial introduction to mature implementation. The paper reports on policies, practices, and issues related to the design of curriculum, pedagogy, and assessment from 2000 to 2022, covering four cycles of senior secondary mathematics curriculum development, implementation, monitoring, evaluation, and review.

The growth of computing power has had an enormous impact on how mathematical calculations are carried out by all people, from meeting simple everyday needs such as shopping to using models of highly complex systems, such as predicting weather. As computers and digital devices have become more accessible, mathematics curricula, teaching, and assessment have had to respond accordingly. In the Australian state of Victoria, for its senior secondary mathematics examinations, students were permitted to use the then newly accessible scientific calculators, rather than four figure logarithm tables or slide rules from 1978. These examinations were, and still are, very high stakes for students and their schools, as the grades are used for both end-of-school certification and for university entrance. Because of the importance of the examinations, related policies are generally quickly adopted by teachers of Year 12 (the last year of school) and in lower year levels as appropriate. After 1978, digital technology developed quickly. By 1997, graphics calculators (at first scientific calculators with multi-line screens and the capacity to graph functions and create tables) were sufficiently affordable to be permitted in the calculus-based examinations for the intermediate subject (Mathematical Methods) and the advanced subject (Specialist Mathematics). One year later, the examiners set the questions assuming that all students had a graphics calculator. By 2000, graphics calculator use was assumed by the examiners for the elementary subject (Further Mathematics) a non-calculus data analysis and discrete mathematics subject. During the 1990s, it became evident that graphics calculators with symbolic capability (symbolic algebra and calculus) were evolving from very expensive calculators for professionals into the school market. The futuristic scenario imagined by Wilf in “The Disk with the College Education” was becoming reality [1]. Hence, a team of researchers, some of whom also were examiners for the school subjects, began to analyze the likely impact of allowing CAS use in the VCE examinations [2,3,4]. From the start, it was very clear that allowing CAS would have a much greater impact on examination questions and solutions than allowing graphics calculators and that teachers and students would need considerable support to use these more complicated devices well. The change would have to be handled carefully. This paper looks back on the two decades of that change, drawing on the perspectives of six long term contributors.

We will show how the deliberate alignment between curriculum, assessment, and pedagogy, has been critical to the successful adoption of a technology-active curriculum and assessment, in particular for the external examinations. This initiative needed a positive policy framework; strong and informed leadership; clear expression of intention with respect to curriculum and high-stakes assessment; a sound research basis with careful monitoring of teachers’ opinions; and substantial professional learning and resource support for pedagogy, all maintained over an extended period.

Expectations and practices change over time, and there has been, and continues to be, genuine critical discourse in Victoria by different stakeholders on what is reasonable, what is mathematically desirable, and what technology policies maintain a suitable balance for sub-groups of the student cohort, and for what pathways and purposes. This paper reflects various aspects of that journey from several perspectives, each variously concerned with what is best for students, making it all work, and progressing contemporary curriculum development.

1.1. Strategic, Tactical and Technical Design

We consider the management of the shift to using mathematically-able software as a complex example of educational design. We follow Burkhardt [5] in distinguishing three aspects of design: strategic, tactical, and technical. There is no hierarchy of importance because all three interconnect and influence whether an educational initiative is a success. Burkhardt gives a working definition of strategic design:

Strategic design focuses on the design implications of the interactions of the products, and the processes for their use, with the whole user system it aims to serve. [5] (p. 1)

In the present case, the user system includes teachers, students and parents, employers and universities, experts, and indeed the whole community because of the importance of retaining their confidence in the quality of the Victorian education system. The strategic design of the shift to mathematically-able software, as described below, shows the value of well-paced change in line with clear long-term intentions, consultation with stakeholders, and planned professional development for teachers. Burkhardt’s tactical design is focused on the overall internal structure of a product—in this case the mathematics study designs that are outlined below. It is here that the intention that students learn to use technology as part of learning mathematics and also develop appropriate by-hand skills is set out for teachers.

In the later parts of the paper, we discuss aspects of the technical design of this initiative, with an emphasis on assessment. This aspect of design is focused on the mathematical tasks that students and teachers do in the classroom and in assessment. Good technical design supports students to learn important mathematics and provides for valid and equitable assessment of this learning [6].

1.2. Information Gathering

The information and opinions expressed in this paper arise from the reflections of six expert long-term participants in this initiative, supplemented by reviews of curriculum and assessment documents, including the examination papers since 2000. (Note that we use the word ‘curriculum’ as the official specification of what students should be taught and learn). Author Leigh-Lancaster was the Mathematics Manager at the VCAA and led curriculum and assessment reviews for the period under discussion. His work included liaising with teachers, academics, and examination panels, and supervising the development of advice for teachers, support materials, and programs. Author Stacey is a mathematics education researcher who led the major research study that accompanied the first pilot CAS subject (reviewed in [2,3]) and has also had many other involvements with teacher education, curriculum, and assessment in Victoria. To broaden and test the authors’ views, we sought the views of leading educators in Victoria who had been involved in the CAS initiative for some time. Four of these educators provided written responses to a series of questions sent by the authors, thereby becoming the consultants for this study. Together these four people have many roles: as teachers and mathematics leaders in their schools, review panel members, examination panel members, examination assessors, textbook authors, advisors to other schools, and active members of professional associations, and over time, all of them have been involved in various subject revisions and developments initiated by the VCAA. The consultants carefully thought back over their own experiences and those of their students in using CAS to assess the success and challenges of the initiative, and to describe the changes that have happened. They consulted personal and public documents to support, explain, and discuss the conclusions that they reached with concrete examples.

1.3. Background Research and Scholarship

Research has both informed and followed aspects of the development described in this paper. The review papers by Stacey [2,3] give an overview of the research conducted on this initiative, and many of the research papers cited later in the present article describe research on specific questions. The intention of this paper, however, is to focus on design issues, both strategic and technical. In the early phase, there was limited scholarly material related to strategic design, as systems around the world were only beginning to implement the structures for introducing CAS technology that were being developed (see, for example [7,8]). Naturally, these structures had to be implemented and progressively adapted, before formal investigation could take place. During the period from 2000 to 2010, a few early research studies on large-scale initiatives emerged and there was ongoing personal professional communication on strategic and technical design (including matters of policy, process, and implementation) between leaders of senior secondary mathematics curriculum and assessment in educational jurisdictions actively working in the field, including the USA, France, Denmark, Victoria, Australia, and the International Baccalaureate Organisation. Broader research and analysis subsequently took place (for example, [9]).

2. Outline of VCE Mathematics Study Designs (2000–2022)

In the state of Victoria, senior secondary school curriculum and assessment is specified and controlled by the VCAA. The state’s curriculum content is broadly in line with the Australian Curriculum with some modifications. For mathematics, a stronger endorsement and expectation of technology use in Victoria is one of the main differences from other Australian states and territories. There are three mathematics subjects that students can select for senior secondary school (Years 11 and 12) in Victoria. It is not compulsory to study mathematics as part of the VCE. Students can choose to do more than one mathematics subject. These three subjects can be broadly classified as elementary (data analysis and discrete mathematics and applications), intermediate (functions, algebra, calculus, probability and statistics), and advanced (extending the intermediate subject and including complex numbers, vectors, differential equations and the like). The intermediate subject is required as background for the advanced subject, and students who do the advanced subject typically take them simultaneously. Students can also choose to do both the elementary and the intermediate subject.

The VCE Mathematics study design [10] develops these subjects as a sequence of four semester units over 2 years, Units 1 and 2 normally completed in Year 11 and Units 3 and 4 completed in Year 12, with detailed content for each unit organized under areas of study (e.g., data analysis, probability and statistics; functions, relations and graphs; or calculus), and topics (e.g., investigating and modelling time series, continuous random variables, or vector calculus) as applicable.

In every subject, for each unit and the areas of study, students are intended to meet three outcomes for senior secondary mathematics:

• develop mathematical concepts, knowledge, and skills (Outcome 1);
• apply mathematics to analyze, investigate, and model a variety of contexts and solve practical and theoretical problems in situations that range from well-defined and familiar to open-ended and unfamiliar (Outcome 2); and
• use technology effectively as a tool for working mathematically (Outcome 3).

Each outcome is elaborated by key knowledge and key skill statements for each mathematics subject. For Outcome 1 these explicitly incorporate expectations for by-hand computation, and for Outcome 3 they explicitly incorporate expectations for the use of technology.

The study design describes the assessment for each outcome and the areas of study. Units 1 and 2 assessments are conducted fully within the school with the VCAA providing guidelines and advice. For Units 3 and 4, the VCAA regulates school-based assessment, worth a total of 34% of the final student score, and the external examinations held at the end of Unit 4 worth a total of 66% of the final score. School-based assessment is subject to audit, and results are statistically moderated with respect to the external examinations. The questions for each external examination are written by a centrally appointed panel of examiners; all students do the examinations in their schools at one time; and the examination scripts are marked anonymously by centrally appointed assessors, many of whom are experienced current teachers of the subject. Examination scores are combined with the school assessments to create a final grade for each subject. After the examination, the questions are made public [11] and the chief assessors for each subject provide reports on overall student performance to assist teachers in preparing students in the future. For each subject there are two examinations for a total of 3 hours. Multiple choice questions are worth one mark each and the component parts of longer constructed response questions (typically worth a total in the range of 10 to 20 marks) are generally worth one to four marks each.

School-based assessment involves students in mathematical investigation, modelling, or problem-solving on three extended tasks devised by teachers according to VCAA specifications. These provide opportunities for students to show how they are able to use the technology of their choice to model situations, represent problems or data, test what-if scenarios, and do computation (numerical, graphical, statistical, symbolic). In contrast, in the external examinations, technology is used in order to solve questions that are intended to take only a few minutes each. This technology use is much more constrained than the technology use by some students in school-based assessments. However, because the examinations have a high public profile and are compulsory for the student cohort, it is technology use in the examinations that has been of most interest and concern to stakeholders, and consequently that is the focus of this paper.

The three-subject senior secondary Units 3 and 4 mathematics curriculum structure has been stable since the early 1990s. There are regular curriculum reviews that have resulted in some changes, but the intentions of the subjects and the target audience for each remain broadly the same. Approximately 50,000 students do the VCE examinations each year. About 30,000 of these students complete the examinations in the elementary mathematics subject (currently named Further Mathematics in Units 3 and 4), approximately 16,000 in the intermediate subject (Mathematical Methods), and approximately 5,000 in the advanced subject (Specialist Mathematics). The exact subject names have varied over time and have not always been the same for all four units of each subject.

3. Strategic Management of Technology Change

As noted above, a major theme of mathematics teaching and assessment has been adapting to the changes in mathematically-able technology in a way that is reasonably accessible to all schools. There are many aspects to this, at all levels of education, involving for example classroom teaching, suitable curriculum content, and teacher preparation. High-stakes examinations, such as those for VCE Mathematics, play a dual role of leading change in schools as well as adapting to it, whilst always needing to maintain high public confidence. They also play a key role in meeting prerequisite requirements for many university courses. In particular, the intermediate subject is a prerequisite for very many tertiary STEM courses and others such as economics and medicine (see, for example, [12]). Carefully considered strategic design has been essential.

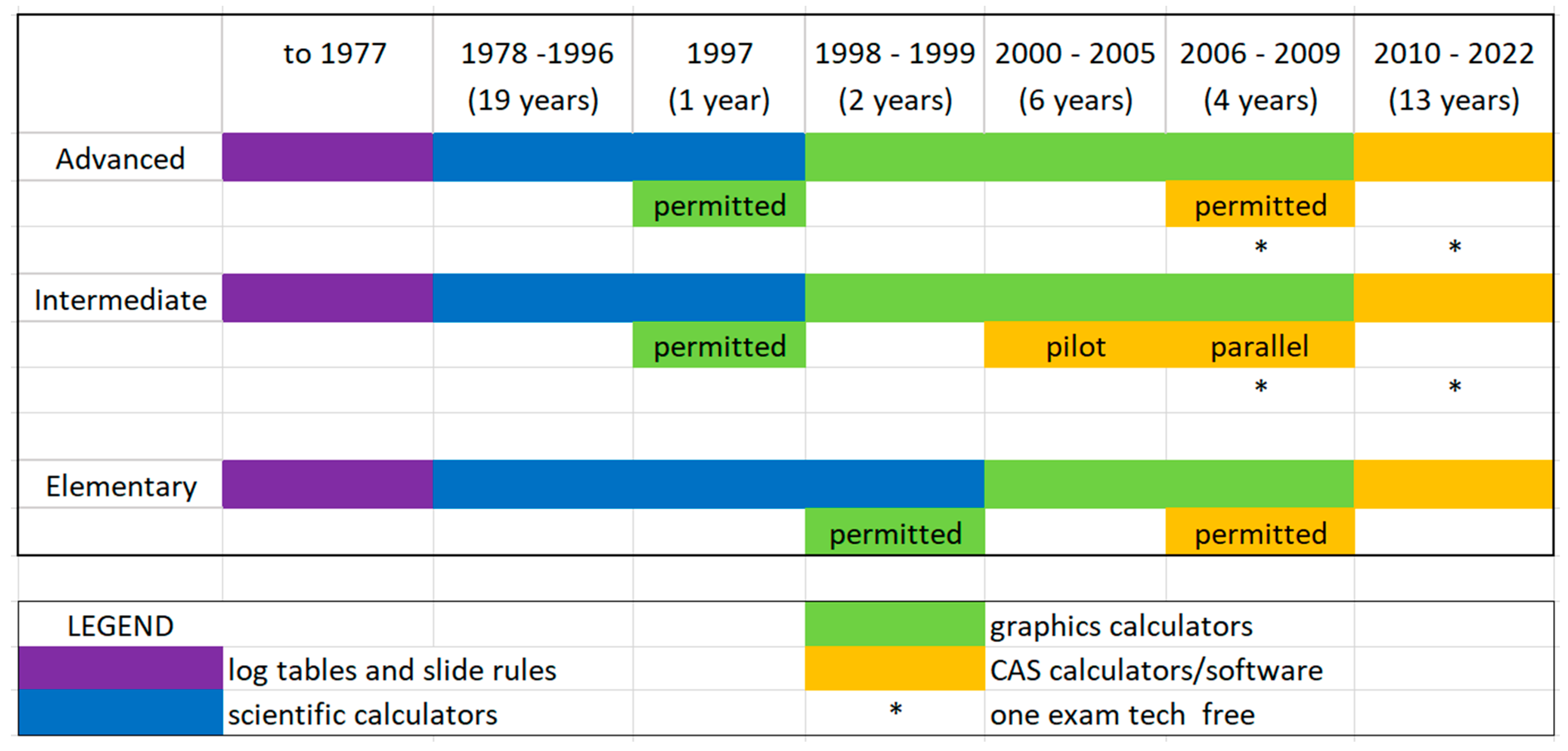
Figure 1 summarizes the changes in the rules about technology in final senior secondary mathematics examinations in Victoria since the advent of personal digital technology. For more details, see [2,13]. Figure 1 shows the technology that examiners assume students can use as they solve the examination questions, moving over time from no technology through scientific, graphics, to CAS capabilities. The examinations contain no questions specifically about the technology or to explicitly test its use; rather students make question-by-question choices to use or not use the specific functionality of technology to answer mathematical questions. The figure also shows that at some times, technology has been permitted rather than assumed. Some students had the permitted technology whilst others did not. At these times, examiners took care in designing questions that students using the new technology were not advantaged. In the late 1990s, permitting graphics calculators was intended as a bridging measure, giving time for teachers to learn about the new capabilities, for schools to gear up with suitable equipment, and as an equity measure for the technology to become more affordable (for example through a second-hand market developing). It was also important that those who did two mathematics subjects were not required to own two calculators. Since 2011, this has been an important reason for assuming CAS in the elementary mathematics subject. The symbolic functionality of the CAS has limited use in the largely non-algebraic questions. Both CAS and non-CAS graphics calculators provide the full range of other relevant functionality for this subject, numerical, graphical, statistical, and financial aspects.

As noted above, the likely impact of CAS technology on the examinations in the advanced and intermediate level subjects was substantial enough to preclude the introduction of CAS with the ‘permitted to assumed’ strategy used for graphics calculators. Hence, the incorporation of CAS technology has required a three-stage process over two decades: closely researched pilot, parallel implementation with a phased transition, then universal implementation. From 2001, when graphics calculators were the assumed technology for all examinations, restricted cohorts undertook a modified version of the Mathematics Methods course assuming an approved CAS calculator or software. The separate examinations in the modified subject used common questions with the standard course where possible (around 75%). These restricted cohorts began with a strongly researched pilot in just three schools (each using a different brand of CAS calculator) that developed into a clearly flagged policy-driven transition that gave schools’ time to increase teachers’ skills and prepare students in earlier year levels for the change [3,14]. By 2009, around half of the intermediate mathematics student cohorts were enrolled in the modified CAS-assumed subject, supporting a judgement that the whole system could reasonably shift. Hence, CAS became the assumed technology for all senior secondary mathematics subjects from 2010, with a 1-year staggering for the elementary subject as previously described. This is an instance of successful strategic design implemented over a 10-year period [5].

3.1. A No-Technology Examination

Following consultation with teachers and universities, particularly in response to concerns (but not convincing evidence) that students using CAS may not develop adequate by-hand skills in algebra, from 2006 a new structure for examinations in advanced and intermediate mathematics was adopted. No technology was permitted in the 1-hour Examination 1 (40 marks), whilst the 2-hour Examination 2 (80 marks) assumed access to the designated technology. This use of a no-technology examination continues. In VCAA consultations, this model was supported by a majority of teachers, with a large minority supporting the then status-quo of technology being assumed in both examinations, and with a very small minority preferring no use of technology in examinations. Garner and Pierce [15] provided an insight into the varying views that teachers and students even in one school had on the values of mathematics with and without technology. It is likely that without the two-component model, public confidence (including from the tertiary sector) that students are learning important aspects of mathematics may not have been adequately assured. At the same time, the 1:2 overall mark weighting sends a strong signal that the curriculum recognizes that in professional use of mathematics, people have access to enabling technology and use it as applicable. Students should be prepared for this. Research summarized in [3] showed that there was no evidence from the common ‘no technology’ Examination 1 of 2006–2009 that students using CAS developed weaker by-hand skills than students using graphics calculators (see also [16]).

A decade on, we asked for the views of the four expert teachers whom we consulted in writing this paper. Consultants 1, 3, and 4 strongly supported retaining the no-technology component and Consultant 2 stated that allowing technology in both examinations was equally viable, providing teachers were given sufficient support. Reasons for support of the no-technology component were variously that it promotes memory, logical thinking and structure, mental calculation and algebra skills, and knowledge of algorithms. Consultant 1, who has been both a teacher and examiner, noted that it is possible to test understanding of algorithms in a technology-assumed examination, but such ‘show-that’ questions are very time consuming. She cited Specialist Mathematics Examination 1, 2021, Question 3c as a straightforward question that tested the procedure for finding a confidence interval but required no technology use or detailed calculations. Students were given the information that Pr(−1.96 < Z < 1.96) = 0.95 and Pr(−3 < Z < 3) = 0.9973 and asked (among other things) to find an approximate confidence interval for the mean lifetime of new light globes given that the mean of a random sample of 25 light globes was 250 weeks, with a population standard deviation of 10 weeks. The question requires students to link the 95% confidence interval to the 0.95 probability, to know how the Z score is derived from sample mean and standard deviation, and to use simple algebra to manipulate the inequality to find the confidence interval. Consultant 1 commented that in contrast, in Examination 2, students could use the calculator to locate the confidence interval quickly, then move onto ‘something more interesting’.

Consultant 3 commented that some of his students are reluctant to use their device to solve problems in Examination 2 (where CAS is assumed), because they feel they may not score all available points if they do not show working. The examination general instructions specify that “where more than 1 mark is available, appropriate working must be shown”. Consequently, he addresses in class how to write a clear solution incorporating CAS use: writing down the mathematics that is needed to validate the method, process, and solution, without the use of technology syntax. This consideration had also arisen with the earlier use of graphics calculators when, for example, doing calculations with probability distributions. Ball and Stacey found this issue arose even in the first year of the CAS pilot and gave suggestions as to how it could be addressed [17]. VCAA examination reports also address this issue (see, for example, 2006, 2011, and 2021 VCE Mathematical Methods examination 2 reports in [11]). Essentially, mark allocation for constructed responses has a formulation, computation, and interpretation structure. Boers and Jones in a very early experiment with CAS in university-level examinations commented that underuse of CAS was more common than overuse [18].

3.2. The Computer Based Examination (2013 to 2021)

From 2013 to 2021, the VCAA ran a trial Computer-Based Examination (CBE) for Mathematical Methods involving several hundred students at Years 11 and 12 that chose to use Mathematica on computers in their teaching and as the CAS technology for students. Over the years, the number of schools varied between 10 and 20. While the curriculum and the assessment (school-based and examinations) were the same as for the standard cohort, the mode of delivery and response to Examination 2 differed. For the CBE trial, Mathematica was used to develop two specially designed notebooks, one that produced the examination, the other that ran the Mathematical Methods Examination 2 as a notebook (.nb file). Students from both standard and CBE cohorts sat the same no-technology written response Examination 1.

For Examination 2, students in the CBE trial responded to multiple-choice items using radio buttons, with responses automatically saved. The constructed response section provided computation and writing cells for parts and sub-parts of questions (akin to the ‘lines for working’ on the paper-based examination). Students could also insert additional computation and writing cells and annotate graphs as they wished. Analysis of distributions of scores showed students seemed to perform similarly on computer-based and calculator-based examination formats [19].

The CBE was a very good fit for schools that were able to teach using Mathematica as their choice of enabling technology. In the examinations, students were able to develop their own responses using a broader set of functionalities (text, symbolic, numerical, graphical, etc.). The assessors were able to see the students’ formulation of the problem; the output obtained and how it was used; and any commentary, annotations, and interpretations. Assessors had direct evidence for the use of various functionalities of technology, and how these have been used, rather than indirect evidence from calculator-paper examinations. It is interesting to note that for the standard (non-CBE) Examination 2, where students write their constructed responses in examination booklets, assessors have regularly commented that errors in student solutions often arise from inaccurate ‘transfer’ of CAS output to their written working. Examples can be found in 2011, 2018, and 2021 VCE Mathematical Methods Examination 2 reports, or 2009 and 2016 Specialist Mathematics Examination 2 reports [11].

On the other hand, the CBE examination was platform-specific and creating the examinations as notebook files was resource intensive for the VCAA. Moreover, appropriate IT expertise was required at the school to run the digital examination securely. Over the 8 years, there was limited uptake by schools and only a small number of schools moved from the mainstream hand-held CAS devices to the CBE. The level of enrolment was around 3% of the number of students in the cohort. Often the initiative was championed by a leading teacher in a school, and if that person left, others did not necessarily have the required familiarity with Mathematica to continue. With limited uptake and the pressures of COVID restrictions, the CBE program was concluded in 2021. The benefits and disadvantages of platform-specific assessment may need to be reviewed more broadly in coming years, as the interplay between commercial technology companies and formal school assessment changes. At this stage, the authors are not aware of any generic platforms that enable students to choose from a range of CAS and readily evaluate, edit, and re-evaluate automatically embedded computations as part of constructed responses in an examination context. There are moves to shift some examinations in various other subjects entirely on-line, but those examinations are generally text-based and do not require specific computational software for students to construct responses.

4. Teaching, Learning and Examining Mathematics with CAS

In this section, we turn to questions of technical design, especially drawing on the varied experiences of our four consultants in their multiple roles as teachers, examiners, school leaders, and authors. We asked the consultants how examination questions had changed over nearly two decades of CAS use. Whilst there have been minor changes to some of the specified content in the mathematics courses over time, the main content has not changed and the student cohorts seem to have remained stable, so it is reasonable to attribute most changes to adaptation to changing technology. We asked them about changes in how they use CAS calculators or software to teach and do mathematics in class and we asked them what, if any, changes have occurred in how their year-12 students use CAS calculators or software to do mathematics in class. The following main themes emerged, with general agreement across all four consultants. Examples that illustrate the main themes are provided in the following sections.

• Examination questions have been adapted to the continuing expansion of the functionality of CAS calculators over time, in some part influenced by the Victorian curriculum and assessment. Various supplementary apps have been helpful, as students use them to streamline solving standard types of examination questions.
• Some types of examination questions have become more demanding because they are more abstract and have greater use of parameters, and the breadth, depth, and variation in what can be asked has increased.
• Examination questions afford an increased variety of solution approaches with CAS.
• Teachers have shifted from conceptualising CAS technology as a graphics calculator that also does algebra, to a tool with an integrated suite of functionalities and a very useful display interface.
• Students and teachers have increased visualisation through the use of sliders, dynamic displays, animations, and simulations to show or explore behaviour. CAS is often used by students to get a ‘preliminary idea/insight/explore the territory’ before proceeding with further work.
• Teachers put more focus on efficiency and effectiveness in problem-solving approaches, so students will be more strategic about when and how to use the technology (think first, then do). Students give careful consideration as to how marks may be allocated as partial credit for constructed responses in examinations.

4.1. Adapting Questions to Expanded Functionality

The consultants all remarked on the constantly expanding functionality of the devices. CAS can now give solutions to a greater range of question types and algebraic structures. As discussed below, this has been a matter for ongoing monitoring and consideration by examiners as they design questions. Additionally, as Consultant 2 noted,

“students have also been making increasing use of pre-prepared files on their device for use in tests and exams. Many students go into exams with files that serve as organised templates for carrying out the necessary computations for standard questions likely to be on the examination. Some students have additional pre-prepared files and programs for solving particular types of questions. For TI-Nspire users for example, the under-appreciated ‘Notes’ application is ideal for this purpose.”

Over two decades, the technical design of examination questions has been under constant review, to keep up with changes to functionality. The design of examination questions is motivated by three desires: to test mathematically important content, to encourage students to learn mathematics deeply, and to test equitably considering the several brands and models of devices that students can use. The policy in Victoria has always been to allow schools a choice from approved devices or software, rather than prescribing one brand or model that has to be used, but the capabilities of some of the functionalities of each vary, leapfrogging each other over time. In the early years of the initiative, the examination paper was vetted by experts on each approved technology to check that there was no overall advantage to users of any one technology. Consultant 4 expressed a strong conviction that this aspect of equity extends beyond examination questions to having all models of devices well represented in textbooks and teacher support materials, so that all students can be taught about the range of capabilities of their own device.

The consultants all commented that the types of questions in the examinations have remained broadly the same over two decades (as expected because most of the content of the subjects has not undergone major changes), but also that there are important differences. Before CAS, examinations could include only relatively simple functions with well-behaved coefficients suitable for by-hand calculation under the time restrictions of an examination. Now a wider range of functions and combinations of functions are used, and students can be asked to carry out a process (e.g., finding an area) for which they have not been taught a specific by-hand technique (e.g., integration by parts). As predicted in the preliminary studies in the 1990s ([4,20]), there is greater use of parameters replacing numerical coefficients and questions focussing on the effect of varying the values of the parameters. More questions require an expression as an answer, rather than a number. For example, multiple-choice Question 17 of the 2019 Mathematics Methods Examination 2 asked students to select the algebraic expression giving the probability of drawing two marbles of the same colour from a box of n marbles, of which k are red and the rest are green. The marks (and implicitly the time) allocated to a specific process (e.g., solving a matrix equation) have significantly reduced. As well as considering the hard-wired functionality in each CAS device, examiners have had to be aware of the ever-changing additional apps that students can upload to their devices (or perhaps only to certain brands or models). Some questions remaining may have limited mathematical value in the technology-assumed examination. For example, Consultant 3 cited a multiple-choice question (Mathematical Methods Examination 2, 2019) where students had to identify an expression equal to log_x(y) + log_z(y). It is possible (although slow) to do this by testing the two or three most likely expressions, asking for the truth value of the equality. Consultant 3 commented that questions like this now have limited mathematical purpose and have lost some of the opportunity to show the mathematical elegance and prowess that can be tested when CAS is not permitted (e.g., in Examination 1). Consultant 1, however, disagrees, observing that this question still has significant value. Students who are fluent in changing the base of logarithms will find the answer much quicker than others. This is one example of the many technical design decisions that confront those creating the examination questions.

Consultant 3 favorably identified that the greatest change that occurred in the Mathematics Methods examinations due to CAS use is that there are more questions that have a ‘problem-solving’ or an ‘explorative’ structure (e.g., 2016 MM Exam 2 Q4 and 2017 MM Exam 2 Q4). He noted that

“the inviting aspect of these questions is that they require a complete set-up of the question from development of the equation to solving via a CAS, providing a very efficient means for a solution”.

These questions require time to comprehend the solution pathway while also encouraging CAS use (slider options in some cases) to get a sense of the question and then a solution where few marks are allocated to questions. Examination papers a decade or more ago did not exhibit these. Consultant 3 also observed that the techniques of calculus now receive much less emphasis and feels that the mathematics behind the derivative is being lost. On the other hand, many questions now involve a deeper investigation of derivative-related mathematics; for example, questions about tangents and normals.

4.2. Increased Question Demand with CAS Access Assumed

Each of the consultants commented that the overall level of demand across multiple-choice and constructed response questions had increased with CAS assumed for Examination 2, due to the increased use of parameters and general forms, including the behavior of families of functions, their key features, properties and algebraic relationships involving these, and the capacity to handle a broader range of mathematical processes symbolically.

There are typically four or five constructed response questions in the Mathematical Methods Examination 2. Typically, there will be one or two questions (with sub-parts) involving modelling a real-world situation with a family of functions, one or two questions about a family of functions in a theoretical context, and a question involving modelling with the distributions of discrete and continuous random variables. In particular, the theoretical context questions, involving gradients and tangents, areas of regions, and intervals over which properties hold or not, were identified by the four consultants as being of increased demand since CAS has been assumed.

The 20 multiple-choice questions of Mathematical Methods Examination 2 have also evolved to involve more general and conceptual questions, with increased use of parameters in question formulation and/or answer alternatives and the use of general or unspecified functions. The following three multiple-choice questions from 2004, 2011 and 2012 provide an illustration of how the level of demand in a particular type of multiple-choice question has increased, as measured by percent of students correct. These questions are all based on a polynomial function of low degree, their graphs, intercepts, and stationary points. All the questions come from near the end of the multiple-choice section, so they could be expected to be reasonably difficult.

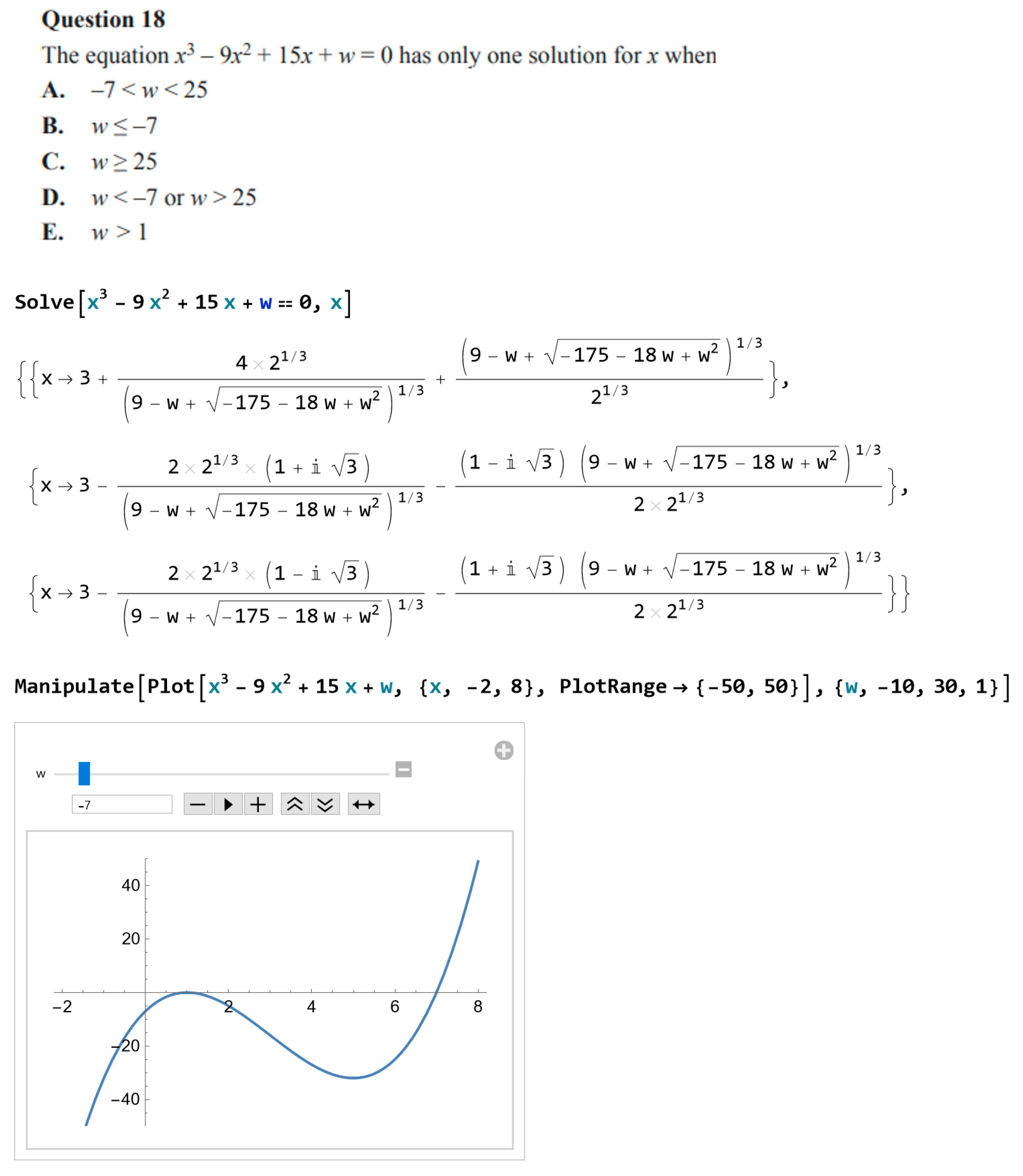
Question 18, from the 2004 Mathematical Methods Examination 1, shown in Figure 2, was answered correctly by 85% of students. It requires the identification of a feature of the graph of a function, at a particular location, with a completely specified rule. While it can be answered without any detailed calculation by drawing on a broad knowledge of the nature of graphs of this kind of function, it can also be readily answered identifying the relevant feature on a graph drawn by the graphics calculator.

For the CAS assumed examination in 2011, the most similar question (also numbered Question 18 so in a similar position in the examination) was answered correctly by only 52% of students. It presented an equation with an undetermined parameter (the constant term) as well as the variable, with no graph, and required finding an interval solution in terms of the parameter. Figure 3 shows the question, followed by CAS software output for solving the given equation, and then a screenshot of a graphics slider image showing the function for w = $-7$. A significant number of students entered the equation and tried to solve for x algebraically on CAS, likely as an automatic go-to strategy given the word ‘solution’. The hand-held TI and CASIO devices of the era got ‘stuck’, while CAS software such as Mathematica returned a complicated-looking explicit formula involving complex numbers. Of course, this was not useful for students of this intermediate level subject. Conceptually, given that the coefficient of x³ is positive, once it is identified that the function has turning points, there is only one correct form of inequality. Calculus could be used to identify the location of the turning points, with corresponding symbolic analysis carried out by hand or using CAS to define the function and carry out and interpret the relevant computations. Alternatively, a graphical approach could be taken. This was the first year that assessors and teachers noted some students tackled the problem by using a slider to animate the graph across the range for values for the parameter. Since then, sliders have become increasingly often used.

Question 16, from 2012 (see Figure 4), took this type of question one step further. It was answered correctly by only 34% of students. It specified only the general type of the function, information about the local maximum and local minimum with parameters for the constant term, no graph, and an interval solution required. The underlying conceptual analysis is the same, and it seems to be addressed very directly in the question, but explicit computational approaches such as those used in the previous questions were not available. The consultants all noted changes like these and expressed varying degrees of concern that the increased demand of questions requires careful consideration so that the intermediate subject does not become less suitable for the intended student cohort.

4.3. Increase in Variety of Approaches and Focus on Efficiency for Examinations

4.3.1. Increased Range of Methods Leading to a Deliberate Choice of Efficient Solutions

It is a long-standing observation that there is an ‘explosion of methods’ for solving problems when technology with multiple representations is available. For example, to find the maximum value of a function, a student might make a table of values, graph the function, and trace along it until the maximum value is reached; use a built-in app to find the maximum value; find where the derivative is zero by hand or by CAS and decide which of these gives the maximum value; or even use an algebraic form that reveals the maximum value through its structure. Further variation of the method arises from the choice to do each step with or without technology. There was an initial strong tendency for teachers to encourage students to use CAS like a calculator—providing step-by-step assistance to essentially unchanged by-hand work, or just to check answers [3,21]. This avoids an explosion of methods. On the other hand, other teachers reported that they almost immediately found great success when students shared various methods, with rich class discussion forging connections between previously isolated topics [3,22].

Consultant 3 observed that there is a strong emphasis given in class to choosing the most efficient CAS methods, especially to save as much time as possible in the examinations. To counteract the sense that CAS can do everything, he sees a growing need to encourage students to look for the best pathway to a solution (often best means the quickest), even if this does not involve CAS, and to look for alternative paths in case a preferred path becomes blocked. He cited a recent examination question where a set of simultaneous equations could be solved by hand quite simply through substitution. However, because of the algebraic form, the calculator solution (chosen by many students) sometimes took a very long time, and on some devices, it did not produce an output.

Some techniques to save time on examinations seem to have little intrinsic value outside of the examination room, but others are mathematically valuable. One mathematically valuable technique is defining functions, which supports an orientation to see a function as an object in its own right, not just as the rule that defines it. For example, in Question 4 in the Mathematical Methods Examination 2, 2021, a probability distribution function was given as a hybrid (piecewise defined) function, and students were asked to find the median and standard deviation. Students who separated the two rules of the hybrid function were less successful than those who began by defining f(x). From a pragmatic point of view, defining functions saves time and the students who did this could then spend more time on later parts of the question. From an epistemological point of view, there is a chance that it encourages students to see functions as mathematical objects. Screen shots of the CAS calculations are shown in Figure 5.

Another mathematically beneficial side effect of using CAS is that students must become more versatile in recognizing mathematical expressions in a variety of formats. Every computer algebra system has a slightly different protocol for how expressions are presented, and these will be different sometimes to the standard output from by-hand algorithms, or other brands of CAS devices. Consultant 4 noted this as a positive effect on students, even though many students find it initially disconcerting. A simple example is in Figure 6. Students learning by-hand algebraic division will calculate the first terms in the quotient as $3x+2$ with one fraction term, whereas the output from this CAS gives four terms in a different order: disconcerting initially for some students, but something they learn to manage. The alternatives offered in multiple-choice examination questions present the correct answer in ‘conventional’ mathematical forms (conventional at least in this educational system), which may differ from the output format of commonly used devices.

4.3.2. Changing Curriculum Content

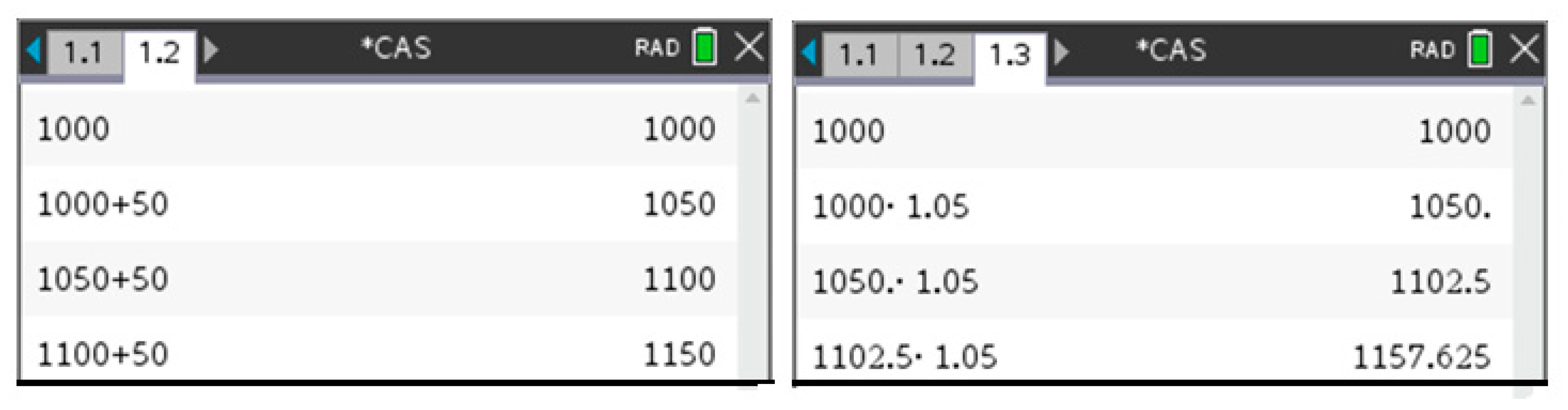
The availability of technology has also resulted in a change to some of the methods taught to students, as well as the approaches they use to solve examination questions. Technology often makes the more straightforward techniques viable. Financial mathematics in the elementary mathematics study design is now explicitly linked with recursion. Consultant 1, for example, explained how she uses recursion functionality to give students at that level a better feel for concepts such as simple and compound interest and the difference between them (see Figure 7). She has less focus on the formulas and encourages these students to use recursion for relevant examination questions.

4.4. CAS Technology as an Integrated Suite of Functionalities with a Display Interface

4.4.1. Increased Use for Visualiation by Students and Teachers

Scientific calculators assist with numerical computation only. However, from the earliest experiments with graphics calculators, teachers appreciated the potential of technology as a dynamic mathematics tool for visualization [22]. All the consultants noted that technology (both functionality and display) has improved over time and consequently the use of visualization has expanded. This expansion is by students exploring and solving problems, and also by teachers when developing students’ understanding of concepts. Sliders have been especially useful. Of course, not all teachers use this. Consultant 4, for example, commented that some teachers still choose to teach functions with the algebra and the graphing quite separate, perhaps especially if they do not have strong technology skills. Consultant 3 gave examples of

“considering the effect of changing the value of a parameter in an exam question, investigating specific and general cases in a modelling task or gaining a sound conceptual understating of the meaning of the average value of a function by manipulating an interactive file prepared by the teacher”.

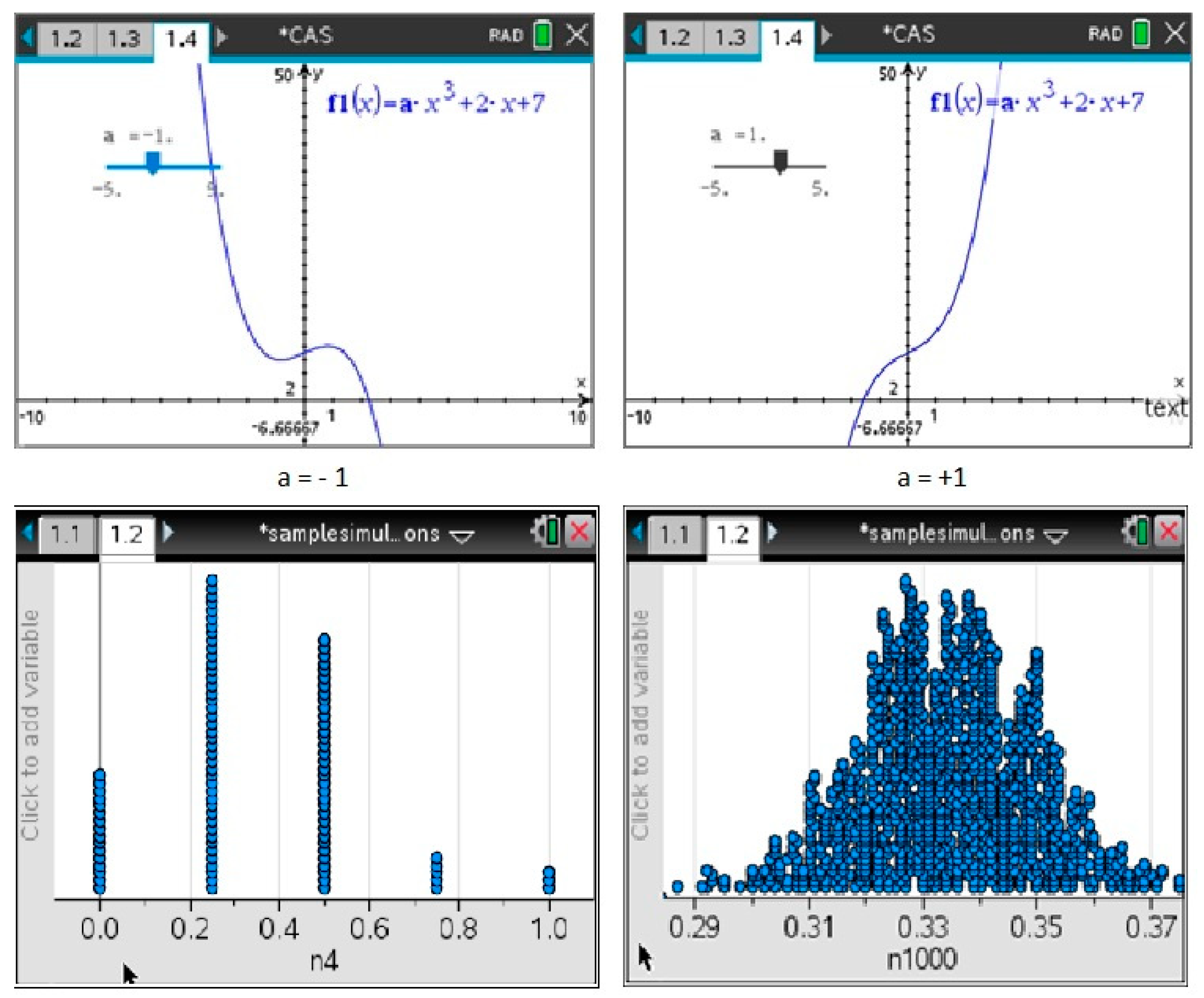
Figure 8 shows two examples used by Consultant 1 to get students to think and to become more engaged in the learning process. She commented that good classroom discussion is supported by the slider visualization on the top row, when she asks questions such as what changes when a changes, and why are there two stationary points when a is negative and none when a is positive. The second row shows two images in a series used to teach that; when the sample size is large, the sample proportion from a binomial distribution is approximately normal. Students can observe and discuss the differences in the distribution of the sample proportion starting with the left-hand screen showing data from 100 samples of size 4 and gradually increasing to end at the right-hand screen showing 1000 samples of size 1000.

Students were also reported using visualization to assist in solving problems, especially in the initial stages of understanding the problem. This is especially so for the tasks that are set in the school-based assessments, as these are more substantial than examination questions. However, Consultant 1 discussed a very difficult problem on a recent examination (only 2% of students received full marks). Using a slider to visualize the situation was a very helpful first step. She comments that it would be helpful if more students used such visualizations to support developing constructed responses in future examinations. Figure 9 gives the question statement and shows the relevant regions for three different values of a using the slider. For small values of a, the area can be found by integrating on the interval [0, a]. However, when a > 1, the area needs to be found in two parts. The calculator screen insert shows a composition of CAS commands first establishing that the area as a function of its endpoint at x = a, creating the equation that puts the integral equal to $\frac{1}{3}$, and then solving this equation for a as a single process. Many students would work this out in steps rather than by one composite command.

4.4.2. Improved Integrated Functionality

The consultants commented on how improved technology in recent years has changed their teaching. They especially liked the greatly improved display capabilities for use in class, and the easy compatibility between applications when making electronic notes. CAS software can create sophisticated CAS documents (notebooks) where text, graphics, and symbolic material can be readily integrated, and worked on by students. CAS software has been evolving these features for some time, while CAS calculators have developed complementary emulators and computer links. These documents can be readily shared, constructed to the style of the user, and employed as presentation tools. So rather than the CAS being a computational device that is separate from written notes, it has become the center of an integrated working environment. Presentation hardware and software has enabled mathematical working to be shared and displayed for all to see, promoting a common discourse. Consultant 4, for example, commented:

“I have my emulator projected onto the screen as part of my teaching using One-Note. I copy a snipped CAS screen onto the work I’m doing at the time so they can look back [at the notes]”.

Consultant 1 reported initial difficulties during the COVID19 pandemic, when schools used remote learning until she mastered sharing CAS and notes screens within the learning management system. However, the value of easily recording good electronic notes from lessons was boosted in this time. Two decades ago, CAS was principally thought of as a tool that could do algebra and calculus; it is now seen as general tool for both teachers and students to do mathematics.

5. Discussion and Conclusions

The section above has reported the main themes in the consultants’ responses, with discussion and additional commentary and examples from the authors on specific points. Taking a wider perspective on the responses of the consultants, we see that they were in broad agreement with each other about the changes, challenges, and advantages that the introduction of CAS has brought to senior mathematics. The lists of changes that they prepared individually had considerable overlap, with most of the major points made by each consultant also being made by one or two others. This gives us increased confidence that similar changes may have been noticed by a wide group of teachers, and that they do indeed arise from real changes in the examination questions and capabilities in technology rather than discourse in the community changing over time. A comprehensive survey is now warranted. When reviewing this article, the consultants (and authors) almost always agreed with the comments attributed to others. Opinions seemed to differ most on judgements of mathematical value at the technical level and about what mathematical practises encourage the best learning. We see this as productive tension among professionals.

A second general observation of the consultants’ responses is that they have all steadily adapted to the changing technological environment in schools, both the whole-school systems and specifically with CAS devices. In Figure 1, we grouped the 13 years from 2010 to 2022 in one ‘CAS assumed’ category. However, whilst there has been little change to strategic and tactical design, the consultants’ responses point to ongoing adjustments to technical design in teaching and assessment.

This paper has outlined a long-term initiative introducing mathematically-able technology into senior secondary school mathematics. Although the tool underpinning the change has been labelled as CAS, it is evident that ‘computer algebra’ is only one of the capabilities of the technology that have been transformational to teaching and learning. Other powerful capabilities are increased visualization for teaching and for solving problems, and multiple representations (algebraic, graphical, and numeric) supporting a variety of approaches for explaining concepts and for solving problems. An increasing range of ‘apps’, for example for statistics and financial mathematics, have changed the problems that students can investigate. What we call “CAS” is, in the terminology of Stacey and Wiliam, acting as both a computational infrastructure and a communications infrastructure [23].

The paper has focused on strategic and technical design of the initiative. At the strategic level, the success of the initiative was supported by a bi-partisan forward-looking political environment; a positive policy framework within the VCAA; strong links with research; and long-term practical support from across the Victorian mathematics community in schools and universities, professional associations, and technology companies. The work of the four consultants for this paper exemplifies these qualities. Whilst nearly all members of the Victorian mathematics community accepted that students should be well prepared for a world where mathematics is typically done in conjunction with technology, the initiative nevertheless challenged mathematical values and long-standing curriculum practices of both enthusiasts and skeptics, so it was essential to find a careful way forward. The strategic design of the initiative was a multi-step evolution, enabling modifications large and small to be implemented over time to achieve recognition of, and a balance between, previous and emerging values. Burkhardt drew attention to several features of strategic design such as incremental change, balancing ambition and realism, and the power of high-stakes assessment that were features of this initiative [5].

At the technical design level, changes in the examination questions provide a good window into the different mathematics experiences that students now have. The examples provided by the four consultants give an insight into the changes that teachers believe are most significant, for both teaching and learning. There seems to be good evidence that, especially with the intermediate subject, there is less emphasis on routine computation (as expected) and that there may be more emphasis on setting up a real-world problem mathematically with a technology-supported solution following (as hoped). It seems that many questions have become more general and abstract (for example asking about properties of functions that are unspecified or include parameters), and this is of concern to some teachers who feel the capacities of the student cohort are possibly being stretched too far. We recognize the tentative nature of the findings about change in this paper, because they arise from individual views of only six people, albeit very well informed. We consider that the conclusions provide important hypotheses that can be investigated with quantitative studies in the future.

Over the two decades, it has been a constant challenge to teachers and examiners to keep up with the changes to CAS technology. Although we call this a ‘mature implementation’ of the CAS initiative, it is likely that the pace of change in the mathematical capability, usability, and integration of technology will not slow down. The challenge of continuing to design; develop; and implement studies, subjects, and assessments that prepare students to use their mathematics beyond school in a rapidly changing technological environment remains.