1. Introduction
Linking different branches of mathematics has always been a very interesting way of approaching problems due to the tools provided by both sides. Some examples of linking differential geometry with graph theory can be found in [
1,
2], where the authors present a representation of vector spaces of even dimension and submanifolds with combinatorial structures. All of them have obtained nice results in their areas.
When we study a submanifold isometrically immersed in a Riemannian manifold
, it is very important to take into account its behaviour with respect to the second fundamental form. Many submanifolds presenting homogeneus behaviour in this sense have been defined: totally geodesic submanifolds, minimal submanifolds, totally umbilical submanifolds and so forth. Most of them have something in common, and they can be characterized by a certain combinatorial structure described in this paper. The idea of this combinatorial structure is influenced by [
3], where the author introduced a graphic representation of submanifolds in order to understand the behaviour of a submanifold with respect to the almost-complex structure.
In fact, we present a new method of submanifold representation by a combinatorial structure in order to understand the behaviour of the second fundamental form. This representation is closely related to a selected local frame field of tangent vector fields, and it depends on it. Thus, it will be more useful in the case of the existence of special local frame fields, for instance, when the ambient Riemannian manifold has an extra structure. On the other hand, sometimes, it is possible to obtain information about the submanifold by using the representation.
The paper is organized as follows. After a general preliminaries section, in which we recall some definitions and results for later use, in
Section 3, we define the new representation and present some examples in which we point out the dependence on the selected local frame field, and we see how to obtain information of the submanifold from such a representation. In
Section 4, we study some general results concerning this representation; specifically, we characterize totally umbilical submanifolds by using it. In
Section 5, we study a Lagrangian submanifold of Kaehler manifolds, in which there exists a distinguished local frame field, and we prove a pure differential geometry theorem (Theorem 3) from the obtained results. Finally, we show other utilities that the representation can have with a well-known example: the Clifford torus.
2. Preliminaries
In this section, we recall some general definitions and basic formulas which we will use later. For more background on the geometry of submanifolds, we recommend the references [
4,
5]. We will recall some more specific notions and results in the following sections, when needed.
From now on, let
M be an isometrically immersed
m-dimensional submanifold of a
n-dimensional Riemannian manifold
, and let us denote by ∇ and
their respective Levi–Civita connections. Then, the
second fundamental form(SFF) is defined as
where
are the extensions of
, respectively. From the
Gauss formula, given a local frame field
of tangent vector fields to
, where the first
m vector fields are tangent to
M and the last
ones are normal to
M, the SFF can be written as
where
. In addition, for each normal vector field to
M,
V, the
shape operator is the (1,1)-tensor field on
M such that
for any
.
From the behaviour of the SFF, some types of submanifolds can be defined. In this context, we would like to point out that a submanifold
M is called
totally geodesic if the SFF vanishes identically, and it is called
minimal if the
mean curvature vector field,
vanishes. Moreover, if for each normal vector field
, the eigenvalues of
,
, are invariant under multiplication by
, that is if
the submanifold is called
austere (see [
6] for more details concerning this type of submanifolds). Finally,
M is called
totally umbilical if
for any tangent vector fields
.
Next, suppose that is of even dimension. A (1,1)-tensor field J on M is called an almost-complex structure on M if, at every point x on M, J is an endomorphism of the tangent space such that . A manifold M with a fixed almost complex structure J is called an almost-complex manifold. A Hermitian metric on is a Riemannian metric g such that for any . An almost complex manifold with a Hermitian metric is called an almost-Hermitian manifold. An almost-Hermitian manifold is called a Kaehler manifold if its almost complex structure is normal (that is, its Nijenhuis tensor field vanishes) and .
A submanifold
M of an almost-Hermitian manifold
is called
totally real if
[
7]. Furthermore, if
, then
M is called a
Lagrangian submanifold. For a
m-dimensional Lagrangian submanifold
M in
, a local orthonormal frame field of tangent vector fields to
is called an
adapted Lagrangian frame field if
are tangent vector fields to
M and
are normal vector fields given by
,
.
3. A New Submanifold Representation
Let be a n-dimensional Riemannian manifold and M be an isometrically immersed m-dimensional submanifold. We now introduce a combinatorial representation procedure in order to understand the behaviour of the SFF of the immersion. We follow these steps:
Let us choose a local orthonormal frame of tangent vector fields to
,
such that
are tangent to
M and
are normal to
M.
We consider a vertex for every field of , labeled with its corresponding natural index.
For with and we have:
- (a)
If , we say that the edge exists if and only if .
- (b)
If , we say that the triangle exists if and only if .
We assign to every edge the weight given by and on every triangle the weight given by .
Finally, notice that we obtain additional visual information by putting the vertices corresponding to tangent fields at an imaginary bottom line and those which correspond to normal fields at a top line.
We are going to use this method with the following examples. For them, let M be a surface isometrically immersed in a Riemannian 4-dimensional manifold .
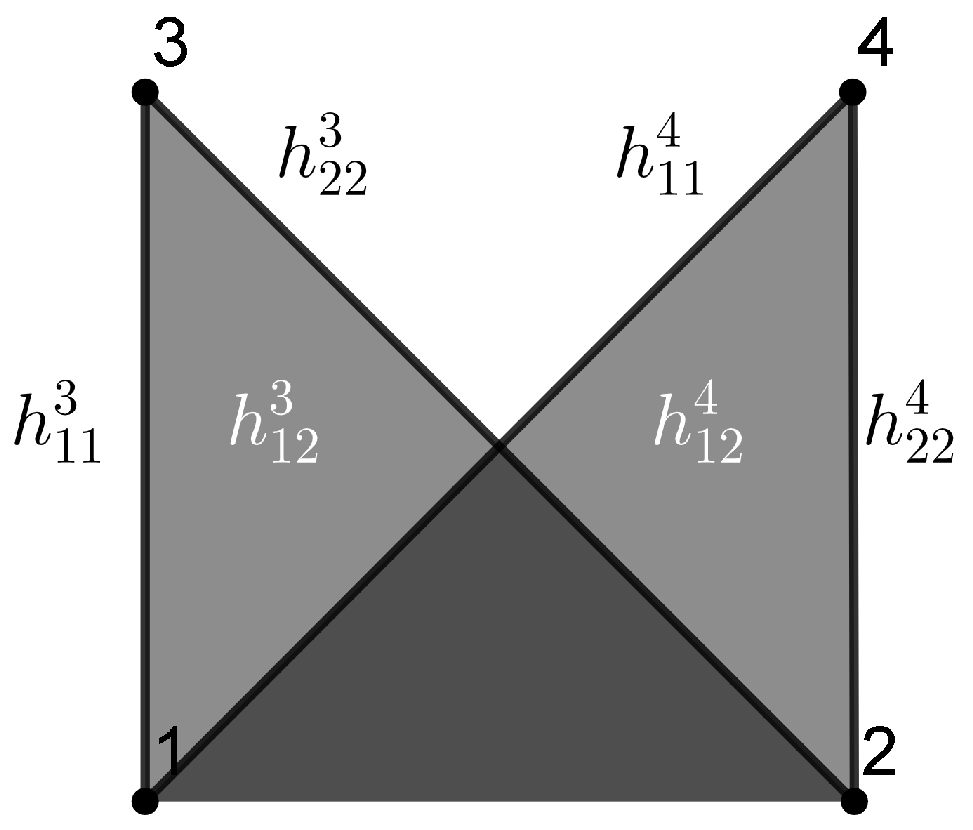
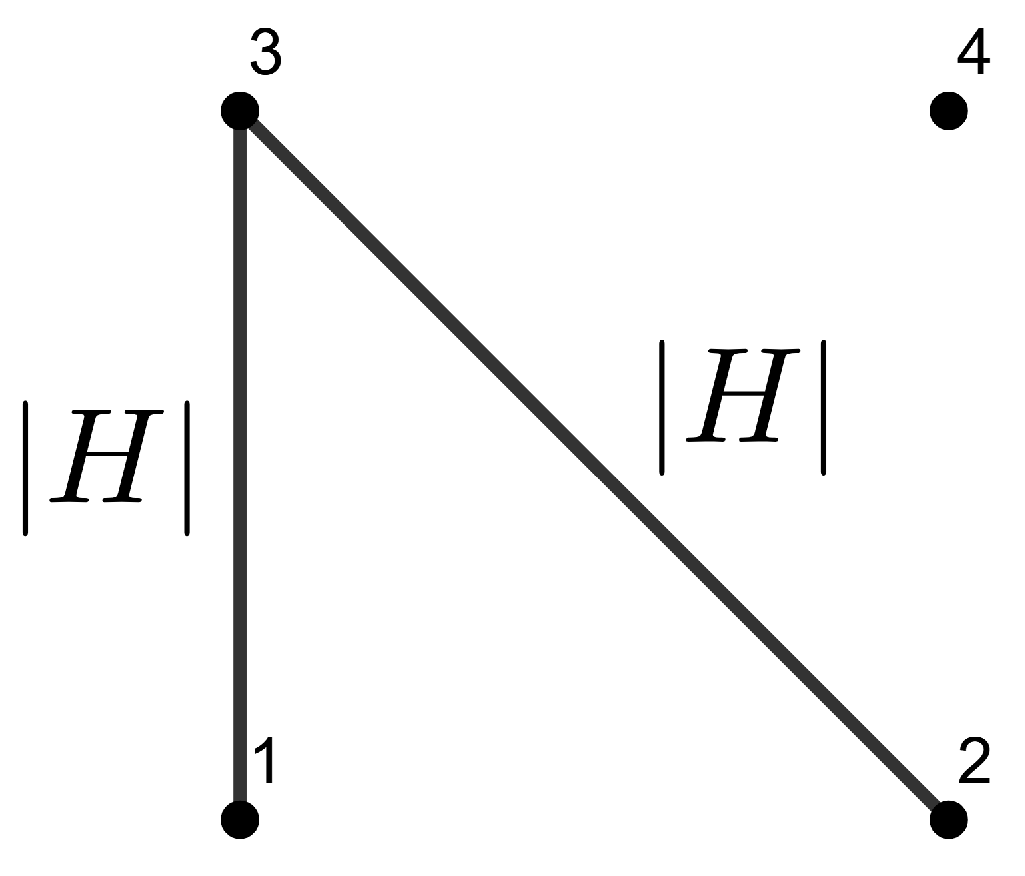
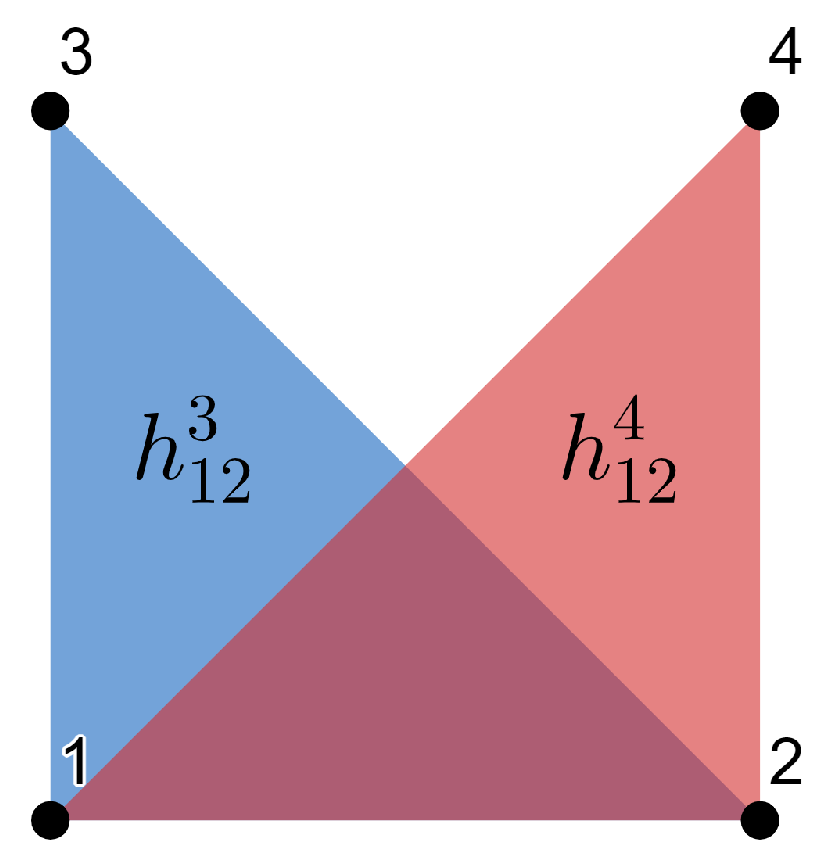
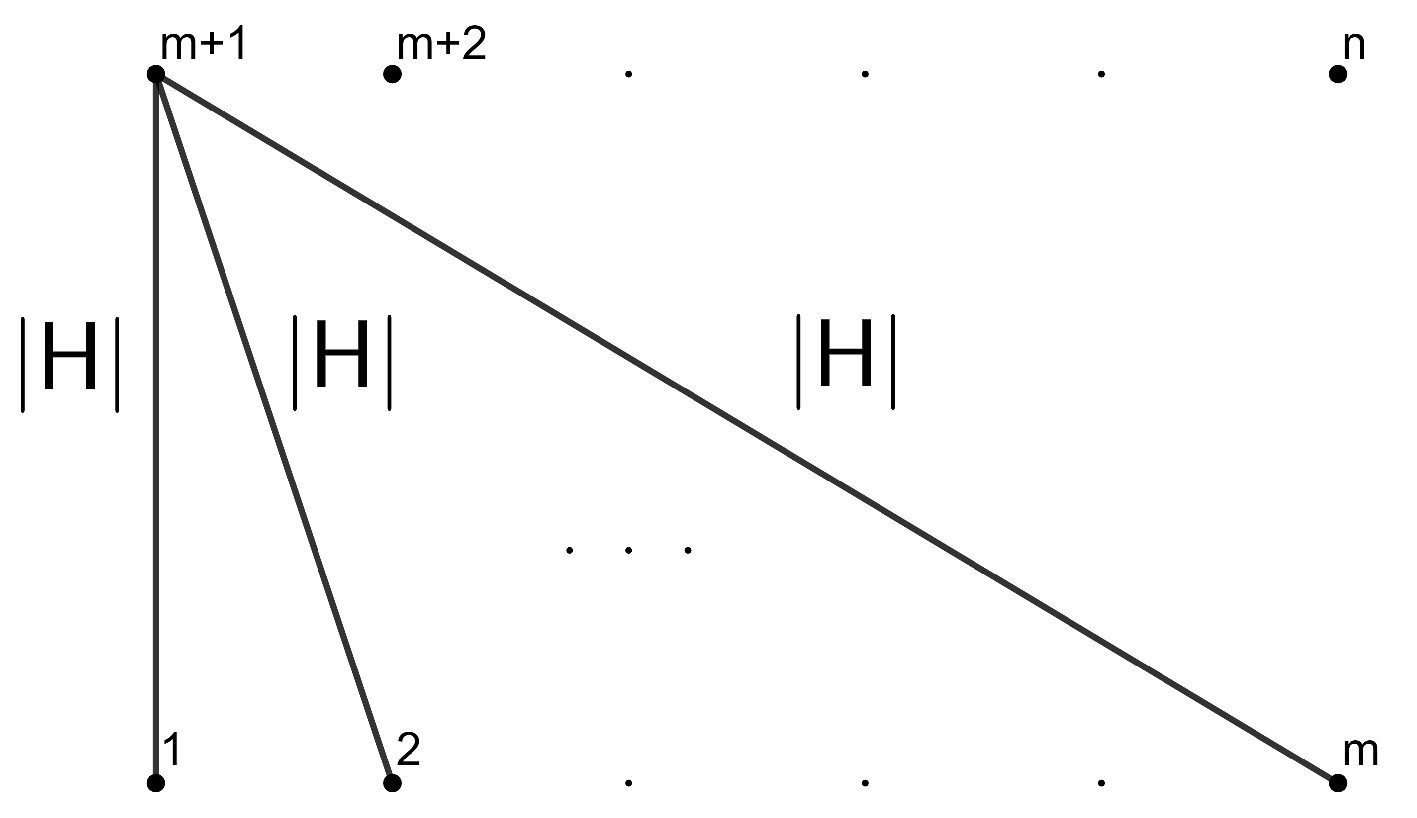
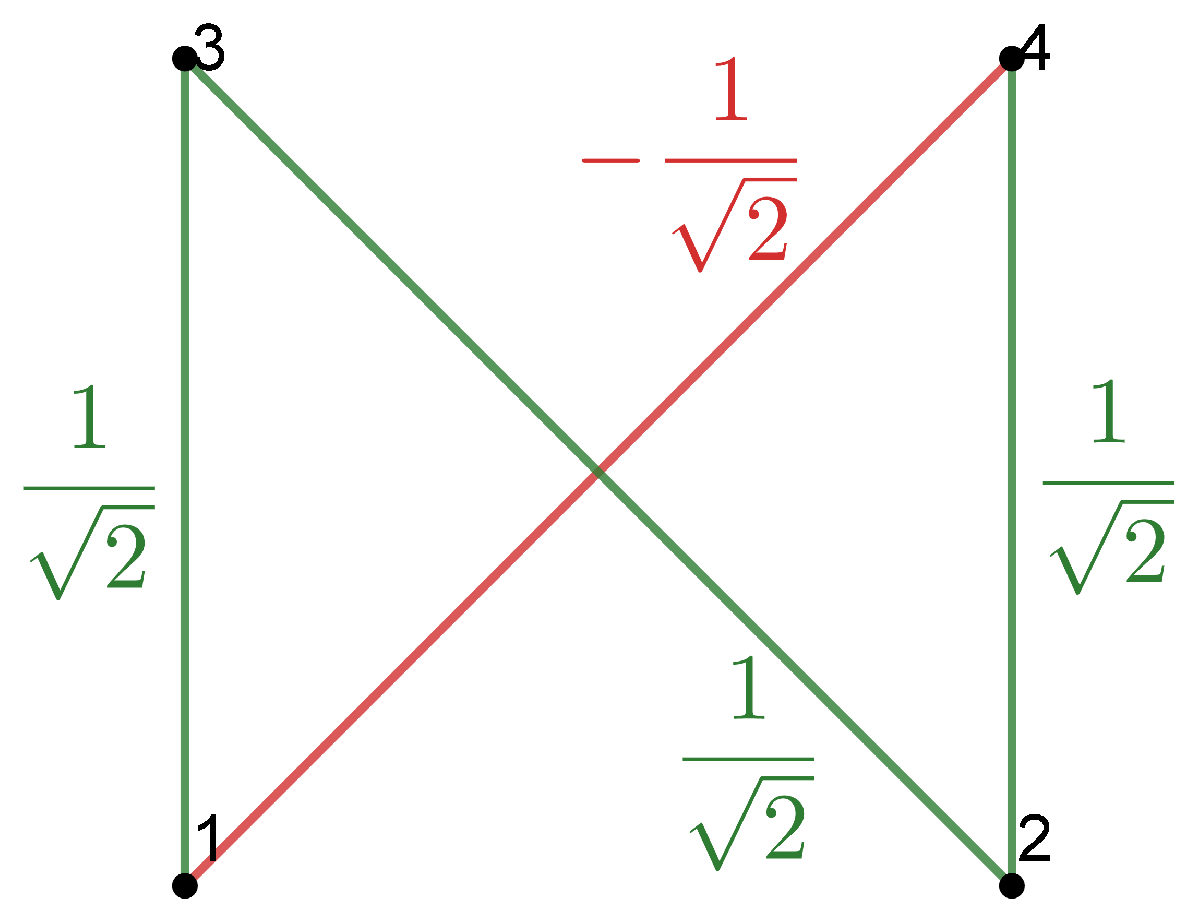
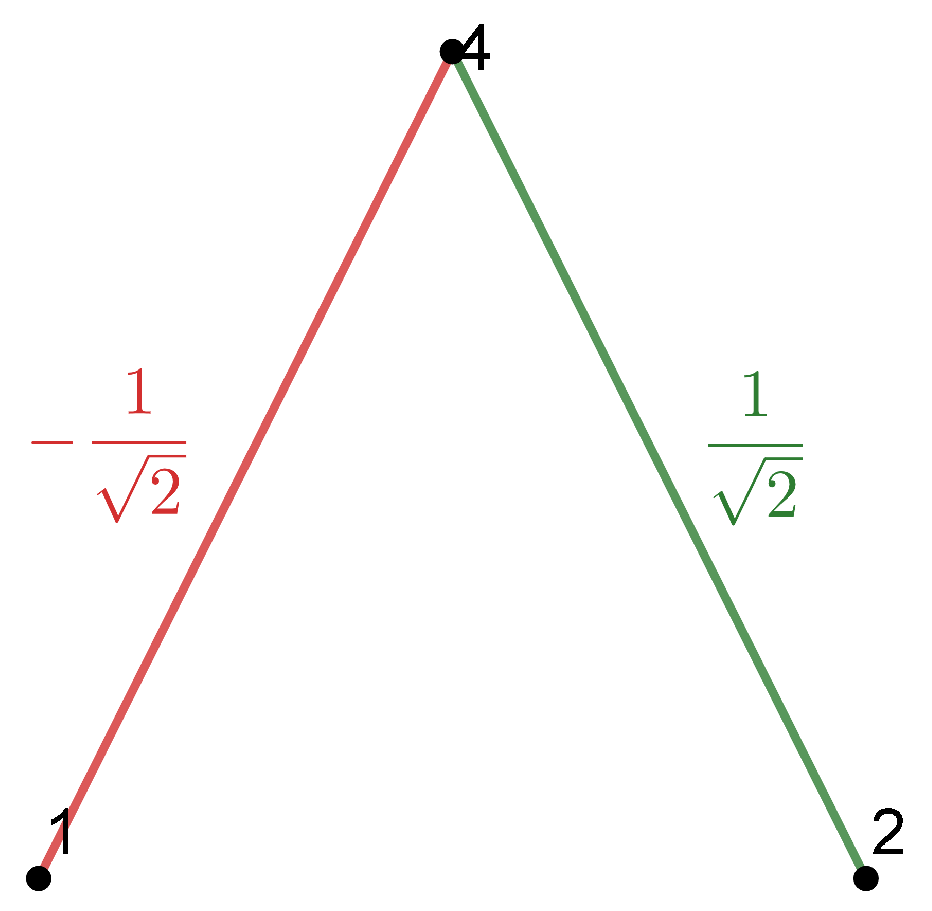
Example 1. Consider a local orthonormal frame , such that are tangent to M and are normal to M. Then we can write the SFF asand we obtain the combinatorial visualization shown in Figure 1. Example 2. Suppose that M is a totally umbilical surface with a non-zero mean curvature H. Then, we can fix the local orthonormal framesuch that are tangent to M and is normal to the other fields. Then, the SFF results inand we obtain the combinatorial visualization shown in Figure 2. Example 3. As above, suppose that M is a totally umbilical surface with a non-zero mean curvature H and consider the local orthonormal frame Then, we obtain the representation drawn in Figure 3 (we use a color code for edges and triangles of the same weight). Remark 1. Examples 2 and 3 show that the representation depends on the chosen local orthonormal frames.
However, this representation allows us to consider the inverse procedure to obtain information concerning the submanifold.
Example 4. Let M again be a surface immersed in a 4-dimensional Riemannian manifold with a local orthonormal frame whose representation can be visualized in Figure 4. In a simple view, we note the absence of edges, which impliesthus, the mean curvature vector field vanishes, and M is a minimal submanifold. 4. General Results
In this section we are going to present some results to point out the utility of this new representation on a general Riemannian manifold.
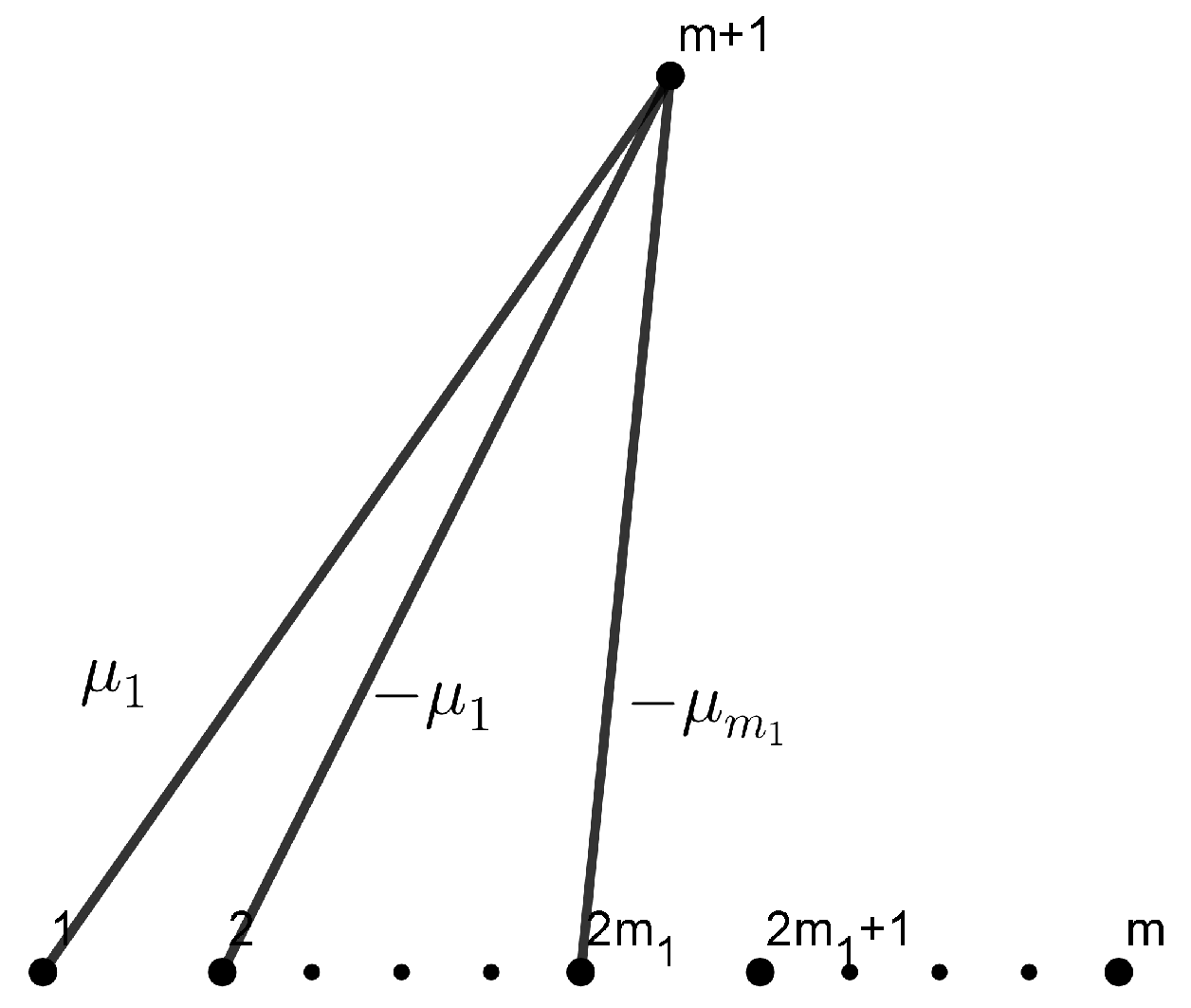
Proposition 1. Let M be a hypersurface isometrically immersed in a -dimensional Riemannian manifold . Then, there exists a local frame field of tangent vector fields to whose representation is that of Figure 5, where denote the eigenvalues of the shape operator . Proof. Let
be a local frame field where
are tangent to
M and
is normal to
M. One of the properties of the shape operator
is that its induced matrix is symmetric. Therefore, by the spectral theorem of symmetric matrices, we know that there exists a local orthonormal frame field
of eigenvectors of
, whose eigenvalues are
, respectively. Then, we obtain the diagonal matrix
Therefore, with respect to the local frame field
, we obtain
We conclude that
, and the representation is that of
Figure 5. □
Corollary 1. A hypersurface M isometrically immersed in a -dimensional Riemannian manifold is an austere submanifold if and only if there exists an orthonormal frame field of tangent vector fields to such that is normal to M and whose representation is Figure 6, where are the non-zero eigenvalues of the shape operator . Theorem 1. The representation of a totally umbilical submanifold with respect to any orthonormal frame field has no triangles.
Proof. Let
M be a
m-dimensional totally umbilical submanifold isometrically immersed in a
n-dimensional Riemannian manifold
, with
H being the mean curvature vector. Consider an orthonormal frame field of the tangent vector field to
,
, such that the first
m vector fields are tangent to
M. Then, it is clear that:
In particular, if , then so for any . Consequently, the representation has no triangles. □
Theorem 2. A (non-minimal) submanifold M isometrically immersed in a Riemannian manifold is totally umbilical if and only if there exists a local orthonormal frame of tangent vector fields to , whose representation is shown in Figure 7. Proof. Firstly, if the submanifold is totally umbilical, consider an orthonormal frame field of the tangent vector field to , such that the first m vector fields are tangent to M and .
Then, from (
1), we easily obtain:
Conversely, suppose that there exists a local orthonormal frame field of the tangent vector field to
,
such that the first
m vector fields are tangent to
M and whose representation is given in
Figure 7.
Then, for such a representation, we get:
Consequently,
. Then, from (
2) and since
is the local orthonormal frame field:
Consequently, by using the linearity of fundamental forms, the submanifold is totally umbilical. □
Proposition 2. A submanifold M is minimal if and only if there exists a frame field whose representation satisfies that the weights of the incident edges of each vertex associated to the normal fields of M add up to zero.
Proof. Let us suppose that
M is minimal. Then, we have:
Therefore, for every . Thus, we conclude the proof of the proposition. □
Corollary 2. If, for a local frame field, the representation only has triangles, the represented submanifold is minimal.
5. Lagrangian Submanifolds of Kaehler Manifolds
In this section, let
be a
-dimensional Kaehler manifold and consider a Lagrangian submanifold
M isometrically immersed in
. Let
be an adapted Lagrangian frame field [
4],
where
is a local frame field for tangent vector fields to
M. We say that the representation obtained by using this adapted Lagrangian frame field is a
Lagrangian representation of M.
Lemma 1. Every Lagrangian representation of a submanifold M of a Kaehler manifold satisfies thatfor any . Proof. Given
, we have
due to the properties of the Kaehler ambient manifold and the anti-symmetry of the almost complex structure
J. By using the symmetry of the SFF, we obtain
which implies (
3). □
Corollary 3. Let M be a Lagrangian submanifold of a Kaehler manifold. If a Lagrangian representation of M has no triangles, then is non-zero if and only if .
Proof. Let us suppose that there exists an edge with . Therefore, from Lemma 1, , which is a contradiction because the representation has no triangles.
The other implication is analogous. □
Theorem 3. Let M be a m-dimensional () Lagrangian and totally umbilical submanifold of a Kaehler manifold. Then, M is minimal.
Proof. Suppose that
M is not minimal; that is, that the mean curvature vector
H is not zero. Let
be an adapted Lagrangian frame field of
M. We now have:
Therefore, , and due to Lemma 1, . However, we know that , which is a contradiction. We conclude that is a minimal submanifold. □
Corollary 4. Any m-dimensional () Lagrangian and totally umbilical submanifold of a Kaehler manifold is totally geodesic.
6. Example: The Clifford Torus
The Clifford torus is a special type of torus with
inside
. It actually lies in the unit sphere
because each point has the same distance to the origin. Then, it is well known that the Clifford torus with the Euclidean metric is an austere submanifold of
[
8]. We are going to reach this conclusion by using this new representation.
Consider
, given by:
The mapping
f is an immersion of
into the unit sphere
, where the image
is the flat torus. The vector fields
form an orthonormal basis of the tangent space
, and the normal vectors
form an orthonormal basis of the normal space. The matrices
and
with respect to the basis
are:
Therefore, the second fundamental form is given by:
In this context, the submanifold representation is presented in
Figure 8 and
Figure 9 (in the representation, we also include a color code to clarify the edges and triangles of the same weight).
We observe that the
Figure 9 is an austere submanifold of
in virtue of Corollary 1.