A Lindley-Type Distribution for Modeling High-Kurtosis Data
Abstract
:1. Introduction
2. ESL Distribution
2.1. Stochastic Representation
- The ESL pdf exhibits a unimodal shape when is equal to 0.5 (see top panels) and a monotonic decreasing shape when is equal to 5 (see bottom panels).
- If and are fixed (see left panels), it is observed that the unimodal and monotonic shapes of the pdf are preserved with each choice of . In this case, the different values of define a set of pdfs with different weights in the tails. The closer to 0 the value of is, the heavier the tail of the ESL pdf.
- For fixed values of and (see right panels), something similar is observed. The unimodal and monotonic shapes of the pdf are preserved even when the parameter varies. Here, different values for also define a set of pdf’s with different weights in the tails. The larger the value of , the heavier the tail of the ESL pdf.
2.2. Reliability Analysis
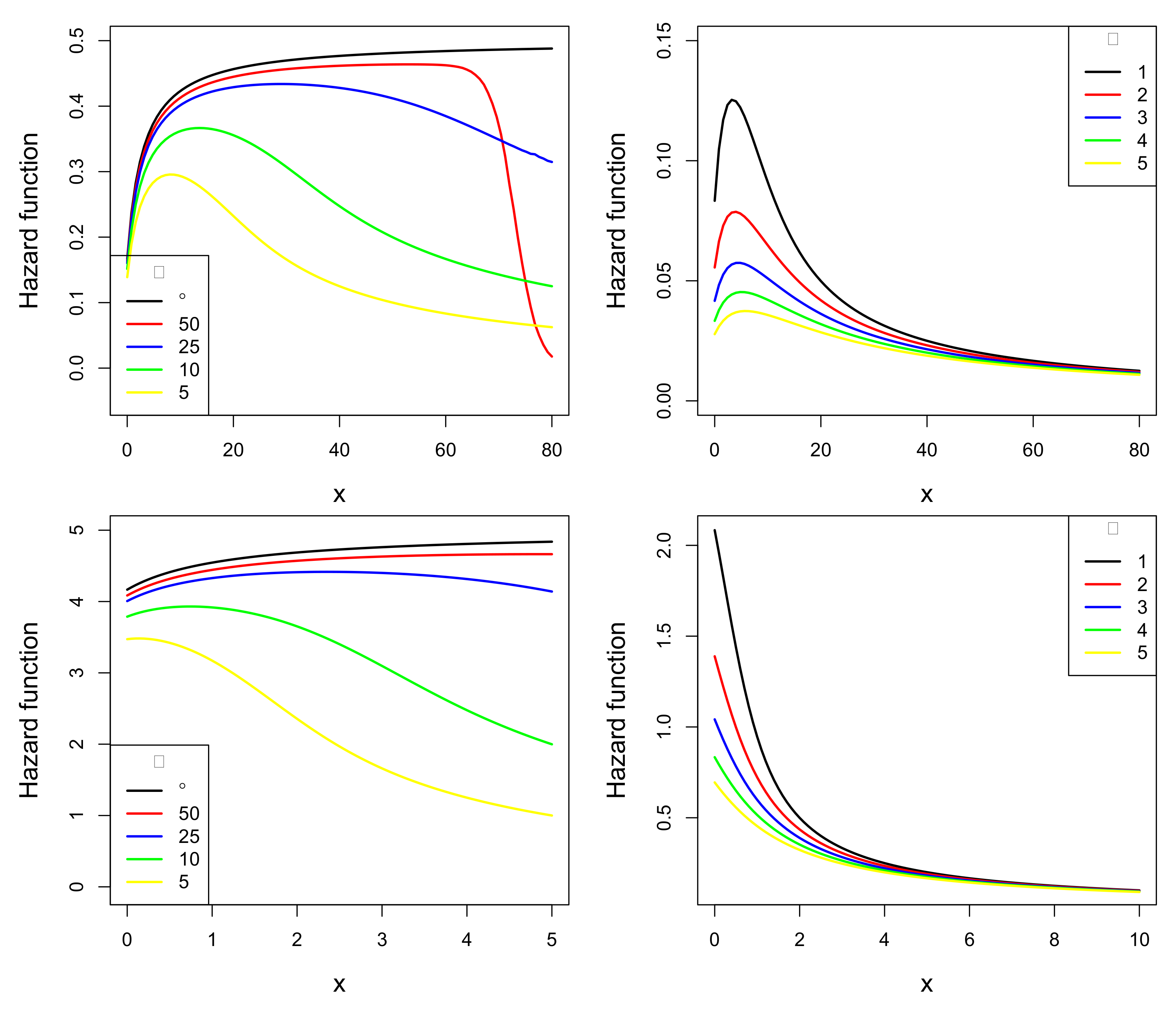
- The ESL hrf can present unimodal or monotonic decreasing shapes.
- In the left panels (), the unimodal shape of the hrf of the ESL distribution approaches the increasing shape of the hrf of the L distribution when assumes a sufficiently large value.
- In the right panels, it is observed that the hrf of the ESL distribution is unimodal when and decreasing when . It is also observed that the unimodal or increasing forms are preserved for the different choices of the parameters and . Thus, the unimodal and monotonic decreasing shape seems to depend on .
2.3. Moments and Related Measurements
3. Parameter Estimation
3.1. Moment Estimation
3.2. Maximum Likelihood Estimation
3.3. Practical Considerations
- The L distribution can be obtained as a limit case of the two-parameter ESL distribution once as .
- Taking into account the kurtosis of the ESL distribution increases as grows, the two-parameter ESL distribution has very heavy tails since as .
- In the choice , the number 100 allows us to obtain a high value for when assumes a value considered small. For example, we get when . Thus, the representation of the ESL random variable given in Proposition (1) assumes a Beta distribution for the variable U in the denominator, thus defining a distribution with extremely heavy tails.
3.4. Simulation Study
- We choose the values 0.5 and 2 for the parameter and the values 3, 4 and 5 for the parameter . In this way, we establish three scenarios where the pdf of the ESL distribution is unimodal (when ) and three other scenarios where the pdf is decreasing (when ).
- Under the consideration of the choices above, we generate 1000 pseudo-random samples of size , 200, 300, 400 and 500 from the two-parameter ESL distribution. Samples are generated as follows:
- (a)
- Generate Y having a L distribution.
- Generate .
- Generate .
- Generate .
- Compute .
- (b)
- Generate X having a ESL distribution.
- Generate .
- Compute .
Step (a) is based on the results proposed by Ghitany et al. [3] for the L distribution, while step (b) is based on the representation of the ESL random variable given in Definition 1. An R code is provided in Appendix A.
- For each sample generated, we obtain the ML estimates by maximizing Equation (9) using the optim function of the R programming language.
4. Real Data Analysis
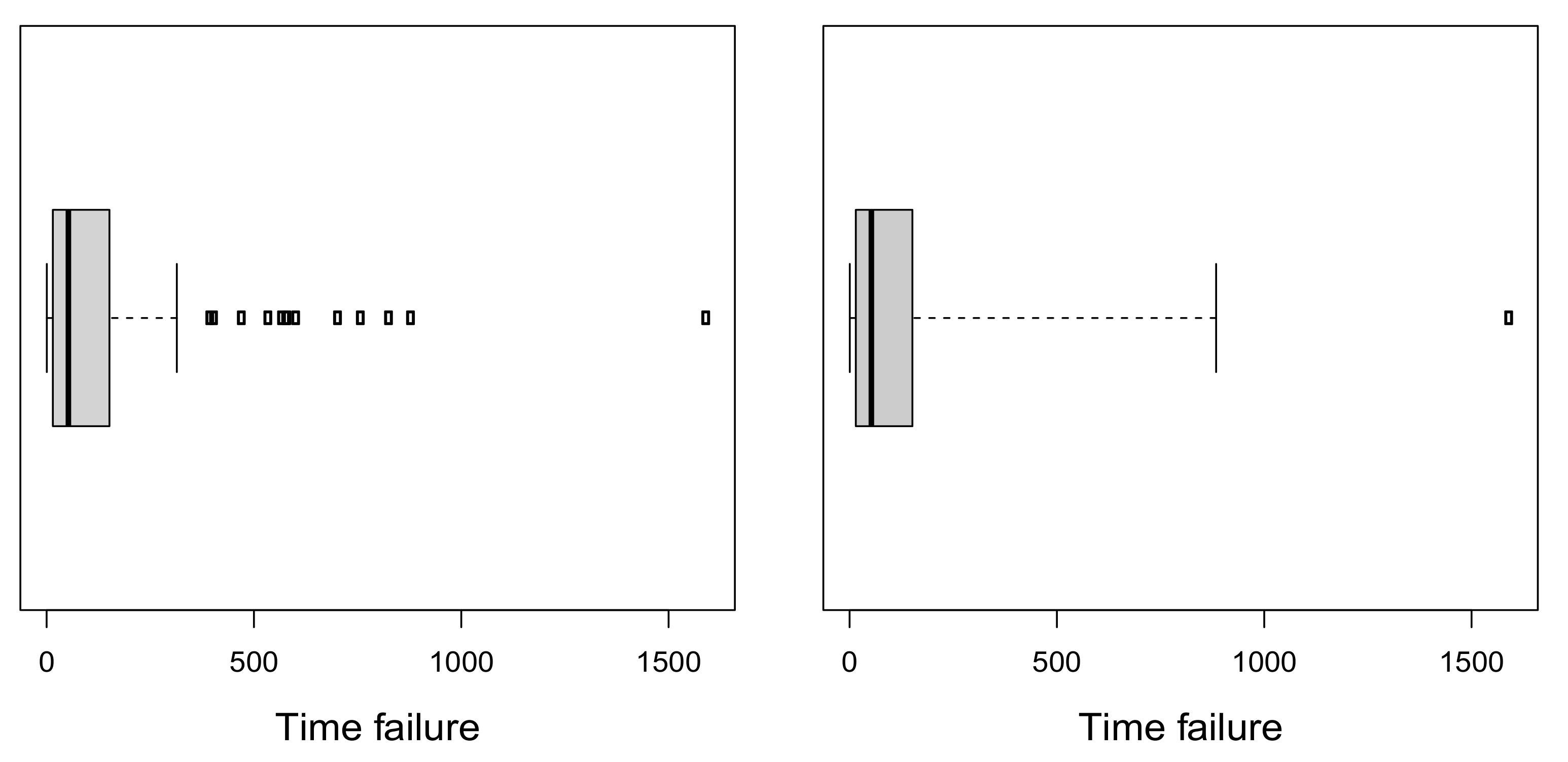
4.1. Time Failures Related to Pascal Programming
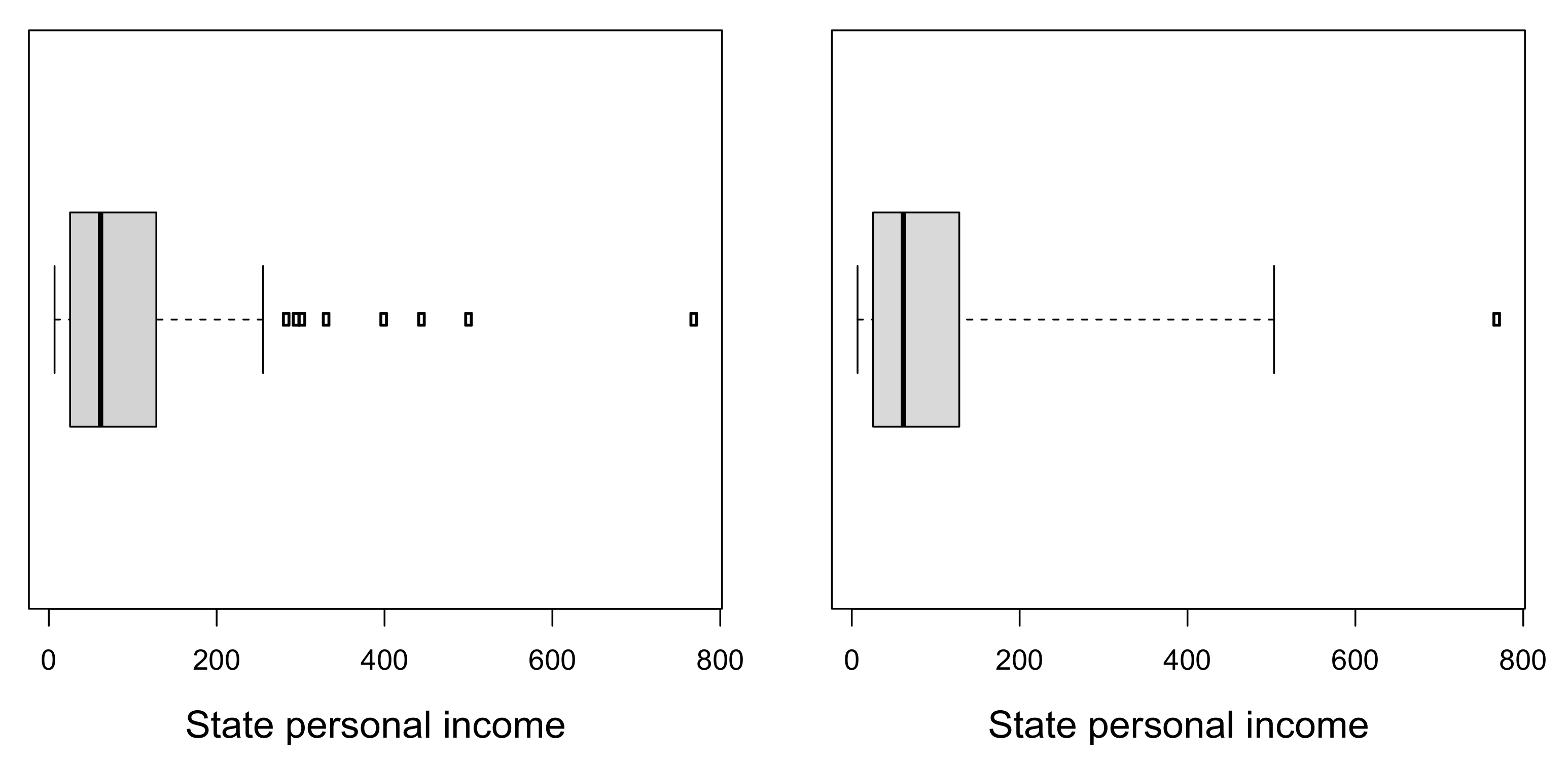
4.2. State Personal Income Data
5. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| L | Lindley |
| LS | Lindley Slash |
| ESL | Extended Slash Lindley |
| PL | Power Lindley |
| ML | Maximum Likelihood |
| probability density function | |
| cdf | cumulative distribution function |
| rf | reliability function |
| hrf | hazard rate function |
Appendix A
Appendix A.1. First Option for the Computation of the ESL pdf
Appendix A.2. Second Option for the Computation of the ESL pdf
Appendix A.3. First Option for the Computation of the ESL cdf
Appendix A.4. Second Option for the Computation of the ESL cdf
Appendix A.5. Code to Generate a Pseudorandom Sample from the ESL Distribution
Appendix B
| 10.293195 | 11.577261 | 12.243384 | 12.448607 | 14.229156 | 14.454129 |
| 14.575292 | 14.581495 | 15.767469 | 16.296835 | 17.258916 | 18.237436 |
| 19.462380 | 20.852964 | 21.778072 | 22.868920 | 23.786644 | 25.045934 |
| 25.678534 | 26.210736 | 28.649564 | 31.716160 | 32.611268 | 34.784360 |
| 36.205164 | 36.293064 | 37.278220 | 37.902896 | 38.536176 | 39.377292 |
| 42.703144 | 43.395580 | 43.956936 | 45.995496 | 46.014968 | 46.241956 |
| 49.466672 | 53.431900 | 56.626672 | 57.749668 | 60.063368 | 60.170928 |
| 63.152360 | 63.333300 | 64.846548 | 65.732720 | 69.341920 | 71.209312 |
| 71.751616 | 72.050072 | 74.079712 | 74.851664 | 78.364336 | 79.104656 |
| 83.903280 | 84.572688 | 87.361632 | 88.870496 | 92.946544 | 98.328688 |
| 104.315120 | 113.216856 | 114.259984 | 115.959680 | 117.639672 | 126.525008 |
| 129.680832 | 133.549208 | 133.728040 | 135.115456 | 153.455776 | 157.633568 |
| 159.800448 | 161.441792 | 166.919248 | 170.033840 | 170.051568 | 176.786352 |
| 231.003152 | 231.594240 | 233.208576 | 255.312928 | 285.923232 | 297.728512 |
| 304.767456 | 333.525344 | 402.096768 | 447.102816 | 503.163328 | 771.470144 |
References
- Lindley, D.V. Fiducial distributions and Bayes’ theorem. J. R. Stat. Soc. 1958, 20, 102–107. [Google Scholar] [CrossRef]
- Lindley, D.V. Introduction to Probability and Statistics from a Bayesian Viewpoint, Part 2, Inference; Cambridge University Press: New York, NY, USA, 1965. [Google Scholar]
- Ghitany, M.E.; Atieh, B.; Nadarajah, S. Lindley distribution and its application. Math. Comput. Simul. 2008, 78, 493–506. [Google Scholar] [CrossRef]
- Ghitany, M.E.; Alqallaf, F.; Al-Mutairi, D.K.; Husain, H.A. A two-parameter weighted Lindley distribution and its applications to survival data. Math. Comput. Simul. 2011, 81, 1190–1201. [Google Scholar] [CrossRef]
- Nadarajah, S.; Bakouch, H.S.; Tahmasbi, R. A generalized Lindley distribution. Sankhya B 2011, 73, 331–359. [Google Scholar] [CrossRef]
- Ghitany, M.E.; Al-Mutairi, D.K.; Balakrishnan, N.; Al-Enezi, L.J. Power Lindley distribution and associated inference. Comput. Stat. Data. Anal. 2013, 64, 20–33. [Google Scholar] [CrossRef]
- Shanker, R.; Mishra, A. A quasi Lindley distribution. Afr. J. Math. Comput. Sci. Res. 2013, 6, 64–71. [Google Scholar]
- Shanker, R.; Sharma, S.; Shanker, R. A two-parameter Lindley distribution for modeling waiting and survival times data. Appl. Math. 2013, 4, 363–368. [Google Scholar] [CrossRef] [Green Version]
- Shanker, R.; Kamlesh, K.K.; Fesshaye, H. A two parameter Lindley distribution: Its properties and applications. Biostat. Biom. Open Access J. 2017, 1, 85–90. [Google Scholar]
- Zakerzadeh, H.; Dolati, A. Generalized Lindley distribution. J. Math. Ext. 2009, 3, 13–25. [Google Scholar]
- Shanker, R.; Shukla, K.K.; Shanker, R.; Tekie, A.L. A three-parameter Lindley distribution. Am. J. Math. Stat. 2017, 7, 15–26. [Google Scholar]
- Ekhosuehi, N.; Opone, F. A three parameter generalized Lindley distribution: Properties and application. Statistica 2018, 78, 233–249. [Google Scholar]
- Gui, W. Statistical properties and applications of the Lindley slash distribution. J. Appl. Statist. Sci. 2012, 20, 283. [Google Scholar]
- Iriarte, Y.A.; Rojas, M.A. Slashed power-Lindley distribution. Commun. Stat.-Theory Methods 2019, 48, 1709–1720. [Google Scholar] [CrossRef]
- Gómez, H.W.; Quintana, F.A.; Torres, F.J. A new family of slash-distributions with elliptical contours. Stat. Probab. Lett. 2007, 77, 717–725. [Google Scholar] [CrossRef]
- Gui, W. A generalization of the slash half normal distribution: Properties and inferences. J. Stat. Theory Pract. 2014, 8, 283–296. [Google Scholar] [CrossRef]
- Iriarte, Y.A.; Gómez, H.W.; Varela, H.; Bolfarine, H. Slashed Rayleigh distribution. Rev. Colomb. Estad. 2015, 38, 31–44. [Google Scholar] [CrossRef]
- Iriarte, Y.A.; Varela, H.; Gómez, H.J.; Gómez, H.W. A gamma-type distribution with applications. Symmetry 2020, 12, 870. [Google Scholar] [CrossRef]
- Gómez, H.J.; Gallardo, D.I.; Santoro, K.I. Slash truncation positive normal distribution and its estimation based on the EM algorithm. Symmetry 2021, 13, 2164. [Google Scholar] [CrossRef]
- Reyes, J.; Barranco-Chamorro, I.; Gallardo, D.I.; Gómez, H.W. Generalized modified slash Birnbaum-Saunders distribution. Symmetry 2018, 10, 724. [Google Scholar] [CrossRef] [Green Version]
- Rojas, M.A.; Bolfarine, H.; Gómez, H.W. An extension of the slash-elliptical distribution. SORT 2014, 38, 215–230. [Google Scholar]
- Johnson, N.L.; Kotz, S.; Balakrishnan, N. Continuous Univariate Distributions, 2nd ed.; John Wile & Sons: Hoboken, NJ, USA, 1995; Volume 2, ISBN 0-471-58494-0. [Google Scholar]
- Andrews, L.C. Special Functions of Mathematics for Engineers, 2nd ed.; SPIE—The International Society for Optical Engineering: Bellingham, WA, USA, 1998. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021. [Google Scholar]
- Diethelm, W.; Tobias, S. fAsianOptions: Rmetrics-EBM and Asian Option Valuation; R Package Version 3042.82; R Foundation for Statistical Computing: Vienna, Austria, 2017. [Google Scholar]
- Byrd, R.H.; Lu, P.; Nocedal, J.; Zhu, C. A limited memory algorithm for bound constrained optimization. SIAM J. Sci. Comput. 1995, 16, 1190–1208. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Automat. Contr. 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Chen, G.; Balakrishnan, N. A general purpose approximate goodness-of-fit test. J. Qual. Technol. 1995, 27, 154–161. [Google Scholar] [CrossRef]
- Hubert, M.; Vandervieren, E. An adjusted boxplot for skewed distributions. Comput. Stat. Data. Anal. 2008, 52, 5186–5201. [Google Scholar] [CrossRef]
- Maechler, M.; Rousseeuw, P.; Croux, C.; Todorov, V.; Ruckstuhl, A.; Salibian-Barrera, M.; Verbeke, T.; Koller, M.; Conceicao, E.L.T.; di Palma, M.A. Robustbase: Basic Robust Statistics; R Package Version 0.95-0; R Foundation for Statistical Computing: Vienna, Austria, 2022. [Google Scholar]
- Lyu, M.R. Handbook of Software Reliability Engineering; IEEE Computer Society Press: Los Alamitos, CA, USA, 1996. [Google Scholar]
- Astorga, J.M.; Iriarte, Y.A.; Gómez, H.W.; Bolfarine, H. Modified slashed generalized exponential distribution. Commun. Stat.-Theory Methods. 2020, 49, 4603–4617. [Google Scholar] [CrossRef]
- Stock, J.H.; Watson, M.W. Introduction to Econometrics, 2nd ed.; Addison Wesley: Boston, MA, USA, 2007. [Google Scholar]




| Parameter | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AE | SD | AB | AE | SD | AB | AE | SD | AB | AE | SD | AB | ||
| 0.5 | 3 | 0.351 | 0.147 | −0.149 | 3.965 | 1.103 | 0.965 | 0.495 | 0.189 | −0.005 | 3.250 | 0.771 | 0.250 |
| 4 | 0.413 | 0.190 | −0.087 | 5.035 | 1.602 | 1.035 | 0.506 | 0.201 | 0.006 | 4.354 | 1.206 | 0.354 | |
| 5 | 0.451 | 0.216 | −0.049 | 6.197 | 2.301 | 1.197 | 0.515 | 0.220 | 0.015 | 5.490 | 1.676 | 0.490 | |
| 2 | 3 | 1.370 | 0.556 | −0.630 | 4.041 | 1.123 | 1.041 | 2.110 | 0.897 | 0.110 | 3.299 | 0.895 | 0.299 |
| 4 | 1.662 | 0.835 | −0.338 | 5.213 | 1.897 | 1.213 | 2.210 | 1.236 | 0.210 | 4.422 | 1.564 | 0.422 | |
| 5 | 1.829 | 0.976 | −0.171 | 6.420 | 2.691 | 1.420 | 2.229 | 1.321 | 0.229 | 5.686 | 2.496 | 0.686 | |
| 0.5 | 3 | 0.381 | 0.128 | −0.119 | 3.637 | 0.681 | 0.637 | 0.499 | 0.134 | −0.001 | 3.113 | 0.482 | 0.113 |
| 4 | 0.438 | 0.167 | −0.062 | 4.623 | 1.025 | 0.623 | 0.501 | 0.138 | 0.001 | 4.160 | 0.736 | 0.160 | |
| 5 | 0.465 | 0.172 | −0.035 | 5.687 | 1.409 | 0.687 | 0.505 | 0.149 | 0.005 | 5.261 | 1.100 | 0.261 | |
| 2 | 3 | 1.508 | 0.526 | −0.492 | 3.699 | 0.756 | 0.699 | 2.043 | 0.688 | 0.043 | 3.131 | 0.595 | 0.131 |
| 4 | 1.778 | 0.744 | −0.222 | 4.684 | 1.160 | 0.684 | 2.070 | 0.755 | 0.070 | 4.207 | 0.940 | 0.207 | |
| 5 | 1.885 | 0.837 | −0.115 | 5.840 | 1.771 | 0.840 | 2.084 | 0.795 | 0.084 | 5.382 | 1.550 | 0.382 | |
| 0.5 | 3 | 0.396 | 0.121 | −0.104 | 3.521 | 0.576 | 0.521 | 0.499 | 0.108 | −0.001 | 3.079 | 0.383 | 0.079 |
| 4 | 0.460 | 0.166 | −0.040 | 4.432 | 0.821 | 0.432 | 0.501 | 0.116 | 0.001 | 4.077 | 0.581 | 0.077 | |
| 5 | 0.478 | 0.157 | −0.022 | 5.467 | 1.105 | 0.467 | 0.504 | 0.115 | 0.004 | 5.160 | 0.814 | 0.160 | |
| 2 | 3 | 1.603 | 0.512 | −0.397 | 3.529 | 0.632 | 0.329 | 2.024 | 0.549 | 0.024 | 3.089 | 0.479 | 0.089 |
| 4 | 1.836 | 0.678 | −0.164 | 4.488 | 0.919 | 0.488 | 2.063 | 0.625 | 0.063 | 4.098 | 0.743 | 0.098 | |
| 5 | 1.910 | 0.749 | −0.090 | 5.581 | 1.270 | 0.581 | 2.075 | 0.667 | 0.075 | 5.213 | 1.118 | 0.213 | |
| 0.5 | 3 | 0.410 | 0.114 | −0.090 | 3.424 | 0.508 | 0.424 | 0.500 | 0.095 | 0.000 | 3.045 | 0.329 | 0.045 |
| 4 | 0.460 | 0.144 | −0.040 | 4.378 | 0.730 | 0.378 | 0.501 | 0.095 | 0.001 | 4.078 | 0.481 | 0.078 | |
| 5 | 0.483 | 0.153 | −0.017 | 5.359 | 0.946 | 0.359 | 0.502 | 0.104 | 0.002 | 5.112 | 0.699 | 0.112 | |
| 2 | 3 | 1.653 | 0.486 | −0.347 | 3.451 | 0.563 | 0.451 | 2.017 | 0.478 | 0.017 | 3.053 | 0.412 | 0.053 |
| 4 | 1.858 | 0.652 | −0.142 | 4.406 | 0.794 | 0.406 | 2.030 | 0.516 | 0.030 | 4.083 | 0.625 | 0.083 | |
| 5 | 1.911 | 0.643 | −0.089 | 5.470 | 1.042 | 0.470 | 2.033 | 0.524 | 0.033 | 5.170 | 0.875 | 0.170 | |
| 0.5 | 3 | 0.418 | 0.112 | −0.082 | 3.384 | 0.477 | 0.384 | 0.500 | 0.088 | 0.000 | 3.024 | 0.293 | 0.024 |
| 4 | 0.468 | 0.142 | −0.032 | 4.334 | 0.716 | 0.334 | 0.500 | 0.091 | 0.000 | 4.012 | 0.473 | 0.012 | |
| 5 | 0.492 | 0.138 | −0.008 | 5.251 | 0.849 | 0.251 | 0.501 | 0.090 | 0.001 | 5.050 | 0.605 | 0.050 | |
| 2 | 3 | 1.663 | 0.464 | −0.337 | 3.434 | 0.520 | 0.434 | 2.015 | 0.426 | 0.015 | 3.051 | 0.364 | 0.051 |
| 4 | 1.869 | 0.601 | −0.131 | 4.361 | 0.742 | 0.361 | 2.028 | 0.472 | 0.028 | 4.080 | 0.572 | 0.080 | |
| 5 | 1.962 | 0.637 | −0.038 | 5.349 | 0.964 | 0.349 | 2.031 | 0.463 | 0.031 | 5.122 | 0.776 | 0.122 | |
| Parameter | L | PL | LS | ESL |
|---|---|---|---|---|
| - | - | - | ||
| () | ||||
| 0.013 | 0.215 | 1.819 | ||
| (0.001) | (0.034) | () | (0.004) | |
| - | 0.480 | 0.799 | 1.284 | |
| (0.030) | 0.148 | (0.003) | ||
| ℓ | −703.450 | −600.236 | −602.341 | −599.780 |
| AIC | 1408.900 | 1204.472 | 1210.683 | 1203.561 |
| BIC | 1411.545 | 1209.761 | 1218.616 | 1208.850 |
| W | 0.353 | 0.160 | 0.119 | 0.084 |
| A | 2.087 | 0.978 | 0.808 | 0.566 |
| Parameter | L | PL | LS | ESL |
|---|---|---|---|---|
| - | - | - | ||
| () | ||||
| 0.019 | 0.083 | 682.380 | 0.312 | |
| (0.001) | (0.019) | 192.712 | (0.089) | |
| - | 0.705 | 2.614 | 3.033 | |
| (0.046) | 1.147 | (0.484) | ||
| ℓ | −553.170 | −536.240 | −536.596 | −534.902 |
| AIC | 1108.341 | 1076.480 | 1079.193 | 1073.804 |
| BIC | 1110.906 | 1081.609 | 1086.886 | 1078.933 |
| 0.140 | 0.084 | 0.074 | 0.051 | |
| 1.003 | 0.653 | 0.579 | 0.432 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rojas, M.A.; Iriarte, Y.A. A Lindley-Type Distribution for Modeling High-Kurtosis Data. Mathematics 2022, 10, 2240. https://doi.org/10.3390/math10132240
Rojas MA, Iriarte YA. A Lindley-Type Distribution for Modeling High-Kurtosis Data. Mathematics. 2022; 10(13):2240. https://doi.org/10.3390/math10132240
Chicago/Turabian StyleRojas, Mario A., and Yuri A. Iriarte. 2022. "A Lindley-Type Distribution for Modeling High-Kurtosis Data" Mathematics 10, no. 13: 2240. https://doi.org/10.3390/math10132240
APA StyleRojas, M. A., & Iriarte, Y. A. (2022). A Lindley-Type Distribution for Modeling High-Kurtosis Data. Mathematics, 10(13), 2240. https://doi.org/10.3390/math10132240






