Abstract
The combination of two elements in a group structure is an element, while, in a hypergroup, the combination of two elements is a non-empty set. The use of hypergroups appears mainly in certain subclasses. For instance, polygroups, which are a special subcategory of hypergroups, are used in many branches of mathematics and basic sciences. On the other hand, in a multi-fuzzy set, an element of a universal set may occur more than once with possibly the same or different membership values. A soft set over a universal set is a mapping from parameters to the family of subsets of the universal set. If we substitute the set of all fuzzy subsets of the universal set instead of crisp subsets, then we obtain fuzzy soft sets. Similarly, multi-fuzzy soft sets can be obtained. In this paper, we combine the multi-fuzzy soft set and polygroup structure, from which we obtain a new soft structure called the multi-fuzzy soft polygroup. We analyze the relation between multi-fuzzy soft sets and polygroups. Some algebraic properties of fuzzy soft polygroups and soft polygroups are extended to multi-fuzzy soft polygroups. Some new operations on a multi-fuzzy soft set are defined. In addition to this, we investigate normal multi-fuzzy soft polygroups and present some of their algebraic properties.
MSC:
20N20; 20N25; 08A72
1. Introduction
The concept of a hyperstructure was first introduced by Marty [1], at the 8th Congress of Scandinavian Mathematicians in 1934, when he defined hypergroups and started to analyze their properties. Indeed, the notion of hypergroups is a generalization of groups. Let H be a non-empty set and ∘ be a function (hyperoperation) from to the family of non-empty subsets of H. Then, is a hypergroup, if ∘ is associative and , for all . The hypergroup is a very general structure. Some researchers considered hypergroups with additional axioms. One of the axioms is the transposition axiom. This axiom is considered by Prenowitz [2,3,4], and then Jantosciak introduced the notion of transposition hypergroups [5]. A transposition hypergroup that has a scalar identity is called a quasicanonical hypergroup [6,7] or polygroup [8,9,10,11]. One can consider the quasicanonical hypergroups as a generalization of canonical hypergroups, introduced in [12]. Examples of polygroups, such as double set algebras, Prenowitz algebras, conjugacy class polygroups and character polygroups, can be found in [11]. This book contains the principal definitions, illustrated with examples and basic results of the theory. The category of polygroups is a category between the category of groups and transposition hypergroups; see Figure 1. More precisely, each group is a polygroup, and each polygroup is a transposition hypergroup. Recently, in [13], an excellent review of the several types of hypergroups was presented. Interesting results can be also found in [14]. The theory of algebraic hyperstructures has become a well-established branch in algebraic theory and it has extensive applications in many branches of mathematics and applied sciences; see [15,16,17,18,19].
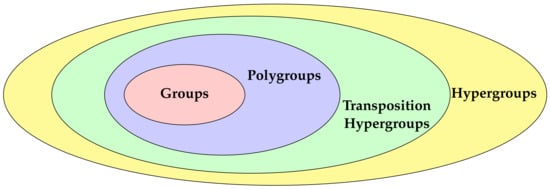
Figure 1.
Each group is a polygroup, each polygroup is a transposition hypergroup, and each transposition hypergroup is a hypergroup.
The theory of fuzzy sets proposed by Zadeh [20] has achieved great success in many fields. Many researchers have applied the theory of fuzzy sets to hyperstructures. Firstly, Zahedi [21] discussed the subject of polygroups and fuzzy subpolygroups, and then Davvaz [22] presented the fuzzy subhypergroup concept, which is a generalization of Rosenfeld’s fuzzy subgroup [23]. There are many articles dealing with the link between fuzzy sets and hyperstructures; see [24,25,26].
Soft set theory, introduced by Molodtsov [27], has been considered as an effective mathematical tool for modeling uncertainties. After Molodsov’s work, different applications of soft sets were investigated in [28,29]. The idea of a fuzzy soft set, which is more general than fuzzy sets and soft sets, was first introduced by Maji et al. [30], and the algebraic properties of this concept were examined. Both of these theories have been applied to algebraic structures and algebraic hyperstructures—for instance, see [31,32].
Sebastian et al. in [33] proposed the concept of the multi-fuzzy set, which is a more general fuzzy set using ordinary fuzzy sets as building blocks; its membership function is an ordered sequence of ordinary fuzzy membership functions. Later, Yang et al. [34] introduced the concept of the multi-fuzzy soft set, which is a combination of the multi-fuzzy set and soft set, and studied its basic operations. They also introduced the application of this concept in decision making. In recent years, multi-fuzzy sets have become a subject of great interest to researchers and have been widely applied to algebraic structures. Some researchers—for instance, Onasanya and Hoskova-Mayerova [35]—studied the concept of multi-fuzzy groups, while Hoskova-Mayerova et al. [36] studied fuzzy multi-hypergroups and also fuzzy multi-polygroups in [37]. Akın [38] studied the concept of multi-fuzzy soft groups as a generalization of fuzzy soft groups, and Kazancı et al. [39] introduced a novel soft hyperstructure called the multi-fuzzy soft hyperstructure and investigated the notion of multi-fuzzy soft hypermodules and some of their structural properties on a hypermodule.
In a multi-fuzzy set, an element of a universal set U may occur more than once with possibly the same or different membership values. For example, if , then the set is a multi-fuzzy set. A soft set over a universe U is a mapping F from parameters to . For example, let be a set of apartments under consideration, and be a set of parameters such that beautiful, expensive, a good view, and near to the city center. If , , and , then is a soft set. If we substitute the set of all fuzzy subsets of U instead of crisp subsets of U, then we obtain fuzzy soft sets. Similarly, we can define multi-fuzzy soft sets.
In this paper, we combine three separated concepts: polygroups (or quasicanonical hypergroups), soft sets and multi-fuzzy sets (as a generalization of fuzzy sets). Previously, the authors have worked only on the one of these subjects or at most two of them. Indeed, we combine the multi-fuzzy soft set and polygroup structure, from which we obtain a new soft structure called the multi-fuzzy soft polygroup. The relation between the generalization of polygroups is indicated in Figure 2. To facilitate our discussion, we first review some basic concepts of the soft set, fuzzy soft set, multi-fuzzy set and polygroup in Section 2. In Section 3, we apply these to the notion of multi-fuzzy soft sets and polygroups and introduce multi-fuzzy soft polygroups. Then, we study some of their structural characterizations in Section 4 and Section 5. Finally, we give the concept of a normal multi-fuzzy soft polygroup and discuss some of their structural characteristics. Finally, some conclusions are pointed out in Section 6.
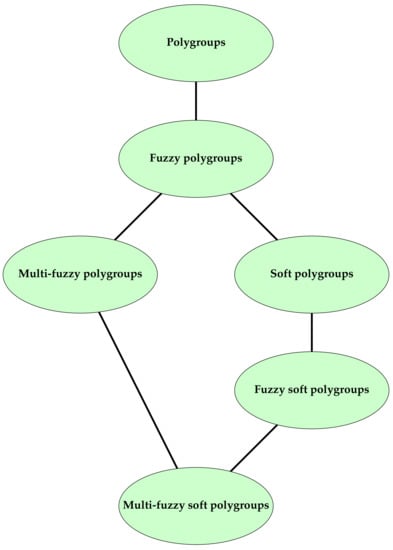
Figure 2.
The relation between generalizations of polygroups.
2. Preliminaries
In this section, we provide some definitions and results of soft set theory that will help in understanding the content of the article [27,28,31,32,40]. Let denote the power set of U, where U is an initial universe set, E is a set of parameters and .
Definition 1
([27]). Let and be a set-valued function. Then, the pair is called a soft set over U. For all and R stand for an arbitrary binary relation between an element of A and an element of U—that is, . In fact, a soft set over U is a parameterized family of subsets of the universe U.
Definition 2
([30,31]). Let and be a mapping. Then, the pair is called a fuzzy soft set over U, where is the collection of all fuzzy subsets of U. That is, for each , is a fuzzy set on U.
Definition 3
([33]). A multi-fuzzy set (MF-set) in U is a set of ordered sequences
The function is said to be the multi membership function of denoted by , and k is called dimension of . The set of all MF-sets of dimension k in U is denoted by .
It is obvious that the one-dimensional MF-set is Zadeh’s fuzzy set, and Atanassov’s intuotionistic fuzzy set is a two-dimensional MF-set with .
Definition 4
([33]). Let . If , then is said to be the null MF-set, defined by . If , then is said to be the absolute MF-set, denoted by .
Definition 5
([33]). Let
Then
- (i)
- if and only if , i.e , and .
- (ii)
- if and only if , i.e , and .
- (iii)
- . That is .
- (iv)
- . That is .
Definition 6
([34]). Let . Then, we call a pair a multi-fuzzy soft set (MFS-set) of dimension k over U. That is, for every , . Here, may be considered a set of a-approximate elements of the multi-fuzzy soft set for .
Let . Denote the set of all MFS-sets of dimension k over U by
Definition 7
([34]). Let and . Then, if and only if and for all .
Definition 8
([34]). Let . Then, is said to be a null MFS-set, denoted by , if for all .
Definition 9
([34]). Let .
- (i)
- The -intersection is defined as , where , for all .
- (ii)
- The -union is defined as , where , for all .
- (iii)
- The union is defined as , where and for all if , if and if .
Definition 10.
Let .
- (i)
- The restricted intersection of and is the MFS-set with where , and for all , . The situation is denoted by .
- (ii)
- The extended intersection of and is the MFS-set , where and for all , if , if and if . In this case, we write .
Definition 11.
Let H be a non-empty set and let be the set of all non-empty subsets of H. A hyperoperation on H is a map and the pair is called a hypergroupoid.
Definition 12
([11,21]). A multi-valued system is called a polygroup where if the following axioms hold for all in P.
- (i)
- ,
- (ii)
- ,
- (iii)
- implies and .
The following elementary properties follow from the axioms:
where .
Let P be a polygroup and K a non-empty subset of P; then, K is called a subpolygroup of P if and is a polygroup.
A subhypergroup N of a hypergroup is normal if [5]. According to [7], a quasicanonical subhypergroup N of a quasicanonical hypergroup H is called normal if and only if it is a member of an appreciated quotient system of H by some congruence relation.
Example 1.
Suppose that H is a subgroup of a group G. Define a system , where and
The algebra of double cosets is a polygroup introduced in (Dresher and Ore [41]).
Example 2.
Consider and define ∘ on P by the following table:
| ∘ | 0 | 1 | 2 | a | b |
| 0 | 0 | 1 | 2 | a | b |
| 1 | 1 | {0,2} | {1,2} | a | b |
| 2 | 2 | {1,2} | {0,1} | a | b |
| a | a | a | a | {0,1,2,b} | {a,b} |
| b | b | b | b | {a,b} | {0,1,2,a} |
Then, P is a canonical hypergroup. Suppose that is the symmetric group on a set with three elements. We consider
with the usual hyperoperation
for all . Then, is a non-commutative polygroup or quasicanonical hypergroup.
3. Multi-Fuzzy Soft Polygroups
The concept of the MF-set was introduced by Sebastian et al. in [33]. By combining the MF-set and soft set, Yang et al. introduced the concept of the MFS-set [34]. Both of these theories have been applied to algebraic structures. At this point, we give a new type of polygroup named the multi-fuzzy soft polygroup (MFS-polygroup). Since the concepts of uncertainty and fuzziness can be better expressed with MFS-sets, their applications in hyperalgebraic structures are extremely important. Thus, in this section, we provide a new connection between the polygroup structure and MFS-set.
Definition 13.
Let P be a polygroup and . Then, is said to be an MFS-polygroup of dimension k over P if and only if, for all and ,
- (i)
- ,
- (ii)
- .
That is, for each , is a multi-fuzzy subpolygroup.
The first condition requires that the polygroup is closed under multi-fuzzy soft hyperoperation ∘ and the second condition is a generalization of the inverse element under ∘.
To better understand this new algebraic structure, consider the following examples.
Example 3.
Let be a polygroup with the Cayley table:
| ∘ | e | a | b | c |
| e | e | a | b | c |
| a | a | a | {e,a,b,c} | c |
| b | b | {e,a,b} | b | {b,c} |
| c | c | {a,c} | c | {e,a,b,c} |
Let be the set of parameters.
Consider the MF-set defined as follows. as follows.
Then, is not an MFS-polygroup of dimension 3 over P since
Example 4.
Consider the polygroup given in Example 3 and define the MF-set as follows.
Then, for all , is an MF-subpolygroup of P. By Definition 13, is an MFS-polygroup of dimension 3 over P.
Example 5.
Consider the polygroup given in Example 3 and define the MF-set as follows.
Then, it is clear to see that and are MF-subpolygroups of P. However, is not an MF-subpolygroup of P since
By Definition 13 is not an MFS-polygroup of dimension 3 over P.
The following example shows that every soft set over P can be seen as an MFS-set of dimension k over P.
Example 6.
Let and be a soft set over P. For all , the MF-set defined by
for all . Then, .
Proposition 1.
Let . If is an MFS-polygroups, then, for all and ,
- (i)
- ,
- (ii)
- .
Proof.
(i) By Definition 13, for all and . Moreover, . This completes the proof of .
(ii) Suppose that . Since and is an MFS-polygroup, then, for all , we obtain
□
The relationship between soft polygroups and MFS-polygroups is given in the following theorem.
Theorem 1.
Let be a soft set over P. Then, is a soft polygroup over P if and only if is an MFS-polygroup.
Proof.
The proof follows by Example 6. □
In Theorem 2, we show that the restricted intersection and the extended intersection of two MFS-polygroups are also an MFS-polygroup.
Theorem 2.
Let be two MFS-polygroups.
- (i)
- is an MFS-polygroup.
- (ii)
- is an MFS-polygroup.
Proof.
(i) By Definition 10 (i), let , where and for all , . Since and are MFS-polygroups, we have for arbitrary and for all
For arbitrary and for all ,
Moreover,
Therefore, is an MFS-polygroup of dimension k over P.
(ii) According to Definition 10 (ii), we can write , . If , then is an MF-subpolygroup of P, since is an MFS-polygroup over P; if , then is an MF-subpolygroup of P, since is an MFS-polygroup over P; if , then is an MF-subpolygroup of P by (i). Therefore, is an MFS-polygroup of dimension k over P. □
The following corollary follows from Theorem 2.
Corollary 1.
Let be a family of MFS-polygroups. If . Then,
- (i)
- is an MFS-polygroup.
- (ii)
- is an MFS-polygroup.
The union of two MFS-polygroups is not an MFS-polygroup. In Theorem 3, we provide a condition for the union to be an MFS-polygroup as well.
Theorem 3.
Let be two MFS-polygroups. If , then is an MFS-polygroup.
Proof.
By Definition 9(iii), we can write , where . Since , it follows that either or for all . If , then is an MF-subpolygroup of P and if , then is an MF-subpolygroup of P. Therefore, is an MFS-polygroup of dimension k over P. □
Theorem 4.
Let be two MFS-polygroups. Then, is an MFS-polygroup.
Proof.
By Definition 9(i), let . We know that for all , is an MF-subpolygroup of P and for all , is an MF-subpolygroup of P and so is for all , because the intersection of two multi-fuzzy subpolygroups is also an MF-subpolygroup. Hence, is an MFS-polygroup of dimension k over P. □
By Theorems 3 and 4, we obtain the following corollary.
Corollary 2.
Let be a family of MFS-polygroups.
- (i)
- If for all and , then is an MFS-polygroup.
- (ii)
- is anMFS-polygroup.
The following theorem gives a condition for the -union of two MFS-polygroups to be an MFS-polygroup.
Theorem 5.
Let be two MFS-polygroups. If or , then is an MFS-polygroup.
Proof.
Suppose that and are MFS-polygroups of dimension k over P. By Definition 9 (ii), we can write , where , and for all . Since and are MFS-polygroups of dimension k over P, we obtain that for all , is an MF-subpolygroup of P and for all , is an MF-subpolygroup of P. By assumption, is an MF-subpolygroup of P for all . Hence, is an MFS-polygroup. □
Definition 14.
The sum of two MFS-sets and of dimension k over P, denoted by , is the MFS-set , where and for all ,
For every ,
The next theorem gives a condition for the sum of two MFS-polygroups to be an MFS-polygroup.
Theorem 6.
Let be two MFS-polygroups. If , then is an MFS-polygroup.
Proof.
The proof is straightforward. □
Definition 15.
Let . The soft set
for all , , is called a t-level soft set of the MFS-set , where is a t-level subset of the MF-set .
The following theorem explores the relation between MFS-polygroups and t-level soft sets.
Theorem 7.
Let . Then, is an MFS-polygroup if and only, if for all and for arbitrary with , the t-level soft set is a soft polygroup over P in Wanga’s sense [40].
Proof.
Let be an MFS-polygroup. Then, for each , is an MF-subpolygroup of P. Suppose that with and . Then, , . Thus,
which implies for all . Therefore, . Moreover, for , we have . It follows that . we obtain that is a subpolygroup of P for all . Consequently, is a soft polygroup over P. Conversely, let be a soft polygroup over P for all . Let for some . Then, obviously, ; consequently, . Thus,
Now, for some . Since, by the assumption, every non-empty t-level soft set is a soft polygroup over P, . Hence, . As a result, we obtain that is an MF-subpolygroup of P for all . Consequently, is an MFS-polygroup of dimension k over P. □
4. The Behavior Image and Inverse Image of MFS-Polygroups
Definition 16.
A pair is called an MF-soft function from to , where and are functions.
Definition 17.
Let , and be an MF- soft function from to .
- (i)
- The image of under the MF-soft function , denoted by , is the MFS-set such that the MF-set for any is characterized by the following MF-membership function:for all .
- (ii)
- The pre-image of under the MF-soft function , denoted by , is the MFS-set such that the MF-set is characterized by the following MF-membership function:for all and .
If φ and ψ are injective (surjective), then is said to be injective (surjective).
Definition 18.
Let , be two polygroups and be an MF-soft function from to . If φ is a strong homomorphism of polygroups, then the pair is called an MF-soft homomorphism. If φ is an isomorphism and ψ is a one-to-one mapping, then is said to be an MF-soft isomorphism.
Theorem 8.
Let be two polygroups and be an MF-soft homomorphism from to . If is an MFS-polygroup, then is an MFS-polygroup.
Proof.
Let , . If or , the proof is straightforward. Assume that there exists , such that and . Since is an MFS-polygroup, it follows that for each
for all . Let . We obtain . Then, we have
Hence,
for all . Then, we have
Moreover, for all where and , we have
Consequently, is an MFS-polygroup. □
Theorem 9.
Let be two polygroups and be an MF-soft homomorphism from to . If is an MFS-polygroup, then is an MFS-polygroup.
Proof.
Let , . For all , we have
Similarly, we obtain . Therefore, we conclude that is an MFS-polygroup. □
5. Normal MFS-Polygroups
In this section, we define normal MFS-polygroups and study some of their basic properties. We proved that the images of normal MFS-polygroups are the normal MFS-polygroups under some conditions.
Definition 19.
Let be an MFS-polygroup. Then, is said to be normal if and only if
for all and .
It is obvious that if is a normal MFS-polygroup, then
for all and .
Theorem 10.
Let be an MFS-polygroup. Then, the following conditions are equivalent:
- (i)
- is a normal MFS-polygroup,
- (ii)
- , for all and ,
- (iii)
- for all and ,
- (iv)
- , for all and .
Proof.
: For any , suppose that and . Then, , where . Since , then . Thus, by hypothesis, we obtain
That is,
: The proof is trivial.
: For any , suppose that and . Then, , where . By , we obtain . Since and letting be a MFS-polygroup, then we have
That is, for all and .
: For any , suppose that and . Then, . Thus, , where . By , we obtain . On the other hand,
Now, let and . Then, and so . By the above result, . Similarly, we obtain . Therefore,
for all and . Hence, is a normal MFS-polygroup. □
Lemma 1.
Let be an MFS-polygroup. If for all and , then
Proof.
Let and . Then,
for all . Since , then . Thus,
If , then , a contradiction. Thus, . Hence, . Consequently, for all and . Similarly, we obtain for all and . □
Theorem 11.
Let be an MFS-polygroup. Then, is normal if and only if
for all and .
Proof.
The proof of Theorem 11 follows from Lemma 1. □
Theorem 12.
Let . Then, is a normal MFS-polygroup if and only if each of its non-empty level subsets is a normal soft polygroup over P.
Proof.
Let be a normal MFS-polygroup. By Theorem 7, is a soft polygroup over P for all . Now, we will show that is normal. Suppose that and . Then, we have
It follows that for all . That is, . We obtain that is a normal subpolygroup of P for all . Consequently, is a normal soft polygroup over P. Conversely, let be a normal soft polygroup over P for all . By Theorem 7, is an MFS-polygroup. That is, is an MF-subpolygroup of P for all . We will show that is normal. Assume that , . Then, . Since is normal, we have . Thus, for all . Therefore,
We obtain that is a normal MF-subpolygroup of P for all . Consequently, is a normal MFS-polygroup. □
Theorem 13.
Let be two normal MFS-polygroups. Then,
- (i)
- is a normal MFS-polygroup.
- (ii)
- is a normal MFS-polygroup.
- (iii)
- If , then is a normal MFS-polygroup.
- (iv)
- is a normal MFS-polygroup.
Theorem 14.
Let be two polygroups and be a surjective multi-fuzzy soft homomorphism from to . If is a normal MFS-polygroup, then is a normal MFS-polygroup.
Proof.
For each and , there exists , such that and . Since is a normal MFS-polygroup, it follows that for each
for all . Let . We obtain . Then, we have
Hence,
for all . Then, we have
Consequently, is a normal MFS-polygroup. □
Theorem 15.
Let be two polygroups and be an MF-soft homomorphism from to . If is a normal MFS-polygroup, then is a normal MFS-polygroup.
Proof.
Let , . For all , we have
Therefore, is a normal MFS-polygroup. □
6. Conclusions
In real life, many problems often involve uncertainties that are difficult to describe and solve with traditional mathematical tools. To investigate these uncertainties, many researchers have proposed mathematical theory to address the problem of uncertainty. Currently, mathematical theories dealing with the problem of uncertainty include fuzzy set theory, soft set theory, multi-fuzzy set theory, probability theory and so on. The purpose of this paper is to apply the MFS-set theory to algebraic hyperstructures, motivated by the study of the algebraic structures of MF-sets. We generalized the concept of fuzzy polygroups and studied the algebraic properties of MFS-sets in polygroup structures. Thus, this paper provides a new connection between polygroup structures and MFS-sets. We hope that our work enhances the understanding of MFS-polygroups for future researchers. To extend this work, one should study the MFS-sets related to various hyperrings, which can be researched further. A solution to a decision-making problem can be investigated using a different algorithm in the future as well.
Author Contributions
Conceptualization, O.K. and B.D.; methodology, O.K., S.H.-M. and B.D.; formal analysis, O.K.; investigation, O.K.; resources, O.K., S.H.-M. and B.D.; writing—original draft preparation, O.K.; writing—review and editing, O.K., S.H.-M. and B.D.; supervision, B.D.; project administration, S.H.-M.; funding acquisition, S.H.-M. All authors have read and agreed to the published version of the manuscript.
Funding
The research was supported by VAROPS, granted by the Ministry of Defence of the Czech Republic.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors are highly grateful to the referees for their constructive suggestions for improving the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Marty, F. Sur une generalization de la notion de group. In Proceedings of the 8th Congress on Mathmatics Scandenaves, Stockholm, Sweden, 14–18 August 1934; pp. 45–49. [Google Scholar]
- Prenowitz, W. Projective geometries as multigroups. Am. J. Math. 1943, 65, 235–256. [Google Scholar] [CrossRef]
- Prenowitz, W. Descriptive geometries as multigroups. Trans. Am. Math. Soc. 1946, 59, 333–380. [Google Scholar] [CrossRef]
- Prenowitz, W. Spherical geometries and mutigroups. Can. J. Math. 1950, 2, 100–119. [Google Scholar] [CrossRef]
- Jantosciak, J. Transposition hypergroups, Noncommutative Join Spaces. J. Algebra 1997, 187, 97–119. [Google Scholar] [CrossRef] [Green Version]
- Bonansinga, P. Quasicanonical hypergroups. Atti Soc. Peloritana Sci. Fis. Mat. Natur. 1981, 27, 9–17. (In Italian) [Google Scholar]
- Massouros, C.G. Quasicanonical hypergroups. In Proceedings of the 4th Internation Congress, on Algebraic Hyperstructures and Applications, Xanthi, Greece, 27–30 June 1990; World Scientific: Singapore, 1991; pp. 129–136. [Google Scholar]
- Ioulidis, S. Polygroups et certains de leurs properietes. Bull. Greek Math. Soc. 1981, 22, 95–104. [Google Scholar]
- Comer, S.D. Polygroups derived from cogroups. J. Algebra 1984, 89, 397–405. [Google Scholar] [CrossRef] [Green Version]
- Comer, S.D. Extension of Polygroups by Polygroups and their Representations Using Color Schemes; Lecture Notes in Mathematics, No 1004, Universal Algebra and Lattice Theory; Springer: Berlin/Heidelberg, Germany, 1982; pp. 91–103. [Google Scholar]
- Davvaz, B. Polygroup Theory and Related Systems; World Scientific Publishing Co. Pte. Ltd.: Hackensack, NJ, USA, 2013. [Google Scholar]
- Mittas, J. Hypergroupes canoniques. Math. Balk. 1972, 2, 165–179. [Google Scholar]
- Massouros, C.; Massouros, G. An overview of the foundations of the hypergroup theory. Mathematics 2021, 9, 1014. [Google Scholar] [CrossRef]
- Massouros, C.; Cristea, I. 1st Symposium on “Hypercompositional Algebra—New Developments and Applications (HAnDA)”. AIP Conf. Proc. 2018, 340001. [Google Scholar] [CrossRef]
- Corsini, P. Prolegomena of Hypergroup Theory, 2nd ed.; Aviani Editor: Tricesimo, Italy, 1993. [Google Scholar]
- Corsini, P.; Leoreanu-Fotea, V. Applications of hyperstructures theory. In Advanced in Mathematics; Kluwer: Dordrecht, The Netherlands, 2003. [Google Scholar]
- Davvaz, B.; Leoreanu-Fotea, V. Hyperring Theory and Applications; Hadronic Press, Inc.: Palm Harber, FL, USA, 2007. [Google Scholar]
- Davvaz, B.; Cristea, I. Fuzzy Algebraic Hyperstructures; Studies in Fuzziness and Soft Computing 321; Springer International Publishing: Cham, Switzerland, 2015. [Google Scholar]
- Vougiouklis, T. Hyperstructures and Their Representations; Hadronic Press: Palm Harbor, FL, USA, 1994. [Google Scholar]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef] [Green Version]
- Zahedi, M.M.; Bolurian, M.; Hasankhani, A. On polygroups and fuzzy subpolygroups. J. Fuzzy Math. 1995, 3, 1–15. [Google Scholar]
- Davvaz, B. Fuzzy Hv-groups. Fuzzy Sets Syst. 1999, 101, 191–195. [Google Scholar] [CrossRef]
- Rosenfeld, A. Fuzzy groups. J. Math. Anal. Appl. 1971, 35, 512–517. [Google Scholar] [CrossRef] [Green Version]
- Corsini, P. A new connection between hypergroups and fuzzy sets. Southeast Asian Bull. Math. 2003, 27, 221–229. [Google Scholar]
- Davvaz, B.; Corsini, P. Generalized fuzzy polygroups. Iran. J. Fuzzy Syst. 2006, 3, 59–75. [Google Scholar]
- Kazancı, O.; Davvaz, B.; Yamak, S. A new characterization of fuzzy n-ary polygroups. Neural Comput. Appl. 2012, 19, 649–655. [Google Scholar] [CrossRef]
- Molodtsov, D. Soft set theory first results. Comp. Math. Appl. 1999, 37, 19–31. [Google Scholar] [CrossRef] [Green Version]
- Aktaş, H.; Çağman, N. Soft sets and soft groups. Inf. Sci. 2007, 177, 2726–2735. [Google Scholar] [CrossRef]
- Maji, P.K.; Biswas, R.; Roy, A.R. Soft set theory. Comp. Math. Appl. 2003, 45, 555–562. [Google Scholar] [CrossRef] [Green Version]
- Maji, P.K.; Biswas, R.; Roy, A.R. Fuzzy soft sets. J. Fuzzy Math. 2001, 9, 589–602. [Google Scholar]
- Aygunoğlu, A.; Aygun, H. Introduction to fuzzy soft groups. Comp. Math. Appl. 2009, 58, 1279–1286. [Google Scholar] [CrossRef] [Green Version]
- Leoreanu-Fotea, V.; Feng, F.; Zhan, J. Fuzzy soft hypergroup. Int. J. Comp. Math. 2012, 89, 1–12. [Google Scholar] [CrossRef]
- Sebastian, S.; Ramakrishnan, T.V. Multi-fuzzy sets: An extension of fuzzy sets. Fuzzy Inf. Eng. 2011, 3, 35–43. [Google Scholar] [CrossRef]
- Yang, Y.; Tan, X.; Meng, C. The multi-fuzzy soft set and its application in decision making. Appl. Math. Modell. 2013, 37, 4915–4923. [Google Scholar] [CrossRef]
- Onasanya, B.O.; Hoskova-Mayerova, S. Multi-fuzzy group induced by multisets. Ital. J. Pure Appl. Math. 2019, 41, 597–604. [Google Scholar]
- Hoskova-Mayerova, S.; Al-Tahan, M.; Davvaz, B. Fuzzy multi-Hypergroups. Mathematics 2020, 8, 244. [Google Scholar] [CrossRef] [Green Version]
- Al-Tahan, M.; Hoskova-Mayerova, S.; Davvaz, B. Fuzzy multi-polygroups. J. Intell. Fuzzy Syst. 2019, 38, 2337–2345. [Google Scholar] [CrossRef]
- Akın, C. Multi-fuzzy soft groups. Soft Comput. 2021, 25, 137–145. [Google Scholar] [CrossRef]
- Kazancı, O.; Hoskova-Mayerova, S.; Davvaz, B. Application multi-fuzzy soft sets in hypermodules. Mathematics 2021, 9, 2182. [Google Scholar] [CrossRef]
- Wanga, J.; Yin, M.; Gua, W. Soft polygroups. Comp. Math. Appl. 2011, 62, 3529–3537. [Google Scholar] [CrossRef] [Green Version]
- Dresher, M.; Ore, O. Theory of Multigroups. Am. J. Math. 1938, 60, 705–733. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).